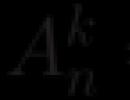Evklid alqoritmi və onun modifikasiyası. Evklidin alqoritmi - ən böyük ortaq bölənin tapılması. Üç və ya daha çox rəqəmin GCD tapılması
Evklid alqoritmi bir cüt tam ədədin ən böyük ümumi bölənini (gcd) tapmaq üçün alqoritmdir.
ən böyük ortaq bölən(GCD) iki ədədi qalıqsız bölən və özü verilmiş iki ədədin hər hansı digər böləninə qalıqsız bölünən ədəddir. Sadəcə olaraq, bu böyük rəqəm, gcd-nin axtarıldığı iki ədədi qalıqsız bölmək olar.
Bölmə ilə GCD tapmaq üçün alqoritm
- Böyük ədədi kiçik olana bölün.
- Qalıq olmadan bölünürsə, daha kiçik rəqəm GCD-dir (döngüdən çıxmalısınız).
- Qalan varsa, deməli daha çox bölmənin qalan hissəsi ilə əvəz olunur.
- 1-ci nöqtəyə keçək.
Misal:
30 və 18 üçün GCD tapın.
30/18 = 1 (qalan 12)
18/12 = 1 (qalan 6)
12/6 = 2 (qalan 0)
Son: GCD 6-nın bölənidir.
gcd(30, 18) = 6
a = 50 b = 130 isə a != 0 və b != 0 : əgər a > b: a = a % b başqa : b = b % a çap (a + b)
Döngədə bölmənin qalan hissəsi a və ya b dəyişəninə yazılır. Dəyişənlərdən ən azı biri sıfır olduqda dövrə başa çatır. Bu o deməkdir ki, digərində GCD var. Bununla belə, hansının olduğunu bilmirik. Beləliklə, GCD üçün bu dəyişənlərin cəmini tapırıq. Dəyişənlərdən biri sıfır olduğundan nəticəyə heç bir təsiri yoxdur.
Çıxarma ilə GCD tapmaq üçün alqoritm
- Böyük ədəddən kiçik olanı çıxarın.
- Əgər 0 çıxırsa, bu, rəqəmlərin bir-birinə bərabər olduğunu və GCD olduğunu bildirir (döngüdən çıxmalısınız).
- Çıxarmanın nəticəsi 0-a bərabər deyilsə, daha böyük rəqəm çıxılmanın nəticəsi ilə əvəz olunur.
- 1-ci nöqtəyə keçək.
Misal:
30 və 18 üçün GCD tapın.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 - 6 = 0
Son: GCD minuend və ya subtrahenddir.
gcd(30, 18) = 6
a = 50 b = 130 isə a != b: əgər a > b: a = a - b başqa : b = b - a çap (a)
GCD (ən böyük ümumi bölən) tapmaq üçün Evklidin alqoritmi
İki qeyri-mənfi tam ədəd verilmişdir və . Onların ən böyük ortaq bölənini tapmaq tələb olunur, yəni. və , və hər ikisinin bölanı olan ən böyük ədəd. Üstündə Ingilis dili"ən böyük ortaq bölən" "ən böyük ümumi bölən" kimi yazılır və ümumi qeydi belədir:
(burada "" bölünmə qabiliyyətini ifadə edir, yəni "" "bölünmə" deməkdir)
Rəqəmlərdən biri sıfıra bərabər, digəri isə sıfırdan fərqli olduqda, onların ən böyük ortaq bölməsi, tərifinə görə, bu ikinci ədəd olacaqdır. Hər iki ədəd sıfır olduqda, nəticə qeyri-müəyyəndir (hər hansı sonsuz böyük ədəd edəcək), biz bu halda ən böyük ümumi bölücünü sıfıra təyin edəcəyik. Buna görə də belə bir qayda haqqında danışa bilərik: əgər ədədlərdən biri sıfıra bərabərdirsə, onda onların ən böyük ortaq bölməsi ikinci ədədə bərabərdir.
Evklid alqoritmi, aşağıda müzakirə olunan, iki ədədin ən böyük ortaq bölənini tapmaq problemini həll edir və üçün.
Bu alqoritm ilk dəfə Evklidin Elementlərində (təqribən eramızdan əvvəl 300-cü ildə) təsvir edilmişdir, baxmayaraq ki, bu alqoritmin daha erkən mənşəyə malik olması tamamilə mümkündür.
Alqoritm
Alqoritmin özü olduqca sadədir və aşağıdakı düsturla təsvir edilmişdir:
İcra
int gcd (int a, int b) ( əgər (b == 0 ) a qaytarır; əks halda gcd (b, a % b) ; )C++ üçlü şərt operatorundan istifadə edərək, alqoritmi daha da qısa şəkildə yazmaq olar:
int gcd (int a, int b) ( qaytarmaq b ? gcd (b, a % b) : a; )Nəhayət, alqoritmin rekursiv olmayan formasını veririk:
int gcd (int a, int b) ( isə (b) ( a % = b; dəyişdirmə (a, b) ; ) a qaytarın; )Düzgünlüyün sübutu
Əvvəlcə qeyd edək ki, Evklid alqoritminin hər iterasiyası ilə onun ikinci arqumenti ciddi şəkildə azalır, buna görə də mənfi olmadığı üçün Evklid alqoritmi həmişə bitir.
üçün düzgünlüyün sübutları hər hansı > üçün bunu göstərməliyik.
Göstərək ki, bərabərliyin sol tərəfindəki qiymət sağdakı həqiqi qiymətə, sağdakı qiymət isə soldakı qiymətə bölünür. Aydındır ki, bu, sol və sağ hissələrin eyni olması demək olacaq ki, bu da Evklidin alqoritminin düzgünlüyünü sübut edəcək.
İşarə et ![]() . Sonra tərifinə görə və .
. Sonra tərifinə görə və .
![]()
Amma sonra belə olur:
![]()
Beləliklə, bəyanatı xatırlayaraq sistemi alırıq:
![]()
İndi aşağıdakı sadə faktdan istifadə edək: əgər bəzi üç ədəd üçün o, tutursa: və , o zaman tutur və: . Bizim vəziyyətimizdə alırıq:
Və ya onun tərifini ilə əvəz etsək, alırıq:
Beləliklə, sübutun yarısını etdik: sol tərəfin sağ tərəfi böldüyünü göstərdik. Sübutun ikinci yarısı oxşar şəkildə edilir.
İş saatları
Alqoritmin işləmə müddəti təxmin edilir Lame teoremi, Evklid alqoritmi ilə Fibonaççi ardıcıllığı arasında təəccüblü bir əlaqə qurur:
Əgər > və bəziləri üçün isə, Evklidin alqoritmi ən çox rekursiv çağırışlar edəcək.
$a$ və $b$ - $gcd(a, b)$ - iki-tu-ral-rəqəmlərin ən böyük ümumi de-li-teli ən böyük ədəddir, bəzi dəstələrdə $a$ və $b$ ədədləridir. izsiz de-lyat-Xiadırlar.
$ GCD (a, b) $ tapmaq üçün aşağıdakı təbii yolla içə bilərsiniz: hər iki ədədi la sadə ədədlərin səlahiyyətləri ilə de-canlandırın: $a = 2^(\alpha_1) \cdot 3^( \alpha_2) \cdot \ldots \cdot p^(\alpha_n)_n$ , $b = 2 ^(\beta_1) \cdot 3^(\beta_2) \cdot \ldots \cdot p^(\beta_n)_n$ , ($\alpha_k$ və $\beta_k$ null ola bilər). Sonra $$gcd(a, b) = 2^(\min(\alpha_1, \beta_1)) \cdot 3^(\min(\alpha_2, \beta_2)) \cdot \ldots \cdot p^(\ dəq( \alpha_n, \beta_n))_n.$$ $ onu əldə edin: $2625 = 2^0 \cdot 3^1 \cdot 5^3 \cdot 7^1, 8100 = 2^2 \cdot 3^4 \cdot 5^ 2 \cdot 7^0$, $gcd(2625, 8100) = 2^0 \cdot 3^1 \cdot 5^2 \cdot 7^0 = 75$ deməkdir.
Bu üsulun əsas çatışmazlığı ondan ibarətdir ki, çoxlu sayda sadə çarpanlara bölmək o qədər də yüzə yaxın deyil, daha dəqiq desək, o qədər də sürətli deyil.
Evklid "Başlanğıc" adlı 7-ci kitabında "iki ədədin ümumi ölçüsünü" tapmağın al-qo-ritmini təsvir edir. Al-go-ritm-san geo-met-ri-che-ski-ni iki kəsimin ümumi ölçüsünün on-hod-de-tion kimi təsvir edir. Bu, daha çoxdan-kəsmədən-azdan-kəsməkdən “after-to-va-tel-no-mu from-nya-ty”yə gəlir. İndi bu al-go-ritm from-ve-walls ən-bol-she-go-go-de-li-te -la iki on-tu- tapmaq üçün al-go-ritm Ev-kli-da kimidir. ral-nyh chi-kəndləri.
Əsas ideya, hansısa əsasda, os-no-van al-go-ritm, ondan ibarətdir ki, $GCD$ chi-sat $a$ və $b$ bərabərdir $ GCD$ chi-sat $b$ və $ ab$. Buradan-bəli, belə çıxır ki, əgər siz $a$-nı $b$ üzərinə qalıqla töksəniz, i.e. $a = b \cdot q + r$, sonra $gcd(a, b) = gcd(b, r)$ şəklində qoyun.
Gözəl geo-met-ri-che-skuyu inter-ter-pre-ta-tion al-go-rit-ma, inter-aktiv-tiv-naya re-a-li-za -tionunu təsvir edək. əvvəl-lo-the-on-the-he.
Yan uzunluqları $a$ və $b$ kənarında olan düzbucaqlı-no-ke-də-shi-va-em max-si-mal-amma-mümkün kvadrat . Düzbucaqlı-mo-kömür-no-ke qalan hissəsində yenidən kənar-şi-va-em üçün mak-si-mal-lakin mümkün kvadratdır. Bütün çıxan düzbucaqlı həddən artıq rənglənməyincə və s. Yüz-ro-ny sa-mo-go-ma-lazi-ko-th kvadrat-ra-ta uzunluğu və $ GCD (a, b) $ bərabər olacaq.
Daha çox fraksiya-amma geo-met-ri-che-sky in-ter-pre-ta-tion op-sa-on eyni və para-ral-lel-am with-ve-de-but arith-me -ti-çe-təsviri al-qo-rit-ma Ev-kli-da.
| In-ter-pre-ta-tion al-go-rit-ma | Al-go-ritm Ev-cli-da |
|---|---|
| Si-mal-amma-th-me-ra (yüz $b$ ilə) kənarlarından kənarda $a$ və $b$ $(a \gt b)$ tərəflərinin uzunluğu olan düzbucaqlıda. Bu əməliyyat mümkün qədər rənglənməmiş hissə üçün təkrarlanır. | Daha böyük $a$ rəqəmi söndürülür, qalanı isə kiçik $b$ rəqəmində söndürülür: $a = b \cdot q_1 + r_1$. |
| Əgər belə kvadratlar bütün düzbucaqlını əhatə edirsə, onda $b$ rəqəmi $GCD$-dır. | Əgər ra-damarların de-lesiyasından $r_1$-ın qalığı nu-lu olarsa, onda daha kiçik olan $b$ $GCD$-dır. |
| Əgər düzbucaqlı-nick (yüz-ro-on-mi $b$ və $r_1$ ilə) qalsa, o, max-si-mal-amma-th-ölçü kvadratlarının ən ağrılı-boyun mümkün sayına malikdir. -ra ($r_1$ tərəfi ilə). | Əgər $r_1$-ın qalığı sıfıra bərabər deyilsə, daha kiçik olan $b$ ədədi, qalanı $r_1$-da söndürülür: $b = r_1 \cdot q_2 + r_2 $. |
| Əgər yüz $r_1$ olan kvadrat bütün düzbucaqlını əhatə edirsə, onda $r_1$ $GCD$-dır. | Əgər ikinci silmə nəticəsində $r_2$-ın qalığı sıfıra bərabərdirsə, onda $r_1$ $GCD$-dır. |
| Əgər düzbucaqlı-nik varsa (yüz-ro-on-mi $r_1$ və $r_2$ ilə), o, max-si-kiçik ölçülü-me-ra kvadratlarının mümkün qədər ağrılı boyuna malikdir. ($r_2$ tərəfi ilə). | Əgər ikinci de-le-ni zamanı $r_2$-ın qalığı sıfıra bərabər deyilsə, o zaman $r_1$ $r_2$ ilə işıqlandırılır: $r_1 = r_2 \cdot q_3 + r_3$ . |
| Və s və bütün sağ bucaq-nick kvadrat-ra-ta-mi olmayana qədər. (Gec və ya tez, bu baş verəcək, çünki yüz kvadrat-ra-ts azaldacaq-sha-ut-sya və hər halda, qalan sağ-mo-kömür-nick quad-ra-ta-nın yarısını çəkə bilərsiniz. yüz-ro-bir vahid ilə -mi). | Və sairə və sair qalan $r_n$ sıfıra bərabər olana qədər (ra-amma və ya daha sonra belə olacaq, çünki -ku qalan-ki reduktor-şa-ut-sya). |
| Yüz mi-kiçik olmayan kvadratın uzunluğu başlanğıc nömrələrin GCD $-dır. | Sonuncu sıfıra bərabər olmayan qalıq cərəyan $r_(n-1)$ orijinal ədədlərin $GCD$-dır. |
Al-go-rhythm Ev-kli-yes müxtəlif şəxsi problemlərin həllində istifadə olunan güclü bir alətdir. Məsələn, o, tam ədədlərdə tənlikləri həll etmək üçün istifadə edir, ədədləri sonsuzluq şəklində təmsil edir - qırılma-nyh (zəncir-ci) heç-heçə-beat, bu, ən-böyük-she-go-go- tapmaq üçün ümumiləşdirilə bilər. iki çox üzvlü de-li-te-la.
Ədəbiyyat
Evklid. Na-ça-la Ev-cli-da. Kitablar VII, X. - M.-L.: GITTL, 1950.
R. Courant, G. Robins. Bu ma-te-ma-ti-ka nədir? - M.: MTsNMO, 2010.
GCD-ni iki əsas yolla tapmaq üçün iki əsas metodu nəzərdən keçirin: Evklid alqoritmindən istifadə və faktorinq. İki, üç və daha çox ədəd üçün hər iki üsulu tətbiq edək.
GCD tapmaq üçün Evklidin alqoritmi
Evklidin alqoritmi iki müsbət ədədin ən böyük ümumi bölənini hesablamağı asanlaşdırır. Biz Evklid alqoritminin düsturlarını və sübutunu Ən Böyük Ümumi Bölən: Müəyyənedici, Nümunələr bölməsində vermişik.
Alqoritmin mahiyyəti ardıcıl olaraq qalığa bölünmə aparmaqdır, bu müddət ərzində bir sıra forma bərabərliyi əldə edilir:
a = b q 1 + r 1 , 0< r 1 < b b = r 1 · q 2 + r 2 , 0 < r 2 < r 1 r 1 = r 2 · q 3 + r 3 , 0 < r 3 < r 2 r 2 = r 3 · q 4 + r 4 , 0 < r 4 < r 3 ⋮ r k - 2 = r k - 1 · q k + r k , 0 < r k < r k - 1 r k - 1 = r k · q k + 1
Bölməni nə vaxt bitirə bilərik rk + 1 = 0, burada r k = gcd (a , b).
Misal 1
64 Və 48 .
Həll
Qeydi təqdim edək: a = 64 , b = 48 .
Evklid alqoritminə əsaslanaraq bölməni həyata keçirəcəyik 64 üstündə 48 .
1-i, qalanı isə 16-nı alırıq. Belə çıxır ki, q 1 = 1, r 1 = 16.
İkinci addım bölməkdir 48 16 ilə 3 alırıq. yəni q2 = 3, Amma r 2 = 0. Beləliklə, 16 rəqəmi şərtdən gələn ədədlər üçün ən böyük ümumi böləndir.
Cavab: gcd(64, 48) = 16.
Misal 2
Nömrələrin GCD-si nədir 111 Və 432 ?
Həll
Bölmək 432 üstündə 111 . Evklidin alqoritminə uyğun olaraq 432 = 111 3 + 99 , 111 = 99 1 + 12 , 99 = 12 8 + 3 , 12 = 3 4 bərabərlik zəncirini alırıq.
Beləliklə, ədədlərin ən böyük ortaq bölməsi 111 Və 432 3-dür.
Cavab: gcd(111, 432) = 3.
Misal 3
661 və 113-ün ən böyük ortaq bölənini tapın.
Həll
Nömrələri ardıcıl olaraq bölüb GCD alacağıq (661 , 113) = 1 . Bu o deməkdir ki, 661 və 113 nisbətən sadə ədədlərdir. Sadə ədədlər cədvəlinə baxsaq, hesablamalara başlamazdan əvvəl bunu anlaya bilərik.
Cavab: gcd(661, 113) = 1.
Nömrələri əsas faktorlara ayırmaqla GCD-nin tapılması
Faktorinq üsulu ilə iki ədədin ən böyük ortaq bölənini tapmaq üçün bu iki ədədi parçalamaqla alınan və onlar üçün ümumi olan bütün sadə amilləri vurmaq lazımdır.
Misal 4
220 və 600 ədədlərini sadə amillərə bölsək, iki məhsul alırıq: 220 = 2 2 5 11 Və 600 = 2 2 2 3 5 5. Bu iki məhsulda ümumi amillər 2, 2 və 5 olacaqdır. Bu o deməkdir ki, NOD (220, 600) = 2 2 5 = 20.
Misal 5
Ədədlərin ən böyük ortaq bölənini tapın 72 Və 96 .
Həll
Ədədlərin bütün sadə amillərini tapın 72 Və 96 :
72 36 18 9 3 1 2 2 2 3 3
96 48 24 12 6 3 1 2 2 2 2 2 3
İki ədəd üçün ümumi sadə amillər: 2, 2, 2 və 3. Bu o deməkdir ki, NOD (72, 96) = 2 2 2 3 = 24.
Cavab: gcd(72, 96) = 24.
İki ədədin ən böyük ortaq bölənini tapmaq qaydası ən böyük ortaq bölənin xassələrinə əsaslanır, ona görə gcd (ma 1 , mb 1) = m gcd (a 1, b 1) , burada m istənilən müsbət tam ədəddir. .
Üç və ya daha çox rəqəmin GCD tapılması
GCD-ni tapmalı olduğumuz ədədlərin sayından asılı olmayaraq, ardıcıl olaraq iki ədədin GCD-ni tapmaqdan ibarət olan eyni alqoritmə uyğun hərəkət edəcəyik. Bu alqoritm aşağıdakı teoremin tətbiqinə əsaslanır: Bir neçə ədədin GCD a 1 , a 2 , … , a kədədinə bərabərdir dk, gcd-nin ardıcıl hesablanmasında tapılır (a 1 , a 2) = d 2, GCD (d 2 , a 3) = d 3 , GCD (d 3 , a 4) = d 4 , … , GCD (d k - 1 , a k) = d k .
Misal 6
78, 294, 570 və dörd ədədin ən böyük ortaq bölənini tapın. 36 .
Həll
Qeydi təqdim edək: a 1 = 78, a 2 = 294, a 3 = 570, a 4 = 36.
78 və 294 rəqəmlərinin GCD-sini tapmaqla başlayaq: d2= GCD (78 , 294) = 6 .
İndi d 3 \u003d GCD (d 2, a 3) \u003d GCD (6, 570) tapmağa başlayaq. Evklid alqoritminə görə 570 = 6 95. Bu o deməkdir ki d 3 = GCD (6 , 570) = 6 .
d 4 \u003d GCD (d 3, a 4) \u003d GCD (6, 36) tapın. 36 6-ya qalıqsız bölünür. Bu, bizə imkan verir d4= GCD (6 , 36) = 6 .
d4 = 6, yəni GCD (78 , 294 , 570 , 36) = 6 .
Cavab:
İndi isə bu və daha çox rəqəmlər üçün GCD-ni hesablamaq üçün başqa üsula baxaq. Ədədlərin bütün ümumi sadə amillərini vurmaqla gcd-ni tapa bilərik.
Misal 7
78 , 294 , 570 və rəqəmlərinin gcd-sini hesablayın 36 .
Həll
Bu ədədləri sadə amillərə bölək: 78 = 2 3 13 , 294 = 2 3 7 7 , 570 = 2 3 5 19 , 36 = 2 2 3 3 .
Bütün dörd ədəd üçün ümumi sadə amillər 2 və 3 rəqəmləri olacaqdır.
Belə çıxır ki, NOD (78, 294, 570, 36) = 2 3 = 6.
Cavab: gcd(78 , 294 , 570 , 36) = 6 .
Mənfi ədədlərin gcd-nin tapılması
Mənfi ədədlərlə məşğul olmalıyıqsa, onda bu ədədlərin modullarından ən böyük ortaq bölücünü tapmaq üçün istifadə edə bilərik. Biz əks işarəli ədədlərin xassəsini bilməklə bunu edə bilərik: ədədlər n Və -n eyni bölücülərə malikdir.
Misal 8
Mənfi tam ədədlərin gcd-sini tapın − 231 Və − 140 .
Həll
Hesablamaları yerinə yetirmək üçün şərtdə verilmiş ədədlərin modullarını götürək. Bunlar 231 və 140 rəqəmləri olacaq. Qısaca deyək: GCD (− 231 , − 140) = GCD (231, 140). İndi iki ədədin sadə amillərini tapmaq üçün Evklid alqoritmini tətbiq edək: 231 = 140 1 + 91 ; 140 = 91 1 + 49; 91 = 49 1 + 42; 49 = 42 1 + 7 və 42 = 7 6. Biz gcd (231, 140) = 7 alırıq .
Və NOD-dan bəri (− 231 , − 140) = GCD (231 , 140) , sonra ədədlərin gcd − 231 Və − 140 bərabərdir 7 .
Cavab: gcd (− 231 , − 140) = 7 .
Misal 9
Üç ədədin gcd-sini təyin edin - 585, 81 və − 189 .
Həll
Yuxarıdakı siyahıdakı mənfi ədədləri onların mütləq qiymətləri ilə əvəz edək, GCD alırıq (− 585 , 81 , − 189) = GCD (585 , 81 , 189) . Sonra bütün verilmiş ədədləri sadə amillərə parçalayırıq: 585 = 3 3 5 13, 81 = 3 3 3 3 və 189 = 3 3 3 7. 3 və 3 əsas amilləri üç ədəd üçün ümumidir. Belə çıxır ki, gcd (585 , 81 , 189) = gcd (- 585 , 81 , - 189) = 9 .
Cavab: GCD (− 585 , 81 , − 189) = 9 .
Mətndə səhv görsəniz, onu vurğulayın və Ctrl+Enter düymələrini basın
Elektron ticarətdə geniş yayılmışdır. Həmçinin, alqoritm xətti Diofant tənliklərinin həllində, davam edən fraksiyaların qurulmasında, Şturm metodunda istifadə olunur. Evklid alqoritmi müasir ədədlər nəzəriyyəsində dörd kvadratın cəminə dair Laqranj teoremi və hesabın əsas teoremi kimi teoremləri sübut etmək üçün əsas vasitədir.
Ensiklopedik YouTube
1 / 5
✪ Riyaziyyat. Natural ədədlər: Evklid alqoritmi. Foxford Onlayn Tədris Mərkəzi
✪ Evklidin alqoritmi
✪ Evklidin alqoritmi, GCD tapmaq üçün sürətli bir yol
✪ Riyaziyyat 71. Ən böyük ortaq bölən. Evklidin Alqoritmi - Əyləncəli Elmlər Akademiyası
✪ 20 while Loop Euclid Python Alqoritmi
Altyazılar
Tarix
Qədim yunan riyaziyyatçıları bu alqoritmi adlandırdılar ἀνθυφαίρεσις və ya ἀνταναίρεσις - "qarşılıqlı çıxma". Bu alqoritm Evklid tərəfindən kəşf edilməmişdir, çünki o, artıq qeyd edilmişdir Topeka Aristotel. Evklidin "Başlanğıcları"nda iki dəfə - ikinin ən böyük ortaq bölənini tapmaq üçün VII kitabda təsvir edilmişdir. natural ədədlər və iki homojen kəmiyyətin ən böyük ümumi ölçüsünü tapmaq üçün X kitabında. Hər iki halda iki seqmentin “ümumi ölçü”nü tapmaq üçün alqoritmin həndəsi təsviri verilir.
Təsvir
Tam ədədlər üçün Evklid alqoritmi
Qoy olsun a (\displaystyle a) Və b (\displaystyle b)- eyni zamanda sıfıra bərabər olmayan tam ədədlər və ədədlər ardıcıllığı
a > b > r 1 > r 2 > r 3 > r 4 > … > rn (\displaystyle a>b>r_(1)>r_(2)>r_(3)>r_(4)>\ \nöqtə \ >r_(n))hər biri ilə müəyyən edilir r k (\displaystyle r_(k))- bu, əvvəlki nömrənin əvvəlkinə bölünməsinin qalığıdır və sondan əvvəlki rəqəm sonuncuya bölünür, yəni:
a = b q 0 + r 1 , (\displaystyle a=bq_(0)+r_(1),) b = r 1 q 1 + r 2 , (\displaystyle b=r_(1)q_(1)+r_(2),) r 1 = r 2 q 2 + r 3 , (\displaystyle r_(1)=r_(2)q_(2)+r_(3),) ⋯ (\displaystyle \cdots) r k − 2 = r k − 1 q k − 1 + r k , (\displaystyle r_(k-2)=r_(k-1)q_(k-1)+r_(k),) ⋯ (\displaystyle \cdots) r n − 2 = r n − 1 q n − 1 + r n , (\displaystyle r_(n-2)=r_(n-1)q_(n-1)+r_(n),) r n − 1 = r n q n . (\displaystyle r_(n-1)=r_(n)q_(n).)Sonra gcd( a, b), ən böyük ortaq bölən a Və b, bərabərdir r n , bu ardıcıllığın sıfırdan fərqli sonuncu üzvü.
Varlıq bu cür r 1 , r 2 , ..., r n , yəni qalıqla bölmək imkanı müstündə n hər hansı bir bütöv üçün m və bütöv n≠ 0 induksiya ilə sübut edilir m.
Düzgünlük bu alqoritm aşağıdakı iki ifadədən irəli gəlir:
- Qoy olsun a = b⋅q + r, onda gcd(a, b) = gcd(b, r).
Sübut
- GCD( r, 0) = r hər hansı bir sıfır üçün r(çünki 0 sıfırdan başqa istənilən tam ədədə bölünür).
Evklidin həndəsi alqoritmi
Uzunluğun iki seqmenti verilsin a Və b. Böyük seqmentdən kiçik seqmenti çıxarın və daha böyük seqmenti yaranan fərqlə əvəz edin. Seqmentlər bərabər olana qədər bu əməliyyatı təkrarlayın. Əgər bu baş verərsə, onda ilkin seqmentlər mütənasibdir və əldə edilən sonuncu seqment onların ən böyük ümumi ölçüsüdür. Əgər ümumi ölçü yoxdursa, deməli proses sonsuzdur. Bu formada alqoritm Evklid tərəfindən təsvir edilir və kompas və hökmdardan istifadə etməklə həyata keçirilir.
Misal
Nümunə etmək üçün gcd-ni tapmaq üçün Evklid alqoritmi istifadə olunacaq a= 1071 və b= 462. Başlamaq üçün 1071-dən 462-dən kiçik bir fərq əldə edənə qədər 462-nin qatını çıxın. 462-ni iki dəfə çıxmalıyıq, ( q 0 = 2), qalan 147 ilə:
1071 = 2 × 462 + 147.
Sonra 147-dən az fərq əldə olunana qədər 462-dən 147-nin qatını çıxırıq. 147-ni üç dəfə çıxarmalıyıq ( q 1 = 3), qalan 21 ilə:
462 = 3 x 147 + 21.
Sonra 21-dən az fərq əldə olunana qədər 147-dən 21-in qatını çıxırıq. 21-i yeddi dəfə çıxarmalıyıq ( q 2 = 7), qalıqsız qalan:
147 = 7 x 21 + 0.
Beləliklə, a > b > ardıcıllığı r 1 > r 2 > r 3 > … > r n bu xüsusi halda belə görünür:
1071 > 462 > 147 > 21.
Sonuncu qalıq sıfır olduğundan alqoritm 21 və gcd(1071, 462) = 21 ilə bitir.
Cədvəl şəklində addımlar aşağıdakı kimi idi:
Proqramlar
Genişləndirilmiş Evklid alqoritmi və Bezout əlaqəsi
Üçün düsturlar r i (\displaystyle r_(i)) bu şəkildə yenidən yazmaq olar:
r 1 = a + b (− q 0) (\displaystyle r_(1)=a+b(-q_(0)) r 2 = b − r 1 q 1 = a (− q 1) + b (1 + q 1 q 0) (\displaystyle r_(2)=b-r_(1)q_(1)=a(-q_() 1))+b(1+q_(1)q_(0))) ⋮ (\displaystyle \vdots) GCD (a , b) = r n = a s + b t (\displaystyle (a,b)=r_(n)=as+bt)Budur s Və t bütöv. Ən böyük ümumi bölücünün bu təsviri Bezout münasibəti adlanır və ədədlər s Və t- əmsallar Bezu . Bezout əlaqəsi Evklidin lemmasının sübutunda açar və arifmetikanın əsas teoremidir.
Davamlı fraksiyalar
Evklidin alqoritmi davam edən kəsrlərlə kifayət qədər sıx bağlıdır. Münasibət a/b davamlı kəsr təmsilini qəbul edir:
a b = [ q 0 ; q 1 , q 2 , ⋯ , q n ] (\displaystyle (\frac (a)(b))=).Bu halda, son həddi olmayan davam edən kəsr Bezout əmsallarının nisbətinə bərabərdir t/s mənfi işarə ilə götürülür:
[ q 0 ; q 1 , q 2 , ⋯ , q n − 1 ] = − t s (\displaystyle =-(\frac (t)(s))).Evklid alqoritmini təyin edən bərabərliklər ardıcıllığı aşağıdakı formada yenidən yazıla bilər:
ab = q 0 + r 0 bbr 0 = q 1 + r 1 r 0 r 0 r 1 = q 2 + r 2 r 1 ⋮ rk − 2 rk − 1 = qk + rkrk − 1 ⋮ r N − 2 r N − 1 = q N (\displaystyle (\begin(aligned)(\frac (a)(b))&=q_(0)+(\frac (r_(0))(b))\\(\frac (b) )(r_(0)))&=q_(1)+(\frac (r_(1))(r_(0)))\\(\frac (r_(0))(r_(1))& =q_(2)+(\frac (r_(2))(r_(1)))\\&()\ \vdots \\(\frac (r_(k-2))(r_(k-1) ))&=q_(k)+(\frac (r_(k))(r_(k-1)))\\&()\ \vdots \\(\frac (r_(N-2))(r_ (N-1)))&=q_(N)\end(düzləşdirilmiş)))Tənliyin sağ tərəfindəki son hədd həmişə aşağıdakı tənliyin sol tərəfinin əksinə bərabərdir. Beləliklə, ilk iki tənlik aşağıdakı formada birləşdirilə bilər:
ab = q 0 + 1 q 1 + r 1 r 0 (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\cfrac (r_() 1))(r_(0))))))Üçüncü bərabərlik ifadənin məxrəcini əvəz etmək üçün istifadə edilə bilər r 1 /r 0, alırıq:
ab = q 0 + 1 q 1 + 1 q 2 + r 2 r 1 (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\) cfrac (1)(q_(2)+(\cfrac (r_(2))(r_(1))))))))Son qalıq nisbəti r k /r k−1 həmişə ardıcıllıqla növbəti bərabərlikdən istifadə etməklə əvəz edilə bilər və s. sonuncu tənliyə qədər. Nəticə davamlı kəsirdir:
a b = q 0 + 1 q 1 + 1 q 2 + 1 ⋱ + 1 q N = [ q 0 ; q 1 , q 2 , … , q N ] (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\cfrac (1)(q_) (2)+(\cfrac (1)(\ddots +(\cfrac (1)(q_(N)))))))))=)Çoxhədlilər üçün ümumiləşdirilmiş Evklid alqoritmi
Evklidin alqoritmi və genişləndirilmiş Evklidin alqoritmi təbii olaraq polinomların halqasına ümumiləşdirilir. k[x] ixtiyari sahə üzərində bir dəyişəndən k, çünki belə çoxhədlilər üçün qalığa bölmə əməliyyatı müəyyən edilmişdir. Çoxhədlər üçün Evklidin alqoritmi icra edilərkən, Evklidin tam ədədlər alqoritmi kimi, çoxhədli qalıqlar ardıcıllığı (PRS) alınır.
Üzük nümunəsi Z[x]
Z[x] -dən f(x) polinomunun əmsallarının tərifinə görə cont(f) gcd olsun - məzmun polinom. f(x)-in cont(f)-ə bölünməsi əmsalı adlanır primitiv hissəçoxhədli f(x) və primpart(f(x)) ilə işarələnir. Bu təriflər iki çoxhədlinin gcd-sini tapmaq üçün lazım olacaq p 1 (x) Və p 2 (x) Z[x] halqasında. Tam ədədlər üzərində çoxhədlilər üçün aşağıdakılar doğrudur:
C o n t ((\displaystyle davam() NODNOD ( c o n t (p 1 (x)) , c o n t (p 2 (x)) ) , (\displaystyle \(davamı(p_(1)(x)),davam(p_(2)(x))\),)
P r i m p a r t ((\displaystyle primpart() GCD ( p 1 (x) , p 2 (x) )) = (\displaystyle \(p_(1)(x),p_(2)(x)\))=) GCD ( p r i m p a r t (p 1 (x)), p r i m p a r t (p 2 (x)) ) . (\displaystyle \(primpart(p_(1)(x)),primpart(p_(2)(x))\).)
Beləliklə, iki ixtiyari çoxhədlinin gcd-nin tapılması məsələsi primitiv çoxhədlilərin gcd-nin tapılması məsələsinə endirilir.
Z[x]-dən iki ibtidai çoxhədli p 1 (x) və p 2 (x) olsun ki, onların səlahiyyətləri arasındakı əlaqə təmin edilir: deg(p 1 (x)) = m və deg(p 2 (x)) ) = n, m > n. Çoxhədlilərin qalığa bölünməsi dividendlərin ən yüksək əmsalının bölənin ən yüksək əmsalına dəqiq bölünməsini nəzərdə tutur, ümumi halda qalığa bölmə aparıla bilməz. Buna görə də, yalançı bölgü alqoritmi təqdim olunur, buna baxmayaraq, tam ədədlər üzərində çoxhədlər çoxluğuna aid olacaq yalançı hissə və psevdoqalıq (prem) əldə etməyə imkan verir.
Pseudo-bölmə dedikdə, bölmənin özündən əvvəl çoxhədlinin vurulması nəzərdə tutulur. p 1 (x) (\displaystyle p_(1)(x))üstündə (l c (p 2 (x))) m − n + 1 (\displaystyle (lc(p_(2)(x)))^(m-n+1)), yəni
L c (p 2 (x)) m − n + 1 p 1 (x) = p 2 (x) q (x) + r 2 (x) , dərəcə (r (x))< deg (p 2 (x)) , {\displaystyle lc(p_{2}(x))^{m-n+1}p_{1}(x)=p_{2}(x)q(x)+r_{2}(x),\deg(r(x))<\deg(p_{2}(x)),}
harada q (x) (\displaystyle q(x)) Və r (x) (\displaystyle r(x))- müvafiq olaraq psevdopartial və yalançı qalıq.
Belə ki, p 1 (x) , p 2 (x) ∈ Z [ x ] (\displaystyle p_(1)(x),p_(2)(x)\Z[x]-də), üstəlik dərəcə (p 1) = n 1 ≥ dərəcə (p 2) = n 2 (\displaystyle \deg(p_(1))=n_(1)\geq \deq(p_(2))=n_(2) ). Sonra Evklidin alqoritmi aşağıdakı addımlardan ibarətdir:
1. GCD məzmununun hesablanması:
C:= (\displaystyle c:=) GCD ( c o n t (p 1) , c o n t (p 2) ) (\displaystyle \(davamı(p_(1)),davam(p_(2))\)).
2. Primitiv hissələrin hesablanması:
P 1 ′ (x) := p r i m p a r t (p 1 (x)) ; (\displaystyle p_(1)"(x):=primpart(p_(1)(x));)
P 2 ′ (x) := p r i m p a r t (p 2 (x)) . (\displaystyle p_(2)"(x):=primpart(p_(2)(x)).)
3. Çoxhədli qalıqların ardıcıllığının qurulması:
P 1 ′ (x) , (\displaystyle p_(1)"(x),)
P 2 ′ (x) , (\displaystyle p_(2)"(x),)
P 3 (x) := prem (p 1 ′ (x) , p 2 ′ (x)) , (\displaystyle p_(3)(x):=prem(p_(1)"(x),p_(2) )"(x)))
P 4 (x) := prem (p 2 ′ (x) , p 3 (x)) , (\displaystyle p_(4)(x):=prem(p_(2)"(x),p_(3) (x)))
P 5 (x) := prem (p 3 (x) , p 4 (x)) , (\displaystyle p_(5)(x):=prem(p_(3)(x),p_(4)(x) )))
. . . (\displaystyle ...)
P h (x) := p r e m (p h − 2 (x) , p h − 1 (x)) . (\displaystyle p_(h)(x):=prem(p_(h-2)(x),p_(h-1)(x)).)