Nurk kahe lõikuva tasandi vahel: määratlus, leidmise näited. Sirgete vaheline nurk Otsige sirgete vahele teravnurka
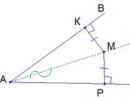
\(\blacktriangleright\) Dihedraalnurk on nurk, mille moodustavad kaks pooltasapinda ja sirgjoon \(a\) , mis on nende ühine piir.
\(\blacktriangleright\) Tasapindade \(\xi\) ja \(\pi\) vahelise nurga leidmiseks peate leidma lineaarnurga vürtsikas või otse) tasapindade \(\xi\) ja \(\pi\) moodustatud kahetahulisest nurgast:
1. samm: olgu \(\xi\cap\pi=a\) (tasapindade lõikejoon). Tasapinnal \(\xi\) märgime suvalise punkti \(F\) ja joonistame \(FA\perp a\) ;
2. samm: joonistage \(FG\perp \pi\) ;
3. samm: vastavalt TTP-le (\(FG\) - risti, \(FA\) - kaldus, \(AG\) - projektsioon) on meil: \(AG\perp a\) ;
4. samm: nurka \(\angle FAG\) nimetatakse tasapindade \(\xi\) ja \(\pi\) moodustatud kahetahulise nurga lineaarnurgaks.
Pange tähele, et kolmnurk \(AG\) on täisnurkne kolmnurk.
Pange tähele ka seda, et sel viisil konstrueeritud tasand \(AFG\) on risti nii tasanditega \(\xi\) kui ka \(\pi\) . Seetõttu võib seda öelda ka teisiti: tasapindadevaheline nurk\(\xi\) ja \(\pi\) on nurk kahe ristuva sirge \(c\in \xi\) ja \(b\in\pi\) vahel, mis moodustavad tasandiga \(\xi\) risti ) ja \(\pi\) .
Ülesanne 1 #2875
Ülesande tase: raskem kui eksam
Antud on nelinurkne püramiid, mille kõik servad on võrdsed ja mille alus on ruut. Leidke \(6\cos \alpha\) , kus \(\alpha\) on selle külgnevate külgpindade vaheline nurk.
Olgu \(SABCD\) antud püramiid (\(S\) on tipp), mille servad on võrdsed \(a\) . Seetõttu on kõik külgpinnad võrdsed võrdkülgsed kolmnurgad. Leidke tahkude \(SAD\) ja \(SCD\) vaheline nurk.
Joonistame \(CH\perp SD\) . Sest \(\kolmnurk SAD=\kolmnurk SCD\), siis on \(AH\) ka \(\triangle SAD\) kõrgus. Seetõttu on definitsiooni järgi \(\angle AHC=\alpha\) lineaarne kahetahuline nurk tahkude \(SAD\) ja \(SCD\) vahel.
Kuna alus on ruut, siis \(AC=a\sqrt2\) . Pange tähele ka seda, et \(CH=AH\) on võrdkülgse kolmnurga kõrgus küljega \(a\) , seega \(CH=AH=\frac(\sqrt3)2a\) .
Seejärel koosinusteoreemiga \(\kolmnurk AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]
Vastus: -2
Ülesanne 2 #2876
Ülesande tase: raskem kui eksam
Tasapinnad \(\pi_1\) ja \(\pi_2\) lõikuvad nurga all, mille koosinus on võrdne \(0,2\) . Tasapinnad \(\pi_2\) ja \(\pi_3\) lõikuvad täisnurga all ning tasandite \(\pi_1\) ja \(\pi_2\) lõikejoon on paralleelne tasapinnad \(\pi_2\) ja \(\ pi_3\) . Leidke tasandite \(\pi_1\) ja \(\pi_3\) vahelise nurga siinus.
Olgu \(\pi_1\) ja \(\pi_2\) lõikejoon sirge \(a\) , \(\pi_2\) ja \(\pi_3\) lõikejoon on sirge \ (b\) ja lõikejoon \(\pi_3\) ja \(\pi_1\) on sirgjoon \(c\) . Kuna \(a\parallel b\) , siis \(c\parallel a\parallel b\) (vastavalt teoreemile teoreetilise viite jaotisest "Geomeetria ruumis" \(\rightarrow\) "Sissejuhatus stereomeetriasse, paralleelsus”).
Märkige punktid \(A\in a, B\in b\) nii, et \(AB\perp a, AB\perp b\) (see on võimalik, kuna \(a\paralleel b\) ). Märkige \(C\in c\), nii et \(BC\perp c\) , seega \(BC\perp b\) . Seejärel \(AC\perp c\) ja \(AC\perp a\) .
Tõepoolest, kuna \(AB\perp b, BC\perp b\) , siis \(b\) on risti tasapinnaga \(ABC\) . Kuna \(c\parallel a\parallel b\) , siis sirged \(a\) ja \(c\) on samuti risti tasapinnaga \(ABC\) ja seega mis tahes sirge sellelt tasapinnalt, eriti rida \ (AC\) .
Sellest järeldub \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Selgub, et \(\kolmnurk ABC\) on ristkülikukujuline, mis tähendab \[\sin \angle BCA=\cos \angle BAC=0,2.\]
Vastus: 0,2
Ülesanne 3 #2877
Ülesande tase: raskem kui eksam
Antud sirged \(a, b, c\), mis lõikuvad ühes punktis ja nurk nende kahe vahel on võrdne \(60^\circ\) . Leidke \(\cos^(-1)\alpha\) , kus \(\alpha\) on nurk joonte \(a\) ja \(c\) moodustatud tasandi ja joonte moodustatud tasandi vahel \(b\ ) ja \(c\) . Esitage oma vastus kraadides.
Olgu sirged ristuvad punktis \(O\) . Kuna nende kahe vaheline nurk on võrdne \(60^\circ\) , ei saa kõik kolm sirget asuda samal tasapinnal. Märgime joonele \(a\) punkti \(A\) ja joonistame \(AB\perp b\) ja \(AC\perp c\) . Siis \(\kolmnurk AOB=\kolmnurk AOC\) ristkülikukujulisena hüpotenuusis ja teravnurgas. Seega \(OB=OC\) ja \(AB=AC\) .
Teeme \(AH\perp (BOC)\) . Siis kolme risti teoreemiga \(HC\perp c\) , \(HB\perp b\) . Kuna \(AB=AC\) , siis \(\kolmnurk AHB=\kolmnurk AHC\) ristkülikukujulisena piki hüpotenuusi ja jalga. Seetõttu \(HB=HC\) . Seega on \(OH\) nurga \(BOC\) poolitaja (kuna punkt \(H\) on nurga külgedest võrdsel kaugusel).
Pange tähele, et sel viisil oleme konstrueerinud ka kahetahulise nurga lineaarnurga, mille moodustab tasapind, mille moodustavad sirged \(a\) ja \(c\) ning tasapind, mille moodustavad sirged \(b\) ja \( c\) . See on nurk \(ACH\) .
Otsime selle nurga üles. Kuna valisime punkti \(A\) suvaliselt, siis valime selle nii, et \(OA=2\) . Seejärel ristkülikukujuliselt \(\kolmnurk AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Kuna \(OH\) on poolitaja, siis \(\angle HOC=30^\circ\) , ristkülikukujulises \(\kolmnurgas HOC\): \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Seejärel ristkülikukujulisest \(\kolmnurgast ACH\): \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]
Vastus: 3
Ülesanne 4 #2910
Ülesande tase: raskem kui eksam
Tasapinnad \(\pi_1\) ja \(\pi_2\) lõikuvad piki joont \(l\) , mis sisaldab punkte \(M\) ja \(N\) . Lõigud \(MA\) ja \(MB\) on risti joonega \(l\) ja asuvad vastavalt tasapindadel \(\pi_1\) ja \(\pi_2\) ning \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Leidke \(3\cos\alpha\) , kus \(\alpha\) on nurk tasapindade \(\pi_1\) ja \(\pi_2\) vahel.
Kolmnurk \(AMN\) on täisnurkne, \(AN^2 = AM^2 + MN^2\) , kust \ Kolmnurk \(BMN\) on täisnurkne, \(BN^2 = BM^2 + MN^2\) , kust \ Kirjutame kolmnurga \(AMB\) koosinusteoreemi: \ Siis \ Kuna tasapindadevaheline nurk \(\alpha\) on teravnurk ja \(\angle AMB\) osutus nüriks, siis \(\cos\alpha=\dfrac5(12)\) . Siis \
Vastus: 1.25
Ülesanne 5 #2911
Ülesande tase: raskem kui eksam
\(ABCDA_1B_1C_1D_1\) on rööptahukas, \(ABCD\) on ruut küljega \(a\) , punkt \(M\) on punktist \(A_1\) tasapinnale langetatud risti alus. ((ABCD)\) , pealegi on \(M\) ruudu \(ABCD\) diagonaalide lõikepunkt. On teada, et \(A_1M = \dfrac(\sqrt(3))(2)a\). Leidke nurk tasapindade \((ABCD)\) ja \((AA_1B_1B)\) vahel. Esitage oma vastus kraadides.
Konstrueerime \(MN\) risti \(AB\)-ga, nagu on näidatud joonisel.
Kuna \(ABCD\) on ruut küljega \(a\) ja \(MN\perp AB\) ja \(BC\perp AB\) , siis \(MN\paralleel BC\) . Kuna \(M\) on ruudu diagonaalide lõikepunkt, siis \(M\) on \(AC\) keskpunkt, seega on \(MN\) keskmine joon Ja \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) on \(A_1N\) projektsioon tasapinnale \((ABCD)\) ja \(MN\) on risti \(AB\) , siis kolme perpendikulaari teoreemi järgi \( A_1N\) on risti nurgaga \(AB \) ning tasapindade \((ABCD)\) ja \((AA_1B_1B)\) vaheline nurk on \(\nurk A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]
Vastus: 60
Ülesanne 6 #1854
Ülesande tase: raskem kui eksam
Ruudus \(ABCD\) : \(O\) on diagonaalide lõikepunkt; \(S\) ei asu ruudu tasapinnal, \(SO \perp ABC\) . Leidke nurk tasapindade \(ASD\) ja \(ABC\) vahel, kui \(SO = 5\) ja \(AB = 10\) .
Täisnurksed kolmnurgad \(\kolmnurk SAO\) ja \(\kolmnurk SDO\) on kahes küljes võrdsed ja nendevaheline nurk (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , sest \(O\) on ruudu diagonaalide lõikepunkt, \(SO\) on ühine külg) \(\Paremnool\) \(AS = SD\) \(\Paremnool\) \(\kolmnurk ASD\) on võrdhaarne. Punkt \(K\) on \(AD\) keskpunkt, siis \(SK\) on kolmnurga \(\kolmnurk ASD\) kõrgus ja \(OK\) on kolmnurga kõrgus \ (AOD\) \(\ Paremnool\) tasapind \(SOK\) on risti tasapindadega \(ASD\) ja \(ABC\) \(\Rightarrow\) \(\angle SKO\) on lineaarnurk, mis on võrdne vajaliku kahetahulise nurgani.
In \(\kolmnurk SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\kolmnurk SOK\) on võrdhaarne täisnurkne kolmnurk \(\Rightarrow\) \(\angle SKO = 45^\circ\) .
Vastus: 45
Ülesanne 7 #1855
Ülesande tase: raskem kui eksam
Ruudus \(ABCD\) : \(O\) on diagonaalide lõikepunkt; \(S\) ei asu ruudu tasapinnal, \(SO \perp ABC\) . Leidke nurk tasapindade \(ASD\) ja \(BSC\) vahel, kui \(SO = 5\) ja \(AB = 10\) .
Täisnurksed kolmnurgad \(\kolmnurk SAO\) , \(\kolmnurk SDO\) , \(\kolmnurk SOB\) ja \(\kolmnurk SOC\) on kahes küljes võrdsed ja nendevaheline nurk (\(SO \perp ABC) \) \(\Paremnool\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) , sest \(O\) on ruudu diagonaalide lõikepunkt, \(SO\) on ühine külg) \(\Paremnool\) \(AS = DS = BS = CS\) \(\Paremnool\) \(\kolmnurk ASD\) ja \(\kolmnurk BSC\) on võrdhaarsed. Punkt \(K\) on \(AD\) keskpunkt, siis \(SK\) on kolmnurga \(\kolmnurk ASD\) kõrgus ja \(OK\) on kolmnurga kõrgus \ (AOD\) \(\ Paremnool\) tasapind \(SOK\) on risti tasapinnaga \(ASD\) . Punkt \(L\) on \(BC\) keskpunkt, siis \(SL\) on kolmnurga \(\kolmnurk BSC\) kõrgus ja \(OL\) on kolmnurga \ kõrgus (BOC\) \(\ Paremnool\) tasapind \(SOL\) (teise nimega tasapind \(SOK\) ) on risti tasapinnaga \(BSC\) . Seega saame, et \(\angle KSL\) on lineaarnurk, mis võrdub soovitud kahetahulise nurgaga.
\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Paremnool\) \(OL = 5\) ; \(SK = SL\) – kõrgused võrdsed võrdhaarsed kolmnurgad, mille võib leida Pythagorase teoreemi abil: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Seda on näha \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Paremnool\) kolmnurga jaoks \(\kolmnurk KSL\) vastupidine teoreem Pythagorase \(\Rightarrow\) \(\kolmnurk KSL\) – täisnurkne kolmnurk \(\Rightarrow\) \(\angle KSL = 90^\circ\) .
Vastus: 90
Õpilaste ettevalmistamine matemaatika eksamiks algab reeglina põhivalemite kordamisega, sealhulgas nende valemite kordamisega, mis võimaldavad teil määrata tasapindade vahelise nurga. Hoolimata asjaolust, et see geomeetria osa on raames piisavalt üksikasjalikult käsitletud kooli õppekava, peavad paljud lõpetajad põhimaterjali kordama. Mõistes tasapindade vahelise nurga leidmist, oskavad gümnasistid ülesande lahendamise käigus kiiresti õige vastuse välja arvutada ning ühtse riigieksami alusel loota korralikele hinnetele.
Peamised nüansid
Et kahetahulise nurga leidmise küsimus raskusi ei tekitaks, soovitame järgida lahendusalgoritmi, mis aitab eksamiülesannetega toime tulla.
Kõigepealt peate määrama joone, mida mööda tasapinnad ristuvad.
Seejärel peate sellel sirgel valima punkti ja joonistama sellele kaks risti.
Järgmine samm on leidmine trigonomeetriline funktsioon kahetahuline nurk, mille moodustavad ristid. Kõige mugavam on seda teha saadud kolmnurga abil, mille osaks on nurk.
Vastuseks on nurga väärtus või selle trigonomeetriline funktsioon.
Eksamieksamiks valmistumine koos Shkolkovoga on teie edu võti
Eelmisel päeval tunni ajal eksami sooritamine paljud õpilased seisavad silmitsi definitsioonide ja valemite leidmise probleemiga, mis võimaldavad teil arvutada kahe tasapinna vahelise nurga. Kooliõpik pole alati käepärast täpselt siis, kui seda vaja läheb. Ja selleks, et leida vajalikke valemeid ja näiteid nende õigeks rakendamiseks, sealhulgas Internetist lennukitevahelise nurga leidmiseks, peate mõnikord kulutama palju aega.
Matemaatikaportaal "Shkolkovo" pakub uut lähenemist riigieksamiks valmistumisel. Meie veebisaidi tunnid aitavad õpilastel tuvastada enda jaoks kõige keerulisemad lõigud ja täita teadmistes lünki.
Oleme koostanud ja selgelt esitanud kogu vajaliku materjali. Põhimõisted ja valemid on esitatud jaotises "Teoreetiline viide".
Materjali paremaks omandamiseks soovitame harjutada ka vastavaid harjutusi. Jaotises Kataloog on esitatud suur valik erineva keerukusega ülesandeid, näiteks sisse lülitatud. Kõik ülesanded sisaldavad üksikasjalikku algoritmi õige vastuse leidmiseks. Saidil olevate harjutuste loendit täiendatakse ja uuendatakse pidevalt.
Harjutades ülesannete lahendamist, mille puhul on vaja leida kahe tasapinna vaheline nurk, on õpilastel võimalus salvestada kõik ülesanded veebis "Lemmikute" alla. Tänu sellele saavad nad tema juurde vajalik arv kordi tagasi pöörduda ja tema lahenduse edenemist kooliõpetaja või juhendajaga arutada.
Artiklis räägitakse tasapindadevahelise nurga leidmisest. Pärast definitsiooni toomist seame graafilise illustratsiooni, kaalume üksikasjalikku meetodit koordinaatide leidmiseks meetodi järgi. Saame ristumistasandite valemi, mis sisaldab normaalvektorite koordinaate.
Materjalis kasutatakse andmeid ja mõisteid, mida on varem uuritud artiklites, mis käsitlevad tasapinda ja joont ruumis. Alustuseks on vaja liikuda edasi arutluskäigu juurde, mis võimaldab kahe ristuva tasandi vahelise nurga määramisel teatud lähenemisviisi.
Antud on kaks lõikuvat tasandit γ 1 ja γ 2. Nende ristmik saab tähise c . χ tasandi ehitus on seotud nende tasandite lõikepunktiga. Tasand χ läbib punkti M sirgjoonena c. Tasapinnad γ 1 ja γ 2 lõigatakse χ tasandi abil. Aktsepteerime sirge a jaoks γ 1 ja χ lõikuva sirge ning sirge b jaoks γ 2 ja χ ristmiku tähistusi. Saame, et sirgete a ja b lõikepunkt annab punkti M .
Punkti M asukoht ei mõjuta nurka lõikuvate sirgete a ja b vahel ning punkt M asub sirgel c, mida läbib tasapind χ.
Vaja on konstrueerida tasapind χ 1, mis on risti sirgega c ja erineb tasapinnast χ . Tasapindade γ 1 ja γ 2 lõikepunkt χ 1 abil saab sirgeid a 1 ja b 1 .
Näha on, et χ ja χ 1 konstrueerimisel on sirged a ja b risti sirgega c, siis a 1, b 1 on risti sirgega c. Leides sirge a ja a 1 tasapinnal γ 1, mis on risti sirgega c, siis võib neid lugeda paralleelseks. Samamoodi näitab b ja b 1 asukoht tasapinnal γ 2 sirge c perpendikulaarsusega nende paralleelsust. See tähendab, et on vaja teha tasandi χ 1 paralleelne ülekanne χ-le, kus saame kaks kokkulangevat sirget a ja a 1 , b ja b 1 . Saame, et ristuvate sirgete a ja b vaheline nurk on 1 võrdne nurgaga ristuvad sirged a ja b.
Mõelge allolevale joonisele.
Seda otsust tõendab asjaolu, et ristuvate sirgete a ja b vahel on nurk, mis ei sõltu punkti M asukohast, see tähendab lõikepunktist. Need jooned paiknevad tasapindadel γ 1 ja γ 2 . Tegelikult võib saadud nurka pidada kahe ristuva tasandi vaheliseks nurgaks.
Liigume edasi olemasolevate ristuvate tasandite γ 1 ja γ 2 vahelise nurga määramisega.
Definitsioon 1
Nurk kahe lõikuva tasandi γ 1 ja γ 2 vahel nimetame sirgete a ja b lõikepunktist moodustatud nurka, kus tasapinnad γ 1 ja γ 2 lõikuvad sirgega c risti oleva tasandiga χ.
Mõelge allolevale joonisele.
Määratluse võib esitada muul kujul. Tasapindade γ 1 ja γ 2 ristumiskohas, kus c on sirge, millel need ristuvad, märkige punkt M, mille kaudu tõmmake sirgega c risti olevad jooned a ja b, mis asuvad tasapindadel γ 1 ja γ 2 , siis sirgete a ja b vaheline nurk on tasapindade vaheline nurk. Praktikas on see rakendatav tasapindadevahelise nurga moodustamisel.
Ristumiskohas moodustub nurk, mille väärtus on väiksem kui 90 kraadi, see tähendab, et nurga astmemõõt kehtib seda tüüpi intervallil (0, 90] ) Samas nimetatakse neid tasapindu risti. kui ristumiskohas tekib täisnurk.Paralleeltasandite vaheline nurk loetakse võrdseks nulliga.
Tavaline viis ristuvate tasandite vahelise nurga leidmiseks on teha lisakonstruktsioone. See aitab seda täpselt määrata ja seda saab teha kolmnurga võrdsus- või sarnasusmärkide, siinuste, nurga koosinuste abil.
Kaaluge probleemide lahendamist, kasutades näidet ploki C 2 ühtse riigieksami probleemidest.
Näide 1
Antud on ristkülikukujuline rööptahukas A B C D A 1 B 1 C 1 D 1, kus külg A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, punkt E eraldab külje A A 1 suhtega 4: 3. Leidke nurk tasapindade A B C ja B E D 1 vahel.
Lahendus
Selguse huvides peate tegema joonise. Me saame sellest aru
Visuaalne esitus on vajalik selleks, et tasanditevahelise nurga all töötamine oleks mugavam.
Teeme definitsiooni sirgjoonele, mida mööda tasandid A B C ja B E D 1 ristuvad. Punkt B on ühine punkt. Peab leidma teise ühine punkt ristmikud. Vaatleme sirgeid D A ja D 1 E , mis asuvad samal tasapinnal A D D 1 . Nende asukoht ei näita paralleelsust, mis tähendab, et neil on ühine lõikepunkt.
Kuid sirge D A asub tasapinnal A B C ja D 1 E tasapinnal B E D 1 . Seega saame, et read D A Ja D 1 E neil on ühine lõikepunkt, mis on ühine ka tasapindadele A B C ja B E D 1 . Näitab joonte lõikepunkti D A ja D 1 E täht F. Siit saame, et B F on sirge, mida mööda tasandid A B C ja B E D 1 ristuvad.
Mõelge allolevale joonisele.
Vastuse saamiseks on vaja konstrueerida tasapindadel A B C ja B E D 1 paiknevad sirgjooned läbipääsuga punktist, mis asub sirgel B F ja on sellega risti. Seejärel peetakse nende joonte vahelist nurka soovitud nurgaks tasandite A B C ja B E D 1 vahel.
Siit on näha, et punkt A on punkti E projektsioon tasapinnale AB C. Tuleb tõmmata sirge BF täisnurga all lõikuv sirge punktis M. On näha, et sirge AM on sirge EM projektsioon tasapinnale ABC, mis põhineb teoreemil nende ristide AM ⊥ BF kohta. Mõelge allolevale joonisele.
∠ A M E on soovitud nurk, mille moodustavad tasapinnad A B C ja B E D 1 . Saadud kolmnurgast A E M leiame nurga siinuse, koosinuse või puutuja, mille järel nurga enda, ainult selle kahe teadaoleva küljega. Tingimusel on meil, et AE pikkus leitakse järgmiselt: sirge AA 1 jagatakse punktiga E suhtega 4: 3, mis tähendab, et joone kogupikkus on 7 osa, siis AE \u003d 4 osa. Leiame A.M.
Tuleb arvestada täisnurkse kolmnurgaga A B F. Meil on täisnurk A kõrgusega A M. Tingimusest A B \u003d 2 leiame pikkuse A F kolmnurkade D D 1 F ja A E F sarnasuse järgi. Saame, et A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4
Kolmnurgast A B F on vaja Pythagorase teoreemi abil leida külje B F pikkus. Saame, et B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Külje A M pikkus leitakse läbi kolmnurga A B F ala. Meil on, et pindala võib olla võrdne nii S A B C = 1 2 · A B · A F kui ka S A B C = 1 2 · B F · A M .
Saame, et A M = A B A F B F = 2 4 2 5 = 4 5 5
Siis leiame kolmnurga A E M nurga puutuja väärtuse. Saame:
t g ∠ A M E = A E A M = 4 4 5 5 = 5
Tasapindade A B C ja B E D 1 lõikumisel saadud soovitud nurk võrdub a r c t g 5 , siis saame lihtsustamisel a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .
Vastus: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .
Mõned lõikuvate joonte vahelise nurga leidmise juhtumid on toodud kasutades koordinaattasand Umbes x y z ja koordinaatide meetod. Vaatleme üksikasjalikumalt.
Kui on antud ülesanne, kus on vaja leida nurk ristuvate tasandite γ 1 ja γ 2 vahel, tähistame soovitud nurka α-ga.
Siis näitab antud koordinaatsüsteem, et meil on ristuvate tasandite γ 1 ja γ 2 normaalvektorite koordinaadid. Seejärel märgime, et n 1 → = n 1 x , n 1 y , n 1 z on tasandi γ 1 normaalvektor ja n 2 → = (n 2 x , n 2 y , n 2 z) - tasapind γ 2 . Mõelge nende tasandite vahelise nurga üksikasjalikule leidmisele vastavalt vektorite koordinaatidele.
On vaja määrata sirgjoon, mida mööda tasapinnad γ 1 ja γ 2 lõikuvad tähega c. Sirgel koos on punkt M, mille kaudu joonistame tasapinna χ, mis on risti c-ga. Tasapind χ piki sirgeid a ja b lõikub tasapindadega γ 1 ja γ 2 punktis M . definitsioonist järeldub, et nurk lõikuvate tasandite γ 1 ja γ 2 vahel on võrdne nendele tasapindadele kuuluvate vastavalt ristuvate sirgete a ja b nurgaga.
Tasapinnal χ jätame punktist M kõrvale normaalvektorid ja tähistame neid n 1 → ja n 2 →. Vektor n 1 → paikneb sirgega a ja vektor n 2 → sirgega b risti oleval sirgel. Seetõttu saame selle antud lennukχ sirge a normaalvektor on võrdne n 1 → ja sirge b korral n 2 → . Mõelge allolevale joonisele.
Siit saame valemi, mille abil saame vektorite koordinaatide abil arvutada ristuvate sirgete nurga siinuse. Leidsime, et sirgete a ja b vahelise nurga koosinus on sama mis koosinus lõikuvate tasandite γ 1 ja γ 2 vahel on tuletatud valemist cos α = cos n 1 → , n 2 → ^ = n 1 xn 2 x + n 1 y n 2 y + n 1 z n 2 zn 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, kus meil on, et n 1 → = (n 1 x, n 1 y, n 1 z) ja n 2 → = (n 2 x, n 2 y, n 2 z) on kujutatud tasandite vektorite koordinaadid.
Ristumisjoonte vaheline nurk arvutatakse valemi abil
α = kaar cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 zn 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2
Näide 2
Tingimuse järgi on antud rööptahukas А В С D A 1 B 1 C 1 D 1 , kus A B \u003d 2, A D \u003d 3, A A 1 \u003d 7 ja punkt E eraldab külge A A 1 4: 3. Leidke nurk tasapindade A B C ja B E D 1 vahel.
Lahendus
Seda on näha tingimusest, et selle küljed on paarikaupa risti. See tähendab, et on vaja kasutusele võtta koordinaatsüsteem O x y z, mille tipp on punktis C ja koordinaatteljed O x, O y, O z. Vajalik on panna suund vastavatele külgedele. Mõelge allolevale joonisele.
Lõikuvad lennukid A B C Ja B E D 1 moodustavad nurga, mille saab leida valemiga 2 x 2 + n 2 y 2 + n 2 z 2 , kus n 1 → = (n 1 x , n 1 y , n 1 z) ja n 2 → = (n 2 x , n 2 y , n 2 z ) on nende tasandite normaalvektorid. On vaja määrata koordinaadid. Jooniselt näeme, et koordinaatide telg O x y langeb tasapinnal A B C kokku, mis tähendab, et normaalvektori k → koordinaadid on võrdsed väärtusega n 1 → = k → = (0, 0, 1) .
Tasapinna B E D 1 normaalvektor on B E → ja B D 1 → vektorkorrutis, kus nende koordinaadid leitakse koordinaatide järgi äärmuslikud punktid B, E, D 1 , mis määratakse ülesande seisukorra alusel.
Saame, et B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Kuna A E E A 1 = 4 3 , siis punktide A 2 , 3 , 0 , A 1 2 , 3 , 7 koordinaatidest leiame E 2 , 3 , 4 . Saame, et BE → = (2 , 0 , 4) , BD 1 → = 2 , - 3 , 7 n 2 → = BE → × BD 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)
Leitud koordinaadid on vaja asendada kaarekoosinuse läbiva nurga arvutamise valemiga. Saame
α = kaar cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = kaar cos 6 6 6 = kaar cos 6 6
Koordinaatide meetod annab sarnase tulemuse.
Vastus: a r c cos 6 6 .
Lõpuülesannet vaadeldakse selleks, et leida ristuvate tasandite vaheline nurk olemasolevate teadaolevate tasandite võrranditega.
Näide 3
Arvutage nurga siinus, koosinus ja nurga väärtus, mille moodustavad kaks ristuvat sirget, mis on defineeritud O xyz koordinaatsüsteemis ja on antud võrranditega 2 x - 4 y + z + 1 = 0 ja 3 y - z-1 = 0.
Lahendus
Vormiga A x + B y + C z + D = 0 sirge üldvõrrandi teemat uurides selgus, et A, B, C on normaalvektori koordinaatidega võrdsed koefitsiendid. Seega on n 1 → = 2 , - 4 , 1 ja n 2 → = 0 , 3 , - 1 antud sirgete normaalvektorid.
Tasapindade normaalvektorite koordinaadid on vaja asendada ristuvate tasandite soovitud nurga arvutamise valemis. Siis me saame selle
α = a rc cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210
Seega saame nurga koosinuse kuju cos α = 13 210 . Siis ei ole ristuvate sirgete nurk nüri. Asendades trigonomeetrilise identiteedi, saame, et nurga siinuse väärtus on võrdne avaldisega. Me arvutame ja saame selle
sin α = 1 - cos 2 α = 1 - 13 210 = 41 210
Vastus: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
Süstimine φ üldvõrrandid A 1 x + B 1 y + C 1 = 0 ja A 2 x + B 2 y + C 2 = 0, arvutatakse järgmise valemiga:
Süstimine φ kahe sirge vahel kanoonilised võrrandid(x-x 1) / m 1 \u003d (y-y 1) / n 1 ja (x-x 2) / m 2 \u003d (y-y 2) / n 2, arvutatakse järgmise valemiga:
Kaugus punktist jooneni
Iga ruumi tasapinda saab kujutada kui lineaarvõrrand helistas üldvõrrand lennuk
Erijuhtumid.
o Kui võrrandis (8), siis tasand läbib alguspunkti.
o (,) abil on tasapind paralleelne vastavalt teljega (telg, telg).
o Kui (,) tasapind on paralleelne tasapinnaga (tasand, tasapind).
Lahendus: kasutage (7)
Vastus: tasapinna üldvõrrand.
Näide.
Tasapind ristkülikukujulises koordinaatsüsteemis Oxyz on antud tasandi üldvõrrandiga 
. Kirjutage üles kõigi selle tasapinna normaalvektorite koordinaadid.
Teame, et tasandi üldvõrrandis olevate muutujate x, y ja z koefitsiendid on selle tasandi normaalvektori vastavad koordinaadid. Seetõttu antud tasandi normaalvektor 
on koordinaadid. Kõikide normaalvektorite hulga saab esitada järgmiselt.
Kirjutage tasapinna võrrand, kui ristkülikukujulises koordinaatsüsteemis Oxyz läbib see punkti 
, aga 
on selle tasandi normaalvektor.
Pakume sellele probleemile kaks lahendust.
Sellest olukorrast, mis meil on. Asendame need andmed punkti läbiva tasapinna üldvõrrandisse:
Kirjutage koordinaattasandiga Oyz paralleelse ja punkti läbiva tasapinna üldvõrrand 
.
Tasapinna, mis on paralleelne koordinaattasandiga Oyz, saab anda vormi tasandi üldise mittetäieliku võrrandiga. Alates punktist 
kuulub tingimuse järgi tasapinnale, siis peavad selle punkti koordinaadid rahuldama tasandi võrrandit ehk võrdsus peab olema tõene. Siit leiame. Seega on soovitud võrrandil vorm.
Lahendus. Vektorkorrutis definitsiooni 10.26 järgi on vektoritega p ja q ortogonaalne. Seetõttu on see soovitud tasapinnaga ortogonaalne ja vektori võib võtta selle normaalvektoriks. Leia vektori n koordinaadid:
st 
. Kasutades valemit (11.1), saame
Avades selles võrrandis sulgud, jõuame lõpliku vastuseni.
Vastus: 
.
Kirjutame normaalvektori vormi ümber ja leiame selle pikkuse:
Vastavalt ülaltoodule:
Vastus: 
Paralleeltasanditel on sama normaalvektor. 1) Võrrandist leiame tasapinna normaalvektori:.
2) Koostame tasandi võrrandi vastavalt punktile ja normaalvektorile: 
Vastus:
Ruumi tasapinna vektorvõrrand
Tasapinna parameetriline võrrand ruumis
Antud punkti läbiva tasandi võrrand, mis on risti antud vektoriga
Laske sisse kolmemõõtmeline ruum on määratud ristkülikukujuline Descartes'i koordinaatsüsteem. Sõnastame järgmise probleemi:
Kirjutage võrrand antud punkti läbivale tasapinnale M(x 0, y 0, z 0) antud vektoriga risti n = ( A, B, C} .
Lahendus. Las olla P(x, y, z) on suvaline punkt ruumis. Punkt P kuulub tasapinnale siis ja ainult siis, kui vektor MP = {x − x 0, y − y 0, z − z 0) vektori suhtes ortogonaalne n = {A, B, C) (joonis 1).
Olles kirjutanud nende vektorite ortogonaalsuse tingimuse (n, MP) = 0 koordinaatide kujul, saame:
|
A(x − x 0) + B(y − y 0) + C(z − z 0) = 0 |
Tasapinna võrrand kolme punktiga
Vektorkujul
Koordinaatides
Tasapindade vastastikune paigutus ruumis
on kahe tasandi üldvõrrandid. Seejärel:
1) kui 
, siis tasapinnad langevad kokku;
2) kui 
, siis on tasapinnad paralleelsed;
3) kui või , siis tasandid lõikuvad ja võrrandisüsteem
(6)
on antud tasandite lõikejoone võrrandid.
|
Lahendus: Koostame sirge kanoonilised võrrandid valemiga: Vastus: |
Võtame saadud võrrandid ja “nööpme maha”, näiteks vasakpoolse tüki: . Nüüd võrdsustame selle tüki mis tahes numbrile(pidage meeles, et seal oli juba null), näiteks ühele: . Kuna , siis peavad ka ülejäänud kaks "tükki" olema võrdsed ühega. Põhimõtteliselt peate süsteemi lahendama: |
Kirjutage parameetrilised võrrandid järgmistele ridadele: 
Lahendus: Sirged on antud kanooniliste võrranditega ja esimeses etapis tuleks leida mõni sirgele kuuluv punkt ja selle suunavektor.
a) võrranditest 
eemalda punkt ja suunavektor: . Võite valida mõne muu punkti (kuidas seda teha, on kirjeldatud ülal), kuid parem on võtta kõige ilmsem. Muide, vigade vältimiseks asendage võrrandites alati selle koordinaadid.
Koostame selle sirge parameetrilised võrrandid: 
Parameetriliste võrrandite mugavus seisneb selles, et nende abiga on väga lihtne leida teisi sirge punkte. Näiteks leiame punkti, mille koordinaadid vastavad näiteks parameetri väärtusele: 
Seega: b) Vaatleme kanoonilisi võrrandeid 
. Punkti valik on siin lihtne, kuid salakaval: (olge ettevaatlik, et koordinaate ei segaks!!!). Kuidas juhtvektorit välja tõmmata? Võite vaielda, millega see sirge on paralleelne, või kasutada lihtsat formaalset nippi: proportsioon on "y" ja "z", nii et kirjutame suunavektori ja paneme ülejäänud ruumi nulli: .
Koostame sirge parameetrilised võrrandid: 
c) Kirjutame võrrandid ümber kujul , see tähendab, et "Z" võib olla ükskõik milline. Ja kui on, siis olgu näiteks . Seega kuulub punkt sellele reale. Suunavektori leidmiseks kasutame järgmist formaalset tehnikat: algvõrrandites on "x" ja "y" ning suunavektorisse nendesse kohtadesse kirjutame nullid: . Ülejäänud kohas panime üksus: . Ühe asemel sobib mis tahes arv, välja arvatud null.
Kirjutame sirge parameetrilised võrrandid: 
nurk ruumisirgete vahel nimetame mis tahes külgnevaid nurki, mille moodustavad kaks sirget, mis on tõmmatud läbi andmetega paralleelse suvalise punkti.
Olgu ruumis antud kaks sirget:
Ilmselgelt võib joonte vahelist nurka φ võtta nende suunavektorite ja vahelise nurgana. Kuna , siis vektoritevahelise nurga koosinuse valemi järgi saame
Kahe sirge paralleelsuse ja perpendikulaarsuse tingimused on samaväärsed nende suunavektorite paralleelsuse ja perpendikulaarsuse tingimustega ja:
Kaks otse on paralleelsed siis ja ainult siis, kui nende vastavad koefitsiendid on proportsionaalsed, st. l 1 paralleel l 2 siis ja ainult paralleelselt 
.
Kaks otse risti siis ja ainult siis, kui vastavate koefitsientide korrutiste summa on võrdne nulliga: .
Kell eesmärk sirge ja tasapinna vahel
Lase rida d- ei ole risti tasapinnaga θ;
d′− sirge projektsioon d tasapinnale θ;
Sirgete vahelistest nurkadest väikseim d Ja d"me helistame nurk sirge ja tasapinna vahel.
Tähistame seda kui φ=( d,θ)
Kui d⊥θ , siis ( d,θ)=π/2
Oi→j→k→− ristkülikukujuline koordinaatsüsteem.
Tasapinnaline võrrand:
θ: Ax+Kõrval+cz+D=0
Leiame, et sirge on antud punkti ja suunavektoriga: d[M 0,lk→]
Vektor n→(A,B,C)⊥θ
Siis jääb üle välja selgitada vektorite vaheline nurk n→ ja lk→ tähistage seda kui γ=( n→,lk→).
Kui nurk γ<π/2 , то искомый угол φ=π/2−γ .
Kui nurk γ>π/2 , siis vajalik nurk φ=γ−π/2
sinφ=sin(2π−γ)=cosγ
sinφ=sin(γ−2π)=−cosγ
Siis nurk sirge ja tasapinna vahel saab arvutada järgmise valemi abil:
sinφ=∣cosγ∣=∣ ∣ Ap 1+bp 2+cp 3∣ ∣ √A 2+B 2+C 2√lk 21+lk 22+lk 23
29. küsimus. Ruutvormi mõiste. Ruutvormide märgimääratlus.
Ruutvorm j (x 1, x 2, ..., x n) n reaalset muutujat x 1, x 2, ..., x n nimetatakse vormi summaks 
, (1)
kus aij on mõningaid numbreid, mida nimetatakse koefitsientideks. Ilma üldistust kaotamata võime seda eeldada aij = a ji.
Ruutvormi nimetatakse kehtiv, kui aij
О GR. Ruutkujuline maatriks nimetatakse maatriksiks, mis koosneb selle koefitsientidest. Ruutvorm (1) vastab ainulaadsele sümmeetrilisele maatriksile 
st. A T = A. Seetõttu saab ruutkuju (1) kirjutada maatriksi kujul j ( X) = x T Ah, kus x T = (X 1 X 2 … x n). (2)
Ja vastupidi, mis tahes sümmeetriline maatriks (2) vastab ainulaadsele ruutvormile kuni muutujate tähistuseni.
Ruutvormi aste nimetatakse selle maatriksi auastmeks. Ruutvormi nimetatakse mitte-degenereerunud, kui selle maatriks on mitteainsuseline AGA. (tuletage meelde, et maatriks AGA nimetatakse mittedegeneratiivseks, kui selle determinant on nullist erinev). Vastasel juhul on ruutvorm degenereerunud.
positiivne kindel(või rangelt positiivne), kui
j ( X) > 0 , kellelegi X = (X 1 , X 2 , …, x n), välja arvatud X = (0, 0, …, 0).
Maatriks AGA positiivne kindel ruutvorm j ( X) nimetatakse ka positiivseks kindlaks. Seetõttu vastab positiivne kindel ruutvorm ainulaadsele positiivsele kindlale maatriksile ja vastupidi.
Ruutkuju (1) nimetatakse negatiivne kindel(või rangelt negatiivne), kui
j ( X) < 0, для любого X = (X 1 , X 2 , …, x n), välja arvatud X = (0, 0, …, 0).
Sarnaselt ülaltoodule nimetatakse negatiivse-määratletud ruutmaatriksit ka negatiivseks-kindlaks.
Seetõttu on positiivselt (negatiivselt) kindel ruutvorm j ( X) jõuab minimaalse (maksimaalse) väärtuseni j ( X*) = 0 jaoks X* = (0, 0, …, 0).
Pange tähele, et enamik ruutvorme ei ole märgikindlad, st nad ei ole positiivsed ega negatiivsed. Sellised ruutvormid kaovad mitte ainult koordinaatsüsteemi alguspunktis, vaid ka teistes punktides.
Millal n> 2, ruutvormi märgimääratluse kontrollimiseks on vaja erikriteeriume. Vaatleme neid.
Suured alaealised ruutvorme nimetatakse alaealisteks:
see tähendab, et need on alaealised järgus 1, 2, …, n maatriksid AGA, mis asub vasakus ülanurgas, viimane neist ühtib maatriksi determinandiga AGA.
Positiivse määratuse kriteerium (Sylvesteri kriteerium)
X) = x T Ah on positiivne kindel, on vajalik ja piisav, et kõik maatriksi peamised alaealised AGA olid positiivsed, see tähendab: M 1 > 0, M 2 > 0, …, M n > 0. Negatiivse kindluse kriteerium Selleks, et ruutvorm j ( X) = x T Ah on negatiivne kindel, siis on vajalik ja piisav, et selle paarisjärjekorras põhimollid on positiivsed ja paaritu järjekorra põhimollid negatiivsed, st: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n
Ma teen lühidalt. Kahe sirge vaheline nurk on võrdne nende suunavektorite vahelise nurgaga. Seega, kui teil õnnestub leida suunavektorite a \u003d (x 1; y 1; z 1) ja b \u003d (x 2; y 2; z 2) koordinaadid, saate nurga leida. Täpsemalt nurga koosinus vastavalt valemile:
Vaatame, kuidas see valem konkreetsetel näidetel töötab:
Ülesanne. Punktid E ja F on märgitud kuubis ABCDA 1 B 1 C 1 D 1 - vastavalt servade A 1 B 1 ja B 1 C 1 keskpunktid. Leidke nurk sirgete AE ja BF vahel.
Kuna kuubi serv ei ole määratud, siis määrame AB = 1. Tutvustame standardse koordinaatsüsteemi: alguspunkt on punktis A ja x, y, z teljed on suunatud vastavalt AB, AD ja AA 1 suunas. . Ühiklõik on võrdne AB = 1. Nüüd leiame oma sirgete suunavektorite koordinaadid.
Leia vektori AE koordinaadid. Selleks vajame punkte A = (0; 0; 0) ja E = (0,5; 0; 1). Kuna punkt E on lõigu A 1 B 1 keskpunkt, on selle koordinaadid võrdsed otste koordinaatide aritmeetilise keskmisega. Pange tähele, et vektori AE alguspunkt ühtib alguspunktiga, seega AE = (0,5; 0; 1).
Nüüd käsitleme BF-vektorit. Samamoodi analüüsime punkte B = (1; 0; 0) ja F = (1; 0,5; 1), sest F - segmendi B 1 C 1 keskosa. Meil on:
BF = (1 - 1; 0,5 - 0; 1 - 0) = (0; 0,5; 1).
Niisiis, suunavektorid on valmis. Joontevahelise nurga koosinus on suunavektorite vahelise nurga koosinus, seega on meil:
Ülesanne. Korrapärases kolmnurkses prismas ABCA 1 B 1 C 1, mille kõik servad on võrdsed 1-ga, on märgitud punktid D ja E - vastavalt servade A 1 B 1 ja B 1 C 1 keskpunktid. Leidke nurk sirgete AD ja BE vahel.
Tutvustame standardset koordinaatsüsteemi: alguspunkt on punktis A, x-telg on suunatud piki AB, z - mööda AA 1 . Suuname y-telje nii, et OXY tasand langeb kokku ABC tasandiga. Ühiklõik on võrdne AB = 1. Leidke soovitud sirgete suunavektorite koordinaadid.
Kõigepealt leiame AD vektori koordinaadid. Vaatleme punkte: A = (0; 0; 0) ja D = (0,5; 0; 1), sest D - segmendi A 1 B 1 keskosa. Kuna vektori AD algus langeb kokku alguspunktiga, saame AD = (0,5; 0; 1).
Nüüd leiame vektori BE koordinaadid. Punkti B = (1; 0; 0) on lihtne arvutada. Punktiga E - segmendi keskpaik C 1 B 1 - on veidi keerulisem. Meil on:
Jääb üle leida nurga koosinus:
Ülesanne. Korrapärases kuusnurkses prismas ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, mille kõik servad on võrdsed 1-ga, on märgitud punktid K ja L - servade A 1 B 1 ja B 1 C 1 keskpunktid, vastavalt. Leidke sirgete AK ja BL vaheline nurk.
Tutvustame prisma standardset koordinaatide süsteemi: asetame koordinaatide alguspunkti alumise aluse keskele, suuname x-telje mööda FC-d, y-telje läbi lõikude AB ja DE keskpunktide ning z-telje. vertikaalselt ülespoole. Ühiklõik on jällegi võrdne AB = 1. Kirjutame välja meile huvipakkuvate punktide koordinaadid:
Punktid K ja L on vastavalt lõikude A 1 B 1 ja B 1 C 1 keskpunktid, seega leitakse nende koordinaadid läbi aritmeetilise keskmise. Teades punkte, leiame suunavektorite AK ja BL koordinaadid:
Nüüd leiame nurga koosinuse:
Ülesanne. Paremal nelinurkne püramiid SABCD, mille kõik servad on võrdsed 1-ga, on märgitud punktid E ja F - vastavalt külgede SB ja SC keskpunktid. Leidke nurk sirgete AE ja BF vahel.
Tutvustame standardset koordinaatsüsteemi: alguspunkt on punktis A, x- ja y-telg on suunatud vastavalt AB ja AD ning z-telg vertikaalselt ülespoole. Ühiku segment on võrdne AB = 1.
Punktid E ja F on vastavalt lõikude SB ja SC keskpunktid, seega leitakse nende koordinaadid otste aritmeetilise keskmisena. Kirjutame üles meile huvipakkuvate punktide koordinaadid:
A = (0; 0; 0); B = (1; 0; 0)
Teades punkte, leiame suunavektorite AE ja BF koordinaadid:
Vektori AE koordinaadid langevad kokku punkti E koordinaatidega, kuna punkt A on alguspunkt. Jääb üle leida nurga koosinus:
