İki kəsişən müstəvi arasındakı bucaq: tərif, tapma nümunələri. Düz xətlər arasındakı bucaq Düz xətlər arasında iti bucaq tapın

\(\blacktrianglerright\) Dihedral bucaq iki yarımmüstəvi və onların ümumi sərhədi olan \(a\) düz xəttinin yaratdığı bucaqdır.

\(\blacktrianglerright\) \(\xi\) və \(\pi\) müstəviləri arasındakı bucağı tapmaq üçün xətti bucağı tapmaq lazımdır. ədviyyatlı və ya düz) \(\xi\) və \(\pi\) müstəvilərinin yaratdığı dihedral bucağın:

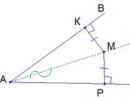
Addım 1: qoy \(\xi\cap\pi=a\) (təyyarələrin kəsişmə xətti). \(\xi\) müstəvisində ixtiyari nöqtəni qeyd edirik \(F\) və çəkirik \(FA\perp a\) ;

Addım 2: çəkmək \(FG\perp \pi\) ;

Addım 3: TTP-yə uyğun olaraq (\(FG\) - perpendikulyar, \(FA\) - oblique, \(AG\) - proyeksiya) bizdə: \(AG\perp a\) ;

Addım 4: \(\bucaq FAG\) bucağı \(\xi\) və \(\pi\) müstəvilərinin yaratdığı dihedral bucağın xətti bucağı adlanır.

Qeyd edək ki, \(AG\) üçbucaq düzbucaqlıdır.
Onu da qeyd edək ki, bu şəkildə qurulmuş \(AFG\) müstəvisi həm \(\xi\) və \(\pi\) müstəvilərinə perpendikulyardır. Buna görə də başqa cür də demək olar: təyyarələr arasındakı bucaq\(\xi\) və \(\pi\) iki kəsişən xətlər arasındakı bucaqdır \(c\in \xi\) və \(b\in\pi\) \(\xi\-ə perpendikulyar müstəvi təşkil edir. ), və \(\pi\) .

Tapşırıq 1 №2875

Tapşırıq səviyyəsi: İmtahandan daha çətindir

Bütün kənarları bərabər olan və əsası kvadrat olan dördbucaqlı bir piramida nəzərə alınmaqla. \(6\cos \alpha\) tapın, burada \(\alpha\) onun bitişik yan üzləri arasındakı bucaqdır.

\(SABCD\) kənarları \(a\) -ə bərabər olan verilmiş piramida (\(S\) təpədir) olsun. Buna görə də bütün yan üzlər bərabər bərabərtərəfli üçbucaqlardır. \(SAD\) və \(SCD\) üzləri arasındakı bucağı tapın.

Gəlin \(CH\perp SD\) çəkək. Çünki \(\üçbucaq SAD=\üçbucaq SCD\), onda \(AH\) da \(\üçbucaq SAD\) hündürlüyü olacaq. Buna görə də, tərifə əsasən, \(\bucaq AHC=\alfa\) \(SAD\) və \(SCD\) üzləri arasındakı xətti dihedral bucaqdır.
Baza kvadrat olduğundan, \(AC=a\sqrt2\) . Onu da qeyd edək ki, \(CH=AH\) tərəfi \(a\) olan bərabərtərəfli üçbucağın hündürlüyüdür, buna görə də \(CH=AH=\frac(\sqrt3)2a\) .
Sonra \(\üçbucaq AHC\) kosinus teoremi ilə: \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Cavab: -2

Tapşırıq 2 №2876

Tapşırıq səviyyəsi: İmtahandan daha çətindir

\(\pi_1\) və \(\pi_2\) müstəviləri kosinusu \(0,2\) -ə bərabər olan bucaq altında kəsişir. \(\pi_2\) və \(\pi_3\) müstəviləri düz bucaq altında kəsişir, \(\pi_1\) və \(\pi_2\) müstəvilərinin kəsişmə xətti isə kəsişmə xəttinə paraleldir. təyyarələr \(\pi_2\) və \(\ pi_3\) . \(\pi_1\) və \(\pi_3\) müstəviləri arasındakı bucağın sinusunu tapın.

\(\pi_1\) və \(\pi_2\) xətlərinin kəsişmə xətti \(a\) xətti, \(\pi_2\) və \(\pi_3\) kəsişmə xətti \ xətti olsun. (b\) , və kəsişmə xətti \(\pi_3\) və \(\pi_1\) düz xəttdir \(c\) . \(a\paralel b\) olduğundan, sonra \(c\paralel a\paralel b\) (“Kosmosda həndəsə” nəzəri istinad bölməsindən teoremə uyğun olaraq \(\sağ ox\) “Stereometriyaya giriş, paralellik”).

\(A\in a, B\in b\) nöqtələrini qeyd edin ki, \(AB\perp a, AB\perp b\) (bu mümkündür, çünki \(a\paralel b\) ). Qeyd edək ki, \(C\in c\) belə ki \(BC\perp c\) , deməli \(BC\perp b\) . Sonra \(AC\perp c\) və \(AC\perp a\) .
Həqiqətən, \(AB\perp b, BC\perp b\) olduğundan, \(b\) \(ABC\) müstəvisinə perpendikulyardır. \(c\paralel a\paralel b\) olduğundan, \(a\) və \(c\) xətləri də \(ABC\) müstəvisinə və deməli, bu müstəvidən istənilən xəttə, xüsusən də perpendikulyardır. , \ (AC\) xəttinə.

Buna görə də belə çıxır \(\bucaq BAC=\bucaq (\pi_1, \pi_2)\), \(\bucaq ABC=\bucaq (\pi_2, \pi_3)=90^\circ\), \(\bucaq BCA=\bucaq (\pi_3, \pi_1)\). Belə çıxır ki, \(\üçbucaq ABC\) düzbucaqlıdır, yəni \[\sin \bucaq BCA=\cos \bucaq BAC=0,2.\]

Cavab: 0.2

Tapşırıq 3 №2877

Tapşırıq səviyyəsi: İmtahandan daha çətindir

Verilmiş xətlər \(a, b, c\) bir nöqtədə kəsişir və onların hər ikisi arasındakı bucaq \(60^\circ\) -ə bərabərdir. \(\cos^(-1)\alpha\) tapın, burada \(\alpha\) \(a\) və \(c\) xətlərinin yaratdığı müstəvi ilə xətlərin yaratdığı müstəvi arasındakı bucaqdır. \(b\ ) və \(c\) . Cavabınızı dərəcələrlə verin.

Xətlərin \(O\) nöqtəsində kəsişməsinə icazə verin. Onların hər ikisi arasındakı bucaq \(60^\circ\) -ə bərabər olduğundan, hər üç xətt eyni müstəvidə uzana bilməz. \(a\) xəttində \(A\) nöqtəsini qeyd edək və \(AB\perp b\) və \(AC\perp c\) çəkək. Sonra \(\üçbucaq AOB=\üçbucaq AOC\) hipotenuzada və iti bucaqda düzbucaqlı kimi. Beləliklə, \(OB=OC\) və \(AB=AC\) .
Gəlin \(AH\perp (BOC)\) edək. Sonra üç perpendikulyar teoremlə \(HC\perp c\) , \(HB\perp b\) . \(AB=AC\) olduğundan \(\üçbucaq AHB=\üçbucaq AHC\) hipotenuz və ayaq boyunca düzbucaqlı kimi. Beləliklə, \(HB=HC\) . Beləliklə, \(OH\) ​​\(BOC\) bucağının bisektorudur (çünki \(H\) nöqtəsi bucağın tərəflərindən bərabər məsafədədir).

Qeyd edək ki, bu yolla biz \(a\) və \(c\) xətlərinin yaratdığı müstəvi ilə \(b\) və \( xətlərinin yaratdığı müstəvi ilə dihedral bucağın xətti bucağını da qurmuşuq. c\) . Bu \(ACH\) bucağıdır.

Gəlin bu küncü tapaq. Biz \(A\) nöqtəsini özbaşına seçdiyimiz üçün onu elə seçək ki, \(OA=2\) . Sonra düzbucaqlı \(\üçbucaq AOC\) şəklində: \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]\(OH\) ​​bissektrisa olduğundan, \(\bucaq HOC=30^\circ\) , buna görə də düzbucaqlı \(\üçbucaq HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Sonra düzbucaqlı \(\üçbucaq ACH\) dən: \[\cos\bucaq \alpha=\cos\bucaq ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Cavab: 3

Tapşırıq 4 № 2910

Tapşırıq səviyyəsi: İmtahandan daha çətindir

\(\pi_1\) və \(\pi_2\) təyyarələri \(M\) və \(N\) nöqtələrini ehtiva edən \(l\) xətti boyunca kəsişir. \(MA\) və \(MB\) seqmentləri \(l\) xəttinə perpendikulyardır və müvafiq olaraq \(\pi_1\) və \(\pi_2\) və \(MN = 15) müstəvilərində yerləşir. \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . \(3\cos\alpha\) tapın, burada \(\alpha\) \(\pi_1\) və \(\pi_2\) müstəviləri arasındakı bucaqdır.

\(AMN\) üçbucaq düzbucaqlıdır, \(AN^2 = AM^2 + MN^2\) , buradan \ \(BMN\) üçbucaq düzbucaqlıdır, \(BN^2 = BM^2 + MN^2\) , buradan \ \(AMB\) üçbucağı üçün kosinus teoremini yazırıq: \ Sonra \ Təyyarələr arasındakı \(\alpha\) bucaq iti bucaq olduğundan və \(\bucaq AMB\) küt olduğu üçün \(\cos\alpha=\dfrac5(12)\) . Sonra \

Cavab: 1.25

Tapşırıq 5 № 2911

Tapşırıq səviyyəsi: İmtahandan daha çətindir

\(ABCDA_1B_1C_1D_1\) paralelepipeddir, \(ABCD\) tərəfi \(a\) olan kvadratdır, \(M\) nöqtəsi \(A_1\) nöqtəsindən müstəviyə endirilmiş perpendikulyarın əsasıdır \ ((ABCD)\) , üstəlik, \(M\) kvadratın diaqonallarının kəsişmə nöqtəsidir \(ABCD\) . Məlumdur ki \(A_1M = \dfrac(\sqrt(3))(2)a\). \((ABCD)\) və \((AA_1B_1B)\) müstəviləri arasındakı bucağı tapın. Cavabınızı dərəcələrlə verin.

Şəkildə göstərildiyi kimi \(MN\) \(AB\) nöqtəsinə perpendikulyar qururuq.

\(ABCD\) tərəfi \(a\) və \(MN\perp AB\) və \(BC\perp AB\) olan kvadrat olduğundan, \(MN\paralel BC\) . \(M\) kvadratın diaqonallarının kəsişmə nöqtəsi olduğundan, \(M\) \(AC\) -in orta nöqtəsidir, ona görə də \(MN\) orta xətt Və \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) \(A_1N\) müstəvisinə proyeksiyasıdır \((ABCD)\) və \(MN\) \(AB\) müstəvisinə perpendikulyardır, onda üç perpendikulyar teoremlə \( A_1N\) \(AB \) -ə perpendikulyardır və \((ABCD)\) və \((AA_1B_1B)\) müstəviləri arasındakı bucaq \(\bucaq A_1NM\) -dir.
\[\mathrm(tg)\, \bucaq A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Sağ ox\qquad\bucaq A_1NM = 60^(\circ)\]

Cavab: 60

Tapşırıq 6 №1854

Tapşırıq səviyyəsi: İmtahandan daha çətindir

\(ABCD\) kvadratında: \(O\) diaqonalların kəsişmə nöqtəsidir; \(S\) kvadrat müstəvisində deyil, \(SO \perp ABC\) . \(SO = 5\) və \(AB = 10\) olduqda \(ASD\) və \(ABC\) müstəviləri arasındakı bucağı tapın.

Düzgün üçbucaqlar \(\üçbucaq SAO\) və \(\üçbucaq SDO\) iki tərəfdən bərabərdir və aralarındakı bucaq (\(SO \perp ABC\) \(\Rightarrow\) \(\bucaq SOA = \bucaq SOD = 90^\circ\); \(AO = DO\) , çünki \(O\) kvadratın diaqonallarının kəsişmə nöqtəsidir, \(SO\) ümumi tərəfdir) \(\Sağ ox\) \(AS = SD\) \(\Rightarrow\) \(\üçbucaq ASD\) ikitərəflidir. \(K\) nöqtəsi \(AD\) nöqtəsinin orta nöqtəsidir, sonra \(SK\) üçbucağın hündürlüyü \(\triangle ASD\) , \(OK\) isə üçbucağın hündürlüyüdür \ (AOD\) \(\ Sağarrow\) müstəvisi \(SOK\) \(ASD\) müstəvilərinə perpendikulyardır və \(ABC\) \(\Sağ ox\) \(\SKO bucağı) bərabər xətti bucaqdır tələb olunan dihedral bucağa.

\(\üçbucaq SKO\) içində: \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\üçbucaq SOK\) ikitərəfli düzbucaqlı üçbucaqdır \(\Rightarrow\) \(\bucaq SKO = 45^\circ\) .

Cavab: 45

Tapşırıq 7 №1855

Tapşırıq səviyyəsi: İmtahandan daha çətindir

\(ABCD\) kvadratında: \(O\) diaqonalların kəsişmə nöqtəsidir; \(S\) kvadrat müstəvisində deyil, \(SO \perp ABC\) . \(SO = 5\) və \(AB = 10\) olduqda \(ASD\) və \(BSC\) müstəviləri arasındakı bucağı tapın.

Düzgün üçbucaqlar \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) və \(\triangle SOC\) iki tərəfdən bərabərdir və onların arasındakı bucaq (\(SO \perp ABC) \) \(\Sağ ox\) \(\bucaq SOA = \bucaq SOD = \bucaq SOB = \bucaq SOC = 90^\circ\); \(AO = OD = OB = OC\) , çünki \(O\) kvadratın diaqonallarının kəsişmə nöqtəsidir, \(SO\) ümumi tərəfdir) \(\Sağ ox\) \(AS = DS = BS = CS\) \(\Sağ ox\) \(\üçbucaq ASD\) və \(\üçbucaq BSC\) ikitərəflidir. \(K\) nöqtəsi \(AD\) nöqtəsinin orta nöqtəsidir, sonra \(SK\) üçbucağın hündürlüyü \(\triangle ASD\) , \(OK\) isə üçbucağın hündürlüyüdür \ (AOD\) \(\ Sağarrow\) müstəvi \(SOK\) müstəvisinə perpendikulyardır \(ASD\) . \(L\) nöqtəsi \(BC\) nöqtəsinin orta nöqtəsidir, sonra \(SL\) üçbucağın hündürlüyü \(\triangle BSC\) , \(OL\) isə üçbucağın hündürlüyüdür \ (BOC\) \(\ Rightarrow\) müstəvi \(SOL\) (aka müstəvi \(SOK\) ) \(BSC\) müstəvisinə perpendikulyardır. Beləliklə, əldə edirik ki, \(\bucaq KSL\) istənilən dihedral bucağa bərabər olan xətti bucaqdır.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Sağ ox\) \(OL = 5\) ; \(SK = SL\) – hündürlüklər bərabərdir ikitərəfli üçbucaqlar Pifaqor teoremindən istifadə etməklə tapıla bilər: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Bunu görmək olar \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Sağ ox\) üçbucaq üçün \(\üçbucaq KSL\) tərs teorem Pifaqor \(\Sağ ox\) \(\üçbucaq KSL\) – düz üçbucaq \(\Sağ ox\) \(\KSL bucağı = 90^\circ\) .

Cavab: 90

Şagirdlərin riyaziyyatdan imtahana hazırlanması, bir qayda olaraq, təyyarələr arasındakı bucağı müəyyən etməyə imkan verən əsas düsturların təkrarlanması ilə başlayır. Bu həndəsə bölməsi çərçivəsində kifayət qədər ətraflı əhatə olunmasına baxmayaraq məktəb kurikulumu, bir çox məzun əsas materialı təkrarlamalıdır. Təyyarələr arasındakı bucağı necə tapacağını anlayan orta məktəb şagirdləri problemin həlli zamanı düzgün cavabı tez hesablaya və vahid dövlət imtahanı əsasında layiqli bal toplamağa arxalana biləcəklər.

Əsas nüanslar

Dihedral bucağı necə tapmaq sualının çətinlik yaratmaması üçün imtahan tapşırıqlarının öhdəsindən gəlməyə kömək edəcək həll alqoritminə əməl etməyi tövsiyə edirik.

Əvvəlcə təyyarələrin kəsişdiyi xətti müəyyənləşdirməlisiniz.

Sonra bu xəttdə bir nöqtə seçmək və ona iki perpendikulyar çəkmək lazımdır.

Növbəti addım tapmaqdır triqonometrik funksiya perpendikulyarların əmələ gətirdiyi dihedral bucaq. Küncün bir hissəsi olduğu ortaya çıxan üçbucağın köməyi ilə bunu etmək ən rahatdır.

Cavab bucağın qiyməti və ya onun triqonometrik funksiyası olacaq.

Şkolkovo ilə birlikdə imtahan testinə hazırlıq uğurunuzun açarıdır

Bir gün əvvəl dərs zamanı imtahandan keçmək bir çox tələbələr 2 təyyarə arasındakı bucağı hesablamağa imkan verən tərif və düsturların tapılması problemi ilə qarşılaşırlar. Məktəb dərsliyi həmişə lazım olduğu anda əlinizdə olmur. Lazımi düsturları və onların düzgün tətbiqi nümunələrini tapmaq, o cümlədən İnternetdə təyyarələr arasındakı bucağı tapmaq üçün bəzən çox vaxt sərf etməlisiniz.

"Şkolkovo" riyaziyyat portalı dövlət imtahanına hazırlaşmaq üçün yeni yanaşma təklif edir. Veb saytımızdakı dərslər tələbələrə özləri üçün ən çətin bölmələri müəyyənləşdirməyə və bilik boşluqlarını doldurmağa kömək edəcək.

Biz bütün lazımi materialları hazırlamışıq və aydın şəkildə təqdim etmişik. Əsas təriflər və düsturlar "Nəzəri istinad" bölməsində təqdim olunur.

Materialı daha yaxşı mənimsəmək üçün biz də müvafiq məşqlər etməyi təklif edirik. Müxtəlif mürəkkəblik dərəcələrində tapşırıqların böyük seçimi, məsələn, Kataloq bölməsində təqdim olunur. Bütün tapşırıqlarda düzgün cavabı tapmaq üçün ətraflı alqoritm var. Saytdakı məşqlərin siyahısı daim əlavə olunur və yenilənir.

İki müstəvi arasında bucağı tapmaq tələb olunan məsələlərin həllində məşq edən tələbələr istənilən tapşırığı onlayn olaraq “Sevimlilər”ə saxlamaq imkanı əldə edirlər. Bunun sayəsində onlar lazımi sayda ona qayıda və məktəb müəllimi və ya tərbiyəçi ilə onun həllinin gedişatını müzakirə edə biləcəklər.

Məqalədə təyyarələr arasındakı bucağı tapmaqdan bəhs edilir. Tərifi gətirdikdən sonra qrafik təsvir quracağıq, metodla koordinatları tapmaq üçün ətraflı metodu nəzərdən keçirəcəyik. Normal vektorların koordinatlarını ehtiva edən kəsişən müstəvilər üçün düstur alırıq.

Materialda kosmosda təyyarə və xətt haqqında məqalələrdə əvvəllər öyrənilmiş məlumat və anlayışlardan istifadə olunacaq. Başlamaq üçün, kəsişən iki təyyarə arasındakı bucağı təyin etmək üçün müəyyən bir yanaşmaya imkan verən əsaslandırmaya keçmək lazımdır.

İki kəsişən γ 1 və γ 2 müstəviləri verilmişdir. Onların kəsişməsi c təyinatını alacaq. χ müstəvisinin qurulması bu müstəvilərin kəsişməsi ilə bağlıdır. χ müstəvisi M nöqtəsindən c düz xətti kimi keçir. γ 1 və γ 2 müstəviləri χ müstəvisindən istifadə edərək kəsişəcək. a xətti üçün γ 1 və χ, b xətti üçün isə γ 2 və χ kəsişən xəttin təyinatlarını qəbul edirik. Alırıq ki, a və b xətlərinin kəsişməsi M nöqtəsini verir.

M nöqtəsinin yeri kəsişən a və b xətləri arasındakı bucağa təsir göstərmir və M nöqtəsi χ müstəvisinin keçdiyi c xəttində yerləşir.

c xəttinə perpendikulyar və χ müstəvisindən fərqli χ 1 müstəvisi qurmaq lazımdır. χ 1 köməyi ilə γ 1 və γ 2 təyyarələrinin kəsişməsi a 1 və b 1 xətlərinin təyinatını alacaq.

Görünür ki, χ və χ 1-i qurarkən a və b xətləri c xəttinə perpendikulyar, sonra a 1, b 1 c xəttinə perpendikulyar olur. c xəttinə perpendikulyarlığı olan γ 1 müstəvisində a və a 1 xətlərini tapsaq, onları paralel hesab etmək olar. Eyni şəkildə b və b 1-in c xəttinin perpendikulyarlığı ilə γ 2 müstəvisində yerləşməsi onların paralelliyini göstərir. Bu o deməkdir ki, χ 1 müstəvisini χ-ə paralel köçürmək lazımdır, burada iki üst-üstə düşən a və a 1 , b və b 1 xəttini alırıq. Alırıq ki, kəsişən a və b xətləri arasındakı bucaq 1-dir bucağa bərabərdir kəsişən a və b xətləri.

Aşağıdakı rəqəmi nəzərdən keçirin.

Bu mühakimə onunla sübut olunur ki, kəsişən a və b xətləri arasında M nöqtəsinin, yəni kəsişmə nöqtəsinin yerindən asılı olmayan bucaq var. Bu xətlər γ 1 və γ 2 müstəvilərində yerləşir. Əslində, yaranan bucağı kəsişən iki müstəvi arasındakı bucaq kimi düşünmək olar.

Mövcud kəsişən γ 1 və γ 2 müstəviləri arasındakı bucağı təyin etməyə davam edək.

Tərif 1

İki kəsişən müstəvi arasındakı bucaq γ 1 və γ 2γ 1 və γ 2 müstəvilərinin c xəttinə perpendikulyar olan χ müstəvisi ilə kəsişdiyi a və b xətlərinin kəsişməsindən yaranan bucağa deyilir.

Aşağıdakı rəqəmi nəzərdən keçirin.

Tərif başqa formada təqdim edilə bilər. γ 1 və γ 2 müstəvilərinin kəsişməsində, burada c onların kəsişdiyi xəttdir, c xəttinə perpendikulyar olan və γ 1 və γ 2 müstəvilərində uzanan a və b xətlərini çəkən M nöqtəsini qeyd edin. , onda a və b xətləri arasındakı bucaq müstəvilər arasındakı bucaq olacaqdır. Təcrübədə bu, təyyarələr arasında bucaq qurmaq üçün tətbiq olunur.

Kəsişmədə dəyəri 90 dərəcədən az olan bucaq əmələ gəlir, yəni bucağın dərəcə ölçüsü bu tip intervalda (0, 90] keçərlidir. Eyni zamanda bu müstəvilərə perpendikulyar deyilir. kəsişməsində düz bucaq yaranarsa.paralel müstəvilər arasındakı bucaq sıfıra bərabər hesab edilir.

Kəsişən təyyarələr arasındakı bucağı tapmağın adi yolu əlavə konstruksiyaların yerinə yetirilməsidir. Bu, onu dəqiqliklə müəyyən etməyə kömək edir və bu, üçbucağın bərabərlik və ya oxşarlıq əlamətlərindən, sinuslardan, bucağın kosinuslarından istifadə etməklə edilə bilər.

C 2 blokunun Vahid Dövlət İmtahanının problemlərindən bir nümunə istifadə edərək problemlərin həllini nəzərdən keçirin.

Misal 1

Düzbucaqlı paralelepiped A B C D A 1 B 1 C 1 D 1 verilir, burada A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, E nöqtəsi A A 1 tərəfini 4: 3 nisbətində ayırır. A B C və B E D müstəviləri arasındakı bucağı tapın 1 .

Həll

Aydınlıq üçün bir rəsm çəkməlisiniz. Bunu anlayırıq

Təyyarələr arasındakı bucaqla işləməyi daha rahat etmək üçün vizual təsvir lazımdır.

A B C və B E D 1 müstəvilərinin kəsişdiyi düz xəttin tərifini edirik. B nöqtəsi ümumi nöqtədir. Başqasını tapmaq lazımdır ortaq nöqtə kəsişmələr. Eyni müstəvidə yerləşən D A və D 1 E xətlərini nəzərdən keçirək A D D 1 . Onların yeri paralelliyi göstərmir, yəni ümumi kəsişmə nöqtəsi var.

Bununla belə, D A xətti A B C müstəvisində, D 1 E isə B E D 1 müstəvisində yerləşir. Beləliklə, xətləri əldə edirik D A Və D 1 E A B C və B E D 1 müstəviləri üçün də ümumi olan ümumi kəsişmə nöqtəsi var. Xətlərin kəsişmə nöqtəsini göstərir D A və D 1 E F hərfi. Buradan alırıq ki, B F A B C və B E D 1 müstəvilərinin kəsişdiyi düz xəttdir.

Aşağıdakı rəqəmi nəzərdən keçirin.

Cavab almaq üçün B F xəttində yerləşən və ona perpendikulyar olan nöqtədən keçməklə A B C və B E D 1 müstəvilərində yerləşən düz xətlər çəkmək lazımdır. Sonra bu xətlər arasında yaranan bucaq A B C və B E D 1 müstəviləri arasında istənilən bucaq hesab olunur.

Buradan görünür ki, A nöqtəsi E nöqtəsinin AB C müstəvisinə proyeksiyasıdır. BF xəttini M nöqtəsində düz bucaq altında kəsən xətt çəkmək lazımdır. AM həmin AM ⊥ BF perpendikulyarları haqqında teoremə əsaslanan EM xəttinin ABC müstəvisinə proyeksiyasıdır. Aşağıdakı rəqəmi nəzərdən keçirin.

∠ A M E A B C və B E D 1 müstəvilərinin yaratdığı istənilən bucaqdır. Yaranan A E M üçbucağından bucağın sinusunu, kosinusunu və ya tangensini, ondan sonra bucağın özünü yalnız iki məlum tərəfi ilə tapa bilərik. Şərtlə, AE-nin uzunluğunun bu şəkildə tapılmasına sahibik: AA 1 xətti E nöqtəsinə 4: 3 nisbətində bölünür, yəni xəttin ümumi uzunluğu 7 hissədir, sonra AE \u003d 4 hissə. A.M.

Düzbucaqlı A B F üçbucağını nəzərdən keçirmək lazımdır. Hündürlüyü A M olan düz A bucağımız var. A B \u003d 2 şərtindən sonra D D 1 F və A E F üçbucaqlarının oxşarlığına görə A F uzunluğunu tapa bilərik. Alırıq ki, A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Pifaqor teoremindən istifadə edərək A B F üçbucağından B F tərəfinin uzunluğunu tapmaq lazımdır. Alırıq ki, B F   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . A M tərəfinin uzunluğu A B F üçbucağının sahəsi ilə tapılır. Bizdə var ki, sahə həm S A B C = 1 2 · A B · A F, həm də S A B C = 1 2 · B F · A M -ə bərabər ola bilər.

Alırıq ki, A M = A B A F B F = 2 4 2 5 = 4 5 5

Onda A E M üçbucağının bucağının tangensinin qiymətini tapa bilərik. Alırıq:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

A B C və B E D 1 müstəvilərinin kəsişməsindən alınan arzu olunan bucaq a r c t g 5-ə bərabərdir, onda sadələşdirildikdə r c t g 5 = a r c sin 30 6 = a r c cos 6 6 alırıq.

Cavab: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

istifadə edərək kəsişən xətlər arasındakı bucağı tapmaq üçün bəzi hallar verilmişdir koordinat müstəvisi x y z və koordinat metodu haqqında. Daha ətraflı nəzərdən keçirək.

Əgər kəsişən γ 1 və γ 2 müstəviləri arasındakı bucağı tapmaq lazım olan yerdə məsələ verilirsə, istənilən bucağı α ilə işarə edirik.

Onda verilmiş koordinat sistemi göstərir ki, bizdə kəsişən γ 1 və γ 2 müstəvilərinin normal vektorlarının koordinatları var. Sonra işarə edirik ki, n 1 → = n 1 x, n 1 y, n 1 z müstəvinin normal vektoru γ 1 , və n 2 → = (n 2 x , n 2 y , n 2 z) - üçün təyyarə γ 2. Vektorların koordinatlarına uyğun olaraq bu müstəvilər arasında yerləşən bucağın ətraflı tapılmasını nəzərdən keçirək.

γ 1 və γ 2 müstəvilərinin c hərfi ilə kəsişdiyi düz xətti təyin etmək lazımdır. Xəttdə M nöqtəsi var, onun vasitəsilə c-yə perpendikulyar χ müstəvisi çəkirik. a və b xətləri boyunca χ müstəvisi M nöqtəsində γ 1 və γ 2 müstəviləri ilə kəsişir. tərifdən belə çıxır ki, kəsişən γ 1 və γ 2 müstəviləri arasındakı bucaq müvafiq olaraq bu müstəvilərə aid olan a və b kəsişən xətlərin bucağına bərabərdir.

χ müstəvisində M nöqtəsindən normal vektorları kənara qoyuruq və onları n 1 → və n 2 → işarələyirik. n 1 → vektoru a xəttinə perpendikulyar, n 2 → vektoru isə b xəttinə perpendikulyar olan xətt üzərində yerləşir. Beləliklə, biz bunu əldə edirik verilmiş təyyarəχ a xəttinin normal vektoru n 1 → və b düz xətti üçün n 2 → -ə bərabərdir. Aşağıdakı rəqəmi nəzərdən keçirin.

Buradan vektorların koordinatlarından istifadə edərək kəsişən xətlərin bucağının sinusunu hesablaya biləcəyimiz bir düstur alırıq. Biz müəyyən etdik ki, a və b xətləri arasındakı bucağın kosinusu kəsişən γ 1 və γ 2 müstəviləri arasındakı kosinusla eynidir cos α = cos n 1 → , n 2 → ^ = n 1 xn düsturundan alınır. 2 x + n 1 y n 2 y + n 1 z n 2 zn 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , burada n 1 → = (n 1 x , n 1 y , n 1 z) və n 2 → = (n 2 x , n 2 y , n 2 z) təmsil olunan müstəvilərin vektorlarının koordinatlarıdır.

Düsturdan istifadə edərək kəsişən xətlər arasındakı bucaq hesablanır

α = qövs cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 zn 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Misal 2

Şərtlə paralelepiped А В С D A 1 B 1 C 1 D 1 verilir , burada A B \u003d 2, A D \u003d 3, A A 1 \u003d 7 və E nöqtəsi A A 1 4: 3 tərəfini ayırır. A B C və B E D müstəviləri arasındakı bucağı tapın 1 .

Həll

Onun tərəflərinin qoşa perpendikulyar olması şərtindən də görünür. Bu o deməkdir ki, C nöqtəsində təpəsi olan O x y z koordinat sistemini və O x, O y, O z koordinat oxlarını tətbiq etmək lazımdır. İstiqaməti uyğun tərəflərə qoymaq lazımdır. Aşağıdakı rəqəmi nəzərdən keçirin.

Kəsişən təyyarələr A B C Və B E D 1 2 x 2 + n 2 y 2 + n 2 z 2 düsturu ilə tapıla bilən bucaq əmələ gətirir, burada n 1 → = (n 1 x , n 1 y , n 1 z) və n 2 → = (n) 2 x , n 2 y , n 2 z ) bu müstəvilərin normal vektorlarıdır. Koordinatları müəyyən etmək lazımdır. Şəkildən görürük ki, O x y koordinat oxu A B C müstəvisində üst-üstə düşür, bu o deməkdir ki, normal k → vektorunun koordinatları n 1 → = k → = (0, 0, 1) qiymətinə bərabərdir.

B E D 1 müstəvisinin normal vektoru B E → və B D 1 → -nin vektor məhsuludur, burada onların koordinatları koordinatlarla tapılır. ekstremal nöqtələr Problemin vəziyyətinə əsasən təyin olunan B, E, D 1.

B (0 , 3 , 0) , D 1 (2 , 0 , 7) alırıq. A E E A 1 = 4 3 olduğu üçün A 2, 3, 0, A 1 2, 3, 7 nöqtələrinin koordinatlarından E 2, 3, 4 nöqtələrini tapırıq. Alırıq ki, BE → = (2 , 0 , 4) , BD 1 → = 2 , - 3 , 7 n 2 → = BE → × BD 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Tapılmış koordinatları qövs kosinusu vasitəsilə bucağı hesablamaq üçün düsturla əvəz etmək lazımdır. alırıq

α = arc cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = arc cos 6 6 6 = arc cos 6 6

Koordinat metodu oxşar nəticə verir.

Cavab: a r c cos 6 6 .

Müstəvilərin mövcud məlum tənlikləri ilə kəsişən müstəvilər arasındakı bucağı tapmaq üçün yekun məsələ nəzərdən keçirilir.

Misal 3

O xyz koordinat sistemində təyin olunan və 2 x - 4 y + z + 1 = 0 və 3 y - tənlikləri ilə verilən bucağın sinusunu, kosinusunu və kəsişən iki xəttin yaratdığı bucağın qiymətini hesablayın. z - 1 = 0.

Həll

A x + B y + C z + D = 0 formalı düz xəttin ümumi tənliyi mövzusu öyrənilərkən məlum olmuşdur ki, A, B, C normal vektorun koordinatlarına bərabər olan əmsallardır. Deməli, n 1 → = 2 , - 4 , 1 və n 2 → = 0 , 3 , - 1 verilmiş xətlərin normal vektorlarıdır.

Təyyarələrin normal vektorlarının koordinatlarını kəsişən müstəvilərin istənilən bucağını hesablamaq üçün düsturla əvəz etmək lazımdır. Sonra bunu anlayırıq

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Deməli, bucağın kosinusu cos α = 13 210 formasını alır. Onda kəsişən xətlərin bucağı küt deyil. Triqonometrik eyniliyi əvəz edərək, bucağın sinusunun dəyərinin ifadəyə bərabər olduğunu alırıq. Hesablayırıq və alırıq

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Cavab: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Mətndə səhv görsəniz, onu vurğulayın və Ctrl+Enter düymələrini basın

Enjeksiyon φ ümumi tənliklər A 1 x + B 1 y + C 1 = 0 və A 2 x + B 2 y + C 2 = 0, düsturla hesablanır:

Enjeksiyon φ iki düz xətt arasında kanonik tənliklər(x-x 1) / m 1 \u003d (y-y 1) / n 1 və (x-x 2) / m 2 \u003d (y-y 2) / n 2, düsturla hesablanır:

Nöqtədən xəttə qədər olan məsafə

Kosmosdakı hər bir müstəvi kimi təmsil oluna bilər xətti tənlikçağırdı ümumi tənlik təyyarə

Xüsusi hallar.

o (8) tənliyindədirsə, müstəvi başlanğıc nöqtəsindən keçir.

o (,) ilə müstəvi müvafiq olaraq oxa (ox, ox) paraleldir.

o (,) müstəvi müstəviyə paralel olduqda(təyyarə, müstəvi).

Həll yolu: istifadə edin (7)

Cavab: təyyarənin ümumi tənliyi.

Misal.

Oxyz düzbucaqlı koordinat sistemindəki müstəvi təyyarənin ümumi tənliyi ilə verilir. . Bu müstəvidə bütün normal vektorların koordinatlarını yazın.

Biz bilirik ki, müstəvinin ümumi tənliyində x, y və z dəyişənlərinin əmsalları həmin müstəvinin normal vektorunun uyğun koordinatlarıdır. Buna görə də verilmiş müstəvinin normal vektoru koordinatlarına malikdir. Bütün normal vektorların çoxluğu kimi verilə bilər.

Düzbucaqlı koordinat sistemində Oxyz fəzada bir nöqtədən keçirsə, təyyarənin tənliyini yazın. , Amma bu müstəvinin normal vektorudur.

Bu problemin iki həllini təqdim edirik.

Bizdə olan şəraitdən. Bu məlumatları nöqtədən keçən təyyarənin ümumi tənliyinə əvəz edirik:

Oyz koordinat müstəvisinə paralel və nöqtədən keçən müstəvi üçün ümumi tənliyi yazın. .

Oyz koordinat müstəvisinə paralel olan müstəvi formanın müstəvisinin ümumi natamam tənliyi ilə verilə bilər. Məsələdən bəri şərtlə müstəviyə aiddir, onda bu nöqtənin koordinatları müstəvi tənliyini təmin etməlidir, yəni bərabərlik doğru olmalıdır. Buradan tapırıq. Beləliklə, istənilən tənlik formaya malikdir.

Həll. 10.26 tərifinə görə vektor məhsulu p və q vektorlarına ortoqonaldır. Buna görə də o, istənilən müstəviyə ortoqonaldır və vektor onun normal vektoru kimi götürülə bilər. n vektorunun koordinatlarını tapın:

yəni . (11.1) düsturundan istifadə edərək əldə edirik

Bu tənlikdəki mötərizələri açaraq son cavaba gəlirik.

Cavab: .

Normal vektoru formada yenidən yazaq və uzunluğunu tapaq:

Yuxarıda göstərilənlərə əsasən:

Cavab verin:

Paralel təyyarələrin eyni normal vektoru var. 1) Tənlikdən təyyarənin normal vektorunu tapırıq:.

2) Nöqtə və normal vektora görə müstəvi tənliyini tərtib edirik:

Cavab verin:

Kosmosda təyyarənin vektor tənliyi

Kosmosda müstəvinin parametrik tənliyi

Verilmiş vektora perpendikulyar verilmiş nöqtədən keçən müstəvi tənliyi

İcazə verin üçölçülü məkan düzbucaqlı Dekart koordinat sistemi müəyyən edilmişdir. Aşağıdakı problemi formalaşdıraq:

Verilmiş nöqtədən keçən müstəvi üçün tənlik yazın M(x 0, y 0, z 0) verilmiş vektora perpendikulyar n = ( A, B, C} .

Həll. Qoy olsun P(x, y, z) fəzada ixtiyari nöqtədir. Nöqtə P vektor olduğu halda müstəviyə aiddir millət vəkili = {x − x 0, y − y 0, z − z 0) vektora ortoqonal n = {A, B, C) (Şəkil 1).

Bu vektorlar üçün ortoqonallıq şərtini yazaraq (n, millət vəkili) = 0 koordinat şəklində alırıq:

A(x − x 0) + B(y − y 0) + C(z − z 0) = 0

Təyyarənin üç nöqtəli tənliyi

Vektor şəklində

Koordinatlarda

Kosmosda təyyarələrin qarşılıqlı yerləşməsi

iki təyyarənin ümumi tənlikləridir. Sonra:

1) əgər , sonra təyyarələr üst-üstə düşür;

2) əgər , onda təyyarələr paraleldir;

3) və ya olarsa, müstəvilər kəsişir və tənliklər sistemi

(6)

verilmiş müstəvilərin kəsişmə xəttinin tənlikləridir.

Həll: Düz xəttin kanonik tənliklərini düsturla tərtib edirik: Cavab verin:

Yaranan tənlikləri götürürük və zehni olaraq "bağlayırıq", məsələn, sol parça: . İndi bu parçanı bərabərləşdiririk istənilən nömrəyə(xatırlayın ki, artıq sıfır var idi), məsələn, birinə: . Çünki , onda digər iki "parça" da birinə bərabər olmalıdır. Əsasən, sistemi həll etməlisiniz:

Aşağıdakı sətirlər üçün parametrik tənlikləri yazın:

Həll: Xətlər kanonik tənliklərlə verilir və birinci mərhələdə xəttə və onun istiqamət vektoruna aid olan nöqtə tapmaq lazımdır.

a) Tənliklərdən nöqtəni və istiqamət vektorunu çıxarın: . Başqa bir nöqtə seçə bilərsiniz (bunu necə etmək yuxarıda təsvir edilmişdir), lakin ən bariz olanı götürmək daha yaxşıdır. Yeri gəlmişkən, səhvlərdən qaçınmaq üçün həmişə onun koordinatlarını tənliklərdə əvəz edin.

Bu düz xəttin parametrik tənliklərini tərtib edək:

Parametrik tənliklərin rahatlığı ondan ibarətdir ki, onların köməyi ilə xəttin digər nöqtələrini tapmaq çox asandır. Məsələn, koordinatları parametrin dəyərinə uyğun gələn bir nöqtə tapaq:

Beləliklə: b) Kanonik tənlikləri nəzərdən keçirək . Burada bir nöqtənin seçimi sadədir, lakin məkrlidir: (koordinatları qarışdırmamağa diqqət yetirin!!!). Bələdçi vektorunu necə çıxarmaq olar? Bu xəttin nəyə paralel olduğunu təxmin edə bilərsiniz və ya sadə formal hiylədən istifadə edə bilərsiniz: nisbət "Y" və "Z"dir, ona görə də istiqamət vektorunu yazırıq və qalan boşluğa sıfır qoyuruq: .

Düz xəttin parametrik tənliklərini tərtib edirik:

c) Tənlikləri formada yenidən yazaq, yəni "Z" hər şey ola bilər. Və əgər varsa, o zaman, məsələn, . Beləliklə, nöqtə bu xəttə aiddir. İstiqamət vektorunu tapmaq üçün aşağıdakı formal texnikadan istifadə edirik: ilkin tənliklərdə "x" və "y" var və bu yerlərdə istiqamət vektorunu yazırıq. sıfırlar: . Qalan yerə qoyuruq vahid: . Bir əvəzinə, sıfırdan başqa hər hansı bir rəqəm edəcək.

Düz xəttin parametrik tənliklərini yazırıq:

künc kosmosdakı düz xətlər arasında verilənlərə paralel ixtiyari bir nöqtədən çəkilmiş iki düz xəttin yaratdığı hər hansı bir bitişik bucaq adlandıracağıq.

Kosmosda iki düz xətt verilsin:

Aydındır ki, xətlər arasındakı φ bucağı onların istiqamət vektorları və arasındakı bucaq kimi qəbul edilə bilər. dan bəri, onda vektorlar arasındakı bucağın kosinusu üçün düstura görə alırıq

İki xəttin paralellik və perpendikulyarlıq şərtləri onların istiqamət vektorlarının paralellik və perpendikulyarlıq şərtlərinə ekvivalentdir və:

İki düz paraleldirlər yalnız və yalnız onların müvafiq əmsalları mütənasib olduqda, yəni. l 1 paralel l 2 və yalnız paralel olarsa .

İki düz perpendikulyar yalnız və yalnız müvafiq əmsalların hasillərinin cəmi sıfıra bərabər olduqda: .

At xətt və təyyarə arasında məqsəd

Qoy xətt d- θ müstəvisinə perpendikulyar deyil;
d′− düz xəttin proyeksiyası dθ təyyarəsinə;
Düz xətlər arasındakı bucaqların ən kiçiki d Və d' zəng edəcəyik xətt və müstəvi arasındakı bucaq.
Onu φ=( kimi işarə edək d,θ)
Əgər d⊥θ , onda ( d,θ)=π/2

Oi→j→k→− düzbucaqlı koordinat sistemi.
Müstəvi tənliyi:

θ: balta+By+cz+D=0

Xəttin nöqtə və istiqamət vektoru ilə verildiyini hesab edirik: d[M 0,səh→]
Vektor n→(A,B,C)⊥θ
Sonra vektorlar arasındakı bucağı tapmaq qalır n→ və səh→, onu γ=( kimi işarələyin n→,səh→).

Əgər bucaq γ<π/2 , то искомый угол φ=π/2−γ .

Əgər bucaq γ>π/2 , onda tələb olunan bucaq φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Sonra, xətt və müstəvi arasındakı bucaq düsturla hesablana bilər:

sinφ=∣cosγ∣=∣ ∣ Ap 1+bp 2+cp 3∣ ∣ √A 2+B 2+C 2√səh 21+səh 22+səh 23

Sual 29. Kvadrat forma anlayışı. Kvadrat formaların işarə-müəyyənliyi.

Kvadrat forma j (x 1, x 2, ..., x n) n real dəyişənlər x 1, x 2, ..., x n formanın cəmi adlanır
, (1)

harada aij əmsal adlanan bəzi ədədlərdir. Ümumiliyi itirmədən bunu güman edə bilərik aij = bir ji.

Kvadrat forma deyilir etibarlı,əgər aij О GR. Kvadrat formanın matrisiəmsallarından ibarət matris adlanır. Kvadrat forma (1) unikal simmetrik matrisə uyğun gəlir
yəni. A T = A. Buna görə də (1) kvadrat forması j () matris şəklində yazıla bilər. X) = x T Ah, harada x T = (X 1 X 2 … x n). (2)

Və əksinə, istənilən simmetrik matris (2) dəyişənlərin qeydinə qədər unikal kvadrat formaya uyğun gəlir.

Kvadrat formanın rütbəsi onun matrisinin dərəcəsi adlanır. Kvadrat forma deyilir degenerativ olmayan,əgər onun matrisi tək deyilsə AMMA. (xatırlayın ki, matris AMMA determinantı sıfırdan fərqli olarsa qeyri-degenerativ adlanır). Əks halda, kvadrat forma degenerativ olur.

müsbət müəyyən(və ya ciddi müsbət) əgər

j ( X) > 0 , hər kəs üçün X = (X 1 , X 2 , …, x n), istisna olmaqla X = (0, 0, …, 0).

Matris AMMA müsbət müəyyən kvadrat forma j ( X) müsbət təyin də deyilir. Buna görə də müsbət müəyyən kvadrat forma unikal müsbət müəyyən matrisə uyğun gəlir və əksinə.

Kvadrat forma (1) adlanır mənfi müəyyən(və ya ciddi mənfi) əgər

j ( X) < 0, для любого X = (X 1 , X 2 , …, x n), istisna olmaqla X = (0, 0, …, 0).

Yuxarıdakı kimi, mənfi-müəyyən kvadratik matris də mənfi müəyyən adlanır.

Buna görə də müsbət (mənfi) müəyyən kvadrat forma j ( X) minimum (maksimum) qiymətə çatır j ( X*) = 0 üçün X* = (0, 0, …, 0).

Qeyd edək ki, kvadrat formaların əksəriyyəti işarə-müəyyən deyil, yəni nə müsbət, nə də mənfidir. Belə kvadrat formalar təkcə koordinat sisteminin başlanğıcında deyil, digər nöqtələrdə də yox olur.

Nə vaxt n> 2, kvadrat formanın işarə-müəyyənliyini yoxlamaq üçün xüsusi meyarlar tələb olunur. Gəlin onları nəzərdən keçirək.

Böyük Azyaşlılar kvadrat forma kiçik adlanır:

yəni bunlar 1, 2, … dərəcəli yetkinlik yaşına çatmayanlardır. n matrislər AMMA, yuxarı sol küncdə yerləşir, onlardan sonuncusu matrisin determinantı ilə üst-üstə düşür AMMA.

Müsbət müəyyənlik meyarı (Silvester meyarı)

X) = x T Ah müsbət müəyyəndir, matrisin bütün əsas kiçiklərinin olması zəruri və kifayətdir AMMA müsbət idi, yəni: M 1 > 0, M 2 > 0, …, M n > 0. Mənfi əminlik meyarı Kvadrat forma üçün j ( X) = x T Ah mənfi müəyyəndir, zəruri və kafidir ki, onun cüt düzənli əsas kiçikləri müsbət, tək düzənliləri isə mənfi olsun, yəni: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

Qısa danışacağam. İki xətt arasındakı bucaq onların istiqamət vektorları arasındakı bucağa bərabərdir. Beləliklə, a \u003d (x 1; y 1; z 1) və b \u003d (x 2; y 2; z 2) istiqamət vektorlarının koordinatlarını tapa bilsəniz, bucağı tapa bilərsiniz. Daha dəqiq desək, düstura görə bucağın kosinusu:

Bu düsturun konkret nümunələrdə necə işlədiyini görək:

Bir tapşırıq. E və F nöqtələri ABCDA 1 B 1 C 1 D 1 kubunda qeyd olunur - müvafiq olaraq A 1 B 1 və B 1 C 1 kənarlarının orta nöqtələri. AE və BF xətləri arasındakı bucağı tapın.

Kubun kənarı göstərilmədiyi üçün biz AB = 1 təyin edirik. Standart koordinat sistemini təqdim edirik: başlanğıc nöqtəsi A nöqtəsindədir və x, y, z oxları müvafiq olaraq AB, AD və AA 1 boyunca yönəldilmişdir. . Vahid seqment AB = 1-ə bərabərdir. İndi xətlərimiz üçün istiqamət vektorlarının koordinatlarını tapaq.

AE vektorunun koordinatlarını tapın. Bunun üçün bizə A = (0; 0; 0) və E = (0,5; 0; 1) nöqtələri lazımdır. E nöqtəsi A 1 B 1 seqmentinin ortası olduğundan onun koordinatları ucların koordinatlarının arifmetik ortasına bərabərdir. Qeyd edək ki, AE vektorunun mənşəyi mənbə ilə üst-üstə düşür, ona görə də AE = (0,5; 0; 1).

İndi BF vektoru ilə məşğul olaq. Eynilə, B = (1; 0; 0) və F = (1; 0.5; 1) nöqtələrini təhlil edirik, çünki F - B 1 C 1 seqmentinin ortası. Bizdə:
BF = (1 - 1; 0,5 - 0; 1 - 0) = (0; 0,5; 1).

Beləliklə, istiqamət vektorları hazırdır. Xətlər arasındakı bucağın kosinusu istiqamət vektorları arasındakı bucağın kosinusudur, buna görə də biz var:

Bir tapşırıq. Bütün kənarları 1-ə bərabər olan müntəzəm üçbucaqlı ABCA 1 B 1 C 1 prizmasında D və E nöqtələri qeyd olunur - müvafiq olaraq A 1 B 1 və B 1 C 1 kənarlarının orta nöqtələri. AD və BE xətləri arasındakı bucağı tapın.

Standart koordinat sistemini təqdim edək: mənşəyi A nöqtəsindədir, x oxu AB boyunca, z - AA 1 boyunca yönəldilmişdir. Y oxunu elə istiqamətləndiririk ki, OXY müstəvisi ABC müstəvisi ilə üst-üstə düşsün. Vahid seqment AB = 1-ə bərabərdir. İstənilən xətlər üçün istiqamət vektorlarının koordinatlarını tapın.

Əvvəlcə AD vektorunun koordinatlarını tapaq. Nöqtələrə nəzər salın: A = (0; 0; 0) və D = (0.5; 0; 1), çünki D - seqmentin ortası A 1 B 1 . AD vektorunun başlanğıcı mənbə ilə üst-üstə düşdüyündən AD = (0,5; 0; 1) alırıq.

İndi BE vektorunun koordinatlarını tapaq. B nöqtəsini = (1; 0; 0) hesablamaq asandır. E nöqtəsi ilə - C 1 B 1 seqmentinin ortası - bir az daha mürəkkəbdir. Bizdə:

Bucağın kosinusunu tapmaq qalır:

Bir tapşırıq. Bütün kənarları 1-ə bərabər olan müntəzəm altıbucaqlı ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 prizmasında K və L nöqtələri qeyd olunur - A 1 B 1 və B 1 C 1 kənarlarının orta nöqtələri, müvafiq olaraq. AK və BL xətləri arasındakı bucağı tapın.

Prizma üçün standart koordinat sistemini təqdim edirik: koordinatların mənşəyini aşağı bazanın mərkəzinə yerləşdiririk, x oxunu FC boyunca, y oxunu AB və DE seqmentlərinin orta nöqtələri vasitəsilə və z oxunu istiqamətləndiririk. şaquli yuxarı. Vahid seqment yenidən AB = 1-ə bərabərdir. Bizi maraqlandıran nöqtələrin koordinatlarını yazaq:

K və L nöqtələri müvafiq olaraq A 1 B 1 və B 1 C 1 seqmentlərinin orta nöqtələridir, ona görə də onların koordinatları arifmetik orta ilə tapılır. Nöqtələri bilməklə AK və BL istiqamət vektorlarının koordinatlarını tapırıq:

İndi bucağın kosinusunu tapaq:

Bir tapşırıq. Sağda dördbucaqlı piramida Bütün kənarları 1-ə bərabər olan SABCD, E və F nöqtələri qeyd olunur - müvafiq olaraq SB və SC tərəflərinin orta nöqtələri. AE və BF xətləri arasındakı bucağı tapın.

Standart koordinat sistemini təqdim edirik: mənşəyi A nöqtəsindədir, x və y oxları müvafiq olaraq AB və AD boyunca, z oxu isə şaquli olaraq yuxarıya doğru yönəldilmişdir. Vahid seqment AB = 1-ə bərabərdir.

E və F nöqtələri müvafiq olaraq SB və SC seqmentlərinin orta nöqtələridir, ona görə də onların koordinatları uçların arifmetik ortası kimi tapılır. Bizi maraqlandıran nöqtələrin koordinatlarını yazırıq:
A = (0; 0; 0); B = (1; 0; 0)

Nöqtələri bilməklə AE və BF istiqamət vektorlarının koordinatlarını tapırıq:

AE vektorunun koordinatları E nöqtəsinin koordinatları ilə üst-üstə düşür, çünki A nöqtəsi başlanğıcdır. Bucağın kosinusunu tapmaq qalır: