How to learn to solve derivatives of a complex function. Find the derivative: algorithm and examples of solutions. "Unpacking" a complex function

The operation of finding a derivative is called differentiation.

As a result of solving problems of finding derivatives of the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716) were the first to work in the field of finding derivatives.

Therefore, in our time, in order to find the derivative of any function, it is not necessary to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but only need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.

To find the derivative, you need an expression under the stroke sign break down simple functions and determine what actions (product, sum, quotient) these functions are related. Further, we find the derivatives of elementary functions in the table of derivatives, and the formulas for the derivatives of the product, sum and quotient - in the rules of differentiation. The table of derivatives and differentiation rules are given after the first two examples.

Example 1 Find the derivative of a function

Decision. From the rules of differentiation we find out that the derivative of the sum of functions is the sum of derivatives of functions, i.e.

From the table of derivatives, we find out that the derivative of "X" is equal to one, and the derivative of the sine is cosine. We substitute these values in the sum of derivatives and find the derivative required by the condition of the problem:

Example 2 Find the derivative of a function

Decision. Differentiate as a derivative of the sum, in which the second term with a constant factor, it can be taken out of the sign of the derivative:

If there are still questions about where something comes from, they, as a rule, become clear after reading the table of derivatives and the simplest rules of differentiation. We are going to them right now.

Table of derivatives of simple functions

1. Derivative of a constant (number). Any number (1, 2, 5, 200...) that is in the function expression. Always zero. This is very important to remember, as it is required very often
2. Derivative of the independent variable. Most often "x". Always equal to one. This is also important to remember
3. Derivative of degree. When solving problems, you need to convert non-square roots to a power.
4. Derivative of a variable to the power of -1
5. Derivative square root
6. Sine derivative
7. Cosine derivative
8. Tangent derivative
9. Derivative of cotangent
10. Derivative of the arcsine
11. Derivative of arc cosine
12. Derivative of arc tangent
13. Derivative of the inverse tangent
14. Derivative of natural logarithm
15. Derivative of a logarithmic function
16. Derivative of the exponent
17. Derivative of exponential function

Differentiation rules

1. Derivative of the sum or difference
2. Derivative of a product
2a. Derivative of an expression multiplied by a constant factor
3. Derivative of the quotient
4. Derivative of a complex function

Rule 1If functions

are differentiable at some point , then at the same point the functions

and

those. the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions.

Consequence. If two differentiable functions differ by a constant, then their derivatives are, i.e.

Rule 2If functions

are differentiable at some point , then their product is also differentiable at the same point

and

those. the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other.

Consequence 1. The constant factor can be taken out of the sign of the derivative:

Consequence 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each of the factors and all the others.

For example, for three multipliers:

Rule 3If functions

differentiable at some point and , then at this point their quotient is also differentiable.u/v , and

those. the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator.

Where to look on other pages

When finding the derivative of the product and the quotient in real problems, it is always necessary to apply several differentiation rules at once, so more examples on these derivatives are in the article."The derivative of a product and a quotient".

Comment. You should not confuse a constant (that is, a number) as a term in the sum and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. This is a typical mistake that occurs at the initial stage of studying derivatives, but as you solve several one-two-part examples average student no longer makes this mistake.

And if, when differentiating a product or a quotient, you have a term u"v, wherein u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (such a case is analyzed in example 10).

Another common mistake is the mechanical solution of the derivative of a complex function as the derivative of a simple function. So derivative of a complex function devoted to a separate article. But first we will learn to find derivatives of simple functions.

Along the way, you can not do without transformations of expressions. To do this, you may need to open in new windows manuals Actions with powers and roots and Actions with fractions .

If you are looking for solutions to derivatives with powers and roots, that is, when the function looks like , then follow the lesson " Derivative of the sum of fractions with powers and roots".

If you have a task like , then you are in the lesson "Derivatives of simple trigonometric functions".

Step by step examples - how to find the derivative

Example 3 Find the derivative of a function

Decision. We determine the parts of the function expression: the entire expression represents the product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the product differentiation rule: the derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other:

Next, we apply the rule of differentiation of the sum: the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum, the second term with a minus sign. In each sum, we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, "x" turns into one, and minus 5 - into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We get the following values of derivatives:

We substitute the found derivatives into the sum of products and obtain the derivative of the entire function required by the condition of the problem:

And you can check the solution of the problem on the derivative on .

Example 4 Find the derivative of a function

Decision. We are required to find the derivative of the quotient. We apply the formula for differentiating a quotient: the derivative of a quotient of two functions is equal to a fraction whose numerator is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator. We get:

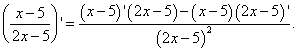
We have already found the derivative of the factors in the numerator in Example 2. Let's also not forget that the product, which is the second factor in the numerator in the current example, is taken with a minus sign:

If you are looking for solutions to such problems in which you need to find the derivative of a function, where there is a continuous pile of roots and degrees, such as, for example, then welcome to class "The derivative of the sum of fractions with powers and roots" .

If you need to learn more about the derivatives of sines, cosines, tangents and other trigonometric functions, that is, when the function looks like , then you have a lesson "Derivatives of simple trigonometric functions" .

Example 5 Find the derivative of a function

Decision. In this function, we see a product, one of the factors of which is the square root of the independent variable, with the derivative of which we familiarized ourselves in the table of derivatives. According to the product differentiation rule and the tabular value of the derivative of the square root, we get:

You can check the solution of the derivative problem on derivative calculator online .

Example 6 Find the derivative of a function

Decision. In this function, we see the quotient, the dividend of which is the square root of the independent variable. According to the rule of differentiation of the quotient, which we repeated and applied in example 4, and the tabular value of the derivative of the square root, we get:

To get rid of the fraction in the numerator, multiply the numerator and denominator by .

Examples are given of calculating derivatives using the derivative formula complex function.

Content

See also: Proof of the formula for the derivative of a complex function

Basic formulas

Here we give examples of calculating derivatives of the following functions:
; ; ; ; .

If a function can be represented as a complex function in the following form:
,
then its derivative is determined by the formula:
.
In the examples below, we will write this formula in the following form:
.
where .
Here, the subscripts or , located under the sign of the derivative, denote the variable with respect to which differentiation is performed.

Usually, in tables of derivatives, the derivatives of functions from the variable x are given. However, x is a formal parameter. The variable x can be replaced by any other variable. Therefore, when differentiating a function from a variable , we simply change, in the table of derivatives, the variable x to the variable u .

Simple examples

Example 1

Find the derivative of a complex function
.

Let's write down given function in equivalent form:
.
In the table of derivatives we find:
;
.

According to the formula for the derivative of a complex function, we have:
.
Here .

Example 2

Find derivative
.

We take out the constant 5 beyond the sign of the derivative and from the table of derivatives we find:
.

.
Here .

Example 3

Find the derivative
.

We take out the constant -1 for the sign of the derivative and from the table of derivatives we find:
;
From the table of derivatives we find:
.

We apply the formula for the derivative of a complex function:
.
Here .

More complex examples

In more difficult examples we apply the rule of differentiation of a complex function several times. In doing so, we calculate the derivative from the end. That is, we break the function into its component parts and find the derivatives of the simplest parts using derivative table. We also apply sum differentiation rules, products and fractions . Then we make substitutions and apply the formula for the derivative of a complex function.

Example 4

Find the derivative
.

We select the simplest part of the formula and find its derivative. .

.
Here we have used the notation
.

We find the derivative of the next part of the original function, applying the results obtained. We apply the rule of differentiation of the sum:
.

Once again, we apply the rule of differentiation of a complex function.

.
Here .

Example 5

Find the derivative of a function
.

We select the simplest part of the formula and find its derivative from the table of derivatives. .

We apply the rule of differentiation of a complex function.
.
Here
.

We differentiate the next part, applying the results obtained.
.
Here
.

Let's differentiate the next part.

.
Here
.

Now we find the derivative of the desired function.

.
Here
.

complex derivatives. Logarithmic derivative.
Derivative of exponential function

We continue to improve our differentiation technique. In this lesson, we will consolidate the material covered, consider more complex derivatives, and also get acquainted with new tricks and tricks for finding the derivative, in particular, with the logarithmic derivative.

Those readers who have a low level of preparation should refer to the article How to find the derivative? Solution examples which will allow you to raise your skills almost from scratch. Next, you need to carefully study the page Derivative of a compound function, understand and resolve all the examples I have given. This lesson is logically the third in a row, and after mastering it, you will confidently differentiate fairly complex functions. It is undesirable to stick to the position “Where else? And that’s enough!”, since all examples and solutions are taken from real control works and often encountered in practice.

Let's start with repetition. On the lesson Derivative of a compound function we have considered a number of examples with detailed comments. During the study of differential calculus and other sections mathematical analysis- you will have to differentiate very often, and it is not always convenient (and not always necessary) to paint examples in great detail. Therefore, we will practice in the oral finding of derivatives. The most suitable "candidates" for this are derivatives of the simplest of complex functions, for example:

According to the rule of differentiation of a complex function :

When studying other matan topics in the future, such a detailed record is most often not required, it is assumed that the student is able to find similar derivatives on autopilot. Let's imagine that at 3 o'clock in the morning the phone rang, and a pleasant voice asked: "What is the derivative of the tangent of two x?". This should be followed by an almost instantaneous and polite response: .

The first example will be immediately intended for independent solution.

Example 1

Find the following derivatives orally, in one step, for example: . To complete the task, you only need to use table of derivatives of elementary functions(if she hasn't already remembered). If you have any difficulties, I recommend re-reading the lesson Derivative of a compound function.

, , ,
, , ,
, , ,

, , ,

, ,

Answers at the end of the lesson

Complex derivatives

After preliminary artillery preparation, examples with 3-4-5 attachments of functions will be less scary. Perhaps the following two examples will seem complicated to some, but if they are understood (someone suffers), then almost everything else in differential calculus will seem like a child's joke.

Example 2

Find the derivative of a function

As already noted, when finding the derivative of a complex function, first of all, it is necessary right UNDERSTAND INVESTMENTS. In cases where there are doubts, I remind you of a useful trick: we take the experimental value "x", for example, and try (mentally or on a draft) to substitute this value into the "terrible expression".

1) First we need to calculate the expression, so the sum is the deepest nesting.

2) Then you need to calculate the logarithm:

4) Then cube the cosine:

5) At the fifth step, the difference:

6) And finally, the outermost function is the square root:

Complex Function Differentiation Formula are applied in reverse order, from the outermost function to the innermost. We decide:

Seems to be no error...

(1) We take the derivative of the square root.

(2) We take the derivative of the difference using the rule

(3) The derivative of the triple is equal to zero. In the second term, we take the derivative of the degree (cube).

(4) We take the derivative of the cosine.

(5) We take the derivative of the logarithm.

(6) Finally, we take the derivative of the deepest nesting .

It may seem too difficult, but this is not the most brutal example. Take, for example, Kuznetsov's collection and you will appreciate all the charm and simplicity of the analyzed derivative. I noticed that they like to give a similar thing at the exam to check whether the student understands how to find the derivative of a complex function, or does not understand.

The following example is for a standalone solution.

Example 3

Find the derivative of a function

Hint: First we apply the rules of linearity and the rule of differentiation of the product

Full solution and answer at the end of the lesson.

It's time to move on to something more compact and prettier.
It is not uncommon for a situation where the product of not two, but three functions is given in an example. How to find the derivative of the product of three factors?

Example 4

Find the derivative of a function

First, we look, but is it possible to turn the product of three functions into a product of two functions? For example, if we had two polynomials in the product, then we could open the brackets. But in this example, all functions are different: degree, exponent and logarithm.

In such cases, it is necessary successively apply the product differentiation rule twice

The trick is that for "y" we denote the product of two functions: , and for "ve" - the logarithm:. Why can this be done? Is it - this is not the product of two factors and the rule does not work?! There is nothing complicated:

Now it remains to apply the rule a second time to bracket:

You can still pervert and take something out of brackets, but in this case it is better to leave the answer in this form - it will be easier to check.

The above example can be solved in the second way:

Both solutions are absolutely equivalent.

Example 5

Find the derivative of a function

This is an example for an independent solution, in the sample it is solved in the first way.

Consider similar examples with fractions.

Example 6

Find the derivative of a function

Here you can go in several ways:

Or like this:

But the solution can be written more compactly if, first of all, we use the rule of differentiation of the quotient , taking for the whole numerator:

In principle, the example is solved, and if it is left in this form, it will not be a mistake. But if you have time, it is always advisable to check on a draft, but is it possible to simplify the answer? We bring the expression of the numerator to a common denominator and get rid of the three-story fraction:

The disadvantage of additional simplifications is that there is a risk of making a mistake not when finding a derivative, but when banal school transformations. On the other hand, teachers often reject the task and ask to “bring it to mind” the derivative.

A simpler example for a do-it-yourself solution:

Example 7

Find the derivative of a function

We continue to master the techniques for finding the derivative, and now we will consider a typical case when a “terrible” logarithm is proposed for differentiation

Example 8

Find the derivative of a function

Here you can go a long way, using the rule of differentiation of a complex function:

But the very first step immediately plunges you into despondency - you have to take an unpleasant derivative of a fractional degree, and then also from a fraction.

So before how to take the derivative of the “fancy” logarithm, it is previously simplified using well-known school properties:

! If you have a practice notebook handy, copy these formulas right there. If you don't have a notebook, draw them on a piece of paper, as the rest of the lesson's examples will revolve around these formulas.

The solution itself can be formulated like this:

Let's transform the function:

We find the derivative:

The preliminary transformation of the function itself greatly simplified the solution. Thus, when a similar logarithm is proposed for differentiation, it is always advisable to “break it down”.

And now a couple of simple examples for an independent solution:

Example 9

Find the derivative of a function

Example 10

Find the derivative of a function

All transformations and answers at the end of the lesson.

logarithmic derivative

If the derivative of logarithms is such sweet music, then the question arises, is it possible in some cases to organize the logarithm artificially? Can! And even necessary.

Example 11

Find the derivative of a function

Similar examples we have recently considered. What to do? One can successively apply the rule of differentiation of the quotient, and then the rule of differentiation of the product. The disadvantage of this method is that you get a huge three-story fraction, which you don’t want to deal with at all.

But in theory and practice there is such a wonderful thing as the logarithmic derivative. Logarithms can be organized artificially by "hanging" them on both sides:

Note : because function can take negative values, then, generally speaking, you need to use modules: , which disappear as a result of differentiation. However, the current design is also acceptable, where by default the complex values. But if with all rigor, then in both cases it is necessary to make a reservation that.

Now you need to “break down” the logarithm of the right side as much as possible (formulas in front of your eyes?). I will describe this process in great detail:

Let's start with the differentiation.
We conclude both parts with a stroke:

The derivative of the right side is quite simple, I will not comment on it, because if you are reading this text, you should be able to handle it with confidence.

What about the left side?

On the left side we have complex function. I foresee the question: “Why, is there one letter “y” under the logarithm?”.

The fact is that this "one letter y" - IS A FUNCTION IN ITSELF(if it is not very clear, refer to the article Derivative of a function implicitly specified). Therefore, the logarithm is an external function, and "y" is an internal function. And we use the compound function differentiation rule :

On the left side, as if by magic, we have a derivative. Further, according to the rule of proportion, we throw the “y” from the denominator of the left side to the top of the right side:

And now we remember what kind of "game"-function we talked about when differentiating? Let's look at the condition:

Final answer:

Example 12

Find the derivative of a function

This is a do-it-yourself example. Sample design of an example of this type at the end of the lesson.

With the help of the logarithmic derivative, it was possible to solve any of examples No. 4-7, another thing is that the functions there are simpler, and, perhaps, the use of the logarithmic derivative is not very justified.

Derivative of exponential function

We have not considered this function yet. An exponential function is a function that has and the degree and base depend on "x". A classic example that will be given to you in any textbook or at any lecture:

How to find the derivative of an exponential function?

It is necessary to use the technique just considered - the logarithmic derivative. We hang logarithms on both sides:

As a rule, the degree is taken out from under the logarithm on the right side:

As a result, on the right side we have a product of two functions, which will be differentiated according to the standard formula .

We find the derivative, for this we enclose both parts under strokes:

The next steps are easy:

Finally:

If some transformation is not entirely clear, please re-read the explanations of Example 11 carefully.

In practical tasks, the exponential function will always be more complicated than the considered lecture example.

Example 13

Find the derivative of a function

We use the logarithmic derivative.

On the right side we have a constant and the product of two factors - "x" and "logarithm of the logarithm of x" (another logarithm is nested under the logarithm). When differentiating a constant, as we remember, it is better to immediately take it out of the sign of the derivative so that it does not get in the way; and, of course, apply the familiar rule :

Since you came here, you probably already managed to see this formula in the textbook

and make a face like this:

Friend, don't worry! In fact, everything is simple to disgrace. You will definitely understand everything. Only one request - read the article slowly try to understand every step. I wrote as simply and clearly as possible, but you still need to delve into the idea. And be sure to solve the tasks from the article.

What is a complex function?

Imagine that you are moving to another apartment and therefore you are packing things in big boxes. Let it be necessary to collect some small items, for example, school stationery. If you just throw them in a huge box, they will get lost among other things. To avoid this, you first put them, for example, in a bag, which you then put in a large box, after which you seal it. This "hardest" process is shown in the diagram below:

It would seem, where does the mathematics? And besides, a complex function is formed in EXACTLY THE SAME way! Only we “pack” not notebooks and pens, but \ (x \), while different “packages” and “boxes” serve.

For example, let's take x and "pack" it into a function:

As a result, we get, of course, \(\cos⁡x\). This is our "bag of things". And now we put it in a "box" - we pack it, for example, into a cubic function.

What will happen in the end? Yes, that's right, there will be a "package with things in a box", that is, "cosine of x cubed."

The resulting construction is a complex function. It differs from the simple one in that SEVERAL “impacts” (packages) are applied to one X in a row and it turns out, as it were, “a function from a function” - “a package in a package”.

AT school course there are very few types of these same “packages”, only four:

Let's now "pack" x first into an exponential function with base 7, and then into a trigonometric function. We get:

\(x → 7^x → tg⁡(7^x)\)

And now let's "pack" x twice in trigonometric functions, first in , and then in :

\(x → sin⁡x → ctg⁡ (sin⁡x)\)

Simple, right?

Now write the functions yourself, where x:
- first it is “packed” into a cosine, and then into an exponential function with base \(3\);
- first to the fifth power, and then to the tangent;
- first to the base logarithm \(4\) , then to the power \(-2\).

See the answers to this question at the end of the article.

But can we "pack" x not two, but three times? No problem! And four, and five, and twenty-five times. Here, for example, is a function in which x is "packed" \(4\) times:

\(y=5^(\log_2⁡(\sin⁡(x^4)))\)

But such formulas will not be found in school practice (students are more fortunate - they can be more difficult☺).

"Unpacking" a complex function

Look at the previous function again. Can you figure out the sequence of "packing"? What X was stuffed into first, what then, and so on until the very end. That is, which function is nested in which? Take a piece of paper and write down what you think. You can do this with a chain of arrows, as we wrote above, or in any other way.

Now the correct answer is: first x was “packed” into the \(4\)th power, then the result was packed into the sine, it, in turn, was placed in the logarithm base \(2\), and in the end the whole construction was shoved into the power fives.

That is, it is necessary to unwind the sequence IN THE REVERSE ORDER. And here is a hint how to do it easier: just look at the X - you have to dance from it. Let's look at a few examples.

For example, here is a function: \(y=tg⁡(\log_2⁡x)\). We look at X - what happens to him first? Taken from him. And then? The tangent of the result is taken. And the sequence will be the same:

\(x → \log_2⁡x → tg⁡(\log_2⁡x)\)

Another example: \(y=\cos⁡((x^3))\). We analyze - first x was cubed, and then the cosine was taken from the result. So the sequence will be: \(x → x^3 → \cos⁡((x^3))\). Pay attention, the function seems to be similar to the very first one (where with pictures). But this is a completely different function: here in the cube x (that is, \(\cos⁡((x x x)))\), and there in the cube the cosine \(x\) (that is, \(\cos⁡ x·\cos⁡x·\cos⁡x\)). This difference arises from different "packing" sequences.

The last example (with important information in it): \(y=\sin⁡((2x+5))\). It is clear that here we first performed arithmetic operations with x, then the sine was taken from the result: \(x → 2x+5 → \sin⁡((2x+5))\). And this is an important point: despite the fact that arithmetic operations are not functions in themselves, here they also act as a way of “packing”. Let's delve a little deeper into this subtlety.

As I said above, in simple functions x is "packed" once, and in complex functions - two or more. Moreover, any combination of simple functions (that is, their sum, difference, multiplication or division) is also a simple function. For example, \(x^7\) is a simple function, and so is \(ctg x\). Hence, all their combinations are simple functions:

\(x^7+ ctg x\) - simple,
\(x^7 ctg x\) is simple,
\(\frac(x^7)(ctg x)\) is simple, and so on.

However, if one more function is applied to such a combination, it will already be a complex function, since there will be two “packages”. See diagram:

Okay, let's get on with it now. Write the sequence of "wrapping" functions:
\(y=cos(⁡(sin⁡x))\)
\(y=5^(x^7)\)
\(y=arctg⁡(11^x)\)
\(y=log_2⁡(1+x)\)
The answers are again at the end of the article.

Internal and external functions

Why do we need to understand function nesting? What does this give us? The point is that without such an analysis we will not be able to reliably find the derivatives of the functions discussed above.

And in order to move on, we will need two more concepts: internal and external functions. This is a very simple thing, moreover, in fact, we have already analyzed them above: if we recall our analogy at the very beginning, then the inner function is the “package” and the outer one is the “box”. Those. what X is “wrapped” in first is an internal function, and what the internal is “wrapped” in is already external. Well, it’s understandable why - it’s outside, it means external.

Here in this example: \(y=tg⁡(log_2⁡x)\), the function \(\log_2⁡x\) is internal, and
- external.

And in this one: \(y=\cos⁡((x^3+2x+1))\), \(x^3+2x+1\) is internal, and
- external.

Perform the last practice of analyzing complex functions, and finally, let's move on to the point for which everything was started - we will find derivatives of complex functions:

Fill in the gaps in the table:

Derivative of a compound function

Bravo to us, we still got to the "boss" of this topic - in fact, the derivative of a complex function, and specifically, to that very terrible formula from the beginning of the article.☺

\((f(g(x)))"=f"(g(x))\cdot g"(x)\)

This formula reads like this:

The derivative of a complex function is equal to the product of the derivative of the external function with respect to the constant internal function and the derivative of the internal function.

And immediately look at the parsing scheme "by words" to understand what to relate to:

I hope the terms "derivative" and "product" do not cause difficulties. "Complex function" - we have already dismantled. The catch is in the "derivative of the external function with respect to the constant internal." What it is?

Answer: this is the usual derivative of the outer function, in which only the outer function changes, while the inner one remains the same. Still unclear? Okay, let's take an example.

Let's say we have a function \(y=\sin⁡(x^3)\). It is clear that the inner function here is \(x^3\), and the outer
. Let us now find the derivative of the outer with respect to the constant inner.

Example 2

Find the derivative of a function

1) First we need to calculate the expression, so the sum is the deepest nesting.

2) Then you need to calculate the logarithm:

4) Then cube the cosine:

5) At the fifth step, the difference:

6) And finally, the outermost function is the square root:

Complex Function Differentiation Formula are applied in reverse order, from the outermost function to the innermost. We decide:

Seems to be error-free:

1) We take the derivative of the square root.

2) We take the derivative of the difference using the rule

3) The derivative of the triple is equal to zero. In the second term, we take the derivative of the degree (cube).

4) We take the derivative of the cosine.

6) And finally, we take the derivative of the deepest nesting .

The following example is for a standalone solution.

Example 3

Find the derivative of a function

Hint: First we apply the rules of linearity and the rule of differentiation of the product

Full solution and answer at the end of the lesson.

Example 4

Find the derivative of a function

In such cases, it is necessary successively apply the product differentiation rule twice

Now it remains to apply the rule a second time to bracket:

You can still pervert and take something out of the brackets, but in this case it is better to leave the answer in this form - it will be easier to check.

The above example can be solved in the second way:

Both solutions are absolutely equivalent.

Example 5

Find the derivative of a function

This is an example for an independent solution, in the sample it is solved in the first way.

Consider similar examples with fractions.

Example 6

Find the derivative of a function

Here you can go in several ways:

Or like this:

But the solution can be written more compactly if, first of all, we use the rule of differentiation of the quotient , taking for the whole numerator:

We bring the expression of the numerator to a common denominator and get rid of the three-story fraction:

A simpler example for a do-it-yourself solution:

Example 7

Find the derivative of a function

We continue to master the techniques for finding the derivative, and now we will consider a typical case when a “terrible” logarithm is proposed for differentiation