"දෙපාර්ශ්වික පාලකයෙකු භාවිතා කරමින් ජ්යාමිතික ඉදිකිරීම්" යන මාතෘකාව පිළිබඳ පර්යේෂණ කටයුතු. මූලික ඉදිකිරීම් කාර්යයන් පාලකයෙකු භාවිතයෙන් කළ හැකි ඉදිකිරීම් මොනවාද?
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt="(!LANG:>පාලකය සහ ජ්යාමිතිය සමඟ ඉදිකිරීම්">!}
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="(!LANG:> ලබා දී ඇති ප්‍රශ්නයට සමාන BÚ ඛණ්ඩයක් සාදන්න"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="(!LANG:> දී ඇති ත්‍රිකෝණයකට සමාන කොන් පැත්තක් තැනීම"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="(! LANG:> කෝණ Úsector එකක් තැනීම"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="(!LANG:> ප්‍රොපෙන්ඩික් රේඛා රේඛා තැනීම"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ !} සමද්වීපාද ත්රිකෝණය RAB Q ද උස වේ, එවිට PM a ට ලම්බක වේ.
Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="(!LANG:> කොටසක මධ්‍ය ලක්ෂ්‍යයේ මධ්‍ය ලක්ෂ්යය ගොඩනැගීම ලබා දී ඇත"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}
නාගරික අයවැය අධ්යාපන ආයතනය
සාමාන්යය විස්තීරණ පාසලතනි විෂයයන් පිළිබඳ ගැඹුරු අධ්‍යයනයක් සමඟ අංක 34
MAN, භෞතික විද්යාව සහ ගණිත අංශය
"මාලිමා යන්ත්රයක් සහ සෘජු දාරයක් භාවිතා කරමින් ජ්යාමිතික ඉදිකිරීම්"
සම්පූර්ණ කළේ: 7 "A" පන්තියේ ශිෂ්‍යයා
Batishcheva වික්ටෝරියා
හිස: Koltovskaya V.V.
Voronezh, 2013
3. දී ඇති එකකට සමාන කෝණයක් ඉදිකිරීම.
පී 
ලබා දී ඇති කෝණයේ A ශීර්ෂය කේන්ද්‍ර කර ගත් අත්තනෝමතික කවයක් අඳින්න (රූපය 3). B සහ C කෝණයේ පැති සහිත රවුමේ ඡේදනය වීමේ ලක්ෂ්ය වේ. AB අරය සමඟින්, අපි ලබා දී ඇති අර්ධ රේඛාවේ ආරම්භක ලක්ෂ්යය වන O ලක්ෂ්‍යයේ කේන්ද්‍ර කරගත් රවුමක් අඳින්නෙමු. ලබා දී ඇති අර්ධ රේඛාව සමඟ මෙම කවයේ ඡේදනය වීමේ ලක්ෂ්යය C මගින් දැක්වේ 1
. C කේන්ද්රය සහිත කවයක් විස්තර කරන්න 1 සහ Fig.3
අරය ක්රි.පූ. ලක්ෂ්යය B 1 නිශ්චිත අර්ධ තලයේ ඉදිකරන ලද කවවල ඡේදනය අපේක්ෂිත කෝණයේ පැත්තේ පිහිටා ඇත.
6. ලම්බක රේඛා ඉදිකිරීම.
අපි O ලක්ෂ්‍යයේ කේන්ද්‍රගත වූ අත්තනෝමතික අරය r සහිත රවුමක් අඳින්නෙමු Fig.6. රවුම A සහ B යන ස්ථානවල රේඛාව ඡේදනය කරයි.A සහ B ලකුණු වලින් අපි AB අරය සහිත රවුම් අඳින්නෙමු. මෙලන්කොලි C මෙම කවවල ඡේදනය වීමේ ලක්ෂ්යය වේවා. අත්තනෝමතික අරයක් සහිත කවයක් තැනීමේදී අපට පළමු පියවරේදී A සහ B ලකුණු ලැබුණි.
අපේක්ෂිත රේඛාව C සහ O ලකුණු හරහා ගමන් කරයි.
Fig.6
දන්නා ගැටළු
1.බ්‍රහ්මගුප්තගේ කාර්යය
පැති හතරක් සහිත සෙල්ලිපි හතරක් සාදන්න. එක් විසඳුමක් ඇපලෝනියස්ගේ කවය භාවිතා කරයි.ත්‍රිරෝද රථයක් සහ ත්රිකෝණයක් අතර ඇති ප්‍රතිසමය භාවිතා කර ඇපලෝනියස් ගැටලුව විසඳා ගනිමු. ත්රිකෝණයක කොටා ඇති කවයක් අපි සොයා ගන්නේ කෙසේද: අපි ද්විභාණ්ඩවල ඡේදනය වන ලක්ෂ්යය ගොඩනඟමු, එයින් ලම්බක ත්රිකෝණයේ පැතිවලට, ලම්බකවල පාද (ලම්බකයේ ඡේදනය වීමේ ලක්ෂ්ය) එය පහත් කර ඇත) සහ අපට අවශ්ය රවුමේ ඇති ලකුණු තුනක් ලබා දෙන්න. අපි මෙම කරුණු තුන හරහා රවුමක් අඳින්නෙමු - විසඳුම සූදානම්. ඇපලෝනියස් ගැටලුව සම්බන්ධයෙන් අපි එයම කරන්නෙමු.
2. ඇපලෝනියස්ගේ ගැටලුව
ලබා දී ඇති කව තුනට රවුම් ස්පර්ශකයක් තැනීමට මාලිමා යන්ත්රයක් සහ කෙළින්ම භාවිතා කරන්න. පුරාවෘත්තයට අනුව, පූ 220 දී පමණ පර්ගාහි ඇපලෝනියස් විසින් ගැටලුව සකස් කරන ලදී. ඊ. "ස්පර්ශ" පොතේ, එය නැති වී ගිය නමුත් 1600 දී ප්‍රංශුවා වියටා විසින් ප්‍රතිසංස්කරණය කරන ලදී, "ගැලික් ඇපලෝනියස්", ඔහුගේ සමකාලීනයන් ඔහුව හැඳින්වූ පරිදි.
ලබා දී ඇති කව කිසිවක් අනෙකා තුළ නොපවතී නම්, මෙම ගැටලුවට අත්‍යවශ්‍යයෙන්ම වෙනස් විසඳුම් 8ක් ඇත.
නිත්ය බහුඅස්‍ර ඉදිකිරීම.
පී 
නිවැරදි
(හෝ සමපාර්ශ්වික
)
ත්රිකෝණය
- මේ නිත්ය බහුඅස්රයපැති තුනක් සහිත, නිත්ය බහුඅස්‍රවලින් පළමුවැන්න. සියළුමසමපාර්ශ්වික ත්රිකෝණයක පැති සමාන වේ, සහ සියල්ලකෝණ 60° වේ. සමපාර්ශ්වික ත්රිකෝණයක් තැනීම සඳහා, ඔබ රවුම සමාන කොටස් 3 කට බෙදිය යුතුය. මෙය සිදු කිරීම සඳහා, විෂ්කම්භය එක් කෙළවරක සිට මෙම කවයේ R අරය සහිත චාපයක් ඇඳීම අවශ්ය වේ, අපි පළමු හා දෙවන බෙදීම් ලබා ගනිමු. තෙවන බෙදීම විෂ්කම්භයේ ප්රතිවිරුද්ධ කෙළවරේ ඇත. මෙම ලක්ෂ්ය සම්බන්ධ කිරීම, අපි සමපාර්ශ්වික ත්රිකෝණයක් ලබා ගනිමු.
නිතිපතා ෂඩාස්රාකාර පුළුවන්මාලිමා යන්ත්රයක් සහ කෙලින් තැනීම. පහතඉදිකිරීම් ක්රමය ලබා දී ඇතරවුම කොටස් 6 කට බෙදීමෙන්. අපි සාමාන්ය ෂඩාස්‍රයක පැතිවල සමානාත්මතාවය පරිවරණය කරන ලද කවයේ අරයට භාවිතා කරමු. රවුමේ එක් විෂ්කම්භයක ප්රතිවිරුද්ධ කෙළවරේ සිට, අපි ආර් අරයේ චාප විස්තර කරමු. දී ඇති කවයක් සහිත මෙම චාපවල ඡේදනය වන ස්ථාන එය සමාන කොටස් 6 කට බෙදනු ඇත. සොයාගත් ලකුණු අඛණ්ඩව සම්බන්ධ කිරීම, නිත්ය ෂඩාස්රයක් ලබා ගනී.
සාමාන්ය පෙන්ටගනයක් තැනීම.
පී 
සාමාන්ය පෙන්ටගනය විය හැකමාලිමා යන්ත්රයක් සහ ස්ට්‍රේට්ජ් එකක් භාවිතයෙන් හෝ එය ලබා දී ඇති දෙයකට සවි කිරීමෙන් ඉදිකර ඇතරවුම, හෝ දී ඇති පැත්තක පදනම මත ගොඩනැගීමෙන්. මෙම ක්රියාවලිය යුක්ලිඩ් විසින් විස්තර කර ඇතඔහුගේ මූලද්‍රව්‍යවල, ක්රි.පූ. 300 පමණ. ඊ.
දී ඇති කවයක් තුළ සාමාන්ය පෙන්ටගනයක් තැනීමේ එක් ක්‍රමයක් මෙන්න:
පෙන්ටගනය ලියා ඇති කවයක් සාදා එහි කේන්ද්රය ලෙස නම් කරන්නඕ . (මෙය දකුණු පස ඇති රූප සටහනේ හරිත කවය).
රවුමේ ලක්ෂ්යයක් තෝරන්නඒ , පෙන්ටගනයේ එක් සිරස් එකක් වනු ඇත. හරහා රේඛාවක් අඳින්නඕ හාඒ .
රේඛාවට ලම්බක රේඛාවක් සාදන්නOA ලක්ෂ්යය හරහා ගමන් කිරීමඕ . රවුම සමඟ එහි එක් ඡේදනයක් ලක්ෂ්යයක් ලෙස නම් කරන්නබී .
ලක්ෂ්යයක් ගොඩනඟන්නසී අතර මැදඕ හාබී .
සී ලක්ෂ්යයක් හරහාඒ . රේඛාව සමඟ එහි ඡේදනය සලකුණු කරන්නOB (මුල් කවය ඇතුළත) ලක්ෂ්යයක් ලෙසඩී .
කේන්ද්‍ර කරගත් රවුමක් අඳින්නඒ D ලක්ෂ්යය හරහා, මෙම කවයේ ඡේදනය මුල් (හරිත කවය) සමඟ ලකුණු ලෙස සලකුණු කරන්නඊ හාඑෆ් .
කේන්ද්‍ර කරගත් රවුමක් අඳින්නඊ ලක්ෂ්යයක් හරහාඒ ජී .
කේන්ද්‍ර කරගත් රවුමක් අඳින්නඑෆ් ලක්ෂ්යයක් හරහාඒ . එහි අනෙක් ඡේදනය මුල් කවය සමඟ ලක්ෂ්යයක් ලෙස නම් කරන්නඑච් .
සාමාන්ය පෙන්ටගනයක් සාදන්නAEGHF .
විසඳිය නොහැකි ගැටළු
පහත සඳහන් ඉදිකිරීම් කාර්යයන් තුනක් පුරාණ කාලයේ පිහිටුවා ඇත:
කෝණ ත්රිකෝණය - අත්තනෝමතික කෝණයක් සමාන කොටස් තුනකට බෙදන්න.
වෙනත් වචන වලින් කිවහොත්, කෝණයේ ත්රිකෝණ ඉදිකිරීම අවශ්ය වේ - කිරණ කෝණය සමාන කොටස් තුනකට බෙදයි. P. L. Vanzel 1837 දී ඔප්පු කළේ ගැටලුව විසඳිය හැක්කේ, උදාහරණයක් ලෙස, ත්රිකෝණය α = 360°/n කෝණ සඳහා ශක්‍ය වන විට පමණක් බව, n පූර්ණ සංඛ්‍යාව 3 න් බෙදිය නොහැකි නම්, කෙසේ වෙතත්, පුවත්පත් වල කලින් කලට ප්‍රකාශයට පත් කරන ලදී. (වැරදි) මාලිමා යන්ත්රයක් සහ සෘජු දාරයක් සහිත කෝණයක් ට්‍රයිසෙක්ට් කිරීමේ ක්රම.
කියුබ් දෙගුණ කිරීම - මාලිමා යන්ත්රයක් සහ පාලකයෙකු සහිත ඝනකයක් තැනීම පිළිබඳ සම්භාව්ය පුරාණ ගැටළුවක් වන අතර, එහි පරිමාව ලබා දී ඇති ඝනකයක පරිමාව මෙන් දෙගුණයක් වේ.
නූතන අංකනයේදී, ගැටළුව සමීකරණය විසඳීම දක්වා අඩු වේ. ඒ සියල්ල දිග කොටසක් ගොඩනැගීමේ ගැටලුවට පැමිණේ. P. Wanzel 1837 දී මාලිමා යන්ත්රයක් සහ සෘජුකෝණාස්‍රයක් ආධාරයෙන් මෙම ගැටලුව විසඳිය නොහැකි බව ඔප්පු කළේය.
රවුම වර්ග කිරීම - දී ඇති කවයකට සමාන ප්‍රමාණයේ චතුරස්‍රයක මාලිමා යන්ත්රයක් සහ පාලකයෙකු භාවිතයෙන් ඉදිකිරීම් සෙවීමේ කාර්යය.
ඔබ දන්නා පරිදි, මාලිමා යන්ත්රයක් සහ පාලකයෙකු ආධාරයෙන්, ඔබට අංක ගණිත මෙහෙයුම් 4ම සිදු කර නිස්සාරණය කළ හැකිය. වර්ගමුලය; එබැවින්, වෘත්තයක වර්ගීකරණය කළ හැක්කේ, එවැනි සීමිත මෙහෙයුම් සංඛ්‍යාවක ආධාරයෙන්, π දිග කොටසක් ගොඩනැගිය හැකි නම් පමණි. මේ අනුව, මෙම ගැටලුවේ නොවිසඳීම අනුගමනය කරන්නේ π අංකයේ වීජීය නොවන ස්වභාවය (අත්‍රාසය) වන අතර එය 1882 දී ලින්ඩමන් විසින් ඔප්පු කරන ලදී.
මාලිමා යන්ත්රයක් සහ පාලකයෙකු ආධාරයෙන් විසඳිය නොහැකි තවත් ප්‍රසිද්ධ ගැටලුවකිත්‍රිකෝණයක් තැනීම සඳහා ලබා දී ඇති දිග ඛණ්ඩ තුනකින් .
එපමණක් නොව, ත්‍රිකෝණාකාරයක් තිබියදී පවා මෙම ගැටළුව විසඳිය නොහැක.
මාලිමා යන්ත්රයක් සහ ස්ට්‍රේට්ජ් එකක් පමණක් භාවිතා කර ගැටලු තුනම විසඳිය නොහැකි බව ඔප්පු වූයේ 19 වැනි සියවසේදීය. ගලෝයිස් න්‍යාය මත පදනම් වූ වීජීය ක්රම මගින් ඉදිකිරීමේ හැකියාව පිළිබඳ ප්‍රශ්නය සම්පූර්ණයෙන්ම විසඳනු ලැබේ.
ඔබ එය දන්නවද...
(ජ්යාමිතික ඉදිකිරීම් ඉතිහාසයෙන්)
වරෙක, නිත්ය බහුඅස්‍ර තැනීම සඳහා අද්භූත අර්ථයක් ආයෝජනය කරන ලදී.
එබැවින්, පයිතගරස් විසින් ආරම්භ කරන ලද ආගමික හා දාර්ශනික ඉගැන්වීම්වල අනුගාමිකයින් සහ ජීවත් වූ පයිතගරස්වරු පුරාණ ග්රීසිය (වී I-I වීසියවස් ක්රි.පූ BC), සාමාන්ය පෙන්ටගනයක විකර්ණ මගින් සාදන ලද තරු බහුඅස්‍රයක් ඔවුන්ගේ එකමුතුවේ සලකුණක් ලෙස පිළිගනු ලැබේ.
සමහර නිත්ය බහුඅස්‍රවල දැඩි ජ්යාමිතික ඉදි කිරීම් සඳහා වූ නීති "ආරම්භය" නම් ග්‍රන්ථයේ දක්වා ඇත්තේ පැරණි ග්‍රීක ගණිතඥ යුක්ලිඩ් විසිනි.IIIතුල. ක්රි.පූ. මෙම ඉදිකිරීම් සිදු කිරීම සඳහා, යුක්ලිඩ් යෝජනා කළේ පාලකයෙකු සහ මාලිමා යන්ත්රයක් පමණක් භාවිතා කරන අතර, එකල කකුල් සම්බන්ධ කිරීම සඳහා උකුල් උපාංගයක් නොතිබුණි (මෙම මෙවලම්වල එවැනි සීමාවක් පුරාණ ගණිතයේ අත්යවශ්ය අවශ්‍යතාවයක් විය).
නිත්ය බහුඅස්‍ර පැරණි තාරකා විද්‍යාවේ බහුලව භාවිතා විය. ගණිතයේ දෘෂ්ටි කෝණයෙන් මෙම සංඛ්යා ගොඩනැගීමට යුක්ලිඩ් උනන්දු වූයේ නම්, පුරාණ ග්‍රීක තාරකා විද්‍යාඥ ක්ලෝඩියස් ටොලමි (ක්රි.ව. 90 - 160 පමණ) සඳහා එය තාරකා විද්‍යාත්මක ගැටලු විසඳීමේ සහායක මෙවලමක් ලෙස අවශ්ය විය. ඉතින්, Almagest හි 1 වන පොතේ, සම්පූර්ණ දසවන පරිච්ඡේදයම නිත්ය පෙන්ටගනයන් සහ decagons ගොඩනැගීම සඳහා කැප කර ඇත.
කෙසේ වෙතත්, තනිකරම විද්‍යාත්මක කෘතිවලට අමතරව, සාමාන්ය බහුඅස්‍ර තැනීම ඉදිකිරීම්කරුවන්, ශිල්පීන් සහ කලාකරුවන් සඳහා පොත්වල අනිවාර්ය අංගයක් විය. ගෘහ නිර්මාණ ශිල්පය, ස්වර්ණාභරණ සහ ලලිත කලාවන්හි මෙම රූප නිරූපණය කිරීමේ හැකියාව දිගු කලක් තිස්සේ අවශ්ය විය.
රෝමානු ගෘහ නිර්මාණ ශිල්පී Vitruvius (ක්රි.පූ. 63-14 පමණ ජීවත් වූ) විසින් රචිත “ගෘහ නිර්මාණ ශිල්පය පිළිබඳ පොත් දහය” පවසන්නේ නගරයේ බිත්ති සැලැස්මේ සාමාන්ය බහුඅස්‍රයක් මෙන් දිස්විය යුතු බවත්, බලකොටුවේ කුළුණු “වටකුරු හෝ බහුඅස්‍ර කළ යුතු බවත්ය. වටලෑමේ ආයුධ මගින් විනාශ කරන ලද චතුරස්රය.
නගර සැලසුම් කිරීම Vitruvius ට මහත් උනන්දුවක් දැක්වූ අතර, ප්රධාන සුළං ඒවා දිගේ හමා නොයන ලෙස වීදි සැලසුම් කිරීම අවශ්ය බව විශ්වාස කළේය. එවැනි සුළං අටක් ඇති බවත් ඒවා යම් දිශාවකට හමන බවත් උපකල්පනය කරන ලදී.
පුනරුද සමයේදී, නිත්ය බහුඅස්‍ර සහ විශේෂයෙන්ම පෙන්ටගනය තැනීම පහසු කාර්යයක් නොවීය. ගණිත ක්රීඩාව, නමුත් බලකොටු ඉදිකිරීම සඳහා අවශ්ය පූර්වාවශ්යතාවයක් විය.
නිත්ය ෂඩාස්රය යනු ශ්‍රේෂ්ඨ ජර්මානු තාරකා විද්‍යාඥයෙකු සහ ගණිතඥයෙකු වන ජොහැන්නස් කෙප්ලර් (1571-1630) විසින් කරන ලද විශේෂ අධ්‍යයනයක විෂයයක් වූ අතර, ඔහු ඔහුගේ අලුත් අවුරුදු තෑග්ග පොතේ හෝ ෂඩාස්රාකාර හිම පියලි ගැන කතා කරයි. හිම පියලි ෂඩාස්රාකාර හැඩයක් ඇති වීමට හේතු ඔහු සාකච්ඡා කළේය, ඔහු විශේෂයෙන් පහත සඳහන් දේ සටහන් කරයි: “... ගුවන් යානය හිඩැස් නොමැතිව ආවරණය කළ හැක්කේ පහත දැක්වෙන සංඛ්යා වලින් පමණි: සමපාර්ශ්වික ත්රිකෝණ, හතරැස් සහ සාමාන්ය ෂඩාස්‍ර. මෙම සංඛ්යා අතර, නිත්ය ෂඩාස්රය විශාලතම ප්රදේශය ආවරණය කරයි.
ජ්යාමිතික ඉදිකිරීම් සම්බන්ධව වඩාත් ප්‍රසිද්ධ විද්‍යාඥයෙකු වූයේ ශ්‍රේෂ්ඨ ජර්මානු චිත්‍ර ශිල්පියෙකු සහ ගණිතඥයෙකු වූ ඇල්බ්‍රෙක්ට් ඩියුරර් (1471-1528), ඔහුගේ "මාර්ගෝපදේශ ..." පොතේ සැලකිය යුතු කොටසක් ඔවුන් වෙනුවෙන් කැප කළේය. ඔහු පැති 3. 4, 5 ... 16 ක් සහිත නිත්ය බහුඅස්‍ර ඉදිකිරීම සඳහා නීති යෝජනා කළේය. ඩියුරර් විසින් යෝජනා කරන ලද කවය බෙදීමේ ක්රම විශ්වීය නොවේ; එක් එක් අවස්ථාවෙහිදී, තනි තාක්ෂණයක් භාවිතා වේ.
ඩුරර් කලාත්මක භාවිතයේදී නිත්ය බහුඅස්‍ර තැනීමේ ක්රම භාවිතා කළේය, නිදසුනක් ලෙස, පාකට් සඳහා විවිධ වර්ගයේ ආභරණ සහ රටා නිර්මාණය කිරීමේදී. බොහෝ නිවාසවල පාකට් තට්ටු සොයා ගත් නෙදර්ලන්තයේ සංචාරයකදී එවැනි රටා වල රූප සටහන් ඔහු විසින් සාදන ලදී.
ඩුරර් නිත්ය බහුඅස්‍ර වලින් ආභරණ සාදන ලද අතර ඒවා වළලු වලට සම්බන්ධ කර ඇත (සමපාර්ශ්වික ත්රිකෝණ හයක්, හතරැස් හතරක්, ෂඩාස්‍ර තුනක් හෝ හයක්, හෙප්ටගන් දාහතරක්, අෂ්ටක හතරක්).
නිගමනය
ඒ නිසා,ජ්යාමිතික ඉදිකිරීම් යනු ප්‍රස්ථාරිකව පිළිතුර ලබා ගන්නා ගැටලුවක් විසඳීමේ ක්‍රමයකි. තීරණයේ නිරවද්‍යතාවය මේ මත රඳා පවතින බැවින්, උපරිම නිරවද්‍යතාවයෙන් සහ කාර්යයේ නිරවද්‍යතාවයෙන් යුත් ඇඳීම් මෙවලම් සමඟ ඉදිකිරීම් සිදු කරනු ලැබේ.
මෙම කාර්යයට ස්තූතිවන්ත වන්නට, මාලිමා යන්ත්‍රයේ සම්භවය පිළිබඳ ඉතිහාසය පිළිබඳව මම දැන හඳුනා ගත්තා, ජ්යාමිතික ඉදිකිරීම් වඩාත් විස්තරාත්මකව සිදු කිරීම සඳහා නීති රීති දැනගෙන, නව දැනුම ලබාගෙන එය ප්රායෝගිකව ක්‍රියාත්මක කළෙමි.
මාලිමා යන්ත්රයක් සහ පාලකයෙකු සමඟ ගොඩනැඟීමේ ගැටළු විසඳීම ප්‍රයෝජනවත් විනෝදාස්වාදයක් වන අතර එය ජ්යාමිතික හැඩතල සහ ඒවායේ මූලද්‍රව්‍යවල දන්නා ගුණාංග දෙස නැවුම් බැල්මක් හෙළීමට ඉඩ සලසයි.මෙම ලිපියේ දී, මාලිමා යන්ත්රයක් සහ කෙළින්ම භාවිතා කරන ජ්යාමිතික ඉදිකිරීම් හා සම්බන්ධ වඩාත් හදිසි ගැටළු අපි සලකා බලමු. ප්රධාන කාර්යයන් සලකා බලනු ලබන අතර ඒවායේ විසඳුම් ලබා දෙනු ලැබේ. ලබා දී ඇති ගැටළු සැලකිය යුතු ප්රායෝගික උනන්දුවක් දක්වන අතර, ජ්යාමිතිය පිළිබඳ ලබාගත් දැනුම තහවුරු කර ගැනීමට සහ භාවිතා කළ හැකිය. ප්රායෝගික වැඩ.
මේ අනුව, කාර්යයේ ඉලක්කය සාක්ෂාත් කරගනු ලැබේ, සකසා ඇති කාර්යයන් ඉටු වේ.
අපරාධ පාසල් ළමුන්ගේ කුඩා විද්‍යා ඇකඩමිය
"සොයන්න"
"ගණිතය" කොටස
ද්විත්ව ඒක පාර්ශවීය පාලකය භාවිතා කරමින් ජ්යාමිතික ඉදිකිරීම්
මම වැඩේ කරලා ඉවරයි ඒ
_____________
පන්තියේ ශිෂ්ය
අධීක්ෂක
හැඳින්වීම ……………………………………………………………………………… 3
I. යානයේ ජ්යාමිතික ඉදිකිරීම් ……………………4
I.1. නිර්මාණාත්මක ජ්යාමිතිය පිළිබඳ සාමාන්ය ප්‍රත්‍යක්ෂ. ගණිතමය මෙවලම්වල ප්‍රත්‍යක්ෂ …………………………………………………………………………………….4
I.2. ……………………….....5
I.3. එක් පාලකයෙකු සමඟ ජ්යාමිතික ඉදිකිරීම් ………………………………………….7
මම.4. ද්විත්ව ඒකපාර්ශ්වික පාලකයෙකු ගොඩනැගීම සඳහා ප්රධාන කාර්යයන් ……………………..8
I.5. ඉදිකිරීම් සඳහා විවිධ කාර්යයන් විසඳීම
I.6. ඒකපාර්ශ්වික පාලකයෙකු සමඟ ඉදිකිරීම් ……………………………………………… 20
I.7. මාලිමා යන්ත්‍රය සහ පාලකය සමඟ ද්විත්ව ඒක පාර්ශවීය පාලකය හුවමාරු කිරීමේ හැකියාව....21
නිගමනය …………………………………………………………………… 24
භාවිතා කරන ලද සාහිත්‍ය ලැයිස්තුව …………………………………………………….25
හැදින්වීම
සීමිත ක්රම මගින් ඉදිකිරීම් සඳහා වන ගැටලුවලට මාලිමා යන්ත්රයක් සහ සෘජු දාරයක් සමඟ පමණක් ඉදිකිරීම් සඳහා ඇති ගැටලු ඇතුළත් වේ. පාසල් විෂය මාලාව. එක් පාලකයෙකු සමඟ පමණක් ඉදිකිරීම් ගැටළු විසඳිය හැකිද? බොහෝ විට අතේ මාලිමා යන්ත්රයක් නොමැති අතර පාලකයෙකු සැමවිටම සොයාගත හැකිය.
ජ්යාමිතිය තුළ ඉදිකිරීම් කටයුතු සිත් ඇදගන්නා අංශයකි. එහි ඇති උනන්දුව ජ්යාමිතික අන්තර්ගතයේ අලංකාරය සහ සරල බව නිසාය. මෙම ගැටළු සලකා බැලීමේ හදිසිතාව වැඩි වන්නේ එය ප්රායෝගිකව යෙදුම සොයා ගැනීම නිසාය. මෙම ලිපියේ සලකා බැලූ ගැටළු විසඳීම සඳහා එක් පාලකයෙකු භාවිතා කිරීමේ හැකියාව ඇත විශාල වැදගත්කමක්ප්රායෝගිකව, මන්ද ඛණ්ඩයක් අඩකින් බෙදීම, දී ඇති කොටස දෙගුණ කිරීම යනාදී ගැටළු වලට අපි නිරන්තරයෙන් මුහුණ දෙන්නෙමු.
මෙම ලිපියෙහි, වඩාත් සංකීර්ණ ගැටළු විසඳීම සඳහා ආධාරකයක් ලෙස සේවය කරන ඉදිකිරීම් සඳහා ප්රධාන කාර්යයන් අපි සලකා බලමු.
අත්දැකීම් පෙන්නුම් කරන පරිදි, ඉදිකිරීම් කටයුතු උනන්දුව ඇති කරයි, මානසික ක්රියාකාරිත්වය සක්රිය කිරීමට දායක වේ. ඒවා විසඳන විට, රූපවල ගුණාංග පිළිබඳ දැනුම ක්රියාශීලීව භාවිතා කරනු ලැබේ, තර්ක කිරීමේ හැකියාව වර්ධනය වේ, ජ්යාමිතික ඉදිකිරීම් වල කුසලතා වැඩි දියුණු වේ. එහි ප්රතිඵලයක් වශයෙන්, ජ්යාමිතිය අධ්යයනය කිරීමේ එක් ඉලක්කයක් වන නිර්මාණාත්මක හැකියාවන් වර්ධනය වේ.
උපකල්පනය: මාලිමා යන්ත්රයක් සහ පාලකයෙකු සමඟ විසඳිය හැකි සියලුම ඉදිකිරීම් ගැටළු විසඳිය හැක්කේ ද්වි-පාර්ශ්වික පාලකයෙකු සමඟ පමණි.
අධ්යයන වස්තුව: ඉදිකිරීම් කාර්යයන් සහ ද්වි-පාර්ශ්වික පාලකයෙක්.
අධ්‍යයනයේ අරමුණු: සියලුම ඉදිකිරීම් ගැටළු විසඳිය හැක්කේ ද්විපාර්ශ්වික පාලකයෙකුගේ උපකාරයෙන් පමණක් බව ඔප්පු කිරීම.
පර්යේෂණ අරමුණු: අධ්යයනය කිරීමට න්යායික පදනමඉදිකිරීම් ගැටළු විසඳීම; ද්වි-පාර්ශ්වික පාලකයෙකුගේ උපකාරයෙන් මූලික ගොඩනැගිලි ගැටළු විසඳීම; වඩාත් සංකීර්ණ ඉදිකිරීම් කාර්යයන් සඳහා උදාහරණ දෙන්න; න්යායික හා ප්රායෝගික ද්රව්ය ක්රමවත් කිරීම.
I. ගුවන් යානයේ ජ්යාමිතික ඉදිකිරීම්
I.1. නිර්මාණාත්මක ජ්යාමිතිය පිළිබඳ සාමාන්ය ප්‍රත්‍යක්ෂ. ගණිතමය මෙවලම්වල ප්‍රත්‍යක්ෂ
නිර්මාණාත්මක ජ්යාමිතිය සඳහා, නිශ්චිත මෙවලමක් පිළිබඳ නිවැරදි හා ගණිතමය අරමුණු සඳහා සම්පූර්ණ විස්තරයක් තිබීම අවශ්ය වේ. එවැනි විස්තරයක් axioms ආකාරයෙන් දක්වා ඇත. වියුක්ත ගණිතමය ස්වරූපයෙන් මෙම ප්‍රත්‍යක්ෂ ජ්යාමිතික ඉදිකිරීම් සඳහා භාවිතා කරන සැබෑ ඇඳීම් මෙවලම්වල ගුණාංග ප්‍රකාශ කරයි.
ජ්යාමිතික ඉදිකිරීම් සඳහා බහුලව භාවිතා වන මෙවලම්:පාලකයා (ඒක පාර්ශවික) , මාලිමා යන්ත්‍රය, ද්විපාර්ශ්වික පාලකය (සමාන්තර දාර සහිත) සහ තවත් සමහරක්.
A. Ruler axiom.
පහත දැක්වෙන ජ්යාමිතික ඉදිකිරීම් සිදු කිරීමට පාලකයා ඔබට ඉඩ සලසයි:
අ) ඉදිකරන ලද ලක්ෂ්ය දෙකක් සම්බන්ධ කරන කොටස ඉදිකිරීම;
b) ඉදිකරන ලද ස්ථාන දෙකක් හරහා ගමන් කරන සරල රේඛාවක් සාදන්න;
ඇ) ඉදිකරන ලද ලක්ෂ්‍යයකින් නිකුත් වන සහ වෙනත් තැනූ ලක්ෂ්යයක් හරහා ගමන් කරන කිරණක් තැනීම.
B. මාලිමාවේ අක්ෂය.
මාලිමා යන්ත්‍රය ඔබට පහත ජ්යාමිතික ඉදිකිරීම් සිදු කිරීමට ඉඩ සලසයි:
අ) රවුමේ කේන්ද්රය සහ රවුමේ අරයට (හෝ එහි කෙළවරට) සමාන ඛණ්ඩයක් ගොඩනඟා ඇත්නම් කවයක් සාදන්න;
B. ද්විපාර්ශ්වික පාලකයෙකුගේ ප්‍රත්‍යක්ෂය.
ද්විත්ව ඒක පාර්ශවීය පාලකයා ඔබට පහත දේ කිරීමට ඉඩ දෙයි:
a) Axiom හි ලැයිස්තුගත කර ඇති ඕනෑම ඉදිකිරීමක් සිදු කරන්න;
ආ) ඉදිකරන ලද රේඛාව මගින් අර්ථ දක්වා ඇති එක් එක් අර්ධ තලය තුළ, මෙම රේඛාවට සමාන්තරව රේඛාවක් සාදා එයින් දුරින් ගමන් කරයිඒ, කොහෙද ඒ - දී ඇති පාලකයෙකු සඳහා සවි කර ඇති කොටස (පාලකයෙකුගේ පළල);
ඇ) A සහ B ලක්ෂ්ය දෙකක් ගොඩනගා ඇත්නම්, AB යම් ස්ථාවර ඛණ්ඩයකට වඩා වැඩි වේද යන්න තීරණය කරන්නඒ (පාලක පළල), සහ AB > නම්ඒ , ඉන්පසු පිළිවෙලින් A සහ B ලක්ෂ්ය හරහා ගමන් කරන සමාන්තර රේඛා යුගල දෙකක් සාදන්න, සහ එකිනෙකාගෙන් දුරින් පරතරයඒ .
ඉහත මෙවලම් වලට අමතරව, ඔබට ජ්යාමිතික ඉදි කිරීම් සඳහා වෙනත් මෙවලම් භාවිතා කළ හැකිය: අත්තනෝමතික කෝණයක්, චතුරස්රයක්, ලකුණු සහිත පාලකයෙක්, සෘජු කෝණ යුගලයක්, විශේෂ වක්ර ඇඳීම සඳහා විවිධ උපාංග ආදිය.
I.2. ගොඩනැගිලි ගැටළු විසඳීම සඳහා පොදු මූලධර්ම
ගොඩනැගීමේ කාර්යය වෙනත් රූපයක් ලබා දී ඇත්නම් සහ අපේක්ෂිත රූපයේ මූලද්‍රව්‍ය සහ මෙම රූපයේ මූලද්‍රව්‍ය අතර යම් සම්බන්ධතා පෙන්නුම් කරන්නේ නම්, ඇඟවුම් කර ඇති මෙවලම් සමඟ නිශ්චිත රූපයක් තැනීම අවශ්ය වේ.
ගැටලුවේ කොන්දේසි සපුරාලන සෑම රූපයක්ම හැඳින්වේතීරණයමෙම කාර්යය.
විසඳුමක් සොයන්න ඉදිකිරීම් කර්තව්‍යය යන්නෙන් අදහස් කරන්නේ එය සීමිත මූලික ඉදිකිරීම් සංඛ්‍යාවකට අඩු කිරීමයි, එනම් මූලික ඉදිකිරීම්වල සීමිත අනුපිළිවෙලක් දැක්වීමට, ඉන් පසුව අපේක්ෂිත රූපය නිර්මාණාත්මක ජ්‍යාමිතියේ පිළිගත් ප්‍රත්‍යයන් අනුව ගොඩනගා ඇති බවට දැනටමත් සලකනු ලැබේ. පිළිගත හැකි මූලික ඉදිකිරීම් ලැයිස්තුව, සහ, ඒ අනුව, ගැටළුව විසඳීමේ පාඨමාලාව, ඉදිකිරීම් සඳහා කුමන ආකාරයේ මෙවලම් භාවිතා කරන්නේද යන්න මත රඳා පවතී.
ඉදිකිරීම් ගැටළුව විසඳන්න - අදහස් කරන්නේ, සියලු විසඳුම් සොයන්න .
අවසාන අර්ථ දැක්වීමට යම් පැහැදිලි කිරීමක් අවශ්ය වේ. ගැටලුවේ කොන්දේසි තෘප්තිමත් කරන රූප හැඩයෙන් හෝ ප්‍රමාණයෙන් සහ ගුවන් යානයේ පිහිටීම අනුව වෙනස් විය හැකිය. කිසියම් ස්ථානයකට සාපේක්ෂව අපේක්ෂිත රූපයේ නිශ්චිත ස්ථානයක් සඳහා ගැටලුවේ තත්වය සපයන්නේද නැද්ද යන්න මත, ඉදිකිරීම් ගැටලුවේ සූත්‍රගත කිරීම මත පදනම්ව යානයේ පිහිටීමෙහි වෙනස්කම් සැලකිල්ලට ගනී හෝ සැලකිල්ලට නොගනී. සංඛ්යා.
ගැටලුවකට විසඳුමක් සොයාගතහොත්, අනාගතයේදී මෙම විසඳුම "සමස්තයක් ලෙස" භාවිතා කිරීමට අවසර ඇත, එනම්, එය මූලික ඉදිකිරීම් වලට බෙදීමකින් තොරව.
සරල ජ්යාමිතික ඉදිකිරීම් ගැටළු ගණනාවක් ඇත, විශේෂයෙන් බොහෝ විට වඩාත් සංකීර්ණ ගැටළු විසඳීමේ සංරචක ලෙස ඇතුළත් වේ. අපි ඒවා මූලික ජ්යාමිතික ඉදිකිරීම් ගැටළු ලෙස හඳුන්වනු ඇත. මූලික කාර්යයන් ලැයිස්තුව, ඇත්ත වශයෙන්ම, කොන්දේසි සහිත ය. වඩාත් පොදු කාර්යයන් පහත සඳහන් කාර්යයන් ඇතුළත් වේ:
මෙම කොටස අඩකින් බෙදන්න.
මෙම කෝණය අඩකින් බෙදන්න.
දී ඇති එකට සමාන කොටසක දී ඇති රේඛාවක් මත ඉදිකිරීම.
දී ඇති එකකට සමාන කෝණයක් ගොඩනැගීම.
දී ඇති රේඛාවකට සමාන්තරව දී ඇති ලක්ෂ්යයක් හරහා ගමන් කරන රේඛාවක් තැනීම.
දී ඇති ලක්ෂ්යයක් හරහා සහ දී ඇති රේඛාවකට ලම්බකව ගමන් කරන රේඛාවක් තැනීම.
මේ සම්බන්ධයෙන් කොටස බෙදීම.
පැති තුනක් ලබා දී ඇති ත්රිකෝණයක් ඉදිකිරීම.
පැත්තක් සහ යාබද කෝණ දෙකක් ලබා දී ඇති ත්රිකෝණයක් ඉදිකිරීම.
පැති දෙකක් සහ ඒවා අතර කෝණයක් ලබා දී ඇති ත්රිකෝණයක් ඉදිකිරීම.
ඕනෑම තරමක් සංකීර්ණ ඉදිකිරීම් ගැටළුවක් විසඳීමේදී, ගැටලුව විසඳීමට මාර්ගයක් සොයා ගැනීමට, ගැටලුවට සියලු විසඳුම් ලබා ගැනීමට, ගැටලුව විසඳීමේ හැකියාව සඳහා කොන්දේසි සොයා ගැනීමට තර්ක කරන්නේ කෙසේද යන ප්‍රශ්නය පැන නගී. , නිර්මාණාත්මක ගැටළු විසඳීමේදී, ඔවුන් පහත පියවර හතරකින් සමන්විත විසඳුම් යෝජනා ක්රමය භාවිතා කරයි:
1) විශ්ලේෂණය;
2) ඉදිකිරීම්;
3) සාක්ෂි;
4) පර්යේෂණ.
I.3. එක් පාලකයෙකු සමඟ ජ්යාමිතික ඉදි කිරීම්
අපි පාලකයා දෘෂ්ටිකෝණ දෙකකින් සලකා බලමු: පාලකයෙකු ලෙස සහ ද්විපාර්ශ්වික පාලකයෙකු ලෙස.
1. ද්විත්ව ඒක පාර්ශවීය පාලකයාපළල ඒ දුරින් පිහිටා ඇති සමාන්තර දාර සහිත පාලකයෙකු අපි අමතන්නෙමු ඒ එකිනෙකින් සෘජුව ගොඩ නැගීමට හැකි වන පරිදි:
a) අත්තනෝමතික රේඛාවක්;
b) ගැටළුව විසඳීමේ ක්රියාවලියේදී ලබා දී ඇති හෝ ලබාගත් ලකුණු දෙකක් හරහා ගමන් කරන සරල රේඛාවක්;
ඇ) සමාන්තර රේඛා, ඒ සෑම එකක්ම එක් ලක්ෂයක් හරහා ගමන් කරයි, ඒවා අතර දුර ප්රමාණයට වඩා වැඩි යඒ (මෙම ඉදිකිරීම් අතරතුර, පාලකයා එහි සමාන්තර දාර දෙකෙන් එකක් ලබා දී ඇති ලක්ෂ්ය දෙකෙන් එකක් ඇති බව එවැනි ස්ථානයක සිටී; මෙම අවස්ථාවේ දී, අපි සෘජු ඉදිකිරීමක් ගැන කතා කරමු).
මෙම ඉදිකිරීමෙහි පාලකයාගේ පළල නියත ලෙස සලකනු ලබන අතර, එබැවින්, විසඳීමේ ක්රියාවලියේදී නම් නිශ්චිත කාර්යයලබාගත් සමහර ලකුණු සම්බන්ධයෙන් සෘජු ඉදිකිරීමක් සිදු කිරීමට අවශ්ය වනු ඇතඑහෙත්හා හිදී , එවිට අපි දිග බව ඔප්පු කළ යුතුයිABවැඩි දිග ඒ .
එය දත්ත වලින් එකක් නම් හෝ ඉදිකරන ලද රේඛා දෙකක ඡේදනය නම් අපි ගොඩනඟන ලද ලක්ෂ්යයක් සලකා බලමු; අනෙක් අතට, ඉදිකරන ලද හෝ ලබා දී ඇති ලක්ෂ්ය හරහා එය ගමන් කරන්නේ නම් අපි ඉදිකරන ලද රේඛාවක් සලකා බලමු.
ද්විත්ව ඒක පාර්ශවීය පාලකයෙකු භාවිතා කරමින්, ඔබට පහත සඳහන් දෑ ගොඩනගා ගත හැකිය.
අ) ඕනෑම ලක්ෂ්ය දෙකක් හරහා රේඛාවක් ඇඳිය හැකි නමුත් එකක් පමණි.
b) රේඛාව කුමක් වුවත්, තලයේ හරියටම රේඛා දෙකක් එයට සමාන්තරව සහ දුරින් ඇත.ඒ .
ඇ) AB හි A සහ B ලකුණු දෙකක් හරහා ඒ සමාන්තර යුගල දෙකක් ඇද ගත හැකියසෘජු; AB = ඒ සමාන්තර රේඛා යුගලයක් ඇද ගත හැකි අතර, ඒවා අතර දුර සමාන වේඒ .
එකයි දෙකයි තුනයි දුන්නොත් අලුතින් පොයින්ට් හදන්න බෑ
(රූපය 1);
ලකුණු හතරක් ලබා දී ඇත්නම්, ඒවායින් තුනක් (හෝ හතරම) එකම සරල රේඛාවක පිහිටා තිබේ නම්, වෙනත් කිසිදු ලක්ෂ්යයක් ගොඩනගා ගත නොහැක (රූපය 2);
සමාන්තර චලිතයක සිරස් අතට ස්ථාන හතරක් ලබා දී ඇති අතර, ගොඩනගා ගත හැක්කේ එක් ලක්ෂ්යයක් පමණි - එහි කේන්ද්රය. (රූපය 3).
ඉහත කරුණු පිළිගත් පසු, දෙපැත්තේ පාලකයෙකු විසින් විසඳන ලද ගැටළු අපි වෙන වෙනම සලකා බලමු.
මම.4. ද්විත්ව ඒක පාර්ශවීය පාලකයෙකු ගොඩනැගීමේ මූලික කාර්යයන්
1
.
ABC කෝණයේ ද්වි අංශය ගොඩනඟන්න.
තීරණය: (රූපය 4)
ඒ (හිදී සී) හා බී (AB), සහ බී = ඩී .
බී ලබා ගන්න ඩී- ද්වි අංශය ABC.
ඇත්ත වශයෙන්ම, ලබාගෙන ඇත
සමාන්තර චලිතය ඉදිකිරීම වේ
රොම්බස්, එහි උස සමාන බැවින්. හිදීඩී –
රොම්බස් වල විකර්ණය ද්වි අංශය වේ ABC. Fig.4
2
.
ලබා දී ඇති කෝණය ABC දෙගුණ කරන්න
තීරණය : (රූපය 5) a) ඒ (AB),
ඒ (හිදී සී)= ඩී , B සහ ලකුණු හරහා ඩී
බී සෘජුවම;
b) ලකුණු B හරහා සහඩී එම් බී
සෘජුවම,බී Ç a = එෆ් .
ලබාගන්න Ð AB එෆ් = 2 Ð ABC .
Fig.5
3 . මෙම රේඛාවට එම් එන් මෙහි
A ලක්ෂ්‍යයට ලම්බක අඳින්න
තීරණය : (රූපය 6)
1) (AA 1) || (VV 1) || (SS 1) -
සෘජුවම (ඇතුළත (එම් එන්),
සමඟ Î (එම් එන්)); 2) A සහ B හරහා
එම් || n - සෘජුව,
එම් Ç (SS 1) = ඩී .
අපට ලැබෙනවා (ඒ ඩී ) (එම් එන් ).
Fig.6.
4
.
දී ඇති කරුණක් හරහා බොරු නොකියයි
මෙම රේඛාව, ලම්බකයක් අඳින්න
දක්වා මෙම සරල රේඛාව.
තීරණය: මෙම ලක්ෂ්යය හරහා අපි අඳින්නෙමු
දී ඇති එකක් ඡේදනය වන රේඛා දෙකක්
සරල රේඛාව AB, සහ ප්රතිඵලයේ කෝණ දෙගුණ කරන්න
දී ඇති එකකට යාබද ත්රිකෝණ
කෙලින්ම. OA එන් = 2 OAB සහ
ඕ.වී එන් = 2 OVA (රූපය 7).
Fig.7
5. දී ඇති රේඛාවකට අදාළව දී ඇති එකකට සමමිතික ලක්ෂ්යයක් සාදන්න.
තීරණය: ගැටලුව 4 බලන්න. (O ලක්ෂ්යය ලක්ෂ්‍යයට සමමිතික වේඑන්. Fig.7)
6. සරල රේඛාවක් අඳින්න මෙයට සමාන්තරව
පී 
රේඛාව එම්
එන්
, A ලක්ෂ්යය හරහා, නැත
M රේඛාවට අයත් වේ එන් .
විසඳුම 1: (රූපය 8)
1)(AA 1) || (VV 1) || (SS 1) || (DD 1 ) || (KK 1) -
– සෘජුවම, (SA)Ç (BB 1) \u003d C 2;
2) (C 2 K) Ç (DD 1 ) = එෆ් .
(එහෙත් එෆ් ) යනු අපේක්ෂිත රේඛාවයි.
රූපය 8
විසඳුම 2 . Fig.8 හි 1 අංකනය කර ඇත
සරල රේඛා අනුපිළිවෙල,
එයින් 1, 2 සහ 3 සමාන්තර වේ
සෘජු ඉදිකිරීම්;
(එහෙත් එෆ්) || (එම් එන්).
Fig.8 1
7
.
මෙම කොටස AB අඩකින් බෙදන්න.
විසඳුම 1 (රූපය 9) (පාලකයාගේ පළල ලබා දී ඇති කොටසේ දිගට වඩා අඩු වූ විට නඩුව සඳහා පමණි). සමාන්තර රේඛා යුගල දෙකක් කෙලින්ම අඳින්න
මෙම කොටසෙහි කෙළවර, පසුව විකර්ණය
ප්රතිඵලයක් ලෙස rhombus. O යනු AB හි මධ්‍ය ලක්ෂ්යය වේ.
සහල්. නවය.
විසඳුම 2 (රූපය 9,a)
1) a || (AB) සහ බී || (AB) - සෘජුවම;
2
) (AR), (AR)Ç
a = C, (AP) Ç
බී
=
ඩී
;
3) (ඩී හිදී) Ç a = M, (CB) Ç බී = එන් ;
4) (එම් එන් ) Ç (AB) = K;
5) (ඩී දක්වා) Ç (එහෙත් එන් ) = එෆ් ;
6) (දී එෆ් ) Ç බී = ඩී 1, (බී එෆ් ) Ç a \u003d C 1;
7) (ඩී හිදී ) Ç (එහෙත් ඩී 1) = X,
(AC 1) Ç (CB) = Z.
8) (X Z) Ç (AB) = O. අපට AO = OB ලැබේ.
රූපය 9, a
විසඳුම 3 .(සහල්. 9b)
දන්නා පරිදි , මැද trapezoid දී
පදනම්, ඡේදනය වීමේ ලක්ෂ්යය
විකර්ණ සහ ඡේදනය වීමේ ලක්ෂ්යය
පැති දිගු
එකම රේඛාවක වැතිර සිටින්න.
1) එම් || (AB) - සෘජුවම;
2) සී Î එම් , ඩී Î එම් , (AC) Ç (හිදී ඩී ) = දක්වා; Fig.9,b
3) (CB) Ç (එහෙත් ඩී ) = එෆ් ; 4) (කේ එෆ් ) Ç (AB) = O. අපට AO = OB ලැබේ.
I.5. විවිධ ගොඩනැගිලි ගැටළු විසඳීම
ද්වි-පාර්ශ්වික පාලකයෙකු සමඟ පමණක් ඉදිකිරීම් සඳහා පහත සඳහන් ගැටළු විසඳීමේදී, සමාන්තර රේඛා සෘජුව ඉදි කිරීම සහ ඉහත ප්රධාන ගැටළු හත භාවිතා කරනු ලැබේ.
1. මෙම ලක්ෂ්යය හරහා අන්‍යෝන්‍ය වශයෙන් ලම්බක රේඛා දෙකක් අඳින්න.
ආර් 
විසඳුමක්:
මෙම ලක්ෂ්යය හරහා යන්න
අත්තනෝමතික රේඛා දෙකක්,
ඊට පස්සේ බයිස්ක්ටර්ස්
යාබද කොන්. (රූපය 10)
Fig.10
2. ලබා දී ඇති කොටස A ඩී දී ඇති දිග.
දිග කොටසක් සාදන්න.
ආර් 
විසඳුමක්
:
වියදම් කරමු එම්
ඒහා
h
||
එම්
ඔස්සේ
කරුණ A. f || (එහෙත් ඩී ) , කේ || (දැන්වීම) සෘජුවම.
අපි AB සහ AC අඳිමු, එහිදී B =f එම් ,
a C = එම් කේ . දන්නා ආකාරයෙන්
AB සහ AC දෙකට බෙදන්න සහ
ත්රිකෝණයේ මධ්යන්ය අඳින්න
ABC. මධ්යන්යයන්ගේ දේපල මගින්
ත්රිකෝණය, ඔහ් ඩී = - අවශ්ය
කොටස (රූපය 11)
සහල්. එකොළොස්
3. දිග රේඛා ඛණ්ඩයක් සාදන්න
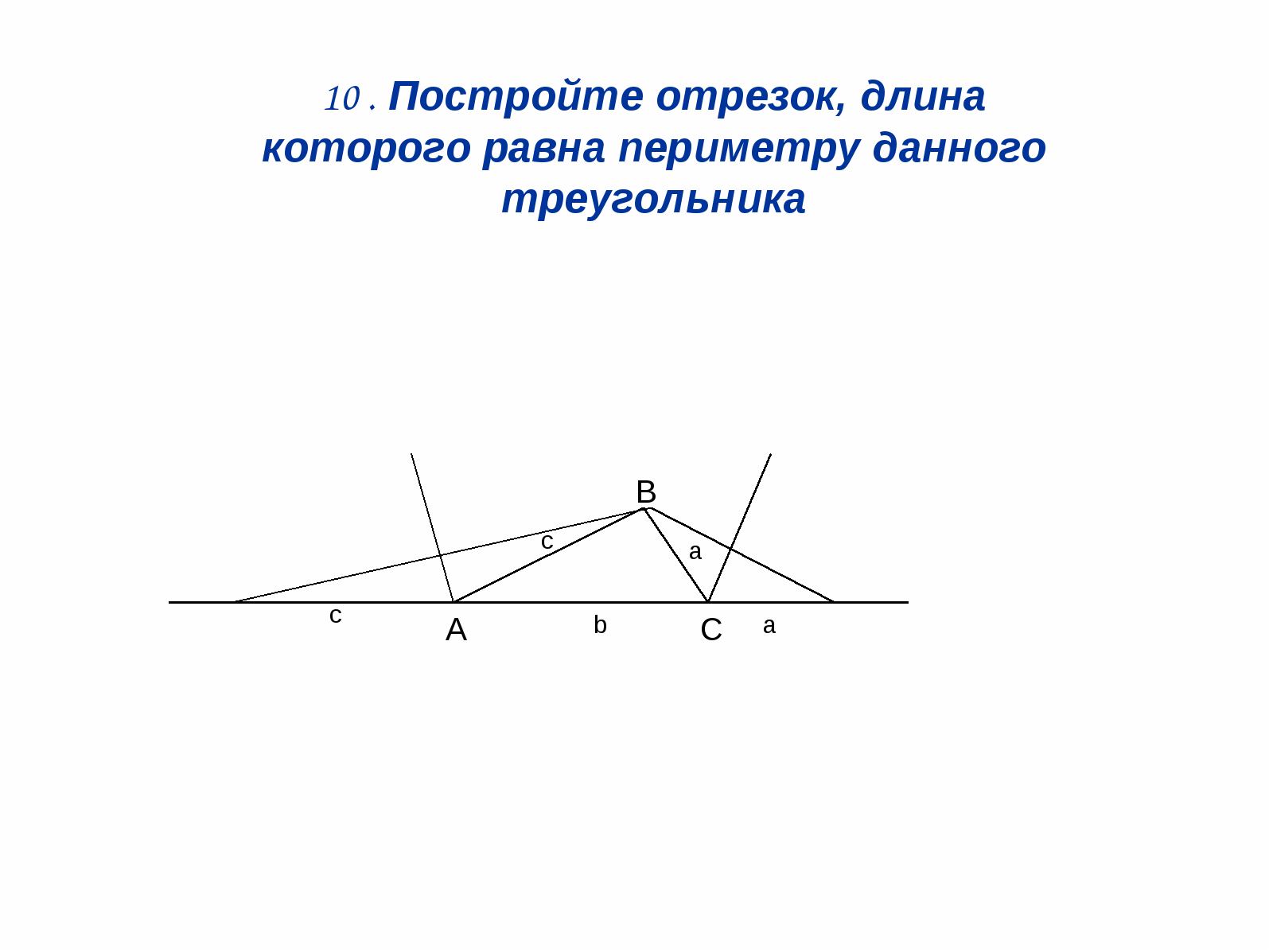ත්රිකෝණයේ පරිමිතියට සමාන වේ.
තීරණය: (රූපය 12). අපි බයිසෙක්ටර් හදමු
ත්රිකෝණයේ පිටත කොන් දෙකක්, සහ පසුව
3 කඳු මුදුන් හිදී ලම්බක අඳින්න
මෙම දෙබිඩි වලට.
ද = a + බී + සමඟ
Fig.12
4. දිග කොටසක් ලබා දී ඇත a. දිග කොටස් සාදන්න 2a, 3a.
ආර් 
විසඳුමක්:
(රූපය 13)
1M එන්) || (AB) සහ (M 1 එන් 1 ) || (එම් එන්) || (එම් 2 එන් 2 ) –
සෘජුවම;
2) (CA) සහ (CB) A සහ B හරහා.
A 1 B 1 සහ A 2 B 2 කොටස් අවශ්ය වේ.
මෙම ගැටලුව සඳහා තවත් විසඳුමක් විය හැකිය
7 ගැටලුවේ විසඳුමෙන් ලබා ගන්න.
සහල්. දහතුන
5. කොටස් දෙකක් සරල රේඛාවක් මත ලබා දී ඇති අතර, ඒවායේ දිග a සහ වේ බී . දිග a + ට සමාන වන කොටස් සාදන්න බී , බී - ඒ, ( ඒ + බී )/2 සහ ( බී - ඒ )/2 .
තීරණය: සහ සඳහා ඒ + බී(රූපය 14, අ)
රූපය 14, a
b) සඳහා ( ඒ + බී)/2 (රූපය 14, ආ)
1) (A 1 B 1) || (A 2 B 2) || (AB) - සෘජුවම;
2) එම් Î (A 2 B 2), (MX) Ç (A 1 B 1) = එන්, (එම් එච්) Ç (A 1 B 1) = පී;
3) (PY) Ç (A 2 B 2) = එල්, (LZ ) Ç (A 1 B 1) = ඕ
අපට ලැබෙන්නේ: එන්
ඕ =
එන්.පී +
PO = 
.
සහල්. 14b
ඇ) සඳහා බී - ඒ(රූපය 14,c)
සහල්. 14, තුළ
ඇ) සඳහා ( බී - ඒ )/2 (රූපය 14d)
සහල්. 14,g
6
.
මෙම කවයේ කේන්ද්රය ගොඩනඟන්න.
තීරණය : (රූපය 15) සරල රේඛාවක් අඳින්න AB,
A සහ B ලක්ෂ්යවල රවුම ඡේදනය කිරීම;
හිරු AB, මෙහි C යනු ඡේදනය වීමේ ලක්ෂ්යය වේ
කවයක් සමඟ.
AB ට සමාන්තරව C ලක්ෂ්යය හරහා අඳින්න
සරල රේඛාව C ඩී; සමඟඩීරවුම තරණය කරයි
ලක්ෂ්යයේඩී.
සම්බන්ධ වීමෙන්ඩීB සහ A සමඟ C, අපට ලැබේ
අපේක්ෂිත ලක්ෂ්යය රවුමේ කේන්ද්රය වේ. සහල්. පහළොව
විසඳුම 2: (රූපය 16) ද්වි-පාර්ශ්වික පාලකයක් භාවිතයෙන් සමාන්තර කෝඩ් දෙකක් සාදන්නදැන්වීම හාක්රි.පූ . අපි සමද්වීපක trapezoid ලබා ගනිමුඒ බී සී ඩී. ඉඩ දෙන්නකේ හාපී - රේඛා ඡේදනය වීමේ ස්ථානAC හාBD , AB හාඩීසී . එවිට රේඛාවපී කේ ඒවාට ලම්බකව trapezoid පාදවල මැද ලක්ෂ්ය හරහා ගමන් කරයි, එයින් අදහස් කරන්නේ එය ලබා දී ඇති කවයේ කේන්ද්රය හරහා ගමන් කරන බවයි. ඒ හා සමානව තවත් එවැනි සරල රේඛාවක් ගොඩනඟා, අපි රවුමේ කේන්ද්රය සොයා ගනිමු.
සහල්. දහසය
7. රවුමක චාපයක් ලබා දී ඇත. රවුමේ කේන්ද්රය ගොඩනඟන්න
තීරණය . (රූපය 17) මෙම චාපයේ A, B සහ C යන ලක්ෂ්ය තුනක් සලකුණු කරමු, AB කොටසේ කෙළවරට රූලරයක් සවි කර එහි දාර රවුම් කරමු. අපට සමාන්තර රේඛා දෙකක් ලැබේ. පාලකයාගේ පිහිටීම වෙනස් කිරීමෙන්, තවත් සමාන්තර සරල රේඛා දෙකක් අඳින්න. අපි රොම්බස් (සමාන උසකින් යුත් සමාන්තර චලිතයක්) ලබා ගනිමු. රොම්බස් වල විකර්ණවලින් එකක් වන්නේ ඛණ්ඩයට ලම්බක ද්විභාණ්ඩයයි.AB , රොම්බස් වල විකර්ණය අනෙක් විකර්ණයේ ලම්බක ද්වි අංශය මත පිහිටා ඇති බැවින්. ඒ හා සමානව, අපි ඛණ්ඩයට ලම්බක ද්විභාණ්ඩය ගොඩනඟමුAC . ඉදිකරන ලද මැදපෙරදිගවල ඡේදනය වන ලක්ෂ්යය අපේක්ෂිත චක්රයේ කේන්ද්රය වේ.
සහල්. 17
8. AB ඛණ්ඩයක් ලබා දී, එයට සමාන්තර නොවන l රේඛාවක් සහ ඒ මත M ලක්ෂ්යයක් ලබා දී ඇත. එක් ද්විත්ව ඒකපාර්ශ්වික පාලකයක් භාවිතා කරමින්, L රේඛාවේ ඡේදනය වීමේ ලක්ෂ්ය AB අරය කවයක් සමඟ M කේන්ද්‍රයෙන් සාදන්න.
තීරණය: (රූපය 18)
අපි ත්රිකෝණය සම්පූර්ණ කරමුABM සමාන්තර චලිතයටABNM . අපි බයිසෙක්ටර් MT සහ ගොඩනඟමුමෙනෙවියඅතර කෝණඑම්.එන්සහ සෘජුඑල් . අපි කාරණය හරහා යමුඑන් මෙම දෙබිඩි වලට සමාන්තර රේඛා:NQ || මෙනෙවිය, NR || එම්.ටී. එම්.ටී│ මෙනෙවියයාබද කෝණවල ද්විභාණ්ඩ ලෙස. අදහස් කරන්නේ,NQ │ MT, එනම් ත්රිකෝණයකNMQද්විභාණ්ඩය උස වේ, එබැවින් ත්රිකෝණය සමද්විපාද වේ:MQ = එම්.එන්. එලෙසම,මහතා = එම්.එන්. ලකුණුප්‍රශ්නයහාආර්කැමති.
සහල්. දහඅට
9. l රේඛාවක් සහ L ට සමාන්තරව OA ඛණ්ඩයක් ලබා දී ඇත. එක් ද්විත්ව ඒකපාර්ශ්වික පාලකයක් භාවිතා කරමින්, O හි කේන්ද්‍රගත වූ අරය OA කවයක් සමඟ l රේඛාවේ ඡේදනය වීමේ ලක්ෂ්ය සාදන්න.
තීරණය: (රූපය 19, අ)
අපි සරල රේඛාවක් අඳින්නෙමුඑල් 1 , රේඛාවට සමාන්තරවOA සහ එය දුරින්ඒ . අපි කෙලින්ම ගනිමුඑල් අත්තනෝමතික ලක්ෂ්යයබී . ඉඩ දෙන්නබී 1 - රේඛා ඡේදනය වීමේ ලක්ෂ්යයOB හාඑල් 1 . අපි කාරණය හරහා යමුබී 1 සෘජු, සමාන්තරAB ; මෙම රේඛාව රේඛාව ඡේදනය කරයිOA ලක්ෂ්යයේඒ 1 . අපි දැන් කරුණු හරහා යමුඕ හාඒ 1 සමාන්තර රේඛා යුගලයක්, අතර දුර සමාන වේඒ (එවැනි රේඛා යුගල දෙකක් තිබිය හැක); ඉඩ දෙන්නx හාx 1 - ලක්ෂ්යය හරහා ගමන් කරන රේඛාවේ ඡේදනය වීමේ ලක්ෂ්යයඕ , සරල රේඛා සමඟඑල් හාඑල් 1 . පරිදිOA 1 = OX 1 සහ ∆OA 1 x 1 ∆ OAX , එවිට ОА = ОХ, ලක්ෂ්යයx කැමති.
ඒ හා සමානව, අපි රවුමේ ඡේදනය වීමේ දෙවන ලක්ෂ්යය සහ සරල රේඛාව - ලක්ෂ්යය ගොඩනඟමුවයි(Fig.18,b).
සහල්. 18,ඒ
සහල්. 18b
I.6.ඒකපාර්ශ්වික පාලකයෙකු සමඟ ඉදිකිරීම්
ඩබ්ලිව් 
මෙහිදී අපි විශේෂ අවස්ථාවක් සලකා බලමු: ලකුණු P ලබා දීමට ඉඩ දෙන්න,ප්‍රශ්නය, ආර් 1
හාප්‍රශ්නය 1
. තවද ඔවුන් trapezoid හි සිරස්වල පිහිටා ඇත.
1. ඛණ්ඩය පී ප්‍රශ්නය අඩකින්
තීරණය රූපය 19 හි පෙන්වා ඇත
ලබා දී ඇති ලකුණු P,ප්‍රශ්නය, ආර් 1 හාප්‍රශ්නය 1 සහ සමාන්තර රේඛා
ආර්ප්‍රශ්නය, ආර් 1 ප්‍රශ්නය 1 . පී වියදම් කරමුප්‍රශ්නය 1 ප්‍රශ්නයආර් 1 = බී , RR 1 QQ 1 = ඒ
ලකුණු A සහ B. AB සම්බන්ධ කරන්න ආර්ප්‍රශ්නය = එෆ්- මැද
කොටස Pප්‍රශ්නය.
සහල්. දහනවය
2. ද්විත්ව කොටස ආර් 1 ප්‍රශ්නය 1.
ආර් 
විසඳුමක්
රූප සටහන 20. අපි ගොඩනඟමු
ලක්ෂ්යයඑෆ්- කොටසේ මැද ආර්ප්‍රශ්නයසහ එය සම්බන්ධ කරන්න
සමගප්‍රශ්නය 1. ආර් 1 ප්‍රශ්නය FQ 1 = M. අපි RM ක්‍රියාත්මක කරමු. ආර්එම් ආර් 1 ප්‍රශ්නය 1 = ආර්
සමානාත්මතාවයRQසහ ආර් 1 ප්‍රශ්නය 1 සමානතාවයෙන් අනුගමනය කරයි
ත්රිකෝණ 
ආර්එම්එෆ්හා ආර්එම්ප්‍රශ්නය 1
,
එෆ්එම්ප්‍රශ්නයහා ආර් 1
එම්ප්‍රශ්නය 1
, සහ සමානාත්මතාවය ආර්එෆ්හාFQ.
සහල්. 20
3
.
දිග කොටසක් සාදන්න
n
ආර්
1
ප්‍රශ්නය
1
.
එම් – 1 සමාන කොටස් Pප්‍රශ්නය 2 , ප්‍රශ්නය 2 ප්‍රශ්නය 3, … ප්‍රශ්නය එම් -1 ප්‍රශ්නය එම්
ඉන්පසු අපි ගොඩනඟමු (RR 1 ) හාප්‍රශ්නය එම් ප්‍රශ්නය 1 සහ සම්බන්ධ කරන්න
ලකුණු සමඟ ඔවුන්ගේ ඡේදනය ලක්ෂ්යය A
ප්‍රශ්නය 2 , ප්‍රශ්නය 3, … ප්‍රශ්නය එම් ලැබුනාඑම් -1 සෘජු
බෙදනවාආර් 1 ප්‍රශ්නය 1 මතඑම් සමාන කොටස්.
සදහාඑම් = 4 විසඳුම රූප සටහන 22 හි දක්වා ඇත
Fig.22
I.7. මාලිමා සහ පාලකය සමඟ ද්විත්ව ඒක පාර්ශවීය පාලකය හුවමාරු කිරීමේ හැකියාව
ද්වි-පාර්ශ්වික පාලකයෙකු මාලිමා යන්ත්රයක් සහ පාලකයෙකු සමඟ හුවමාරු කළ හැකි බව අපි ඔප්පු කරමු. මෙය සිදු කිරීම සඳහා, අපි පහත සඳහන් ප්රකාශයන් ඔප්පු කරමු:
යෝජනාව 1: මාලිමා යන්ත්රයක් සහ කෙලින් කළ හැකි සියලුම ඉදිකිරීම් ද්වි-පාර්ශ්වික කෙළින්ම කළ හැකිය.
මාලිමා යන්ත්රයක් සහ රූලයක් සමඟින් තැනීමේදී, පාලකයා ලක්ෂ්ය දෙකක් හරහා සරල රේඛාවක් අඳින අතර, මාලිමා යන්ත්‍රය රවුමක් සාදන බැවින් (දී ඇති එකට සමාන වූ ලක්ෂ්ය සමූහයක් සොයා ගනී), එවිට මාලිමා යන්ත්‍රය සහ පාලකය සහිත සියලුම ඉදිකිරීම් අඩු කරනු ලැබේ. සරල රේඛා දෙකක්, රවුම් දෙකක් සහ සරල රේඛාවක් සහිත කවයක් ඡේදනය කිරීම.
රේඛා දෙකක ඡේදනය පාලකයෙකු භාවිතයෙන් ඇද ගත හැකිය.
රවුමක සහ සරල රේඛාවක ඡේදනය (රූපය 23):
ගොඩනැගිල්ල:AB කොටස ලබා දීමට ඉඩ දෙන්න - රවුමේ අරය, සරල රේඛාවඑල් , O කවයේ කේන්ද්රය, එවිට:
1) අපි වැය කරන්නේ OS ||එල් , OS = AB.
2) අපි වැය කරන්නේ OS ||කේසහ a මත දුරස්ථ.
3) අපි වියදම් කරනවාOD, OD එල් = ඩී; OD k) තේල්ස් ප්‍රමේයයේ අනුපිළිවෙලින්
4) සමානාත්මතාවයේ සංක්රාන්ති නීතිය අනුව
5) සලකා බලන්නOMQE. OMQEOM || සිට සමාන්තර චලිතයකිEQසහ OE ||MC(රේඛීය පැති සමාන්තර වේ). මෙය රොම්බස් බව ඔප්පු කරමු.
5.1) හැසිරීමQZ OCහාQG මත, එවිටQG = QZ = ඒ.
5.2) OMQ = RQM(හරස් බොරු); OS =මත, ඔප්පු කළ යුතු විය.
රවුම් දෙකක ඡේදනය: සමාන.
ප්‍රකාශය 2: ද්වි-පාර්ශ්වික පාලකයෙකු සමඟ කළ හැකි සියලුම ඉදිකිරීම් මාලිමා යන්ත්රයක් සහ කෙළින්ම කළ හැකිය.
මෙය සිදු කිරීම සඳහා, අපි මාලිමා යන්ත්රයක් සහ පාලකයෙකු භාවිතා කරමින් ද්වි-පාර්ශ්වික පාලකයෙකු සඳහා සම්මත ඉදිකිරීම් සිදු කරන්නෙමු.
1) ලක්ෂ්ය දෙකක රේඛාවක් පාලකයෙකු භාවිතයෙන් පහසුවෙන් ඇද ගත හැකිය.
2) ලබා දී ඇති රේඛාවට සමාන්තරව සහ දුරස්ථ රේඛාවක් ඉදිකිරීම දී ඇති දුර:
2.1) රේඛාවක් ලබා දෙන්නකේසහ දිග කොටසකිඒ.
2.2) අපි අත්තනෝමතික රේඛාවක් ගොඩනඟමුබී කේ, ඉඩ දෙන්නකේ බී= බී.
2.3) මතබීතිත දෙපසබීසරල රේඛාවක් මතබීදිගක් වෙන් කරන්නඒ, ලකුණු ඉඩ දෙන්නසීහාඩී.
2.4) ලක්ෂ්යයක් හරහාසීසරල රේඛාවක් සාදන්නc කේ.
2.5) ලක්ෂ්යයක් හරහාඩීසරල රේඛාවක් සාදන්නඈ කේ.
2.6) සෘජුcහාඈ- කැමති, සිටක්රි.පූහාBDසමානඒඉදි කිරීම් මගින් සහ රේඛාව අතර දුර ප්රමාණයට සමාන වේකේසහ සෘජු
3) එකිනෙකට සමාන්තරව රේඛා තැනීම සහ ලබා දී ඇති ලක්ෂ්ය දෙකක් හරහා ගමන් කිරීම සහ ලබා දී ඇති කොටසට සමාන වන දුර අතර දුර:
3.1) ලකුණු දෙන්න ඉඩ දෙන්නඒහාබීසහ දිග කොටසකිඒ.
3.2) ලක්ෂ්යයක් කේන්ද්‍ර කරගත් රවුමක් අඳින්නඒසහ අරයඒ.
3.3) අපි ලක්ෂ්යයක් හරහා දී ඇති කවයකට ස්පර්ශකයක් ගොඩනඟමුබී; එවැනි ස්පර්ශක දෙකක් තිබේ නම්බීරවුමෙන් පිටත පිහිටා ඇත (නම්AB> ඒ), එකක් නම්බීරවුම මත පිහිටා ඇත (නම්AB= ඒ), නම් නැතබීරවුම ඇතුළත පිහිටා ඇත (AB< ඒ) මෙම ස්පර්ශකය අපේක්ෂිත රේඛා වලින් එකකි; ලක්ෂ්යය හරහා යාමට ඉතිරිව ඇතඒඑයට සමාන්තරව සරල රේඛාවක්.
3.4) එක් රේඛාවක් ස්පර්ශකයක් ලෙස රවුමේ අරයට ලම්බක වන බැවින්, දෙවැන්න ද එයට ලම්බක වේ (ඒවා සමාන්තර බැවින්), එබැවින් ඒවා අතර දුර අරයට සමාන වන අතර එය ඉදිකිරීම් අනුව සමාන වේ. දක්වාඒඅවශ්ය වූයේ කුමක්ද.
මේ අනුව, ද්විත්ව ඒකපාර්ශ්වික පාලකයෙකුගේ සහ මාලිමා යන්ත්‍රයේ සහ පාලකයෙකුගේ හුවමාරු හැකියාව අපි ඔප්පු කර ඇත්තෙමු.
නිගමනය: ද්විත්ව ඒක පාර්ශවීය පාලකයෙකු මාලිමා යන්ත්‍ර සහ පාලකයෙකු සමඟ හුවමාරු කළ හැකිය.
නිගමනය
එබැවින්, මාලිමා යන්ත්රයක් සහ පාලකයෙකුගේ ආධාරයෙන් සම්භාව්ය ඉදිකිරීම් ගැටළු විසඳීම සඳහා එක් පාලකයෙකු භාවිතා කිරීමේ හැකියාව පිළිබඳ ප්‍රශ්නය සලකා බලා විසඳා ඇත. සමාන්තර දාර සහිත එක් පාලකයෙකු පමණක් භාවිතයෙන් ඉදිකිරීම් ගැටළු විසඳිය හැකි බව පෙනේ. වඩාත් සංකීර්ණ ගැටළු විසඳන විට, මෙම ලිපියේ සලකා බලනු ලබන ඊනියා මූලික ඉදිකිරීම් මත අනාගතයේ දී විශ්වාසය තැබිය යුතුය.
ඉදිරිපත් කරන ලද ද්රව්ය ගණිත පාඩම් වල, ගණිත කවයක පන්තිවල පමණක් නොව ප්රායෝගික ක්‍රියාකාරකම් වලදීද කෙලින්ම යෙදිය හැකිය.
භාවිතා කළ සාහිත්‍ය ලැයිස්තුව
Aliyev A.V. ජ්යාමිතික ඉදිකිරීම්. පාසලේ ගණිතය. 1978 අංක 3
ග්ලේසර් ජී.අයි. පාසලේ ගණිත ඉතිහාසය. එම්., බුද්ධත්වය. 1981.
ඩෙප්මන් අයි.යා. ගණිතය පොතක පිටු පිටුපස. එම්.. අධ්යාපනය. 1989.
පයිතගරස්ගේ අඩිපාරේ එලෙන්ස්කි ශා. එම්., ඩෙට්ගිස්. 1961.
තරුණ ගණිතඥයෙකුගේ විශ්වකෝෂ ශබ්දකෝෂය. M., Pedagogy. 1985
ඉදිකිරීම් ගැටළු වලදී, අපි ඉදිකිරීම් සලකා බලමු ජ්යාමිතික රූපයපාලකයෙකු සහ මාලිමා යන්ත්‍රයකින් කළ හැකි දේ.
පාලකයෙකු සමඟ, ඔබට:
අත්තනෝමතික රේඛාව;
දී ඇති ලක්ෂ්යයක් හරහා ගමන් කරන අත්තනෝමතික රේඛාවක්;
ලබා දී ඇති ලක්ෂ්ය දෙකක් හරහා ගමන් කරන සරල රේඛාවක්.
මාලිමා යන්ත්රයක් භාවිතා කරමින්, දී ඇති කේන්ද්‍රයකින් ලබා දී ඇති අරයක කවයක් ඔබට විස්තර කළ හැකිය.
දී ඇති ලක්ෂ්‍යයකින් දී ඇති රේඛාවක් මත කොටසක් ඇඳීමට මාලිමා යන්ත්රයක් භාවිතා කළ හැකිය.
ඉදිකිරීම් සඳහා ප්රධාන කාර්යයන් සලකා බලන්න.
කාර්යය 1. a, b, c ලබා දී ඇති පැති සහිත ත්රිකෝණයක් සාදන්න (රූපය 1).
තීරණය. පාලකයෙකුගේ සහාය ඇතිව, අත්තනෝමතික සරල රේඛාවක් අඳින්න සහ එය මත අත්තනෝමතික ලක්ෂ්යයක් ගන්න. a ට සමාන මාලිමා විවරයක් සහිතව, අපි කේන්ද්රය B සහ අරය a සහිත කවයක් විස්තර කරමු. C රේඛාව සමඟ එහි ඡේදනය වීමේ ලක්ෂ්යය වීමට ඉඩ දෙන්න. c ට සමාන මාලිමා විවරයක් සමඟ, අපි B කේන්ද්‍රයේ සිට කවයක් විස්තර කරමු, සහ b ට සමාන මාලිමා විවරයක් සමඟ - C මධ්යයේ සිට රවුමක්. A මෙම කවවල ඡේදනය වීමේ ලක්ෂ්යය ලෙස සලකමු. ABC ත්‍රිකෝණයට a, b, c ට සමාන පැති ඇත.
අදහස් දක්වන්න. රේඛා කොටස් තුනක් ත්රිකෝණයක පැති ලෙස ක්‍රියා කිරීමට නම්, ඒවායින් විශාල ප්‍රමාණය අනෙක් දෙකේ එකතුවට වඩා අඩු වීම අවශ්ය වේ (සහ< b + с).
කාර්යය 2.
තීරණය. ශීර්ෂය A සහ OM කදම්භ සහිත මෙම කෝණය රූප සටහන 2 හි පෙන්වා ඇත.
දී ඇති කෝණයේ A ශීර්ෂය කේන්ද්‍ර කර ගත් අත්තනෝමතික කවයක් අඳින්න. B සහ C කෝණයෙහි පැති සමග රවුමේ ඡේදනය වීමේ ලක්ෂ්යයන් (රූපය 3, a). O ලක්ෂ්‍යයේ කේන්ද්රය සහිත AB අරය සහිත රවුමක් අඳිමු - මෙම කිරණෙහි ආරම්භක ස්ථානය (රූපය 3, b). ලබා දී ඇති කිරණ සමඟ මෙම කවයේ ඡේදනය වීමේ ලක්ෂ්යය С 1 ලෙස දැක්වේ. අපි C 1 කේන්ද්රය සහ BC අරය සහිත කවයක් විස්තර කරමු. රවුම් දෙකක ඡේදනය වන ලක්ෂ්යය B 1 අපේක්ෂිත කෝණයේ පැත්තේ පිහිටා ඇත. මෙය සමානාත්මතාවයෙන් Δ ABC \u003d Δ OB 1 C 1 (ත්රිකෝණවල සමානාත්මතාවය සඳහා තුන්වන නිර්ණායකය) අනුගමනය කරයි.
කාර්යය 3.ලබා දී ඇති කෝණයෙහි බයිසෙක්ටරය ගොඩනඟන්න (රූපය 4).
තීරණය. දී ඇති කෝණයක A ශීර්ෂයෙන්, මධ්යයේ සිට, අපි අත්තනෝමතික අරය කවයක් අඳින්නෙමු. B සහ C කෝණයේ පැති සමග එහි ඡේදනය වීමේ ලක්ෂ්යයන් වේ. එකම අරය සහිත B සහ C ලකුණු වලින් අපි කවයන් විස්තර කරමු. A. Ray AD කෝණය A අඩකින් බෙදීමට වඩා වෙනස්, D ඔවුන්ගේ ඡේදනය වීමට ඉඩ දෙන්න. මෙය සමානාත්මතාවයෙන් ΔABD = ΔACD (ත්රිකෝණවල සමානාත්මතාවය සඳහා තුන්වන නිර්ණායකය) අනුගමනය කරයි.
කාර්යය 4.මෙම කොටසට මධ්යස්ථ ලම්බකයක් අඳින්න (රූපය 5).
තීරණය. අත්තනෝමතික නමුත් සමාන මාලිමා විවරයක් (විශාල 1/2 AB), අපි A සහ B ලක්ෂ්යවල මධ්‍යස්ථාන සහිත චාප දෙකක් විස්තර කරමු, ඒවා C සහ D සමහර ස්ථානවල ඡේදනය වේ. සරල රේඛා CD අවශ්ය ලම්බක වනු ඇත. ඇත්ත වශයෙන්ම, ඉදිකිරීම් වලින් දැකිය හැකි පරිදි, එක් එක් ලක්ෂ්ය C සහ D A සහ B ට සමානව දුරස් වේ; එබැවින්, මෙම ලක්ෂ්ය AB ඛණ්ඩයට ලම්බක ද්වි අංශය මත පිහිටා තිබිය යුතුය.
කාර්යය 5.මෙම කොටස අඩකින් බෙදන්න. එය ගැටළුව 4 ලෙසම විසඳනු ලැබේ (රූපය 5 බලන්න).
කාර්යය 6.දී ඇති ලක්ෂ්යයක් හරහා, දී ඇති රේඛාවට ලම්බකව රේඛාවක් අඳින්න.
තීරණය. අවස්ථා දෙකක් හැකි ය:
1) ලබා දී ඇති ලක්ෂ්යය O ලබා දී ඇති සරල රේඛාවේ පිහිටා ඇත a (රූපය 6).
O ලක්ෂ්‍යයෙන් අපි අත්තනෝමතික අරයක් සහිත කවයක් අඳින්නෙමු, එය A සහ B ලක්ෂ්‍යවලදී a රේඛාව ඡේදනය වේ. A සහ B ලක්ෂ්‍යවලින් අපි එකම අරය සහිත රවුම් අඳින්නෙමු. О 1 ඔවුන්ගේ ඡේදනය වීම O ට වඩා වෙනස් වීමට ඉඩ දෙන්න. අපට ОО 1 ⊥ AB ලැබේ. ඇත්ත වශයෙන්ම, O සහ O 1 යන ලක්ෂ්ය AB ඛණ්ඩයේ කෙළවරට සමාන දුරින් පිහිටා ඇති අතර, එම නිසා, මෙම කොටසට ලම්බක ද්වි අංශය මත පිහිටයි.
උදාහරණයක්
රේඛාවක් අඩකින් බෙදීම
බෙදීමේ ගැටලුව. මෙම කොටස බෙදීමට මාලිමා යන්ත්රයක් සහ කෙලවරක් භාවිතා කරන්න ABසමාන කොටස් දෙකකට. විසඳුම් වලින් එකක් රූපයේ දැක්වේ:
- මාලිමා යන්ත්‍ර ලක්ෂ්ය කේන්ද්‍ර කර ගත් රවුම් අඳියි ඒහා බීඅරය AB.
- ඡේදනය වීමේ ස්ථාන සොයා ගැනීම පීහා ප්‍රශ්නයඉදිකරන ලද කව දෙකක් (චාප).
- පාලකයෙකු මත, ලකුණු හරහා ගමන් කරන කොටසක් හෝ රේඛාවක් අඳින්න පීහා ප්‍රශ්නය.
- කොටසේ මැද ලක්ෂ්යය සොයා ගැනීම AB- ඡේදනය වන ස්ථානය ABහා PQ.
විධිමත් අර්ථ දැක්වීම
ඉදිකිරීම් ගැටළු තලයේ සියලුම ලක්ෂ්යවල කට්ටලය, තලයේ සියලුම රේඛා කට්ටලය සහ තලයේ සියලුම කවවල කට්ටලය සලකා බලයි, ඒවා හරහා පහත සඳහන් මෙහෙයුම් සඳහා අවසර ඇත:
- සියලුම ලක්ෂ්ය සමූහයෙන් ලක්ෂ්යයක් තෝරන්න:
- අත්තනෝමතික ලක්ෂ්යය
- දී ඇති රේඛාවක අත්තනෝමතික ලක්ෂ්යය
- දී ඇති කවයක් මත අත්තනෝමතික ලක්ෂ්යය
- ලබා දී ඇති රේඛා දෙකක ඡේදනය වීමේ ලක්ෂ්යය
- දී ඇති රේඛාවක සහ දී ඇති කවයක ඡේදනය / ස්පර්ශක ලක්ෂ්ය
- ලබා දී ඇති කව දෙකක ඡේදනය / ස්පර්ශක ලක්ෂ්ය
- "හරහා පාලකයන්»සියලු පේළි කට්ටලයෙන් රේඛාවක් තෝරන්න:
- අත්තනෝමතික රේඛාව
- දී ඇති ලක්ෂ්යයක් හරහා ගමන් කරන අත්තනෝමතික රේඛාවක්
- ලබා දී ඇති ලක්ෂ්ය දෙකක් හරහා ගමන් කරන රේඛාවක්
- "හරහා මාලිමා යන්ත්‍රය»සියලු කවයන් සමූහයෙන් කවයක් තෝරන්න:
- අත්තනෝමතික කවය
- අත්තනෝමතික කවය කේන්ද්‍රගත කර ඇත ලබා දී ඇති ලක්ෂ්යය
- දී ඇති ලක්ෂ්ය දෙකක් අතර දුරට සමාන අරයක් සහිත අත්තනෝමතික කවයක්
- දී ඇති ලක්ෂ්‍යයක කේන්ද්‍රගත වූ සහ දී ඇති ලක්ෂ්ය දෙකක් අතර දුරට සමාන අරයක් සහිත කවයක්
ගැටලුවේ තත්වයන් තුළ, යම් යම් කරුණු සමූහයක් නියම කර ඇත. සීමිත මෙහෙයුම් සංඛ්‍යාවක් භාවිතා කරමින්, මුල් කට්ටලය සමඟ දී ඇති සම්බන්ධතාවයක ඇති ඉහත අවසර ලත් මෙහෙයුම් අතරින් තවත් ලක්ෂ්ය කට්ටලයක් තැනීම අවශ්ය වේ.
ඉදිකිරීම් ගැටලුවේ විසඳුම අත්යවශ්ය කොටස් තුනක් අඩංගු වේ:
- දී ඇති කට්ටලයක් තැනීමේ ක්‍රමයේ විස්තරය.
- විස්තර කර ඇති ආකාරයට ගොඩනගා ඇති කට්ටලය ඇත්ත වශයෙන්ම මුල් කට්ටලය සමඟ දී ඇති සම්බන්ධතාවයක ඇති බවට සාක්ෂියකි. සාමාන්‍යයෙන් ප්‍රමේයයක නිත්ය සාධනයක් ලෙස ගොඩ නැගීමේ සාධනය සිදු කරනු ලබන්නේ, ප්‍රත්‍යක්ෂ සහ අනෙකුත් ඔප්පු කරන ලද ප්‍රමේයයන් මත ය.
- විස්තර කරන ලද ඉදිකිරීම් ක්රමය විශ්ලේෂණය කිරීම ආරම්භක කොන්දේසි වල විවිධ ප්‍රභේද සඳහා එහි යෙදීම් සඳහා මෙන්ම විස්තර කරන ලද ක්රමය මගින් ලබාගත් විසඳුමේ සුවිශේෂත්වය හෝ අද්විතීයභාවය සඳහා.
දන්නා ගැටළු
- ලබා දී ඇති කව තුනකට රවුම් ස්පර්ශකයක් ගොඩනැගීමේ ඇපලෝනියස්ගේ ගැටලුව. ලබා දී ඇති කව කිසිවක් අනෙකා තුළ නොපවතී නම්, මෙම ගැටලුවට අත්‍යවශ්‍යයෙන්ම වෙනස් විසඳුම් 8ක් ඇත.
- බ්‍රහ්මගුප්තගේ ප්‍රශ්නය එහි හතර පැත්තේ සෙල්ලිපි කළ චතුරස්රයක් තැනීමයි.
නිත්ය බහුඅස්‍ර ඉදිකිරීම
පැරණි ජ්‍යාමිතිකයන් නිවැරදිව ගොඩනගන්නේ කෙසේදැයි දැන සිටියහ n-gons සඳහා , , සහ .
හැකි සහ කළ නොහැකි ඉදිකිරීම්
සියලුම ඉදිකිරීම් සමහර සමීකරණයකට විසඳුම් වලට වඩා වැඩි දෙයක් නොවන අතර මෙම සමීකරණයේ සංගුණක ලබා දී ඇති කොටස්වල දිගට සම්බන්ධ වේ. එමනිසා, අංකයක් තැනීම ගැන කතා කිරීම පහසුය - යම් ආකාරයක සමීකරණයකට චිත්රක විසඳුමක්. ඉහත අවශ්‍යතා රාමුව තුළ, පහත සඳහන් ඉදිකිරීම් කළ හැකිය:
- රේඛීය සමීකරණ සඳහා විසඳුම් ඉදිකිරීම.
- චතුරස්රාකාර සමීකරණවල විසඳුම් ඉදිකිරීම.
වෙනත් වචන වලින් කිවහොත්, මුල් සංඛ්යා (ඛණ්ඩවල දිග) වර්ගමූලය භාවිතා කරමින් අංක ගණිත ප්‍රකාශනවලට සමාන සංඛ්යා පමණක් තැනීමට හැකිය. උදාහරණයක් වශයෙන්,
වෙනස්කම් සහ සාමාන්යකරණයන්
- තනි මාලිමා යන්ත්රයක් සහිත ඉදිකිරීම්. Mohr-Mascheroni ප්රමේයය අනුව, එක් මාලිමා යන්ත්රයක් ආධාරයෙන්, ඔබට මාලිමා යන්ත්රයක් සහ පාලකයෙකු සමඟ ගොඩනගා ගත හැකි ඕනෑම රූපයක් ගොඩනගා ගත හැකිය. මෙම අවස්ථාවෙහිදී, එය මත ලකුණු දෙකක් ලබා දී ඇත්නම්, රේඛාවක් ඉදිකරනු ලැබේ.
- තනි පාලකයෙකු සමඟ ඉදිකිරීම්.එක් පාලකයෙකුගේ උපකාරයෙන් සිදු කළ හැක්කේ ප්රක්ෂේපිත ලෙස වෙනස් නොවන ඉදිකිරීම් පමණක් බව දැකීම පහසුය. විශේෂයෙන්, කොටස සමාන කොටස් දෙකකට බෙදීමට හෝ අඳින ලද රවුමේ කේන්ද්රය සොයා ගැනීමට පවා නොහැකි ය. නමුත් සලකුණු කරන ලද කේන්ද්‍රයක් සහිත ගුවන් යානයේ පෙර-ඇඳි කවයක් තිබේ නම්, පාලකයෙකු භාවිතා කරමින්, ඔබට මාලිමා යන්ත්රයක් සහ පාලකයෙකු (Poncelet-Steiner theorem) සමඟ සමාන ඉදිකිරීම් අඳින්න පුළුවන්. ඉංග්රීසි)), 1833. පාලකයා මත සෙරිෆ් දෙකක් තිබේ නම්, එහි ආධාරයෙන් ඉදිකිරීම් මාලිමා යන්ත්රයක් සහ පාලකයෙකුගේ ආධාරයෙන් ඉදිකිරීම් වලට සමාන වේ (නැපෝලියන් මෙය ඔප්පු කිරීමේදී වැදගත් පියවරක් ගත්තේය).
- සීමිත මෙවලම් සහිත ඉදිකිරීම්.මේ ආකාරයේ ගැටළු වලදී, මෙවලම් (ගැටළුවේ සම්භාව්ය සූත්‍රගත කිරීමට ප්‍රතිවිරුද්ධව) පරමාදර්ශී නොවන නමුත් සීමිත යැයි සැලකේ: පාලකයෙකු භාවිතයෙන් ලකුණු දෙකක් හරහා සරල රේඛාවක් ඇඳිය හැක්කේ මෙම ලක්ෂ්ය අතර දුර නිශ්චිතව නොඉක්මවන්නේ නම් පමණි. අගය; මාලිමා යන්ත්‍රයකින් අඳින ලද කව වල අරය ඉහලින්, පහලින් හෝ ඉහලින් සහ පහලින් සීමා කළ හැක.
- පැතලි ඔරිගාමි සහිත ගොඩනැගිල්ල. Khujit නීති බලන්න
ද බලන්න
- ගතික ජ්යාමිතික වැඩසටහන් මඟින් පරිගණකයක් මත මාලිමා යන්ත්රයක් සහ කෙලින් ඇඳීමට ඔබට ඉඩ සලසයි.
සටහන්
සාහිත්යය
- A. ඇඩ්ලර්ජ්‍යාමිතික ඉදිකිරීම් න්‍යාය / G. M. Fikhtengolts විසින් ජර්මානු භාෂාවෙන් පරිවර්තනය කරන ලදී. - තුන්වන සංස්කරණය. - L.: Uchpedgiz, 1940. - 232 p.
- I. I. ඇලෙක්සැන්ඩ්රොව්ඉදිකිරීම් සඳහා ජ්යාමිතික ගැටළු එකතු කිරීම. - දහඅටවන සංස්කරණය. - එම් .: උච්පෙඩ්ගිස්, 1950. - 176 පි.
- B.I. Argunov, M. B. Balk. - දෙවන සංස්කරණය. - එම් .: උච්පෙඩ්ගිස්, 1957. - 268 පි.
- A. M. Voronetsමාලිමා යන්ත්‍රයක ජ්යාමිතිය. - M.-L.: ONTI, 1934. - 40 පි. - (ජනප්රිය ගණිත පුස්තකාලය යටතේ සාමාන්ය සංස්කරණය L. A. Lyusternik).
- V. A. ගයිලර්විසඳිය නොහැකි ඉදිකිරීම් ගැටළු // සිසිලනකාරකය. - 1999. - අංක 12. - S. 115-118.
- V. A. කිරිචෙන්කෝමාලිමා යන්ත්‍ර සහ පාලකයා සහ ගැලෝයිස් න්‍යාය සහිත ඉදිකිරීම් // ගිම්හාන පාසල"නූතන ගණිතය". - ඩබ්නා, 2005.
- යූ අයි මනින් IV පොත. ජ්යාමිතිය // ප්රාථමික ගණිතයේ විශ්වකෝෂය. - එම් .: Fizmatgiz, 1963. - 568 පි.
- Y. පීටර්සන්ජ්යාමිතික ඉදිකිරීම් ගැටළු විසඳීම සඳහා ක්රම සහ න්යායන්. - එම් .: ඊ ලිස්නර් සහ යූ රෝමන් ගේ මුද්‍රණාලය, 1892. - 114 පි.
- V. V. Prasolovසම්භාව්ය ගොඩනැගිලි ගැටළු තුනක්. ඝනකයක් දෙගුණ කිරීම, කෝණයක ත්රිකෝණය, රවුම වර්ග කිරීම. - එම් .: Nauka, 1992. - 80 p. - (ගණිතය පිළිබඳ ජනප්රිය දේශන).
- ජේ. ස්ටයිනර්සරල රේඛාවක් සහ ස්ථාවර කවයක් භාවිතයෙන් සිදු කරන ලද ජ්යාමිතික ඉදිකිරීම්. - එම් .: උච්පෙඩ්ගිස්, 1939. - 80 පි.
- ගණිතය පිළිබඳ විකල්ප පාඨමාලාව. 7-9 / Comp. I. L. Nikolskaya. - එම් .: අධ්යාපනය, 1991. - S. 80. - 383 පි. - ISBN 5-09-001287-3
විකිමීඩියා පදනම. 2010 .
වෙනත් ශබ්ද කෝෂවල "මාලිමා යන්ත්රයක් සහ පාලකයෙකු සමඟ ඉදිකිරීම්" යනු කුමක්දැයි බලන්න:
පාලකයන් - Akademika VseTools හි වැඩ කරන වට්ටම් කූපනයක් ලබා ගන්න හෝ VseTools හි විකිණීමට ඇති නොමිලේ නැව්ගත කිරීම සමඟ පාලකයින් ලාභදායී ලෙස මිලදී ගන්න
පුරාණ කාලයේ සිට දන්නා යුක්ලීඩීය ජ්යාමිතිය අංශය. ඉදිකිරීම් කාර්යයන් වලදී, පහත සඳහන් මෙහෙයුම් සිදු කළ හැකිය: තලයේ අත්තනෝමතික ලක්ෂ්යයක්, ඉදිකරන ලද එක් රේඛාවක ලක්ෂ්යයක් හෝ ඉදිකරන ලද රේඛා දෙකක සන්ධිස්ථානයක් සලකුණු කරන්න. ...... විකිපීඩියා සහය ඇතිව
මාලිමා යන්ත්රයක් සහ සෘජු දාරයක් ආධාරයෙන් ඉදි කිරීම් පුරාණ කාලයේ සිට දන්නා යුක්ලීඩීය ජ්‍යාමිතියෙහි කොටසකි. ඉදිකිරීම් කටයුතු වලදී, පහත සඳහන් මෙහෙයුම් සිදු කළ හැකිය: තලයේ අත්තනෝමතික ලක්ෂ්යයක්, ඉදිකරන ලද එක් රේඛාවක ලක්ෂ්යයක් හෝ ලක්ෂ්යයක් සලකුණු කරන්න ... ... විකිපීඩියා
උදා., එස්., භාවිතා කරන්න. සංයුක්ත. බොහෝ විට රූප විද්යාව: (නැත) කුමක්ද? ඉදිකිරීම් කුමක් සඳහාද? ඉදිකිරීම්, (බලන්න) කුමක්ද? ගොඩනැගීම කුමක්ද? ගොඩනැගීම, කුමක් ගැනද? ගොඩනැගීම ගැන; pl. මොනවාද? ඉදිකිරීම්, (නැත) කුමක්ද? ඉදිකිරීම්, ඇයි? ඉදිකිරීම්, (බලන්න) කුමක්ද? ඉදිකිරීම් වඩා? ... ... Dmitriev ශබ්දකෝෂය
