Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt="(!LANG:>Construction with ruler and compass Geometry">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="(!LANG:> Construct a segment equal to the given Ú Problem A B"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="(!LANG:> Constructing an angle equal to a given one Consider triangles"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="(!LANG:> Constructing an angle bisector Problem Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="(!LANG:> Construction of perpendicular lines Ú Problem Given a line"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ !} isosceles triangle RAB Q is also the height, then PM is perpendicular to a.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="(!LANG:> Constructing the midpoint of a segment Task Ú Construct the midpoint of a given"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}

Municipal budgetary educational institution

average comprehensive school No. 34 with in-depth study of individual subjects

MAN, Physics and Mathematics Section

"Geometric constructions using a compass and straightedge"

Completed by: student of 7 "A" class

Batishcheva Victoria

Head: Koltovskaya V.V.

Voronezh, 2013

3. Construction of an angle equal to a given one.

P draw an arbitrary circle centered at the vertex A of the given angle (Fig. 3). Let B and C be the intersection points of the circle with the sides of the angle. With radius AB, we draw a circle centered at the point O, the starting point of the given half-line. The point of intersection of this circle with the given half-line is denoted by C 1 . Describe a circle with center C 1 and Fig.3

radius BC. Point B 1 the intersection of the constructed circles in the specified half-plane lies on the side of the desired angle.

6. Construction of perpendicular lines.

We draw a circle with an arbitrary radius r centered at the point O Fig.6. The circle intersects the line at points A and B.From points A and B we draw circles with radius AB. Let melancholy C be the point of intersection of these circles. We got points A and B at the first step, when constructing a circle with an arbitrary radius.

The desired line passes through the points C and O.

Fig.6

Known Issues

1.Brahmagupta's task

Construct an inscribed quadrilateral with four sides. One solution uses the circle of Apollonius.Let's solve the Apollonius problem using the analogy between a tricycle and a triangle. How do we find a circle inscribed in a triangle: we build the intersection point of the bisectors, drop the perpendiculars from it to the sides of the triangle, the bases of the perpendiculars (the points of intersection of the perpendicular with the side on which it is lowered) and give us three points lying on the required circle. We draw a circle through these three points - the solution is ready. We will do the same with the Apollonius problem.

2. Apollonius' problem

Use a compass and straightedge to construct a circle tangent to the three given circles. According to legend, the problem was formulated by Apollonius of Perga around 220 BC. e. in the book "Touch", which was lost, but was restored in 1600 by François Vieta, "Gallic Apollonius", as his contemporaries called him.

If none of the given circles lies inside the other, then this problem has 8 essentially different solutions.

Construction of regular polygons.

P

correct (or equilateral ) triangle - this regular polygonwith three sides, the first of the regular polygons. Everything sides of an equilateral triangle are equal, and all the angles are 60°. To construct an equilateral triangle, you need to divide the circle into 3 equal parts. To do this, it is necessary to draw an arc with a radius R of this circle from only one end of the diameter, we get the first and second divisions. The third division is at the opposite end of the diameter. Connecting these points, we get an equilateral triangle.

Regular hexagon canbuild with a compass and straightedge. Belowthe construction method is givenby dividing the circle into 6 parts. We use the equality of the sides of a regular hexagon to the radius of the circumscribed circle. From the opposite ends of one of the diameters of the circle, we describe arcs of radius R. The intersection points of these arcs with a given circle will divide it into 6 equal parts. Consistently connecting the points found, a regular hexagon is obtained.

Construction of a regular pentagon.

P
regular pentagon can beconstructed using a compass and straightedge, or by fitting it into a givencircle, or by building on the basis of a given side. This process is described by Euclidin his Elements, about 300 BC. e.

Here is one method for constructing a regular pentagon in a given circle:

Construct a circle in which the pentagon will be inscribed and designate its center asO . (This is the green circle in the diagram on the right).

Pick a point on the circleA , which will be one of the vertices of the pentagon. Draw a line throughO AndA .

Construct a line perpendicular to the lineOA passing through the pointO . Designate one of its intersections with the circle as a pointB .

Build a pointC midway betweenO AndB .

C through a pointA . Mark its intersection with the lineOB (inside the original circle) as a pointD .

Draw a circle centered atA through point D, mark the intersection of this circle with the original (green circle) as pointsE AndF .

Draw a circle centered atE through a pointA G .

Draw a circle centered atF through a pointA . Designate its other intersection with the original circle as a pointH .

Build a regular pentagonAEGHF .

Unsolvable problems

The following three construction tasks were set in antiquity:

Angle trisection - split an arbitrary angle into three equal parts.

In other words, it is necessary to construct the trisectors of the angle - the rays dividing the angle into three equal parts. P. L. Vanzel proved in 1837 that the problem is solvable only when, for example, the trisection is feasible for angles α = 360°/n, provided that the integer n is not divisible by 3. However, in the press from time to time published (incorrect) methods for trisecting an angle with a compass and straightedge.

Doubling the Cube - a classic ancient problem on the construction of a cube with a compass and a ruler, the volume of which is twice the volume of a given cube.

In modern notation, the problem is reduced to solving the equation. It all comes down to the problem of constructing a segment of length. P. Wanzel proved in 1837 that this problem cannot be solved with the help of a compass and straightedge.

Squaring the circle - the task of finding a construction using a compass and a ruler of a square that is equal in area to a given circle.

As you know, with the help of a compass and a ruler, you can perform all 4 arithmetic operations and extract square root; hence it follows that the squaring of a circle is possible if and only if, with the help of a finite number of such operations, it is possible to construct a segment of length π. Thus, the unsolvability of this problem follows from the non-algebraic nature (transcendence) of the number π, which was proved in 1882 by Lindemann.

Another well-known problem that cannot be solved with the help of a compass and a ruler isconstruction of a triangle by three given lengths of bisectors .

Moreover, this problem remains unsolvable even in the presence of a trisector.

Only in the 19th century was it proved that all three problems were unsolvable using only a compass and straightedge. The question of the possibility of construction is completely solved by algebraic methods based on the Galois theory.

DO YOU KNOW THAT...

(from the history of geometric constructions)

Once upon a time, a mystical meaning was invested in the construction of regular polygons.

So, the Pythagoreans, followers of the religious and philosophical teachings founded by Pythagoras, and who lived in ancient greece (V I-I Vcenturies BC BC), adopted as a sign of their union a star polygon formed by the diagonals of a regular pentagon.

The rules for the strict geometric construction of some regular polygons are set out in the book "Beginnings" by the ancient Greek mathematician Euclid, who lived inIIIin. BC. To perform these constructions, Euclid suggested using only a ruler and a compass, which at that time did not have a hinged device for connecting the legs (such a limitation in tools was an indispensable requirement of ancient mathematics).

Regular polygons were widely used in ancient astronomy. If Euclid was interested in the construction of these figures from the point of view of mathematics, then for the ancient Greek astronomer Claudius Ptolemy (about 90 - 160 AD) it turned out to be necessary as an auxiliary tool in solving astronomical problems. So, in the 1st book of the Almagest, the entire tenth chapter is devoted to the construction of regular pentagons and decagons.

However, in addition to purely scientific works, the construction of regular polygons was an integral part of books for builders, artisans, and artists. The ability to depict these figures has long been required in architecture, jewelry, and fine arts.

The “Ten Books on Architecture” by the Roman architect Vitruvius (who lived around 63-14 BC) says that the city walls should look like a regular polygon in plan, and the towers of the fortress “should be made round or polygonal, because the quadrilateral rather destroyed by siege weapons.

The planning of cities was of great interest to Vitruvius, who believed that it was necessary to plan the streets so that the main winds did not blow along them. It was assumed that there were eight such winds and that they blow in certain directions.

During the Renaissance, the construction of regular polygons, and in particular the pentagon, was not an easy task. math game, but was a necessary prerequisite for the construction of fortresses.

The regular hexagon was the subject of a special study by the great German astronomer and mathematician Johannes Kepler (1571-1630), which he talks about in his book New Year's Gift, or about hexagonal snowflakes. He discussed the reasons why snowflakes have a hexagonal shape, he notes, in particular, the following: “... the plane can be covered without gaps only by the following figures: equilateral triangles, squares and regular hexagons. Among these figures, the regular hexagon covers the largest area.

One of the most famous scientists involved in geometric constructions was the great German artist and mathematician Albrecht Dürer (1471 -1528), who devoted a significant part of his book "Guidelines ..." to them. He proposed rules for constructing regular polygons with 3. 4, 5 ... 16 sides. The methods for dividing the circle proposed by Dürer are not universal; in each case, an individual technique is used.

Durer applied the methods of constructing regular polygons in artistic practice, for example, when creating various kinds of ornaments and patterns for parquet. Sketches of such patterns were made by him during a trip to the Netherlands, where parquet floors were found in many houses.

Durer made ornaments from regular polygons, which are connected into rings (rings of six equilateral triangles, four quadrangles, three or six hexagons, fourteen heptagons, four octagons).

Conclusion

So,geometric constructions is a method of solving a problem in which the answer is obtained graphically. Constructions are carried out with drawing tools with maximum accuracy and accuracy of work, since the correctness of the decision depends on this.

Thanks to this work, I got acquainted with the history of the origin of the compass, got to know the rules for performing geometric constructions in more detail, gained new knowledge and put it into practice.
Solving problems on building with a compass and a ruler is a useful pastime that allows you to take a fresh look at the known properties of geometric shapes and their elements.In this paper, we consider the most urgent problems associated with geometric constructions using a compass and straightedge. The main tasks are considered and their solutions are given. The given problems are of considerable practical interest, consolidate the knowledge gained in geometry and can be used to practical work.
Thus, the goal of the work is achieved, the tasks set are fulfilled.

SMALL ACADEMY OF SCIENCES OF SCHOOLCHILDREN OF THE CRIMEA

"FINDER"

Section "Mathematics"

GEOMETRIC CONSTRUCTION USING THE DOUBLE-SIDED RULER

I've done the work but

_____________

class student

scientific adviser

INTRODUCTION…………………………………………………………………..…..3

I. GEOMETRIC CONSTRUCTIONS ON THE PLANE ………………...4

I.1. General axioms of constructive geometry. Axioms of mathematical tools………………………………………………………………………..4

I.2. ……………………….....5

I.3. Geometric constructions with one ruler ……………………………..7

I.4. The main tasks for building a double-sided ruler………………..8

I.5. Solving various tasks for the construction

I.6. Constructions with a one-sided ruler…………………………………….....20

I.7. Interchangeability of double-sided ruler with compass and ruler….21

CONCLUSION………………………………………………………………….24

List of used literature………………………………..………….25

Introduction

Problems for construction by limited means include problems for construction only with a compass and a straightedge, which are considered in school curriculum. Is it possible to solve construction problems with only one ruler? Often there is no compass at hand, and a ruler can always be found.

Construction tasks in geometry is a fascinating section. Interest in it is due to the beauty and simplicity of geometric content. The urgency of considering these problems increases due to the fact that it finds application in practice. The ability to use one ruler to solve the problems considered in this paper has great importance in practice, because we are constantly faced with problems of dividing a segment in half, doubling a given segment, etc.

In this paper, we consider the main tasks for the construction, which serve as a support in solving more complex problems.

As experience shows, construction tasks arouse interest, contribute to the activation of mental activity. When solving them, knowledge about the properties of figures is actively used, the ability to reason is developed, the skills of geometric constructions are improved. As a result, constructive abilities are developed, which is one of the goals of studying geometry.

Hypothesis: all construction problems that can be solved with a compass and ruler can only be solved with a two-sided ruler.

Object of study: construction tasks and a two-sided ruler.

Objectives of the study: to prove that all construction problems can be solved only with the help of a two-sided ruler.

Research objectives: to study theoretical basis solving construction problems; solve basic building problems with the help of a two-sided ruler; give examples of more complex construction tasks; systematize theoretical and practical material.

I. GEOMETRIC CONSTRUCTIONS ON THE PLANE

I.1. General axioms of constructive geometry. Axioms of mathematical tools

For constructive geometry, it is necessary to have an accurate and, for mathematical purposes, a complete description of a particular tool. Such a description is given in the form of axioms. These axioms in an abstract mathematical form express those properties of real drawing tools that are used for geometric constructions.

The most commonly used tools for geometric constructions are:ruler (one-sided) , compass, bilateral ruler (with parallel edges) and some others.

A. Ruler axiom.

The ruler allows you to perform the following geometric constructions:
a) construct a segment connecting two constructed points;

b) construct a straight line passing through two constructed points;

c) construct a ray emanating from a constructed point and passing through another constructed point.

B. Axiom of the compass.

The compass allows you to perform the following geometric constructions:
a) construct a circle if the center of the circle and a segment equal to the radius of the circle (or its ends) are constructed;

B. The axiom of a two-sided ruler.

The double-sided ruler allows you to:

a) perform any of the constructions listed in axiom A;

b) in each of the half-planes defined by the constructed line, construct a line parallel to this line and passing from it at a distancebut, where but - a segment fixed for a given ruler (width of a ruler);

c) if two points A and B are constructed, then determine whether AB will be greater than some fixed segmentbut (ruler width), and if AB >but , then construct two pairs of parallel lines passing through points A and B, respectively, and spaced from one another at a distancebut .

In addition to the above tools, you can use other tools for geometric constructions: an arbitrary angle, a square, a ruler with marks, a pair of right angles, various devices for drawing special curves, etc.

I.2. General principles for solving building problems

Building task consists in the fact that it is required to construct a certain figure with the indicated tools, if some other figure is given and certain relations between the elements of the desired figure and the elements of this figure are indicated.

Each figure that satisfies the conditions of the problem is calleddecision this task.

Find a solution construction task means to reduce it to a finite number of basic constructions, i.e., to indicate a finite sequence of basic constructions, after which the desired figure will already be considered built by virtue of the accepted axioms of constructive geometry. The list of admissible basic constructions, and, consequently, the course of solving the problem, essentially depends on what kind of tools are used for constructions.

Solve the construction problem - means, find all solutions .

The last definition needs some clarification. Figures that satisfy the conditions of the problem can differ both in shape or size, and in position on the plane. Differences in position on the plane are taken into account or not taken into account depending on the formulation of the construction problem itself, on whether the condition of the problem provides for or does not provide for a certain location of the desired figure relative to any given figures.

If a solution to a problem is found, then in the future it is allowed to use this solution "as a whole", i.e., without dividing it into basic constructions.

There are a number of simple geometric construction problems, which are especially often included as components in the solution of more complex problems. We will call them elementary geometric construction problems. The list of elementary tasks is, of course, conditional. The most common tasks include the following:

Divide this segment in half.

Divide this angle in half.

Construction on a given line of a segment equal to the given one.

Constructing an angle equal to a given one.

Constructing a line passing through a given point parallel to a given line.

Construction of a line passing through a given point and perpendicular to a given line.

The division of the segment in this respect.

Construction of a triangle given three sides.

Construction of a triangle given a side and two adjacent angles.

Construction of a triangle given two sides and an angle between them.

When solving any somewhat complex construction problem, the question arises of how to reason in order to find a way to solve the problem, to obtain all solutions to the problem, to find out the conditions for the possibility of solving the problem, etc. Therefore, when solving constructive problems, they use the solution scheme consisting of the following four steps:

1) analysis;
2) construction;
3) proof;
4) research.

I.3. Geometric constructions with one ruler

We will consider the ruler from two points of view: as a ruler and as a two-sided ruler.

1. double sided ruler width but we will call a ruler with parallel edges located at a distance but from each other, making it possible to directly build:

a) an arbitrary line;

b) a straight line passing through two points given or obtained in the process of solving the problem;

c) parallel lines, each of which passes through one of the points, the distance between which is greater thanbut (during this construction, the ruler is in such a position that each of its two parallel edges has one of the two given points; in this case, we will speak of a direct construction).

The width of the ruler in this construction is considered constant, and therefore, if in the process of solving specific task there will be a need to perform a direct construction with respect to some obtained pointsBUT And IN , then we must prove that the lengthAB more length but .

We will consider a point constructed if it is one of the data or is the intersection of two constructed lines; in turn, we will consider a line constructed if it passes through the constructed or given points.

Using a double-sided ruler, you can build the following.

a) A line can be drawn through any two points, but only one.

b) Whatever the line, there are exactly two lines in the plane parallel to it and at a distance from ita .

c) Through two points A and B at AB but it is possible to draw two pairs of parallel direct; at AB = but a pair of parallel lines can be drawn, the distance between which is equal tobut .

If one, two, three points are given, then no new points can be constructed

(Figure 1);

if four points are given, some three of which (or all four) lie on the same straight line, then no other points can be constructed (Fig. 2);

given four points lying at the vertices of a parallelogram, only one point can be constructed - its center. (Fig.3).

Having accepted the above, we consider separately the problems solved by a two-sided ruler.

I.4. Basic tasks on building a double-sided ruler

1
. Construct the bisector of angle ABC.

Solution: (Fig. 4)

but  (IN C) And b  (AB), and  b = D .

Get B D- bisector  ABC.

Indeed, obtained by

parallelogram construction is

rhombus, since its heights are equal. IND –

the diagonal of the rhombus is the bisector ABC. Fig.4

2
. Double the given angle ABC

Solution : (Fig. 5) a) but  (AB),

but  (IN C)= D , through points B and D

b directly;

b) through points B andD m  b

directly,b Ç a = F .

Get Ð AB F = 2 Ð ABC .

Fig.5

3 . To this line M N in this

draw a perpendicular to point A

Solution : (Fig.6)

1) (AA 1) || (VV 1) || (SS 1 ) –

directly (in (M N),

FROM Î (M N)); 2) through A and B

m || n - directly,

m Ç (SS 1 ) = D .

We get (A D )  (M N ).

Fig.6.

4
. Through a given point not lying on

this line, draw a perpendicular

to this straight line.

Solution: Through this point O we draw

two lines intersecting a given

straight line AB, and double the angles of the resulting

triangles adjacent to a given

straight.  OA N = 2  OAB and

OV N = 2  OVA (Fig. 7).

Fig.7

5. Construct a point symmetrical to a given one with respect to a given line.

Solution: see problem 4. (the point O is symmetrical to the pointN. Fig.7)

6. Draw a straight line parallel to this

P
line M N , through point A, not

belonging to the line M N .

Solution 1: (Fig. 8)

1)(AA 1 ) || (VV 1) || (SS 1) || (DD 1 ) || (KK 1) -

– directly, (CA)Ç (BB 1) \u003d C 2;

2) (C 2 K) Ç (DD 1 ) = F .

(BUT F ) is the desired line.

Figure 8

Solution 2 . In Fig.8 1 is numbered

sequence of straight lines,

of which 1, 2 and 3 are parallel in

direct construction;

(BUT F) || (M N).

Fig.8 1

7
. Divide this segment AB in half.

Solution 1 (Fig. 9) (only for the case when the width of the ruler is less than the length of the given segment). Draw directly two pairs of parallel lines through

the ends of this segment, and then the diagonal

the resulting rhombus. O is the midpoint of AB.

Rice. nine.

Solution 2 (Fig. 9, a)

1) a || (AB) and b || (AB) - directly;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D IN) Ç a = M, (CB) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D TO) Ç (BUT N ) = F ;

6) (In F ) Ç b = D 1, (B F ) Ç a \u003d C 1;

7) (D IN ) Ç (BUT D 1 ) = X,

(AC 1 ) Ç (CB) = Z.

8) (X Z) Ç (AB) = O. We get AO = OB.

Fig. 9, a

Solution 3 .( Rice. 9b)

As is known , in the middle trapezoid

bases, point of intersection

diagonals and intersection point

side extensions

lie on the same line.

1) m || (AB) - directly;

2) C Î m , D Î m , (AC) Ç (IN D ) = TO; Fig.9,b

3) (CB) Ç (BUT D ) = F ; 4) (K F ) Ç (AB) = O. We get AO = OB.

I.5. Solving various building problems

In solving the following problems on the construction of only a two-sided ruler, the direct construction of parallel lines and the seven main problems above are used.

1. Draw two mutually perpendicular lines through this point.

R Solution: pass through this point

two arbitrary lines,

and then the bisectors

adjacent corners. (Fig.10)

Fig.10

2. Given segment A D a given length.

Construct a segment whose length is .

R
solution : Let's spend m  but And h || m across

point A. f || (BUT D ) , k || (AD) directly.

Let's draw AB and AC, where B =f  m ,

a C = m  k . In a known way

Divide AB and AC in half and

draw the medians of the triangle

ABC. By the property of medians

triangle, oh D = - desired

segment (Fig.11)

Rice. eleven

3. Construct a line segment whose length is

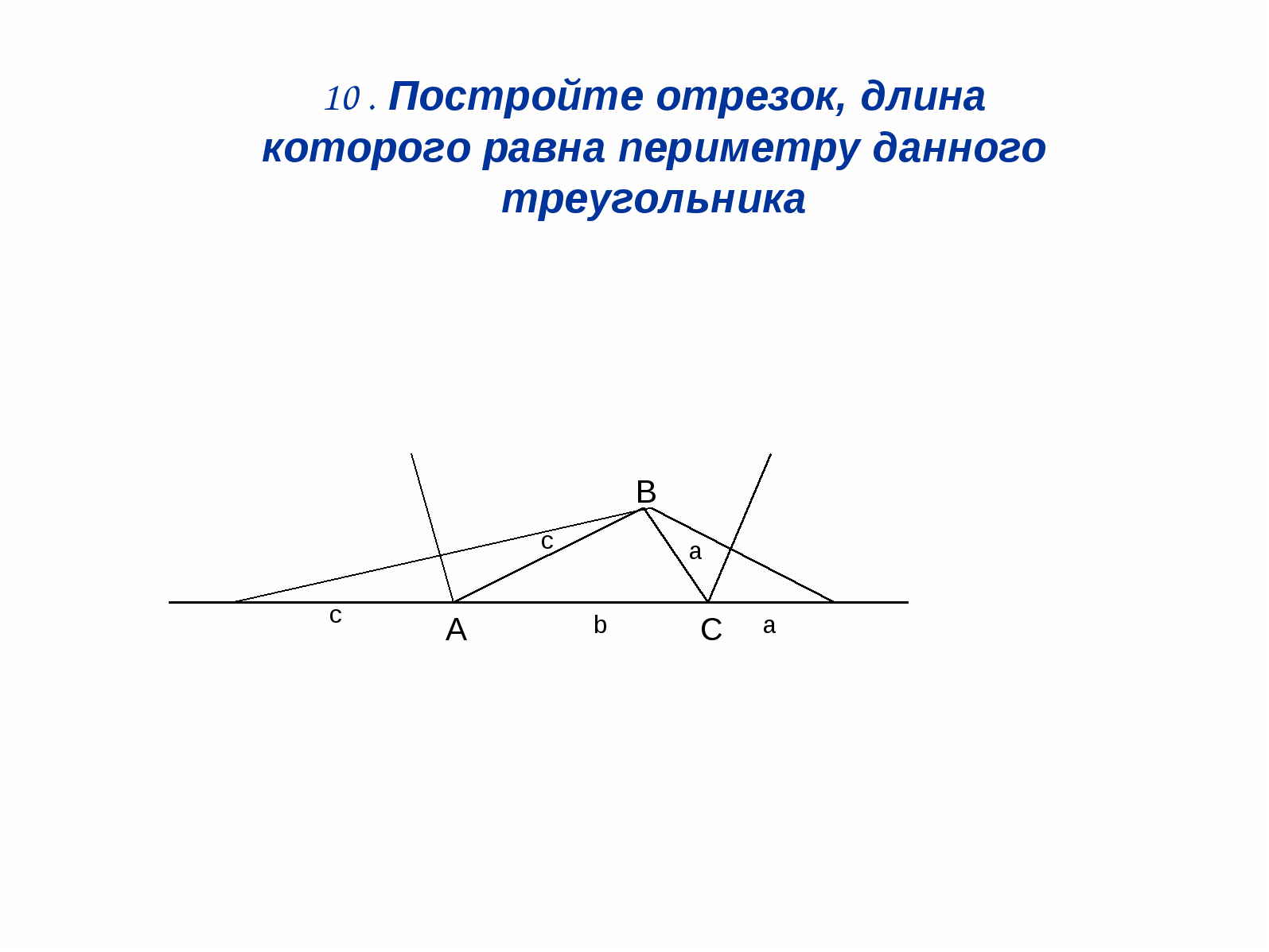equal to the perimeter of the triangle.

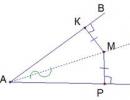
Solution: (Fig. 12). Let's build bisectors

two outer corners of the triangle, and then

3 peaks IN draw perpendiculars

to these bisectors.

DE = a + b + with

Fig.12

4. Given a segment of length a. Construct length segments 2a, 3a.

R Solution: (Fig. 13)

1M N) || (AB) and (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

Directly;

2) (CA) and (CB) through A and B.

Segments A 1 B 1 and A 2 B 2 are required.

Another solution to this problem can be

get from the solution of problem 7.

Rice. 13

5. Two segments are given on a straight line, the lengths of which are a and b . Construct segments whose lengths are equal to a + b , b - but, ( a + b )/2 and ( b - a )/2 .

Solution: and for a + b(Fig. 14, a)

Fig. 14, a

b) for ( a + b)/2 (Fig. 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) - directly;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1) = N, (M H) Ç (A 1 B 1) = P;

3) (PY) Ç (A 2 B 2) = L, (LZ ) Ç (A 1 B 1) = O

We get: N O = NP + PO =
.

Rice. 14b

c) for b - but(Fig. 14, c)

Rice. 14,in

c) for ( b - a )/2 (Fig. 14d)

Rice. 14, g

6
. Construct the center of this circle.

Solution : (Fig. 15) Draw a straight line AB,

intersecting the circle at points A and B;

Sun  AB, where C is the point of intersection

with a circle.

Draw through point C parallel to AB

straight line C D; FROMDcrosses the circle

at the pointD.

By connectingDwith B and A with C, we get

the desired point is the center of the circle. Rice. 15

Solution 2: (Fig. 16) Construct two parallel chords using a two-sided rulerAD AndBC . We get an isosceles trapezoidABCD. Let beK AndP - points of intersection of linesAC AndBD , AB AndDC . Then the lineP K passes through the midpoints of the bases of the trapezoid perpendicular to them, which means it passes through the center of the given circle. Having similarly constructed another such straight line, we find the center of the circle.

Rice. 16

7. An arc of a circle is given. Construct the center of the circle

Solution . (Fig. 17) Let's mark three points A, B and C on this arc. Let's attach a ruler to the ends of the segment AB and circle its edges. We get two parallel lines. By changing the position of the ruler, draw two more parallel straight lines. We get a rhombus (parallelogram with equal heights). One of the diagonals of the rhombus is the perpendicular bisector to the segmentAB , since the diagonal of the rhombus lies on the perpendicular bisector of the other diagonal. Similarly, we construct the perpendicular bisector to the segmentAC . The intersection point of the constructed midperpendiculars is the center of the desired circle.

Rice. 17

8. Given a segment AB, a line l not parallel to it, and a point M on it. Using one double-sided ruler, construct the points of intersection of line l with a circle of radius AB with center M.

Solution: (Fig.18)

Let's complete the triangleABM to parallelogramABNM . Let us construct the bisectors MT andMSangles betweenMNand directl . Let's pass through the pointN lines parallel to these bisectors:NQ || MS, NR || MT. MT│ MSas bisectors of adjacent angles. Means,NQ │ MT, that is, in a triangleNMQThe bisector is the height, so the triangle is isosceles:MQ = MN. Likewise,MR = MN. pointsQAndRdesired.

Rice. eighteen

9. Given a line l and a segment OA parallel to l. Using one double-sided ruler, construct the points of intersection of line l with a circle of radius OA centered at O.

Solution: (Fig. 19, a)

Let's draw a straight linel 1 , parallel to the lineOA and at a distance from ita . Let's take it straightl arbitrary pointB . Let beB 1 - point of intersection of linesOB Andl 1 . Let's pass through the pointB 1 straight, parallelAB ; this line intersects the lineOA at the pointA 1 . Let's now pass through the pointsO AndA 1 a pair of parallel lines, the distance between which is equal toa (there can be two such pairs of lines); let beX AndX 1 - the point of intersection of the line passing through the pointO , with straight linesl Andl 1 . BecauseOA 1 = OX 1 and ∆OA 1 X 1 ∆ OAX , then ОА = ОХ, pointX desired.

Similarly, we construct the second point of intersection of the circle and the straight line - the pointY(Fig.18,b).

Rice. 18,a

Rice. 18b

I.6.Constructions with a one-sided ruler

Z
Here we consider a special case: let the points P be given,Q, R 1 AndQ 1 . and they lie at the vertices of the trapezoid.

1. Divide segment P Q in half

Solution shown in figure 19

Given points P,Q, R 1 AndQ 1 and parallel lines

RQ, R 1 Q 1 . Let's spend RQ 1  QR 1 = B , RR 1  QQ 1 = A

Connect points A and B. AB RQ = F- middle

segment PQ.

Rice. 19

2. Double segment R 1 Q 1.

R
solution shown in Figure 20. Let's build

pointF- the middle of the segment RQand connect it

fromQ 1. R 1 Q FQ 1 = M. Let's carry out RM. RM R 1 Q 1 = R

equalityRQand R 1 Q 1 follows from the similarity

triangles RMFAnd RMQ 1 ,

FMQAnd R 1 MQ 1 , and the equality РFAndFQ.

Rice. twenty

3
. Construct a length segment n  R 1 Q 1 .

m – 1 equal segments PQ 2 , Q 2 Q 3, … Q m -1 Q m

Then we build (RR 1 ) AndQ m Q 1 and connect

their intersection point A with the points

Q 2 , Q 3, … Q m Receivedm -1 direct

divideR 1 Q 1 on them equal parts.

Form = 4 the solution is shown in figure 22

Fig.22

I.7. Interchangeability of double-sided ruler with compass and ruler

Let us prove that a two-sided ruler is interchangeable with a compass and a ruler. To do this, we prove the following assertions:

Proposition 1: all constructions that can be done with a compass and straightedge can be done with a two-sided straightedge.

Since when constructing with a compass and a ruler, the ruler draws a straight line through two points, and the compass constructs a circle (finds a set of points equidistant from the given one), then all constructions with a compass and ruler are reduced to constructing the intersection of two straight lines, two circles and a circle with a straight line.

The intersection of two lines can be drawn using a ruler.

The intersection of a circle and a straight line (Fig. 23):

Building:Let the segment AB be given - the radius of the circle, the straight linel , the center of the circle O, then:

1) We spend OS ||l , OS = AB.

2) We spend OS ||kand remote on a.

3) We spendOD, OD l = D; OD k) By corollary of the Thales theorem

4) According to the law of transitivity of equalities

5) ConsiderOMQE. OMQEis a parallelogram, since OM ||EQand OE ||MC(linear sides are parallel). Let's prove that this is a rhombus.

5.1) ConductQZ OCAndQG ON, thenQG = QZ = a.

5.2)  OMQ =  RQM(cross lying);  OS =ON, which was to be proved.

Intersection of two circles: similar.

Statement 2: all constructions feasible with a two-sided ruler are feasible with a compass and straightedge.

To do this, we will perform constructions that are standard for a two-sided ruler using a compass and a ruler.

1) A two-point line is easily drawn using a ruler.

2) Construction of a line parallel to the given one and remote from it on given distance:

2.1) Let a line be givenkand a segment of lengtha.

2.2) We build an arbitrary lineb k, let bek b= B.

2.3) Onbon either side of the dotBon a straight linebset aside a lengtha, let the pointsCAndD.

2.4) Through a pointCbuild a straight linec k.

2.5) Through a pointDbuild a straight lined k.

2.6) DirectcAndd– desired, sinceBCAndBDequalaby construction and are equal to the distance between the linekand direct

3) Construction of lines parallel to each other and passing through two given points, and the distance between the distance between which is equal to the given segment:

3.1) Let points be givenAAndBand a segment of lengtha.

3.2) Draw a circle centered at a pointAand radiusa.

3.3) We construct a tangent to a given circle through a pointB; there are two such tangents, ifBlies outside the circle (ifAB> a), one ifBlies on the circle (ifAB= a), none ifBlies inside the circle (AB< a). This tangent is one of the desired lines; left to pass through the pointAstraight line parallel to it.

3.4) Since one of the lines is perpendicular to the radius of the circle as a tangent, the second is also perpendicular to it (since they are parallel), therefore, the distance between them is equal to the radius, which, by construction, is equal toawhich is what was required.

Thus, we have proved the interchangeability of a double-sided ruler and a compass and a ruler.

Conclusion: a double-sided ruler is interchangeable with compasses and a ruler.

Conclusion

So, the question of the possibility of using one ruler for solving classical construction problems with the help of a compass and a ruler has been considered and solved. It turns out that construction problems can be solved using only one ruler with parallel edges. When solving more complex problems, one should rely in the future on the so-called basic constructions considered in this paper.

The material presented can be directly applied not only in mathematics lessons, in the classes of a mathematical circle, but also in practical activities.

List of used literature

Aliyev A.V. Geometric constructions. Mathematics at school. 1978 No. 3

Glazer G.I. History of mathematics at school. M., Enlightenment. 1981.

Depman I.Ya. Behind the pages of a mathematics textbook. M.. Education. 1989.

Elensky Sh. In the footsteps of Pythagoras. M., Detgiz. 1961.

Encyclopedic Dictionary of a Young Mathematician. M., Pedagogy. 1985

In construction problems, we will consider the construction geometric figure which can be done with a ruler and a compass.

With a ruler, you can:

arbitrary line;

an arbitrary line passing through a given point;

a straight line passing through two given points.

Using a compass, you can describe a circle of a given radius from a given center.

A compass can be used to draw a segment on a given line from a given point.

Consider the main tasks for the construction.

Task 1. Construct a triangle with given sides a, b, c (Fig. 1).

Solution. With the help of a ruler, draw an arbitrary straight line and take an arbitrary point B on it. With a compass opening equal to a, we describe a circle with center B and radius a. Let C be the point of its intersection with the line. With a compass opening equal to c, we describe a circle from the center B, and with a compass opening equal to b - a circle from the center C. Let A be the intersection point of these circles. Triangle ABC has sides equal to a, b, c.

Comment. In order for three line segments to serve as sides of a triangle, it is necessary that the larger of them be less than the sum of the other two (and< b + с).

Task 2.

Solution. This angle with vertex A and beam OM are shown in Figure 2.

Draw an arbitrary circle centered at the vertex A of the given angle. Let B and C be the points of intersection of the circle with the sides of the angle (Fig. 3, a). Let's draw a circle with radius AB with the center at the point O - the starting point of this ray (Fig. 3, b). The point of intersection of this circle with the given ray will be denoted as С 1 . Let us describe a circle with center C 1 and radius BC. Point B 1 of the intersection of two circles lies on the side of the desired angle. This follows from the equality Δ ABC \u003d Δ OB 1 C 1 (the third criterion for the equality of triangles).

Task 3. Construct the bisector of the given angle (Fig. 4).

Solution. From vertex A of a given angle, as from the center, we draw a circle of arbitrary radius. Let B and C be the points of its intersection with the sides of the angle. From points B and C with the same radius we describe circles. Let D be their intersection point, different from A. Ray AD divides angle A in half. This follows from the equality ΔABD = ΔACD (the third criterion for the equality of triangles).

Task 4. Draw a median perpendicular to this segment (Fig. 5).

Solution. With an arbitrary but identical compass opening (large 1/2 AB), we describe two arcs with centers at points A and B, which will intersect each other at some points C and D. The straight line CD will be the required perpendicular. Indeed, as can be seen from the construction, each of the points C and D is equally distant from A and B; therefore, these points must lie on the perpendicular bisector to segment AB.

Task 5. Divide this segment in half. It is solved in the same way as problem 4 (see Fig. 5).

Task 6. Through a given point, draw a line perpendicular to the given line.

Solution. Two cases are possible:

1) the given point O lies on the given straight line a (Fig. 6).

From point O we draw a circle with an arbitrary radius that intersects the line a at points A and B. From points A and B we draw circles with the same radius. Let О 1 be their intersection point different from О. We get ОО 1 ⊥ AB. Indeed, the points O and O 1 are equidistant from the ends of the segment AB and, therefore, lie on the perpendicular bisector to this segment.

Example

Splitting a line in half

Bisection problem. Use a compass and straightedge to divide this segment AB into two equal parts. One of the solutions is shown in the figure:

• Compasses draw circles centered at points A And B radius AB.
• Finding intersection points P And Q two constructed circles (arcs).
• On a ruler, draw a segment or a line passing through the points P And Q.
• Finding the midpoint of the segment AB- point of intersection AB And PQ.

Formal definition

Construction problems consider the set of all points of the plane, the set of all lines of the plane, and the set of all circles of the plane, over which the following operations are allowed:

1. Select a point from the set of all points:
   1. arbitrary point
   2. arbitrary point on a given line
   3. arbitrary point on a given circle
   4. point of intersection of two given lines
   5. points of intersection / tangency of a given line and a given circle
   6. points of intersection/tangency of two given circles
2. "Via rulers» select a line from the set of all lines:
   1. arbitrary line
   2. an arbitrary line passing through a given point
   3. a line passing through two given points
3. "Via compass» select a circle from the set of all circles:
   1. arbitrary circle
   2. arbitrary circle centered at given point
   3. an arbitrary circle with a radius equal to the distance between two given points
   4. a circle centered at a given point and with a radius equal to the distance between two given points

In the conditions of the problem, a certain set of points is specified. It is required, using a finite number of operations, to construct another set of points from among the above allowed operations, which is in a given relationship with the original set.

The solution of the construction problem contains three essential parts:

1. Description of the method for constructing a given set.
2. A proof that the set constructed in the described way is indeed in a given relationship with the original set. Usually the proof of the construction is done as a regular proof of a theorem, relying on axioms and other proved theorems.
3. Analysis of the described construction method for its applicability to different variants of initial conditions, as well as for the uniqueness or non-uniqueness of the solution obtained by the described method.

Known Issues

• Apollonius' problem of constructing a circle tangent to three given circles. If none of the given circles lies inside the other, then this problem has 8 essentially different solutions.
• Brahmagupta's problem of constructing an inscribed quadrilateral on its four sides.

Construction of regular polygons

Ancient geometers knew how to construct correct n-gons for , , and .

Possible and impossible constructions

All constructions are nothing more than solutions to some equation, and the coefficients of this equation are related to the lengths of the given segments. Therefore, it is convenient to talk about the construction of a number - a graphical solution to an equation of a certain type. Within the framework of the above requirements, the following constructions are possible:

• Construction of Solutions to Linear Equations.
• Construction of solutions of quadratic equations.

In other words, it is possible to construct only numbers equal to arithmetic expressions using the square root of the original numbers (lengths of segments). For example,

Variations and Generalizations

• Constructions with a single compass. According to the Mohr-Mascheroni theorem, with the help of one compass, you can build any figure that can be built with a compass and a ruler. In this case, a line is considered to be constructed if two points are given on it.
• Constructions with a single ruler. It is easy to see that only projectively invariant constructions can be carried out with the help of one ruler. In particular, it is impossible even to split the segment into two equal parts, or to find the center of the drawn circle. But if there is a pre-drawn circle on the plane with a marked center, using a ruler, you can draw the same constructions as with a compass and a ruler (the Poncelet-Steiner theorem ( English)), 1833. If there are two serifs on the ruler, then constructions with the help of it are equivalent to constructions with the help of a compass and a ruler (Napoleon made an important step in proving this).
• Constructions with limited tools. In problems of this kind, tools (in contrast to the classical formulation of the problem) are considered not ideal, but limited: a straight line through two points can be drawn using a ruler only if the distance between these points does not exceed a certain value; the radius of circles drawn with a compass can be limited from above, below, or both above and below.
• Building with flat origami. see Khujit rules

see also

• Dynamic geometry programs allow you to draw with a compass and straightedge on a computer.

Notes

Literature

• A. Adler Theory of geometric constructions / Translated from German by G. M. Fikhtengolts. - Third edition. - L.: Uchpedgiz, 1940. - 232 p.
• I. I. Alexandrov Collection of geometric problems for the construction. - Eighteenth edition. - M .: Uchpedgiz, 1950. - 176 p.
• B. I. Argunov, M. B. Balk. - Second edition. - M .: Uchpedgiz, 1957. - 268 p.
• A. M. Voronets The geometry of a compass. - M.-L.: ONTI, 1934. - 40 p. - (Popular math library under general edition L. A. Lyusternik).
• V. A. Geiler Unsolvable construction problems // coolant. - 1999. - No. 12. - S. 115-118.
• V. A. Kirichenko Constructions with compasses and ruler and Galois theory // Summer school"Modern Mathematics". - Dubna, 2005.
• Yu. I. Manin Book IV. Geometry // Encyclopedia of elementary mathematics. - M .: Fizmatgiz, 1963. - 568 p.
• Y. Petersen Methods and theories for solving geometric construction problems. - M .: Printing house of E. Lissner and Yu. Roman, 1892. - 114 p.
• V. V. Prasolov Three classic building problems. Doubling a cube, trisection of an angle, squaring a circle. - M .: Nauka, 1992. - 80 p. - (Popular lectures on mathematics).
• J. Steiner Geometric constructions performed using a straight line and a fixed circle. - M .: Uchpedgiz, 1939. - 80 p.
• Optional course in mathematics. 7-9 / Comp. I. L. Nikolskaya. - M .: Education, 1991. - S. 80. - 383 p. - ISBN 5-09-001287-3

Wikimedia Foundation. 2010 .

See what "Construction with a compass and ruler" is in other dictionaries:

Rulers - get a working discount coupon at Akademika VseTools or profitably buy rulers with free shipping on sale at VseTools

Section of Euclidean geometry, known since ancient times. In construction tasks, the following operations are possible: Mark an arbitrary point on the plane, a point on one of the constructed lines, or an intersection point of two constructed lines. With the help of ... ... Wikipedia

Constructions with the help of a compass and straightedge A section of Euclidean geometry known since ancient times. In construction tasks, the following operations are possible: Mark an arbitrary point on the plane, a point on one of the constructed lines, or a point ... ... Wikipedia

Ex., s., use. comp. often Morphology: (no) what? construction for what? construction, (see) what? building what? building, about what? about building; pl. what? construction, (no) what? constructions, why? constructions, (see) what? construction than? ... ... Dictionary of Dmitriev