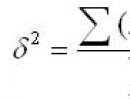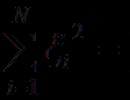Antiderivatiivne ja määramata integraalesitlus. Tunni "Määramatu integraal. Arvutusmeetodid" ettekanne. Kahe muutuja funktsiooni äärmus

slaid 1

slaid 2

Ajalooline teave Integraalarvutus tekkis vajadusest luua üldine meetod Pindalade, mahtude ja raskuskeskmete leidmine. Embrüonaalsel kujul kasutas seda meetodit Archimedes. Seda arendati süstemaatiliselt 17. sajandil Cavalieri, Torricelli, Fermami ja Pascali töödes. 1659. aastal lõi I. Barrow seose ala leidmise probleemi ja puutuja leidmise probleemi vahel. Newton ja Leib-Nitz 17. sajandi 70ndatel juhtisid selle seose mainitud konkreetsetest geomeetrilistest probleemidest kõrvale. Nii tekkis seos integraal- ja diferentsiaalarvutuse vahel. Seda ühendust kasutasid Newton, Leibniz ja nende õpilased integratsioonitehnika arendamiseks. Integratsioonimeetodid saavutasid oma praeguse seisu peamiselt L. Euleri töödes. M. V. Ostrogradsko-Go ja P. L. Tšebõševi tööd lõpetasid nende meetodite väljatöötamise.

slaid 3

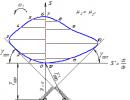
Integraali mõiste. Olgu sirge MN antud võrrandiga Ja me peame leidma kõverjoonelise trapetsi aABb pindala F. Jagame lõigu ab n osaks (võrdsed või ebavõrdsed) ja konstrueerime astmelise kujundi, mis on näidatud joonisel 1 viirutusega. Selle pindala, selle pindala on võrdne (1) Kui võtame kasutusele tähise, siis valem (1) võtab vorm (3) Soovitav pindala on summa (3) piir lõpmatult suure n korral. Leibniz võttis kasutusele selle piiri tähistuse (4) Kui (kaldkiri s) on sõna summa (summa) algustäht, tähistab avaldis E üksikute terminite tüüpilist vormi. Leibniz hakkas väljendit nimetama integraaliks – ladinakeelsest sõnast integralis – integraaliks. J. B. Fourier parandas Leibnizi tähistust, andes sellele vormi Siin on x-i alg- ja lõppväärtused selgelt näidatud.

slaid 4

Integratsiooni ja diferentseerumise seos. Vaatleme konstanti ja b muutujat. Siis on integraal b funktsioon. Selle funktsiooni erinevus on

slaid 5

primitiivne funktsioon. Olgu funktsioon funktsiooni tuletis, T.S. On funktsioonide erinevus: siis nimetatakse funktsiooni funktsiooni antiderivatiiviks

slaid 6

Näide antiderivaadi leidmisest. Funktsioon on antiderivaat T.S. Funktsioonil on diferentsiaal Funktsioon on funktsiooni antiderivaat

Slaid 7

Määramatu integraal. Antud avaldise määramatu integraal Selle antiderivatiivse funktsiooni kõige üldisemat vormi nimetatakse. Tähistatakse avaldise määramatut integraali Avaldist nimetatakse alamintegraaliks, funktsiooni nimetatakse alamintegraalfunktsiooniks, muutuja x on integratsiooni muutuja. Antud funktsiooni määramatu integraali leidmist nimetatakse integreerimiseks.

Primitiivne. Diferentsiaalarvutuse ülesanne on leida selle tuletis antud funktsiooni suhtes. Integraalarvutuse ülesanne: leida funktsioon, teades selle tuletist. Funktsiooni F(x) nimetatakse funktsiooni f(x) antituletiseks antud intervallil, kui selle intervalli mis tahes x korral on võrdus F ʹ (x)=f(x) tõene.

Teoreem. Kui funktsioon F(x) on funktsiooni f(x) antituletis mingil intervallil, siis on selle funktsiooni kõigi antiderivatiivide hulk kujul F(x)+C, kus C R. y x 0 Geomeetriliselt: F( x)+C on perekonna kõver, mis on saadud igaühest paralleeltranslatsiooni teel piki OS-i telge. C integraalkõver

Näide 2. Leia kõik tuletisvastased funktsioonid f(x)=2x ja esita need geomeetriliselt. y x

Integrand - integrand - määramata integraali märk х - integratsioonimuutuja F(x)+C - kõigi antiderivaatide hulk C - integratsiooni konstant Antiderivatiivse funktsiooni leidmise protsessi nimetatakse integreerimiseks ja matemaatika osa integraalarvutuseks.

Määramata integraali omadused Määramatu integraali diferentsiaal on võrdne integrandiga ja määramata integraali tuletis on võrdne integrandiga:

Integreerimise põhimeetodid. Otsese integratsiooni meetod. Otsene integreerimine on integraalide arvutamise meetod, milles need taandatakse tabeliteks, rakendades neile määramata integraali põhiomadusi. Sel juhul muundatakse integrand tavaliselt sobival viisil.

Anoshina O.V.

Peamine kirjandus

1. V. S. Šipatšov, Kõrgem matemaatika. Põhikursus: õpik ja
bakalaureuse töötuba [Vene Föderatsiooni haridusministeeriumi tunnistus] / V. S.
Šipatšov; toim. A. N. Tihhonova. - 8. väljaanne, muudetud. ja täiendav Moskva: Yurayt, 2015. - 447 lk.
2. V. S. Šipatšov, Kõrgem matemaatika. Täielik kursus: õpik
akad. Bakalaureusekraad [UMO tunnistus] / V. S. Šipatšov; toim. AGA.
N. Tihhonova. - 4. väljaanne, Rev. ja täiendav - Moskva: Yurayt, 2015. - 608
Koos
3. Danko P.E., Popov A.G., Koževnikova T..Ja. kõrgem matemaatika
harjutustes ja ülesannetes. [Tekst] / P.E. Danko, A.G. Popov, T.Ya.
Koževnikov. Kell 2 - M .: lõpetanud kool, 2007. - 304+415c.

Aruandlus

1.
Test. Teostatakse vastavalt:
Ülesanded ja juhendid ekspertiisi sooritamiseks
distsipliinil "RAKENDUSMATEMAATIKA", Jekaterinburg, FGAOU
VO "Vene Riiklik Kutsepedagoogika
Ülikool", 2016 - 30. a.
Võimalus kontrolltööd vali viimase numbri järgi
rekordite raamat.
2.
Eksam

Määramata integraal, selle omadused ja arvutamine Antiderivatiivne ja määramata integraal

Definitsioon. Kutsutakse funktsioon F x
tuletisvastane funktsioon f x defineeritud sisse
mingi intervall, kui F x f x jaoks
iga x sellest intervallist.
Näiteks cos x funktsioon on
primitiivne patufunktsioonid x , sest
cos x sin x .

Ilmselgelt, kui F x on antiderivaat
funktsioonid f x , siis on ka F x C , kus C on mingi konstant
tuletisevastane funktsioon f x .
Kui F x on mingi antiderivaat
funktsioon f x , siis mis tahes vormi funktsioon
F x F x C on samuti
tuletisevastane funktsioon f x ja mis tahes
primitiivset saab esitada sellisel kujul.

Definitsioon. Kõikide tervik
funktsiooni f x antiderivaadid,
mõnel määratletud
vahepealset nimetatakse
määramatu integraal
funktsioonid f x sellel intervallil ja
tähistatakse f x dx .

Kui F x on mingi funktsiooni antiderivaat
f x , siis kirjutavad nad f x dx F x C , kuigi
õigem oleks kirjutada f x dx F x C .
Meie kirjutame väljakujunenud traditsiooni kohaselt
f x dx F x C .
Seega sama sümbol
f x dx tähistab tervikut
funktsiooni f x antiderivaatide komplekt,
ja selle komplekti mis tahes elemente.

Integraalsed omadused

Määramatu integraali tuletis on
integrand ja selle erinevus integrandist. Tõesti:
1. (f (x) dx) (F (x) C) F (x) f (x);
2.d f (x)dx (f (x)dx) dx f (x)dx.

Integraalsed omadused

3. Määramatu integraal alates
diferentsiaal pidevalt (x)
diferentseeruv funktsioon on võrdne iseendaga
see funktsioon kuni konstandini:
d (x) (x) dx (x) C,
kuna (x) on (x) antiderivaat.

Integraalsed omadused

4. Kui funktsioonidel f1 x ja f 2 x on
antiderivaadid, siis funktsioon f1 x f 2 x
on ka antiderivaat ja
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx Kf x dx ;
6. f x dx f x C ;
7. f x x dx F x C .

1. dx x C .
a 1
x
2. x a dx
C, (a 1).
a 1
dx
3. ln x C .
x
x
a
4.a x dx
C.
aastal a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8,2 ctgx C .
sin x
dx
9. 2tgx C .
cos x
dx
arctgx C .
10.
2
1 x

Määramata integraalide tabel

11.
dx
arcsin x C .
1x2
dx
1
x
12. 2 2 arctaan C .
a
a
a x
13.
14.
15.
dx
a2x2
x
arcsin C ..
a
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
a 2 x 2 2a log a x C .
dx
16.
x2 a
log x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
19.
20.
dx
ch 2 x thx C .
dx
cthx C.
2
sh x

Diferentsiaalide omadused

Integreerimisel on seda mugav kasutada
omadused: 1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3.xdxdx,
2
1 3
2
4. x dx dx .
3

Näited

Näide. Arvutage cos 5xdx.
Lahendus. Integraalide tabelist leiame
cos xdx sin x C .
Teisendame selle integraali tabeliks,
kasutades ära asjaolu, et d ax adx .
Seejärel:
d5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5x
5
5
1
= sin 5 x C .
5

Näited

Näide. Arvuta x
3 x 1 dx.
Lahendus. Kuna integraalmärgi all
on siis nelja liikme summa
laiendage integraali nelja summana
integraalid:
2
3
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4x2
3
x C
3
4
2

Muutuja tüübi sõltumatus

Integraalide arvutamisel on see mugav
kasutage järgmisi omadusi
integraalid:
Kui f x dx F x C , siis
f x b dx F x b C .
Kui f x dx F x C , siis
1
f ax b dx F ax b C .
a

Näide

Arvuta
1
6
2
3
x
dx
2
3
x
C
.
3 6
5

Integratsioonimeetodid Integreerimine osade kaupa

See meetod põhineb valemil udv uv vdu .
Osade kaupa integreerimise meetodil võetakse järgmised integraalid:
a) x n sin xdx, kus n 1,2...k;
b) x n e x dx , kus n 1,2...k ;
c) x n arctgxdx , kus n 0, 1, 2,... k . ;
d) x n ln xdx , kus n 0, 1, 2,... k .
Integraalide a) ja b) arvutamisel sisestage
n 1
tähistus: x n u , siis du nx dx , ja näiteks
sin xdx dv , siis v cos x .
Integraalide c), d) arvutamisel märgi u jaoks funktsioon
arctgx , ln x ja dv jaoks võtavad nad x n dx .

Näited

Näide. Arvutage x cos xdx .
Lahendus.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .

Näited

Näide. Arvutama
x ln xdx
dx
u ln x, du
x
x2
dv xdx, v
2
x2
x 2 dx
ln x
=
2
2 x
x2
1
x2
1x2
ln x xdx
ln x
C.
=
2
2
2
2 2

Muutuv asendusmeetod

Olgu nõutav f x dx , ja leidmine
otse korja primitiivne
f x puhul me ei saa, aga me teame seda
ta on olemas. Sageli leitud
antiderivaat, lisades uue muutuja,
valemi järgi
f x dx f t t dt , kus x t ja t on uus
muutuv

Ruuttrinoomi sisaldavate funktsioonide integreerimine

Mõelge integraalile
axb
dx ,
x px q
sisaldab ruudukujulist trinoomi in
integrandi nimetaja
väljendid. Võetakse ka selline integraal
muutujate meetodi muutmine,
varem tuvastatud
nimetaja on täisruut.
2

Näide

Arvutama
dx
.
x4x5
Lahendus. Teisendame x 2 4 x 5,
2
täisruudu valimine valemi a b 2 a 2 2ab b 2 järgi.
Siis saame:
x2 4x5 x2 2x2 4 4 5
x 2 2 2 x 4 1 x 2 2 1
x 2 t
dx
dx
dt
x t 2
2
2
2
x 2 1 dx dt
x4x5
t1
arctgt C arctg x 2 C.

Näide

Otsi
1 x
1 x
2
dx
tdt
1 t
2
x t, x t 2,
dx2tdt
2
t2
1 t
2
dt
1 t
1 t
d (t 2 1)
t
2
1
2
2tdt
2
dt
log(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln(x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt

Kindel integraal, selle peamised omadused. Newtoni-Leibnizi valem. Kindla integraali rakendused.

Määratletud integraali mõiste viib selleni
kõverjoonelise ala leidmise probleem
trapetsikujuline.
Olgu antud mingi intervall
pidev funktsioon y f (x) 0
Ülesanne:
Joonistage selle graafik ja leidke joonise F ala,
selle kõveraga piiratud kaks sirget x = a ja x
= b ja altpoolt - punktide vaheline abstsisstelje segment
x = a ja x = b.

Figuuri aABb nimetatakse
kõverjooneline trapets

Definitsioon

b
f(x)dx
Kindla integraali all
a
sellest pidev funktsioon f(x)
see segment on arusaadav
vastav juurdekasv
primitiivne, see tähendab
F (b) F (a) F (x) /
b
a
Arvud a ja b on integratsiooni piirid,
on integratsiooni intervall.

Reegel:

Kindel integraal on võrdne erinevusega
antiderivatiivse integrandi väärtused
funktsioonid ülemise ja alumise piiri jaoks
integratsiooni.
Tutvustame erinevuse tähistust
b
F (b) F (a) F (x) / a
b
f (x)dx F (b) F (a)
a
Newtoni-Leibnizi valem.

Kindla integraali põhiomadused.

1) Kindla integraali väärtus ei sõltu
integratsioonimuutuja tähistus, st.
b
b
a
a
f (x)dx f (t)dt
kus x ja t on suvalised tähed.
2) Kindel integraal samaga
väljaspool
integratsioon on null
a
f (x)dx F (a) F (a) 0
a

3) Integratsiooni piiride ümberkorraldamisel
kindel integraal pöörab oma märgi ümber
b
a
f (x)dx F (b) F (a) F (a) F (b) f (x)dx
a
b
(liituv omadus)
4) Kui intervall on jagatud lõplikuks arvuks
osaintervallid, siis kindel integraal,
ülevõetud intervall on võrdne defineeritud summaga
integraalid, mis võtavad üle kõik selle osaintervallid.
b
c
b
f(x)dx f(x)dx
c
a
a
f(x)dx

5) Konstantse kordaja saab välja võtta
kindla integraali märgi jaoks.
6) Algebra kindel integraal
lõpliku arvu pidevate summad
funktsioonid on võrdne sama algebraga
summa kindlad integraalid nendest
funktsioonid.

3. Muutuja muutumine kindlas integraalis.

3. Muutuja asendamine teatud
lahutamatu.
b
f (x)dx f (t) (t)dt
a
a(), b(), (t)
kus
t[; ] , funktsioonid (t) ja (t) on pidevalt sisse lülitatud;
5
Näide:
1
=
x 1dx
=
x 1 5
t04
x 1 t
dt dx
4
0
3
2
t dt t 2
3
4
0
2
2
16
1
t t 40 4 2 0
5
3
3
3
3

Valed integraalid.

Valed integraalid.
Definitsioon. Olgu funktsioon f(x) defineeritud
lõpmatu intervall , kus b< + . Если
on olemas
b
lim
f(x)dx,
b
a
siis seda piiri nimetatakse sobimatuks
funktsiooni f(x) integraal intervallil
}