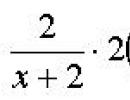Prognoosi koostamine vähimruutude meetodil. Näide probleemi lahendamisest. Lineaarse paari regressioonianalüüs Vähimruutude arvutamine
Eksperimentaalsete andmete lähendamine on meetod, mis põhineb katseliselt saadud andmete asendamisel analüütilise funktsiooniga, mis läbib või langeb sõlmpunktides kõige lähemalt algväärtustele (katse või katse käigus saadud andmed). Praegu on analüütilise funktsiooni määratlemiseks kaks võimalust:
Konstrueerides n-kraadise interpolatsioonipolünoomi, mis läbib otse läbi kõigi punktide antud andmemassiivi. Sel juhul esitatakse lähendusfunktsioon järgmiselt: interpolatsioonipolünoom Lagrange'i kujul või interpolatsioonipolünom Newtoni kujul.
Konstrueerides n-kraadise lähendava polünoomi, mis läbib punktide lähedal antud andmemassiivist. Seega ühtlustab ligikaudne funktsioon kõik juhuslikud mürad (või vead), mis võivad katse ajal tekkida: katse ajal mõõdetud väärtused sõltuvad juhuslikest teguritest, mis kõikuvad vastavalt oma juhuslikele seadustele (mõõtmis- või instrumendivead, ebatäpsus või katseviga vead). Sel juhul määratakse ligikaudne funktsioon vähimruutude meetodil.
Vähima ruudu meetod(ingliskeelses kirjanduses Ordinary Least Squares, OLS) on matemaatiline meetod, mis põhineb ligikaudse funktsiooni määratlusel, mis on üles ehitatud antud katseandmete massiivi punktide lähimasse lähedusse. Alg- ja lähendusfunktsioonide F(x) lähedus määratakse numbrilise mõõduga, nimelt: katseandmete ruudus hälvete summa lähenduskõverast F(x) peaks olema väikseim.
Vähimruutude meetodil koostatud sobituskõver
Kasutatakse vähimruutude meetodit:
Ülemääratud võrrandisüsteemide lahendamiseks, kui võrrandite arv ületab tundmatute arvu;
Otsida lahendust tavaliste (mitte ülemääratletud) mittelineaarsete võrrandisüsteemide puhul;
Punktväärtuste lähendamiseks mõne lähendusfunktsiooni abil.
Vähimruutude meetodil lähendav funktsioon määratakse kindlaks antud katseandmete massiivi arvutatud lähendusfunktsiooni hälbete miinimumsumma tingimusest. See vähimruutude meetodi kriteerium on kirjutatud järgmise avaldisena:

Arvutatud lähendusfunktsiooni väärtused sõlmpunktides,
Määratud massiiv katseandmeid sõlmepunktides.
Ruutkriteeriumil on mitmeid "häid" omadusi, nagu diferentseeritavus, mis pakub polünoomiliste lähendusfunktsioonidega aproksimeerimisprobleemile ainulaadse lahenduse.
Sõltuvalt ülesande tingimustest on lähendusfunktsioon polünoom astmega m
Lähendamisfunktsiooni aste ei sõltu sõlmpunktide arvust, kuid selle mõõde peab alati olema väiksem kui antud katseandmete massiivi dimensioon (punktide arv).
![]()
∙ Kui lähendava funktsiooni aste on m=1, siis lähendame tabelifunktsiooni sirgjoonega (lineaarne regressioon).
∙ Kui lähendamisfunktsiooni aste on m=2, siis lähendame tabelifunktsiooni ruutparabooliga (ruutlähendus).
∙ Kui lähendava funktsiooni aste on m=3, siis lähendame tabelifunktsiooni kuupparabooliga (kuupproksimatsioon).
Üldjuhul, kui antud tabeliväärtuste jaoks on vaja konstrueerida ligikaudne polünoom kraadiga m, kirjutatakse kõigi sõlmpunktide hälvete minimaalse ruudusumma tingimus ümber järgmisel kujul:
![]() - astme m lähendava polünoomi tundmatud koefitsiendid;
- astme m lähendava polünoomi tundmatud koefitsiendid;
Määratud tabeli väärtuste arv.
Funktsiooni miinimumi olemasolu vajalik tingimus on selle osatuletise võrdsus nulliga tundmatute muutujate suhtes ![]() . Selle tulemusena saame järgmise võrrandisüsteemi:
. Selle tulemusena saame järgmise võrrandisüsteemi:

Teisendame saadud lineaarset võrrandisüsteemi: avage sulud ja liigutage vabad liikmed avaldise paremale poole. Selle tulemusena kirjutatakse saadud lineaarsete algebraavaldiste süsteem järgmisel kujul:

Seda lineaarsete algebraavaldiste süsteemi saab maatriksi kujul ümber kirjutada:

Selle tulemusena saadi lineaarvõrrandi süsteem mõõtmetega m + 1, mis koosneb m + 1 tundmatust. Seda süsteemi saab lahendada mis tahes lineaarsete algebraliste võrrandite lahendamise meetodiga (näiteks Gaussi meetod). Lahenduse tulemusena leitakse aproksimeeriva funktsiooni tundmatud parameetrid, mis annavad minimaalse lähendusfunktsiooni ruutude hälbete summa algandmetest, s.o. parim võimalik ruutlähendus. Tuleb meeles pidada, et kui algandmete isegi üks väärtus muutub, muudavad kõik koefitsiendid oma väärtusi, kuna need on täielikult määratud algandmetega.
Algandmete lähendamine lineaarse sõltuvuse järgi
(lineaarne regressioon)
Vaatleme näiteks ligikaudse funktsiooni määramise meetodit, mis on antud lineaarse seosena. Vähimruutude meetodi kohaselt kirjutatakse hälvete ruutude miinimumsumma tingimus järgmiselt:
Tabeli sõlmpunktide koordinaadid;
Lähendava funktsiooni tundmatud koefitsiendid, mis on antud lineaarse seosena.
Funktsiooni miinimumi olemasolu vajalik tingimus on selle osatuletise võrdsus nulliga tundmatute muutujate suhtes. Selle tulemusena saame järgmise võrrandisüsteemi:

Teisendame saadud lineaarset võrrandisüsteemi.

Lahendame saadud lineaarvõrrandisüsteemi. Lähendava funktsiooni koefitsiendid analüütilisel kujul määratakse järgmiselt (Crameri meetod):

Need koefitsiendid annavad lineaarse lähendusfunktsiooni konstrueerimise vastavalt kriteeriumile, mille eesmärk on minimeerida ligikaudse funktsiooni ruutude summa antud tabeliväärtustest (eksperimentaalsed andmed).
Algoritm vähimruutude meetodi rakendamiseks
1. Algandmed:
Arvestades eksperimentaalsete andmete massiivi mõõtmiste arvuga N
On antud lähendava polünoomi aste (m).
2. Arvutusalgoritm:
2.1. Mõõtmetega võrrandisüsteemi koostamiseks määratakse koefitsiendid

Võrrandisüsteemi koefitsiendid (võrrandi vasak pool)
![]()
![]() - võrrandisüsteemi ruutmaatriksi veeru numbri indeks
- võrrandisüsteemi ruutmaatriksi veeru numbri indeks

Lineaarvõrrandisüsteemi vabaliikmed (võrrandi parem pool)
![]() - võrrandisüsteemi ruutmaatriksi reanumbri indeks
- võrrandisüsteemi ruutmaatriksi reanumbri indeks
2.2. Mõõtmega lineaarvõrrandisüsteemi moodustamine .

2.3. Lineaarvõrrandisüsteemi lahendus astme m lähendava polünoomi tundmatute kordajate määramiseks.
2.4 Lähendava polünoomi algväärtustest kõigi sõlmepunktide ruudu hälvete summa määramine

Ruuthälvete summa leitud väärtus on minimaalne võimalik.
Ühtlustamine muude funktsioonidega
Tuleb märkida, et algandmete lähendamisel vastavalt vähimruutude meetodile kasutatakse mõnikord lähendava funktsioonina logaritmilist funktsiooni, eksponentsiaalfunktsiooni ja võimsusfunktsiooni.
Logi ligikaudne
Mõelge juhtumile, kui ligikaudne funktsioon on antud vormi logaritmilise funktsiooniga:
Vähimruutude meetodi olemus on trendimudeli parameetrite leidmisel, mis kõige paremini kirjeldab mõne juhusliku nähtuse arengutrendi ajas või ruumis (trend on joon, mis iseloomustab selle arengu trendi). Vähimruutude meetodi (OLS) ülesanne on leida mitte ainult mõni trendimudel, vaid leida parim või optimaalne mudel. See mudel on optimaalne, kui vaadeldud tegelike väärtuste ja vastavate arvutatud trendi väärtuste ruudu hälvete summa on minimaalne (väikseim):
kus on standardhälve vaadeldava tegeliku väärtuse vahel
ja vastav arvutatud trendi väärtus,
uuritava nähtuse tegelik (täheldatud) väärtus,
trendimudeli hinnanguline väärtus,
Uuritava nähtuse vaatluste arv.
MNC-d kasutatakse harva iseseisvalt. Reeglina kasutatakse seda korrelatsiooniuuringutes enamasti ainult vajaliku tehnikana. Tuleb meeles pidada, et LSM-i teabebaas saab olla ainult usaldusväärne statistiline jada ja vaatluste arv ei tohiks olla väiksem kui 4, vastasel juhul võivad LSM-i silumisprotseduurid kaotada oma mõistuse.
OLS-i tööriistakomplekt on taandatud järgmistele protseduuridele.
Esimene protseduur. Selgub, kas valitud faktori-argumendi muutumisel on üldse kalduvus resultantatribuuti muuta või teisisõnu, kas on seos " juures " ja " X ».
Teine protseduur. Määratakse kindlaks, milline joon (trajektoor) suudab seda trendi kõige paremini kirjeldada või iseloomustada.
Kolmas protseduur.
Näide. Oletame, et meil on andmed uuritava talu keskmise päevalillesaagi kohta (tabel 9.1).
Tabel 9.1
|
Vaatluse number |
||||||||||
|
Tootlikkus, c/ha |
Kuna meie riigis ei ole päevalille tootmise tehnoloogiatase viimase 10 aasta jooksul palju muutunud, siis suure tõenäosusega sõltusid saagikuse kõikumised analüüsitud perioodil väga palju ilmastiku- ja kliimatingimuste kõikumisest. Kas see on tõsi?
Esimene MNC protseduur. Kontrollimisel on hüpotees päevalille saagikuse muutumise trendi olemasolust sõltuvalt ilmastiku- ja kliimatingimuste muutustest analüüsitud 10 aasta jooksul.
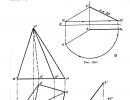
Selles näites " y » on soovitav võtta päevalille saak ja « x » on vaadeldud aasta number analüüsitud perioodil. Hüpoteesi kontrollimine mis tahes seose olemasolu kohta " x " ja " y » saab teha kahel viisil: käsitsi ja arvutiprogrammide abil. Loomulikult lahendatakse see probleem arvutitehnoloogia olemasoluga iseenesest. Kuid selleks, et OLS-i tööriistakomplekti paremini mõista, on soovitatav testida hüpoteesi seose olemasolu kohta " x " ja " y » käsitsi, kui käepärast on vaid pliiats ja tavaline kalkulaator. Sellistel juhtudel saab trendi olemasolu hüpoteesi visuaalselt kõige paremini kontrollida analüüsitava aegrea graafilise kujutise asukoha - korrelatsioonivälja järgi:


Meie näite korrelatsiooniväli asub aeglaselt tõusva joone ümber. See viitab iseenesest teatud trendi olemasolule päevalille saagikuse muutumises. Ühegi trendi olemasolust ei saa rääkida ainult siis, kui korrelatsiooniväli näeb välja nagu ring, ring, rangelt vertikaalne või rangelt horisontaalne pilv või koosneb juhuslikult hajutatud punktidest. Kõigil muudel juhtudel on vaja kinnitada hüpoteesi seose olemasolu kohta " x " ja " y ja jätkake uurimistööd.
Teine MNC protseduur. Selgitatakse, milline joon (trajektoor) suudab kõige paremini kirjeldada või iseloomustada päevalille saagikuse muutuste trendi analüüsitud perioodil.
Arvutitehnoloogia olemasolu korral toimub optimaalse trendi valik automaatselt. "Käsitsi" töötlemisega toimub optimaalse funktsiooni valik reeglina visuaalselt - korrelatsioonivälja asukoha järgi. See tähendab, et vastavalt diagrammi tüübile valitakse empiirilisele trendile (tegelikule trajektoorile) kõige paremini sobiv joone võrrand.
Nagu teate, on looduses tohutult erinevaid funktsionaalseid sõltuvusi, mistõttu on isegi väikest osa neist väga raske visuaalselt analüüsida. Õnneks saab reaalses majanduspraktikas enamikku seoseid täpselt kirjeldada kas parabooli, hüperbooli või sirgjoonega. Sellega seoses saate parima funktsiooni valiku "käsitsi" abil piirduda ainult nende kolme mudeliga.
|
Hüperbool: |
||
|
|
|
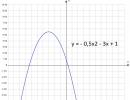
Teist järku parabool: ![]() :
:

On lihtne näha, et meie näites iseloomustab päevalillesaagi muutuste trendi analüüsitud 10 aasta jooksul kõige paremini sirgjoon, seega on regressioonivõrrandiks sirge võrrand.
Kolmas protseduur. Arvutatakse välja seda sirget iseloomustava regressioonivõrrandi parameetrid ehk teisisõnu määratakse analüütiline valem, mis kirjeldab parimat trendimudelit.
Regressioonivõrrandi parameetrite väärtuste leidmine, meie puhul parameetrid ja , on LSM-i tuum. See protsess taandub normaalvõrrandisüsteemi lahendamiseks.
 (9.2)
(9.2)
Seda võrrandisüsteemi saab Gaussi meetodil üsna lihtsalt lahendada. Tuletame meelde, et lahenduse tulemusena leitakse meie näites parameetrite väärtused ja. Seega on leitud regressioonivõrrandil järgmine vorm: ![]()
Ekstrapoleerimine - see on teadusliku uurimistöö meetod, mis põhineb mineviku ja praeguste suundumuste, mustrite, seoste levitamisel prognoositava objekti tulevase arenguga. Ekstrapoleerimismeetodid hõlmavad liikuva keskmise meetod, eksponentsiaalse silumise meetod, vähimruutude meetod.
Essents vähimruutude meetod seisneb vaadeldud ja arvutatud väärtuste vaheliste ruutude hälvete summa minimeerimises. Arvutatud väärtused leitakse vastavalt valitud võrrandile - regressioonivõrrandile. Mida väiksem on vahemaa tegelike väärtuste ja arvutatud väärtuste vahel, seda täpsem on regressioonivõrrandil põhinev prognoos.
Kõvera valiku aluseks on uuritava nähtuse olemuse teoreetiline analüüs, mille muutust kuvatakse aegreaga. Mõnikord võetakse arvesse ka seeria tasemete kasvu olemust. Seega, kui toodangu kasvu oodatakse aritmeetilises progressioonis, siis silumine toimub sirgjooneliselt. Kui selgub, et kasv on eksponentsiaalne, siis tuleks silumine teha eksponentsiaalfunktsiooni järgi.
Vähimruutude meetodi töövalem : Y t+1 = a*X + b, kus t + 1 on prognoosiperiood; Уt+1 – prognoositav näitaja; a ja b - koefitsiendid; X - aja sümbol.
Koefitsiendid a ja b arvutatakse järgmiste valemite abil:
kus Uf - dünaamika seeria tegelikud väärtused; n on aegrea tasemete arv;
Aegridade silumine vähimruutude meetodil peegeldab uuritava nähtuse arengumustreid. Trendi analüütilises väljenduses käsitletakse aega sõltumatu muutujana ja seeria tasemed toimivad selle sõltumatu muutuja funktsioonina.
Nähtuse areng ei sõltu sellest, mitu aastat on alguspunktist möödunud, vaid sellest, millised tegurid, mis suunas ja millise intensiivsusega selle arengut mõjutasid. Sellest on selge, et nähtuse areng ajas ilmneb nende tegurite toime tulemusena.
Kõvera tüübi õige seadmine, analüütilise sõltuvuse tüüp ajast, on üks keerulisemaid eelennustusanalüüsi ülesandeid. .
Trendi kirjeldava funktsiooni tüübi valik, mille parameetrid määratakse vähimruutude meetodil, on enamikul juhtudel empiiriline, konstrueerides mitmeid funktsioone ja võrreldes neid omavahel juurkeskmise väärtusega. -ruutviga arvutatakse järgmise valemiga:
kus Uf - dünaamika seeria tegelikud väärtused; Ur – aegrea arvutatud (silutud) väärtused; n on aegrea tasemete arv; p on trendi (arengutrendi) kirjeldavates valemites määratletud parameetrite arv.
Vähimruutude meetodi puudused :
- kui püütakse kirjeldada uuritavat majandusnähtust matemaatilise võrrandi abil, on prognoos lühikest aega täpne ja regressioonivõrrand tuleks uue teabe ilmnemisel ümber arvutada;
- regressioonivõrrandi valiku keerukus, mis on lahendatav standardsete arvutiprogrammide abil.
Näide vähimruutude meetodi kasutamisest prognoosi koostamiseks
Ülesanne . Regiooni tööpuuduse taset iseloomustavad andmed, %
- Koostage piirkonna töötuse määra prognoos novembriks, detsembriks, jaanuariks, kasutades meetodeid: liikuv keskmine, eksponentsiaalne silumine, vähimruutud.
- Arvutage saadud prognooside vead iga meetodi abil.
- Võrrelge saadud tulemusi, tehke järeldused.
Vähimruutude lahendus
Lahenduse jaoks koostame tabeli, milles teeme vajalikud arvutused:
Määratleme aja sümboli kui prognoosibaasi perioodide järjestikuse numeratsiooni (veerg 3). Arvutage veerud 4 ja 5. Arvutage seeria Ur väärtused, mis määratakse valemiga Y t + 1 = a * X + b, kus t + 1 on prognoosiperiood; Уt+1 – prognoositav näitaja; a ja b - koefitsiendid; X - aja sümbol.
Koefitsiendid a ja b määratakse järgmiste valemitega:
kus Uf - dünaamika seeria tegelikud väärtused; n on aegrea tasemete arv.
a = / = - 0,17
b = 22,13 / 10 - (-0,17) * 55 / 10 \u003d 3,15
Arvutame keskmise suhtelise vea järgmise valemi abil:
ε = 28,63/10 = 2,86% prognoosi täpsus kõrge.
Järeldus : Arvutustes saadud tulemuste võrdlemine liikuva keskmise meetod , eksponentsiaalne silumine ja vähimruutude meetodit, võime öelda, et eksponentsiaalse silumise meetodil tehtud arvutuste keskmine suhteline viga jääb 20-50% vahemikku. See tähendab, et ennustuse täpsus on antud juhul vaid rahuldav.
Esimesel ja kolmandal juhul on prognoosi täpsus kõrge, kuna keskmine suhteline viga on alla 10%. Kuid libiseva keskmise meetod võimaldas saada usaldusväärsemaid tulemusi (novembri prognoos - 1,52%, prognoos detsembriks - 1,53%, prognoos jaanuariks - 1,49%), kuna keskmine suhteline viga selle meetodi kasutamisel on väikseim - 1 ,13%.
Seda kasutatakse ökonomeetrias laialdaselt selle parameetrite selge majandusliku tõlgendamise vormis.
Lineaarne regressioon taandatakse vormi võrrandi leidmiseks
või
Tüüpvõrrand võimaldab antud parameetri väärtusi X neil on efektiivse tunnuse teoreetilised väärtused, asendades sellega teguri tegelikud väärtused X.
Lineaarse regressiooni loomine taandub selle parameetrite hindamisele − a ja sisse. Lineaarse regressiooni parameetrite hinnanguid saab leida erinevate meetoditega.
Klassikaline lähenemine lineaarse regressiooni parameetrite hindamisel põhineb vähimruudud(MNK).
LSM võimaldab selliseid parameetrite hinnanguid saada a ja sisse, mille all on resultanttunnuse tegelike väärtuste ruudu hälvete summa (y) arvutatud (teoreetilisest) minimaalne:
Funktsiooni miinimumi leidmiseks on vaja arvutada iga parameetri osatuletised a ja b ja võrdsusta need nulliga.
Tähistage S, seejärel:
Valemit teisendades saame parameetrite hindamiseks järgmise normaalvõrrandi süsteemi a ja sisse:
Lahendades normaalvõrrandisüsteemi (3.5) kas muutujate järjestikuse elimineerimise meetodil või determinantide meetodil, leiame soovitud parameetrite hinnangud a ja sisse.
Parameeter sisse nimetatakse regressioonikoefitsiendiks. Selle väärtus näitab tulemuse keskmist muutust teguri muutusega ühe ühiku võrra.
Regressioonivõrrandit täiendatakse alati ühenduse tiheduse näitajaga. Lineaarse regressiooni kasutamisel toimib sellise indikaatorina lineaarne korrelatsioonikordaja. Lineaarse korrelatsioonikoefitsiendi valemit on mitmesuguseid modifikatsioone. Mõned neist on loetletud allpool:
Nagu teate, on lineaarne korrelatsioonikordaja piirides: -1 ≤ ≤ 1.
Lineaarfunktsiooni valiku kvaliteedi hindamiseks arvutatakse ruut
Nimetatud lineaarne korrelatsioonikordaja määramiskoefitsient . Determinatsioonikordaja iseloomustab efektiivtunnuse dispersiooni osakaalu y, seletatav regressiooniga saadud tunnuse koguvariatsioonis:
Vastavalt sellele iseloomustab väärtus 1 - dispersiooni osakaalu y, põhjustatud muude tegurite mõjust, mida mudelis arvesse ei võeta.
Küsimused enesekontrolliks
1. Vähimruutude meetodi olemus?
2. Mitu muutujat annab paaripõhise regressiooni?
3. Milline koefitsient määrab muutuste vahelise seose tiheduse?
4. Millistes piirides määratakse determinatsioonikoefitsient?
5. Parameetri b hindamine korrelatsioon-regressioonanalüüsis?
1. Christopher Dougherty. Sissejuhatus ökonomeetriasse. - M.: INFRA - M, 2001 - 402 lk.
2. S.A. Boroditš. Ökonomeetria. Minsk LLC "Uued teadmised" 2001.
3. R.U. Rakhmetova Ökonomeetria lühikursus. Õpetus. Almatõ. 2004. -78s.
4. I.I. Eliseeva, ökonomeetria. - M.: "Finants ja statistika", 2002
5. Igakuine info- ja analüütiline ajakiri.
Mittelineaarsed majandusmudelid. Mittelineaarsed regressioonimudelid. Muutuv teisendus.
Mittelineaarsed majandusmudelid..
Muutuv teisendus.
elastsuse koefitsient.
Kui majandusnähtuste vahel on mittelineaarsed seosed, siis väljendatakse neid vastavate mittelineaarsete funktsioonide abil: näiteks võrdkülgne hüperbool , teise astme paraboolid jne.
Mittelineaarseid regressioone on kahte klassi:
1. Regressioonid, mis on analüüsis sisalduvate selgitavate muutujate suhtes mittelineaarsed, kuid hinnanguliste parameetrite suhtes lineaarsed, näiteks:
Erineva astme polünoomid - , ;
Võrdkülgne hüperbool - ;
Poollogaritmiline funktsioon - .
2. Regressioonid, mis on hinnangulistes parameetrites mittelineaarsed, näiteks:
Võimsus - ;
Demonstratiivne -;
Eksponentsiaalne - .
Saadud atribuudi üksikute väärtuste ruutude kõrvalekallete kogusumma juures keskmisest väärtusest on põhjustatud paljude tegurite mõjust. Tinglikult jagame kogu põhjuste komplekti kahte rühma: uuritud faktorit x ja muud tegurid.
Kui tegur tulemust ei mõjuta, siis on graafikul olev regressioonisirge teljega paralleelne oh ja
Siis tuleneb kogu saadud atribuudi dispersioon muude tegurite mõjust ja hälvete ruudu summa langeb kokku jääkväärtusega. Kui muud tegurid tulemust ei mõjuta, siis sa sidusid Koos X funktsionaalselt ja ruutude jääksumma on null. Sel juhul on regressiooniga seletatav ruutude hälvete summa võrdne ruutude kogusummaga.
Kuna kõik korrelatsioonivälja punktid ei asu regressioonisirgel, toimub nende hajumine alati nagu teguri mõjul. X, st regressioon juures peal X, ja põhjustatud muude põhjuste toimest (seletamatu variatsioon). Regressioonijoone sobivus prognoosile sõltub sellest, milline osa tunnuse koguvariatsioonist juures seletatud variatsiooni
Ilmselgelt, kui regressioonist tingitud hälvete ruudu summa on suurem kui ruutude jääksumma, siis on regressioonivõrrand statistiliselt oluline ja tegur X mõjutab oluliselt tulemust. y.
, st tunnuse sõltumatu varieerumise vabaduse arvuga. Vabadusastmete arv on seotud üldkogumi n ühikute arvu ja sellest määratud konstantide arvuga. Seoses uuritava probleemiga peaks vabadusastmete arv näitama, kui paljudest sõltumatutest kõrvalekalletest P
Regressioonivõrrandi kui terviku olulisuse hinnang antakse abiga F- Fisheri kriteerium. Sel juhul esitatakse nullhüpotees, et regressioonikordaja on võrdne nulliga, s.t. b= 0 ja sellest ka tegur X tulemust ei mõjuta y.
F-kriteeriumi otsesele arvutamisele eelneb dispersioonianalüüs. Selle kesksel kohal on muutuja hälvete ruutude kogusumma laiendamine juures keskmisest väärtusest juures kaheks osaks - "seletatud" ja "seletamatu":
Hälvete ruudu summa;
Regressiooniga seletatud hälbe ruutude summa;
Hälbe ruudu jääksumma.
Igasugune hälvete ruudu summa on seotud vabadusastmete arvuga , st tunnuse sõltumatu varieerumise vabaduse arvuga. Vabadusastmete arv on seotud rahvastikuühikute arvuga n ja sellest määratud konstantide arvuga. Seoses uuritava probleemiga peaks vabadusastmete arv näitama, kui paljudest sõltumatutest kõrvalekalletest P Võimalik on etteantud ruutude summa moodustamiseks.
Dispersioon vabadusastme kohtaD.
F-suhted (F-kriteerium):
Kui nullhüpotees on tõene, siis tegur ja jääkvariatsioonid ei erine üksteisest. H 0 puhul on ümberlükkamine vajalik selleks, et teguri dispersioon ületaks jääki mitu korda. Inglise statistik Snedecor töötas välja kriitiliste väärtuste tabelid F-suhted nullhüpoteesi erinevatel olulisuse tasanditel ja erineval arvul vabadusastmetel. Tabeli väärtus F-kriteerium on dispersioonide suhte maksimaalne väärtus, mis võib tekkida, kui need lahknevad juhuslikult nullhüpoteesi esinemise tõenäosuse teatud tasemel. Arvutatud väärtus F-suhe tunnistatakse usaldusväärseks, kui o on suurem kui tabel.
Sel juhul lükatakse nullhüpotees tunnuste seose puudumise kohta tagasi ja tehakse järeldus selle seose olulisuse kohta: F fakt > F tabel H 0 lükatakse tagasi.
Kui väärtus on väiksem kui tabel F fakt ‹, F tabel, siis on nullhüpoteesi tõenäosus suurem kui etteantud tase ja seda ei saa tagasi lükata ilma tõsise riskita teha vale järelduse seose olemasolu kohta. Sel juhul peetakse regressioonivõrrandit statistiliselt ebaoluliseks. N o ei kaldu kõrvale.
Regressioonikordaja standardviga
Regressioonikordaja olulisuse hindamiseks võrreldakse selle väärtust standardveaga, st määratakse tegelik väärtus t-Õpilase test: mida seejärel võrreldakse tabeli väärtusega teatud olulisuse tasemel ja vabadusastmete arvuga ( n- 2).
Parameetri standardviga a:
Lineaarse korrelatsioonikordaja olulisust kontrollitakse vea suuruse alusel korrelatsioonikordaja r:
Funktsiooni täielik dispersioon X:
Mitmekordne lineaarne regressioon
Mudeli ehitamine
Mitmekordne regressioon on efektiivse tunnuse regressioon kahe või enama teguriga, st vormi mudel
Regressioon võib anda modelleerimisel hea tulemuse, kui jätta tähelepanuta teiste uuritavat objekti mõjutavate tegurite mõju. Üksikute majandusmuutujate käitumist ei saa kontrollida, st ei ole võimalik tagada kõigi muude tingimuste võrdsust ühe uuritava teguri mõju hindamiseks. Sel juhul peaksite proovima tuvastada muude tegurite mõju, lisades need mudelisse, st koostama mitmekordse regressiooni võrrandi: y = a+b 1 x 1 +b 2 +…+b p x p + .
Mitmekordse regressiooni põhieesmärk on luua suure hulga teguritega mudel, määrates samal ajal igaühe mõju individuaalselt, samuti nende kumulatiivset mõju modelleeritavale näitajale. Mudeli spetsifikatsioon sisaldab kahte küsimuste valdkonda: tegurite valik ja regressioonivõrrandi tüübi valik
Vähima ruudu meetod kasutatakse regressioonivõrrandi parameetrite hindamiseks.Üks tunnustevaheliste stohhastiliste seoste uurimise meetodeid on regressioonanalüüs.
Regressioonanalüüs on regressioonivõrrandi tuletamine, mida kasutatakse juhusliku suuruse (tunnuse-tulemuse) keskmise väärtuse leidmiseks, kui on teada mõne teise (või mõne muu) muutuja (tunnuse-teguri) väärtus. See sisaldab järgmisi samme.
- seose vormi valik (analüütilise regressioonivõrrandi tüüp);
- võrrandi parameetrite hindamine;
- analüütilise regressioonivõrrandi kvaliteedi hindamine.
Lineaarse paarisuhte korral on regressioonivõrrand järgmine: y i =a+b·x i +u i . Selle võrrandi a ja b parameetrid on hinnatud statistilise vaatluse x ja y andmete põhjal. Sellise hindamise tulemuseks on võrrand: , kus , - parameetrite a ja b hinnangud, - regressioonivõrrandiga saadud efektiivse tunnuse (muutuja) väärtus (arvutuslik väärtus).
Parameetrite hindamiseks kasutatakse kõige sagedamini vähimruutude meetod (LSM).
Vähimruutude meetod annab regressioonivõrrandi parameetrite parimad (järjekindlad, tõhusad ja erapooletud) hinnangud. Kuid ainult juhul, kui teatud eeldused juhusliku liikme (u) ja sõltumatu muutuja (x) kohta on täidetud (vt OLS-i eeldusi).
Lineaarpaarvõrrandi parameetrite hindamise ülesanne vähimruutude meetodil koosneb järgmisest: selliste parameetrite hinnangute saamiseks , mille puhul efektiivse tunnuse tegelike väärtuste y i ruutude kõrvalekallete summa arvutatud väärtustest on minimaalne.
Formaalselt OLS-i kriteerium võib kirjutada nii:  .
.
Vähimruutude meetodite klassifikatsioon
- Vähima ruudu meetod.
- Maksimaalse tõenäosuse meetod (tavalise klassikalise lineaarse regressioonimudeli puhul eeldatakse regressioonijääkide normaalsust).
- GLSM-i üldistatud vähimruutude meetodit kasutatakse vea autokorrelatsiooni ja heteroskedastilisuse korral.
- Kaalutud vähimruutude meetod (GLSM-i erijuhtum heteroskedastiliste jääkidega).
Illustreerige olemust klassikaline vähimruutude meetod graafiliselt. Selleks koostame punktdiagrammi vastavalt vaatlusandmetele (x i , y i , i=1;n) ristkülikukujulises koordinaatsüsteemis (sellist punktgraafikut nimetatakse korrelatsiooniväljaks). Proovime leida sirge, mis on korrelatsioonivälja punktidele kõige lähemal. Vähimruutude meetodi järgi valitakse joon nii, et korrelatsioonivälja punktide ja selle sirge vahelise ruuduga vertikaalsete kauguste summa oleks minimaalne. 
Selle probleemi matemaatiline tähistus:  .
.
Väärtused y i ja x i =1...n on meile teada, need on vaatlusandmed. Funktsioonis S on need konstandid. Selle funktsiooni muutujad on parameetrite nõutavad hinnangud - , . 2 muutuja funktsiooni miinimumi leidmiseks on vaja arvutada selle funktsiooni osatuletised iga parameetri suhtes ja võrdsustada need nulliga, s.t.  .
.
Selle tulemusel saame kahe normaalse lineaarvõrrandi süsteemi: 
Selle süsteemi lahendamisel leiame vajalikud parameetrite hinnangud: 
Regressioonivõrrandi parameetrite arvutamise õigsust saab kontrollida summade võrdlemisel (arvutuste ümardamise tõttu on võimalik mõningane ebakõla).
Parameetrite hinnangute arvutamiseks saate koostada tabeli 1.
Regressioonikordaja b märk näitab seose suunda (kui b > 0 on seos otsene, kui b<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Formaalselt on parameetri a väärtus y keskmine väärtus x puhul, mis võrdub nulliga. Kui märgiteguril ei ole ega saa olla nullväärtust, siis pole parameetri a ülaltoodud tõlgendusel mõtet.
Tunnustevahelise seose tiheduse hindamine
tehakse lineaarse paari korrelatsiooni koefitsiendiga - r x,y . Seda saab arvutada järgmise valemi abil:  . Lisaks saab lineaarse paari korrelatsiooni koefitsiendi määrata regressioonikordaja b kaudu:
. Lisaks saab lineaarse paari korrelatsiooni koefitsiendi määrata regressioonikordaja b kaudu:  .
.
Paari korrelatsiooni lineaarse koefitsiendi lubatud väärtuste vahemik on –1 kuni +1. Korrelatsioonikordaja märk näitab seose suunda. Kui r x, y >0, siis on ühendus otsene; kui r x, y<0, то связь обратная.
Kui see koefitsient on moodulis ühtsuse lähedane, siis võib tunnuste vahelist seost tõlgendada üsna tiheda lineaarsena. Kui selle moodul on võrdne ühega ê r x , y ê =1, siis on tunnuste vaheline seos funktsionaalne lineaarne. Kui tunnused x ja y on lineaarselt sõltumatud, siis r x,y on nullilähedane.
Tabelit 1 saab kasutada ka r x,y arvutamiseks.
Saadud regressioonivõrrandi kvaliteedi hindamiseks arvutatakse teoreetiline määramiskordaja - R 2 yx:  ,
,
kus d 2 on regressioonivõrrandiga seletatav dispersioon y;
e 2 - jääk (regressioonivõrrandiga seletamatu) dispersioon y ;
s 2 y - kogu (kogu) dispersioon y .
Determinantkoefitsient iseloomustab regressiooniga (ja järelikult faktoriga x) seletatava tulemuseks oleva tunnuse y variatsiooni (dispersiooni) osakaalu koguvariatsioonis (dispersioonis) y. Määramiskoefitsient R 2 yx võtab väärtused vahemikus 0 kuni 1. Vastavalt sellele iseloomustab väärtus 1-R 2 yx dispersiooni y osakaalu, mis on põhjustatud muude mudelis arvestamata tegurite mõjust ja spetsifikatsioonivigadest.
Paaritud lineaarse regressiooniga R 2 yx =r 2 yx .