Calculation of mathematical expectation and variance. Expected value. Expectation of a continuous random variable

Magnitude

Basic numerical characteristics of random

The density distribution law characterizes a random variable. But often it is unknown, and one has to limit oneself to less information. Sometimes it is even more profitable to use numbers that describe a random variable in total. Such numbers are called numerical characteristics random variable. Let's look at the main ones.

Definition:The mathematical expectation M(X) of a discrete random variable is the sum of the products of all possible values of this quantity and their probabilities:

If a discrete random variable X takes a countably many possible values, then

Moreover, the mathematical expectation exists if this series is absolutely convergent.

From the definition it follows that M(X) a discrete random variable is a non-random (constant) variable.

Example: Let X– number of occurrences of the event A in one test, P(A) = p. We need to find the mathematical expectation X.

Solution: Let's create a tabular distribution law X:

X	0	1
P	1 - p	p

Let's find the mathematical expectation:

Thus, the mathematical expectation of the number of occurrences of an event in one trial is equal to the probability of this event.

Origin of the term expected value associated with initial period the emergence of probability theory (XVI-XVII centuries), when the scope of its application was limited to gambling. The player was interested in the average value of the expected win, i.e. mathematical expectation of winning.

Let's consider probabilistic meaning of mathematical expectation.

Let it be produced n tests in which the random variable X accepted m 1 times value x 1, m 2 times value x 2, and so on, and finally she accepted m k times value x k, and m 1 + m 2 +…+ + m k = n.

Then the sum of all values taken by the random variable X, is equal x 1 m 1 +x 2 m 2 +…+x k m k.

Arithmetic mean of all values taken by a random variable X,equals:

since is the relative frequency of a value for any value i = 1, …, k.

As is known, if the number of tests n is sufficiently large, then the relative frequency is approximately equal to the probability of the event occurring, therefore,

Thus, .

Conclusion:The mathematical expectation of a discrete random variable is approximately equal (the more accurately, the greater the number of tests) to the arithmetic mean of the observed values of the random variable.

Let's consider the basic properties of mathematical expectation.

Property 1:The mathematical expectation of a constant value is equal to the constant value itself:

M(C) = C.

Proof: Constant WITH can be considered , which has one possible meaning WITH and accepts it with probability p = 1. Hence, M(C) = C 1= S.

Let's define product of a constant variable C and a discrete random variable X as a discrete random variable CX, the possible values of which are equal to the products of the constant WITH to possible values X CX equal to the probabilities of the corresponding possible values X:

CX	C	C	…	C
X			…
R			…

Property 2:The constant factor can be taken out of the mathematical expectation sign:

M(CX) = CM(X).

Proof: Let the random variable X is given by the law of probability distribution:

X			…
P			…

Let's write the law of probability distribution of a random variable CX:

CX	C	C	…	C
P			…

M(CX) = C +C =C + ) = C M(X).

Definition:Two random variables are called independent if the distribution law of one of them does not depend on what possible values the other variable took. Otherwise, the random variables are dependent.

Definition:Several random variables are said to be mutually independent if the distribution laws of any number of them do not depend on what possible values the remaining variables took.

Let's define product of independent discrete random variables X and Y as a discrete random variable XY, the possible values of which are equal to the products of each possible value X for every possible value Y. Probabilities of possible values XY are equal to the products of the probabilities of possible values of the factors.

Let the distributions of random variables be given X And Y:

X			…
P			…

Y			…
G			…

Then the distribution of the random variable XY has the form:

XY			…
P			…

Some works may be equal. In this case, the probability of a possible value of the product is equal to the sum of the corresponding probabilities. For example, if = , then the probability of the value is

Property 3:The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations:

M(XY) = M(X) M(Y).

Proof: Let independent random variables X And Y are specified by their own probability distribution laws:

X
P

Y
G

To simplify the calculations, we will limit ourselves to a small number of possible values. In the general case the proof is similar.

Let's create a law of distribution of a random variable XY:

XY
P

M(XY) =

M(X) M(Y).

Consequence:The mathematical expectation of the product of several mutually independent random variables is equal to the product of their mathematical expectations.

Proof: Let us prove for three mutually independent random variables X,Y,Z. Random variables XY And Z independent, then we get:

M(XYZ) = M(XY Z) = M(XY) M(Z) = M(X) M(Y) M(Z).

For an arbitrary number of mutually independent random variables, the proof is carried out by the method of mathematical induction.

Example: Independent random variables X And Y

X	5	2
P	0,6	0,1	0,3

Y	7	9
G	0,8	0,2

Need to find M(XY).

Solution: Since random variables X And Y are independent, then M(XY)=M(X) M(Y)=(5 0,6+2 0,1+4 0,3) (7 0,8+9 0,2)= 4,4 7,4 = =32,56.

Let's define sum of discrete random variables X and Y as a discrete random variable X+Y, the possible values of which are equal to the sums of each possible value X with every possible value Y. Probabilities of possible values X+Y for independent random variables X And Y are equal to the products of the probabilities of the terms, and for dependent random variables - to the products of the probability of one term by the conditional probability of the second.

If = and the probabilities of these values are respectively equal, then the probability (the same as ) is equal to .

Property 4:The mathematical expectation of the sum of two random variables (dependent or independent) is equal to the sum of the mathematical expectations of the terms:

M(X+Y) = M(X) + M(Y).

Proof: Let two random variables X And Y are given by the following distribution laws:

X
P

Y
G

To simplify the conclusion, we will limit ourselves to two possible values of each quantity. In the general case the proof is similar.

Let's compose all possible values of a random variable X+Y(assume, for simplicity, that these values are different; if not, then the proof is similar):

X+Y
P

Let's find the mathematical expectation of this value.

M(X+Y) = + + + +

Let's prove that + = .

Event X = ( its probability P(X = ) entails the event that the random variable X+Y will take the value or (the probability of this event, according to the addition theorem, is equal to ) and vice versa. Then = .

The equalities = = = are proved in a similar way

Substituting the right-hand sides of these equalities into the resulting formula for the mathematical expectation, we obtain:

M(X + Y) = + ) = M(X) + M(Y).

Consequence:The mathematical expectation of the sum of several random variables is equal to the sum of the mathematical expectations of the terms.

Proof: Let us prove for three random variables X,Y,Z. Let's find the mathematical expectation of random variables X+Y And Z:

M(X+Y+Z)=M((X+Y Z)=M(X+Y) M(Z)=M(X)+M(Y)+M(Z)

For an arbitrary number of random variables, the proof is carried out by the method of mathematical induction.

Example: Find the average of the sum of the number of points that can be obtained when throwing two dice.

Solution: Let X– the number of points that can appear on the first die, Y- On the second. It is obvious that random variables X And Y have the same distributions. Let's write down the distribution data X And Y into one table:

X	1	2	3	4	5	6
Y	1	2	3	4	5	6
P	1/6	1/6	1/6	1/6	1/6	1/6

M(X) = M(Y) (1+2+3+4+5+6) = =

M(X + Y) = 7.

So, the average value of the sum of the number of points that can appear when throwing two dice is 7 .

Theorem:The mathematical expectation M(X) of the number of occurrences of event A in n independent trials is equal to the product of the number of trials and the probability of the occurrence of the event in each trial: M(X) = np.

Proof: Let X– number of occurrences of the event A V n independent tests. Obviously the total number X occurrences of the event A in these trials is the sum of the number of occurrences of the event in individual trials. Then, if the number of occurrences of an event in the first trial, in the second, and so on, finally, is the number of occurrences of the event in n-th test, then the total number of occurrences of the event is calculated by the formula:

By property 4 of mathematical expectation we have:

M(X) = M( ) + … + M( ).

Since the mathematical expectation of the number of occurrences of an event in one trial is equal to the probability of the event, then

M( ) = M( )= … = M( ) = p.

Hence, M(X) = np.

Example: The probability of hitting the target when firing from a gun is p = 0.6. Find the average number of hits if made 10 shots.

Solution: The hit for each shot does not depend on the outcomes of other shots, therefore the events under consideration are independent and, therefore, the required mathematical expectation is equal to:

M(X) = np = 10 0,6 = 6.

So the average number of hits is 6.

Now consider the mathematical expectation of a continuous random variable.

Definition:The mathematical expectation of a continuous random variable X, the possible values of which belong to the interval,called the definite integral:

where f(x) is the probability distribution density.

If possible values of a continuous random variable X belong to the entire Ox axis, then

It is assumed that this improper integral converges absolutely, i.e. the integral converges If this requirement were not met, then the value of the integral would depend on the rate at which (separately) the lower limit tends to -∞, and the upper limit tends to +∞.

It can be proven that all properties of the mathematical expectation of a discrete random variable are preserved for a continuous random variable. The proof is based on the properties of definite and improper integrals.

It is obvious that the mathematical expectation M(X) greater than the smallest and less than the largest possible value of the random variable X. Those. on the number axis, possible values of a random variable are located to the left and to the right of its mathematical expectation. In this sense, the mathematical expectation M(X) characterizes the location of the distribution and is therefore often called distribution center.

Chapter 6.

Numerical characteristics of random variables

Mathematical expectation and its properties

To solve many practical problems, knowledge of all possible values of a random variable and their probabilities is not always required. Moreover, sometimes the distribution law of the random variable under study is simply unknown. However, it is necessary to highlight some features of this random variable, in other words, numerical characteristics.

Numerical characteristics– these are some numbers that characterize certain properties, distinctive features of a random variable.

For example, the average value of a random variable, the average spread of all values of a random variable around its average, etc. The main purpose of numerical characteristics is to express in a concise form the most important features of the distribution of the random variable under study. Numerical characteristics play a huge role in probability theory. They help solve, even without knowledge of the laws of distribution, many important practical problems.

Among all the numerical characteristics, we first highlight position characteristics. These are characteristics that fix the position of a random variable on the numerical axis, i.e. a certain average value around which the remaining values of the random variable are grouped.

Of the characteristics of a position, the greatest role in probability theory is played by the mathematical expectation.

Expected value sometimes called simply the mean of a random variable. It is a kind of distribution center.

Expectation of a discrete random variable

Let us first consider the concept of mathematical expectation for a discrete random variable.

Before introducing a formal definition, let us solve the following simple problem.

Example 6.1. Let a certain shooter fire 100 shots at a target. As a result, the following picture was obtained: 50 shots - hitting the "eight", 20 shots - hitting the "nine" and 30 - hitting the "ten". What is the average score for one shot?

Solution This problem is obvious and boils down to finding the average value of 100 numbers, namely, points.

We transform the fraction by dividing the numerator by the denominator term by term, and present the average value in the form of the following formula:

Let us now assume that the number of points in one shot are the values of some discrete random variable X. From the problem statement it is clear that X 1 =8; X 2 =9; X 3 =10. The relative frequencies of occurrence of these values are known, which, as is known, when large number tests are approximately equal to the probabilities of the corresponding values, i.e. R 1 ≈0,5;R 2 ≈0,2; R 3 ≈0.3. So, . The value on the right side is the mathematical expectation of a discrete random variable.

Mathematical expectation of a discrete random variable X is the sum of the products of all its possible values and the probabilities of these values.

Let the discrete random variable X is given by its distribution series:

X	X 1	X 2	…	X n
R	R 1	R 2	…	R n

Then the mathematical expectation M(X) of a discrete random variable is determined by the following formula:

If a discrete random variable takes on an infinite countable set of values, then the mathematical expectation is expressed by the formula:

Moreover, the mathematical expectation exists if the series on the right side of the equality converges absolutely.

Example 6.2 . Find the mathematical expectation of winning X under the conditions of example 5.1.

Solution . Recall that the distribution series X has the following form:

X
R	0,7	0,2	0,1

We get M(X)=0∙0.7+10∙0.2+50∙0.1=7. Obviously, 7 rubles is a fair price for a ticket in this lottery, without various costs, for example, associated with the distribution or production of tickets. ■

Example 6.3 . Let the random variable X is the number of occurrences of some event A in one test. The probability of this event is R. Find M(X).

Solution. Obviously, the possible values of the random variable are: X 1 =0 – event A didn't show up and X 2 =1 – event A appeared. The distribution series looks like:

X
R	1−R	R

Then M(X) = 0∙(1−R)+1∙R= R. ■

So, the mathematical expectation of the number of occurrences of an event in one trial is equal to the probability of this event.

At the beginning of the paragraph there was given specific task, where the relationship between the mathematical expectation and the average value of a random variable was indicated. Let us explain this in general terms.

Let it be produced k tests in which the random variable X accepted k 1 time value X 1 ; k 2 times the value X 2, etc. and finally k n times value xn. It's obvious that k 1 +k 2 +…+k n = k. Let us find the arithmetic mean of all these values, we have

Note that a fraction is the relative frequency of occurrence of a value x i V k tests. With a large number of tests, the relative frequency is approximately equal to the probability, i.e. . It follows that

Thus, the mathematical expectation is approximately equal to the arithmetic mean of the observed values of the random variable, and the more accurate the greater the number of tests - this is probabilistic meaning of mathematical expectation.

The expected value is sometimes called center distribution of a random variable, since it is obvious that the possible values of the random variable are located on the numerical axis to the left and to the right of its mathematical expectation.

Let us now move on to the concept of mathematical expectation for a continuous random variable.

There will also be tasks for independent decision, to which you can see the answers.

Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. The expected value is often called simply the average. random variable. Dispersion of a random variable - characteristic of dispersion, spread of a random variable about its mathematical expectation.

In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.

Expectation of a discrete random variable

Let's come to the concept of mathematical expectation. Let the mass of some substance be distributed between the points of the x-axis x1 , x 2 , ..., x n. Moreover, each material point has a corresponding mass with a probability of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.

The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:

Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for someone who buys one ticket?

Solution. We find the average payoff if total amount winnings, which is equal to 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, divide by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:

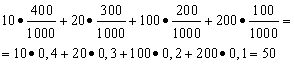
On the other hand, in these conditions, the winning amount is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.

Example 2. The publisher decided to publish a new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 - the bookstore and 30 - the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.

Find the publisher's expected profit.

Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:

Number	Profit xi	Probability pi	xi p i
500	-125000	0,20	-25000
1000	-50000	0,40	-20000
2000	100000	0,25	25000
3000	250000	0,10	25000
4000	400000	0,05	20000
Total:		1,00	25000

Thus, we obtain the mathematical expectation of the publisher’s profit:

Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.

Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:

Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .

Hint: find the probability of random variable values by Bernoulli's formula .

Properties of mathematical expectation

Let's consider the properties of mathematical expectation.

Property 1. The mathematical expectation of a constant value is equal to this constant:

Property 2. The constant factor can be taken out of the mathematical expectation sign:

Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:

Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:

Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:

When you can’t limit yourself only to mathematical expectation

In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.

Let the random variables X And Y are given by the following distribution laws:

Meaning X	Probability
-0,1	0,1
-0,01	0,2
0	0,4
0,01	0,2
0,1	0,1

Meaning Y	Probability
-20	0,3
-10	0,1
0	0,2
10	0,1
20	0,3

The mathematical expectations of these quantities are the same - equal to zero:

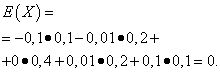
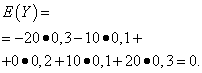
However, their distribution patterns are different. Random value X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the share of high- and low-paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.

Variance of a discrete random variable

Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:

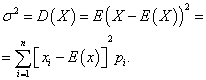
The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:

Example 5. Calculate variances and standard deviations of random variables X And Y, the distribution laws of which are given in the tables above.

Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:

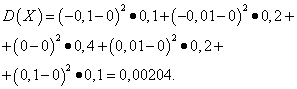
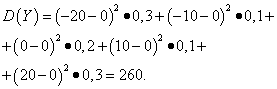
Then the standard deviations of random variables X And Y make up

Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.

Example 6. The investor has 4 alternative project investments. The table summarizes the expected profit in these projects with the corresponding probability.

Project 1	Project 2	Project 3	Project 4
500, P=1	1000, P=0,5	500, P=0,5	500, P=0,5
	0, P=0,5	1000, P=0,25	10500, P=0,25
		0, P=0,25	9500, P=0,25

Find the mathematical expectation, variance and standard deviation for each alternative.

Solution. Let us show how these values are calculated for the 3rd alternative:

The table summarizes the found values for all alternatives.

All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.

Dispersion properties

Let us present the properties of dispersion.

Property 1. The variance of a constant value is zero:

Property 2. The constant factor can be taken out of the dispersion sign by squaring it:

Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:

Where .

Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:

Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.

Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:

E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,

where we get the probabilities: p= 0.3 and 1 − p = 0,7 .

Law of distribution of a random variable:

X	−3	7
p	0,3	0,7

We calculate the variance of this random variable using the formula from property 3 of dispersion:

D(X) = 2,7 + 34,3 − 16 = 21 .

Find the mathematical expectation of a random variable yourself, and then look at the solution

Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.

Example 9. There are 6 white and 4 black balls in an urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.

Solution. Random value X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:

X	0	1	2	3
p	1/30	3/10	1/2	1/6

Hence the mathematical expectation of this random variable:

M(X) = 3/10 + 1 + 1/2 = 1,8 .

The variance of a given random variable is:

D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .

Expectation and variance of a continuous random variable

For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.

To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.

The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .

Expectation is the probability distribution of a random variable

Mathematical expectation, definition, mathematical expectation of discrete and continuous random variables, sample, conditional expectation, calculation, properties, problems, estimation of expectation, dispersion, distribution function, formulas, calculation examples

Expand contents

Collapse content

Mathematical expectation is the definition

One of the most important concepts in mathematical statistics and probability theory, characterizing the distribution of values or probabilities of a random variable. Usually expressed as weighted average all possible parameters of a random variable. Widely used in technical analysis, research number series, the study of continuous and long-term processes. It is important in assessing risks, predicting price indicators when trading on financial markets, and is used in developing strategies and methods of gaming tactics in the theory of gambling.

Mathematical expectation is the average value of a random variable, the probability distribution of a random variable is considered in probability theory.

Mathematical expectation is a measure of the average value of a random variable in probability theory. Expectation of a random variable x denoted by M(x).

Mathematical expectation is

Mathematical expectation is in probability theory, a weighted average of all possible values that a random variable can take.

Mathematical expectation is the sum of the products of all possible values of a random variable and the probabilities of these values.

Mathematical expectation is the average benefit from a particular decision, provided that such a decision can be considered within the framework of the theory of large numbers and long distance.

Mathematical expectation is in gambling theory, the amount of winnings a player can earn or lose, on average, for each bet. In gambling parlance, this is sometimes called the "player's edge" (if it is positive for the player) or the "house edge" (if it is negative for the player).

Mathematical expectation is the percentage of profit per win multiplied by the average profit, minus the probability of loss multiplied by the average loss.

Mathematical expectation of a random variable in mathematical theory

One of the important numerical characteristics of a random variable is its mathematical expectation. Let us introduce the concept of a system of random variables. Let's consider a set of random variables that are the results of the same random experiment. If is one of the possible values of the system, then the event corresponds to a certain probability that satisfies Kolmogorov’s axioms. A function defined for any possible values of random variables is called a joint distribution law. This function allows you to calculate the probabilities of any events from. In particular, the joint distribution law of random variables and, which take values from the set and, is given by probabilities.

The term “mathematical expectation” was introduced by Pierre Simon Marquis de Laplace (1795) and comes from the concept of “expected value of winnings,” which first appeared in the 17th century in the theory of gambling in the works of Blaise Pascal and Christiaan Huygens. However, the first complete theoretical understanding and assessment of this concept was given by Pafnuty Lvovich Chebyshev (mid-19th century).

Random distribution law numerical quantities(distribution function and distribution series or probability density) completely describe the behavior of a random variable. But in a number of problems, it is enough to know some numerical characteristics of the quantity under study (for example, its average value and possible deviation from it) in order to answer the question posed. The main numerical characteristics of random variables are the mathematical expectation, variance, mode and median.

The mathematical expectation of a discrete random variable is the sum of the products of its possible values and their corresponding probabilities. Sometimes the mathematical expectation is called a weighted average, since it is approximately equal to the arithmetic mean of the observed values of a random variable over a large number of experiments. From the definition of mathematical expectation it follows that its value is no less than the smallest possible value of a random variable and no more than the largest. The mathematical expectation of a random variable is a non-random (constant) variable.

The mathematical expectation has a simple physical meaning: if you place a unit mass on a straight line, placing some mass at some points (for discrete distribution), or by “smearing” it with a certain density (for absolutely continuous distribution), then the point corresponding to the mathematical expectation will be the coordinate of the “center of gravity” of the line.

The average value of a random variable is a certain number that is, as it were, its “representative” and replaces it in roughly approximate calculations. When we say: “the average lamp operating time is 100 hours” or “the average point of impact is shifted relative to the target by 2 m to the right,” we are indicating a certain numerical characteristic of a random variable that describes its location on the numerical axis, i.e. "position characteristics".

Of the characteristics of a position in probability theory, the most important role is played by the mathematical expectation of a random variable, which is sometimes called simply the average value of a random variable.

Consider the random variable X, having possible values x1, x2, …, xn with probabilities p1, p2, …, pn. We need to characterize with some number the position of the values of a random variable on the x-axis, taking into account the fact that these values have different probabilities. For this purpose, it is natural to use the so-called “weighted average” of the values xi, and each value xi during averaging should be taken into account with a “weight” proportional to the probability of this value. Thus, we will calculate the average of the random variable X, which we denote M |X|:

This weighted average is called the mathematical expectation of the random variable. Thus, we introduced into consideration one of the most important concepts of probability theory - the concept of mathematical expectation. The mathematical expectation of a random variable is the sum of the products of all possible values of a random variable and the probabilities of these values.

X is connected by a peculiar dependence with the arithmetic mean of the observed values of the random variable over a large number of experiments. This dependence is of the same type as the dependence between frequency and probability, namely: with a large number of experiments, the arithmetic mean of the observed values of a random variable approaches (converges in probability) to its mathematical expectation. From the presence of a connection between frequency and probability, one can deduce as a consequence the presence of a similar connection between the arithmetic mean and the mathematical expectation. Indeed, consider the random variable X, characterized by a distribution series:

Let it be produced N independent experiments, in each of which the value X takes on a certain value. Let's assume that the value x1 appeared m1 times, value x2 appeared m2 times, general meaning xi appeared mi times. Let us calculate the arithmetic mean of the observed values of the value X, which, in contrast to the mathematical expectation M|X| we denote M*|X|:

With increasing number of experiments N frequencies pi will approach (converge in probability) the corresponding probabilities. Consequently, the arithmetic mean of the observed values of the random variable M|X| with an increase in the number of experiments it will approach (converge in probability) to its mathematical expectation. The connection between the arithmetic mean and mathematical expectation formulated above constitutes the content of one of the forms of the law of large numbers.

We already know that all forms of the law of large numbers state the fact that some averages are stable over a large number of experiments. Here we are talking about the stability of the arithmetic mean from a series of observations of the same quantity. With a small number of experiments, the arithmetic mean of their results is random; with a sufficient increase in the number of experiments, it becomes “almost non-random” and, stabilizing, approaches a constant value - the mathematical expectation.

The stability of averages over a large number of experiments can be easily verified experimentally. For example, when weighing a body in a laboratory on precise scales, as a result of weighing we obtain a new value each time; To reduce observation error, we weigh the body several times and use the arithmetic mean of the obtained values. It is easy to see that with a further increase in the number of experiments (weighings), the arithmetic mean reacts to this increase less and less and, with a sufficiently large number of experiments, practically ceases to change.

It should be noted that the most important characteristic of the position of a random variable - the mathematical expectation - does not exist for all random variables. It is possible to compose examples of such random variables for which the mathematical expectation does not exist, since the corresponding sum or integral diverges. However, such cases are not of significant interest for practice. Typically, the random variables we deal with have a limited range of possible values and, of course, have a mathematical expectation.

In addition to the most important characteristics of the position of a random variable - the mathematical expectation - in practice, other characteristics of the position are sometimes used, in particular, the mode and median of the random variable.

The mode of a random variable is its most probable value. The term "most probable value" strictly speaking applies only to discontinuous quantities; for a continuous quantity, the mode is the value at which the probability density is maximum. The figures show the mode for discontinuous and continuous random variables, respectively.

If the distribution polygon (distribution curve) has more than one maximum, the distribution is called "multimodal".

Sometimes there are distributions that have a minimum in the middle rather than a maximum. Such distributions are called “anti-modal”.

In the general case, the mode and mathematical expectation of a random variable do not coincide. In the particular case, when the distribution is symmetrical and modal (i.e. has a mode) and there is a mathematical expectation, then it coincides with the mode and center of symmetry of the distribution.

Another position characteristic is often used - the so-called median of a random variable. This characteristic is usually used only for continuous random variables, although it can be formally defined for a discontinuous variable. Geometrically, the median is the abscissa of the point at which the area enclosed by the distribution curve is divided in half.

In the case of a symmetric modal distribution, the median coincides with the mathematical expectation and mode.

The mathematical expectation is the average value of a random variable - numerical characteristic probability distribution of a random variable. In the most general way, the mathematical expectation of a random variable X(w) is defined as the Lebesgue integral with respect to the probability measure R in the original probability space:

The mathematical expectation can also be calculated as the Lebesgue integral of X by probability distribution px quantities X:

The concept of a random variable with infinite mathematical expectation can be defined in a natural way. A typical example is the return times of some random walks.

Using the mathematical expectation, many numerical and functional characteristics of a distribution are determined (as the mathematical expectation of the corresponding functions of a random variable), for example, the generating function, characteristic function, moments of any order, in particular dispersion, covariance.

The mathematical expectation is a characteristic of the location of the values of a random variable (the average value of its distribution). In this capacity, the mathematical expectation serves as some “typical” distribution parameter and its role is similar to the role of the static moment - the coordinate of the center of gravity of the mass distribution - in mechanics. From other characteristics of the location with the help of which the distribution is described in general terms - medians, modes, mathematical expectation differs in the greater value that it and the corresponding scattering characteristic - dispersion - have in the limit theorems of probability theory. The meaning of mathematical expectation is revealed most fully by the law of large numbers (Chebyshev's inequality) and the strengthened law of large numbers.

Expectation of a discrete random variable

Let there be some random variable that can take one of several numerical values (for example, the number of points when throwing a dice can be 1, 2, 3, 4, 5 or 6). Often in practice, for such a value, the question arises: what value does it take “on average” with a large number of tests? What will be our average income (or loss) from each of the risky transactions?

Let's say there is some kind of lottery. We want to understand whether it is profitable or not to participate in it (or even participate repeatedly, regularly). Let’s say that every fourth ticket is a winner, the prize will be 300 rubles, and the price of any ticket will be 100 rubles. With an infinitely large number of participations, this is what happens. In three quarters of cases we will lose, every three losses will cost 300 rubles. In every fourth case we will win 200 rubles. (prize minus cost), that is, for four participations we lose on average 100 rubles, for one - on average 25 rubles. In total, the average rate of our ruin will be 25 rubles per ticket.

We throw the dice. If it is not cheating (without shifting the center of gravity, etc.), then how many points will we have on average at a time? Since each option is equally likely, we simply take the arithmetic mean and get 3.5. Since this is AVERAGE, there is no need to be indignant that no specific roll will give 3.5 points - well, this cube does not have a face with such a number!

Now let's summarize our examples:

Let's look at the picture just given. On the left is a table of the distribution of a random variable. The value X can take one of n possible values (shown in the top line). There cannot be any other meanings. Under each possible value, its probability is written below. On the right is the formula, where M(X) is called the mathematical expectation. The meaning of this value is that with a large number of tests (with a large sample), the average value will tend to this same mathematical expectation.

Let's return again to the same playing cube. The mathematical expectation of the number of points when throwing is 3.5 (calculate it yourself using the formula if you don’t believe me). Let's say you threw it a couple of times. The results were 4 and 6. The average was 5, which is far from 3.5. They threw it one more time, they got 3, that is, on average (4 + 6 + 3)/3 = 4.3333... Somehow far from the mathematical expectation. Now do a crazy experiment - roll the cube 1000 times! And even if the average is not exactly 3.5, it will be close to that.

Let's calculate the mathematical expectation for the lottery described above. The plate will look like this:

Then the mathematical expectation will be, as we established above:

Another thing is that it would be difficult to do it “on the fingers” without a formula if there were more options. Well, let's say there would be 75% losing tickets, 20% winning tickets and 5% especially winning ones.

Now some properties of mathematical expectation.

It's easy to prove:

The constant factor can be taken out as a sign of the mathematical expectation, that is:

This is a special case of the linearity property of the mathematical expectation.

Another consequence of the linearity of the mathematical expectation:

that is, the mathematical expectation of the sum of random variables is equal to the sum of the mathematical expectations of random variables.

Let X, Y be independent random variables, Then:

This is also easy to prove) Work XY itself is a random variable, and if the initial values could take n And m values accordingly, then XY can take nm values. The probability of each value is calculated based on the fact that the probabilities independent events multiply. As a result, we get this:

Expectation of a continuous random variable

Continuous random variables have such a characteristic as distribution density (probability density). It essentially characterizes the situation that some values from the set real numbers a random variable takes more often, some less often. For example, consider this graph:

Here X- actual random variable, f(x)- distribution density. Judging by this graph, during experiments the value X will often be a number close to zero. The chances are exceeded 3 or be smaller -3 rather purely theoretical.

Let, for example, there be a uniform distribution:

This is quite consistent with intuitive understanding. Let's say, if we receive many random real numbers with a uniform distribution, each of the segment |0; 1| , then the arithmetic mean should be about 0.5.

The properties of mathematical expectation - linearity, etc., applicable for discrete random variables, are also applicable here.

Relationship between mathematical expectation and other statistical indicators

In statistical analysis, along with the mathematical expectation, there is a system of interdependent indicators that reflect the homogeneity of phenomena and the stability of processes. Variation indicators often have no independent meaning and are used for further data analysis. The exception is the coefficient of variation, which characterizes the homogeneity of the data, which is a valuable statistical characteristic.

The degree of variability or stability of processes in statistical science can be measured using several indicators.

The most important indicator characterizing the variability of a random variable is Dispersion, which is most closely and directly related to the mathematical expectation. This parameter is actively used in other types of statistical analysis (hypothesis testing, analysis of cause-and-effect relationships, etc.). Like the average linear deviation, variance also reflects the extent of the spread of data around the mean value.

It is useful to translate the language of signs into the language of words. It turns out that the dispersion is the average square of the deviations. That is, the average value is first calculated, then the difference between each original and average value is taken, squared, added, and then divided by the number of values in the population. The difference between an individual value and the average reflects the measure of deviation. It is squared so that all deviations become exclusively positive numbers and to avoid mutual destruction of positive and negative deviations when summing them up. Then, given the squared deviations, we simply calculate the arithmetic mean. Average - square - deviations. The deviations are squared and the average is calculated. The answer to the magic word “dispersion” lies in just three words.

However, in its pure form, such as the arithmetic mean, or index, dispersion is not used. It is rather an auxiliary and intermediate indicator that is used for other types of statistical analysis. It doesn't even have a normal unit of measurement. Judging by the formula, this is the square of the unit of measurement of the original data.

Let us measure a random variable N times, for example, we measure the wind speed ten times and want to find the average value. How is the average value related to the distribution function?

Or we will roll the dice a large number of times. The number of points that will appear on the dice with each throw is a random variable and can take any natural value from 1 to 6. The arithmetic mean of the dropped points calculated for all dice throws is also a random variable, but for large N it tends to a very specific number - mathematical expectation Mx. IN in this case Mx = 3.5.

How did you get this value? Let in N tests n1 once you get 1 point, n2 once - 2 points and so on. Then the number of outcomes in which one point fell:

Similarly for outcomes when 2, 3, 4, 5 and 6 points are rolled.

Let us now assume that we know the distribution law of the random variable x, that is, we know that the random variable x can take values x1, x2, ..., xk with probabilities p1, p2, ..., pk.

The mathematical expectation Mx of a random variable x is equal to:

The mathematical expectation is not always a reasonable estimate of some random variable. Thus, to estimate the average salary, it is more reasonable to use the concept of median, that is, such a value that the number of people receiving a salary lower than the median and a greater one coincide.

The probability p1 that the random variable x will be less than x1/2, and the probability p2 that the random variable x will be greater than x1/2, are the same and equal to 1/2. The median is not determined uniquely for all distributions.

Standard or Standard Deviation in statistics, the degree of deviation of observational data or sets from the AVERAGE value is called. Denoted by the letters s or s. A small standard deviation indicates that the data clusters around the mean, while a large standard deviation indicates that the initial data are located far from it. The standard deviation is square root quantity called dispersion. It is the average of the sum of the squared differences of the initial data that deviate from the average value. The standard deviation of a random variable is the square root of the variance:

Example. Under test conditions when shooting at a target, calculate the dispersion and standard deviation of the random variable:

Variation- fluctuation, changeability of the value of a characteristic among units of the population. Individual numerical values of a characteristic found in the population under study are called variants of values. Insufficient average value for full characteristics population forces us to supplement the average values with indicators that allow us to assess the typicality of these averages by measuring the variability (variation) of the characteristic being studied. The coefficient of variation is calculated using the formula:

Range of variation(R) represents the difference between the maximum and minimum values of the attribute in the population being studied. This indicator gives the most general idea about the variability of the studied characteristic, since it shows the difference only between the limiting values of the options. Dependence on the extreme values of a characteristic gives the scope of variation an unstable, random character.

Average linear deviation represents the arithmetic mean of the absolute (modulo) deviations of all values of the analyzed population from their average value:

Mathematical expectation in gambling theory

Mathematical expectation is The average amount of money a gambler can win or lose on a given bet. This is a very important concept for the player because it is fundamental to the assessment of most gaming situations. Mathematical expectation is also the optimal tool for analyzing basic card layouts and gaming situations.

Let's say you're playing a coin game with a friend, betting equally $1 each time, no matter what comes up. Tails means you win, heads means you lose. The odds are one to one that it will come up heads, so you bet $1 to $1. Thus, your mathematical expectation is zero, because From a mathematical point of view, you cannot know whether you will lead or lose after two throws or after 200.

Your hourly gain is zero. Hourly winnings are the amount of money you expect to win in an hour. You can toss a coin 500 times in an hour, but you won't win or lose because... your chances are neither positive nor negative. If you look at it, from the point of view of a serious player, this betting system is not bad. But this is simply a waste of time.

But let's say someone wants to bet $2 against your $1 on the same game. Then you immediately have a positive expectation of 50 cents from each bet. Why 50 cents? On average, you win one bet and lose the second. Bet the first dollar and you will lose $1, bet the second and you will win $2. You bet $1 twice and are ahead by $1. So each of your one-dollar bets gave you 50 cents.

If a coin appears 500 times in one hour, your hourly winnings will already be $250, because... On average, you lost one dollar 250 times and won two dollars 250 times. $500 minus $250 equals $250, which is the total winnings. Please note that the expected value, which is the average amount you win per bet, is 50 cents. You won $250 by betting a dollar 500 times, which equals 50 cents per bet.

Mathematical expectation has nothing to do with short-term results. Your opponent, who decided to bet $2 against you, could beat you on the first ten rolls in a row, but you, having a 2 to 1 betting advantage, all other things being equal, will earn 50 cents on every $1 bet in any circumstances. It makes no difference whether you win or lose one bet or several bets, as long as you have enough cash to comfortably cover the costs. If you continue to bet in the same way, then over a long period of time your winnings will approach the sum of the expectations in individual throws.

Every time you make a best bet (a bet that may turn out to be profitable in the long run), when the odds are in your favor, you are bound to win something on it, no matter whether you lose it or not in the given hand. Conversely, if you make an underdog bet (a bet that is unprofitable in the long run) when the odds are against you, you lose something regardless of whether you win or lose the hand.

You place a bet with the best outcome if your expectation is positive, and it is positive if the odds are on your side. When you place a bet with the worst outcome, you have a negative expectation, which happens when the odds are against you. Serious players only bet on the best outcome; if the worst happens, they fold. What does the odds mean in your favor? You may end up winning more than the real odds bring. The real odds of landing heads are 1 to 1, but you get 2 to 1 due to the odds ratio. In this case, the odds are in your favor. You definitely get the best outcome with a positive expectation of 50 cents per bet.

Here's more complex example mathematical expectation. A friend writes down numbers from one to five and bets $5 against your $1 that you won't guess the number. Should you agree to such a bet? What is the expectation here?

On average you will be wrong four times. Based on this, the odds against you guessing the number are 4 to 1. The odds against you losing a dollar on one attempt. However, you win 5 to 1, with the possibility of losing 4 to 1. So the odds are in your favor, you can take the bet and hope for the best outcome. If you make this bet five times, on average you will lose $1 four times and win $5 once. Based on this, for all five attempts you will earn $1 with a positive mathematical expectation of 20 cents per bet.

A player who is going to win more than he bets, as in the example above, is taking chances. On the contrary, he ruins his chances when he expects to win less than he bets. A bettor can have either a positive or a negative expectation, which depends on whether he wins or ruins the odds.

If you bet $50 to win $10 with a 4 to 1 chance of winning, you will get a negative expectation of $2 because On average, you will win $10 four times and lose $50 once, which shows that the loss per bet will be $10. But if you bet $30 to win $10, with the same odds of winning 4 to 1, then in this case you have a positive expectation of $2, because you again win $10 four times and lose $30 once, for a profit of $10. These examples show that the first bet is bad, and the second is good.

Mathematical expectation is the center of any game situation. When a bookmaker encourages football fans to bet $11 to win $10, he has a positive expectation of 50 cents on every $10. If the casino pays even money from the pass line in craps, then the casino's positive expectation will be approximately $1.40 for every $100, because This game is structured so that anyone who bets on this line loses 50.7% on average and wins 49.3% of the total time. Undoubtedly, it is this seemingly minimal positive expectation that brings enormous profits to casino owners around the world. As Vegas World casino owner Bob Stupak noted, “a one-thousandth of one percent negative probability over a long enough distance will ruin richest man in the world".

Expectation when playing Poker

The game of Poker is the most revealing and a clear example from the point of view of using the theory and properties of mathematical expectation.

Expected Value in Poker is the average benefit from a particular decision, provided that such a decision can be considered within the framework of the theory of large numbers and long distance. A successful poker game is to always accept moves with positive expected value.

The mathematical meaning of the mathematical expectation when playing poker is that we often encounter random variables when making decisions (we don’t know what cards the opponent has in his hands, what cards will come in subsequent rounds of betting). We must consider each of the solutions from the point of view of large number theory, which states that with a sufficiently large sample, the average value of a random variable will tend to its mathematical expectation.

Among the particular formulas for calculating the mathematical expectation, the following is most applicable in poker:

When playing poker, the expected value can be calculated for both bets and calls. In the first case, fold equity should be taken into account, in the second, the bank’s own odds. When assessing the mathematical expectation of a particular move, you should remember that a fold always has a zero expectation. Thus, discarding cards will always be a more profitable decision than any negative move.

Expectation tells you what you can expect (profit or loss) for every dollar you risk. Casinos make money because the mathematical expectation of all games played in them is in favor of the casino. With a long enough series of games, you can expect that the client will lose his money, since the “odds” are in favor of the casino. However, professional casino players limit their games to short periods of time, thereby stacking the odds in their favor. The same goes for investing. If your expectation is positive, you can make more money by making many trades in a short period of time. Expectation is your percentage of profit per win multiplied by your average profit, minus your probability of loss multiplied by your average loss.

Poker can also be considered from the standpoint of mathematical expectation. You may assume that a certain move is profitable, but in some cases it may not be the best because another move is more profitable. Let's say you hit a full house in five-card draw poker. Your opponent makes a bet. You know that if you raise the bet, he will respond. Therefore, raising seems to be the best tactic. But if you do raise the bet, the remaining two players will definitely fold. But if you call, you have full confidence that the other two players behind you will do the same. When you raise your bet you get one unit, and when you just call you get two. Thus, calling gives you a higher positive expected value and will be the best tactic.

The mathematical expectation can also give an idea of which poker tactics are less profitable and which are more profitable. For example, if you play a certain hand and you think your loss will average 75 cents including ante, then you should play that hand because this is better than folding when the ante is $1.

Another important reason to understand the concept of expected value is that it gives you a sense of peace of mind whether you win the bet or not: if you made a good bet or folded at the right time, you will know that you have earned or saved a certain amount of money that the weaker player could not save. It's much harder to fold if you're upset because your opponent drew a stronger hand. With all this, the money you save by not playing instead of betting is added to your winnings for the night or month.

Just remember that if you changed your hands, your opponent would have called you, and as you will see in the Fundamental Theorem of Poker article, this is just one of your advantages. You should be happy when this happens. You can even learn to enjoy losing a hand because you know that other players in your position would have lost much more.

As discussed in the coin game example at the beginning, the hourly profit ratio is related to the mathematical expectation, and this concept especially important for professional players. When you go to play poker, you should mentally estimate how much you can win in an hour of play. In most cases you will need to rely on your intuition and experience, but you can also use some math. For example, you are playing draw lowball and you see three players bet $10 and then trade two cards, which is a very bad tactic, you can figure out that every time they bet $10, they lose about $2. Each of them does this eight times per hour, which means that all three of them lose approximately $48 per hour. You are one of the remaining four players who are approximately equal, so these four players (and you among them) must split $48, each making a profit of $12 per hour. Your hourly odds in this case are simply equal to your share of the amount of money lost by three bad players in an hour.

Over a long period of time, the player’s total winnings are the sum of his mathematical expectations in individual hands. The more hands you play with positive expectation, the more you win, and conversely, the more hands you play with negative expectation, the more you lose. As a result, you should choose a game that can maximize your positive anticipation or negate your negative anticipation so that you can maximize your hourly winnings.

Positive mathematical expectation in gaming strategy

If you know how to count cards, you can have an advantage over the casino, as long as they don't notice and throw you out. Casinos love drunk players and don't tolerate card counting players. The advantage will allow you to win over time. larger number times than to lose. Good money management using expected value calculations can help you extract more profit from your edge and reduce your losses. Without an advantage, you're better off giving the money to charity. In the game on the stock exchange, the advantage is given by the game system, which creates greater profits than losses, price differences and commissions. No amount of money management can save a bad gaming system.

A positive expectation is defined as a value greater than zero. The larger this number, the stronger the statistical expectation. If the value is less than zero, then the mathematical expectation will also be negative. The larger the module of the negative value, the worse the situation. If the result is zero, then the wait is break-even. You can only win when you have a positive mathematical expectation and a reasonable playing system. Playing by intuition leads to disaster.

Mathematical expectation and stock trading

Mathematical expectation is a fairly widely used and popular statistical indicator when carrying out exchange trading in financial markets. First of all, this parameter is used to analyze the success of trading. It is not difficult to guess that the higher this value, the more reasons to consider the trade being studied successful. Of course, analysis of a trader’s work cannot be carried out using this parameter alone. However, the calculated value, in combination with other methods of assessing the quality of work, can significantly increase the accuracy of the analysis.

The mathematical expectation is often calculated in trading account monitoring services, which allows you to quickly evaluate the work performed on the deposit. The exceptions include strategies that use “sitting out” unprofitable trades. A trader may be lucky for some time, and therefore there may be no losses in his work at all. In this case, it will not be possible to be guided only by the mathematical expectation, because the risks used in the work will not be taken into account.

In market trading, the mathematical expectation is most often used when predicting the profitability of any trading strategy or when predicting a trader's income based on statistical data from his previous trades.

With regard to money management, it is very important to understand that when making trades with negative expectations, there is no money management scheme that can definitely bring high profits. If you continue to play the stock market under these conditions, then regardless of how you manage your money, you will lose your entire account, no matter how large it was to begin with.

This axiom is true not only for games or trades with negative expectation, it is also true for games with equal chances. Therefore, the only time you have a chance to profit in the long term is if you take trades with positive expected value.

The difference between negative expectation and positive expectation is the difference between life and death. It doesn't matter how positive or how negative the expectation is; All that matters is whether it is positive or negative. Therefore, before considering money management, you should find a game with positive expectation.

If you don't have that game, then all the money management in the world won't save you. On the other hand, if you have a positive expectation, you can, through proper money management, turn it into an exponential growth function. It doesn't matter how small the positive expectation is! In other words, it doesn't matter how profitable a trading system is based on a single contract. If you have a system that wins $10 per contract per trade (after commissions and slippage), you can use money management techniques to make it more profitable than a system that averages $1,000 per trade (after deduction of commissions and slippage).

What matters is not how profitable the system was, but how certain the system can be said to show at least minimal profit in the future. Therefore, the most important preparation a trader can make is to ensure that the system will show a positive expected value in the future.

In order to have a positive expected value in the future, it is very important not to limit the degrees of freedom of your system. This is achieved not only by eliminating or reducing the number of parameters to be optimized, but also by reducing as many system rules as possible. Every parameter you add, every rule you make, every tiny change you make to the system reduces the number of degrees of freedom. Ideally, you need to build a fairly primitive and simple system, which will consistently generate small profits in almost any market. Again, it is important for you to understand that it does not matter how profitable the system is, as long as it is profitable. The money you make in trading will be made through effective money management.

A trading system is simply a tool that gives you a positive expected value so that you can use money management. Systems that work (show at least minimal profits) in only one or a few markets, or have different rules or parameters for different markets, will most likely not work in real time for long. The problem with most technically oriented traders is that they spend too much time and effort optimizing the various rules and parameter values of the trading system. This gives completely opposite results. Instead of wasting energy and computer time on increasing the profits of the trading system, direct your energy to increasing the level of reliability of obtaining a minimum profit.

Knowing that money management is just a numbers game that requires the use of positive expectations, a trader can stop searching for the "holy grail" of stock trading. Instead, he can start testing his trading method, find out how logical this method is, and whether it gives positive expectations. Proper money management methods, applied to any, even very mediocre trading methods, will do the rest of the work themselves.

For any trader to succeed in his work, he needs to solve three most important tasks: . To ensure that the number of successful transactions exceeds the inevitable mistakes and miscalculations; Set up your trading system so that you have the opportunity to earn money as often as possible; Achieve stable positive results from your operations.

And here, for us working traders, mathematical expectation can be of great help. This term is one of the key ones in probability theory. With its help, you can give an average estimate of some random value. The mathematical expectation of a random variable is similar to the center of gravity, if you imagine all possible probabilities as points with different masses.

In relation to a trading strategy, the mathematical expectation of profit (or loss) is most often used to evaluate its effectiveness. This parameter is defined as the sum of the products of given levels of profit and loss and the probability of their occurrence. For example, the developed trading strategy assumes that 37% of all transactions will bring profit, and the remaining part - 63% - will be unprofitable. At the same time, the average income from a successful transaction will be $7, and the average loss will be $1.4. Let's calculate the mathematical expectation of trading using this system:

What does this number mean? It says that, following the rules of this system, on average we will receive $1,708 from each closed transaction. Since the resulting efficiency rating is greater than zero, such a system can be used for real work. If, as a result of the calculation, the mathematical expectation turns out to be negative, then this already indicates an average loss and such trading will lead to ruin.

The amount of profit per transaction can also be expressed as a relative value in the form of %. For example:

– percentage of income per 1 transaction - 5%;

– percentage of successful trading operations - 62%;

– percentage of loss per 1 transaction - 3%;

– percentage of unsuccessful transactions - 38%;

That is, the average trade will bring 1.96%.

It is possible to develop a system that, despite the predominance of unprofitable trades, will produce a positive result, since its MO>0.

However, waiting alone is not enough. It is difficult to make money if the system gives very few trading signals. In this case, its profitability will be comparable to bank interest. Let each operation produce on average only 0.5 dollars, but what if the system involves 1000 operations per year? This will be a very significant amount in a relatively short time. It logically follows from this that another distinctive feature of a good trading system can be considered a short period of holding positions.

Sources and links

dic.academic.ru – academic online dictionary

mathematics.ru – educational website in mathematics

nsu.ru – educational website of Novosibirsk state university

webmath.ru – educational portal for students, applicants and schoolchildren.

exponenta.ru educational mathematical website

ru.tradimo.com – free online school trading

crypto.hut2.ru – multidisciplinary information resource

poker-wiki.ru – free encyclopedia of poker

sernam.ru – Science Library selected natural science publications

reshim.su – website WE WILL SOLVE test coursework problems

unfx.ru – Forex on UNFX: training, trading signals, trust management

slovopedia.com – Big encyclopedic Dictionary Slovopedia

pokermansion.3dn.ru – Your guide in the world of poker

statanaliz.info – information blog “ Statistical analysis data"

forex-trader.rf – Forex-Trader portal

megafx.ru – current Forex analytics

fx-by.com – everything for a trader

2. Basics of probability theory

Expected value

Consider a random variable with numerical values. It is often useful to associate a number with this function - its “mean value” or, as they say, “average value”, “index of central tendency”. For a number of reasons, some of which will become clear later, the mathematical expectation is usually used as the “average value”.

Definition 3. Mathematical expectation of a random variable X called number

those. the mathematical expectation of a random variable is a weighted sum of the values of a random variable with weights equal to the probabilities of the corresponding elementary events.

Example 6. Let's calculate the mathematical expectation of the number that appears on the top face of the die. It follows directly from Definition 3 that

Statement 2. Let the random variable X takes values x 1, x 2,…, xm. Then the equality is true

(5)

those. The mathematical expectation of a random variable is a weighted sum of the values of the random variable with weights equal to the probabilities that the random variable takes certain values.

Unlike (4), where the summation is carried out directly over elementary events, a random event can consist of several elementary events.

Sometimes relation (5) is taken as the definition of mathematical expectation. However, using Definition 3, as shown below, it is easier to establish the properties of the mathematical expectation necessary for constructing probabilistic models of real phenomena than using relation (5).

To prove relation (5), we group into (4) terms with identical values of the random variable:

Since the constant factor can be taken out of the sign of the sum, then

By determining the probability of an event

Using the last two relations we obtain the required:

The concept of mathematical expectation in probabilistic-statistical theory corresponds to the concept of the center of gravity in mechanics. Let's put it in points x 1, x 2,…, xm on the mass number axis P(X= x 1 ), P(X= x 2 ),…, P(X= x m) respectively. Then equality (5) shows that the center of gravity of this system of material points coincides with the mathematical expectation, which shows the naturalness of Definition 3.

Statement 3. Let X- random value, M(X)– its mathematical expectation, A– a certain number. Then

1) M(a)=a; 2) M(X-M(X))=0; 3M[(X- a) 2 ]= M[(X- M(X)) 2 ]+(a- M(X)) 2 .

To prove this, let us first consider a random variable that is constant, i.e. the function maps the space of elementary events to a single point A. Since the constant multiplier can be taken beyond the sign of the sum, then

If each member of a sum is divided into two terms, then the whole sum is divided into two sums, of which the first is made up of the first terms, and the second is made up of the second. Therefore, the mathematical expectation of the sum of two random variables X+Y, defined on the same space of elementary events, is equal to the sum of mathematical expectations M(X) And M(U) these random variables:

M(X+Y) = M(X) + M(Y).

And therefore M(X-M(X)) = M(X) - M(M(X)). As shown above, M(M(X)) = M(X). Hence, M(X-M(X)) = M(X) - M(X) = 0.

Because the (X - a) 2 = ((X – M(X)) + (M(X) - a)} 2 = (X - M(X)) 2 + 2(X - M(X))(M(X) - a) + (M(X) – a) 2 , That M[(X - a) 2 ] =M(X - M(X)) 2 + M{2(X - M(X))(M(X) - a)} + M[(M(X) – a) 2 ]. Let's simplify the last equality. As shown at the beginning of the proof of Statement 3, the mathematical expectation of a constant is the constant itself, and therefore M[(M(X) – a) 2 ] = (M(X) – a) 2 . Since the constant multiplier can be taken beyond the sign of the sum, then M{2(X - M(X))(M(X) - a)} = 2(M(X) - a)M(X - M(X)). The right side of the last equality is 0 because, as shown above, M(X-M(X))=0. Hence, M[(X- a) 2 ]= M[(X- M(X)) 2 ]+(a- M(X)) 2 , which was what needed to be proven.

From the above it follows that M[(X- a) 2 ] reaches a minimum A, equal M[(X- M(X)) 2 ], at a = M(X), since the second term in equality 3) is always non-negative and equals 0 only for the specified value A.

Statement 4. Let the random variable X takes values x 1, x 2,…, xm, and f is some function of the numerical argument. Then

To prove this, let’s group on the right side of equality (4), which defines the mathematical expectation, terms with the same values:

Using the fact that the constant factor can be taken out of the sign of the sum, and the definition of the probability of a random event (2), we obtain

Q.E.D.

Statement 5. Let X And U– random variables defined on the same space of elementary events, A And b- some numbers. Then M(aX+ bY)= aM(X)+ bM(Y).

Using the definition of the mathematical expectation and the properties of the summation symbol, we obtain a chain of equalities:

The required has been proven.

The above shows how the mathematical expectation depends on the transition to another reference point and to another unit of measurement (transition Y=aX+b), as well as to functions of random variables. The results obtained are constantly used in technical and economic analysis, in assessing the financial and economic activities of an enterprise, during the transition from one currency to another in foreign economic calculations, in regulatory and technical documentation, etc. The results under consideration allow the use of the same calculation formulas for various parameters scale and shift.