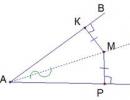
Definition of the velocity vector. The velocity vector at any point of the trajectory is tangent to it. Instantaneous center of speed
To characterize the speed of movement, the concept of speed is introduced.
Definition:
The average speed of the point for the time interval from to  called a vector quantity equal to the ratio of the increment of the radius vector of a point over this period of time to its duration
called a vector quantity equal to the ratio of the increment of the radius vector of a point over this period of time to its duration  .
.
 - average speed.
- average speed.

Definition: The speed (or instantaneous speed) of a point is called a vector quantity equal to the first time derivative of the radius vector.


The velocity vector characterizes the movement, both in magnitude and in direction. The velocity vector is always directed tangentially to the trajectory in the direction of motion.
Definition: The speed modulus is equal to the first time derivative of the distance traveled.

Let us expand the velocity vector in terms of the basis of a rectangular Cartesian coordinate system:
 , where V x , V y , V z are the projections of the velocity vector on the corresponding axis, which are respectively equal to:
, where V x , V y , V z are the projections of the velocity vector on the corresponding axis, which are respectively equal to:

where  is the X projection of the radius vector of the material point.
is the X projection of the radius vector of the material point.
 In the coordinate representation, the velocity vector has the form:
In the coordinate representation, the velocity vector has the form:
Velocity vector modulus in coordinate representation:
Reverse ratio.
Let's represent the radius velocity vector by means of a definite and indefinite integral:


where t, t 0 are the initial and final moments of time.
Representation of the distance traveled through the modulus of speed by means of a definite and indefinite integral.


§4. The acceleration vector.
To characterize the rate of change of the velocity vector of a point in mechanics, the concept of acceleration is introduced.
Definition:
Average acceleration for the time interval from  before
before  called a vector quantity equal to the ratio of the increment of the velocity vector of a point for a given time interval to its value.
called a vector quantity equal to the ratio of the increment of the velocity vector of a point for a given time interval to its value.

Definition: Acceleration (or instantaneous acceleration) of a point is called a vector quantity, numerically equal to the first time derivative of the speed of the point under consideration or, what is the same, the second time derivative of the radius vector of this point:

Acceleration can be entered through the limit of the average acceleration:

The two acceleration records entered are equivalent.
Let us expand the acceleration vector in terms of the basis of a rectangular Cartesian coordinate system:
where a x , a y , a z are projections of the acceleration vector onto the axis.
Coordinate representation of the module of the acceleration vector:
Inverse ratios:
 ;
;

Consider the motion of a material point along a plane curve. Acceleration is always directed inside the concavity of the curve or trajectory. We introduce two unit vectors:  , which is directed tangentially to the trajectory and
, which is directed tangentially to the trajectory and  - directed perpendicular to the trajectory to the center of the curve.
- directed perpendicular to the trajectory to the center of the curve.
 ;
;
Let us expand the acceleration vector in given directions.
 - tangential acceleration.
- tangential acceleration.
Definition: Tangential acceleration is a vector quantity that characterizes the rate of change of the velocity vector modulo.
 - vector representation.
- vector representation.
 - scalar representation.
- scalar representation.
 - normal acceleration.
- normal acceleration.
Definition: Normal acceleration characterizes the rate of change of the velocity vector in the direction and is calculated by the formula:
 -where R is the radius of curvature of the trajectory at the point M
-where R is the radius of curvature of the trajectory at the point M
If the trajectory is a circle, then R is the radius of the circle.
In scalar representation:

It follows from the properties of the components of the total acceleration that the total acceleration is directed towards the concavity of the trajectory.
The total acceleration modulus is:

Similarly for the full acceleration vector:

In this topic, we will consider a very special kind of non-uniform motion. Based on the opposition to uniform motion, not uniform motion- this is movement with unequal speed, along any trajectory. What is the characteristic of uniformly accelerated motion? This is an uneven movement, but which "equally accelerating". Acceleration is associated with an increase in speed. Remember the word "equal", we get an equal increase in speed. And how to understand "an equal increase in speed", how to evaluate the speed is equally increasing or not? To do this, we need to detect the time, estimate the speed through the same time interval. For example, a car starts moving, in the first two seconds it develops a speed of up to 10 m/s, in the next two seconds 20 m/s, after another two seconds it is already moving at a speed of 30 m/s. Every two seconds, the speed increases and each time by 10 m/s. This is uniformly accelerated motion.

The physical quantity that characterizes how much each time the speed increases is called acceleration.
Can a cyclist's movement be considered uniformly accelerated if, after stopping, his speed is 7 km/h in the first minute, 9 km/h in the second, and 12 km/h in the third? It is forbidden! The cyclist accelerates, but not equally, first accelerating by 7 km/h (7-0), then by 2 km/h (9-7), then by 3 km/h (12-9).
Usually, the movement with increasing speed is called accelerated movement. Movement with decreasing speed - slow motion. But physicists call any motion with a changing speed accelerated motion. Whether the car starts off (speed increases!), or slows down (speed decreases!), in any case, it moves with acceleration.

Uniformly accelerated motion- this is such a movement of a body in which its speed for any equal intervals of time changes(may increase or decrease) equally
body acceleration
Acceleration characterizes the rate of change of speed. This is the number by which the speed changes every second. If the modulo acceleration of the body is large, this means that the body quickly picks up speed (when it accelerates) or quickly loses it (when decelerating). Acceleration- this is a physical vector quantity, numerically equal to the ratio of the change in speed to the period of time during which this change occurred.
Let's determine the acceleration in the following problem. At the initial moment of time, the speed of the ship was 3 m/s, at the end of the first second the speed of the ship became 5 m/s, at the end of the second - 7 m/s, at the end of the third - 9 m/s, etc. Obviously, . But how do we determine? We consider the speed difference in one second. In the first second 5-3=2, in the second second 7-5=2, in the third 9-7=2. But what if the speeds are not given for every second? Such a task: starting speed ship 3 m / s, at the end of the second second - 7 m / s, at the end of the fourth 11 m / s. In this case, you need 11-7 = 4, then 4/2 = 2. We divide the speed difference by the time interval. 


This formula is most often used in solving problems in a modified form:

The formula is not written in vector form, so we write the "+" sign when the body accelerates, the "-" sign - when it slows down.
Direction of the acceleration vector
The direction of the acceleration vector is shown in the figures

In this figure, the car is moving in a positive direction along the Ox axis, the velocity vector always coincides with the direction of movement (directed to the right). When the acceleration vector coincides with the direction of speed, this means that the car is accelerating. The acceleration is positive.
During acceleration, the direction of acceleration coincides with the direction of speed. The acceleration is positive.

In this picture, the car is moving in the positive direction along the Ox axis, the velocity vector is the same as the direction of motion (rightward), the acceleration is NOT the same as the direction of the speed, which means that the car is decelerating. The acceleration is negative.
When braking, the direction of acceleration is opposite to the direction of speed. The acceleration is negative.
Let's figure out why the acceleration is negative when braking. For example, in the first second, the ship dropped speed from 9m/s to 7m/s, in the second second to 5m/s, in the third to 3m/s. The speed changes to "-2m/s". 3-5=-2; 5-7=-2; 7-9=-2m/s. That's where the negative acceleration value comes from.
When solving problems, if the body slows down, the acceleration in the formulas is substituted with a minus sign!!!
Moving with uniformly accelerated motion


An additional formula called untimely

Formula in coordinates

Communication with medium speed
At uniformly accelerated motion the average speed can be calculated as the arithmetic mean of the initial and final speed

From this rule follows a formula that is very convenient to use when solving many problems

Path ratio
If the body moves uniformly accelerated, the initial speed is zero, then the paths traveled in successive equal time intervals are related as a series of odd numbers.
The main thing to remember
1) What is uniformly accelerated motion;
2) What characterizes acceleration;
3) Acceleration is a vector. If the body accelerates, the acceleration is positive; if it slows down, the acceleration is negative;
3) Direction of the acceleration vector;
4) Formulas, units of measurement in SI
Exercises
Two trains go towards each other: one - accelerated to the north, the other - slowly to the south. How are train accelerations directed?
Same to the north. Because the first train has the same acceleration in the direction of movement, and the second has the opposite movement (it slows down).
The trajectory of the movement of a material point through the radius vector
Having forgotten this section of mathematics, in my memory the equations of motion of a material point have always been represented using the dependence familiar to all of us y(x), and looking at the text of the task, I was a little taken aback when I saw the vectors. It turned out that there is a representation of the trajectory of a material point using radius-vector- a vector that specifies the position of a point in space relative to some pre-fixed point, called the origin.
The formula for the trajectory of a material point, in addition to the radius vector, is described in the same way orts- unit vectors i, j, k in our case coinciding with the axes of the coordinate system. And, finally, consider an example of the equation for the trajectory of a material point (in two-dimensional space):

What is interesting in this example? The trajectory of the point movement is given by sines and cosines, what do you think the graph will look like in the familiar representation of y(x) ? “Probably some kind of creepy,” you thought, but everything is not as difficult as it seems! Let's try to build the trajectory of the material point y(x), if it moves according to the law presented above:

Here I noticed the square of the cosine, if you see the square of the sine or cosine in any example, this means that you need to apply the basic trigonometric identity, which I did (second formula) and transformed the coordinate formula y to substitute the change formula into it instead of the sine x:

As a result, the terrible law of motion of a point turned out to be ordinary parabola whose branches are directed downwards. I hope you understand the approximate algorithm for constructing the dependence y(x) from the representation of motion through the radius vector. Now let's move on to our main question: how to find the velocity and acceleration vector of a material point, as well as their modules.
Material point velocity vector

Everyone knows that the speed of a material point is the value of the distance traveled by the point per unit time, that is, the derivative of the formula for the law of motion. To find the velocity vector, you need to take the derivative with respect to time. Let's look at a specific example of finding the velocity vector.
An example of finding the velocity vector
We have the law of displacement of a material point:

Now you need to take the derivative of this polynomial, if you forgot how this is done, then here you are. As a result, the velocity vector will look like this:

Everything turned out to be easier than you thought, now let's find the acceleration vector of a material point according to the same law presented above.
How to find the acceleration vector of a material point

Point acceleration vector this is a vector quantity that characterizes the change in the module and direction of the speed of a point over time. To find the acceleration vector of a material point in our example, you need to take the derivative, but from the velocity vector formula presented just above:

Point velocity vector modulus
Now let's find the modulus of the velocity vector of a material point. As you know from the 9th grade, the modulus of a vector is its length, in rectangular Cartesian coordinates it is equal to square root from the sum of the squares of its coordinates. And where do you ask from the velocity vector we obtained above to take its coordinates? Everything is very simple:

Now it is enough just to substitute the time specified in the task and get a specific numerical value.
Acceleration vector modulus
As you understood from what was written above (and from the 9th grade), finding the module of the acceleration vector occurs in the same way as the module of the velocity vector: we extract the square root from the sum of the squares of the vector coordinates, everything is simple! Well, here's an example for you:

As you can see, the acceleration of a material point according to the law given above does not depend on time and has a constant magnitude and direction.
More examples of solutions to the problem of finding the velocity and acceleration vector
And here you can find examples of solving other problems in physics. And for those who do not quite understand how to find the velocity and acceleration vector, here are a couple more examples from the network without any extra explanation, I hope they will help you.

If you have any questions, you can ask them in the comments.
Velocity is a vector quantity that characterizes not only the speed of the particle's movement along the trajectory, but also the direction in which the particle moves at each moment of time.
Average speed over time from t1 before t2 is equal to the ratio of the movement during this time to the time interval for which this movement took place:
The fact that this is the average speed we will note by enclosing the average value in angle brackets:<...>, as done above.
The above formula for the mean velocity vector is a direct consequence of the general mathematical definition mean value<f(x)> arbitrary function f(x) on the interval [ a,b]:
![]()
Really
The average speed may be too rough characteristic of the movement. For example, the average speed over a period of oscillations is always zero, regardless of the nature of these oscillations, for the simple reason that over a period - by the definition of a period - an oscillating body will return to its starting point and, therefore, the displacement over a period is always zero. For this and a number of other reasons, instantaneous speed is introduced - the speed in this moment time. In the future, implying instantaneous speed, we will write simply: “speed”, omitting the words “instantaneous” or “at a given moment of time” whenever this cannot lead to misunderstandings. To obtain speed at a moment of time t gotta do the obvious thing: Calculate the ratio limit when aiming for a span of time t2 – t1 to zero. Let's rename: t1 = t And t 2 \u003d t + and rewrite the upper relation as:
Speed at time t is equal to the limit of the ratio of movement in time to the time interval during which this movement took place, when the latter tends to zero
![]()

Rice. 2.5. To the definition of instantaneous speed.
At the moment, we do not consider the question of the existence of this limit, assuming that it exists. Note that if there is a finite displacement and a finite interval of time, then and are their limit values: an infinitesimal displacement and an infinitely small interval of time. So the right side of the definition of speed
is nothing more than a fraction - a quotient of division by , so the last ratio can be rewritten and is quite often used in the form
By geometric sense derivative, the velocity vector at each point of the trajectory is directed tangentially to the trajectory at this point in its direction of motion.
Video 2.1. The velocity vector is directed tangentially to the trajectory. Sharpener experiment.
Any vector can be expanded in a basis (for unit vectors of the basis, in other words, unit vectors that determine the positive directions of the axes OX,OY,oz we use the notation , , or , respectively). The coefficients of this expansion are the projections of the vector onto the corresponding axes. The following is important: in the algebra of vectors, it is proved that the expansion in terms of the basis is unique. Let us expand the radius vector of some moving material point in terms of the basis
Taking into account the constancy of the Cartesian unit vectors , , , we will differentiate this expression with respect to time
On the other hand, the expansion in terms of the basis of the velocity vector has the form
comparing the last two expressions, taking into account the uniqueness of the expansion of any vector in terms of the basis, gives the following result: the projections of the velocity vector on the Cartesian axes are equal to the time derivatives of the corresponding coordinates, that is
![]()
![]()
![]()
The modulus of the velocity vector is
![]()
Let's get one more, important, expression for the modulus of the velocity vector.
It has already been noted that for the value || less and less different from the corresponding path (see Fig. 2). That's why

and in the limit (>0)
In other words, the modulus of speed is the derivative of the distance traveled with respect to time.
Finally we have:
Average modulus of the velocity vector, is defined as follows:
The average value of the module of the velocity vector is equal to the ratio of the distance traveled to the time during which this path was traveled:
Here s(t1,t2)- path in time from t1 before t2 and correspondingly, s(t0,t2)- path in time from t0 before t2 And s(t0,t2)- path in time from t0 before t1.
The average velocity vector, or simply the average velocity as above, is
![]()
Note that, first of all, this is a vector, its module - the module of the average velocity vector should not be confused with the average value of the module of the velocity vector. In the general case, they are not equal: the modulus of the average vector is not at all equal to the average modulus of this vector. Two operations: the calculation of the module and the calculation of the average, in the general case, cannot be swapped.
Consider an example. Let the point move in one direction. On fig. 2.6. shows a graph of the path she traveled s at the time (for the time from 0 before t). Using physical meaning speed, use this graph to find the point in time at which the instantaneous speed is equal to the average ground speed for the first seconds of the point's movement.

Rice. 2.6. Determination of the instantaneous and average speed of the body
Velocity modulus at a given time
![]()
being the derivative of the path with respect to time, it is equal to the angular coefficient of the rocking to the dependence graph to the point corresponding to the moment of time t*. The average module of speed for a period of time from 0 before t* is the slope of the secant passing through the points of the same graph corresponding to the beginning t = 0 and end t = t* time interval. We need to find such a moment in time t* when both slopes are the same. To do this, we draw a straight line through the origin of coordinates, tangent to the trajectory. As can be seen from the figure, the point of contact of this straight line s(t) and gives t*. In our example, we get
Speed is one of the main characteristics. It expresses the very essence of movement, i.e. determines the difference that exists between a stationary body and a moving body.
The SI unit for speed is m/s.
It is important to remember that speed is a vector quantity. The direction of the velocity vector is determined by the movement. The velocity vector is always directed tangentially to the trajectory at the point through which the moving body passes (Fig. 1).
For example, consider the wheel of a moving car. The wheel rotates and all points of the wheel move in circles. Spray flying from the wheel will fly along tangents to these circles, indicating the direction of the velocity vectors of the individual points of the wheel.
Thus, the speed characterizes the direction of motion of the body (the direction of the velocity vector) and the speed of its movement (modulus of the velocity vector).
Negative speed
Can the speed of a body be negative? Yes maybe. If the speed of the body is negative, this means that the body is moving in the direction opposite to the direction of the coordinate axis in the selected frame of reference. Figure 2 shows the movement of the bus and the car. The speed of the car is negative and the speed of the bus is positive. It should be remembered that speaking of the sign of the velocity, we mean the projection of the velocity vector onto the coordinate axis.

Uniform and uneven movement
In general, the speed depends on time. According to the nature of the dependence of speed on time, the movement is uniform and uneven.
DEFINITION
Uniform movement is a movement with a constant modulo speed.
In the case of uneven movement, they talk about:
Examples of solving problems on the topic "Speed"
EXAMPLE 1
| The task | The car passed the first half of the way between two settlements at a speed of 90 km/h, and the other half at a speed of 54 km/h. Determine the average speed of the car. |
| Solution | It would be incorrect to calculate the average speed of a car as the arithmetic mean of the two indicated speeds. Let's use the definition of average speed: Since rectilinear uniform motion is assumed, the signs of the vectors can be omitted. The time spent by the car on the passage of the entire segment of the path: where is the time taken to complete the first half of the journey, and is the time taken to complete the second half of the journey.
The total displacement is equal to the distance between settlements, i.e. . Substituting these ratios into the formula for the average speed, we get: We translate the speeds in individual sections into the SI system: Then the average speed of the car is:
|
| Answer | The average speed of the car is 18.8 m/s |
EXAMPLE 2
| The task | A car travels for 10 seconds at a speed of 10 m/s and then travels for another 2 minutes at a speed of 25 m/s. Determine the average speed of the car. |
| Solution | Let's make a drawing. |