ebavõrdsuse lahendus režiimis võrgus lahendus peaaegu iga antud ebavõrdsus võrgus. Matemaatiline ebavõrdsus võrgus matemaatika lahendamiseks. Leia kiiresti ebavõrdsuse lahendus režiimis võrgus. Veebisait www.site võimaldab leida lahendus peaaegu iga antud algebraline, trigonomeetriline või transtsendentaalne ebavõrdsus võrgus. Õppides peaaegu iga matemaatika haru erinevatel etappidel, peate otsustama ebavõrdsus võrgus. Kohe vastuse ja mis kõige tähtsam täpse vastuse saamiseks vajate ressurssi, mis seda võimaldab. Tänu saidile www.site lahendada ebavõrdsus võrgus võtab paar minutit. www.site peamine eelis matemaatika lahendamisel ebavõrdsus võrgus- see on antud vastuse kiirus ja täpsus. Sait suudab lahendada mis tahes algebraline ebavõrdsus võrgus, trigonomeetrilised ebavõrdsused võrgus, transtsendentaalne ebavõrdsus võrgus ja ebavõrdsused tundmatute parameetritega režiimis võrgus. Ebavõrdsused toimida võimsa matemaatilise aparaadina lahendusi praktilisi probleeme. Abiga matemaatilised ebavõrdsused võimalik on väljendada fakte ja suhteid, mis võivad esmapilgul tunduda segased ja keerulised. Teadmata kogused ebavõrdsused leiate probleemi sõnastades matemaatilised keel kujul ebavõrdsused Ja otsustama vastu võetud ülesanne režiimis võrgus veebisaidil www.sait. Ükskõik milline algebraline ebavõrdsus, trigonomeetriline ebavõrdsus või ebavõrdsused sisaldavad transtsendentaalne funktsioone, mida saate hõlpsalt kasutada otsustama Internetis ja saate täpse vastuse. Õppimine loodusteadused, seisate paratamatult silmitsi vajadusega lahendusi ebavõrdsusele. Sel juhul peab vastus olema täpne ja tuleb režiimis kohe kätte saada võrgus. Seetõttu jaoks lahendada matemaatilisi ebavõrdsusi võrgus soovitame saiti www.site, millest saab teie jaoks asendamatu kalkulaator algebraliste võrratuste lahendamine võrgus, trigonomeetrilised ebavõrdsused võrgus ja transtsendentaalne ebavõrdsus võrgus või ebavõrdsused tundmatute parameetritega. Praktilisteks probleemideks erinevatele veebilahenduste leidmisel matemaatilised ebavõrdsused ressurss www.. Lahendamine ebavõrdsus võrgus ise, on kasulik saadud vastust kontrollida kasutades ebavõrdsuse võrgulahendus veebisaidil www.sait. Peate ebavõrdsuse õigesti kirjutama ja kohe kätte saama online lahendus, misjärel jääb üle vaid võrrelda vastust oma ebavõrdsuse lahendusega. Vastuse kontrollimine ei kesta rohkem kui minut, sellest piisab lahendada ebavõrdsus võrgus ja võrrelge vastuseid. See aitab teil vältida vigu otsus ja parandage vastus õigeaegselt ebavõrdsuse lahendamine võrgus kas algebraline, trigonomeetriline, transtsendentaalne või ebavõrdsus tundmatute parameetritega.

Arvude moodul kutsutakse seda numbrit ennast, kui see ei ole negatiivne, või sama numbrit vastupidise märgiga, kui see on negatiivne.

Näiteks arvu 6 moodul on 6 ja arvu -6 moodul on samuti 6.

See tähendab, et arvu moodulit mõistetakse absoluutväärtusena, selle arvu absoluutväärtusena, võtmata arvesse selle märki.

See on tähistatud järgmiselt: |6|, | X|, |A| jne.

(Lisateavet leiate jaotisest "Numbrimoodul").

Mooduliga võrrandid.

Näide 1 . Lahenda võrrand|10 X - 5| = 15.

Lahendus.

Reegli kohaselt on võrrand võrdne kahe võrrandi kombinatsiooniga:

10X - 5 = 15
10X - 5 = -15

Otsustame:

10X = 15 + 5 = 20
10X = -15 + 5 = -10

X = 20: 10
X = -10: 10

X = 2
X = -1

Vastus: X 1 = 2, X 2 = -1.

Näide 2 . Lahenda võrrand|2 X + 1| = X + 2.

Lahendus.

Kuna moodul on mittenegatiivne arv, siis X+ 2 ≥ 0. Vastavalt:

X ≥ -2.

Teeme kaks võrrandit:

2X + 1 = X + 2
2X + 1 = -(X + 2)

Otsustame:

2X + 1 = X + 2
2X + 1 = -X - 2

2X - X = 2 - 1
2X + X = -2 - 1

X = 1
X = -1

Mõlemad numbrid on suuremad kui -2. Nii et mõlemad on võrrandi juured.

Vastus: X 1 = -1, X 2 = 1.

Näide 3 . Lahenda võrrand

|X + 3| - 1
————— = 4
X - 1

Lahendus.

Võrrand on mõttekas, kui nimetaja ei ole võrdne nulliga- tähendab, kui X≠ 1. Võtame seda tingimust arvesse. Meie esimene toiming on lihtne – me mitte lihtsalt ei vabane murdosast, vaid teisendame selle nii, et saaksime mooduli puhtal kujul:

|X+ 3| - 1 = 4 · ( X - 1),

|X + 3| - 1 = 4X - 4,

|X + 3| = 4X - 4 + 1,

|X + 3| = 4X - 3.

Nüüd on võrrandi vasakul küljel mooduli all ainult avaldis. Lase käia.
Arvu moodul on mittenegatiivne arv – see tähendab, et see peab olema suurem kui null või võrdne nulliga. Vastavalt sellele lahendame ebavõrdsuse:

4X - 3 ≥ 0

4X ≥ 3

X ≥ 3/4

Seega on meil teine ​​tingimus: võrrandi juur peab olema vähemalt 3/4.

Vastavalt reeglile koostame kahe võrrandi komplekti ja lahendame need:

X + 3 = 4X - 3
X + 3 = -(4X - 3)

X + 3 = 4X - 3
X + 3 = -4X + 3

X - 4X = -3 - 3
X + 4X = 3 - 3

X = 2
X = 0

Saime kaks vastust. Kontrollime, kas need on algvõrrandi juured.

Meil oli kaks tingimust: võrrandi juur ei tohi olla võrdne 1-ga ja see peab olema vähemalt 3/4. See on X ≠ 1, X≥ 3/4. Mõlemad tingimused vastavad ainult ühele kahest saadud vastusest – numbrile 2. See tähendab, et ainult see on algvõrrandi juur.

Vastus: X = 2.

Ebavõrdsused mooduliga.

Näide 1 . Lahendage ebavõrdsus| X - 3| < 4

Lahendus.

Mooduli reegel ütleb:

|A| = A, Kui A ≥ 0.

|A| = -A, Kui A < 0.

Moodul võib sisaldada nii mittenegatiivseid kui ka negatiivseid numbreid. Seega peame kaaluma mõlemat juhtumit: X- 3 ≥ 0 ja X - 3 < 0.

1) Millal X- 3 ≥ 0 meie esialgne ebavõrdsus jääb samaks, ainult ilma mooduli märgita:
X - 3 < 4.

2) Millal X - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(X - 3) < 4.

Sulgude avamisel saame:

-X + 3 < 4.

Seega jõudsime nendest kahest tingimusest kahe ebavõrdsuse süsteemi ühendamiseni:

X - 3 ≥ 0
X - 3 < 4

X - 3 < 0
-X + 3 < 4

Lahendame need:

X ≥ 3
X < 7

X < 3
X > -1

Niisiis, meie vastus on kahe komplekti liit:

3 ≤ X < 7 U -1 < X < 3.

Määrake väikseim ja kõrgeim väärtus. Need on -1 ja 7. Veelgi enam X suurem kui -1, kuid väiksem kui 7.
Pealegi, X≥ 3. See tähendab, et ebavõrdsuse lahendus on kogu arvude hulk vahemikus -1 kuni 7, välja arvatud need äärmuslikud arvud.

Vastus: -1 < X < 7.

Või: X ∈ (-1; 7).

Lisandmoodulid.

1) Meie ebavõrdsuse lahendamiseks on lihtsam ja lühem viis – graafiliselt. Selleks peate joonistama horisontaaltelje (joonis 1).

Väljend | X - 3| < 4 означает, что расстояние от точки X punktini 3 on väiksem kui neli ühikut. Märgime teljele numbri 3 ja loendame sellest vasakule ja paremale 4 jaotust. Vasakul jõuame punktini -1, paremal - punktini 7. Seega punktid X me lihtsalt nägime neid ilma neid arvutamata.

Veelgi enam, ebavõrdsuse tingimuse kohaselt ei kuulu -1 ja 7 ise lahenduste hulka. Seega saame vastuse:

1 < X < 7.

2) Kuid on veel üks lahendus, mis on isegi graafilisest meetodist lihtsam. Selleks tuleb meie ebavõrdsus esitada järgmisel kujul:

4 < X - 3 < 4.

Nii see ju moodulireegli järgi on. Mittenegatiivne arv 4 ja sarnane negatiivne arv -4 on ebavõrdsuse lahendamise piirid.

4 + 3 < X < 4 + 3

1 < X < 7.

Näide 2 . Lahendage ebavõrdsus| X - 2| ≥ 5

Lahendus.

See näide erineb oluliselt eelmisest. Vasak pool on suurem kui 5 või võrdne 5. C geomeetriline punkt Vaatepunktist on ebavõrdsuse lahenduseks kõik arvud, mis asuvad punktist 2 vähemalt 5 ühiku kaugusel (joonis 2). Graafik näitab, et need kõik on arvud, mis on väiksemad või võrdsed -3 ja suuremad või võrdsed 7. See tähendab, et oleme vastuse juba saanud.

Vastus: -3 ≥ X ≥ 7.

Teel lahendame sama ebavõrdsuse, paigutades vaba liikme ümber vasakule ja paremale vastupidise märgiga:

5 ≥ X - 2 ≥ 5

5 + 2 ≥ X ≥ 5 + 2

Vastus on sama: -3 ≥ X ≥ 7.

Või: X ∈ [-3; 7]

Näide on lahendatud.

Näide 3 . Lahendage ebavõrdsus 6 X 2 - | X| - 2 ≤ 0

Lahendus.

Number X võib olla positiivne, negatiivne või null. Seetõttu peame arvestama kõigi kolme asjaoluga. Nagu teate, võetakse neid arvesse kahes ebavõrdsuses: X≥ 0 ja X < 0. При X≥ 0 kirjutame lihtsalt oma esialgse ebavõrdsuse ümber nii, nagu see on, ainult ilma mooduli märgita:

6x 2 - X - 2 ≤ 0.

Nüüd teisest juhtumist: kui X < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6X 2 - (-X) - 2 ≤ 0.

Sulgude laiendamine:

6X 2 + X - 2 ≤ 0.

Seega saime kaks võrrandisüsteemi:

6X 2 - X - 2 ≤ 0
X ≥ 0

6X 2 + X - 2 ≤ 0
X < 0

Peame lahendama süsteemide ebavõrdsused – ja see tähendab, et peame leidma kahe ruutvõrrandi juured. Selleks võrdsustame võrratuste vasakpoolsed küljed nulliga.

Alustame esimesest:

6X 2 - X - 2 = 0.

Ruutvõrrandi lahendamine - vt jaotist „Ruudvõrrand”. Nimetame vastuse kohe:

X 1 = -1/2, x 2 = 2/3.

Esimesest võrratuste süsteemist saame, et algse võrratuse lahendus on kogu arvude hulk vahemikus -1/2 kuni 2/3. Lahenduste liidu kirjutame aadressil X ≥ 0:
[-1/2; 2/3].

Nüüd lahendame teise ruutvõrrandi:

6X 2 + X - 2 = 0.

Selle juured:

X 1 = -2/3, X 2 = 1/2.

Järeldus: millal X < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Kombineerime kaks vastust ja saame lõpliku vastuse: lahenduseks on kogu arvude komplekt vahemikus -2/3 kuni 2/3, sealhulgas need äärmuslikud arvud.

Vastus: -2/3 ≤ X ≤ 2/3.

Või: X ∈ [-2/3; 2/3].

LÄBIVAATATUD

Pedagoogiline nõukogu MOU

"Zashizhemskaya keskkool"

Protokoll nr 1

NÕUSTUD

Personalidirektori asetäitja

_______ /Sidorkina R.L./

MA KINNITASIN

Peaõpetaja:

A. P. Konakov

korraldus nr 63

Mooduliga võrrandite ja võrratuste lahendamine

Uurimine

Programmi koostasid:

kõrgema matemaatika õpetaja

Sidorkina R.L.

Zashizhemye küla, 2014

Sisukord

Sissejuhatus……………………………………………………………………………………3

Lihtsamad võrrandid ja võrratused mooduliga………………………5

Mooduliga võrrandite ja võrratuste graafiline lahendamine………….8

Muud viisid moodulitega võrrandite ja võrratuste lahendamiseks.........10

Järeldus………………………………………………………..16

Viited…………………………………………………………18

1. Sissejuhatus

Absoluutväärtuse (mooduli) mõiste on arvu üks olulisemaid tunnuseid nii reaal- kui ka kompleksarvude valdkonnas.

Seda mõistet kasutatakse laialdaselt mitte ainult koolimatemaatikakursuse erinevates osades, vaid ka kursustel kõrgem matemaatika, ülikoolides õppinud füüsikat ja tehnikateadusi. Näiteks ligikaudsete arvutuste teoorias kasutatakse ligikaudse arvu absoluutsete ja suhteliste vigade mõisteid. Mehaanikas ja geomeetrias uuritakse vektori ja selle pikkuse (vektori mooduli) mõisteid. IN matemaatiline analüüs arvu absoluutväärtuse mõiste sisaldub selliste põhimõistete definitsioonides nagu piir, piiratud funktsioon jne. Absoluutväärtustega seotud probleeme leidub sageli matemaatikaolümpiaadidel, sisseastumiseksamidülikoolidele ja ühtsele riigieksamile. Seetõttu sai meie jaoks oluline uurida selle teema mõningaid aspekte.

Kodu eesmärk Meie töö on uurida erinevaid meetodeid võrrandite ja moodulitega võrratuste lahendamiseks.

See eesmärk tuleb saavutada järgmiste probleemide lahendamisega ülesandeid:

Uurige mooduli määratlust ja mõningaid omadusi.

Õppige moodulitega lihtsate võrrandite ja võrratuste lahendamist ekvivalentsete üleminekute kaudu

Vaatleme erinevaid meetodeid võrrandite ja mooduli võrratuste lahendamiseks.

Objekt uuringud on teatud tüüpi võrrandid ja mooduli võrratused.

Üksus uuringud - erinevad meetodid võrrandite ja võrratuste lahendamiseks mooduliga, nimelt: graafiline meetod, geomeetrilise tõlgendamise meetod, identiteedi kasutamine, märkide teoreemi rakendamine, tagajärjele ülemineku meetod, intervallide meetod, positiivse teguriga korrutamise meetod, moodulite paljastamise meetod.

Uuringu käigus kasutati selliseid meetodeid nagu selleteemalise kirjanduse uurimine ja praktiline meetod.

Oma töö käigus uurisime selliseid allikaid nagu:

1. “Suur matemaatikaentsüklopeedia” koolinoortele ja üliõpilastele;

Matemaatika. Ühtne riigieksam - 2011-2012. Tüüpilised eksamivalikud. / Toimetanud A.L. Semenova, I.V. Jaštšenko.

Entsüklopeedia “Ma tunnen maailma” Matemaatika;

;

1. 1. Lihtsamad võrrandid ja võrratused mooduliga

Lihtsaimateks võrranditeks loeme võrrandeid, mis on lahendatud ühe järgmistest samaväärsetest üleminekutest:

Näited lihtsate võrrandite lahendamisest.

Näide 1 Lahendame võrrandi
.

Lahendus.

Vastus.
.

Näide 2 Lahendame võrrandi.

Lahendus.

Vastus.
.

Näide 3 Lahendame võrrandi
.

Lahendus.

Vastus.
.

Võrrandite jada lahendatakse järgmise teoreemi abil.

Teoreem.4 Moodulite summa on võrdne alammoodulsuuruste algebralise summaga siis ja ainult siis, kui igal suurusel on märk, millega see algebralises summas sisaldub.

Näide 5 Lahenda võrrand

Lahendus. Kuna , siis on meil vorm , kus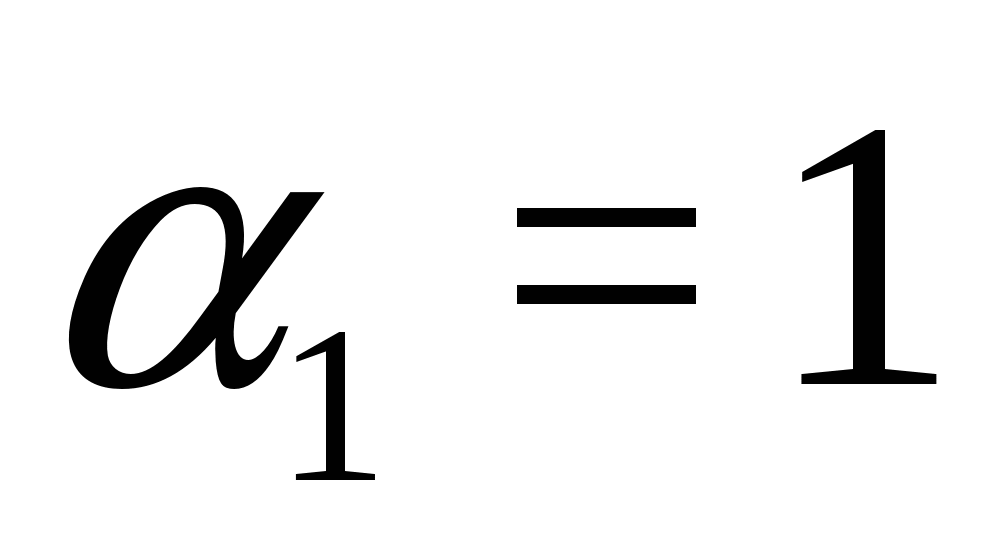
,
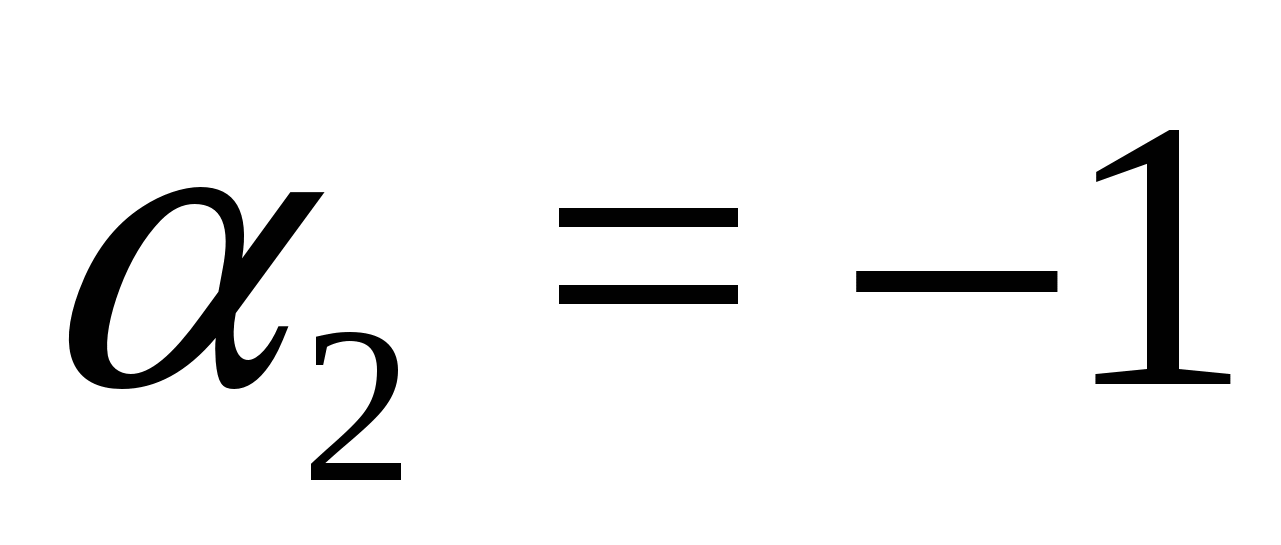. Seetõttu on algne võrrand samaväärne süsteemiga:

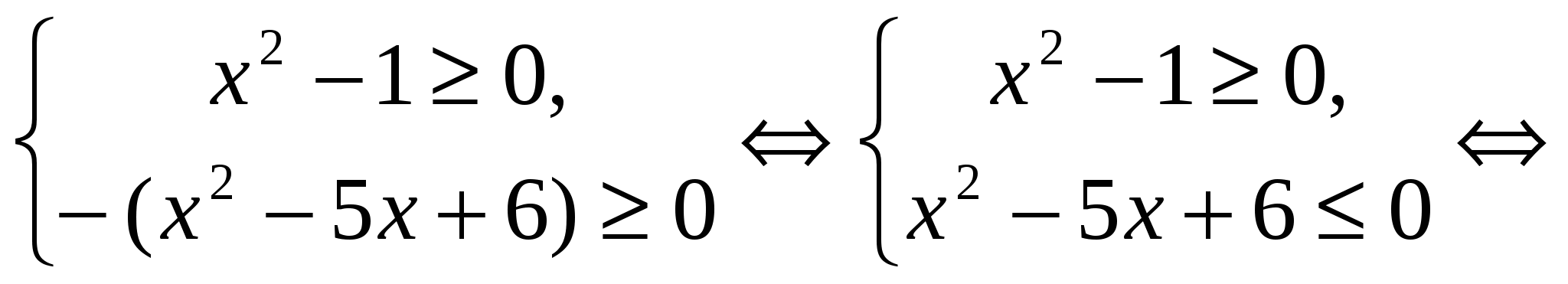
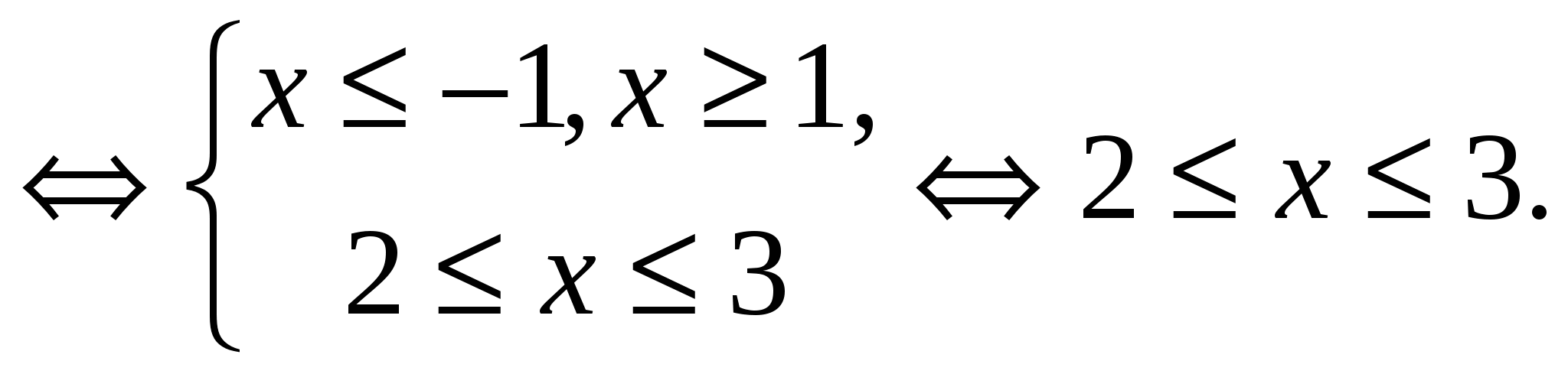
Vastus.
.

Näited lihtsate võrratuste lahendamisest.

Näide 6 Lahendame ebavõrdsuse
.

Lahendus.

Vastus.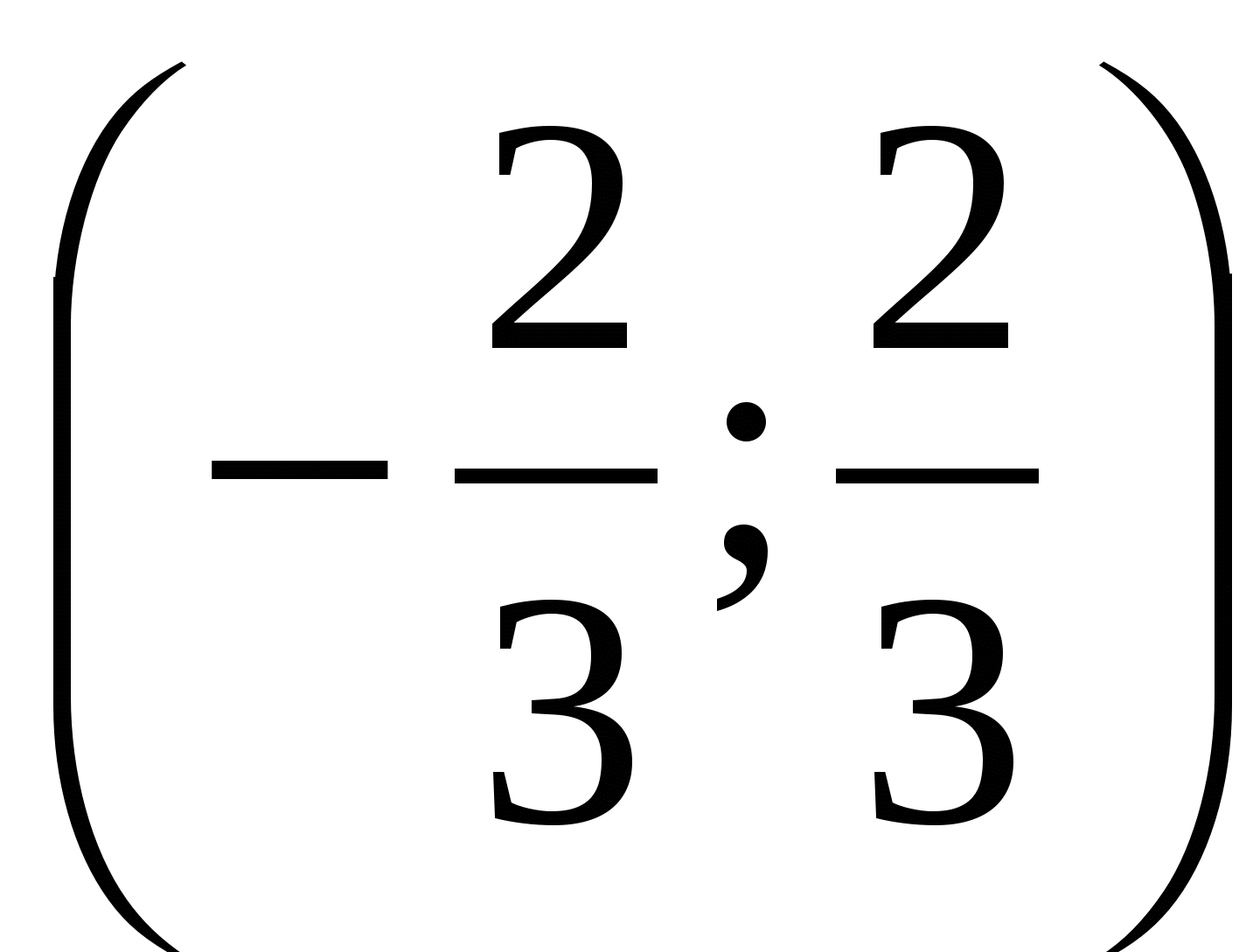
.

Näide 7 Lahendame ebavõrdsuse
.

Lahendus.

Vastus.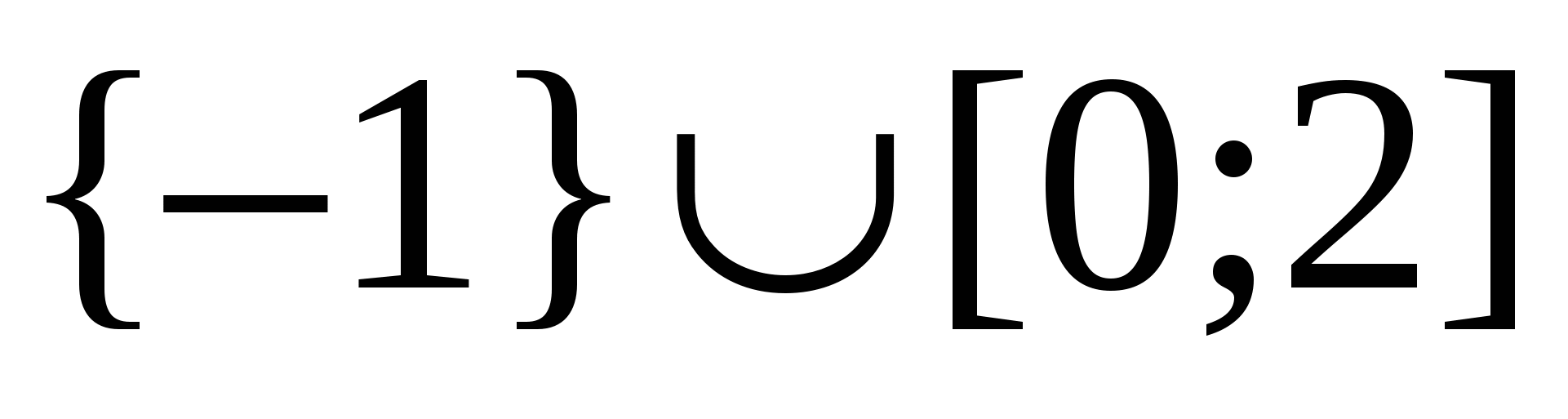
.

Kummalisel kombel, aga
on piisav, et vabaneda mooduli märgist mis tahes ebavõrdsuses.

Näide 8 Lahendage ebavõrdsus

Lahendus.

Vastus.
.

3. Mooduliga võrrandite ja võrratuste graafiline lahendamine

Absoluutväärtuse märki sisaldavate võrrandite lahendamist on sageli palju mugavam lahendada mitte analüütiliselt, vaid graafiliselt (eriti parameetreid sisaldavad võrrandid).

Näide 9(C5, ühtne riigieksam – 2010)

C5. Iga väärtuse jaoksa märkige võrrandi lahendite arv

Lahendus.Joonistame funktsiooni
. Selleks valige terve ruut:

Funktsiooni y = graafiku lõikepunktide arv
horisontaalsete joontega y = a võrdub võrrandi lahendite arvuga.

KOHTA vastus: Kui < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, siis on kaks lahendust.

Muud võimalused võrrandite ja võrratuste lahendamiseks mooduliga

• Mooduli laiendamise meetod

Vaatame näite abil moodulite laiendamise meetodit:

Näide 10 Lahenda võrrand

Lahendus. See võrrand sisaldab rohkem kui ühte moodulit.

Kahe või enama mooduli märgi all olevaid muutujaid sisaldavate võrrandite lahendamise meetod on järgmine.

1. Leidke muutuja väärtused, mille juures iga moodul muutub nulliks: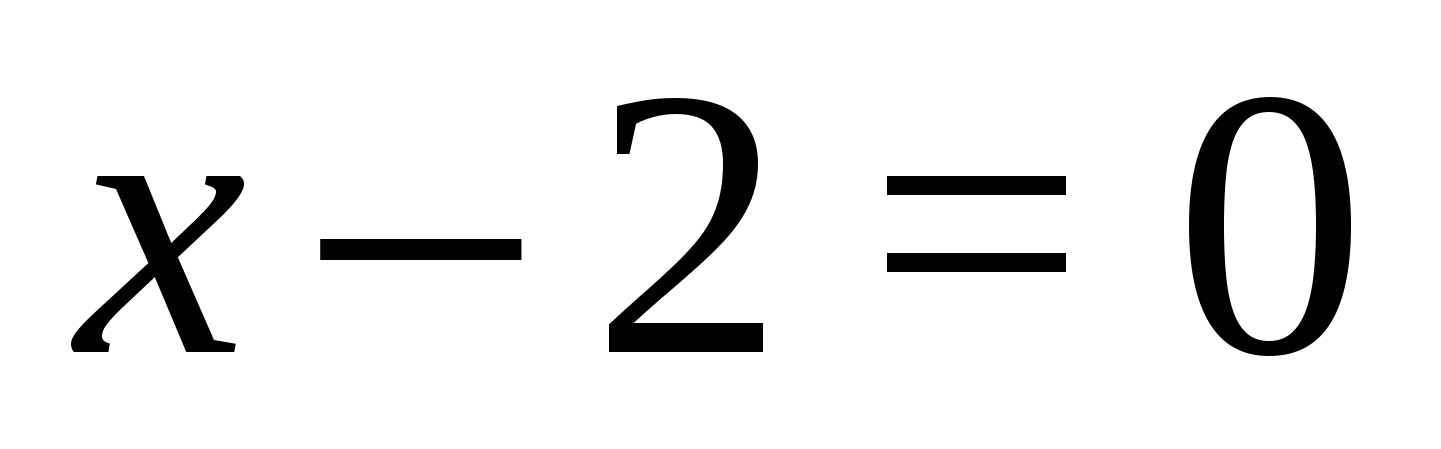
,
;
,
;
,
.

2. Märgi need punktid numbrireale.

3. Vaatleme iga intervalli võrrandit ja määrame moodulite all olevate avaldiste märgid.

1) Millal
või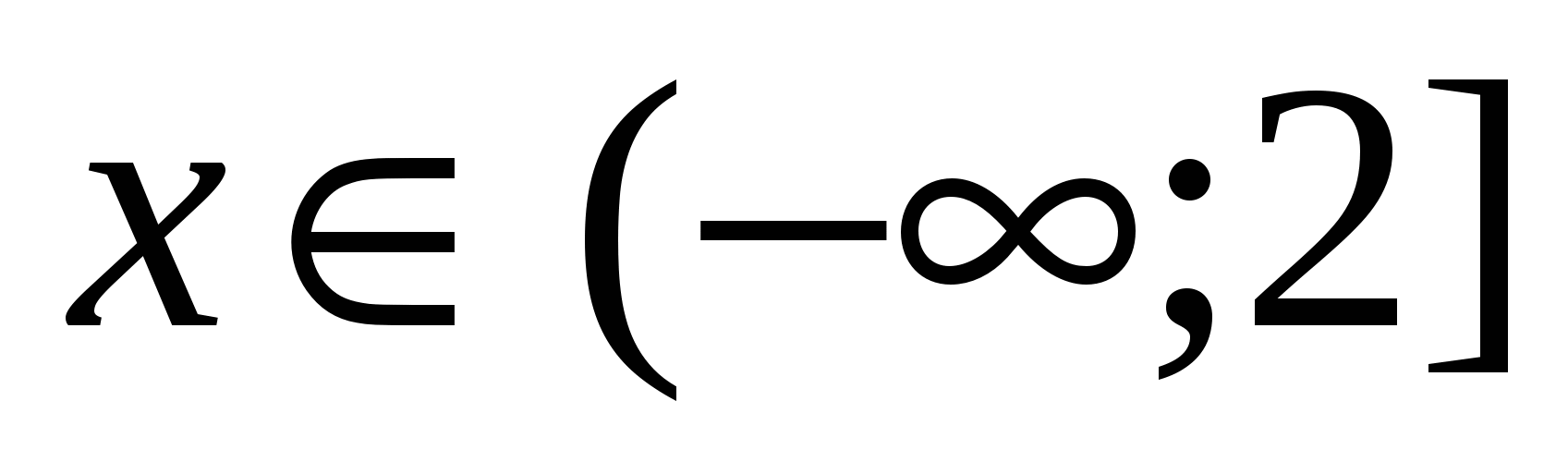
. Selle intervalli iga moodulavaldise märgi määramiseks piisab mis tahes väärtuse võtmisest sellest intervallist ja asendage see avaldisega. Kui saadud väärtus on negatiivne, siis kõigi jaoks alates sellest intervallist on avaldis negatiivne; kui kätte saadakse numbriline väärtus positiivne, mis tähendab kõigi väärtuste puhul alates sellest intervallist on avaldis positiivne.

Võtame väärtuse
vahelt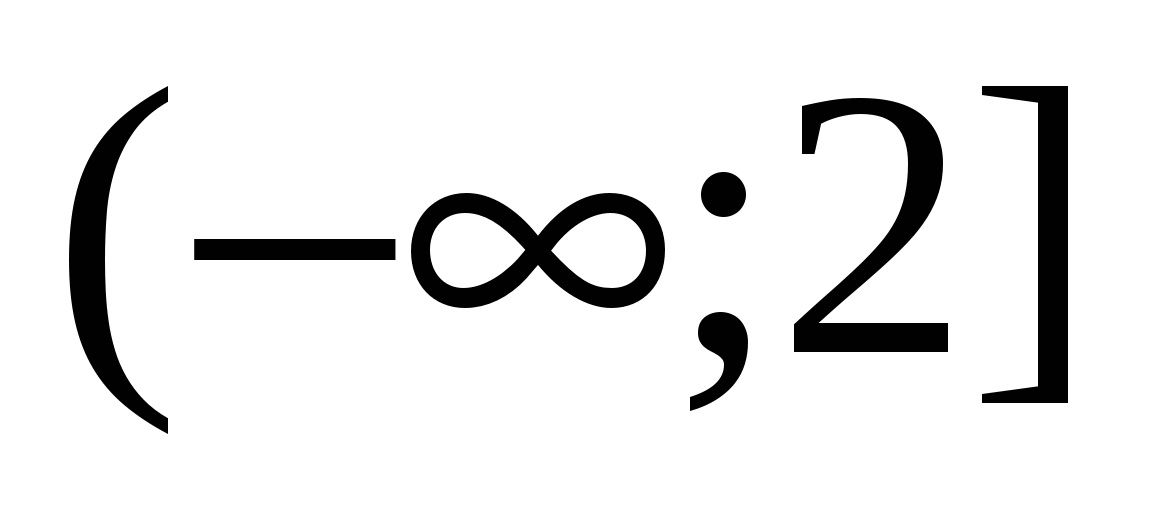
ja asendage selle väärtus avaldisega
, saame
, mis tähendab selles intervallis
negatiivne ja seetõttu "tuleb"" välja" mooduli alt "miinusmärgiga", saame:
.

Selle väärtuse juures , väljendus
saab väärtuse
, mis tähendab, et see on intervallis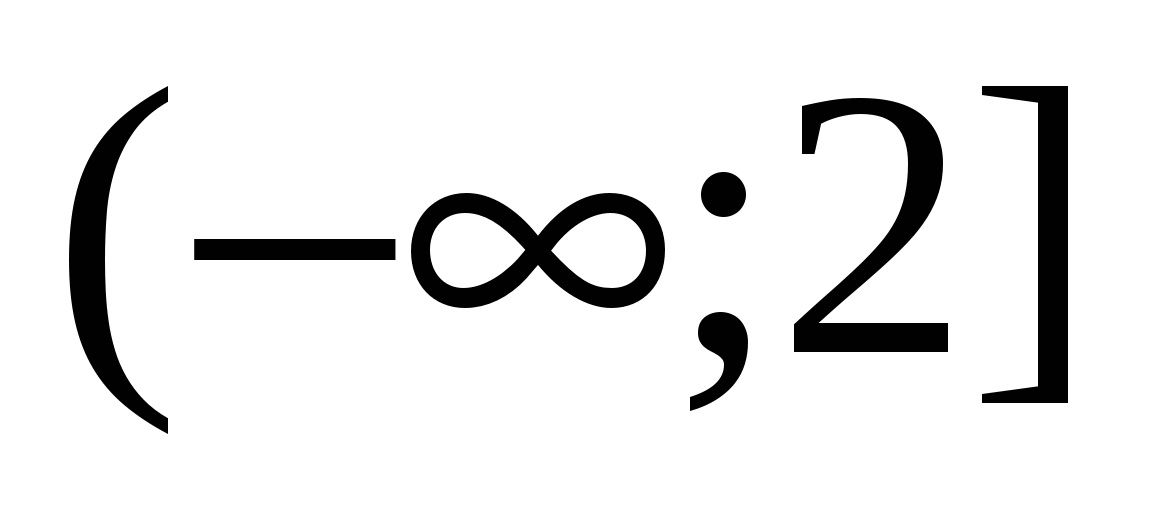
võtab ka negatiivsed väärtused ja "väljub"" moodulist "miinusmärgiga", saame:
.

Väljendus
saab väärtuse
ja "väljub" mooduli alt "miinusmärgiga":
.

Selle intervalli võrrand kujuneb järgmiselt: selle lahendamisel leiame:
.

Saame teada, kas see väärtus sisaldub intervallis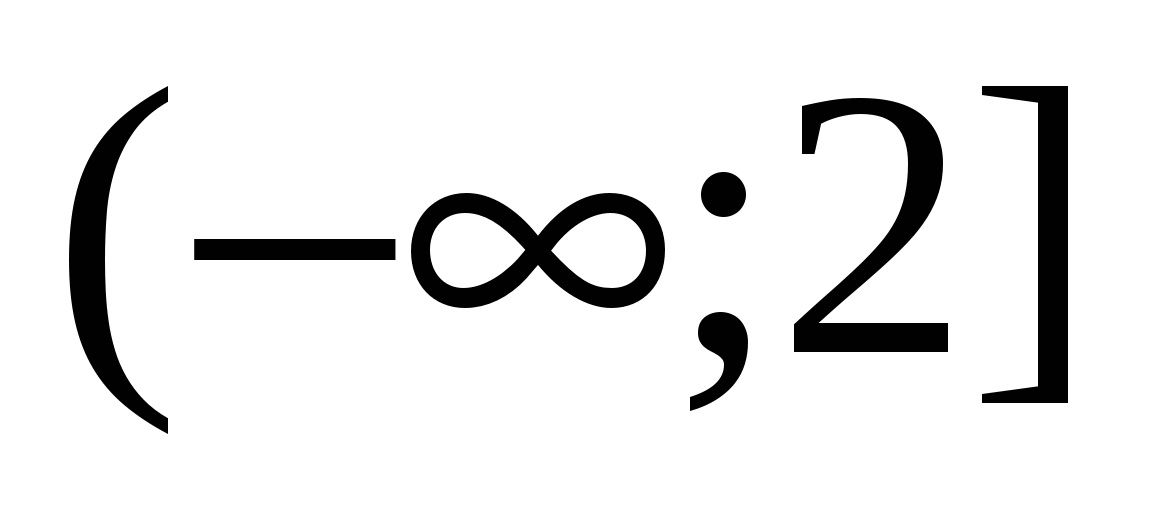
. Selgub, et see on kaasas, mis tähendab
on võrrandi juur.

2) Millal
. Valige mis tahes väärtus sellest lõhest. Lase
. Määrame selle väärtuse juures iga mooduli all oleva avaldise märgi . Selgub, et väljend
positiivsed ja ülejäänud kaks on negatiivsed.

Selle intervalli võrrand on järgmisel kujul: . Selle lahendades leiame
. See väärtus ei sisaldu vahemikus
, mis tähendab, et see ei ole võrrandi juur.

3) Millal
. Valige suvaline väärtus sellest intervallist, oletame
ja asendada iga väljendiga. Leiame, et väljendid
Ja
on positiivsed ja
- negatiivne. Saame järgmise võrrandi: .

Pärast transformatsiooni saame:
, mis tähendab, et võrrandil pole sellel intervallil juuri.

4) Millal
. On lihtne kindlaks teha, et kõik selle intervalli avaldised on positiivsed, mis tähendab, et saame võrrandi: ,
,
mis sisaldub intervallis ja on võrrandi juur.

Vastus.
,
.

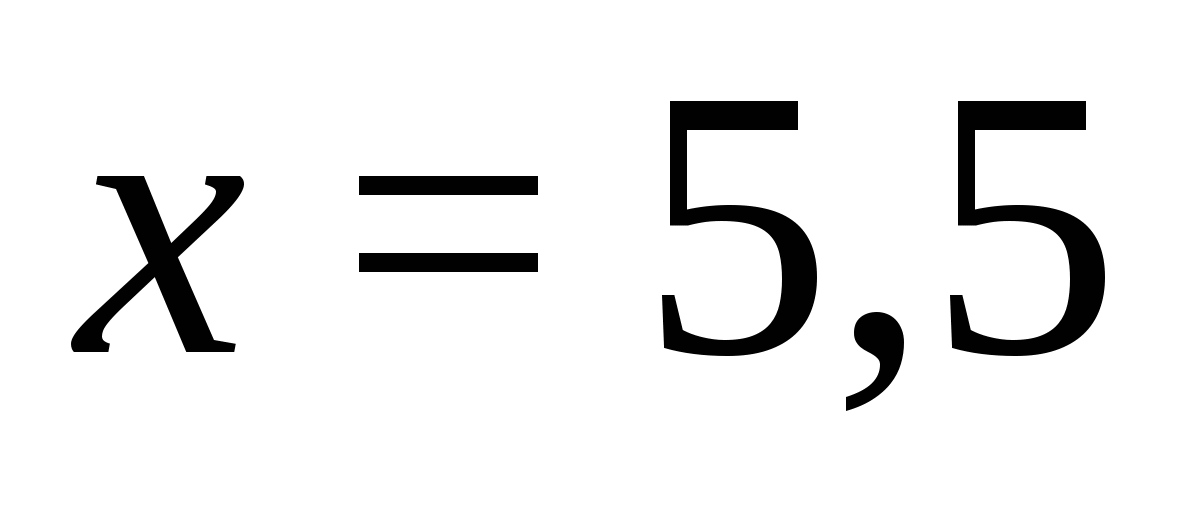• Mittenegatiivsete avaldiste mooduleid sisaldavate võrrandite lahendamine

Näide 11 Kui suur on võrrandi juurte summa (juur, kui see on olemas)

Lahendus. Mõelge väljendile

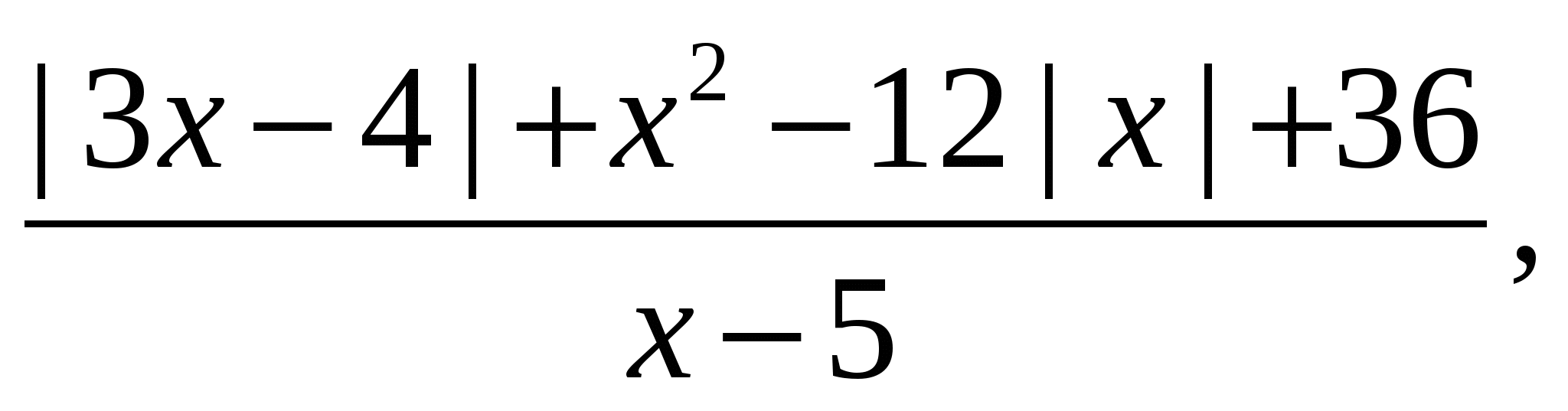ja teisendage see vormiks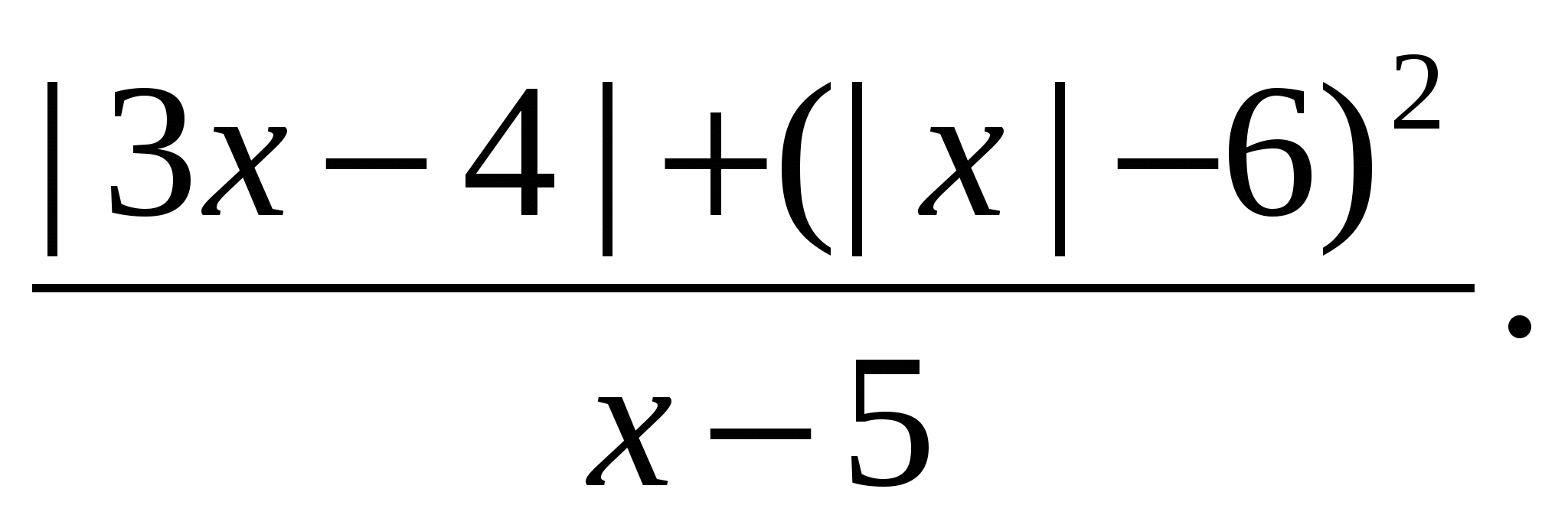

On ilmne, et murru lugeja on muutuja mis tahes väärtuse puhul positiivne arv. See tähendab, et murdosa avaldis on positiivne, kui
(sest
). Teisendame saadud avaldise tingimusel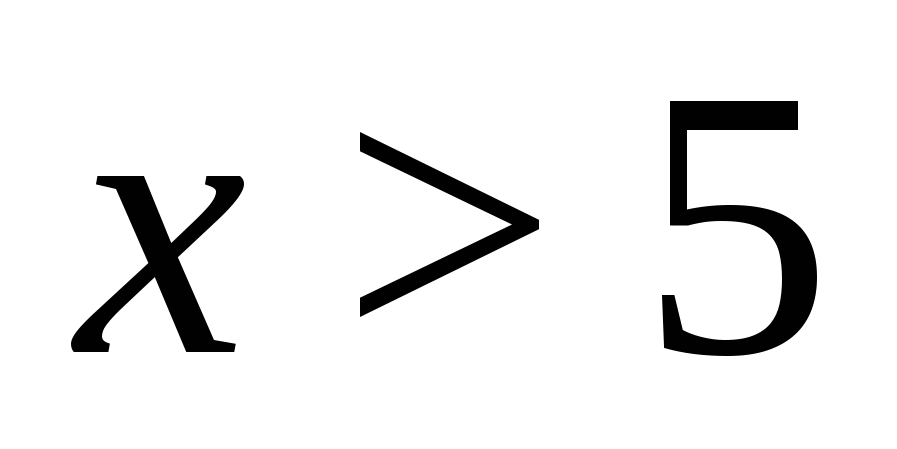
. Saame algse võrrandiga samaväärse võrrandi:

Vastus.
.

Näide 12 Lahenda võrrand

Lahendus. Kuna võrrandi vasak pool on mittenegatiivne, peab muutuja kõigi lubatud väärtuste korral võrrandi juurte hulgal olema ka selle parem pool mittenegatiivne, seega tingimus
, sellel intervallil on mõlema murru nimetajad võrdsed ja jääb üle võrrand lahendada
. Selle lahendamine ja piiranguga arvestamine
, saame

Vastus.
.

• Võrrandite lahendamine geomeetrilise tõlgenduse abil

Väljendi geomeetriline tähendus
- abstsissidega punkte ühendava koordinaattelje segmendi pikkus Ja . Algebralise ülesande tõlkimine geomeetrilisse keelde võimaldab sageli vältida tülikaid arvutusi.

Näide 13 Lahendame võrrandi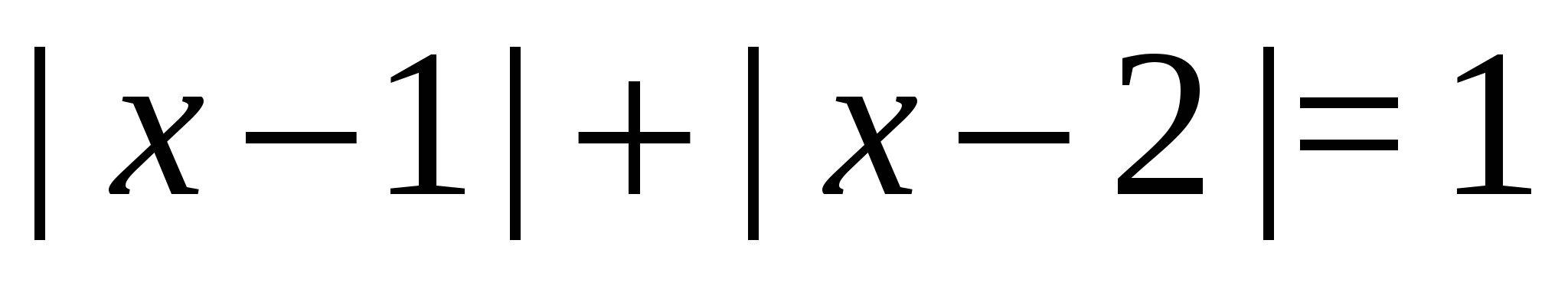
.

Lahendus. Põhjendame järgmiselt: mooduli geomeetrilise tõlgenduse põhjal on võrrandi vasak pool kauguste summa teatud punktist abstsissiga. kahele fikseeritud punktile abstsissidega 1 ja 2. Seejärel kõik punktid abstsissidega lõigust
neil on nõutav omadus, kuid väljaspool seda segmenti asuvatel punktidel ei ole.

Vastus.
.

Näide 14 Lahendage ebavõrdsus
.

Lahendus. Kujutame koordinaatjoonel punkte, kauguste summat, millest punktideni
Ja täpselt võrdne . Need on kõik segmendi punktid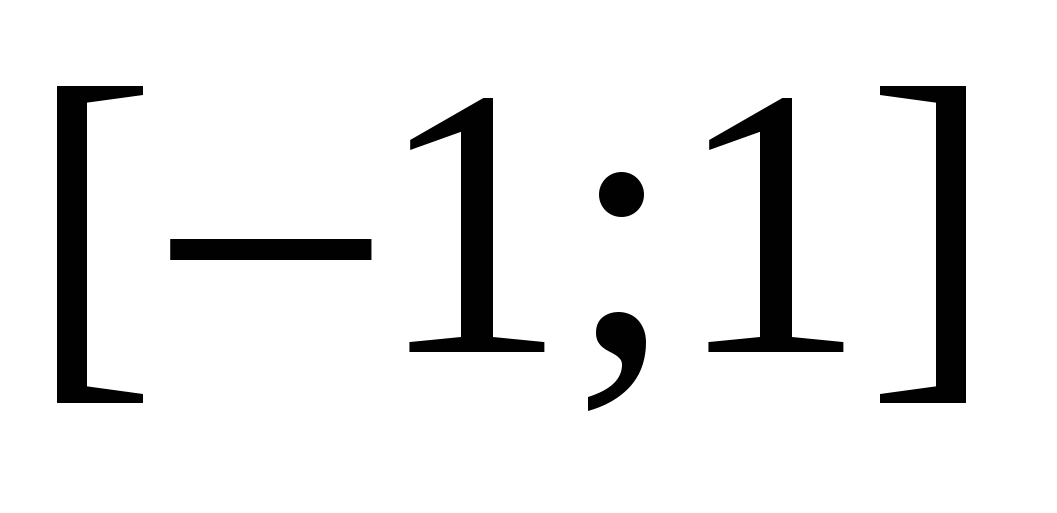
. Kõikide numbrite jaoks väljaspool sellest segmendist kauguste summa on suurem kui kaks.

Vastus.
.

Näide(C3, ühtne riigieksam – 2010) 15 Lahenda võrrand

Lahendus. Identiteedi rakendamine kaks korda
, saame võrrandi

mille lahendus on intervall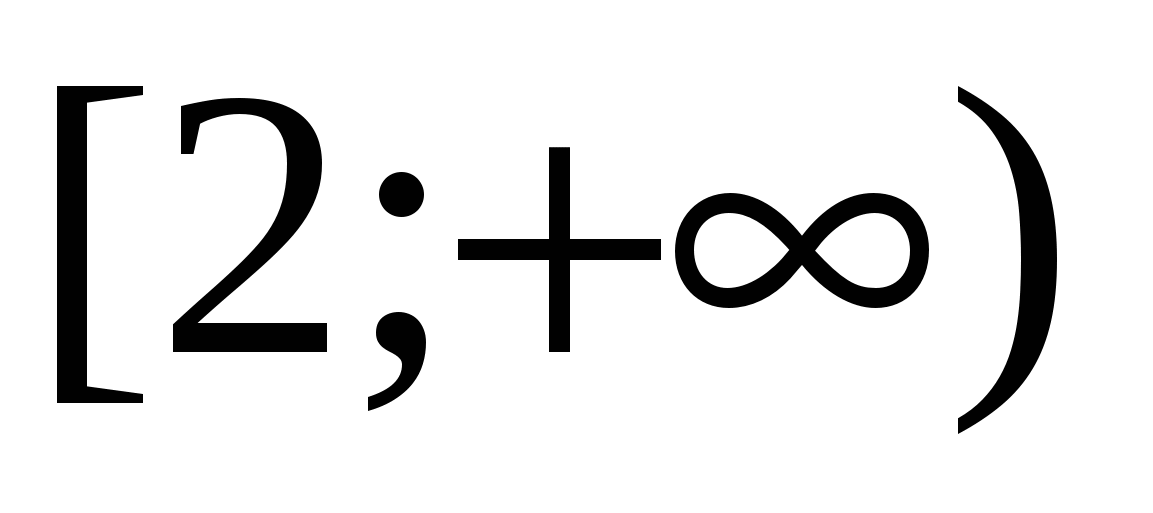
.

Vastus.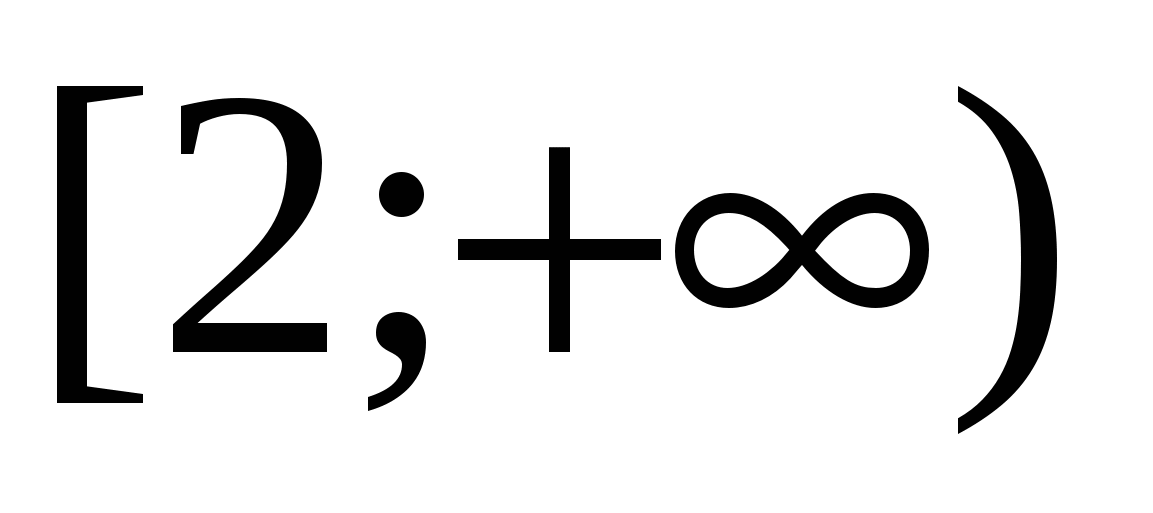
.

Näide(C3, ühtne riigieksam – 2011) 16 17 Lahenda võrrand

Lahendus. .

Vastus.
.

• Märgiteoreemi rakendamine võrrandite lahendamisel

Sõnastame teoreemi, mis on mugav moodulite erinevuste korrutistele või jagatistele ebavõrdsuste lahendamiseks:

18. teoreem Kahe avaldise moodulite erinevuse märk langeb kokku nende avaldiste ruutude erinevuse märgiga. ei kao muutuja ühegi väärtuse korral. See tähendab, et kogu määratluspiirkonnas on funktsioon konstantse märgiga. Arvutades näiteks
, leiame, et funktsioon võtab ainult positiivseid väärtusi.

Vastus.
.

Intervallmeetod võimaldab moodulitega lahendada keerulisemaid võrrandeid ja võrratusi, kuid sel juhul on sellel veidi erinev eesmärk. Asi on järgmine. Leiame kõigi alammoodulavaldiste juured ja jagame arvulise telje nende avaldiste konstantse märgi intervallideks. See võimaldab teil neid intervalle järjest läbides üheaegselt vabaneda kõigist moodulitest ja lahendada tavalise võrrandi või võrratuse (kontrollides samas, et leitud vastus sisaldub selles intervallis).

• Võrrandite lahendamine positiivse teguriga korrutamise teel

Järeldus.

Oma töö kokkuvõtteks võime öelda järgmist.

Töö eesmärgiks oli uurida erinevaid meetodeid võrrandite ja moodulitega võrratuste lahendamiseks.

Vaadeldakse mõningaid kõige lihtsamate võrrandite ja mooduliga võrratuste variante, mis on lahendatavad ekvivalentsete üleminekute abil, samuti moodulite summa teoreemi; graafiline viis võrrandite lahendamiseks. Peab ütlema, et sisse koolikursus matemaatikud, need on kõige sagedamini kasutatavad lahendusmeetodid. Graafiline meetod on eriti aktuaalne ülesannete lahendamisel C 5 kontrollist ja mõõtmisest Ühtse riigieksami materjalid.

Järgmiseks uurisime mitme näite varal muid võimalusi võrrandite ja võrratuste lahendamiseks moodulitega, nimelt: moodulite paljastamise meetodit; mittenegatiivsete avaldiste mooduleid sisaldavate võrrandite lahendamine; võrrandite lahendamine geomeetrilise tõlgenduse abil; identiteeti kasutades
; märgiteoreemi rakendamine; võrrandite lahendamine, minnes tagajärjele, korrutades positiivse teguriga, aga ka võrratuste lahendamine intervallide meetodil.

Seega jõudsime uuringu käigus järgmistele järeldustele.

Peame moodulite paljastamise meetodit, graafilist meetodit ja intervallide meetodit kõige universaalsemaks ja rakendatavaks kõige suurema hulga probleemide korral. See usk tekkis otsuse tulemusena suur numberülesanded ühtse riigieksami, ainemeistrivõistluste, olümpiaadiülesannete testimise ja mõõtmise materjalidest, samuti selleteemalise kirjanduse õppimine. Väga oluliseks peame ka identiteedi tundmist ja rakendamist
, kuna seda kasutatakse mitte ainult võrrandite ja võrratuste lahendamiseks, vaid ka paljude avaldiste teisendamiseks radikaalidega. Ülejäänud lahendusmeetodid, mida oleme kaalunud, pakuvad kindlasti suurt huvi matemaatilise silmaringi laiendamise ja üldise matemaatiline areng. Seetõttu kavatseme neid kasutada riikliku lõpliku sertifitseerimise ettevalmistamiseks Ühtne riigieksami vorm ja ettevalmistus kõrgkoolis õppimiseks.

Bibliograafia.

“Suur matemaatikaentsüklopeedia” koolilastele ja üliõpilastele;

Matemaatika. Ühtne riigieksam - 2011, 2012. Mudeleksami võimalused. / Toimetanud A.L. Semenova, I.V. Jaštšenko.

M.Ya. Võgodski. Algmatemaatika käsiraamat

"Uusim kooliõpilaste teatmik";

Entsüklopeedia “Ma uurin maailma. Matemaatika";

;

See artikkel on pühendatud erinevate võrrandite ja võrratuste lahendamise tehnikatele, mis sisaldavad
muutuja mooduli märgi all.

Kui kohtate eksamil mooduliga võrrandit või võrratust, saate selle lahendada järgmiselt
teadmata üldse mingeid erimeetodeid ja kasutades ainult mooduli definitsiooni. Kas see on tõsi,
Selleks võib kuluda poolteist tundi väärtuslikku eksamiaega.

Seetõttu tahame teile rääkida tehnikatest, mis lihtsustavad selliste probleemide lahendamist.

Kõigepealt meenutagem seda

Mõelgem Erinevat tüüpi mooduliga võrrandid. (Liikume ebavõrdsuse juurde hiljem.)

Moodul vasakul, number paremal

See on kõige lihtsam juhtum. Lahendame võrrandi

On ainult kaks numbrit, mille moodulid on võrdsed neljaga. Need on 4 ja −4. Seetõttu võrrand
võrdub kahe lihtsa kombinatsiooniga:

Teisel võrrandil pole lahendeid. Esimese lahendused: x = 0 ja x = 5.

Vastus: 0; 5.

Muutuv nii mooduli all kui ka väljaspool moodulit

Siin peame moodulit definitsiooni järgi laiendama. . . või mõtle!

Võrrand jaguneb kaheks juhuks, sõltuvalt mooduli all oleva avaldise märgist.
Teisisõnu, see on samaväärne kahe süsteemi kombinatsiooniga:

Esimese süsteemi lahendus: . Teisel süsteemil pole lahendusi.
Vastus: 1.

Esimene juhtum: x ≥ 3. Eemaldage moodul:

Arv, mis on negatiivne, ei vasta tingimusele x ≥ 3 ega ole seetõttu algse võrrandi juur.

Uurime, kas see rahuldab see tingimus number . Selleks koostame erinevuse ja määrame selle märgi:

See tähendab, et see on suurem kui kolm ja seetõttu on see algvõrrandi juur

Teine juhtum: x< 3. Снимаем модуль:

Number . suurem kui , ja seepärast ei vasta tingimusele x< 3. Проверим :

Tähendab,. on algse võrrandi juur.

Kas eemaldada moodul definitsiooni järgi? Sellele on isegi hirmutav mõelda, sest diskriminant pole täiuslik ruut. Kasutagem parem järgmist kaalutlust: võrrand kujul |A| = B on samaväärne kahe süsteemi kombinatsiooniga:

Sama asi, kuid veidi erinev:

Teisisõnu lahendame kaks võrrandit A = B ja A = −B ning seejärel valime juured, mis vastavad tingimusele B ≥ 0.

Alustame. Kõigepealt lahendame esimese võrrandi:

Seejärel lahendame teise võrrandi:

Nüüd kontrollime igal juhul parema külje märki:

Seetõttu sobivad ainult ja.

Ruutvõrrandid asendusega |x| = t

Lahendame võrrandi:

Kuna , on mugav teha asendus |x| = t. Saame:

Vastus: ±1.

Moodul võrdne mooduliga

Me räägime võrranditest kujul |A| = |B|. See on saatuse kingitus. Moodulit definitsiooni järgi ei avalikustata! See on lihtne:

Vaatleme näiteks võrrandit: . See on samaväärne järgmise komplektiga:

Jääb lahendada kõik hulga võrrandid ja vastus üles kirjutada.

Kaks või enam moodulit

Lahendame võrrandi:

Ärme hakka iga mooduliga eraldi vaeva nägema ja ava seda definitsiooni järgi – valikuvõimalusi tuleb liiga palju. On ratsionaalsem viis - intervallmeetod.

Mooduli avaldised kaovad punktides x = 1, x = 2 ja x = 3. Need punktid jagavad arvujoone neljaks intervalliks (intervalliks). Märgime need punktid arvureale ja asetame saadud intervallidele iga mooduli all oleva avaldise jaoks märgid. (Märkide järjekord kattub võrrandi vastavate moodulite järjestusega.)

Seega peame arvestama nelja juhtumiga - kui x on igas intervallis.

Juhtum 1: x ≥ 3. Kõik moodulid eemaldatakse "plussiga":

Saadud väärtus x = 5 rahuldab tingimust x ≥ 3 ja on seetõttu algse võrrandi juur.

Juhtum 2: 2 ≤ x ≤ 3. Viimane moodul eemaldatakse nüüd "miinusega":

Sobiv on ka saadud väärtus x - see kuulub vaadeldavasse intervalli.

Juhtum 3: 1 ≤ x ≤ 2. Teine ja kolmas moodul eemaldatakse "miinusega":

Me oleme saanud vaadeldavast intervallist mis tahes x jaoks õige arvulise võrdsuse, mis on selle võrrandi lahendus.

Juhtum 4: x ≤ 1 ≤ 1. Teine ja kolmas moodul eemaldatakse "miinusega":

Ei midagi uut. Teame juba, et x = 1 on lahendus.

Vastus: ∪ (5).

Moodul moodulis

Lahendame võrrandi:

Alustame sisemooduli avamisega.

1) x ≤ 3. Saame:

Mooduli all olev avaldis kaob kell . See punkt kuulub kõnealusele
vahel. Seetõttu peame analüüsima kahte alamjuhtumit.

1.1) Sel juhul saame:

See x väärtus ei sobi, kuna see ei kuulu vaadeldavasse intervalli.

1.2) . Seejärel:

See x väärtus pole samuti hea.

Seega ei ole x ≤ 3 jaoks lahendusi. Liigume edasi teise juhtumi juurde.

2) x ≥ 3. Meil ​​on:

Siin on meil vedanud: avaldis x + 2 on vaadeldavas intervallis positiivne! Seetõttu ei ole enam alamjuhtumeid: moodul eemaldatakse "plussiga":

See x väärtus on vaadeldavas intervallis ja on seega algvõrrandi juur.

Nii lahendatakse kõik seda tüüpi probleemid - avame pesastatud moodulid ükshaaval, alustades sisemisest.