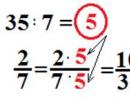Give examples of decimals and ordinary fractions. Decimal fractions. Her Majesty fraction: what is it

A decimal fraction differs from an ordinary fraction in that its denominator is a place value.

For example:

Decimal fractions are separated from ordinary fractions into a separate form, which led to their own rules for comparing, adding, subtracting, multiplying and dividing these fractions. In principle, you can work with decimal fractions using the rules of ordinary fractions. Own rules for converting decimal fractions simplify calculations, and rules for converting ordinary fractions to decimals, and vice versa, serve as a link between these types of fractions.

Writing and reading decimal fractions allows you to write them down, compare them, and perform operations on them according to rules very similar to the rules for operations with natural numbers.

The system of decimal fractions and operations on them was first outlined in the 15th century. Samarkand mathematician and astronomer Dzhemshid ibn-Masudal-Kashi in the book “The Key to the Art of Counting”.

The whole part of the decimal fraction is separated from the fractional part by a comma; in some countries (the USA) they put a period. If a decimal fraction does not have an integer part, then the number 0 is placed before the decimal point.

You can add any number of zeros to the fractional part of a decimal on the right; this does not change the value of the fraction. The fractional part of a decimal is read at the last significant digit.

For example:
0.3 - three tenths
0.75 - seventy-five hundredths
0.000005 - five millionths.

Reading the whole part of a decimal is the same as reading natural numbers.

For example:
27.5 - twenty seven...;
1.57 - one...

After the whole part of the decimal fraction the word “whole” is pronounced.

For example:
10.7 - ten point seven

0.67 - zero point sixty-seven hundredths.

Decimal places are the digits of the fractional part. The fractional part is not read by digits (unlike natural numbers), but as a whole, therefore the fractional part of a decimal fraction is determined by the last significant digit on the right. The place system of the fractional part of the decimal is somewhat different than that of natural numbers.

1st digit after busy - tenths digit
2nd decimal place - hundredths place
3rd decimal place - thousandths place
4th decimal place - ten-thousandth place
5th decimal place - hundred thousandths place
6th decimal place - millionth place
The 7th decimal place is the ten-millionth place
The 8th decimal place is the hundred millionth place

The first three digits are most often used in calculations. The large digit capacity of the fractional part of decimals is used only in specific branches of knowledge where infinitesimal quantities are calculated.

Converting a decimal to a mixed fraction consists of the following: the number before the decimal point is written as an integer part of the mixed fraction; the number after the decimal point is the numerator of its fractional part, and in the denominator of the fractional part write a unit with as many zeros as there are digits after the decimal point.

Common fraction

Quarters

Orderliness. a And b there is a rule that allows one to uniquely identify one and only one of the three between them relations : « < », « >" or " = ". This rule is called ordering rule and is formulated as follows: two non-negative numbers and are related by the same relation as two integers and ; two non-positive numbers a And b are related by the same relation as two non-negative numbers and ; if suddenly a non-negative, but b- negative, then a > b. style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png" border="0">
Adding Fractions
Addition operation. For any rational numbers a And b there is a so-called summation rule c. Moreover, the number itself c called amount numbers a And b and is denoted by , and the process of finding such a number is called summation. The summation rule has the following form: .
Multiplication operation. For any rational numbers a And b there is a so-called multiplication rule, which assigns them some rational number c. Moreover, the number itself c called work numbers a And b and is denoted by , and the process of finding such a number is also called multiplication. The multiplication rule looks like this: .
Transitivity order relations. For any triple of rational numbers a , b And c If a less b And b less c, That a less c, and if a equals b And b equals c, That a equals c. 6435">Commutativity of addition. Changing the places of rational terms does not change the sum.
Associativity addition. The order in which three rational numbers are added does not affect the result.
Availability zero. There is a rational number 0 that preserves every other rational number when added.
The presence of opposite numbers. Any rational number has an opposite rational number, which when added to gives 0.
Commutativity of multiplication. Changing the places of rational factors does not change the product.
Associativity of multiplication. The order in which three rational numbers are multiplied does not affect the result.
Availability units. There is a rational number 1 that preserves every other rational number when multiplied.
Availability reciprocal numbers. Any rational number has an inverse rational number, which when multiplied by gives 1.
Distributivity multiplication relative to addition. The multiplication operation is coordinated with the addition operation through the distribution law:
Connection of the order relation with the operation of addition. The same rational number can be added to the left and right sides of a rational inequality. max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/51/358b88fcdff63378040f8d9ab9ba5048.png" border="0">
Axiom of Archimedes. Whatever the rational number a, you can take so many units that their sum exceeds a. style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png" border="0">

Additional properties

All other properties inherent in rational numbers are not distinguished as basic ones, because, generally speaking, they are no longer based directly on the properties of integers, but can be proven based on the given basic properties or directly by the definition of some mathematical object. There are a lot of such additional properties. It makes sense to list only a few of them here.

Style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png" border="0">

Countability of a set

Numbering of rational numbers

To estimate the number of rational numbers, you need to find power there are many of them. It is easy to prove that the set of rational numbers countably. To do this, it is enough to give an algorithm that numbers rational numbers, i.e., establishes bijection between sets of rational and natural numbers.

The simplest of these algorithms looks like this. An endless table of ordinary fractions is compiled, on each i-th line in each j the th column of which the fraction is located. For definiteness, it is assumed that the rows and columns of this table are numbered starting from one. Table cells are denoted by , where i- the number of the table row in which the cell is located, and j- column number.

The resulting table is traversed using a “snake” according to the following formal algorithm.

These rules are searched from top to bottom and the next position is selected based on the first match.

In the process of such a traversal, each new rational number is associated with another natural number. That is, the fraction 1/1 is assigned to the number 1, the fraction 2/1 to the number 2, etc. It should be noted that only irreducible fractions are numbered. A formal sign of irreducibility is equality to one greatest common divisor numerator and denominator of the fraction.

Following this algorithm, we can enumerate all positive rational numbers. This means that the set of positive rational numbers is countable. It is easy to establish a bijection between the sets of positive and negative rational numbers by simply assigning to each rational number its opposite. That. the set of negative rational numbers is also countable. Their union is also countable by the property of countable sets. The set of rational numbers is also countable as the union of a countable set with a finite one.

The statement about the countability of the set of rational numbers may cause some confusion, since at first glance it seems that it is much more extensive than the set of natural numbers. In fact, this is not so and there are enough natural numbers to enumerate all rational ones.

Lack of rational numbers

The hypotenuse of such a triangle cannot be expressed by any rational number

Rational numbers of the form 1 / n at large n can be measured arbitrarily small quantities. This fact creates the misleading impression that rational numbers can measure any geometric distances. It is easy to show that this is not true.

From Pythagorean theorem it is known that hypotenuse rectangular triangle expressed as Square root amounts squares his legs. That. the length of the hypotenuse of an isosceles right triangle with a unit leg is equal to , i.e., the number whose square is 2.

If we assume that a number can be represented by some rational number, then there is such an integer m and such a natural number n, that , and the fraction is irreducible, i.e. numbers m And n- mutually simple.

If , then , i.e. m 2 = 2n 2. Therefore, the number m 2 is even, but the product of two odd numbers is odd, which means that the number itself m also even. So there is a natural number k, such that the number m can be represented in the form m = 2k. Number square m In this sense m 2 = 4k 2, but on the other hand m 2 = 2n 2 means 4 k 2 = 2n 2, or n 2 = 2k 2. As shown earlier for the number m, this means that the number n- even as m. But then they are not relatively prime, since both are bisected. The resulting contradiction proves that it is not a rational number.

Already in elementary school, students are exposed to fractions. And then they appear in every topic. You cannot forget actions with these numbers. Therefore, you need to know all the information about ordinary and decimal fractions. These concepts are not complicated, the main thing is to understand everything in order.

Why are fractions needed?

The world around us consists of entire objects. Therefore, there is no need for shares. But everyday life constantly pushes people to work with parts of objects and things.

For example, chocolate consists of several pieces. Consider a situation where his tile is formed by twelve rectangles. If you divide it into two, you get 6 parts. It can easily be divided into three. But it will not be possible to give five people a whole number of chocolate slices.

By the way, these slices are already fractions. And their further division leads to the appearance of more complex numbers.

What is a "fraction"?

This is a number made up of parts of a unit. Outwardly, it looks like two numbers separated by a horizontal or slash. This feature is called fractional. The number written at the top (left) is called the numerator. What is at the bottom (right) is the denominator.

Essentially, the slash turns out to be a division sign. That is, the numerator can be called the dividend, and the denominator can be called the divisor.

What fractions are there?

In mathematics there are only two types: ordinary and decimal fractions. Schoolchildren become acquainted with the first ones in elementary school, calling them simply “fractions.” The latter will be learned in 5th grade. That's when these names appear.

Common fractions are all those that are written as two numbers separated by a line. For example, 4/7. A decimal is a number in which the fractional part has a positional notation and is separated from the whole number by a comma. For example, 4.7. Students need to clearly understand that the two examples given are completely different numbers.

Every simple fraction can be written as a decimal. This statement is almost always true in reverse. There are rules that allow you to write a decimal fraction as a common fraction.

What subtypes do these types of fractions have?

It is better to start in chronological order, as they are studied. Common fractions come first. Among them, 5 subspecies can be distinguished.

Correct. Its numerator is always less than its denominator.

Wrong. Its numerator is greater than or equal to its denominator.

Reducible/irreducible. It may turn out to be either right or wrong. Another important thing is whether the numerator and denominator have common factors. If there are, then it is necessary to divide both parts of the fraction by them, that is, reduce it.

Mixed. An integer is assigned to its usual regular (irregular) fractional part. Moreover, it is always on the left.

Composite. It is formed from two fractions divided by each other. That is, it contains three fractional lines at once.

Decimal fractions have only two subtypes:

finite, that is, one whose fractional part is limited (has an end);

infinite - a number whose digits after the decimal point do not end (they can be written endlessly).

How to convert a decimal fraction to a common fraction?

If this is a finite number, then an association is applied based on the rule - as I hear, so I write. That is, you need to read it correctly and write it down, but without a comma, but with a fractional bar.

As a hint about the required denominator, you need to remember that it is always one and several zeros. You need to write as many of the latter as there are digits in the fractional part of the number in question.

How to convert decimal fractions into ordinary fractions if their integer part is missing, that is, equal to zero? For example, 0.9 or 0.05. After applying the specified rule, it turns out that you need to write zero integers. But it is not indicated. All that remains is to write down the fractional parts. The first number will have a denominator of 10, the second will have a denominator of 100. That is, the given examples will have the following numbers as answers: 9/10, 5/100. Moreover, it turns out that the latter can be reduced by 5. Therefore, the result for it needs to be written as 1/20.

How can you convert a decimal fraction into an ordinary fraction if its integer part is different from zero? For example, 5.23 or 13.00108. In both examples, the whole part is read and its value is written. In the first case it is 5, in the second it is 13. Then you need to move on to the fractional part. The same operation is supposed to be carried out with them. The first number appears 23/100, the second - 108/100000. The second value needs to be reduced again. The answer gives the following mixed fractions: 5 23/100 and 13 27/25000.

How to convert an infinite decimal fraction to an ordinary fraction?

If it is non-periodic, then such an operation will not be possible. This fact is due to the fact that each decimal fraction is always converted to either a finite or a periodic fraction.

The only thing you can do with such a fraction is round it. But then the decimal will be approximately equal to that infinite. It can already be turned into an ordinary one. But the reverse process: converting to decimal will never give the initial value. That is, infinite non-periodic fractions are not converted into ordinary fractions. This needs to be remembered.

How to write an infinite periodic fraction as an ordinary fraction?

In these numbers, there are always one or more digits after the decimal point that are repeated. They are called a period. For example, 0.3(3). Here "3" is in the period. They are classified as rational because they can be converted into ordinary fractions.

Those who have encountered periodic fractions know that they can be pure or mixed. In the first case, the period starts immediately from the comma. In the second, the fractional part begins with some numbers, and then the repetition begins.

The rule by which you need to write an infinite decimal as a common fraction will be different for the two types of numbers indicated. It is quite easy to write pure periodic fractions as ordinary fractions. As with finite ones, they need to be converted: write down the period in the numerator, and the denominator will be the number 9, repeated as many times as the number of digits the period contains.

For example, 0,(5). The number does not have an integer part, so you need to immediately start with the fractional part. Write 5 as the numerator and 9 as the denominator. That is, the answer will be the fraction 5/9.

The rule on how to write an ordinary decimal periodic fraction that is mixed.

Look at the length of the period. That's how many 9s the denominator will have.

Write down the denominator: first nines, then zeros.

To determine the numerator, you need to write down the difference of two numbers. All numbers after the decimal point will be minified, along with the period. Deductible - it is without a period.

For example, 0.5(8) - write the periodic decimal fraction as a common fraction. The fractional part before the period contains one digit. So there will be one zero. There is also only one number in the period - 8. That is, there is only one nine. That is, you need to write 90 in the denominator.

To determine the numerator, you need to subtract 5 from 58. It turns out 53. For example, you would have to write the answer as 53/90.

How are fractions converted to decimals?

The simplest option is a number whose denominator is the number 10, 100, etc. Then the denominator is simply discarded, and a comma is placed between the fractional and integer parts.

There are situations when the denominator easily turns into 10, 100, etc. For example, the numbers 5, 20, 25. It is enough to multiply them by 2, 5 and 4, respectively. You just need to multiply not only the denominator, but also the numerator by the same number.

For all other cases, a simple rule is useful: divide the numerator by the denominator. In this case, you may get two possible answers: a finite or a periodic decimal fraction.

Operations with ordinary fractions

Addition and subtraction

Students become acquainted with them earlier than others. Moreover, at first the fractions have the same denominators, and then they have different ones. General rules can be reduced to this plan.

Find the least common multiple of the denominators.

Write additional factors for all ordinary fractions.

Multiply the numerators and denominators by the factors specified for them.

Add (subtract) the numerators of the fractions and leave the common denominator unchanged.

If the numerator of the minuend is less than the subtrahend, then we need to find out whether we have a mixed number or a proper fraction.

In the first case, you need to borrow one from the whole part. Add the denominator to the numerator of the fraction. And then do the subtraction.

In the second, it is necessary to apply the rule of subtracting a larger number from a smaller number. That is, from the module of the subtrahend, subtract the module of the minuend, and in response put a “-” sign.

Look carefully at the result of addition (subtraction). If you get an improper fraction, then you need to select the whole part. That is, divide the numerator by the denominator.

Multiplication and division

To perform them, fractions do not need to be reduced to a common denominator. This makes it easier to perform actions. But they still require you to follow the rules.

When multiplying fractions, you need to look at the numbers in the numerators and denominators. If any numerator and denominator have a common factor, then they can be reduced.

Multiply the numerators.

Multiply the denominators.

If the result is a reducible fraction, then it must be simplified again.

When dividing, you must first replace division with multiplication, and the divisor (second fraction) with the reciprocal fraction (swap the numerator and denominator).

Then proceed as with multiplication (starting from point 1).

In tasks where you need to multiply (divide) by a whole number, the latter should be written as an improper fraction. That is, with a denominator of 1. Then act as described above.

Operations with decimals

Addition and subtraction

Of course, you can always convert a decimal into a fraction. And act according to the plan already described. But sometimes it is more convenient to act without this translation. Then the rules for their addition and subtraction will be exactly the same.

Equalize the number of digits in the fractional part of the number, that is, after the decimal point. Add the missing number of zeros to it.

Write the fractions so that the comma is below the comma.

Add (subtract) like natural numbers.

Remove the comma.

Multiplication and division

It is important that you do not need to add zeros here. Fractions should be left as they are given in the example. And then go according to plan.

To multiply, you need to write the fractions one below the other, ignoring the commas.

Multiply like natural numbers.

Place a comma in the answer, counting from the right end of the answer as many digits as they are in the fractional parts of both factors.

To divide, you must first transform the divisor: make it a natural number. That is, multiply it by 10, 100, etc., depending on how many digits are in the fractional part of the divisor.

Multiply the dividend by the same number.

Divide a decimal fraction by a natural number.

Place a comma in your answer at the moment when the division of the whole part ends.

What if one example contains both types of fractions?

Yes, in mathematics there are often examples in which you need to perform operations on ordinary and decimal fractions. In such tasks there are two possible solutions. You need to objectively weigh the numbers and choose the optimal one.

First way: represent ordinary decimals

It is suitable if division or translation results in finite fractions. If at least one number gives a periodic part, then this technique is prohibited. Therefore, even if you don’t like working with ordinary fractions, you will have to count them.

Second way: write decimal fractions as ordinary

This technique turns out to be convenient if the part after the decimal point contains 1-2 digits. If there are more of them, you may end up with a very large common fraction and decimal notation will make the task faster and easier to calculate. Therefore, you always need to soberly evaluate the task and choose the simplest solution method.

When studying the queen of all sciences - mathematics, at some point everyone comes across fractions. Although this concept (like the types of fractions themselves or mathematical operations with them) is not at all complicated, you need to treat it carefully, because in real life outside of school it will be very useful. So, let's refresh our knowledge about fractions: what they are, what they are for, what types they are and how to perform various arithmetic operations with them.

Her Majesty fraction: what is it

In mathematics, fractions are numbers, each of which consists of one or more parts of a unit. Such fractions are also called ordinary or simple. As a rule, they are written in the form of two numbers that are separated by a horizontal or slash line, it is called a “fractional” line. For example: ½, ¾.
The upper, or first, of these numbers is the numerator (shows how many parts are taken from the number), and the lower, or second, is the denominator (demonstrates how many parts the unit is divided into).
The fraction bar actually functions as a division sign. For example, 7:9=7/9
Traditionally, common fractions are less than one. While decimals can be larger than it.

What are fractions for? Yes, for everything, because in the real world, not all numbers are integers. For example, two schoolgirls in the cafeteria bought one delicious chocolate bar together. When they were about to share dessert, they met a friend and decided to treat her too. However, now it is necessary to correctly divide the chocolate bar, considering that it consists of 12 squares.
At first, the girls wanted to divide everything equally, and then each would get four pieces. But, after thinking it over, they decided to treat their friend, not 1/3, but 1/4 of the chocolate. And since the schoolgirls did not study fractions well, they did not take into account that in such a situation they would end up with 9 pieces, which are very difficult to divide into two. This fairly simple example shows how important it is to be able to correctly find a part of a number. But in life there are many more such cases.

Types of fractions: ordinary and decimal

All mathematical fractions are divided into two large categories: ordinary and decimal. The features of the first of them were described in the previous paragraph, so now it’s worth paying attention to the second.
Decimal is a positional notation of a fraction of a number, which is written in writing separated by a comma, without a dash or slash. For example: 0.75, 0.5.
In fact, a decimal fraction is identical to an ordinary fraction, however, its denominator is always one followed by zeros - hence its name.
The number preceding the comma is an integer part, and everything after it is a fraction. Any simple fraction can be converted to a decimal. Thus, the decimal fractions indicated in the previous example can be written as usual: ¾ and ½.

It is worth noting that both decimal and ordinary fractions can be either positive or negative. If they are preceded by a “-” sign, this fraction is negative, if “+” is a positive fraction.

Subtypes of ordinary fractions

There are these types of simple fractions.

Correct. Their numerator value is always less than that of the denominator. For example: 7/8. It is a proper fraction because the numerator 7 is less than the denominator 8. Improper. In such fractions, either the numerator and denominator are equal to each other (8/8), or the value of the lower number is less than the upper one (9/8). Mixed. This is the name of a proper fraction written together with a whole number: 8 ½. It is understood as the sum of this number and a fraction. By the way, it’s quite easy to make an improper fraction appear in its place. To do this, 8 needs to be written as 16/2+1/2=17/2. Composite. As the name implies, they consist of several fractional lines: ½ / ¾. Reducible / irreducible. These can include both proper and improper fractions. It all depends on whether the numerator and denominator can be divided by the same number. For example, 6/9 is a reducible fraction, because both of its components can be divided by 3 and the result is 2/3. But 7/9 is irreducible, since 7 and 9 are prime numbers that do not have a common divisor and cannot be reduced.

Subtypes of decimal fraction

Unlike a simple fraction, a decimal fraction is divided into only 2 types.

Finite - received this name due to the fact that after the decimal point it has a limited (finite) number of digits: 19.25. An infinite fraction is a number with an infinite number of digits after the decimal point. For example, when dividing 10 by 3, the result will be an infinite fraction 3.333...

Adding Fractions

Carrying out various arithmetic manipulations with fractions is a little more difficult than with ordinary numbers. However, if you understand the basic rules, solving any example with them will not be difficult.
So, in order to add fractions together, first of all, you need to make sure that both terms have the same denominators. To do this, you have to find the smallest number that can be divided without a remainder into the denominators of the summands.
For example: 2/3+3/4. The least common multiple for them will be 12, therefore, it is necessary that this number be in each denominator. To do this, we multiply the numerator and denominator of the first fraction by 4, it turns out 8/12, we do the same with the second term, but only multiply by 3 - 9/12. Now you can easily solve the example: 8/12+9/12= 17/12. The resulting fraction is an incorrect value because the numerator is greater than the denominator. It can and should be transformed into a correct mixed one by dividing 17:12 = 1 and 5/12.
When mixed fractions are added, operations are performed first with whole numbers, and then with fractions.
If the example contains a decimal fraction and a regular fraction, it is necessary to make both simple, then bring them to the same denominator and add them. For example 3.1+1/2. The number 3.1 can be written as a mixed fraction of 3 and 1/10 or as an improper fraction - 31/10. The common denominator for the terms will be 10, so you need to multiply the numerator and denominator of 1/2 by 5 alternately, you get 5/10. Then you can easily calculate everything: 31/10+5/10=35/10. The result obtained is an improper reducible fraction, we bring it into normal form, reducing it by 5: 7/2 = 3 and 1/2, or decimal - 3.5.
When adding 2 decimal fractions, it is important that there are the same number of digits after the decimal point. If this is not the case, you just need to add the required number of zeros, because in a decimal fraction this can be done painlessly. For example, 3.5+3.005. To solve this problem, you need to add 2 zeros to the first number and then add one by one: 3.500+3.005=3.505.

Subtracting Fractions

When subtracting fractions, you should do the same as when adding: reduce to a common denominator, subtract one numerator from another, and, if necessary, convert the result to a mixed fraction.

For example: 16/20-5/10. The common denominator will be 20. You need to bring the second fraction to this denominator by multiplying both its parts by 2, you get 10/20. Now you can solve the example: 16/20-10/20= 6/20. However, this result applies to reducible fractions, so it is worth dividing both sides by 2 and the result is 3/10.

Multiplying fractions

Dividing and multiplying fractions are much simpler operations than addition and subtraction. The fact is that when performing these tasks, there is no need to look for a common denominator.
To multiply fractions, you simply need to multiply both numerators one by one, and then both denominators. Reduce the resulting result if the fraction is a reducible quantity.

For example: 4/9x5/8. After alternate multiplication, the result is 4x5/9x8=20/72. This fraction can be reduced by 4, so the final answer in the example is 5/18.

How to divide fractions

Dividing fractions is also a simple operation; in fact, it still comes down to multiplying them. To divide one fraction by another, you need to invert the second and multiply by the first.

For example, dividing the fractions 5/19 and 5/7. To solve the example, you need to swap the denominator and numerator of the second fraction and multiply: 5/19x7/5=35/95. The result can be reduced by 5 - it turns out 7/19.
If you need to divide a fraction by a prime number, the technique is slightly different. Initially, you should write this number as an improper fraction, and then divide according to the same scheme. For example, 2/13:5 should be written as 2/13: 5/1. Now you need to turn over 5/1 and multiply the resulting fractions: 2/13x1/5= 2/65.
Sometimes you have to divide mixed fractions. You need to treat them as you would with whole numbers: turn them into improper fractions, reverse the divisor and multiply everything. For example, 8 ½: 3. Convert everything into improper fractions: 17/2: 3/1. This is followed by a 3/1 flip and multiplication: 17/2x1/3= 17/6. Now you need to convert the improper fraction to the correct one - 2 whole and 5/6.
So, having figured out what fractions are and how you can perform various arithmetic operations with them, you need to try not to forget about it. After all, people are always more inclined to divide something into parts than to add, so you need to be able to do it correctly.