inequality solution in mode online solution almost any given inequality online. Mathematical inequalities online to solve mathematics. Find quickly inequality solution in mode online. The website www.site allows you to find solution almost any given algebraic, trigonometric or transcendental inequality online. When studying almost any branch of mathematics at different stages you have to decide inequalities online. To get an answer immediately, and most importantly an accurate answer, you need a resource that allows you to do this. Thanks to the site www.site solve inequality online will take a few minutes. The main advantage of www.site when solving mathematical inequalities online- this is the speed and accuracy of the response provided. The site is able to solve any algebraic inequalities online, trigonometric inequalities online, transcendental inequalities online, and inequalities with unknown parameters in mode online. Inequalities serve as a powerful mathematical apparatus solutions practical problems. With the help mathematical inequalities it is possible to express facts and relationships that may seem confusing and complex at first glance. Unknown quantities inequalities can be found by formulating the problem in mathematical language in the form inequalities And decide received task in mode online on the website www.site. Any algebraic inequality, trigonometric inequality or inequalities containing transcendental features you can easily decide online and get the exact answer. Studying natural Sciences, you inevitably face the need solutions to inequalities. In this case, the answer must be accurate and must be obtained immediately in the mode online. Therefore for solve mathematical inequalities online we recommend the site www.site, which will become your indispensable calculator for solving algebraic inequalities online, trigonometric inequalities online, and transcendental inequalities online or inequalities with unknown parameters. For practical problems of finding online solutions to various mathematical inequalities resource www.. Solving inequalities online yourself, it is useful to check the received answer using online solution of inequalities on the website www.site. You need to write the inequality correctly and instantly get online solution, after which all that remains is to compare the answer with your solution to the inequality. Checking the answer will take no more than a minute, it’s enough solve inequality online and compare the answers. This will help you avoid mistakes in decision and correct the answer in time when solving inequalities online either algebraic, trigonometric, transcendental or inequality with unknown parameters.

Modulus of numbers this number itself is called if it is non-negative, or the same number with the opposite sign if it is negative.

For example, the modulus of the number 6 is 6, and the modulus of the number -6 is also 6.

That is, the modulus of a number is understood as the absolute value, the absolute value of this number without taking into account its sign.

It is designated as follows: |6|, | X|, |A| etc.

(More details in the “Number module” section).

Equations with modulus.

Example 1 . Solve the equation|10 X - 5| = 15.

Solution.

According to the rule, the equation is equivalent to the combination of two equations:

10X - 5 = 15
10X - 5 = -15

We decide:

10X = 15 + 5 = 20
10X = -15 + 5 = -10

X = 20: 10
X = -10: 10

X = 2
X = -1

Answer: X 1 = 2, X 2 = -1.

Example 2 . Solve the equation|2 X + 1| = X + 2.

Solution.

Since the modulus is a non-negative number, then X+ 2 ≥ 0. Accordingly:

X ≥ -2.

Let's make two equations:

2X + 1 = X + 2
2X + 1 = -(X + 2)

We decide:

2X + 1 = X + 2
2X + 1 = -X - 2

2X - X = 2 - 1
2X + X = -2 - 1

X = 1
X = -1

Both numbers are greater than -2. So both are roots of the equation.

Answer: X 1 = -1, X 2 = 1.

Example 3 . Solve the equation

|X + 3| - 1
————— = 4
X - 1

Solution.

The equation makes sense if the denominator is not equal to zero- means if X≠ 1. Let's take this condition into account. Our first action is simple - we don’t just get rid of the fraction, but transform it so as to obtain the module in its pure form:

|X+ 3| - 1 = 4 · ( X - 1),

|X + 3| - 1 = 4X - 4,

|X + 3| = 4X - 4 + 1,

|X + 3| = 4X - 3.

Now we have only an expression under the modulus on the left side of the equation. Go ahead.
The modulus of a number is a non-negative number - that is, it must be greater than zero or equal to zero. Accordingly, we solve the inequality:

4X - 3 ≥ 0

4X ≥ 3

X ≥ 3/4

Thus, we have a second condition: the root of the equation must be at least 3/4.

In accordance with the rule, we compose a set of two equations and solve them:

X + 3 = 4X - 3
X + 3 = -(4X - 3)

X + 3 = 4X - 3
X + 3 = -4X + 3

X - 4X = -3 - 3
X + 4X = 3 - 3

X = 2
X = 0

We received two answers. Let's check whether they are roots of the original equation.

We had two conditions: the root of the equation cannot be equal to 1, and it must be at least 3/4. That is X ≠ 1, X≥ 3/4. Both of these conditions correspond to only one of the two answers received - the number 2. This means that only this is the root of the original equation.

Answer: X = 2.

Inequalities with modulus.

Example 1 . Solve inequality| X - 3| < 4

Solution.

The module rule states:

|A| = A, If A ≥ 0.

|A| = -A, If A < 0.

The module can have both non-negative and negative numbers. So we have to consider both cases: X- 3 ≥ 0 and X - 3 < 0.

1) When X- 3 ≥ 0 our original inequality remains as it is, only without the modulus sign:
X - 3 < 4.

2) When X - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(X - 3) < 4.

Opening the brackets, we get:

-X + 3 < 4.

Thus, from these two conditions we came to the unification of two systems of inequalities:

X - 3 ≥ 0
X - 3 < 4

X - 3 < 0
-X + 3 < 4

Let's solve them:

X ≥ 3
X < 7

X < 3
X > -1

So, our answer is a union of two sets:

3 ≤ X < 7 U -1 < X < 3.

Determine the smallest and highest value. These are -1 and 7. Moreover X greater than -1 but less than 7.
Besides, X≥ 3. This means that the solution to the inequality is the entire set of numbers from -1 to 7, excluding these extreme numbers.

Answer: -1 < X < 7.

Or: X ∈ (-1; 7).

Add-ons.

1) There is a simpler and shorter way to solve our inequality - graphically. To do this, you need to draw a horizontal axis (Fig. 1).

Expression | X - 3| < 4 означает, что расстояние от точки X to point 3 is less than four units. We mark the number 3 on the axis and count 4 divisions to the left and to the right of it. On the left we will come to point -1, on the right - to point 7. Thus, the points X we just saw them without calculating them.

Moreover, according to the inequality condition, -1 and 7 themselves are not included in the set of solutions. Thus, we get the answer:

1 < X < 7.

2) But there is another solution that is simpler even than the graphical method. To do this, our inequality must be presented in the following form:

4 < X - 3 < 4.

After all, this is how it is according to the modulus rule. The non-negative number 4 and the similar negative number -4 are the boundaries for solving the inequality.

4 + 3 < X < 4 + 3

1 < X < 7.

Example 2 . Solve inequality| X - 2| ≥ 5

Solution.

This example is significantly different from the previous one. The left side is greater than 5 or equal to 5. C geometric point From the point of view, the solution to the inequality is all numbers that are at a distance of 5 units or more from point 2 (Fig. 2). The graph shows that these are all numbers that are less than or equal to -3 and greater than or equal to 7. This means that we have already received the answer.

Answer: -3 ≥ X ≥ 7.

Along the way, we solve the same inequality by rearranging the free term to the left and to the right with the opposite sign:

5 ≥ X - 2 ≥ 5

5 + 2 ≥ X ≥ 5 + 2

The answer is the same: -3 ≥ X ≥ 7.

Or: X ∈ [-3; 7]

The example is solved.

Example 3 . Solve inequality 6 X 2 - | X| - 2 ≤ 0

Solution.

Number X can be a positive number, negative number, or zero. Therefore, we need to take into account all three circumstances. As you know, they are taken into account in two inequalities: X≥ 0 and X < 0. При X≥ 0 we simply rewrite our original inequality as is, only without the modulus sign:

6x 2 - X - 2 ≤ 0.

Now about the second case: if X < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6X 2 - (-X) - 2 ≤ 0.

Expanding the brackets:

6X 2 + X - 2 ≤ 0.

Thus, we received two systems of equations:

6X 2 - X - 2 ≤ 0
X ≥ 0

6X 2 + X - 2 ≤ 0
X < 0

We need to solve inequalities in systems - and this means we need to find the roots of two quadratic equations. To do this, we equate the left-hand sides of the inequalities to zero.

Let's start with the first one:

6X 2 - X - 2 = 0.

How to solve a quadratic equation - see the section “Quadratic Equation”. We will immediately name the answer:

X 1 = -1/2, x 2 = 2/3.

From the first system of inequalities we obtain that the solution to the original inequality is the entire set of numbers from -1/2 to 2/3. We write the union of solutions at X ≥ 0:
[-1/2; 2/3].

Now let's solve the second quadratic equation:

6X 2 + X - 2 = 0.

Its roots:

X 1 = -2/3, X 2 = 1/2.

Conclusion: when X < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Let's combine the two answers and get the final answer: the solution is the entire set of numbers from -2/3 to 2/3, including these extreme numbers.

Answer: -2/3 ≤ X ≤ 2/3.

Or: X ∈ [-2/3; 2/3].

REVIEWED

Pedagogical Council MOU

"Zashizhemskaya Secondary School"

Protocol No. 1

AGREED

Deputy Director for HR

_______ /Sidorkina R.L./

I APPROVED

Head teacher:

A.P. Konakov

Order No. 63

Solving equations and inequalities with modulus

Research

The program was compiled by:

higher mathematics teacher

Sidorkina R.L.

Zashizhemye village, 2014

Table of contents

Introduction…………………………………………………………………………………3

The simplest equations and inequalities with modulus……………………5

Graphical solution of equations and inequalities with modulus………….8

Other ways to solve equations and inequalities with modulus.........10

Conclusion……………………………………………………..16

References………………………………………………………18

1. Introduction

The concept of absolute value (modulus) is one of the most important characteristics of a number, both in the field of real and complex numbers.

This concept is widely used not only in various sections of the school mathematics course, but also in courses higher mathematics, physics and technical sciences studied in universities. For example, in the theory of approximate calculations, the concepts of absolute and relative errors of an approximate number are used. In mechanics and geometry, the concepts of a vector and its length (vector modulus) are studied. IN mathematical analysis the concept of the absolute value of a number is contained in the definitions of such basic concepts as limit, bounded function, etc. Problems related to absolute values ​​are often found in mathematical olympiads, entrance exams to universities and the Unified State Exam. And so it became important for us to study some aspects of this topic.

Home purpose Our work is to study various methods for solving equations and inequalities with moduli.

This goal must be achieved by solving the following tasks:

Study the definition and some properties of a module.

Master the solution of simple equations and inequalities with modulus through equivalent transitions

Consider various methods for solving equations and inequalities with modulus.

Object studies are some types of equations and inequalities with modulus.

Item research - various methods for solving equations and inequalities with a modulus, namely: graphical method, method of geometric interpretation, use of identity, application of the theorem of signs, method of transition to a consequence, method of intervals, method of multiplication by a positive factor, method of revealing modules.

During the study, methods such as studying the literature on this issue and the practical method were used.

In the course of our work, we examined such sources as:

1. “Big Mathematical Encyclopedia” for schoolchildren and students;

Mathematics. Unified State Examination - 2011-2012. Typical exam options. / Edited by A.L. Semenova, I.V. Yashchenko.

Encyclopedia “I know the world” Mathematics;

;

1. 1. The simplest equations and inequalities with modulus

We will consider the simplest equations to be those solved by one of the following equivalent transitions:

Examples of solving simple equations.

Example 1 Let's solve the equation
.

Solution.

Answer.
.

Example 2 Let's solve the equation.

Solution.

Answer.
.

Example 3 Let's solve the equation
.

Solution.

Answer.
.

A series of equations are solved using the following theorem.

Theorem.4 The sum of modules is equal to the algebraic sum of submodular quantities if and only if each quantity has the sign with which it is included in the algebraic sum.

Example 5 Solve the equation

Solution. Since , then we have an equality of the form , where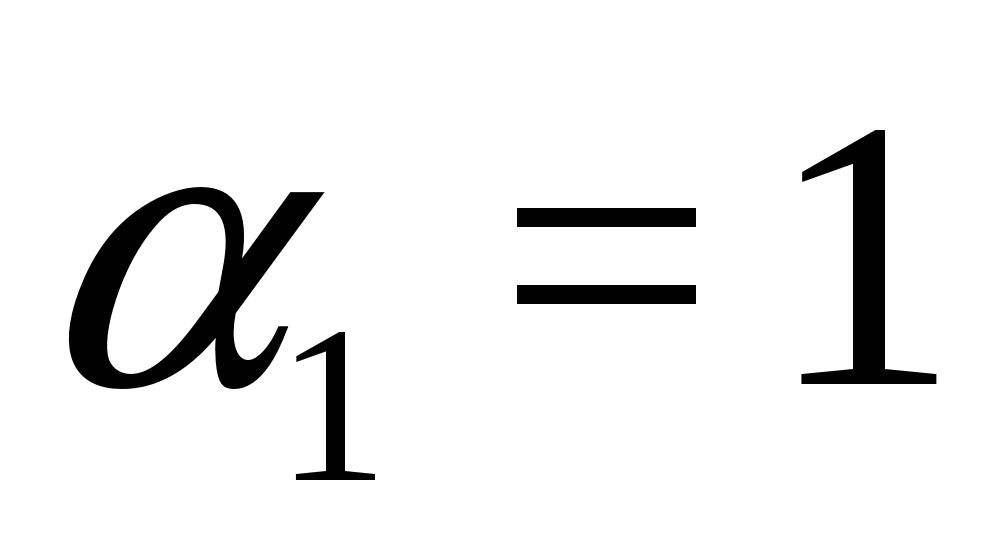
,
. Therefore, the original equation is equivalent to the system:

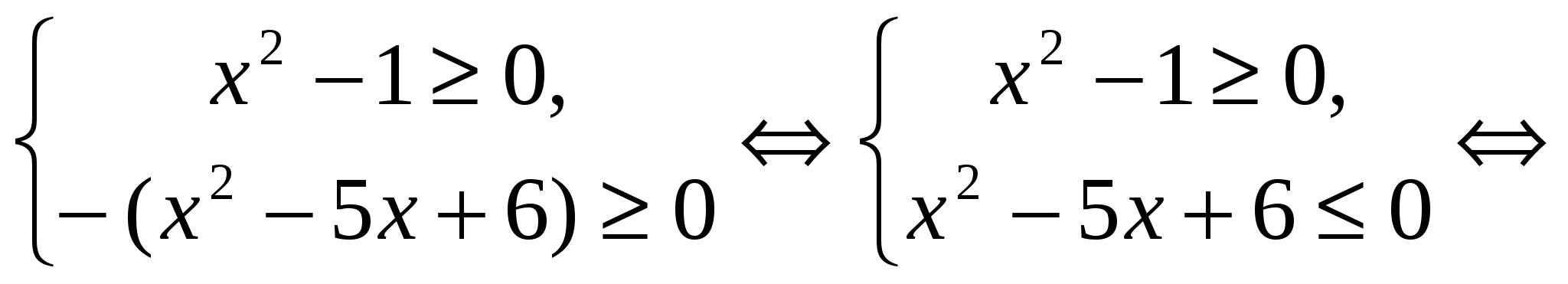
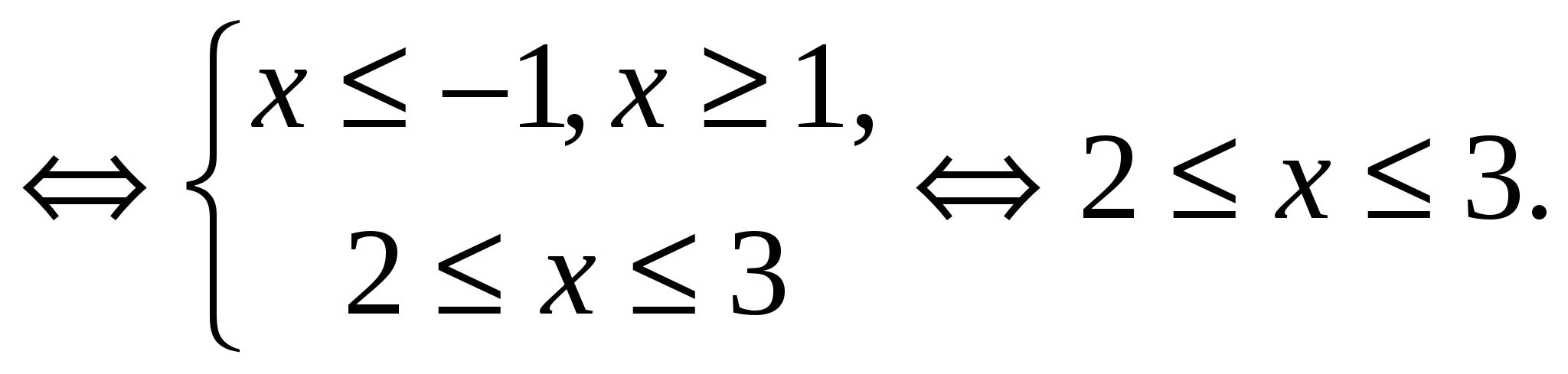
Answer.
.

Examples of solving simple inequalities.

Example 6 Let's solve the inequality
.

Solution.

Answer.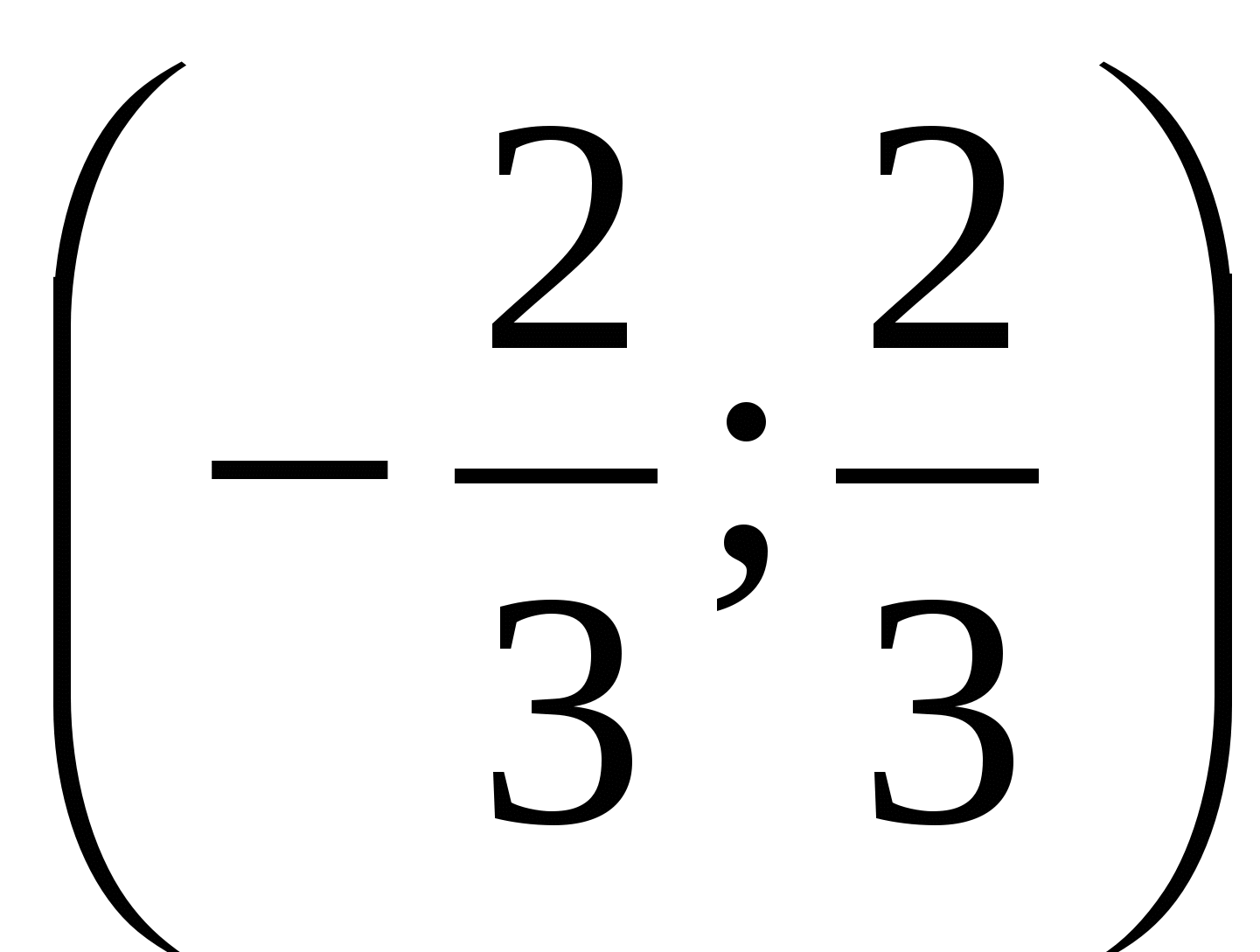
.

Example 7 Let's solve the inequality
.

Solution.

Answer.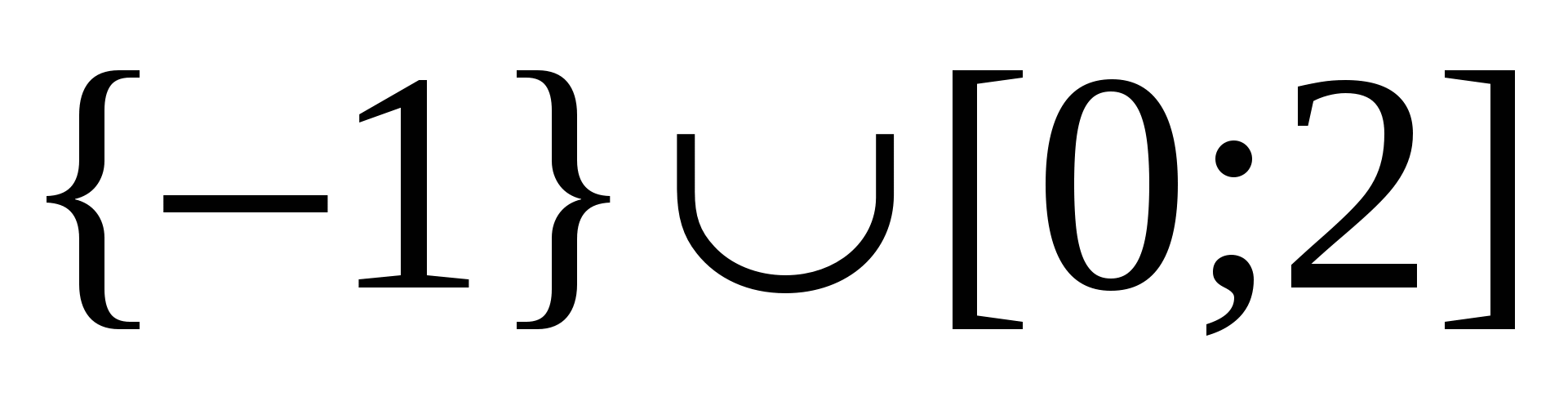
.

Oddly enough, but
is enough to get rid of the modulus sign in any inequalities.

Example 8 Solve inequality

Solution.

Answer.
.

3. Graphical solution of equations and inequalities with modulus

Solving equations containing the sign of an absolute value is often much more convenient to solve not analytically, but graphically (especially equations containing parameters).

Example 9(C5, Unified State Exam - 2010)

C5. For each valuea indicate the number of solutions to the equation

Solution.Let's plot the function
. To do this, select a complete square:

Number of intersection points of the graph of the function y =
with horizontal lines y = a is equal to the number of solutions to the equation.

ABOUT answer: If < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, then there are two solutions.

Other ways to solve equations and inequalities with modulus

• Module Expansion Method

Let's look at the method of expanding modules using an example:

Example 10 Solve the equation

Solution. This equation contains more than one module.

The method for solving equations containing variables under the sign of two or more modules is as follows.

1. Find the values ​​of the variable at which each of the modules becomes zero: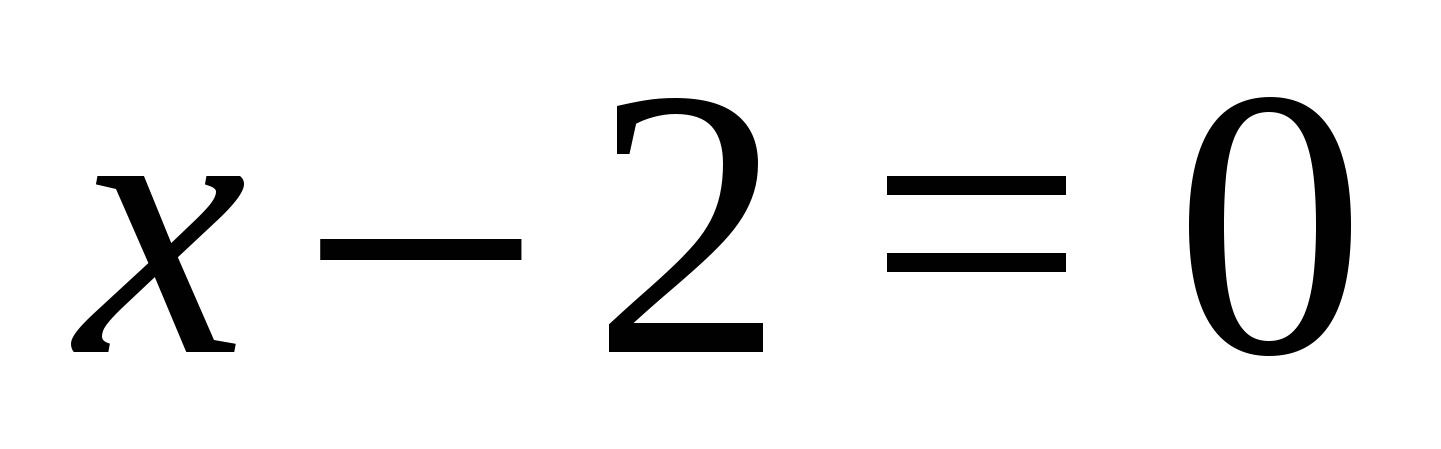
,
;
,
;
,
.

2. Mark these points on the number line.

3. We consider the equation on each of the intervals and set the sign of the expressions that are under the modules.

1) When
or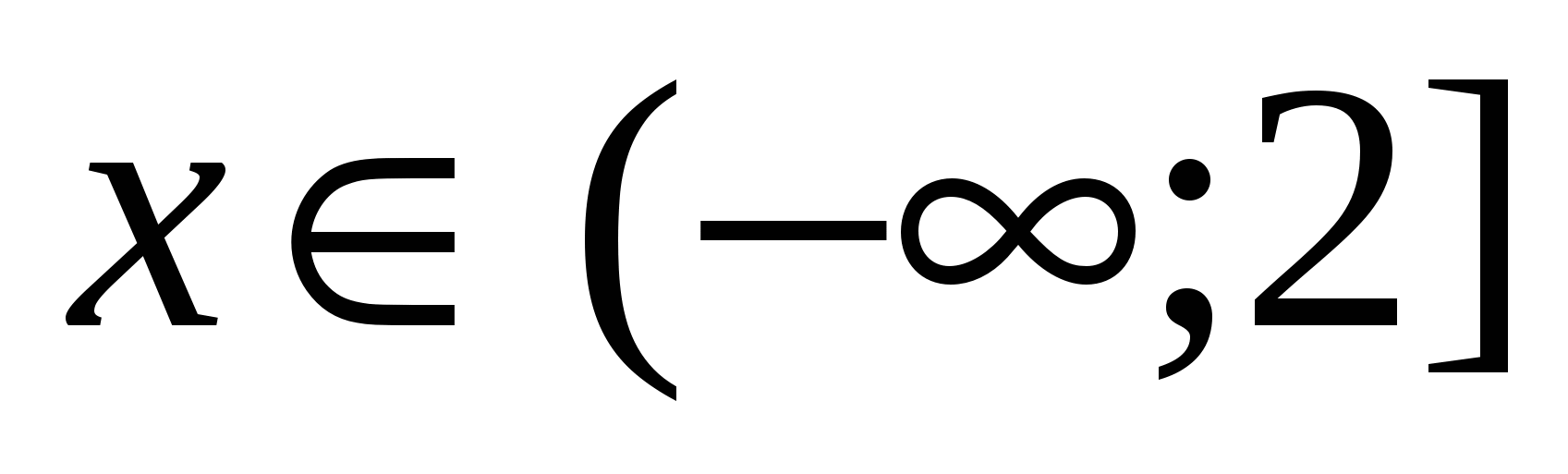
. To determine the sign of each of the modulo expressions on this interval, it is enough to take any value from this interval and substitute it into the expression. If the resulting value is negative, then for all from this interval the expression will be negative; if received numeric value positive, which means for all values from this interval the expression will be positive.

Let's take the value
from between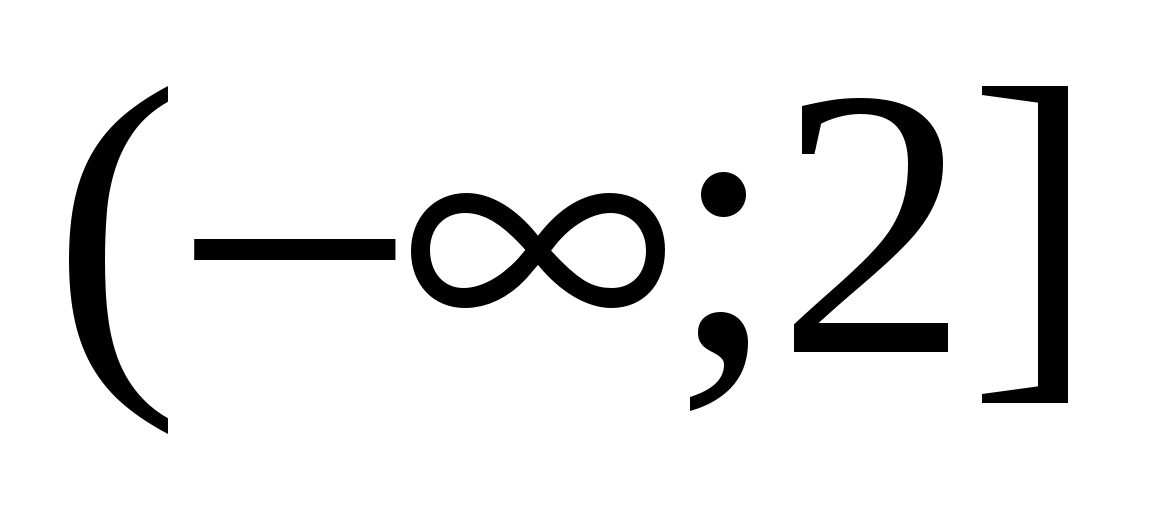
and substitute its value into the expression
, we get
, which means in this interval
negative, and therefore ``will come out"" from under the module with a ``minus" sign", we get:
.

At this value , expression
will get the value
, which means it is in the interval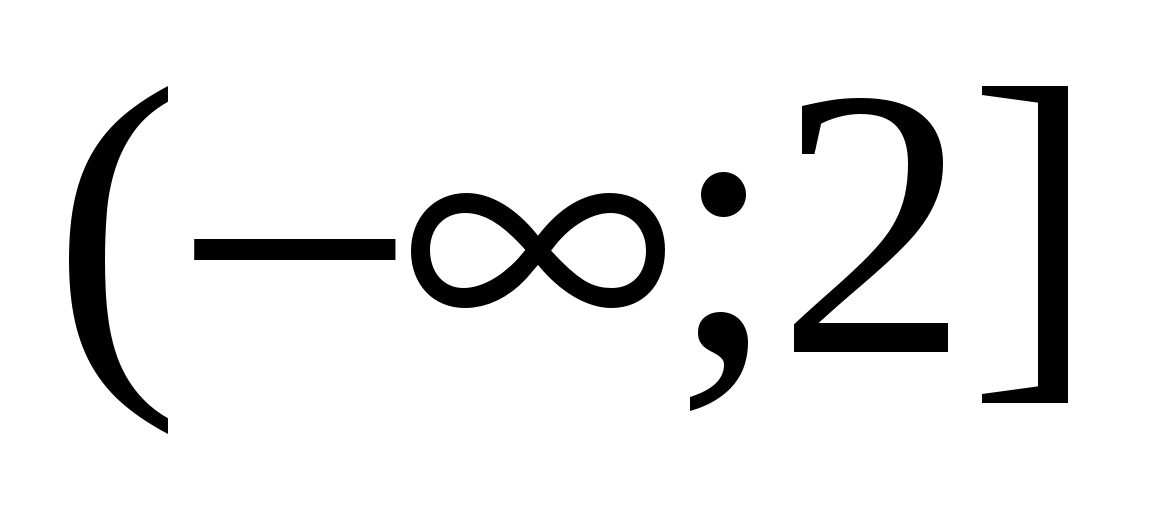
also takes negative values ​​and will ``exit"" the module with a ``minus" sign", we get:
.

Expression
will get the value
and will “exit” from under the module with a ``minus" sign:
.

The equation on this interval will turn out like this: solving it, we find:
.

We find out whether this value is included in the interval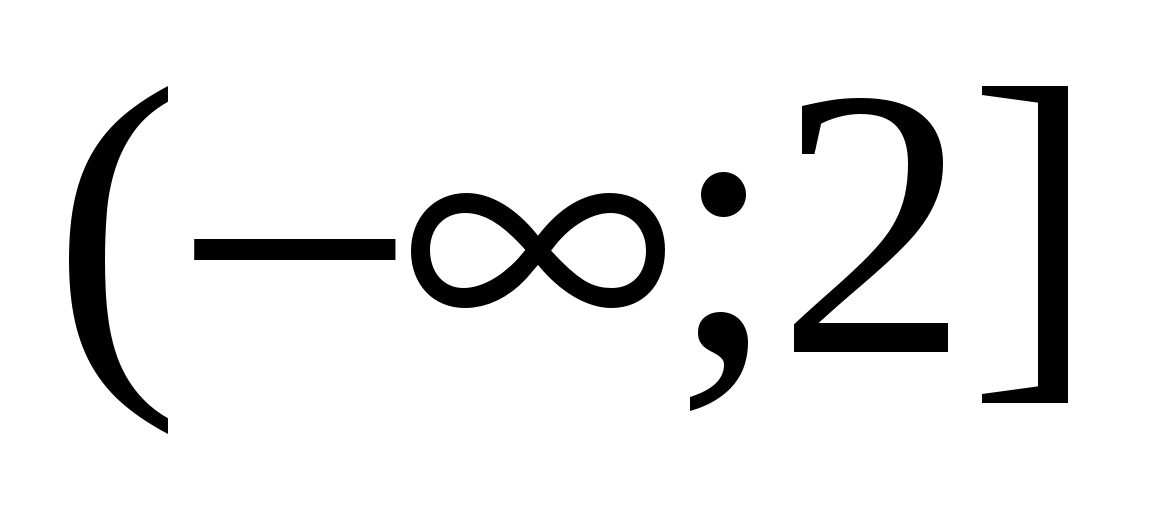
. It turns out that it is included, which means
is the root of the equation.

2) When
. Choose any value from this gap. Let
. We determine the sign of each of the expressions under the modulus at this value . It turns out that the expression
positive and the other two are negative.

The equation on this interval will take the form: . Solving it, we find
. This value is not included in the range
, and therefore is not the root of the equation.

3) When
. Choose an arbitrary value from this interval, let's say
and substitute into each of the expressions. We find that the expressions
And
are positive and
- negative. We get the following equation: .

After transformation, we get:
, which means the equation has no roots on this interval.

4) When
. It is easy to establish that all expressions on this interval are positive, which means we get the equation: ,
,
which is included in the interval and is the root of the equation.

Answer.
,
.

• Solving equations containing moduli of non-negative expressions

Example 11 What is the sum of the roots of the equation (root, if there is one) of the equation

Solution. Consider the expression

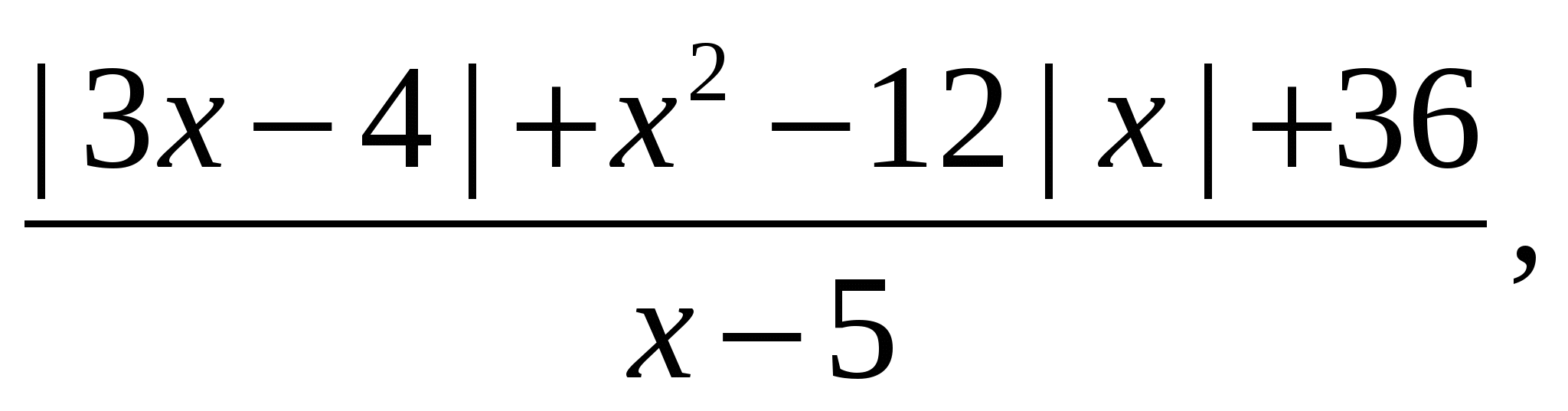and convert it to the form

It is obvious that the numerator of the fraction is a positive number for any value of the variable. This means that a fractional expression is positive if
(because
). Let us transform the resulting expression, provided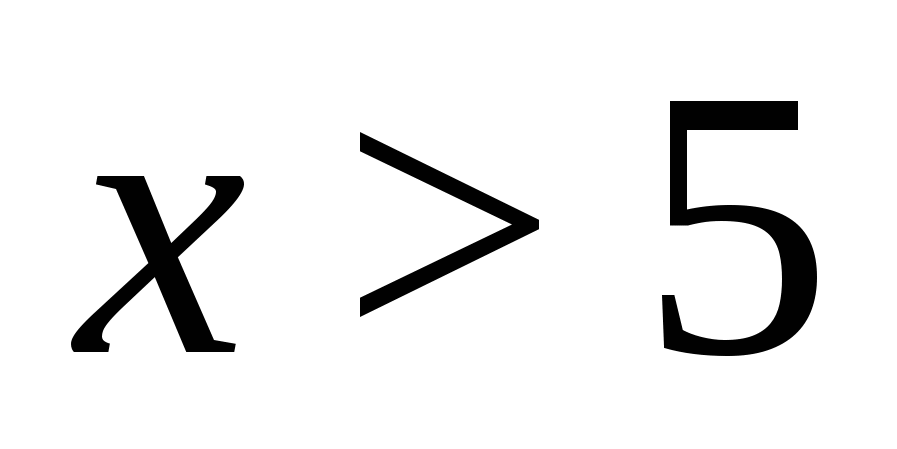
. We obtain an equation equivalent to the original one:

Answer.
.

Example 12 Solve the equation

Solution. Since the left side of the equation is non-negative, for all admissible values ​​of the variable, on the set of roots of the equation its right side must also be non-negative, hence the condition
, on this interval the denominators of both fractions are equal, and it remains to solve the equation
. Solving it and taking into account the constraint
, we get

Answer.
.

• Solving equations using geometric interpretation

Geometric meaning of the expression
- length of the segment of the coordinate axis connecting the points with abscissas And . Translating an algebraic problem into geometric language often allows one to avoid cumbersome calculations.

Example 13 Let's solve the equation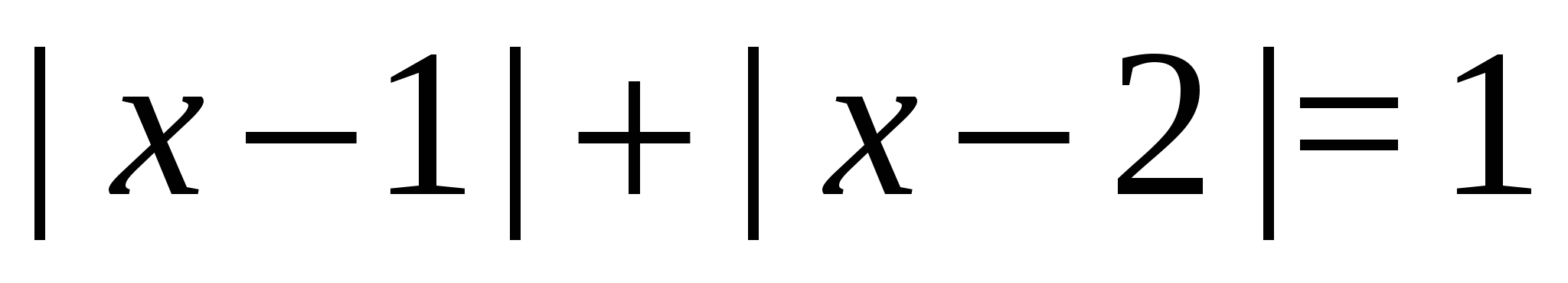
.

Solution. We will reason as follows: based on the geometric interpretation of the module, the left side of the equation is the sum of distances from a certain point with the abscissa to two fixed points with abscissas 1 and 2. Then all points with abscissas from the segment
have the required property, but points located outside this segment do not.

Answer.
.

Example 14 Solve inequality
.

Solution. Let us depict points on the coordinate line, the sum of the distances from which to the points
And exactly equal to . These are all points of the segment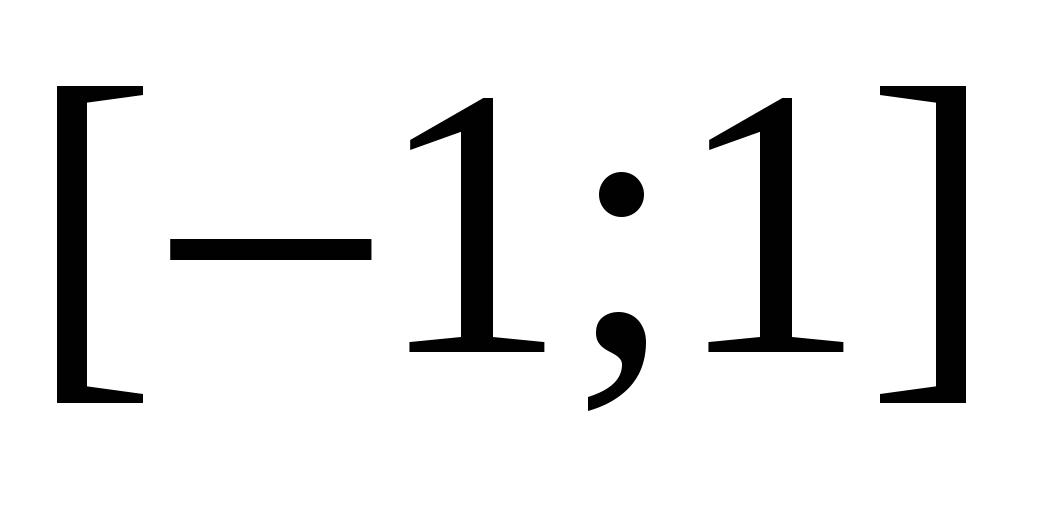
. For all numbers outside of this segment the sum of the distances will be greater than two.

Answer.
.

Example(C3, Unified State Exam - 2010) 15 Solve the equation

Solution. Applying the identity twice
, we get the equation

whose solution is the interval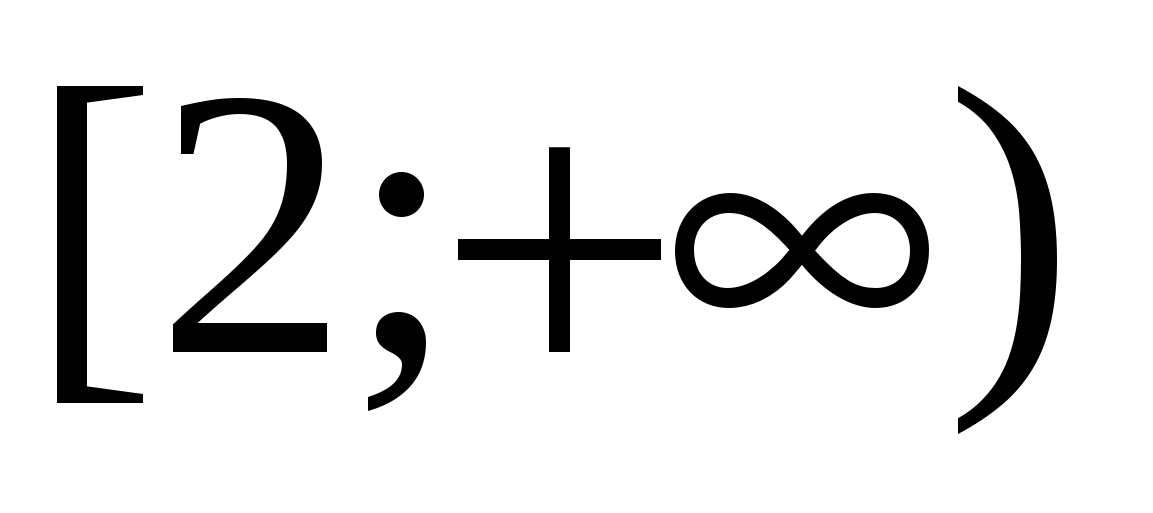
.

Answer.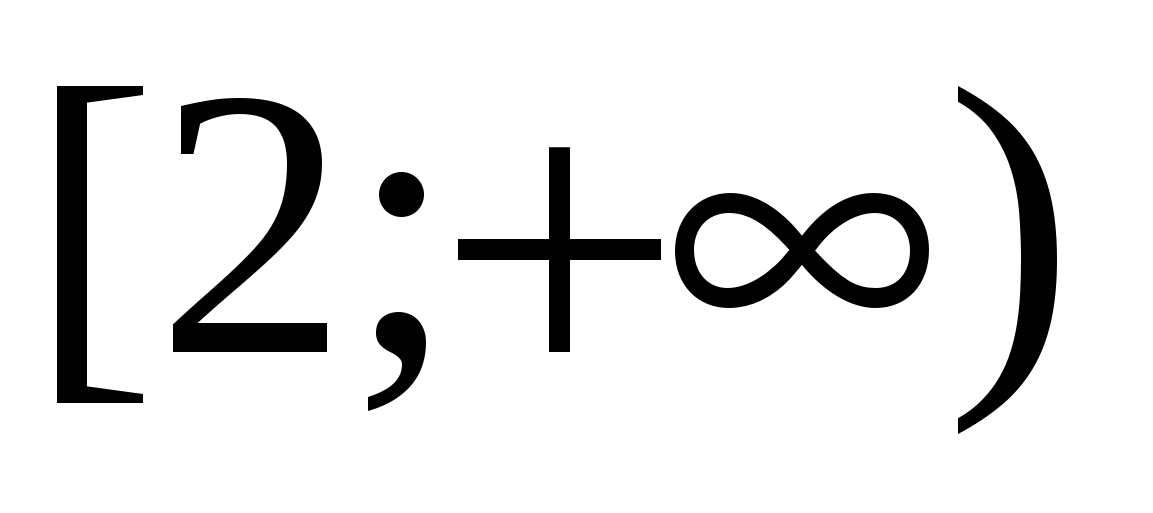
.

Example(C3, Unified State Exam - 2011) 16 17 Solve the equation

Solution. .

Answer.
.

• Application of the sign theorem to solving equations

Let us formulate a theorem convenient for solving inequalities regarding products or quotients of moduli differences:

Theorem 18 The sign of the difference between the moduli of two expressions coincides with the sign of the difference in the squares of these expressions. does not vanish for any value of the variable. This means that throughout the entire domain of definition the function is of constant sign. Calculating, for example,
, we find that the function takes only positive values.

Answer.
.

The interval method allows you to solve more complex equations and inequalities with moduli, but in this case it has a slightly different purpose. The point is as follows. We find the roots of all submodular expressions and divide the numerical axis into intervals of constant sign of these expressions. This allows you, by sequentially going through these intervals, to simultaneously get rid of all modules and solve an ordinary equation or inequality (while checking that the answer found is included in this interval).

• Solving equations by multiplying by a positive factor

Conclusion.

To summarize our work, we can say the following.

The goal of the work was to study various methods for solving equations and inequalities with moduli.

Some varieties of the simplest equations and inequalities with a modulus, solvable using equivalent transitions, as well as the theorem on the sum of moduli, are considered; graphical way to solve equations. It must be said that in school course mathematicians, these are the solution methods that are most often used. The graphical method is especially relevant when solving problems C 5 from control and measuring Unified State Exam materials.

Next, we studied, using several examples, other ways to solve equations and inequalities with modules, namely: the method of revealing modules; solving equations containing moduli of non-negative expressions; solving equations using geometric interpretation; using the identity
; application of the sign theorem; solving equations by going to the consequence, multiplying by a positive factor, as well as solving inequalities by the method of intervals.

Thus, during the study we came to the following conclusions.

We consider the method of revealing modules, the graphical method and the interval method to be the most universal and applicable to the largest number of problems. This belief arose as a result of the decision large number tasks from testing and measuring materials of the Unified State Exam, subject championships, olympiad problems, as well as studying literature on this issue. We also consider the knowledge and application of the identity to be very important
, since it is used not only to solve equations and inequalities, but also to transform many expressions with radicals. The remaining solution methods that we have considered are certainly of great interest in terms of expanding mathematical horizons and general mathematical development. Therefore, we plan to use them to prepare for the state final certification in Unified State Examination form and preparation for studying at a higher educational institution.

Bibliography.

“Big Mathematical Encyclopedia” for schoolchildren and students;

Mathematics. Unified State Examination - 2011, 2012. Model exam options. / Edited by A.L. Semenova, I.V. Yashchenko.

M.Ya. Vygodsky. Handbook of Elementary Mathematics

"The newest schoolchildren's reference book";

Encyclopedia “I explore the world. Mathematics";

;

This article is devoted to techniques for solving various equations and inequalities containing
variable under the modulus sign.

If you come across an equation or inequality with a modulus in the exam, you can solve it by
without knowing any special methods at all and using only the module definition. Is it true,
This may take an hour and a half of precious exam time.

That’s why we want to tell you about techniques that simplify solving such problems.

First of all, let us remember that

Let's consider Various types equations with modulus. (We will move on to inequalities later.)

Module on the left, number on the right

This is the simplest case. Let's solve the equation

There are only two numbers whose modules are equal to four. These are 4 and −4. Therefore the equation
is equivalent to the combination of two simple ones:

The second equation has no solutions. Solutions to the first: x = 0 and x = 5.

Answer: 0; 5.

Variable both under module and outside module

Here we have to expand the module by definition. . . or think!

The equation splits into two cases, depending on the sign of the expression under the modulus.
In other words, it is equivalent to a combination of two systems:

Solution of the first system: . The second system has no solutions.
Answer: 1.

First case: x ≥ 3. Remove the module:

The number, being negative, does not satisfy the condition x ≥ 3 and therefore is not a root of the original equation.

Let's find out if it satisfies this condition number . To do this, we compose the difference and determine its sign:

This means that it is greater than three and therefore is the root of the original equation

Second case: x< 3. Снимаем модуль:

Number . greater than , and therefore does not satisfy the condition x< 3. Проверим :

Means, . is the root of the original equation.

Removing the module by definition? It's scary to even think about it, because the discriminant is not a perfect square. Let's better use the following consideration: an equation of the form |A| = B is equivalent to the combination of two systems:

Same thing, but a little different:

In other words, we solve two equations, A = B and A = −B, and then select roots that satisfy the condition B ≥ 0.

Let's get started. First we solve the first equation:

Then we solve the second equation:

Now in each case we check the sign of the right side:

Therefore, only and are suitable.

Quadratic equations with replacement |x| = t

Let's solve the equation:

Since , it is convenient to make the replacement |x| = t. We get:

Answer: ±1.

Modulus equal to modulus

We are talking about equations of the form |A| = |B|. This is a gift of fate. No module disclosures by definition! It's simple:

For example, consider the equation: . It is equivalent to the following set:

It remains to solve each of the equations of the set and write down the answer.

Two or more modules

Let's solve the equation:

Let's not bother with each module separately and open it by definition - there will be too many options. There is a more rational way - the interval method.

The modulus expressions vanish at the points x = 1, x = 2, and x = 3. These points divide the number line into four intervals (intervals). Let's mark these points on the number line and place signs for each of the expressions under the modules on the resulting intervals. (The order of the signs coincides with the order of the corresponding modules in the equation.)

Thus, we need to consider four cases - when x is in each of the intervals.

Case 1: x ≥ 3. All modules are removed “with a plus”:

The resulting value x = 5 satisfies the condition x ≥ 3 and is therefore the root of the original equation.

Case 2: 2 ≤ x ≤ 3. The last module is now removed “with a minus”:

The resulting value of x is also suitable - it belongs to the interval under consideration.

Case 3: 1 ≤ x ≤ 2. The second and third modules are removed “with a minus”:

We have obtained the correct numerical equality for any x from the interval under consideration; they serve as solutions to this equation.

Case 4: x ≤ 1 ≤ 1. The second and third modules are removed “with a minus”:

Nothing new. We already know that x = 1 is a solution.

Answer: ∪ (5).

Module within a module

Let's solve the equation:

We start by opening the internal module.

1) x ≤ 3. We get:

The expression under the modulus vanishes at . This point belongs to the one in question
between. Therefore, we have to analyze two subcases.

1.1) In this case we get:

This x value is not suitable because it does not belong to the interval under consideration.

1.2) . Then:

This x value is also not good.

So, for x ≤ 3 there are no solutions. Let's move on to the second case.

2) x ≥ 3. We have:

Here we are lucky: the expression x + 2 is positive in the interval under consideration! Therefore, there will no longer be any subcases: the module is removed “with a plus”:

This value of x is in the interval under consideration and is therefore the root of the original equation.

This is how all problems of this type are solved - we open the nested modules one by one, starting with the internal one.