Раньше мы доказывали свойства определенного интеграла, пользуясь его определением, как предела сумм . Совершенно так же можно доказать и основные свойства кратных интегралов. Для простоты мы все функции будем считать непрерывными, так что интегралы от них безусловно имеют смысл.

I. Постоянный множитель можно выносить за знак интеграла, и интеграл от конечной суммы функций равен сумме интегралов от слагаемых:

II. Если область разложена на конечное число частей [например на две части , то интеграл по всей области равен сумме интегралов по всем частям:

III. Если в области , то

В частности :

IV. Если сохраняет знак в области (а), то имеет место теорема о среднем, выражающаяся формулой

где - некоторая точка, лежащая внутри области (а).

В частности, при получаем

где - площадь области .

Аналогичные свойства имеют место и для трехкратного интеграла. Заметим, что при определении двукратного и трехкратного интеграла как предела суммы считается всегда, что область интегрирования конечна и подынтегральная функция во всяком случае ограничена, т. е. существует такое положительное число А, что во всех точках N области интегрирования. Если эти условия не выполнены, то интеграл может существовать как несобственный интеграл аналогично тому, как это имело место для простого определенного интеграла . Мы займемся несобственными кратными интегралами в § 8.

Предостережение.При вычислении несобственных интегралов с особыми точками внутрипромежутка интегрирования нельзямеханически применять формулу Ньютона – Лейбница, поскольку это может привести к ошибкам.

Общее правило: формула Ньютона – Лейбница верна, если первообразная от f(x) в особой точке последней непрерывна.

Пример 2.11.

Рассмотрим несобственный интеграл с особой точкой х = 0. Формула Ньютона–Лейбница, применяемая формально, дает

Однако общее правило здесь не выполняется; для f(x) = 1/x первообразная ln |x| не определена в х = 0 и является бесконечно большой в этой точке, т.е. не является непрерывной в этой точке. Непосредственной проверкой легко убедиться, что интеграл расходится. Действительно,

Полученная неопределенность может быть раскрыта по-разному, поскольку e и d стремятся к нулю независимым образом. В частности, полагая e = d, получаем главное значение несобственного интеграла, равное 0. Если e = 1/n, а d =1/n 2 , т.е. d стремится к 0 быстрее, чем e, то получаем

при и , наоборот,

т.е. интеграл расходится.n

Пример 2.12.

Рассмотрим несобственный интеграл с особой точкой х = 0. Первообразная от функции имеет вид и непрерывна в точке х = 0. Поэтому можно применить формулу Ньютона – Лейбница:

Естественным обобщением понятия определенного интеграла Римана на случай функции нескольких переменных является понятие кратного интеграла. Для случая двух переменных такие интегралы называют двойными.

Рассмотрим в двумерном евклидовом пространстве R ´ R , т.е. на плоскости с декартовой системой координат, множество Е конечной площади S .

Обозначим через (i = 1, …, k ) разбиение множества Е , т.е. такую систему его подмножеств E i , i = 1,. . ., k , что Ø при i ¹ j и (рис. 2.5). Здесь через обозначено подмножество E i без его границы, т.е. внутренние точки подмножества E i , которые вместе с его границей Гр E i образуют замкнутое подмножество E i, . Ясно, что площадь S (E i) подмножества E i совпадает с площадью его внутренней части , поскольку площадь границы ГрE i равна нулю.

Через d(E i) обозначим диаметр множества E i , т.е. максимальное расстояние между двумя его точками. Величину l(t) = d(E i) назовем мелкостью разбиения t. Если функция f(x),x = (x, y), определена на E как функция двух аргументов, то всякую сумму вида

X i Î E i , i = 1, . . . , k, x i = (x i , y i),

зависящую как от функции f и разбиения t , так и от выбора точек x i Î E i Ì t, называют интегральной суммой функции f .

Если для функции f существует ,не зависящий ни от разбиений t , ни от выбора точек (i = 1, …, k), то этот предел называется двойным интегралом Римана от f(x,y) и обозначается

Саму функцию f называют в этом случае интегрируемой по Риману .

Напомним, что в случае функции одного аргумента в качестве множества Е , по которому производится интегрирование, обычно берется отрезок , а в качестве его разбиения t рассматривается разбиение, состоящее из отрезков. В остальном, как нетрудно убедиться, определение двойного интеграла Римана повторяет определение определенного интеграла Римана для функции одного аргумента.

Двойной интеграл Римана от ограниченных функций двух переменных обладает обычными свойствами определенного интеграла для функций одного аргумента – линейностью, аддитивностью относительно множеств, по которым производится интегрирование, сохранение при интегрировании нестрогих неравенств , интегрируемость произведения интегрируемых функций и т.п.

Вычисление кратных интегралов Римана сводится к вычислению повторных интегралов . Рассмотрим случай двойного интеграла Римана. Пусть функция f(x,y) определена на множестве Е, лежащем в декартовом произведении множеств X ´ Y, E Ì X ´ Y.

Повторным интегралом от функции f(x, y) называется интеграл, в котором последовательно выполняется интегрирование по разным переменным, т.е. интеграл вида

Множество E(y) = {x: Î E} Ì X называется сечением множества E, соответствующим заданному y, y Î E y ; множество E y называется – проекцией множества E на ось Y.

Для повторного интеграла используют также такое обозначение:

которое, как и прежнее, означает, что сначала при фиксированном y, y Î E y , проводится интегрирование функции f(x, y) по x по отрезку E (y ), являющемуся сечением множества Е , соответствующим этому y. В результате внутренний интеграл определяет некоторую функцию одной переменной – y. Эта функция интегрируется затем как функция одной переменной, на что указывает символ внешнего интеграла.

При изменении порядка интегрирования получается повторный интеграл вида

где внутреннее интегрирование проводится по y, а внешнее – по x. Как соотносится этот повторный интеграл с повторным интегралом, определенным выше?

Если существует двойной интеграл от функции f , т.е.

то существуют и оба повторных интеграла, причем они одинаковы по величине и равны двойному, т.е.

Подчеркнем, что сформулированное в этом утверждении условие возможности перемены порядка интегрирования в повторных интегралах является лишь достаточным , но не необходимым.

Другие достаточные условия возможности перемены порядка интегрирования в повторных интегралах формулируются следующим образом:

если существует хотя бы один из интегралов

то функция f(x, y) интегрируема по Риману на множестве Е , оба повторных интеграла от нее существуют и равны двойному интегралу. n

Конкретизируем записи проекций и сечений в обозначениях повторных интегралов.

Если множество Е является прямоугольником

то E x = {x: a £ x £ b}, E y = {y: c £ y £ d}; при этом E(y) = E x для любого y, y Î E y . , а E(x) = E y для любого x, x Î E x ..

Формальная запись: "y y Î E y Þ E(y) = E x Ù"x x Î E x Þ E(x) = E y

Если множество Е имеет криволинейную границу и допускает представления

В этом случае повторные интегралы записываются так:

Пример 2.13.

Вычислить двойной интеграл по прямоугольной области, сведя его к повторному .

Поскольку выполняется условие sin 2 (x+ y) =| sin 2 (x + y)|, то проверку выполнимости достаточных условий существования двойного интеграла I в форме существования любого из повторных интегралов

здесь проводить специально не следует и можно сразу переходить к вычислению повторного интеграла

Если он существует, то существует и двойной интеграл, причем I = I 1 . Поскольку

Итак, I = .n

Пример 2.14.

Вычислить двойной интеграл по треугольной области (см. рис. 2.6), сведя его к повторному

Гр(E) = {: x = 0, y = 0, x + y = 2}.

Сначала убедимся в существовании двойного интеграла I. Для этого достаточно убедиться в существовании повторного интеграла

т.е. подынтегральные функции непрерывны на отрезках интегрирования, поскольку все они степенные. Следовательно, интеграл I 1 существует. В этом случае двойной интеграл тоже существует и равен любому повторному, т.е.

Пример 2.15.

Для лучшего понимания связи между понятиями двойного и повторных интегралов рассмотрим следующий пример, который при первом чтении может быть опущен. Задана функция двух переменных f(x, y)

Отметим, что эта функция при фиксированном х нечетна по y , а при фиксированном y – нечетна по x. В качестве множества Е, по которому интегрируется эта функция, возьмем квадрат E = {: -1 £ x £ 1, -1 £ y £ 1 }.

Вначале рассмотрим повторный интеграл

Внутренний интеграл

берется при фиксированном y, -1 £ y £ 1. Поскольку подынтегральная функция при фиксированном y нечетная по x, а интегрирование по этой переменной осуществляется по отрезку [-1, 1], симметричному относительно точки 0, то внутренний интеграл равен 0. Очевидно, что внешний интеграл по переменной y от нулевой функции также равен 0, т.е.

Аналогичные рассуждения для второго повторного интеграла приводят к тому же результату:

Итак, для рассматриваемой функции f(x, y) повторные интегралы существуют и равны друг другу. Однако двойной интеграл от функции f(x, y) не существует. Чтобы убедиться в этом, обратимся к геометрическому смыслу вычисления повторных интегралов.

Для вычисления повторного интеграла

используется разбиение квадрата Е специального вида, равно как и специальным образом проводимый подсчет интегральных сумм. Именно, квадрат Е разбивается на горизонтальные полосы, (см. рис.2.7), а каждая полоса – на маленькие прямоугольники. Каждая полоска соответствует некоторому значению переменной y; например, это может быть ордината горизонтальной оси полосы.

Подсчет интегральных сумм производится так: сначала подсчитывается суммы для каждой полосы в отдельности, т.е. при фиксированном y для разных x, а затем эти промежуточные суммы суммируются для разных полос, т.е. для разных y. Если мелкость разбиения устремить к нулю, то в пределе мы получим указанный выше повторный интеграл.

Ясно, что для второго повторного интеграла

множество Е разбивается вертикальными полосами, соответствующими разным x. Промежуточные суммы подсчитываются внутри каждой полосы по маленьким прямоугольникам, т.е. по y, а затем они суммируются для разных полос, т.е. по х. В пределе, при мелкости разбиения, стремящейся к нулю, получаем соответствующий повторный интеграл.

Чтобы доказать, что двойной интеграл не существует, достаточно привести один пример разбиения, расчет интегральных сумм по которому в пределе при мелкости разбиения, стремящейся к нулю, дает результат, отличный от значения повторных интегралов. Приведем пример такого разбиения, соответствующего полярной системе координат (r, j) (см. рис. 2.8).

В полярной системе координат положение любой точки на плоскости М 0 (x 0 , y 0), где x 0 ,y 0 – декартовы координаты точки М 0 – определяется длиной r 0 радиуса, соединяющего ее с началом координат и углом j 0 , образуемым этим радиусом с положительным направлением оси x (угол отсчитывается против часовой стрелки). Связь между декартовыми и полярными координатами очевидна:

y 0 = r 0 × sinj 0 .

Разбиение строится следующим образом. Сначала квадрат Е разбивается на сектора радиусами, исходящими из центра координат, а затем каждый сектор – на маленькие трапеции линиями, перпендикулярными оси сектора. Подсчет интегральных сумм проводится так: сначала по маленьким трапециям внутри каждого сектора вдоль его оси (по r), а затем – по всем секторам (по j) . Положение каждого сектора характеризуется углом его оси j, а длина его оси r(j) зависит от этого угла:

если или , то ;

если , то ;

если , то

если , то .

Переходя к пределу интегральных сумм полярного разбиения при мелкости разбиения, стремящейся к нулю, получим запись двойного интеграла в полярных координатах. Такую запись можно получить и чисто формальным образом, заменяя декартовы координаты (x, y) на полярные (r, j).

По правилам перехода в интегралах от декартовых координат к полярным следует писать, по определению:

В полярных координатах функция f(x, y) запишется так:

Окончательно имеем

Внутренний интеграл (несобственный) в последней формуле

где функция r(j) указана выше, 0 £ j £ 2p , равен +¥ для любого j, ибо

Следовательно, подынтегральная функция во внешнем интеграле, вычисляемом по j, не определена ни для какого j . Но тогда не определен и сам внешний интеграл, т.е. не определен исходный двойной интеграл.

Отметим, что для функции f(x, y) не выполнено достаточное условие существования двойного интеграла по множеству Е. Покажем, что интеграл

не существует. Действительно,

Аналогично устанавливается такой же результат для интеграла

Скачать с Depositfiles

Лекции 5-6

Тема2. Кратные интегралы.

Двойной интеграл.

Контрольные вопросы.

1. Двойной интеграл, его геометрический и физический смысл

2. Свойства двойного интеграла.

3. Вычисление двойного интеграла в декартовых координатах.

4. Замена переменных в двойном интеграле. Вычисление двойного интеграла в полярных координатах.

Пусть функция z = f (x , y ) определена в ограниченной замкнутой области D плоскости. Разобьём область D произвольным образом на n элементарных замкнутых областей  1 , … , n , имеющих площади   1 , …,   n и диаметры d 1 , …, d n соответственно. Обозначим d наибольший из диаметров областей  1 , … ,  n . В каждой области  k выберем произвольную точку P k (x k ,y k ) и составим интегральную сумму функции f (x,y )

S =
(1)

Определение. Двойным интегралом функции f (x,y ) по области D называется предел интегральной суммы

, (2)

если он существует.

Замечание. Интегральная сумма S зависит от способа разбиения области D и выбора точек P k (k =1, …, n ). Однако, предел
, если он существует, не зависит от способа разбиения области D и выбора точек P k .

Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f (x,y ) непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в D . В дальнейшем будем считать, что все рассматриваемые двойные интегралы существуют.

Геометрический смысл двойного интеграла.

Если f (x,y ) ≥0 в области D , то двойной интеграл (1) равен объему «цилиндрического” тела, изображенного на рисунке:

V =
(3)

Цилиндрическое тело ограничено снизу областью D , сверху  частью поверхности z = f (x , y ), с боков  вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.

Физический смысл двойного интеграла. Масса плоской пластины.

Пусть задана плоская пластина D с известной функцией плотности γ(х, у ), тогда разбивая пластину D на части D i и выбирая произвольные точки
, получим для массы пластины
, или, сравнивая с формулой (2):

(4)

4. Некоторые свойства двойного интеграла.

Линейность. Если С – числовая константа, то

Аддитивность. Если область D « разбита” на области D 1 и D 2 , то

3) Площадь ограниченной области D равна

(5)

Вычисление двойного интеграла в декартовых координатах.

Пусть задана область

Рисунок 1

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Область D заключена в полосе между прямыми x = a , y = b , снизу и сверху ограничена соответственно кривыми y = φ 1 (x ) и y = φ 2 (x ) .

Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:

(7)

Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутреннийинтеграл

по переменной y , п ри этомx считаетсяпостоянной. В результате получится функция от переменной x , а затем вычисляется « внешний” интеграл от этой функции по переменной x .

Замечание. Процесс перехода к повторному интегралу по формуле (7) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.

Пусть теперь область D имеет вид

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Тогда

. (9)

Предположим, что область D можно представить в виде (6) и (8) одновременно. Тогда имеет место равенство

(10)

Переход од одного повторного интеграла к другому в равенстве (10) называется изменением порядка интегрирования в двойном интеграле.

Примеры.

1) Изменить порядок интегрирования в интеграле

Решение. По виду повторного интеграла находим область

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Изобразим область D . По рисунку видим, что эта область расположена в горизонтальной полосе между прямыми y =0, y =2 и между линиями x =0 и x = D

Иногда для упрощения вычислений делают замену переменных:

,
(11)

Если функции (11) непрерывно дифференцируемы и определитель (Якобиан) отличен от нуля в рассматриваемой области:

(12)

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

.

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

.

Пример 2. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

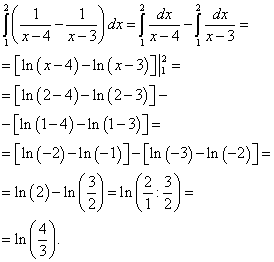
Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

.

Вычисляем первое слагаемое:

Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

.

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

.

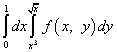Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

.

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

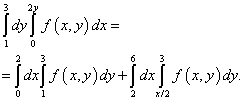
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .