How to draw a four-dimensional cube. A program for drawing a four-dimensional cube. What is a tesseract
As soon as I was able to give lectures after the operation, the first question the students asked was:
When will you draw us a 4-dimensional cube? Ilyas Abdulkhaevich promised us!
I remember that my dear friends sometimes like a moment of mathematical educational activities. Therefore, I will write a part of my lecture for mathematicians here. And I will try without being boring. At some points I read the lecture more strictly, of course.
Let's agree first. 4-dimensional, and even more so 5-6-7- and generally k-dimensional space is not given to us in sensory sensations.
“We are wretched because we are only three-dimensional,” as my Sunday school teacher, who first told me what a 4-dimensional cube is, said. Sunday school was, naturally, extremely religious - mathematical. That time we were studying hyper-cubes. A week before this, mathematical induction, a week after that, Hamiltonian cycles in graphs - accordingly, this is 7th grade.
We cannot touch, smell, hear or see a 4-dimensional cube. What can we do with it? We can imagine it! Because our brain is much more complex than our eyes and hands.
So, in order to understand what a 4-dimensional cube is, let's first understand what is available to us. What is a 3-dimensional cube?
OK OK! I'm not asking you for a clear mathematical definition. Just imagine the simplest and most ordinary three-dimensional cube. Introduced?
Fine.
In order to understand how to generalize a 3-dimensional cube into a 4-dimensional space, let's figure out what a 2-dimensional cube is. It's so simple - it's a square! 
A square has 2 coordinates. The cube has three. Square points are points with two coordinates. The first is from 0 to 1. And the second is from 0 to 1. The points of the cube have three coordinates. And each is any number from 0 to 1.
It is logical to imagine that a 4-dimensional cube is a thing that has 4 coordinates and everything is from 0 to 1.
/* It’s immediately logical to imagine a 1-dimensional cube, which is nothing more than a simple segment from 0 to 1. */
So, wait, how do you draw a 4-dimensional cube? After all, we cannot draw 4-dimensional space on a plane!
But we don’t draw 3-dimensional space on a plane either, we draw it projection onto a 2-dimensional drawing plane. We place the third coordinate (z) at an angle, imagining that the axis from the drawing plane goes “towards us”. 
Now it is completely clear how to draw a 4-dimensional cube. In the same way that we positioned the third axis at a certain angle, let’s take the fourth axis and also position it at a certain angle.
And - voila! -- projection of a 4-dimensional cube onto a plane. 
What? What is this anyway? I always hear whispers from the back desks. Let me explain in more detail what this jumble of lines is.
Look first at the three-dimensional cube. What have we done? We took the square and dragged it along the third axis (z). It's like many, many paper squares glued together in a stack.
It's the same with a 4-dimensional cube. Let's call the fourth axis, for convenience and for science fiction, the “time axis.” We need to take an ordinary three-dimensional cube and drag it through time from the time “now” to the time “in an hour.”
We have a "now" cube. In the picture it is pink. 
And now we drag it along the fourth axis - along the time axis (I showed it in green). And we get the cube of the future - blue. 
Each vertex of the “cube now” leaves a trace in time - a segment. Connecting her present with her future.
In short, without any lyrics: we drew two identical 3-dimensional cubes and connected the corresponding vertices.
Exactly the same as they did with a 3-dimensional cube (draw 2 identical 2-dimensional cubes and connect the vertices).
To draw a 5-dimensional cube, you will have to draw two copies of a 4-dimensional cube (a 4-dimensional cube with fifth coordinate 0 and a 4-dimensional cube with fifth coordinate 1) and connect the corresponding vertices with edges. True, there will be such a jumble of edges on the plane that it will be almost impossible to understand anything.
Once we have imagined a 4-dimensional cube and even been able to draw it, we can explore it in different ways. Remembering to explore it both in your mind and from the picture.
For example. A 2-dimensional cube is bounded on 4 sides by 1-dimensional cubes. This is logical: for each of the 2 coordinates it has both a beginning and an end.
A 3-dimensional cube is bounded on 6 sides by 2-dimensional cubes. For each of the three coordinates it has a beginning and an end.
This means that a 4-dimensional cube must be limited by eight 3-dimensional cubes. For each of the 4 coordinates - on both sides. In the figure above we clearly see 2 faces that limit it along the “time” coordinate.
Here are two cubes (they are slightly oblique because they have 2 dimensions projected onto the plane at an angle), limiting our hypercube on the left and right. 
It is also easy to notice “upper” and “lower”. 
The most difficult thing is to understand visually where “front” and “rear” are. The front one starts from the front edge of the “cube now” and to the front edge of the “cube of the future” - it is red. The rear one is purple. 
They are the most difficult to notice because other cubes are tangled under your feet, which limit the hypercube at a different projected coordinate. But note that the cubes are still different! Here is the picture again, where the “cube of now” and the “cube of the future” are highlighted. 
Of course, it is possible to project a 4-dimensional cube into 3-dimensional space.
The first possible spatial model is clear what it looks like: you need to take 2 cube frames and connect their corresponding vertices with a new edge.
I don't have this model in stock right now. At the lecture, I show students a slightly different 3-dimensional model of a 4-dimensional cube.
You know how a cube is projected onto a plane like this.
It's like we're looking at a cube from above. 
The near edge is, of course, large. And the far edge looks smaller, we see it through the near one.
This is how you can project a 4-dimensional cube. The cube is larger now, we see the cube of the future in the distance, so it looks smaller. 
On the other side. From the top side. 
Directly exactly from the side of the edge: 
From the rib side: 
And the last angle, asymmetrical. From the section “tell me that I looked between his ribs.” 
Well, then you can come up with anything. For example, just as there is a development of a 3-dimensional cube onto a plane (it’s like cutting out a sheet of paper so that when folded you get a cube), the same happens with the development of a 4-dimensional cube into space. It's like cutting out a piece of wood so that by folding it in 4-dimensional space we get a tesseract.
You can study not just a 4-dimensional cube, but n-dimensional cubes in general. For example, is it true that the radius of a sphere circumscribed around an n-dimensional cube is less than the length of the edge of this cube? Or here’s a simpler question: how many vertices does an n-dimensional cube have? How many edges (1-dimensional faces)?
Tesseract (from ancient Greek τέσσερες ἀκτῖνες - four rays) is a four-dimensional hypercube - an analogue of a cube in four-dimensional space.
The image is a projection (perspective) of a four-dimensional cube onto three-dimensional space.
According to the Oxford Dictionary, the word "tesseract" was coined and used in 1888 by Charles Howard Hinton (1853–1907) in his book New era thoughts". Later, some people called the same figure a "tetracube".
Geometry
An ordinary tesseract in Euclidean four-dimensional space is defined as a convex hull of points (±1, ±1, ±1, ±1). In other words, it can be represented as the following set:
The tesseract is limited by eight hyperplanes, the intersection of which with the tesseract itself defines its three-dimensional faces (which are ordinary cubes). Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, the tesseract has 8 3D faces, 24 2D faces, 32 edges and 16 vertices.
Popular description
Let's try to imagine what a hypercube will look like without leaving three-dimensional space.
In a one-dimensional “space” - on a line - we select a segment AB of length L. On a two-dimensional plane at a distance L from AB, we draw a segment DC parallel to it and connect their ends. The result is a square ABCD. Repeating this operation with the plane, we obtain a three-dimensional cube ABCDHEFG. And by shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG
The one-dimensional segment AB serves as the side of the two-dimensional square ABCD, the square - as the side of the cube ABCDHEFG, which, in turn, will be the side of the four-dimensional hypercube. A straight line segment has two boundary points, a square has four vertices, and a cube has eight. In a four-dimensional hypercube, there will thus be 16 vertices: 8 vertices of the original cube and 8 of the one shifted in the fourth dimension. It has 32 edges - 12 each give the initial and final positions of the original cube, and another 8 edges “draw” its eight vertices, which have moved to the fourth dimension. The same reasoning can be done for the faces of a hypercube. In two-dimensional space there is only one (the square itself), a cube has 6 of them (two faces from the moved square and four more that describe its sides). A four-dimensional hypercube has 24 square faces - 12 squares of the original cube in two positions and 12 squares from its twelve edges.
Similarly, we can continue the reasoning for hypercubes more dimensions, but it is much more interesting to see how a four-dimensional hypercube will look for us, residents of three-dimensional space. For this we will use the already familiar method of analogies.
Tesseract unwrapping
Let's take the wire cube ABCDHEFG and look at it with one eye from the side of the edge. We will see and can draw two squares on the plane (its near and far edges), connected by four lines - side edges. Similarly, a four-dimensional hypercube in space three dimensions will look like two cubic “boxes” inserted into each other and connected by eight edges. In this case, the “boxes” themselves - three-dimensional faces - will be projected onto “our” space, and the lines connecting them will stretch in the fourth dimension. You can also try to imagine the cube not in projection, but in a spatial image.
Just as a three-dimensional cube is formed by a square shifted by the length of its face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in perspective will look like some rather complex figure. The part that remained in “our” space is drawn with solid lines, and the part that went into hyperspace is drawn with dotted lines. The four-dimensional hypercube itself consists of an infinite number of cubes, just as a three-dimensional cube can be “cut” into an infinite number of flat squares.
By cutting the six faces of a three-dimensional cube, you can decompose it into a flat figure - a development. It will have a square on each side of the original face, plus one more - the face opposite to it. And the three-dimensional development of a four-dimensional hypercube will consist of the original cube, six cubes “growing” from it, plus one more - the final “hyperface”.
The properties of the tesseract are an extension of the properties geometric shapes smaller dimension into four-dimensional space.
Projections
To two-dimensional space
This structure is difficult to imagine, but it is possible to project a tesseract into two-dimensional or three-dimensional spaces. In addition, projecting onto a plane makes it easy to understand the location of the vertices of a hypercube. In this way, it is possible to obtain images that no longer reflect the spatial relationships within the tesseract, but which illustrate the vertex connection structure, as in the following examples:
To three-dimensional space
The projection of a tesseract onto three-dimensional space represents two nested three-dimensional cubes, the corresponding vertices of which are connected by segments. The inner and outer cubes have different sizes in three-dimensional space, but in four-dimensional space they are equal cubes. To understand the equality of all tesseract cubes, a rotating tesseract model was created.
The six truncated pyramids along the edges of the tesseract are images of equal six cubes.
Stereo pair
A stereo pair of a tesseract is depicted as two projections onto three-dimensional space. This image of the tesseract was designed to represent depth as a fourth dimension. The stereo pair is viewed so that each eye sees only one of these images, a stereoscopic picture appears that reproduces the depth of the tesseract.
Tesseract unwrapping
The surface of a tesseract can be unfolded into eight cubes (similar to how the surface of a cube can be unfolded into six squares). There are 261 different tesseract designs. The unfolding of a tesseract can be calculated by plotting the connected angles on a graph.
Tesseract in art
In Edwina A.'s "New Abbott Plain", the hypercube acts as a narrator.
In one episode of The Adventures of Jimmy Neutron: "Boy Genius", Jimmy invents a four-dimensional hypercube identical to the foldbox from Heinlein's 1963 novel Glory Road.
Robert E. Heinlein has mentioned hypercubes in at least three science fiction stories. In The House of Four Dimensions (The House That Teal Built) (1940), he described a house built like an unwrapped tesseract.
Heinlein's novel Glory Road describes hyper-sized dishes that were larger on the inside than on the outside.
Henry Kuttner's story "Mimsy Were the Borogoves" describes an educational toy for children from the distant future, similar in structure to a tesseract.
In the novel by Alex Garland (1999), the term "tesseract" is used for the three-dimensional unfolding of a four-dimensional hypercube, rather than the hypercube itself. This is a metaphor designed to show that the cognitive system must be broader than the knowable.
The plot of Cube 2: Hypercube centers on eight strangers trapped in a "hypercube", or network of connected cubes.
The television series Andromeda uses tesseract generators as a plot device. They are primarily designed to manipulate space and time.
Painting “The Crucifixion” (Corpus Hypercubus) by Salvador Dali (1954)
The Nextwave comic book depicts a vehicle that includes 5 tesseract zones.
In the album Voivod Nothingface one of the compositions is called “In my hypercube”.
In Anthony Pearce's novel Route Cube, one of the International Development Association's orbiting moons is called a tesseract that has been compressed into 3 dimensions.
In the series “Black Hole School” in the third season there is an episode “Tesseract”. Lucas presses a secret button and the school begins to take shape like a mathematical tesseract.
The term “tesseract” and its derivative term “tesserate” are found in the story “A Wrinkle in Time” by Madeleine L’Engle.
In geometry hypercube- This n-dimensional analogy of a square ( n= 2) and cube ( n= 3). It is a closed convex figure consisting of groups of parallel lines located on opposite edges of the figure, and connected to each other at right angles.
This figure is also known as tesseract(tesseract). The tesseract is to the cube as the cube is to the square. More formally, a tesseract can be described as a regular convex four-dimensional polytope (polyhedron) whose boundary consists of eight cubic cells.
According to the Oxford English Dictionary, the word "tesseract" was coined in 1888 by Charles Howard Hinton and used in his book "A New Era of Thought." The word was derived from the Greek "τεσσερες ακτινες" ("four rays"), in the form of four coordinate axes. In addition, in some sources, the same figure was called tetracube(tetracube).
n-dimensional hypercube is also called n-cube.

A point is a hypercube of dimension 0. If you shift the point by a unit of length, you get a segment of unit length - a hypercube of dimension 1. Further, if you shift the segment by a unit of length in a direction perpendicular to the direction of the segment, you get a cube - a hypercube of dimension 2. Shifting the square by a unit of length in the direction perpendicular to the plane of the square, a cube is obtained - a hypercube of dimension 3. This process can be generalized to any number of dimensions. For example, if you move a cube by one unit of length in the fourth dimension, you get a tesseract.
The hypercube family is one of the few regular polyhedra that can be represented in any dimension.
Elements of a hypercube
Dimension hypercube n has 2 n“sides” (a one-dimensional line has 2 points; a two-dimensional square has 4 sides; a three-dimensional cube has 6 faces; a four-dimensional tesseract has 8 cells). The number of vertices (points) of a hypercube is 2 n(for example, for a cube - 2 3 vertices).
Quantity m-dimensional hypercubes on the boundary n-cube equals
For example, on the boundary of a hypercube there are 8 cubes, 24 squares, 32 edges and 16 vertices.
| n-cube | Name | Vertex (0-face) |
Edge (1-face) |
Edge (2-face) |
Cell (3-face) |
(4-face) | (5-face) | (6-sided) | (7-face) | (8-face) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube | Dot | 1 | ||||||||
| 1-cube | Line segment | 2 | 1 | |||||||
| 2-cube | Square | 4 | 4 | 1 | ||||||
| 3-cube | Cube | 8 | 12 | 6 | 1 | |||||
| 4-cube | Tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5-cube | Penteract | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-cube | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-cube | Hepteract | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-cube | Octeract | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-cube | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projection onto a plane
The formation of a hypercube can be represented in the following way:
- Two points A and B can be connected to form a line segment AB.
- Two parallel segments AB and CD can be connected to form a square ABCD.
- Two parallel squares ABCD and EFGH can be connected to form a cube ABCDEFGH.
- Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to form the hypercube ABCDEFGHIJKLMNOP.
The latter structure is not easy to visualize, but it is possible to depict its projection into two-dimensional or three-dimensional space. Moreover, projections onto a two-dimensional plane can be more useful by allowing the positions of the projected vertices to be rearranged. In this case, it is possible to obtain images that no longer reflect the spatial relationships of the elements within the tesseract, but illustrate the structure of the vertex connections, as in the examples below.
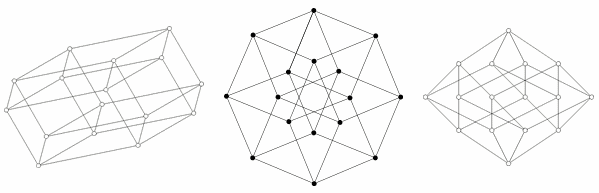
The first illustration shows how, in principle, a tesseract is formed by joining two cubes. This scheme is similar to the scheme for creating a cube from two squares. The second diagram shows that all the edges of the tesseract are the same length. This scheme also forces you to look for cubes connected to each other. In the third diagram, the vertices of the tesseract are located in accordance with the distances along the faces relative to the bottom point. This scheme is interesting because it is used as a basic scheme for the network topology of connecting processors when organizing parallel computing: the distance between any two nodes does not exceed 4 edge lengths, and there are many different paths for balancing the load.
Hypercube in art
The hypercube has appeared in science fiction literature since 1940, when Robert Heinlein, in the story “And He Built a Crooked House,” described a house built in the shape of a tesseract scan. In the story, this Next, this house collapses, turning into a four-dimensional tesseract. After this, the hypercube appears in many books and short stories.
The movie Cube 2: Hypercube is about eight people trapped in a network of hypercubes.
Salvador Dali's painting "Crucifixion (Corpus Hypercubus)", 1954, depicts Jesus crucified on a tesseract scan. This painting can be seen in the Metropolitan Museum of Art in New York.
Conclusion
A hypercube is one of the simplest four-dimensional objects, on the example of which you can see all the complexity and unusualness fourth dimension. And what looks impossible in three dimensions is possible in four, for example, impossible figures. So, for example, the bars of an impossible triangle in four dimensions will be connected at right angles. And this figure will look like this from all viewing points, and will not be distorted, unlike the implementations of an impossible triangle in three-dimensional space (see.
Let's start by explaining what four-dimensional space is.
This is a one-dimensional space, that is, simply the OX axis. Any point on it is characterized by one coordinate.

Now let's draw the OY axis perpendicular to the OX axis. So we get a two-dimensional space, that is, the XOY plane. Any point on it is characterized by two coordinates - abscissa and ordinate.

Let's draw the OZ axis perpendicular to the OX and OY axes. The result is a three-dimensional space in which any point has an abscissa, ordinate and applicate.

It is logical that the fourth axis, OQ, should be perpendicular to the OX, OY and OZ axes at the same time. But we cannot accurately construct such an axis, and therefore we can only try to imagine it. Every point in four-dimensional space has four coordinates: x, y, z and q.
Now let's see how the four-dimensional cube appeared.

The picture shows a figure in one-dimensional space - a line.

If you make a parallel translation of this line along the OY axis, and then connect the corresponding ends of the two resulting lines, you will get a square.

Similarly, if you make a parallel translation of the square along the OZ axis and connect the corresponding vertices, you will get a cube.

And if we make a parallel translation of the cube along the OQ axis and connect the vertices of these two cubes, then we will get a four-dimensional cube. By the way, it's called tesseract.
To draw a cube on a plane, you need it project. Visually it looks like this: 
Let's imagine that it is hanging in the air above the surface wireframe model cube, that is, as if “made of wire,” and above it is a light bulb. If you turn on the light bulb, trace the shadow of the cube with a pencil, and then turn off the light bulb, a projection of the cube will be depicted on the surface.
Let's move on to something a little more complex. Look again at the drawing with the light bulb: as you can see, all the rays converge at one point. It is called vanishing point and is used to build perspective projection(and it can also be parallel, when all the rays are parallel to each other. The result is that the sensation of volume is not created, but it is lighter, and moreover, if the vanishing point is quite far removed from the projected object, then the difference between these two projections is little noticeable). To project a given point onto given plane, using the vanishing point, you need to draw a straight line through the vanishing point and the given point, and then find the intersection point of the resulting straight line and the plane. And in order to project a more complex figure, say, a cube, you need to project each of its vertices, and then connect the corresponding points. It should be noted that algorithm for projecting space onto subspace can be generalized to the case of 4D->3D, not just 3D->2D.
As I said, we can't imagine exactly what the OQ axis looks like, just like the tesseract. But we can get a limited idea of it if we project it onto a volume and then draw it on a computer screen!
Now let's talk about the tesseract projection.

On the left is the projection of the cube onto the plane, and on the right is the tesseract onto the volume. They are quite similar: the projection of a cube looks like two squares, small and large, one inside the other, and whose corresponding vertices are connected by lines. And the projection of the tesseract looks like two cubes, small and large, one inside the other, and whose corresponding vertices are connected. But we have all seen a cube, and we can say with confidence that both a small square and a large one, and four trapezoids above, below, to the right and left of small square, are actually squares, and they are equal. And the tesseract has the same thing. And a large cube, and a small cube, and six truncated pyramids on the sides of a small cube - these are all cubes, and they are equal.
My program can not only draw the projection of a tesseract onto a volume, but also rotate it. Let's look at how this is done.
First, I'll tell you what it is rotation parallel to the plane.
Imagine that the cube rotates around the OZ axis. Then each of its vertices describes a circle around the OZ axis. 
A circle is a flat figure. And the planes of each of these circles are parallel to each other, and in in this case parallel to the XOY plane. That is, we can talk not only about rotation around the OZ axis, but also about rotation parallel to the XOY plane. As we see, for points that rotate parallel to the XOY axis, only the abscissa and ordinate change, while the applicate remains unchanged. And, in fact, we we can talk about rotation around a straight line only when we are dealing with three-dimensional space. In two-dimensional space everything rotates around a point, in four-dimensional space everything rotates around a plane, in five-dimensional space we talk about rotation around a volume. And if we can imagine rotation around a point, then rotation around a plane and volume is something unthinkable. And if we talk about rotation parallel to the plane, then in any n-dimensional space a point can rotate parallel to the plane.
Many of you have probably heard of the rotation matrix. Multiplying the point by it, we get a point rotated parallel to the plane by an angle phi. For two-dimensional space it looks like this: 
How to multiply: x of a point rotated by an angle phi = cosine of the angle phi*ix of the original point minus sine of the angle phi*ig of the original point;
ig of a point rotated by an angle phi = sine of the angle phi * ix of the original point plus cosine of the angle phi * ig of the original point.
Xa`=cosф*Xa - sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, where Xa and Ya are the abscissa and ordinate of the point to be rotated, Xa` and Ya` are the abscissa and ordinate of the already rotated point
For three-dimensional space, this matrix is generalized as follows: 
Rotation parallel to the XOY plane. As you can see, the Z coordinate does not change, but only X and Y change
Xa`=cosф*Xa - sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (essentially, Za`=Za)

Parallel rotation XOZ plane. Nothing new,
Xa`=cosф*Xa + Ya*0 - sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (essentially, Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

And the third matrix.
Xa`=Xa*1 + Ya*0 + Za*0 (essentially, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya - sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
And for the fourth dimension they look like this: 
I think you already understand what to multiply by, so I won’t go into detail again. But I note that it does the same thing as a matrix for rotation parallel to a plane in three-dimensional space! Both of them change only the ordinate and the applicate, and do not touch the other coordinates, so it can be used in the three-dimensional case, simply not paying attention to the fourth coordinate.
But with the projection formula, not everything is so simple. No matter how many forums I read, none of the projection methods worked for me. The parallel one was not suitable for me, since the projection would not look three-dimensional. In some projection formulas, to find a point you need to solve a system of equations (and I don’t know how to teach a computer to solve them), others I simply didn’t understand... In general, I decided to come up with my own way. For this purpose, consider the 2D->1D projection.

pov means "Point of view", ptp means "Point to project" (the point to be projected), and ptp` is the desired point on the OX axis.
Angles povptpB and ptpptp`A are equal as corresponding (the dotted line is parallel to the OX axis, the straight line povptp is a secant).
The x of the point ptp` is equal to the x of the point ptp minus the length of the segment ptp`A. This segment can be found from the triangle ptpptp`A: ptp`A = ptpA/tangent of angle ptpptp`A. We can find this tangent from the triangle povptpB: tangent ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Answer: Xptp`=Xptp-Yptp/tangent of angle ptpptp`A.
I did not describe this algorithm in detail here, since there are a lot of special cases when the formula changes somewhat. If anyone is interested, look at the source code of the program, everything is described there in the comments.
In order to project a point in three-dimensional space onto a plane, we simply consider two planes - XOZ and YOZ, and solve this problem for each of them. In the case of four-dimensional space, it is necessary to consider three planes: XOQ, YOQ and ZOQ.
And finally, about the program. It works like this: initialize sixteen vertices of the tesseract -> depending on the commands entered by the user, rotate it -> project it onto the volume -> depending on the commands entered by the user, rotate its projection -> project onto the plane -> draw.
I wrote the projections and rotations myself. They work according to the formulas I just described. The OpenGL library draws lines and also handles color mixing. And the coordinates of the tesseract vertices are calculated in this way:
Coordinates of the vertices of a line centered at the origin and length 2 - (1) and (-1);
- " - " - square - " - " - and an edge of length 2:
(1; 1), (-1; 1), (1; -1) and (-1; -1);
- " - " - cube - " - " -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1), (-1; -1; -1);
As you can see, a square is one line above the OY axis and one line below the OY axis; a cube is one square in front of the XOY plane, and one behind it; The tesseract is one cube on the other side of the XOYZ volume, and one on this side. But it is much easier to perceive this alternation of ones and minus ones if they are written in a column
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
In the first column, one and minus one alternate. In the second column, first there are two pluses, then two minuses. In the third - four plus ones, and then four minus ones. These were the vertices of the cube. The tesseract has twice as many of them, and therefore it was necessary to write a loop to declare them, otherwise it is very easy to get confused.
My program can also draw anaglyph. Happy owners of 3D glasses can observe a stereoscopic image. There is nothing tricky about drawing a picture; you simply draw two projections onto the plane, for the right and left eyes. But the program becomes much more visual and interesting, and most importantly, it gives a better idea of the four-dimensional world.
Less significant functions are the illumination of one of the edges in red so that turns can be better seen, as well as minor conveniences - regulation of the coordinates of the “eye” points, increasing and decreasing the turning speed.
Archive with the program, source code and instructions for use.
If an unusual incident happened to you, you saw a strange creature or an incomprehensible phenomenon, you can send us your story and it will be published on our website ===> .
The doctrine of multidimensional spaces began to appear in the middle of the 19th century. idea four-dimensional space science fiction writers borrowed from scientists. In their works they told the world about the amazing wonders of the fourth dimension.
The heroes of their works, using the properties of four-dimensional space, could eat the contents of an egg without damaging the shell, and drink a drink without opening the bottle cap. The thieves removed the treasure from the safe through the fourth dimension. Surgeons performed operations on internal organs without cutting the patient's body tissue.
Tesseract
In geometry, a hypercube is an n-dimensional analogy of a square (n = 2) and a cube (n = 3). The four-dimensional analogue of our usual 3-dimensional cube is known as the tesseract. The tesseract is to the cube as the cube is to the square. More formally, a tesseract can be described as a regular convex four-dimensional polyhedron whose boundary consists of eight cubic cells.

Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, the tesseract has 8 3D faces, 24 2D faces, 32 edges and 16 vertices.
By the way, according to the Oxford Dictionary, the word tesseract was coined and used in 1888 by Charles Howard Hinton (1853-1907) in his book A New Age of Thought. Later, some people called the same figure a tetracube (Greek tetra - four) - a four-dimensional cube.

Construction and description
Let's try to imagine what a hypercube will look like without leaving three-dimensional space.
In a one-dimensional “space” - on a line - we select a segment AB of length L. On a two-dimensional plane at a distance L from AB, we draw a segment DC parallel to it and connect their ends. The result is a square CDBA. Repeating this operation with the plane, we obtain a three-dimensional cube CDBAGHFE. And by shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube CDBAGHFEKLJIOPNM.
In a similar way, we can continue our reasoning for hypercubes of a larger number of dimensions, but it is much more interesting to see how a four-dimensional hypercube will look for us, residents of three-dimensional space.
Let's take the wire cube ABCDHEFG and look at it with one eye from the side of the edge. We will see and can draw two squares on the plane (its near and far edges), connected by four lines - side edges. Similarly, a four-dimensional hypercube in three-dimensional space will look like two cubic “boxes” inserted into each other and connected by eight edges. In this case, the “boxes” themselves - three-dimensional faces - will be projected onto “our” space, and the lines connecting them will stretch in the direction of the fourth axis. You can also try to imagine the cube not in projection, but in a spatial image.

Just as a three-dimensional cube is formed by a square shifted by the length of its face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in perspective will look like some rather complex figure. The four-dimensional hypercube itself can be divided into an infinite number of cubes, just as a three-dimensional cube can be “cut” into an infinite number of flat squares.
By cutting the six faces of a three-dimensional cube, you can decompose it into a flat figure - a development. It will have a square on each side of the original face plus one more - the face opposite to it. And the three-dimensional development of a four-dimensional hypercube will consist of the original cube, six cubes “growing” from it, plus one more - the final “hyperface”.

Hypercube in art
The Tesseract is such an interesting figure that it has repeatedly attracted the attention of writers and filmmakers.
Robert E. Heinlein mentioned hypercubes several times. In The House That Teal Built (1940), he described a house built as an unwrapped tesseract and then, due to an earthquake, "folded" in the fourth dimension to become a "real" tesseract. Heinlein's novel Glory Road describes a hyper-sized box that was larger on the inside than on the outside.


Henry Kuttner's story "All Tenali Borogov" describes an educational toy for children from the distant future, similar in structure to a tesseract.
The plot of Cube 2: Hypercube centers on eight strangers trapped in a "hypercube", or network of connected cubes.
A parallel world
Mathematical abstractions gave rise to the idea of existence parallel worlds. These are understood as realities that exist simultaneously with ours, but independently of it. A parallel world can have different sizes: from a small geographical area to an entire universe. In a parallel world, events occur in their own way; it may differ from our world, both in individual details and in almost everything. Moreover, the physical laws of a parallel world are not necessarily similar to the laws of our Universe.
This topic is fertile ground for science fiction writers.
Salvador Dali's painting "The Crucifixion" depicts a tesseract. “Crucifixion or Hypercubic Body” is a painting by the Spanish artist Salvador Dali, painted in 1954. Depicts the crucified Jesus Christ on a tesseract scan. The painting is kept in the Metropolitan Museum of Art in New York

It all started in 1895, when H.G. Wells, with his story “The Door in the Wall,” opened up the existence of parallel worlds to science fiction. In 1923, Wells returned to the idea of parallel worlds and placed in one of them a utopian country where the characters in the novel Men Like Gods go.
The novel did not go unnoticed. In 1926, G. Dent’s story “The Emperor of the Country “If”” appeared. In Dent’s story, for the first time, the idea arose that there could be countries (worlds) whose history could go differently from the history of real countries in our world. And worlds these are no less real than ours.
In 1944, Jorge Luis Borges published the story “The Garden of Forking Paths” in his book Fictional Stories. Here the idea of branching time was finally expressed with utmost clarity.
Despite the appearance of the works listed above, the idea of many worlds began to seriously develop in science fiction only in the late forties of the 20th century, approximately at the same time when a similar idea arose in physics.
One of the pioneers of the new direction in science fiction was John Bixby, who suggested in the story “One Way Street” (1954) that between worlds you can only move in one direction - once you go from your world to a parallel one, you will not return back, but you will move from one world to the next. However, returning to one’s own world is also not excluded - for this it is necessary that the system of worlds be closed.
Clifford Simak's novel A Ring Around the Sun (1982) describes numerous planets Earth, each existing in its own world, but in the same orbit, and these worlds and these planets differ from each other only by a slight (microsecond) shift in time . The numerous Earths visited by the hero of the novel form unified system worlds.
Alfred Bester expressed an interesting view of the branching of worlds in his story “The Man Who Killed Mohammed” (1958). “By changing the past,” the hero of the story argued, “you change it only for yourself.” In other words, after a change in the past, a branch of history arises in which only for the character who made the change does this change exist.
The Strugatsky brothers’ story “Monday Begins on Saturday” (1962) describes the characters’ journeys to different versions of the future described by science fiction writers - in contrast to the travels to different versions of the past that already existed in science fiction.
However, even a simple listing of all the works that touch on the theme of parallel worlds would take too much time. And although science fiction writers, as a rule, do not scientifically substantiate the postulate of multidimensionality, they are right about one thing - this is a hypothesis that has a right to exist.
The fourth dimension of the tesseract is still waiting for us to visit.
Victor Savinov