solutie inegalitatiiîn mod online soluţie aproape orice inegalitate dată online. Matematic inegalități online pentru a rezolva matematica. Găsiți rapid solutie inegalitatiiîn mod online. Site-ul www.site vă permite să găsiți soluţie aproape orice dat algebric, trigonometric sau inegalitatea transcendentală online. Când studiezi aproape orice ramură a matematicii în diferite etape, trebuie să te decizi inegalități online. Pentru a obține un răspuns imediat și, cel mai important, un răspuns precis, aveți nevoie de o resursă care vă permite să faceți acest lucru. Multumesc site-ului www.site rezolva inegalitatea online va dura câteva minute. Principalul avantaj al www.site-ului atunci când rezolvăm matematică inegalități online- aceasta este viteza și acuratețea răspunsului oferit. Site-ul este capabil să rezolve orice inegalități algebrice online, inegalități trigonometrice online, inegalități transcendentale online, și de asemenea inegalităților cu parametri necunoscuți în modul online. Inegalități servesc ca un puternic aparat matematic solutii probleme practice. Cu ajutorul inegalități matematice este posibil să se exprime fapte și relații care pot părea confuze și complexe la prima vedere. Cantitati necunoscute inegalităților poate fi găsit prin formularea problemei în matematic limba în formă inegalitățilorŞi decide sarcină primită în modul online pe site-ul www.site. Orice inegalitatea algebrică, inegalitatea trigonometrică sau inegalităților conţinând transcendental caracteristici pe care le puteți ușor decide online și obțineți răspunsul exact. Studiind stiintele naturii, inevitabil te confrunți cu nevoia soluții la inegalități. În acest caz, răspunsul trebuie să fie corect și trebuie obținut imediat în modul online. Prin urmare pentru Rezolvarea inegalităților matematice online vă recomandăm site-ul www.site, care va deveni calculatorul dumneavoastră indispensabil pentru rezolvarea inegalităților algebrice online, inegalități trigonometrice online, și de asemenea inegalități transcendentale online sau inegalităților cu parametri necunoscuți. Pentru probleme practice de a găsi soluții online la diverse inegalități matematice resursa www.. Rezolvarea inegalități online singur, este util să verificați răspunsul primit folosind soluție online inegalităților pe site-ul www.site. Trebuie să scrieți corect inegalitatea și să obțineți instantaneu soluție online, după care nu mai rămâne decât să compari răspunsul cu soluția ta la inegalitate. Verificarea răspunsului nu va dura mai mult de un minut, este suficient rezolva inegalitatea onlineși comparați răspunsurile. Acest lucru vă va ajuta să evitați greșelile în decizie si corecteaza raspunsul la timp rezolvarea inegalităților online fie el algebric, trigonometric, transcendental sau inegalitate cu parametri necunoscuți.

Modulul numerelor acest număr în sine se numește dacă este nenegativ, sau același număr cu semnul opus dacă este negativ.

De exemplu, modulul numărului 6 este 6, iar modulul numărului -6 este, de asemenea, 6.

Adică modulul unui număr este înțeles ca valoare absolută, valoarea absolută a acestui număr fără a lua în considerare semnul său.

Se desemnează după cum urmează: |6|, | X|, |O| etc.

(Mai multe detalii în secțiunea „Modul de număr”).

Ecuații cu modul.

Exemplul 1 . Rezolvați ecuația|10 X - 5| = 15.

Soluţie.

Conform regulii, ecuația este echivalentă cu combinația a două ecuații:

10X - 5 = 15
10X - 5 = -15

Noi decidem:

10X = 15 + 5 = 20
10X = -15 + 5 = -10

X = 20: 10
X = -10: 10

X = 2
X = -1

Răspuns: X 1 = 2, X 2 = -1.

Exemplul 2 . Rezolvați ecuația|2 X + 1| = X + 2.

Soluţie.

Deoarece modulul este un număr nenegativ, atunci X+ 2 ≥ 0. În consecință:

X ≥ -2.

Să facem două ecuații:

2X + 1 = X + 2
2X + 1 = -(X + 2)

Noi decidem:

2X + 1 = X + 2
2X + 1 = -X - 2

2X - X = 2 - 1
2X + X = -2 - 1

X = 1
X = -1

Ambele numere sunt mai mari decât -2. Deci ambele sunt rădăcini ale ecuației.

Răspuns: X 1 = -1, X 2 = 1.

Exemplul 3 . Rezolvați ecuația

|X + 3| - 1
————— = 4
X - 1

Soluţie.

Ecuația are sens dacă numitorul nu este egal cu zero- înseamnă dacă X≠ 1. Să luăm în considerare această condiție. Prima noastră acțiune este simplă - nu doar scăpăm de fracțiune, ci o transformăm astfel încât să obținem modulul în forma sa pură:

|X+ 3| - 1 = 4 · ( X - 1),

|X + 3| - 1 = 4X - 4,

|X + 3| = 4X - 4 + 1,

|X + 3| = 4X - 3.

Acum avem doar o expresie sub modulul din partea stângă a ecuației. Să mergem mai departe.
Modulul unui număr este un număr nenegativ - adică trebuie să fie mai mare decât zero sau egal cu zero. În consecință, rezolvăm inegalitatea:

4X - 3 ≥ 0

4X ≥ 3

X ≥ 3/4

Astfel, avem o a doua condiție: rădăcina ecuației trebuie să fie cel puțin 3/4.

În conformitate cu regula, compunem un set de două ecuații și le rezolvăm:

X + 3 = 4X - 3
X + 3 = -(4X - 3)

X + 3 = 4X - 3
X + 3 = -4X + 3

X - 4X = -3 - 3
X + 4X = 3 - 3

X = 2
X = 0

Am primit două răspunsuri. Să verificăm dacă sunt rădăcini ale ecuației originale.

Am avut două condiții: rădăcina ecuației nu poate fi egală cu 1 și trebuie să fie cel puțin 3/4. Adică X ≠ 1, X≥ 3/4. Doar unul dintre cele două răspunsuri obținute corespunde ambelor condiții - numărul 2. Aceasta înseamnă că numai aceasta este rădăcina ecuației inițiale.

Răspuns: X = 2.

Inegalități cu modul.

Exemplul 1 . Rezolvați inegalitatea| X - 3| < 4

Soluţie.

Regula modulului spune:

|O| = O, Dacă O ≥ 0.

|O| = -O, Dacă O < 0.

Modulul poate avea atât numere nenegative, cât și numere negative. Deci trebuie să luăm în considerare ambele cazuri: X- 3 ≥ 0 și X - 3 < 0.

1) Când X- 3 ≥ 0 inegalitatea noastră originală rămâne așa cum este, doar fără semnul modulului:
X - 3 < 4.

2) Când X - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(X - 3) < 4.

Deschizând parantezele, obținem:

-X + 3 < 4.

Astfel, din aceste două condiții am ajuns la unificarea a două sisteme de inegalități:

X - 3 ≥ 0
X - 3 < 4

X - 3 < 0
-X + 3 < 4

Să le rezolvăm:

X ≥ 3
X < 7

X < 3
X > -1

Deci, răspunsul nostru este o unire a două seturi:

3 ≤ X < 7 U -1 < X < 3.

Determinați cel mai mic și cea mai mare valoare. Acestea sunt -1 și 7. Mai mult X mai mare de -1 dar mai mic de 7.
In plus, X≥ 3. Aceasta înseamnă că soluția inegalității este întregul set de numere de la -1 la 7, excluzând aceste numere extreme.

Răspuns: -1 < X < 7.

Sau: X ∈ (-1; 7).

Suplimente.

1) Există o modalitate mai simplă și mai scurtă de a ne rezolva inegalitatea - grafic. Pentru a face acest lucru, trebuie să desenați o axă orizontală (Fig. 1).

Expresie | X - 3| < 4 означает, что расстояние от точки X la punctul 3 este mai puțin de patru unități. Marcam numărul 3 pe axă și numărăm 4 diviziuni la stânga și la dreapta acestuia. În stânga vom ajunge la punctul -1, în dreapta - la punctul 7. Astfel, punctele X le-am văzut doar fără să le calculăm.

În plus, conform condiției de inegalitate, -1 și 7 înșiși nu sunt incluse în setul de soluții. Astfel, obținem răspunsul:

1 < X < 7.

2) Dar există o altă soluție care este mai simplă chiar și decât metoda grafică. Pentru a face acest lucru, inegalitatea noastră trebuie să fie prezentată în următoarea formă:

4 < X - 3 < 4.

La urma urmei, așa este în conformitate cu regula modulului. Număr nenegativ 4 și un număr negativ similar -4 sunt limitele pentru rezolvarea inegalității.

4 + 3 < X < 4 + 3

1 < X < 7.

Exemplul 2 . Rezolvați inegalitatea| X - 2| ≥ 5

Soluţie.

Acest exemplu este semnificativ diferit de cel precedent. Partea stângă este mai mare de 5 sau egală cu 5. C punct geometric Din punct de vedere, soluția inegalității sunt toate numerele care se află la o distanță de 5 unități sau mai mult de punctul 2 (Fig. 2). Graficul arată că toate acestea sunt numere mai mici sau egale cu -3 și mai mari sau egale cu 7. Aceasta înseamnă că am primit deja răspunsul.

Răspuns: -3 ≥ X ≥ 7.

Pe parcurs, rezolvăm aceeași inegalitate prin rearanjarea termenului liber la stânga și la dreapta cu semnul opus:

5 ≥ X - 2 ≥ 5

5 + 2 ≥ X ≥ 5 + 2

Răspunsul este același: -3 ≥ X ≥ 7.

Sau: X ∈ [-3; 7]

Exemplul este rezolvat.

Exemplul 3 . Rezolvați inegalitatea 6 X 2 - | X| - 2 ≤ 0

Soluţie.

Număr X poate fi un număr pozitiv, un număr negativ sau zero. Prin urmare, trebuie să luăm în considerare toate cele trei circumstanțe. După cum știți, ele sunt luate în considerare în două inegalități: X≥ 0 și X < 0. При X≥ 0 pur și simplu rescriem inegalitatea noastră originală așa cum este, doar fără semnul modulului:

6x 2 - X - 2 ≤ 0.

Acum despre al doilea caz: dacă X < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6X 2 - (-X) - 2 ≤ 0.

Extinderea parantezelor:

6X 2 + X - 2 ≤ 0.

Astfel, am primit două sisteme de ecuații:

6X 2 - X - 2 ≤ 0
X ≥ 0

6X 2 + X - 2 ≤ 0
X < 0

Trebuie să rezolvăm inegalitățile în sisteme - și asta înseamnă că trebuie să găsim rădăcinile a două ecuații pătratice. Pentru a face acest lucru, echivalăm părțile din stânga ale inegalităților cu zero.

Să începem cu primul:

6X 2 - X - 2 = 0.

Cum se rezolvă o ecuație pătratică - vezi secțiunea „Ecuație pătratică”. Vom numi imediat răspunsul:

X 1 = -1/2, x 2 = 2/3.

Din primul sistem de inegalități obținem că soluția inegalității inițiale este întreaga mulțime de numere de la -1/2 la 2/3. Scriem uniunea de soluții la X ≥ 0:
[-1/2; 2/3].

Acum să rezolvăm a doua ecuație pătratică:

6X 2 + X - 2 = 0.

Rădăcinile sale:

X 1 = -2/3, X 2 = 1/2.

Concluzie: când X < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Să combinăm cele două răspunsuri și să obținem răspunsul final: soluția este întregul set de numere de la -2/3 la 2/3, inclusiv aceste numere extreme.

Răspuns: -2/3 ≤ X ≤ 2/3.

Sau: X ∈ [-2/3; 2/3].

REVIZUT

Consiliul Pedagogic MOU

„Școala Gimnazială Zashizhemskaya”

Protocolul nr. 1

DE ACORD

Director adjunct pentru HR

_______ /Sidorkina R.L./

AM APROBAT

Director:

A.P. Konakov

Ordinul nr. 63

Rezolvarea ecuațiilor și inegalităților cu modul

Munca de cercetare

Programul a fost realizat de:

profesor superior de matematică

Sidorkina R.L.

Satul Zashizhemye, 2014

Cuprins

Introducere…………………………………………………………………………………………… 3

Cele mai simple ecuații și inegalități cu modul……………………5

Rezolvarea grafică a ecuațiilor și inegalităților cu modul………….8

Alte modalităţi de rezolvare a ecuaţiilor şi inegalităţilor cu modul.........10

Concluzie………………………………………………………..16

Referințe………………………………………………………18

1. Introducere

Conceptul de valoare absolută (modul) este una dintre cele mai importante caracteristici ale unui număr, atât în ​​domeniul numerelor reale, cât și al numerelor complexe.

Acest concept este utilizat pe scară largă nu numai în diferite secțiuni ale cursului de matematică școlar, ci și în cursuri matematică superioară, fizica si stiintele tehnice studiate in universitati. De exemplu, în teoria calculelor aproximative se folosesc conceptele de erori absolute și relative ale unui număr aproximativ. În mecanică și geometrie sunt studiate conceptele de vector și lungimea acestuia (modul vectorial). ÎN analiză matematică conceptul de valoare absolută a unui număr este conținut în definițiile unor concepte de bază precum limită, funcție mărginită etc. Problemele legate de valorile absolute se găsesc adesea în olimpiadele matematice, examenele de admitere la universități și la examenul de stat unificat.Și așa a devenit important pentru noi să studiem câteva aspecte ale acestui subiect.

Acasă scop Munca noastră este de a studia diferite metode de rezolvare a ecuațiilor și inegalităților cu module.

Acest obiectiv trebuie atins prin rezolvarea următoarelor sarcini:

Studiați definiția și unele proprietăți ale unui modul.

Stăpânește soluția ecuațiilor simple și a inegalităților cu modul prin tranziții echivalente

Luați în considerare diferite metode de rezolvare a ecuațiilor și inegalităților cu modul.

Obiect studiile sunt niște tipuri de ecuații și inegalități cu modul.

Articol cercetare - diverse metode de rezolvare a ecuatiilor si inegalitatilor cu modul si anume: metoda grafica, metoda de interpretare geometrică, utilizarea identității, aplicarea teoremei semnelor, metoda trecerii la o consecință, metoda intervalelor, metoda înmulțirii cu un factor pozitiv, metoda dezvăluirii modulelor.

Pe parcursul studiului s-au folosit metode precum studierea literaturii pe această temă și metoda practică.

Pe parcursul activității noastre, am examinat surse precum:

1. „Marea Enciclopedie Matematică” pentru școlari și elevi;

Matematică. Examenul Unificat de Stat - 2011-2012. Opțiuni tipice de examen. / Editat de A.L. Semenova, I.V. Iascenko.

Enciclopedia „Cunosc lumea” Matematică;

;

1. 1. Cele mai simple ecuații și inegalități cu modul

Printre cele mai simple ecuații vom include ecuații care pot fi rezolvate prin una dintre următoarele tranziții echivalente:

Exemple de rezolvare a ecuațiilor simple.

Exemplul 1 Să rezolvăm ecuația
.

Soluţie.

Răspuns.
.

Exemplul 2 Să rezolvăm ecuația.

Soluţie.

Răspuns.
.

Exemplul 3 Să rezolvăm ecuația
.

Soluţie.

Răspuns.
.

O serie de ecuații sunt rezolvate folosind următoarea teoremă.

Teorema.4 Suma modulelor este egală cu suma algebrică a mărimilor submodulare dacă și numai dacă fiecare mărime are semnul cu care este inclusă în suma algebrică.

Exemplul 5 Rezolvați ecuația

Soluţie. Din moment ce , atunci avem o egalitate a formei , unde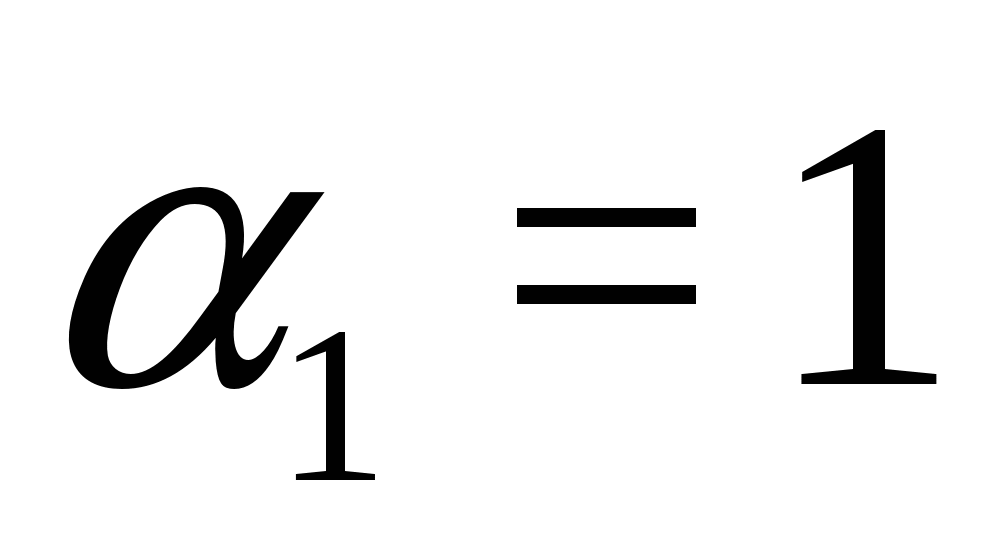
,
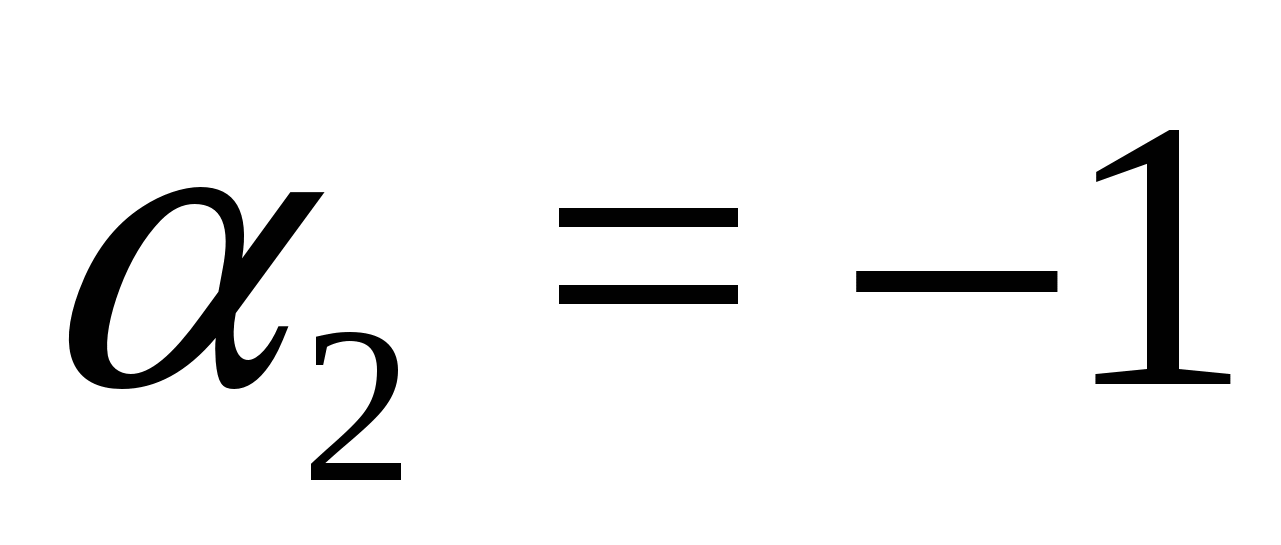. Prin urmare, ecuația inițială este echivalentă cu sistemul:

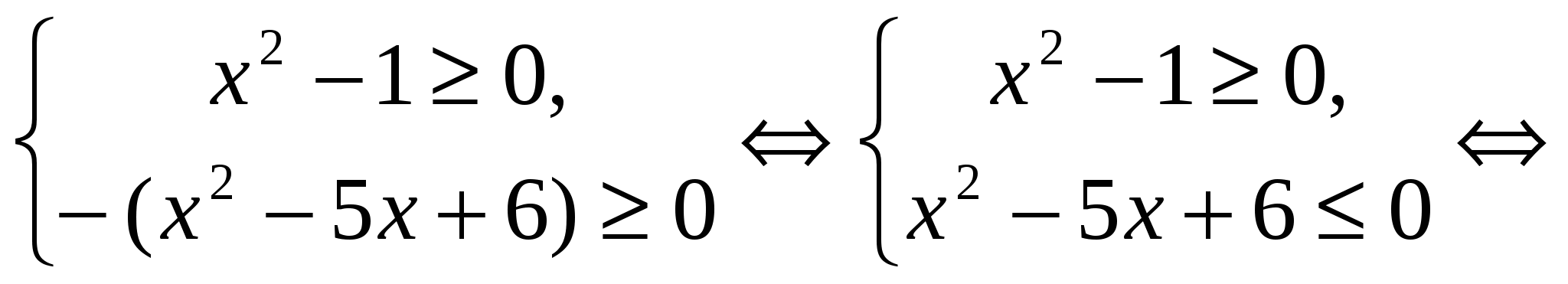
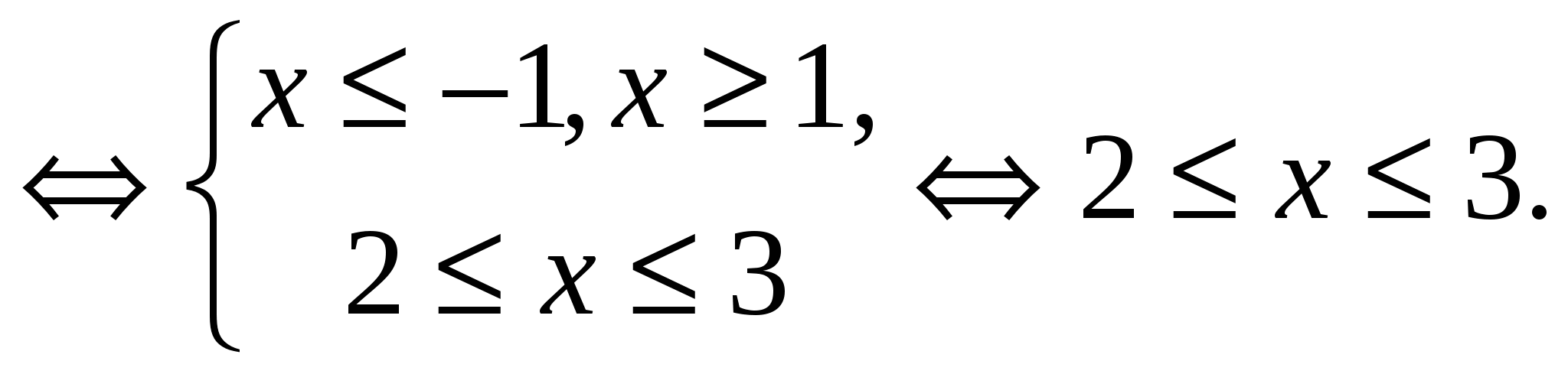
Răspuns.
.

Exemple de rezolvare a inegalităților simple.

Exemplul 6 Să rezolvăm inegalitatea
.

Soluţie.

Răspuns.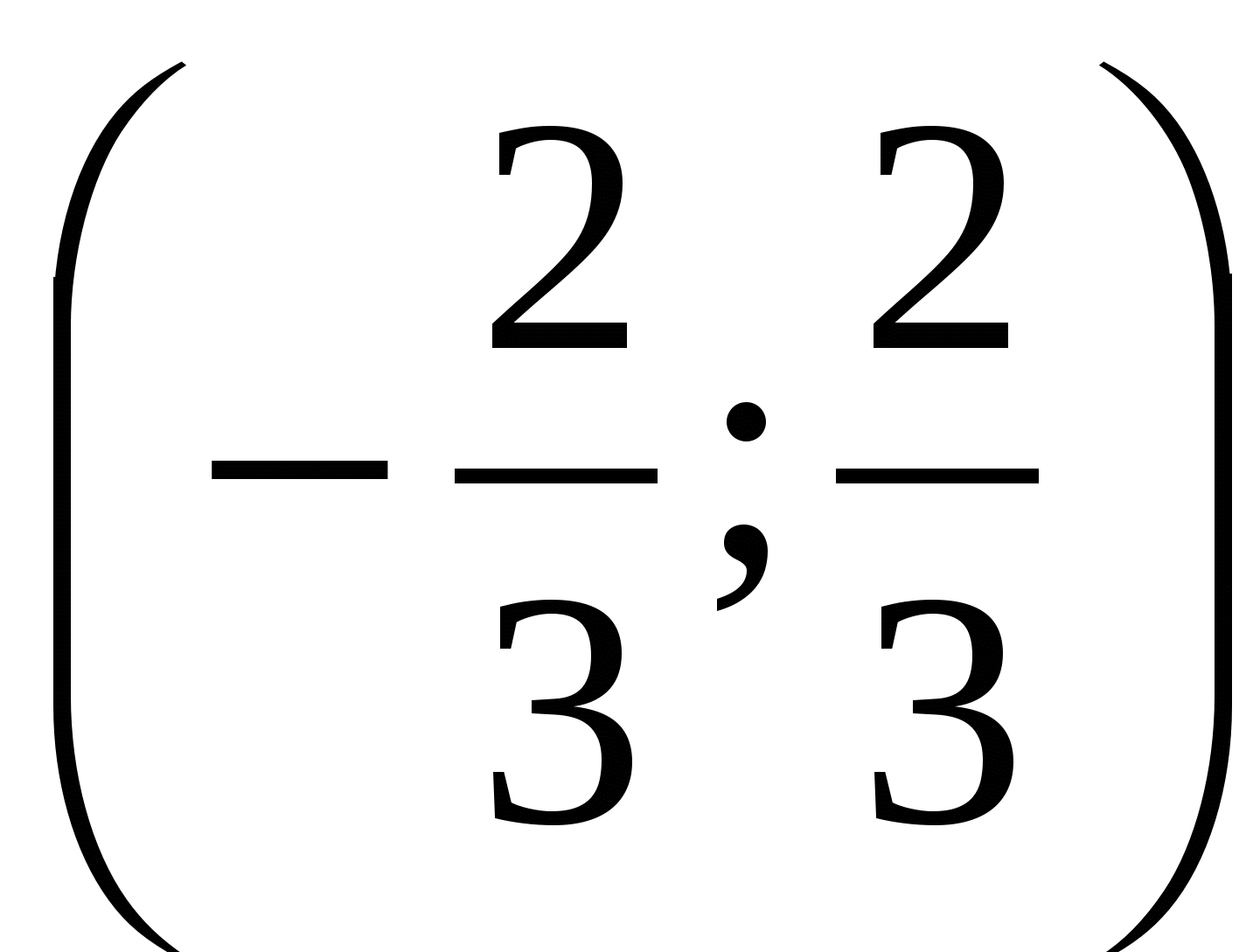
.

Exemplul 7 Să rezolvăm inegalitatea
.

Soluţie.

Răspuns.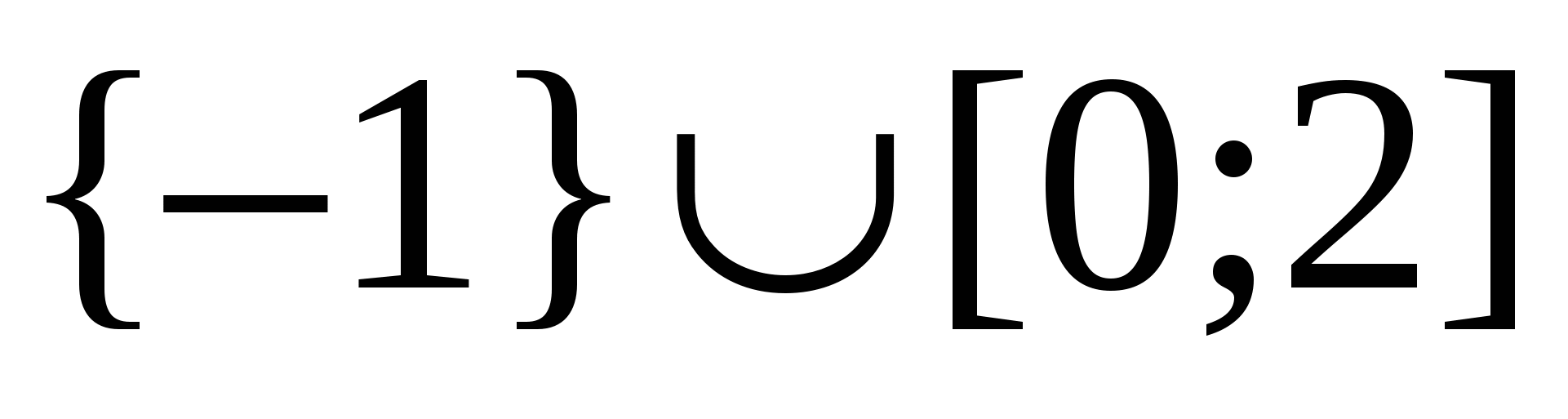
.

Destul de ciudat, dar
este suficient pentru a scăpa de semnul modulului în orice inegalități.

Exemplul 8 Rezolvați inegalitatea

Soluţie.

Răspuns.
.

3. Rezolvarea grafică a ecuațiilor și inegalităților cu modul

Rezolvarea ecuațiilor care conțin semnul unei valori absolute este adesea mult mai convenabilă de rezolvat nu analitic, ci grafic (în special ecuații care conțin parametri).

Exemplul 9(C5, examen de stat unificat - 2010)

C5. Pentru fiecare valoareo indicați numărul de soluții ale ecuației

Soluţie.Să diagramăm funcția
. Pentru a face acest lucru, selectați un pătrat complet:

Numărul de puncte de intersecție ale graficului funcției y =
cu drepte orizontale y = a este egal cu numărul de soluții ale ecuației.

DESPRE răspuns: Dacă < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, atunci există două soluții.

Alte modalități de a rezolva ecuații și inegalități cu modul

• Metoda de extindere a modulului

Să ne uităm la metoda de extindere a modulelor folosind un exemplu:

Exemplul 10 Rezolvați ecuația

Soluţie. Această ecuație conține mai mult de un modul.

Metoda de rezolvare a ecuațiilor care conțin variabile sub semnul a două sau mai multe module este următoarea.

1. Găsiți valorile variabilei la care fiecare dintre module devine zero:
,
;
,
;
,
.

2. Marcați aceste puncte pe dreapta numerică.

3. Considerăm ecuația pe fiecare dintre intervale și stabilim semnul expresiilor care se află sub module.

1) Când
sau
. Pentru a determina semnul fiecăreia dintre expresiile modulo pe acest interval, este suficient să luăm orice valoare din acest interval și substituiți-l în expresie. Dacă valoarea rezultată este negativă, atunci pentru toate din acest interval expresia va fi negativă; dacă este primită valoare numerică pozitiv, ceea ce înseamnă pentru toate valorile din acest interval expresia va fi pozitivă.

Să luăm valoarea
de între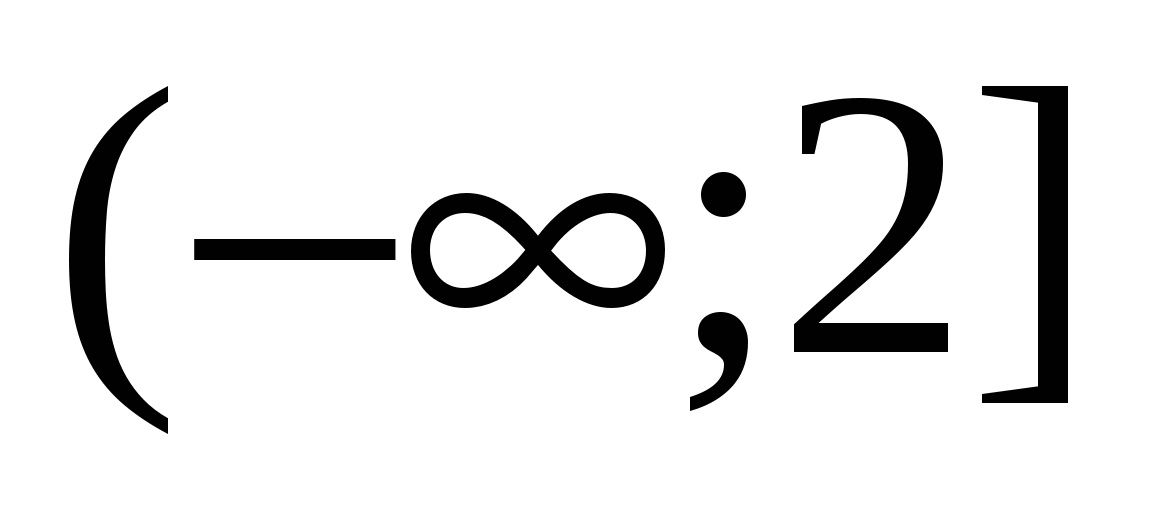
și substituiți valoarea acesteia în expresie
, primim
, ceea ce înseamnă în acest interval
negativ și, prin urmare, „va ieși”” de sub modul cu semnul „minus””, obținem:
.

La această valoare , expresie
va primi valoarea
, ceea ce înseamnă că este în interval
de asemenea, ia valori negative și va „ieși” din modulul cu semnul „minus””, obținem:
.

Expresie
va primi valoarea
și va „ieși” de sub modul cu semnul „minus”:
.

Ecuația din acest interval se va dovedi astfel: rezolvând-o, găsim:
.

Aflăm dacă această valoare este inclusă în interval
. Se dovedește că este inclus, ceea ce înseamnă
este rădăcina ecuației.

2) Când
. Alege orice valoare din acest gol. Lasă
. Determinăm semnul fiecăreia dintre expresiile de sub modul la această valoare . Se pare că expresia
pozitive iar celelalte două sunt negative.

Ecuația de pe acest interval va lua forma: . Rezolvând, găsim
. Această valoare nu este inclusă în interval
, ceea ce înseamnă că nu este rădăcina ecuației.

3) Când
. Alegeți o valoare arbitrară din acest interval, să zicem
și înlocuiți în fiecare dintre expresii. Constatăm că expresiile
Şi
sunt pozitive şi
- negativ. Obținem următoarea ecuație: .

După transformare, obținem:
, ceea ce înseamnă că ecuația nu are rădăcini în acest interval.

4) Când
. Este ușor de stabilit că toate expresiile din acest interval sunt pozitive, ceea ce înseamnă că obținem ecuația: ,
,
care este inclus în interval și este rădăcina ecuației.

Răspuns.
,
.

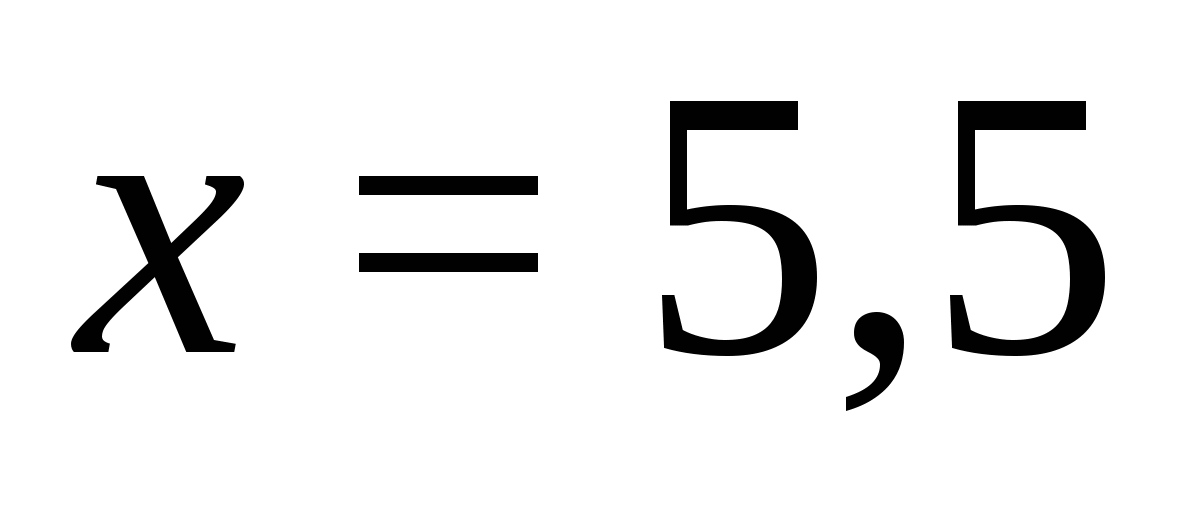• Rezolvarea ecuațiilor care conțin module de expresii nenegative

Exemplul 11 Care este suma rădăcinilor ecuației (rădăcină, dacă există) a ecuației

Soluţie. Luați în considerare expresia

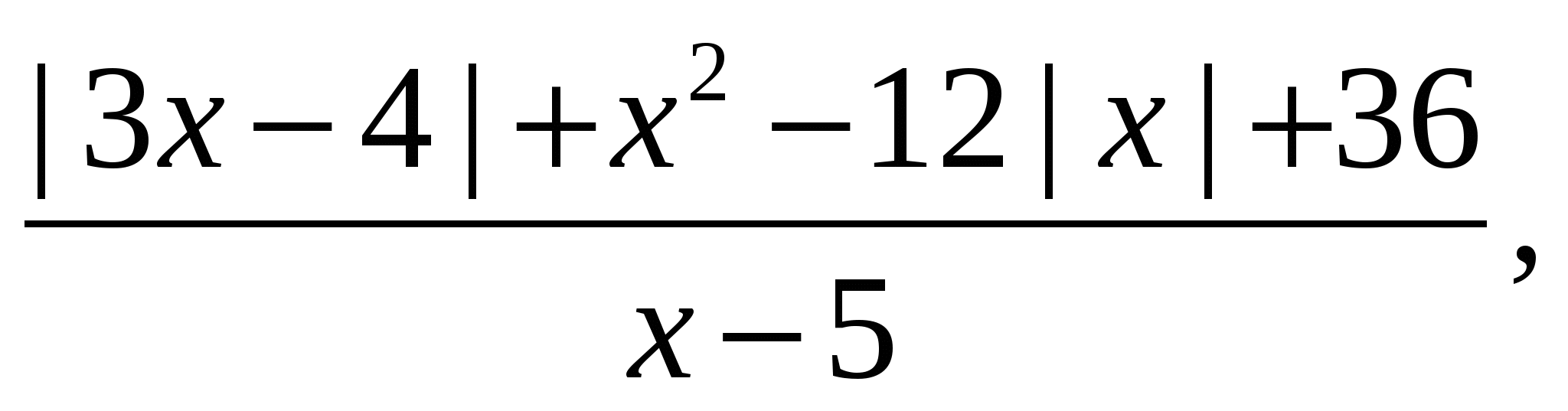și convertiți-l în formă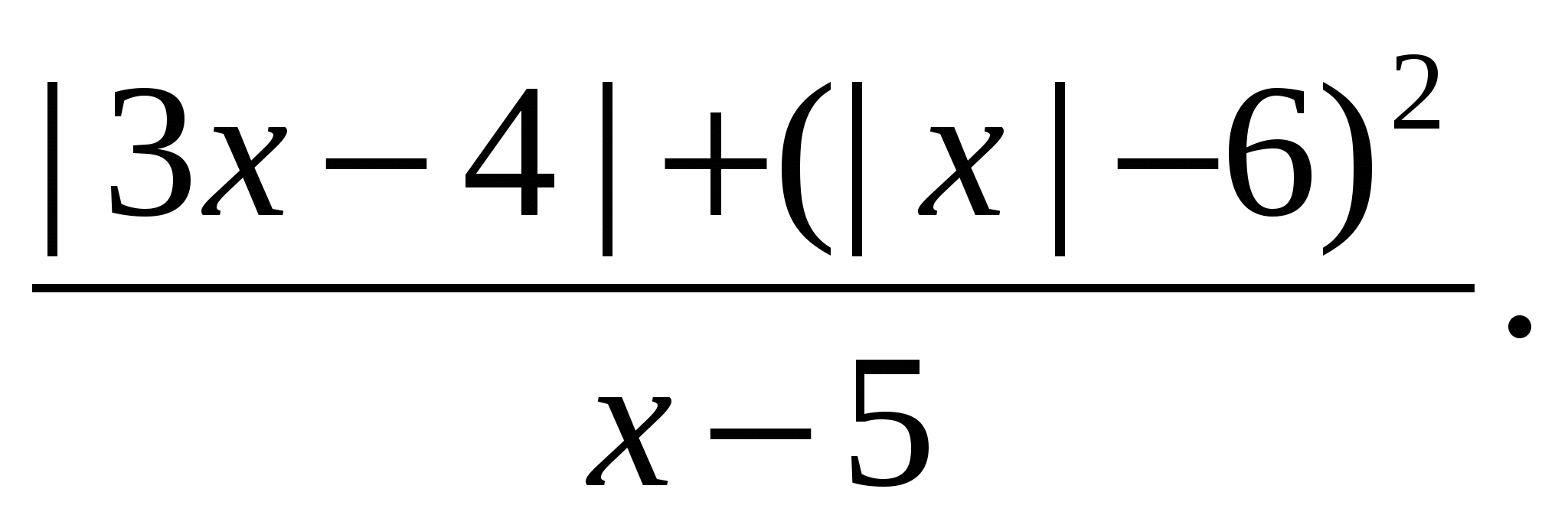

Este evident că numărătorul fracției este un număr pozitiv pentru orice valoare a variabilei. Aceasta înseamnă că o expresie fracțională este pozitivă dacă
(deoarece
). Să transformăm expresia rezultată, cu condiția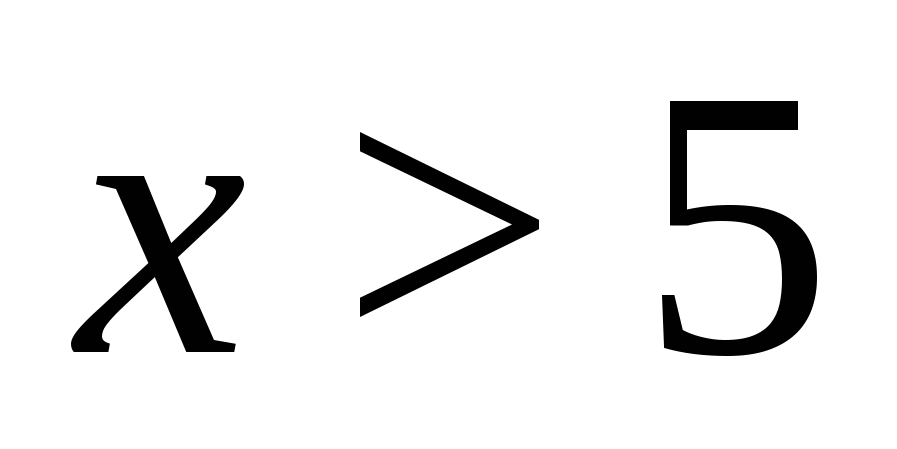
. Obținem o ecuație echivalentă cu cea inițială:

Răspuns.
.

Exemplul 12 Rezolvați ecuația

Soluţie. Deoarece partea stângă a ecuației este nenegativă, pentru toate valorile admisibile ale variabilei, pe mulțimea rădăcinilor ecuației trebuie să fie și partea dreaptă a acesteia, de unde condiția
, pe acest interval numitorii ambelor fracții sunt egali și rămâne de rezolvat ecuația
. Rezolvând-o și ținând cont de constrângere
, primim

Răspuns.
.

• Rezolvarea ecuațiilor folosind interpretarea geometrică

Sensul geometric al expresiei
- lungimea segmentului axei de coordonate care leagă punctele cu abscisele Şi . Traducerea unei probleme algebrice în limbaj geometric permite adesea să se evite calculele greoaie.

Exemplul 13 Să rezolvăm ecuația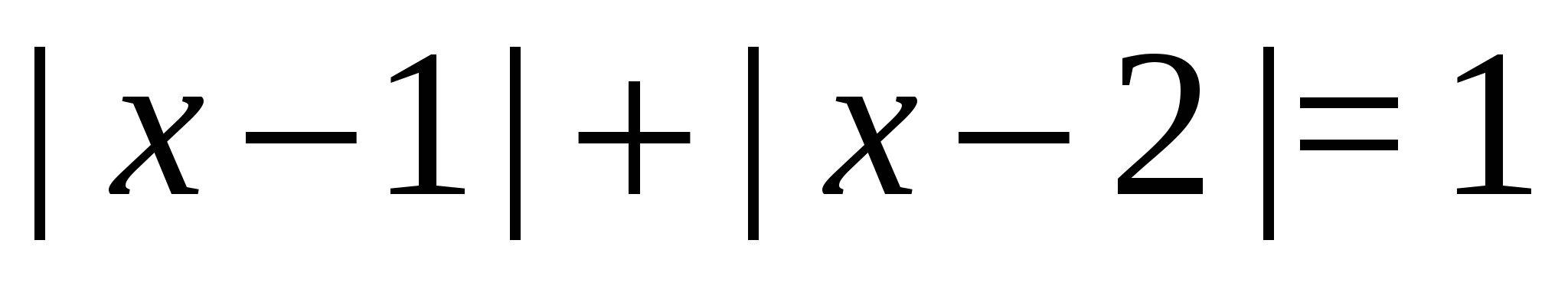
.

Soluţie. Vom raționa astfel: pe baza interpretării geometrice a modulului, partea stângă a ecuației este suma distanțelor de la un anumit punct cu abscisa. la două puncte fixe cu abscisele 1 și 2. Apoi toate punctele cu abscisele din segment
au proprietatea necesară, dar punctele situate în afara acestui segment nu au.

Răspuns.
.

Exemplul 14 Rezolvați inegalitatea
.

Soluţie. Să descriem puncte pe linia de coordonate, suma distanțelor de la care până la puncte
Şi exact egal cu . Acestea sunt toate punctele segmentului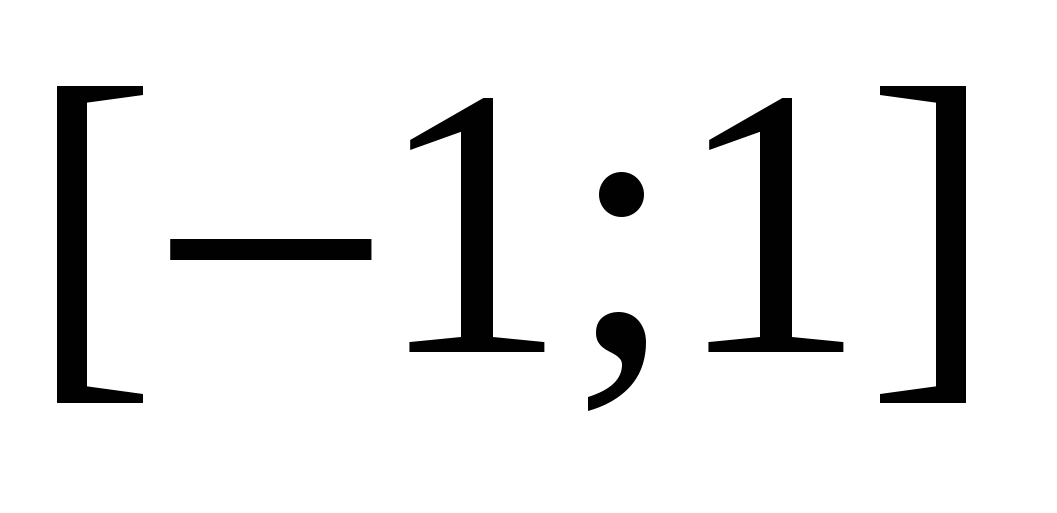
. Pentru toate numerele de afară a acestui segment suma distanțelor va fi mai mare de două.

Răspuns.
.

Exemplu(C3, examen de stat unificat - 2010) 15 Rezolvați ecuația

Soluţie. Aplicând identitatea de două ori
, obținem ecuația

a cărui soluție este intervalul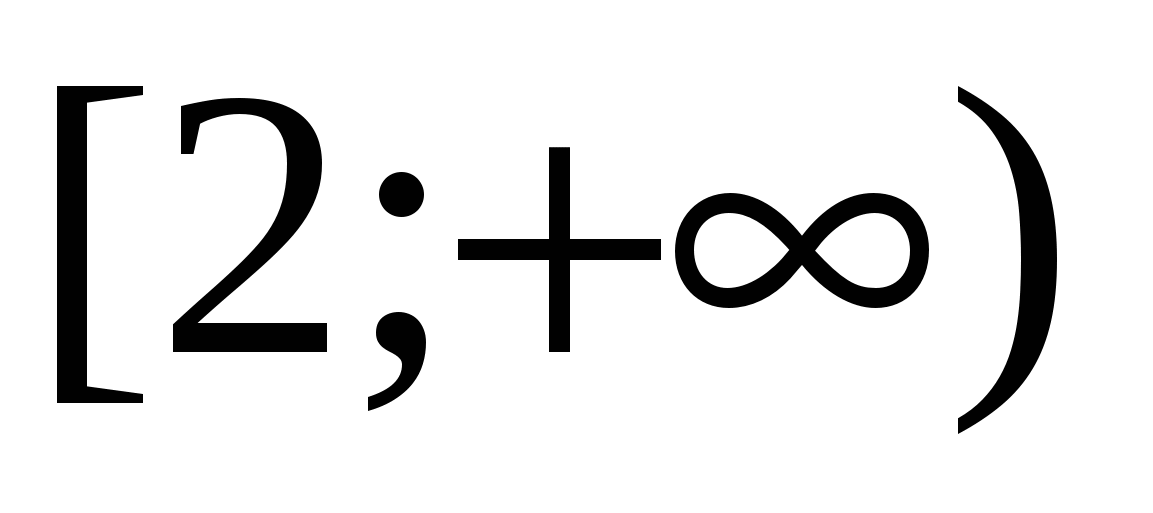
.

Răspuns.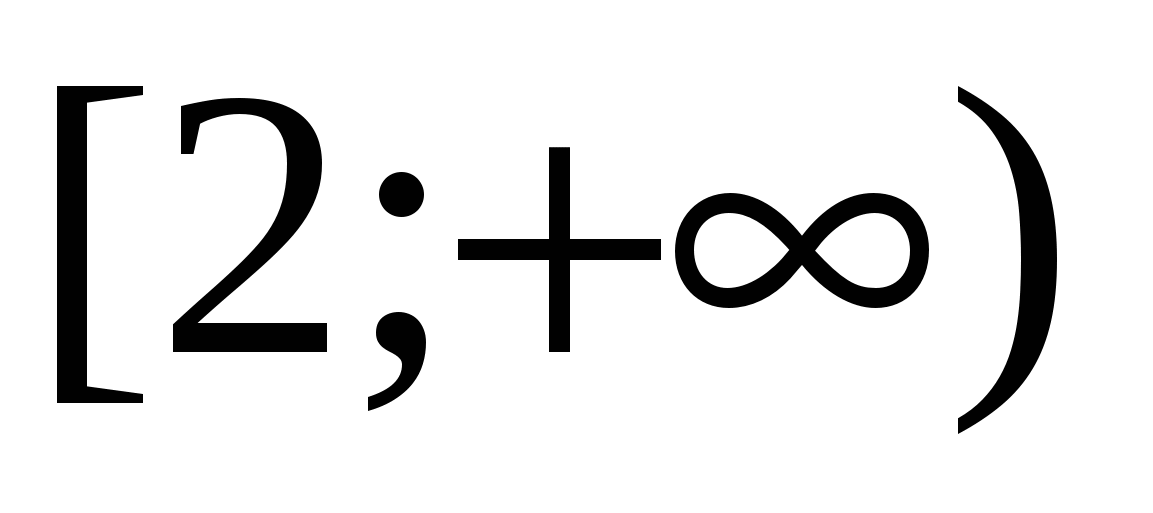
.

Exemplu(C3, examen de stat unificat - 2011) 16 17 Rezolvați ecuația

Soluţie. .

Răspuns.
.

• Aplicarea teoremei semnului la rezolvarea ecuațiilor

Să formulăm o teoremă convenabilă pentru rezolvarea inegalităților privind produsele sau coeficientii diferențelor de module:

Teorema 18 Semnul diferenței dintre modulele a două expresii coincide cu semnul diferenței în pătratele acestor expresii. nu dispare pentru nicio valoare a variabilei. Aceasta înseamnă că funcția este de semn constant în întregul domeniu de definiție. Calcularea, de exemplu,
, constatăm că funcția ia numai valori pozitive.

Răspuns.
.

Metoda intervalului vă permite să rezolvați ecuații și inegalități mai complexe cu module, dar în acest caz are un scop ușor diferit. Ideea este după cum urmează. Găsim rădăcinile tuturor expresiilor submodulare și împărțim axa numerică în intervale de semn constant ale acestor expresii. Acest lucru vă permite să parcurgeți secvențial aceste intervale, să scăpați simultan de toate modulele și să rezolvați o ecuație obișnuită sau o inegalitate (în timp ce verificați dacă răspunsul găsit este inclus în acest interval).

• Rezolvarea ecuațiilor prin înmulțirea cu un factor pozitiv

Concluzie.

Pentru a rezuma munca noastră, putem spune următoarele.

Scopul lucrării a fost studierea diferitelor metode de rezolvare a ecuațiilor și inegalităților cu module.

Sunt luate în considerare unele varietăți ale celor mai simple ecuații și inegalități cu modul, rezolvate folosind tranziții echivalente, precum și teorema asupra sumei modulelor; metoda grafica de rezolvare a ecuatiilor. Trebuie spus că în curs şcolar matematicieni, acestea sunt metodele de rezolvare care sunt cele mai des folosite. Metoda grafică este deosebit de relevantă la rezolvarea problemelor C 5 din control și măsurare Materiale pentru examenul de stat unificat.

În continuare, am studiat, folosind mai multe exemple, alte modalități de rezolvare a ecuațiilor și inegalităților cu module și anume: metoda relevării modulelor; rezolvarea de ecuații care conțin module de expresii nenegative; rezolvarea ecuațiilor folosind interpretarea geometrică; folosind identitatea
; aplicarea teoremei semnului; rezolvarea ecuațiilor mergând la consecință, înmulțirea cu un factor pozitiv, precum și rezolvarea inegalităților prin metoda intervalelor.

Astfel, pe parcursul studiului am ajuns la următoarele concluzii.

Considerăm că metoda dezvăluirii modulelor, metoda grafică și metoda intervalelor sunt cele mai universale și aplicabile celui mai mare număr de probleme. Această convingere a apărut ca urmare a deciziei număr mare sarcini de la testarea și măsurarea materialelor din examenul de stat unificat, campionate de subiecte, probleme de olimpiade, precum și studierea literaturii pe această problemă. De asemenea, considerăm foarte importante cunoașterea și aplicarea identității
, deoarece este folosit nu numai pentru a rezolva ecuații și inegalități, ci și pentru a transforma multe expresii cu radicali. Restul metodelor de rezolvare pe care le-am luat în considerare sunt cu siguranță de mare interes în ceea ce privește extinderea orizontului matematic și general dezvoltare matematică. Prin urmare, intenționăm să le folosim pentru a ne pregăti pentru certificarea finală de stat în Formularul de examinare unificată de statși pregătirea pentru studii la o instituție de învățământ superior.

Lista literaturii folosite.

„Big Mathematical Encyclopedia” pentru școlari și elevi;

Matematică. Examen de stat unificat - 2011, 2012. Opțiuni de examen model. / Editat de A.L. Semenova, I.V. Iascenko.

M.Ya. Vygodski. Manual de matematică elementară

„Cea mai nouă carte de referință pentru școlari”;

Enciclopedie „Explorez lumea. Matematică";

;

Acest articol este dedicat tehnicilor de rezolvare a diferitelor ecuații și inegalități care conțin
variabilă sub semnul modulului.

Dacă întâlniți o ecuație sau o inegalitate cu un modul în examen, o puteți rezolva prin
fără a cunoaște deloc metode speciale și folosind doar definiția modulului. Este adevărat,
Acest lucru poate dura o oră și jumătate de timp prețios pentru examen.

De aceea, vrem să vă vorbim despre tehnici care simplifică rezolvarea unor astfel de probleme.

În primul rând, să ne amintim asta

Să luăm în considerare diverse tipuri ecuații cu modul. (Vom trece la inegalități mai târziu.)

Modul în stânga, numărul în dreapta

Acesta este cel mai simplu caz. Să rezolvăm ecuația

Există doar două numere ale căror module sunt egale cu patru. Acestea sunt 4 și -4. Prin urmare, ecuația
este echivalent cu combinarea a două simple:

A doua ecuație nu are soluții. Soluții la prima: x = 0 și x = 5.

Răspuns: 0; 5.

Variabilă atât sub modul cât și în exterior

Aici trebuie să extindem modulul prin definiție. . . sau gandeste-te!

Ecuația se împarte în două cazuri, în funcție de semnul expresiei sub modul.
Cu alte cuvinte, este echivalent cu o combinație de două sisteme:

Rezolvarea primului sistem: . Al doilea sistem nu are soluții.
Raspuns: 1.

Primul caz: x ≥ 3. Scoateți modulul:

Numărul, fiind negativ, nu satisface condiția x ≥ 3 și, prin urmare, nu este o rădăcină a ecuației inițiale.

Să aflăm dacă satisface această condiție numarul . Pentru a face acest lucru, compunem diferența și determinăm semnul acesteia:

Aceasta înseamnă că este mai mare decât trei și, prin urmare, este rădăcina ecuației originale

Al doilea caz: x< 3. Снимаем модуль:

Numărul . mai mare decât și, prin urmare, nu satisface condiția x< 3. Проверим :

Înseamnă, . este rădăcina ecuației inițiale.

Eliminarea unui modul prin definiție? E înfricoșător chiar și să te gândești la asta, pentru că discriminantul nu este un pătrat perfect. Să folosim mai bine următoarea considerație: o ecuație de forma |A| = B este echivalent cu combinația a două sisteme:

Același lucru, dar puțin diferit:

Cu alte cuvinte, rezolvăm două ecuații, A = B și A = −B, apoi selectăm rădăcini care îndeplinesc condiția B ≥ 0.

Să începem. Mai întâi rezolvăm prima ecuație:

Apoi rezolvăm a doua ecuație:

Acum, în fiecare caz, verificăm semnul din partea dreaptă:

Prin urmare, numai și sunt potrivite.

Ecuații cuadratice cu înlocuire |x| = t

Să rezolvăm ecuația:

Deoarece , este convenabil să faceți înlocuirea |x| = t. Primim:

Răspuns: ±1.

Modulul egal cu modulul

Vorbim de ecuații de forma |A| = |B|. Acesta este un dar al destinului. Fără dezvăluiri de module prin definiție! Este simplu:

De exemplu, luați în considerare ecuația: . Este echivalent cu următorul set:

Rămâne să rezolvi fiecare dintre ecuațiile mulțimii și să notezi răspunsul.

Două sau mai multe module

Să rezolvăm ecuația:

Să nu ne deranjam cu fiecare modul separat și să-l deschidem prin definiție - vor fi prea multe opțiuni. Există o modalitate mai rațională - metoda intervalului.

Expresiile modulului dispar în punctele x = 1, x = 2 și x = 3. Aceste puncte împart linia numerică în patru intervale (intervale). Să notăm aceste puncte pe linia numerică și să plasăm semne pentru fiecare dintre expresiile de sub module pe intervalele rezultate. (Ordinea semnelor coincide cu ordinea modulelor corespunzătoare din ecuație.)

Astfel, trebuie să luăm în considerare patru cazuri - când x este în fiecare dintre intervale.

Cazul 1: x ≥ 3. Toate modulele sunt eliminate „cu un plus”:

Valoarea rezultată x = 5 satisface condiția x ≥ 3 și, prin urmare, este rădăcina ecuației inițiale.

Cazul 2: 2 ≤ x ≤ 3. Ultimul modul este acum eliminat „cu minus”:

Valoarea rezultată a lui x este de asemenea potrivită - aparține intervalului luat în considerare.

Cazul 3: 1 ≤ x ≤ 2. Al doilea și al treilea modul sunt eliminate „cu minus”:

Am obținut egalitatea numerică corectă pentru orice x din intervalul luat în considerare, acestea servesc ca soluții pentru această ecuație.

Cazul 4: x ≤ 1 ≤ 1. Al doilea și al treilea modul sunt eliminate „cu minus”:

Nimic nou. Știm deja că x = 1 este o soluție.

Răspuns: ∪ (5).

Modul în cadrul unui modul

Să rezolvăm ecuația:

Începem prin a deschide modulul intern.

1) x ≤ 3. Se obține:

Expresia sub modul dispare la . Acest punct aparține celui în cauză
între. Prin urmare, trebuie să analizăm două subcazuri.

1.1) În acest caz obținem:

Această valoare x nu este potrivită deoarece nu aparține intervalului luat în considerare.

1.2). Apoi:

Această valoare x nu este, de asemenea, bună.

Deci, pentru x ≤ 3 nu există soluții. Să trecem la al doilea caz.

2) x ≥ 3. Avem:

Aici avem noroc: expresia x + 2 este pozitivă în intervalul luat în considerare! Prin urmare, nu vor mai exista subcazuri: modulul este eliminat „cu un plus”:

Această valoare a lui x se află în intervalul luat în considerare și, prin urmare, este rădăcina ecuației originale.

Așa se rezolvă toate problemele de acest tip - deschidem modulele imbricate unul câte unul, începând cu cel intern.