Distribuție binomială: definiție, formulă, exemple. Distribuție binomială. Distribuții discrete în EXCEL Distribuție binomială formele sale limitative
Să luăm în considerare implementarea schemei Bernoulli, i.e. Se efectuează o serie de teste independente repetate, în fiecare dintre ele un anumit eveniment A are aceeași probabilitate, independent de numărul testului. Și pentru fiecare test există doar două rezultate:
1) evenimentul A - succes;
2) eveniment - eșec,
cu probabilităţi constante
Să introducem în considerare o variabilă aleatoare discretă X - „numărul de apariții ale evenimentului A la n teste" și găsiți legea de distribuție a acestei variabile aleatoare. Valoarea X poate lua următoarele valori:
Probabilitate 
că variabila aleatoare X va lua valoarea x k găsit prin formula lui Bernoulli
Legea de distribuție a unei variabile aleatoare discrete, definită de formula Bernoulli (1), se numește legea distribuției binomiale. Permanent n Şi r (q=1-p), cuprinse în formula (1) se numesc parametrii distribuţiei binomiale.
Denumirea „distribuție binomială” se datorează faptului că partea dreaptă în egalitate (1) este termenul general al expansiunii binomului lui Newton, i.e.
(2)
Și de când p+q=1, atunci partea dreaptă a egalității (2) este egală cu 1
Aceasta înseamnă că
(4)
În egalitate (3) primul termen qnîn partea dreaptă înseamnă probabilitatea ca în n teste, evenimentul A nu va apărea nici măcar o dată, al doilea termen 
probabilitatea ca evenimentul A să apară o dată, al treilea termen este probabilitatea ca evenimentul A să apară de două ori și, în final, ultimul termen r p- probabilitatea ca evenimentul A să se producă exact n dată.
Legea binomială de distribuție a unei variabile aleatoare discrete este prezentată sub forma unui tabel:
| X | 0 | 1 | … | k | … | n |
| R | qn | … | 
|
… | r p |
De bază caracteristici numerice distributie binomiala:
1) așteptări matematice 
(5)
2) dispersie 
(6)
3) abaterea standard 
(7)
4) numărul cel mai probabil de apariții ale evenimentului k 0- acesta este numărul care, pentru un dat n corespunde probabilității binomiale maxime
Pentru dat nŞi r acest număr este determinat de inegalități
(8)
dacă număr pr+r nu este intreg, atunci k 0 egal cu partea întreagă a acestui număr, dacă pr+r este un număr întreg, atunci k 0 are două sensuri
Legea binomială a distribuției probabilităților este utilizată în teoria tirului, în teoria și practica controlului statistic al calității produselor, în teorie la coadă, în teoria fiabilității etc. Această lege poate fi aplicată în toate cazurile în care există o succesiune de teste independente.
Exemplul 1: Testele de calitate au stabilit că din 100 de dispozitive, 90 în medie nu prezintă defecte. Întocmește o lege binomială a distribuției probabilității a numărului de dispozitive de înaltă calitate achiziționate la întâmplare 4.
Soluţie: Evenimentul A, a cărui apariție este verificată, este „un dispozitiv de înaltă calitate achiziționat la întâmplare”. În funcție de condițiile problemei, principalii parametri ai distribuției binomiale sunt:
Variabila aleatorie X este numărul de dispozitive de înaltă calitate din 4 luate, ceea ce înseamnă valorile lui X - Să găsim probabilitățile valorilor lui X folosind formula (1):
Astfel, legea distribuției valorii X este numărul de dispozitive de înaltă calitate din 4 luate:
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Pentru a verifica corectitudinea construcției distribuției, să verificăm cu ce suma probabilităților este egală cu
Răspuns: Legea distribuției
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Exemplul 2: Metoda de tratament folosita duce la recuperare in 95% din cazuri. Au folosit cinci pacienți această metodă. Găsiți cel mai probabil număr de persoane recuperate, precum și caracteristicile numerice ale variabilei aleatoare X - numărul de persoane recuperate din 5 pacienți care au folosit această metodă.
Desigur, atunci când calculați funcția de distribuție cumulativă, ar trebui să utilizați conexiunea menționată între distribuțiile binomiale și beta. Această metodă este în mod evident mai bună decât însumarea directă atunci când n > 10.
În manualele clasice de statistică, pentru a obține valorile distribuției binomiale, se recomandă adesea utilizarea formulelor bazate pe teoreme limită (cum ar fi formula Moivre-Laplace). Trebuie remarcat faptul că din punct de vedere pur computaţional valoarea acestor teoreme este aproape de zero, mai ales acum, când aproape fiecare birou are un computer puternic. Principalul dezavantaj al aproximărilor de mai sus este acuratețea lor complet insuficientă pentru valorile de n caracteristice majorității aplicațiilor. Nu mai puțin un dezavantaj este absența oricăror recomandări clare cu privire la aplicabilitatea uneia sau aceleia aproximări (textele standard oferă doar formulări asimptotice; ele nu sunt însoțite de estimări de acuratețe și, prin urmare, sunt de puțin folos). Aș spune că ambele formule sunt potrivite doar pentru n< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Nu mă gândesc aici la problema găsirii cuantilelor: pentru distribuțiile discrete este banală, iar în acele probleme în care apar astfel de distribuții, nu este, de regulă, relevantă. Dacă mai sunt necesare cuantile, recomand reformularea problemei în așa fel încât să se lucreze cu valorile p (semnificații observate). Iată un exemplu: la implementarea unor algoritmi exhaustivi de căutare, la fiecare pas este necesară testarea ipotezei statistice despre o variabilă aleatoare binomială. Conform abordare clasică La fiecare pas, trebuie să calculați statistica criteriului și să comparați valoarea acesteia cu limita setului critic. Deoarece, totuși, algoritmul este exhaustiv, este necesar să se determine din nou granița setului critic de fiecare dată (la urma urmei, dimensiunea eșantionului se schimbă de la pas la pas), ceea ce crește neproductiv costurile de timp. Abordare modernă recomandă calcularea semnificației observate și compararea acesteia cu probabilitatea de încredere, economisind la căutarea cuantilelor.
Prin urmare, în codurile de mai jos nu există un calcul al funcției inverse în schimb, este dată funcția rev_binomialDF, care calculează probabilitatea p de succes într-o încercare individuală având în vedere numărul dat n de încercări, numărul m de succese în ele; valoarea y a probabilităţii obţinerii acestor m succese. Aceasta folosește conexiunea menționată mai sus dintre distribuțiile binomiale și beta.
De fapt, această funcție vă permite să obțineți limitele intervalelor de încredere. Într-adevăr, să presupunem că în n încercări binomiale avem m succese. După cum se știe, limita din stânga a intervalului de încredere cu două fețe pentru parametrul p cu un nivel de încredere este egală cu 0 dacă m = 0 și for este o soluție a ecuației 
. În mod similar, limita dreaptă este 1 dacă m = n și pentru este o soluție a ecuației 
. Rezultă că pentru a găsi limita stângă trebuie să rezolvăm ecuația relativă 
, și pentru a găsi cea potrivită - ecuația 
. Acestea sunt rezolvate în funcțiile binom_leftCI și binom_rightCI, care returnează limitele superioare și, respectiv, inferioare ale intervalului de încredere cu două fețe.
Aș dori să observ că, dacă nu aveți nevoie de o precizie absolut incredibilă, atunci pentru n suficient de mare puteți utiliza următoarea aproximare [B.L. van der Waerden, Statistica matematică. M: IL, 1960, cap. 2, secțiunea 7]: 
, unde g este o cuantilă a distribuției normale. Valoarea acestei aproximări este că există aproximări foarte simple care vă permit să calculați cuantile ale unei distribuții normale (vezi textul despre calcularea distribuției normale și secțiunea corespunzătoare a acestei cărți de referință). În practica mea (în principal cu n > 100), această aproximare a dat aproximativ 3-4 cifre, ceea ce, de regulă, este destul de suficient.
Pentru a calcula folosind următoarele coduri, veți avea nevoie de fișierele betaDF.h, betaDF.cpp (vezi secțiunea despre distribuția beta), precum și de logGamma.h, logGamma.cpp (vezi Anexa A). De asemenea, puteți vedea un exemplu de utilizare a funcțiilor.
Fișier binomDF.h
| #ifndef __BINOMIAL_H__ #include "betaDF.h" binom dubluDF(încercări duble, succese duble, p dublu); /* * Să fie „încercări” de observații independente * cu probabilitatea „p” de succes în fiecare. |
* Calculați probabilitatea B(reușite|încercări,p) ca numărul * reușite să fie între 0 și „reușite” (inclusiv).
| */ double rev_binomialDF(încercări duble, succese duble, y dublu); /* * Fie cunoscută probabilitatea y a cel puțin m succese * în încercările de testare a schemei Bernoulli. Funcția găsește probabilitatea p* de succes într-o încercare individuală. |
altfel returnează BetaDF(n-m, m+1).valoare(1-p); )/* binomialDF */ ENTRY double rev_binomialDF(double n, double m, double y) /* * Fie probabilitatea y a cel puțin m succese să apară * în n încercări ale schemei Bernoulli. Funcția găsește probabilitatea p* de succes într-o încercare individuală. * * Următoarea relație este utilizată în calcule * * 1 - p = rev_Beta(y|n-m,m+1). */ ( afirmă ((n > 0) && (m >= 0) && (m= 0) && (y 0) && (m >= 0) && (m= 0,5) && (y n Distribuția binomială este una dintre cele mai importante distribuții de probabilitate ale unei variabile aleatoare care variază discret. Distribuția binomială este distribuția de probabilitate a numărului 0) && (m >= 0) && (m m
producerea unui eveniment:
- O n V 0) && (m >= 0) && (m observații reciproc independente
- . Adesea un eveniment 0) && (m >= 0) && (m se numește „succesul” unei observații, iar evenimentul opus se numește „eșec”, dar această desemnare este foarte condiționată. Condiții de distribuție binomială;
- în total efectuate
procese în care evenimentul n poate sau nu să apară; 0) && (m >= 0) && (m eveniment */ ( afirmă ((n > 0) && (m >= 0) && (mîn fiecare încercare poate apărea cu aceeași probabilitate
p Condiții de distribuție binomială testele sunt independente reciproc. 0) && (m >= 0) && (m;
Probabilitatea ca în = 1 - Condiții de distribuție binomială eveniment de testare
va veni exact ori, poate fi calculat folosind formula lui Bernoulli: Unde n- probabilitatea producerii unui eveniment */ ( afirmă ((n > 0) && (m >= 0) && (m q n - */ ( afirmă ((n > 0) && (m >= 0) && (m- probabilitatea producerii evenimentului opus. Să ne dăm seama1 de ce distribuția binomială este legată de formula lui Bernoulli în modul descris mai sus?
,
. Eveniment - numărul de succese la Probabilitatea ca în = 1 - Condiții de distribuție binomială testele sunt împărțite într-un număr de opțiuni, în fiecare dintre acestea succesul este obținut în
.
teste, și eșec - în */ ( afirmă ((n > 0) && (m >= 0) && (m teste. Să luăm în considerare una dintre aceste opțiuni - n - */ ( afirmă ((n > 0) && (m >= 0) && (m B n. Folosind regula de adunare a probabilităților, înmulțim probabilitățile evenimentelor opuse: */ ( afirmă ((n > 0) && (m >= 0) && (m iar dacă notăm
, Asta */ ( afirmă ((n > 0) && (m >= 0) && (m numere de apariție a evenimentului 0) && (m >= 0) && (m(numerele de la 0 la n) este egal cu unu:
unde fiecare termen reprezintă un termen din binomul lui Newton. Prin urmare, distribuția luată în considerare se numește distribuție binomială.
În practică, este adesea necesar să se calculeze probabilitățile „nu mai mult de */ ( afirmă ((n > 0) && (m >= 0) && (m succes in n teste” sau „cel puțin */ ( afirmă ((n > 0) && (m >= 0) && (m succes in n teste". Pentru aceasta se folosesc următoarele formule.
Funcția integrală, adică probabilitate F(*/ ( afirmă ((n > 0) && (m >= 0) && (m) ce este în n eveniment observațional 0) && (m >= 0) && (m nu va mai veni */ ( afirmă ((n > 0) && (m >= 0) && (m dată, poate fi calculat folosind formula:
La rândul său probabilitate F(≥*/ ( afirmă ((n > 0) && (m >= 0) && (m) ce este în n eveniment observațional 0) && (m >= 0) && (m va veni nici mai puțin */ ( afirmă ((n > 0) && (m >= 0) && (m dată, se calculează prin formula:
Uneori este mai convenabil să se calculeze probabilitatea ca n eveniment observațional 0) && (m >= 0) && (m nu va mai veni */ ( afirmă ((n > 0) && (m >= 0) && (m ori, prin probabilitatea evenimentului opus:
.
Ce formulă de utilizat depinde de care dintre ele are suma care conține mai puțini termeni.
Caracteristicile distribuției binomiale se calculează folosind următoarele formule .
Aşteptare matematică: .
Dispersie: .
Abatere standard: .
Distribuție binomială și calcule în MS Excel
Probabilitate binomială P n( */ ( afirmă ((n > 0) && (m >= 0) && (m) și valorile funcției integrale F(*/ ( afirmă ((n > 0) && (m >= 0) && (m) poate fi calculat folosind funcția MS Excel BINOM.DIST. Fereastra pentru calculul corespunzător este prezentată mai jos (clic stânga pentru mărire).
MS Excel vă solicită să introduceți următoarele date:
- numărul de succese;
- numărul de teste;
- probabilitatea de succes;
- integrală - valoare logică: 0 - dacă trebuie să calculați probabilitatea P n( */ ( afirmă ((n > 0) && (m >= 0) && (m) și 1 - dacă probabilitatea F(*/ ( afirmă ((n > 0) && (m >= 0) && (m).
Exemplul 1. Managerul companiei a rezumat informații despre numărul de camere vândute în ultimele 100 de zile. Tabelul rezumă informațiile și calculează probabilitățile ca un anumit număr de camere să fie vândute pe zi.
Ziua se încheie cu un profit dacă sunt vândute 13 sau mai multe camere. Probabilitatea ca ziua să fie lucrată profitabil:
Probabilitatea ca o zi să fie lucrată fără profit:
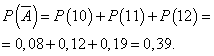
Fie ca probabilitatea ca o zi să fie lucrată cu profit să fie constantă și egală cu 0,61, iar numărul de camere vândute pe zi nu depinde de zi. Apoi putem folosi distribuția binomială, unde evenimentul 0) && (m >= 0) && (m- ziua se va lucra cu profit, - fara profit.
Probabilitatea ca toate cele 6 zile să fie rezolvate cu profit:
.
Obținem același rezultat folosind funcția MS Excel BINOM.DIST (valoarea valorii integrale este 0):
P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.
Probabilitatea ca din 6 zile 4 sau mai multe zile să fie lucrate cu profit:
p 
,
,
Folosind funcția MS Excel BINOM.DIST, calculăm probabilitatea ca din 6 zile nu mai mult de 3 zile să fie finalizate cu profit (valoarea valorii integrale este 1):
P 6 (≤3 ) = BINOM.DIST(3; 6; 0,61; 1) = 0,435.
Probabilitatea ca toate cele 6 zile să fie rezolvate cu pierderi:
,
Putem calcula același indicator folosind funcția MS Excel BINOM.DIST:
P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.
Rezolvați singur problema și apoi vedeți soluția
Exemplul 2.În urnă sunt 2 bile albe și 3 bile negre. Se scoate o minge din urna, se pune culoarea si se pune la loc. Încercarea se repetă de 5 ori. Numărul de apariții de bile albe este discret variabilă aleatoare X, distribuit conform legii binomiale. Întocmește o lege de distribuție a unei variabile aleatoare. Definiți modul, așteptările matematice și dispersia.
Să continuăm să rezolvăm problemele împreună
Exemplul 3. De la serviciul de curierat am mers pe site-uri n= 5 curieri. Fiecare curier este probabil Condiții de distribuție binomială= 0,3, indiferent de altele, este întârziat pentru obiect. Variabilă aleatorie discretă X- numarul de curieri intarziati. Construiți o serie de distribuție pentru această variabilă aleatoare. Găsiți așteptările sale matematice, varianța, abaterea standard. Găsiți probabilitatea ca cel puțin doi curieri să întârzie obiectele.
Capitolul 7.
Legile specifice de distribuție a variabilelor aleatoare
Tipuri de legi de distribuție a variabilelor aleatoare discrete
Fie ca o variabilă aleatorie discretă să ia valorile X 1 , X 2 , …, x n,…. Probabilitățile acestor valori pot fi calculate folosind diverse formule, de exemplu, folosind teoremele de bază ale teoriei probabilităților, formula lui Bernoulli sau alte formule. Pentru unele dintre aceste formule, legea distribuției are propriul nume.
Cele mai comune legi ale distribuției unei variabile aleatoare discrete sunt legea binomială, geometrică, hipergeometrică și Poisson.
Legea distribuției binomiale
Lasă-l să fie produs n procese independente, în fiecare dintre ele evenimentul poate apărea sau nu 0) && (m >= 0) && (m. Probabilitatea ca acest eveniment să apară în fiecare încercare este constantă, nu depinde de numărul încercării și este egală cu r=R(0) && (m >= 0) && (m). De aici probabilitatea ca evenimentul să nu se producă 0) && (m >= 0) && (mîn fiecare test este de asemenea constantă și egală Probabilitatea ca în=1–r. Luați în considerare variabila aleatoare X egal cu numărul de apariţii ale evenimentului 0) && (m >= 0) && (m V n teste. Evident, valorile acestei cantități sunt egale
X 1 =0 – eveniment 0) && (m >= 0) && (m V n testele nu au apărut;
X 2 =1 – eveniment 0) && (m >= 0) && (m V n a apărut o dată în procese;
X 3 =2 – eveniment 0) && (m >= 0) && (m V n testele au apărut de două ori;
…………………………………………………………..
x n +1 = n- eveniment 0) && (m >= 0) && (m V n totul a apărut în timpul testelor n dată.
Probabilitățile acestor valori pot fi calculate folosind formula Bernoulli (4.1):
p La=0, 1, 2, …,n .
Legea distribuției binomiale X, egală cu numărul succes in n Teste Bernoulli, cu probabilitate de succes r.
Deci, o variabilă aleatorie discretă are o distribuție binomială (sau este distribuită conform legii binomiale) dacă valorile sale posibile sunt 0, 1, 2, ..., n, iar probabilitățile corespunzătoare sunt calculate folosind formula (7.1).
Distribuția binomială depinde de două parametrii rŞi n.
Seria de distribuție a unei variabile aleatoare distribuite conform legii binomiale are forma:
| X | … | k | … | n | ||
| R |  | … | … |  |
Exemplu 7.1 . Trei focuri independente sunt trase în țintă. Probabilitatea de a lovi fiecare lovitură este de 0,4. Variabila aleatoare X– numărul de lovituri pe țintă. Construiți-i seria de distribuție.
Soluţie. Valori posibile ale unei variabile aleatorii X sunt X 1 =0; X 2 =1; X 3 =2; X 4 =3. Să găsim probabilitățile corespunzătoare folosind formula lui Bernoulli. Nu este greu de demonstrat că folosirea acestei formule aici este complet justificată. Rețineți că probabilitatea de a nu lovi ținta cu o singură lovitură va fi egală cu 1-0,4=0,6. Primim
Seria de distribuție are următoarea formă:
| X | ||||
| R | 0,216 | 0,432 | 0,288 | 0,064 |
Este ușor de verificat că suma tuturor probabilităților este egală cu 1. Variabila aleatoare în sine X distribuite conform legii binomiale. ■
Să găsim așteptarea și varianța matematică a unei variabile aleatoare distribuite conform legii binomiale.
La rezolvarea Exemplului 6.5, s-a arătat că așteptarea matematică a numărului de apariții ale evenimentului 0) && (m >= 0) && (m V n studii independente, dacă probabilitatea apariției 0) && (m >= 0) && (mîn fiecare test este constantă și egală r, egal n· r
Acest exemplu a folosit o variabilă aleatoare distribuită conform legii binomiale. Prin urmare, soluția la Exemplul 6.5 este în esență o demonstrație a următoarei teoreme.
Teorema 7.1. Așteptarea matematică a unei variabile aleatoare discrete distribuite conform legii binomiale este egală cu produsul dintre numărul de încercări și probabilitatea de „reușită”, i.e. M(X)=n· r.
Teorema 7.2. Varianta unei variabile aleatoare discrete distribuite conform legii binomiale este egală cu produsul dintre numărul de încercări cu probabilitatea de „reușit” și probabilitatea de „eșec”, i.e. D(X)=nрq.
Asimetria și curtoza unei variabile aleatoare distribuite conform legii binomiale sunt determinate de formulele
Aceste formule pot fi obținute folosind conceptul de momente inițiale și centrale.
Legea distribuției binomiale stă la baza multor situații din viața reală. Pentru valori mari n Distribuția binomială poate fi aproximată folosind alte distribuții, în special distribuția Poisson.
Distribuția Poisson
Să fie n Testele Bernoulli, cu numărul de teste n destul de mare. S-a arătat mai devreme că în acest caz (dacă, în plus, probabilitatea r evenimentelor 0) && (m >= 0) && (m foarte mic) pentru a afla probabilitatea ca evenimentul 0) && (m >= 0) && (m apărea T Odată ajuns la teste, puteți utiliza formula Poisson (4.9). Dacă variabila aleatoare Xînseamnă numărul de apariții ale evenimentului 0) && (m >= 0) && (m V n Bernoulli teste, apoi probabilitatea ca X va lua valoarea k poate fi calculat folosind formula
, (7.2)
p λ = nр.
Legea distribuției Poisson se numește distribuția unei variabile aleatoare discrete X, pentru care valorile posibile sunt numere întregi numere nenegative, și probabilitățile r t aceste valori se găsesc folosind formula (7.2).
Magnitudinea λ = nр numit parametru Distribuții Poisson.
O variabilă aleatoare distribuită conform legii lui Poisson poate lua un număr infinit de valori. Deoarece pentru această distribuţie probabilitatea r Apariția unui eveniment în fiecare proces este mică, atunci această distribuție este uneori numită legea evenimentelor rare.
Seria de distribuție a unei variabile aleatoare distribuită conform legii lui Poisson are forma
| X | … | T | … | ||||
| R | … | … |
Este ușor să verificați că suma probabilităților celui de-al doilea rând este egală cu 1. Pentru a face acest lucru, trebuie să vă amintiți că funcția poate fi extinsă într-o serie Maclaurin, care converge pentru orice X. ÎN în acest caz, avem
. (7.3)
După cum sa menționat, legea lui Poisson înlocuiește legea binomială în anumite cazuri limitative. Un exemplu este variabila aleatoare X, ale căror valori sunt egale cu numărul de defecțiuni într-o anumită perioadă de timp în timpul utilizării repetate a unui dispozitiv tehnic. Se presupune că acesta este un dispozitiv extrem de fiabil, de ex. Probabilitatea de eșec într-o singură aplicație este foarte mică.
Pe lângă astfel de cazuri limitative, în practică există variabile aleatoare distribuite conform legii lui Poisson care nu sunt asociate cu distribuția binomială. De exemplu, distribuția Poisson este adesea folosită atunci când se tratează numărul de evenimente care au loc într-o perioadă de timp (numărul de apeluri primite la o centrală telefonică în timpul unei ore, numărul de mașini care sosesc la o spălătorie în timpul unei zile, numărul de opriri ale mașinii pe săptămână etc.). Toate aceste evenimente ar trebui să formeze așa-numitul flux de evenimente, care este unul dintre conceptele de bază ale teoriei cozilor de așteptare. Parametru λ caracterizează intensitatea medie a fluxului de evenimente.
Exemplu 7.2 . La facultate sunt 500 de studenți. Care este probabilitatea ca 1 septembrie să fie ziua de naștere a trei studenți din această secție?
Soluţie . De la numărul de elevi n=500 este destul de mare și r– probabilitatea ca orice elev să se nască la 1 septembrie este egală cu , i.e. este suficient de mic, atunci putem presupune că variabila aleatoare X– numărul elevilor născuți la 1 septembrie este repartizat conform legii lui Poisson cu parametrul λ = n.p.= =1,36986. Apoi, conform formulei (7.2) obținem
Teorema 7.3. Fie variabila aleatoare X distribuite conform legii lui Poisson. Atunci așteptarea și varianța sa matematică sunt egale între ele și egale cu valoarea parametrului λ , adică M(X) = D(X) = λ = n.p..
Dovada. Prin definiția așteptărilor matematice, folosind formula (7.3) și seria de distribuție a unei variabile aleatoare distribuite conform legii lui Poisson, obținem
Înainte de a găsi varianța, găsim mai întâi așteptarea matematică a pătratului variabilei aleatoare luate în considerare. Primim
De aici, prin definiția dispersiei, obținem
Teorema a fost demonstrată.
Folosind conceptele de momente inițiale și centrale, se poate demonstra că pentru o variabilă aleatoare distribuită conform legii lui Poisson, coeficienții de asimetrie și curtoză sunt determinați de formulele
Nu este greu de înțeles că, din moment ce conținutul semantic al parametrului λ = n.p. este pozitivă, atunci o variabilă aleatoare distribuită conform legii lui Poisson are întotdeauna asimetrie și curtoză pozitive.
Nu toate fenomenele sunt măsurate pe o scară cantitativă precum 1, 2, 3... 100500... Un fenomen nu poate lua întotdeauna un număr infinit sau mare de stări diferite. De exemplu, genul unei persoane poate fi M sau F. trăgătorul fie lovește ținta, fie ratează. Puteți vota fie „pentru”, fie „împotrivă”, etc. etc. Cu alte cuvinte, astfel de date reflectă starea unui atribut alternativ - fie „da” (evenimentul a avut loc), fie „nu” (evenimentul nu a avut loc). Evenimentul care apare (rezultatul pozitiv) se mai numește și „succes”.
Se numesc experimente cu astfel de date Schema Bernoulli, în onoarea renumitului matematician elvețian care a constatat că, cu un număr mare de încercări, raportul dintre rezultatele pozitive și numărul total de încercări tinde la probabilitatea apariției acestui eveniment.
Variabilă caracteristică alternativă
Pentru a utiliza aparate matematice în analiză, rezultatele acestor observații trebuie înregistrate în formă numerică. Pentru a face acest lucru, unui rezultat pozitiv i se atribuie numărul 1, un rezultat negativ - 0. Cu alte cuvinte, avem de-a face cu o variabilă care poate lua doar două valori: 0 sau 1.
Ce beneficii se poate obține din asta? De fapt, nu mai puțin decât din date obișnuite. Astfel, este ușor să calculați numărul de rezultate pozitive - doar însumați toate valorile, de exemplu. toate 1 (succes). Puteți merge mai departe, dar acest lucru va necesita să introduceți câteva notații.
Primul lucru de remarcat este că rezultatele pozitive (care sunt egale cu 1) au o anumită probabilitate de a apărea. De exemplu, obținerea capetelor atunci când aruncați o monedă este ½ sau 0,5. Această probabilitate este indicată în mod tradițional de litera latină Condiții de distribuție binomială. Prin urmare, probabilitatea ca un eveniment alternativ să se producă este egală cu 1 - p, care se notează și prin Probabilitatea ca în, adică q = 1 – p. Aceste notații pot fi sistematizate clar sub forma unui tabel de distribuție variabilă X.
Am primit o listă de valori posibile și probabilitățile acestora. Poate fi calculat așteptări matematiceŞi dispersie. Așteptarea este suma produselor tuturor valorilor posibile și probabilitățile lor corespunzătoare:
Să calculăm așteptarea folosind notația din tabelele de mai sus.
Se pare că așteptarea matematică a unui semn alternativ este egală cu probabilitatea acestui eveniment - Condiții de distribuție binomială.
Acum să definim care este varianța unui atribut alternativ. Dispersia este pătratul mediu al abaterilor de la așteptarea matematică. Formula generala(pentru date discrete) are forma:
Prin urmare, varianța atributului alternativ:
Este ușor de observat că această dispersie are un maxim de 0,25 (cu p=0,5).
Abaterea standard este rădăcina varianței:
Valoarea maximă nu depășește 0,5.
După cum puteți vedea, atât așteptarea matematică, cât și varianța atributului alternativ au o formă foarte compactă.
Distribuția binomială a unei variabile aleatoare
Să privim situația dintr-un unghi diferit. Într-adevăr, cui îi pasă că pierderea medie de capete la aruncare este de 0,5? Este chiar imposibil de imaginat. Este mai interesant să punem întrebarea despre numărul de capete care apar pentru un anumit număr de aruncări.
Cu alte cuvinte, cercetătorul este adesea interesat de probabilitatea ca un anumit număr de evenimente de succes să aibă loc. Acesta poate fi numărul de produse defecte din lotul testat (1 - defect, 0 - bun) sau numărul de recuperări (1 - sănătos, 0 - bolnav), etc. Numărul de astfel de „reușite” va fi egal cu suma tuturor valorilor variabilei X, adică numărul de rezultate unice.
Variabila aleatoare Să ne dăm seama se numește binom și ia valori de la 0 la n(la Să ne dăm seama= 0 – toate piesele sunt potrivite, cu Să ne dăm seama = n– toate piesele sunt defecte). Se presupune că toate valorile x independente unele de altele. Să luăm în considerare principalele caracteristici ale unei variabile binomiale, adică vom stabili așteptarea, dispersia și distribuția ei matematică.
Așteptarea unei variabile binomiale este foarte ușor de obținut. Așteptările matematice ale sumei cantităților este suma așteptărilor matematice ale fiecărei mărimi adăugate și este aceeași pentru toată lumea, prin urmare:
De exemplu, așteptarea matematică a numărului de capete scăzute în 100 de aruncări este 100 × 0,5 = 50.
Acum derivăm formula pentru dispersia unei variabile binomiale. Varianța sumei variabilelor aleatoare independente este suma varianțelor. De aici
Abaterea standard, respectiv
Pentru 100 de aruncări de monede, abaterea standard a numărului de capete este
În cele din urmă, luați în considerare distribuția valorii binomului, i.e. probabilitatea ca variabila aleatoare Să ne dăm seama va accepta sensuri diferite k, Unde 0≤k≤n. Pentru o monedă, această problemă ar putea arăta astfel: Care este probabilitatea de a obține 40 de capete la 100 de aruncări?
Pentru a înțelege metoda de calcul, imaginați-vă că moneda este aruncată doar de 4 ori. Oricare parte poate cădea de fiecare dată. Ne întrebăm: care este probabilitatea de a obține 2 capete din 4 aruncări. Fiecare aruncare este independentă una de cealaltă. Aceasta înseamnă că probabilitatea de a obține orice combinație va fi egală cu produsul dintre probabilitățile unui rezultat dat pentru fiecare aruncare individuală. Fie O capete și P cozi. Atunci, de exemplu, una dintre combinațiile care ni se potrivesc poate arăta ca OOPP, adică:
Probabilitatea unei astfel de combinații este egală cu produsul dintre două probabilități de a obține capete și alte două probabilități de a nu obține capete (evenimentul invers, calculat ca 1 - p), adică 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Aceasta este probabilitatea uneia dintre combinațiile care ni se potrivește. Dar întrebarea era despre numărul total de vulturi, și nu despre o anumită ordine. Apoi trebuie să adunați probabilitățile tuturor combinațiilor în care există exact 2 capete. În mod clar, toate sunt la fel (produsul nu se schimbă atunci când se modifică factorii). Prin urmare, trebuie să calculați numărul lor și apoi să le înmulțiți cu probabilitatea unei astfel de combinații. Să numărăm toate combinațiile posibile de 4 aruncări de 2 capete: RROO, RORO, ROOR, ORRO, OROR, OORR. Există 6 opțiuni în total.
Prin urmare, probabilitatea dorită de a obține 2 capete după 4 aruncări este 6×0,0625=0,375.
Cu toate acestea, numărarea în acest fel este plictisitoare. Deja pentru 10 monede, va fi foarte dificil să obțineți numărul total de opțiuni prin forță brută. De aceea oameni deștepți cu mult timp în urmă a inventat o formulă cu care să se calculeze numărul de combinații diferite de n elemente prin k, Unde n- numărul total de elemente, k– numărul de elemente ale căror opțiuni de aranjare sunt calculate. Combinația de formule a n elemente prin k este aceasta:
Lucruri similare se întâmplă în secțiunea de combinatorie. Trimit acolo pe oricine dorește să-și îmbunătățească cunoștințele. De aici, apropo, numele distribuției binomiale (formula de mai sus este un coeficient de extindere a binomului lui Newton).
Formula pentru determinarea probabilității poate fi generalizată cu ușurință la orice mărime nŞi k. Ca urmare, formula pentru distribuția binomială are următoarea formă.
Numărul de combinații care îndeplinesc condiția se înmulțește cu probabilitatea uneia dintre ele.
Pentru utilizare practică Este suficient doar să cunoaștem formula pentru distribuția binomială. Sau poate nici nu știți - mai jos vă arătăm cum să determinați probabilitatea folosind Excel. Dar e mai bine să știi.
Folosind această formulă, calculăm probabilitatea de a obține 40 de capete în 100 de aruncări:
Sau doar 1,08%. Spre comparație, probabilitatea așteptării matematice a acestui experiment, adică 50 de capete, fiind egală cu 7,96%. Probabilitatea maximă a unei valori binomiale aparține valorii corespunzătoare așteptării matematice.
Calcularea probabilității unei distribuții binomiale în Excel
Dacă utilizați doar hârtie și un calculator, calculele folosind formula de distribuție binomială, în ciuda absenței integralelor, sunt destul de dificile. De exemplu, valoarea este 100! – are mai mult de 150 de caractere. Anterior, și chiar acum, se foloseau formule aproximative pentru a calcula astfel de cantități. În acest moment, este recomandabil să folosiți software special, precum MS Excel. Astfel, orice utilizator (chiar și un umanist de pregătire) poate calcula cu ușurință probabilitatea valorii unei variabile aleatoare distribuite binomial.
Pentru a consolida materialul, vom folosi Excel pentru moment ca un calculator obișnuit, adică. Să efectuăm un calcul pas cu pas folosind formula de distribuție binomială. Să calculăm, de exemplu, probabilitatea de a obține 50 de capete. Mai jos este o poză cu pașii de calcul și rezultatul final.
După cum puteți vedea, rezultatele intermediare sunt de o asemenea amploare încât nu se potrivesc în celulă, deși sunt folosite peste tot funcții simple tipuri: FACTOR (calcul factorial), PUTERE (ridicarea unui număr la o putere), precum și operatori de înmulțire și împărțire. Mai mult, acest calcul este destul de greoi în orice caz, nu este compact, pentru că sunt implicate multe celule. Da, și este puțin greu de înțeles imediat.
În general, Excel oferă o funcție gata făcută pentru calcularea probabilităților unei distribuții binomiale. Funcția este numită BINOM.DIST.
Numărul de succese – numărul de teste reușite. Avem 50 dintre ele.
Numărul de teste – număr de aruncări: de 100 de ori.
Probabilitatea de succes – probabilitatea de a obține capete la o aruncare este de 0,5.
Integral – este indicat fie 1, fie 0 Dacă 0, atunci probabilitatea este calculată P(B=k); dacă 1, atunci se va calcula funcția de distribuție binomială, i.e. suma tuturor probabilităților de la B=0 la B=k inclusiv.
Faceți clic pe OK și obțineți același rezultat ca mai sus, doar totul a fost calculat de o funcție.
Foarte convenabil. De dragul experimentului, în loc de ultimul parametru 0, punem 1. Obținem 0,5398. Aceasta înseamnă că, cu 100 de aruncări de monede, probabilitatea de a obține capete între 0 și 50 este de aproape 54%. Dar la început părea că ar trebui să fie de 50%. În general, calculele se fac rapid și ușor.
Un analist real trebuie să înțeleagă cum se comportă funcția (care este distribuția ei), așa că vom calcula probabilitățile pentru toate valorile de la 0 la 100. Adică, vom pune întrebarea: care este probabilitatea ca nici un singur cap va apărea, va apărea acel 1 vultur, 2, 3, 50, 90 sau 100. Calculul este prezentat în imaginea următoare. Linia albastră este distribuția binomială în sine, punctul roșu este probabilitatea pentru un anumit număr de succese k.
Cineva ar putea întreba dacă distribuția binomială este similară cu... Da, foarte asemănătoare. Chiar și Moivre (în 1733) spunea că distribuția binomială cu eșantioane mari se apropie (nu știu cum se numea atunci), dar nimeni nu l-a ascultat. Doar Gauss, și apoi Laplace 60-70 de ani mai târziu, au redescoperit și studiat cu atenție legea distribuției normale. Graficul de mai sus arată clar că probabilitatea maximă cade pe așteptarea matematică și, pe măsură ce se abate de la aceasta, scade brusc. Exact ca legea normală.
Distribuția binomială are o mare semnificație practică, apare destul de des. Folosind Excel, calculele se fac rapid și ușor.
