Lucrări de cercetare pe tema „construcții geometrice folosind o riglă cu două fețe”. Sarcini de construcție de bază Ce construcții se pot face cu ajutorul unei rigle

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Constructie folosind o rigla si busola Geometrie">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Construiți un segment egal cu problema Ú dată A B"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Construirea unui unghi egal cu unul dat Luați în considerare triunghiuri"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Construirea bisectoarei unui unghi Problema Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Construcția liniilor perpendiculare Ú Problemă dată unei linii"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную !} linie dată. Ú Rezolvare 1. Construiți o dreaptă a și un punct M aparținând acestei drepte. 2. Pe razele dreptei a, care emană din punctul M, trasăm segmentele egale MA și MB. M a Apoi construim două cercuri cu centrele A și B de raza AB. Ele se intersectează în două puncte: P și Q. A B 3. Să trasăm o dreaptă prin punctul M și unul dintre aceste puncte, de exemplu dreapta MR, și să demonstrăm că această dreaptă este cea dorită, adică că este perpendiculară pe linie dată. 4. Într-adevăr, din moment ce mediana RM triunghi isoscel RAB Q este de asemenea o înălțime, apoi PM este perpendicular pe a.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Construirea punctului de mijloc al unui segment Sarcină Ú Construiți punctul de mijloc al unui dat"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – !} acest segment. 2. Construiți două cercuri cu 21 de centre A și B de raza AB. Ele se intersectează în punctele P și Q. O 3. Să trasăm o dreaptă PQ. Punctul O al intersecției acestei drepte cu A B segmentul AB este mijlocul dorit al segmentului AB 4. De fapt, triunghiurile APQ și BPQ sunt egale pe trei laturi, prin urmare unghiul 1 = Q unghiul 2 5. Prin urmare, segmentul PO este bisectoarea triunghiului isoscel ARB și aceasta înseamnă mediana, adică punctul O este mijlocul segmentului AB.

Bugetul municipal instituție de învățământ

medie școală gimnazială Nr. 34 cu studiu aprofundat al subiectelor individuale

MAN, secția fizică și matematică

„Construcții geometrice folosind busolă și riglă”

Completat de: elev de clasa a 7-a „A”

Batishcheva Victoria

Șef: Koltovskaya V.V.

Voronej, 2013

3. Construirea unui unghi egal cu cel dat.

P Să desenăm un cerc arbitrar cu un centru la vârful A al unui unghi dat (Fig. 3). Fie B și C punctele de intersecție ale cercului cu laturile unghiului. Cu raza AB desenăm un cerc cu centrul în punctul O, punctul de plecare al acestei semi-linii. Să notăm punctul de intersecție al acestui cerc cu această semi-linie ca C 1 . Să descriem un cerc cu centrul C 1 și Fig.3

raza aeronavei. Punctul B 1 intersecția cercurilor construite în semiplanul indicat se află pe partea unghiului dorit.

6. Construirea liniilor perpendiculare.

Desenăm un cerc cu o rază arbitrară r cu un centru în punctul O din Fig. 6. Cercul intersectează linia în punctele A și B.Din punctele A și B desenăm cercuri cu raza AB. Fie melancolia C punctul de intersecție al acestor cercuri. Punctele A și B am obținut în prima etapă, la construirea unui cerc cu o rază arbitrară.

Linia dreaptă dorită trece prin punctele C și O.


Fig.6

Probleme cunoscute

1.problema lui Brahmagupta

Construiți un patrulater înscris folosind cele patru laturi ale sale. O soluție folosește cercul Apollonius.Să rezolvăm problema lui Apollonius folosind analogia dintre un tricerc și un triunghi. Cum găsim un cerc înscris într-un triunghi: construim punctul de intersecție al bisectoarelor, coborâm perpendiculare din el către laturile triunghiului, bazele perpendicularelor (punctele de intersecție ale perpendicularei cu latura pe care aceasta este aruncat) și ne dă trei puncte situate pe cercul dorit. Desenați un cerc prin aceste trei puncte - soluția este gata. La fel vom face și cu problema lui Apollonius.

2. problema lui Apollonius

Folosind o busolă și o riglă, construiți un cerc tangent la cele trei cercuri date. Potrivit legendei, problema a fost formulată de Apollonius din Perga în jurul anului 220 î.Hr. e. în cartea „Atinge”, care s-a pierdut, dar a fost restaurată în 1600 de François Viète, „Apollonius galic”, așa cum l-au numit contemporanii săi.

Dacă niciunul dintre cercurile date nu se află în interiorul celuilalt, atunci această problemă are 8 soluții semnificativ diferite.


Constructii poligoane regulate.

P

corecta (sau echilateral ) triunghi - Asta poligon regulatcu trei laturi, primul dintre poligoane regulate. Toate laturile unui triunghi regulat sunt egali unul cu celălalt, și toate unghiurile sunt de 60°. Pentru a construi un triunghi echilateral, trebuie să împărțiți cercul în 3 părți egale. Pentru a face acest lucru, este necesar să desenați un arc cu raza R a acestui cerc de la un singur capăt al diametrului, obținem prima și a doua diviziune. A treia diviziune se află la capătul opus al diametrului. Conectând aceste puncte, obținem un triunghi echilateral.

Hexagon obișnuit Canconstruiți folosind o busolă și o riglă. De mai josse da metoda de constructieprin împărțirea cercului în 6 părți. Folosim egalitatea laturilor unui hexagon regulat cu raza cercului circumscris. De la capetele opuse ale unuia dintre diametrele cercului descriem arce cu raza R. Punctele de intersecție ale acestor arce cu un cerc dat îl vor împărți în 6 părţi egale. Prin conectarea secvenţială a punctelor găsite, se obţine un hexagon regulat.

Construcția unui pentagon regulat.

P
un pentagon regulat poate ficonstruit folosind o busolă și o riglă sau potrivindu-l într-un anumitcerc sau construcție bazată pe o latură dată. Acest proces este descris de Euclidîn Elementele sale pe la 300 î.Hr. e.

Iată o metodă pentru a construi un pentagon regulat într-un cerc dat:

    Construiți un cerc în care va fi înscris pentagonul și marcați centrul acestuia caO . (Acesta este cercul verde din diagrama din dreapta).

    Selectați un punct de pe cercO , care va fi unul dintre vârfurile pentagonului. Construiți o linie dreaptă prinO ŞiO .

    Construiți o dreaptă perpendiculară pe dreaptăO.A. , trecând prin punctO . Desemnați una dintre intersecțiile sale cu cercul ca punctB .

    Trasează un punctC la mijloc întreO ŞiB .

    C prin punctO . Marcați intersecția acesteia cu liniaO.B. (în interiorul cercului original) ca punctD .

    Desenați un cerc cu centrul laO prin punctul D, marcați intersecția acestui cerc cu originalul (cercul verde) ca puncteE ŞiF .

    Desenați un cerc cu centrul laE prin punctO G .

    Desenați un cerc cu centrul laF prin punctO . Etichetați cealaltă intersecție cu cercul original ca punctH .

    Construiți un pentagon regulatAEGHF .

Probleme de nerezolvat

Următoarele trei sarcini de construcție au fost stabilite în antichitate:

    Trisecție unghiulară - împărțiți un unghi arbitrar în trei părți egale.

Cu alte cuvinte, este necesar să se construiască trisectoare unghiulară - raze care împart unghiul în trei părți egale. P. L. Wanzel a demonstrat în 1837 că problema este rezolvabilă doar atunci când, de exemplu, trisecția este fezabilă pentru unghiurile α = 360°/n, cu condiția ca întregul n să nu fie divizibil cu 3. Totuși, în presă din când în când (incorect ) sunt publicate metode de trisectare a unui unghi cu compas și riglă.

    Dublarea cubului - problema antică clasică de a construi cu o busolă și o riglă muchia unui cub, al cărui volum este de două ori mai mare decât volumul unui cub dat.

În notația modernă, problema se reduce la rezolvarea ecuației. Totul se reduce la problema construirii unui segment de lungime. P. Wantzel a dovedit în 1837 că această problemă nu poate fi rezolvată folosind o busolă și o muchie dreaptă.

    Pătratarea unui cerc - o sarcină constând în găsirea unei construcții folosind o busolă și o riglă a unui pătrat egal ca suprafață cu cercul dat.

După cum știți, cu ajutorul unei busole și al unei rigle le puteți face pe toate 4 operatii aritmeticeși extracție rădăcină pătrată; rezultă că pătrarea cercului este posibilă dacă și numai dacă, folosind un număr finit de astfel de acțiuni, este posibil să se construiască un segment de lungime π. Astfel, imposibilitatea de rezolvare a acestei probleme rezultă din natura nealgebrică (transcendența) numărului π, care a fost dovedită în 1882 de Lindemann.

O altă problemă binecunoscută care nu poate fi rezolvată folosind o busolă și o riglă esteconstruirea unui triunghi folosind trei lungimi bisectoare date .

Mai mult, această problemă rămâne de nerezolvat chiar și în prezența unui trisector.

Abia în secolul al XIX-lea s-a dovedit că toate cele trei probleme nu erau rezolvate folosind doar o busolă și o linie dreaptă. Problema posibilității de construcție este complet rezolvată metode algebrice, bazat pe teoria Galois.

ȘTIAȚI CĂ...

(din istoria construcțiilor geometrice)


Cândva, s-a investit un sens mistic în construcția de poligoane regulate.

Astfel, pitagoreicii, adepți ai învățăturii religioase și filozofice întemeiate de Pitagora, și care au trăit în Grecia antică (V eu-eu Vsecole î.Hr BC), au adoptat ca semn al unirii lor un poligon în formă de stea format din diagonalele unui pentagon regulat.

Regulile pentru construcția geometrică strictă a unor poligoane regulate sunt stabilite în cartea „Elemente” a matematicianului grec antic Euclid, care a trăit înIIIV. î.Hr Pentru a realiza aceste construcții, Euclid a propus să folosească doar o riglă și o busolă, care la acea vreme nu aveau un dispozitiv articulat pentru conectarea picioarelor (o astfel de limitare a instrumentelor era o cerință imuabilă a matematicii antice).

Poligoanele regulate au fost utilizate pe scară largă în astronomia antică. Dacă Euclid a fost interesat de construcția acestor figuri din punctul de vedere al matematicii, atunci pentru astronomul grec antic Claudius Ptolemeu (aproximativ 90 - 160 d.Hr.) s-a dovedit a fi necesar ca instrument auxiliar în rezolvarea problemelor astronomice. Deci, în cartea I a Almagesților, întregul capitol al zecelea este dedicat construcției de pentagoane și decagoane regulate.

Cu toate acestea, pe lângă lucrările pur științifice, construcția de poligoane regulate a fost o parte integrantă a cărților pentru constructori, meșteri și artiști. Capacitatea de a descrie aceste figuri a fost mult timp cerută în arhitectură, bijuterii și arte plastice.

„Zece cărți de arhitectură” ale arhitectului roman Vitruvius (care a trăit aproximativ în anii 63-14 î.Hr.) spune că zidurile orașului ar trebui să aibă în plan forma unui poligon regulat, iar turnurile cetății „trebuie făcute rotunde sau poligonale. , pentru un patrulater mai degrabă distrus de armele de asediu.”

Dispunerea orașelor a fost de mare interes pentru Vitruvius, care credea că este necesar să se planifice străzile, astfel încât vânturile principale să nu sufle de-a lungul lor. Se presupunea că au fost opt ​​astfel de vânturi și că au suflat în anumite direcții.

În timpul Renașterii, construirea poligoanelor regulate, și în special a pentagonului, nu a fost o sarcină ușoară. joc de matematică, dar a fost o condiție prealabilă necesară pentru construirea de cetăți.

Hexagonul obișnuit a făcut obiectul unui studiu special al marelui astronom și matematician german Johannes Kepler (1571-1630), despre care vorbește în cartea sa „Cadou de Anul Nou sau fulgi de zăpadă hexagonali”. Discută despre motivele pentru care fulgii de zăpadă au formă hexagonală, el notează, în special, următoarele: „... un plan poate fi acoperit fără goluri numai cu următoarele figuri: triunghiuri echilaterale, pătrate și hexagoane regulate. Printre aceste figuri, un hexagon obișnuit acoperă zona cea mai mare»

Unul dintre cei mai faimoși oameni de știință implicați în construcții geometrice a fost marele artist și matematician german Albrecht Durer (1471 -1528), care le-a dedicat o parte semnificativă a cărții sale „Manuale...”. El a propus reguli pentru construirea poligoanelor regulate cu 3, 4, 5... 16 laturi. Metodele de împărțire a unui cerc propuse de Dürer nu sunt universale în fiecare caz specific;

Dürer a folosit metode pentru a construi poligoane regulate în practica artistică, de exemplu, când a creat diferite tipuri de ornamente și modele pentru parchet. A schițat astfel de modele în timpul unei călătorii în Olanda, unde parchet au fost găsite în multe case.

Dürer a compus ornamente din poligoane regulate, care sunt legate în inele (inele de șase triunghiuri echilaterale, patru patrulatere, trei sau șase hexagoane, paisprezece heptagoane, patru octogoane).

Concluzie

Aşa,constructii geometrice este o metodă de rezolvare a unei probleme în care răspunsul se obține grafic. Construcțiile sunt realizate folosind instrumente de desen cu precizie și acuratețe maximă a muncii, deoarece corectitudinea soluției depinde de aceasta.

Datorită acestei lucrări, m-am familiarizat cu istoria originii busolei, m-am familiarizat mai mult cu regulile de realizare a construcțiilor geometrice, am acumulat noi cunoștințe și le-am aplicat în practică.
Rezolvarea problemelor care implică construcția cu busole și o riglă este o distracție utilă care vă permite să aruncați o privire nouă asupra proprietăților cunoscute ale figurilor geometrice și ale elementelor acestora.Această lucrare discută cele mai presante probleme asociate construcțiilor geometrice folosind busole și rigle. Sunt luate în considerare principalele probleme și sunt oferite soluțiile lor. Problemele prezentate prezintă un interes practic semnificativ, consolidează cunoștințele dobândite în geometrie și pot fi folosite pentru munca practica.
Astfel, scopul lucrării a fost atins, sarcinile atribuite au fost îndeplinite.

MICA ACADEMIE DE ȘTIINȚE A ȘCOLARILOR DIN CRIMEA

„CĂUTATOR”

Secțiunea „Matematică”

CONSTRUCȚII GEOMETRICE FOLOSIND O RIGĂ DUBLĂ

A terminat lucrarea O

_____________

Elev la clasă

Supraveghetor stiintific

INTRODUCERE……………………………………………………………………………………………..…..3

I. CONSTRUCȚII GEOMETRICE ÎN AVION…………………4

I.1. Axiome generale ale geometriei constructive. Axiomele instrumentelor matematice……………………………………………………………………………………………..4

I.2. ……………………….....5

I.3. Construcții geometrice cu o singură riglă……………………………..7

eu.4. Sarcini de bază pentru construirea cu o riglă cu două fețe……..8

I.5. Rezolvarea diferitelor probleme de construcție …………………………………12

I.6. Construcții cu riglă unilaterală……………………………………………….20

I.7. Interschimbabilitatea unei rigle cu două fețe cu o busolă și o riglă....21

CONCLUZIE……………………………………………………………………….24

Lista referințelor……………………………..………….25

Introducere

Problemele care implică construcția cu mijloace limitate includ problemele care implică construcția folosind doar busole și o riglă, care sunt luate în considerare în programa școlară. Este posibil să rezolvi problemele de construcție cu o singură riglă? Adesea nu aveți o busolă la îndemână, dar puteți găsi întotdeauna o riglă.

Problemele privind construcțiile în geometrie sunt o secțiune fascinantă. Interesul pentru el se datorează frumuseții și simplității conținutului său geometric. Relevanța luării în considerare a acestor probleme crește datorită faptului că sunt utilizate în practică. Capacitatea de a folosi o riglă pentru a rezolva problemele luate în considerare în această lucrare are mare valoareîn activităţi practice, deoarece Ne confruntăm constant cu probleme de împărțire a unui segment în jumătate, dublare a unui anumit segment etc.

Această lucrare examinează principalele probleme de construcție care servesc drept bază pentru rezolvarea unor probleme mai complexe.

După cum arată experiența, sarcinile de construcție trezesc interes și contribuie la activarea activității mentale. La rezolvarea acestora, se utilizează în mod activ cunoștințele despre proprietățile figurilor, se dezvoltă capacitatea de a raționa și se îmbunătățește abilitățile construcțiilor geometrice. Ca urmare, se dezvoltă abilitățile constructive, care este unul dintre scopurile studierii geometriei.

Ipoteza: toate problemele de construcție care pot fi rezolvate folosind o busolă și o riglă pot fi rezolvate numai folosind o riglă cu două fețe.

Obiect de studiu: sarcini de construcție și riglă cu două fețe.

Obiectivele cercetării: să demonstreze că toate problemele de construcție pot fi rezolvate doar cu ajutorul unei rigle cu două fețe.

Obiectivele cercetării: a studia fundamente teoretice rezolvarea problemelor de construcție; rezolvați probleme de construcție de bază folosind o riglă cu două fețe; dați exemple de sarcini de construcție mai complexe; sistematizarea materialului teoretic și practic.

I. CONSTRUCȚII GEOMETRICE PE AVION

I.1. Axiome generale ale geometriei constructive. Axiomele instrumentelor matematice

Pentru geometria structurală este necesar să existe o precizie și în scopuri matematice descriere completă unul sau altul instrument. Această descriere este dată sub formă de axiome. Aceste axiome în formă matematică abstractă exprimă acele proprietăți ale instrumentelor reale de desen care sunt folosite pentru construcții geometrice.

Cele mai frecvent utilizate instrumente de construcție geometrică sunt:riglă (cu o singură parte) , busolă, cu două fețe riglă (cu margini paralele) si altii unii.

A. Axioma domnitorului.

Rigla vă permite să efectuați următoarele construcții geometrice:
a) construiți un segment care leagă două puncte construite;

b) construiți o dreaptă care trece prin două puncte construite;

c) construiți o rază care emană dintr-un punct construit și trece printr-un alt punct construit.

B. Axioma busolei.

Busola vă permite să efectuați următoarele construcții geometrice:
a) construiți un cerc dacă s-au construit centrul cercului și un segment egal cu raza cercului (sau capetele acestuia);

B. Axioma unei rigle cu două fețe.

Rigla cu două fețe vă permite să:

a) efectuați oricare dintre construcțiile enumerate în axioma A;

b) în fiecare dintre semiplanurile definite de linia construită, construiți o dreaptă paralelă cu această dreaptă și care trece de ea la distanțăO, Unde O - un segment fix pentru o rigla dată (lățimea riglei);

c) dacă sunt construite două puncte A și B, atunci determinați dacă AB va fi mai mare decât un anumit segment fixO (lățimea riglei), iar dacă AB >O , apoi construiți două perechi de drepte paralele care trec prin punctele A și respectiv B și distanțate una de cealaltă la o distanțăO .

Pe lângă instrumentele enumerate, puteți utiliza și alte instrumente pentru construcții geometrice: un unghi arbitrar, un pătrat, o riglă cu semne, o pereche de unghiuri drepte, diverse dispozitive pentru trasarea curbelor speciale etc.

I.2. Principii generale pentru rezolvarea problemelor de construcție

Sarcina de construcție constă în faptul că se cere construirea unei anumite figuri cu instrumentele specificate dacă se dă o altă figură și se indică anumite relații între elementele figurii dorite și elementele acestei figuri.

Fiecare figură care satisface condițiile problemei se numeștedecizie această sarcină.

Găsiți o soluție Sarcina de construcție înseamnă reducerea acestuia la un număr finit de construcții de bază, adică indicarea unei secvențe finite de construcții de bază, după care figura dorită va fi considerată deja construită în virtutea axiomelor acceptate ale geometriei constructive. Lista construcțiilor de bază acceptabile și, în consecință, progresul rezolvării problemei, depinde în mod semnificativ de ce instrumente specifice sunt utilizate pentru construcții.

Rezolvați problema construcției - Mijloace, găsiți toate soluțiile sale .

Ultima definiție necesită unele clarificări. Cifrele care îndeplinesc condițiile problemei pot diferi atât ca formă sau dimensiune, cât și ca poziție în plan. Diferențele de poziție pe plan sunt luate în considerare sau nu sunt luate în considerare în funcție de formularea problemei de construcție în sine, dacă starea problemei prevede sau nu o anumită locație a figurii dorite în raport cu orice figuri date. .

Dacă se găsește o soluție la o problemă, atunci în viitor este permisă utilizarea acestei soluții „în ansamblu”, adică fără a o împărți în construcții de bază.

Există o serie de probleme simple de construcție geometrică, care sunt adesea incluse ca componente în rezolvarea unor probleme mai complexe. Le vom numi probleme de construcție geometrică elementară. Lista sarcinilor elementare este, desigur, condiționată. Sarcinile de bază includ de obicei următoarele:

    Împărțiți acest segment în jumătate.

    Împărțirea unui unghi dat la jumătate.

    Construind pe o dreaptă dată un segment egal cu cel dat.

    Construirea unui unghi egal cu unul dat.

    Construirea unei drepte care trece printr-un punct dat paralel cu o dreaptă dată.

    Construirea unei drepte care trece printr-un punct dat și perpendiculară pe o dreaptă dată.

    Împărțirea unui segment în acest sens.

    Construirea unui triunghi folosind trei laturi date.

    Construirea unui triunghi folosind o latură și două unghiuri adiacente.

    Construirea unui triunghi folosind două laturi și unghiul dintre ele.

La rezolvarea oricărei probleme de construcție oarecum complexă, se pune întrebarea cum să raționăm pentru a găsi o modalitate de rezolvare a problemei, pentru a obține toate soluțiile la problemă, pentru a afla condițiile posibilității de rezolvare a problemei etc. Prin urmare , atunci când rezolvă probleme constructive, ei folosesc o schemă de soluții, constând din următoarele patru etape:

1) analiza;
2) construcție;
3) dovada;
4) cercetare.

I.3. Construcții geometrice cu o singură riglă

Vom considera domnitorul din două puncte de vedere: ca riglă și ca riglă cu două fețe.

1. Riglă cu două fețe lăţime O vom numi o riglă cu margini paralele situate la distanță O unul de celălalt, făcând posibilă construirea directă:

a) o linie dreaptă arbitrară;

b) o dreaptă care trece prin două puncte date sau obţinute în procesul de rezolvare a problemei;

c) drepte paralele, fiecare dintre acestea trecând prin unul dintre punctele, distanțele dintre care sunt mai mariO (în această construcție, rigla este într-o astfel de poziție încât pe fiecare dintre cele două margini paralele ale sale să existe unul dintre cele două puncte date; în acest caz, vom vorbi despre construcția directă).

Lățimea riglei în această construcție este considerată constantă și, prin urmare, dacă se află în proces de rezolvare sarcină specifică va fi nevoie să se realizeze construcţia directă relativ la unele puncte obţinuteOŞi ÎN , atunci trebuie să dovedim că lungimeaAB mai lung O .

Vom considera un punct de construit dacă este unul dintre date sau este intersecția a două drepte construite; la rândul nostru, vom considera o linie dreaptă de construit dacă trece prin punctele construite sau date.

Folosind o riglă cu două fețe, puteți construi următoarele.

a) Prin oricare două puncte puteți trage o linie dreaptă și numai una.

b) Oricare ar fi linia dreaptă, există exact două drepte în plan, paralele cu aceasta și separate de ea printr-o distanțăo .

c) Prin două puncte A și B la ABO se pot trasa două perechi de paralele Drept; cu AB = O puteți desena o pereche de linii paralele, distanța dintre care este egalăO .

Dacă se acordă unul, două, trei puncte, atunci nu se pot construi puncte noi

(Figura 1);

dacă sunt date patru puncte, dintre care trei (sau toate patru) se află pe aceeași linie, atunci nu se pot construi alte puncte (Fig. 2);

Dacă vi se oferă patru puncte situate la vârfurile unui paralelogram, puteți construi un singur punct - centrul său. (Fig.3).

După ce am acceptat cele de mai sus, să luăm în considerare separat problemele rezolvate de o riglă cu două fețe.

eu.4. Sarcini de bază pentru construcția cu o riglă cu două fețe

1
. Construiți bisectoarea unghiului ABC.

Soluţie: (Fig. 4)

O  (ÎN C) Și b  (AB) și b = D .

Primim B D– bisectoare ABC.

Intr-adevar, obtinut de

construirea unui paralelogram este

romb, deoarece înălțimile sale sunt egale. ÎND –

diagonala unui romb este bisectoare ABC. Fig.4

2
. Dublați unghiul dat ABC

Soluţie : (Fig. 5) a) O  (AB),

O (ÎN C)= D , prin punctele B și D

b direct;

b) prin punctele B şiD m  b

direct,b Ç a = F .

Primim Ð AB F = 2 Ð ABC .

Fig.5


3 . La o linie dreaptă dată M N în aceasta

trageți o perpendiculară pe punctul A

Soluţie : (Fig.6)

1) (AA 1) || (BB 1) || (SS 1) –

direct (B(M N),

CU Î (M N)); 2) prin A și B

m || n - direct,

m Ç (SS 1) = D .

Primim (A D ) (M N ).

Fig.6.

4
. Printr-un punct dat nu se întinde pe

linie dată, trage o perpendiculară

La această linie.

Soluţie: Prin acest punct O desenăm

două drepte care intersectează un dat

dreapta AB și dublați unghiurile rezultatului

triunghiuri adiacente acestuia

direct. OA N = 2 OAV și

OB N = 2 OVA (Fig. 7).

Fig.7

5. Construiți un punct simetric față de o dreaptă dată relativ la o dreaptă dată.

Soluţie: vezi problema 4. (punctul O este simetric cu punctulN. Fig.7)

6. Efectuați o linie dreaptă paralel cu acesta

n
drept M N , prin punctul A, nu

aparținând liniei M N .

Soluția 1: (Fig. 8)

1)(AA 1) || (BB 1) || (SS 1) || (DD 1 ) || (КК 1) -

– direct, (SA)Ç (BB1) = C2;

2) (Cu 2 K) Ç (DD 1 ) = F .

(O F ) este linia dreaptă dorită.

Fig 8

Soluția 2 . În Fig. 8 1 este numerotat

succesiune de linii drepte,

dintre care 1, 2 și 3 sunt paralele în

construcție directă;

(O F) || (M N).

Fig.8 1

7
. Împărțiți acest segment AB în jumătate.

Soluția 1. (Fig. 9) (numai pentru cazul în care lățimea riglei este mai mică decât lungimea acestui segment). Desenați direct două perechi de linii paralele

capetele acestui segment și apoi diagonala

rombul rezultat. O – mijloc AB.

Orez. 9.

Soluția 2. (Fig. 9, a)

1) a || (AB) și b || (AB) – direct;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D ÎN) Ç a = M, (SV) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D LA) Ç (O N ) = F ;

6) (B F ) Ç b = D 1, (B F ) Ç a = C1;

7) (D ÎN ) Ç (O D 1) = X,

(AC 1) Ç (SV) = Z.

8) (X Z) Ç (AB) =O. Obținem AO = OB.

Fig.9,a

Soluția 3 .( Orez. 9, b)

După cum se știe , în trapezul mijlociu

baze, punct de intersecție

diagonalele și punctul de intersecție

prelungiri ale laturilor

stați pe aceeași linie dreaptă.

1) m || (AB) – direct;

2) C Î m , D Î m , (AS) Ç (ÎN D ) = LA; Fig.9, b

3) (NE) Ç (O D ) = F ; 4) (K F ) Ç (AB) =O. Obținem AO = OB.

I.5. Rezolvarea diverselor probleme de construcție

În rezolvarea următoarelor probleme de construcție folosind doar o riglă cu două fețe, se utilizează construcția directă a liniilor paralele și cele șapte probleme principale prezentate mai sus.

1. Desenați două drepte reciproc perpendiculare prin acest punct.

R soluţie: să trecem prin acest punct

două linii arbitrare,

și apoi - bisectoare

colțurile adiacente. (Fig.10)

Fig.10

2. Având în vedere un segment A D lungime dată a.

Construiți un segment a cărui lungime este egală cu .

R
decizie : Să ducem la îndeplinire m OŞi h || m prin

punctul A. f || (O D ) , k || (AD) direct.

Să desenăm AB și AC, unde B =f m ,

a C = m k . Într-un mod cunoscut

împărțiți AB și AC în jumătate și

să desenăm medianele triunghiului

ABC. Prin proprietatea medianelor

triunghi, O D = – căutat

segment (Fig. 11)

Orez. 11

3. Construiți un segment a cărui lungime este

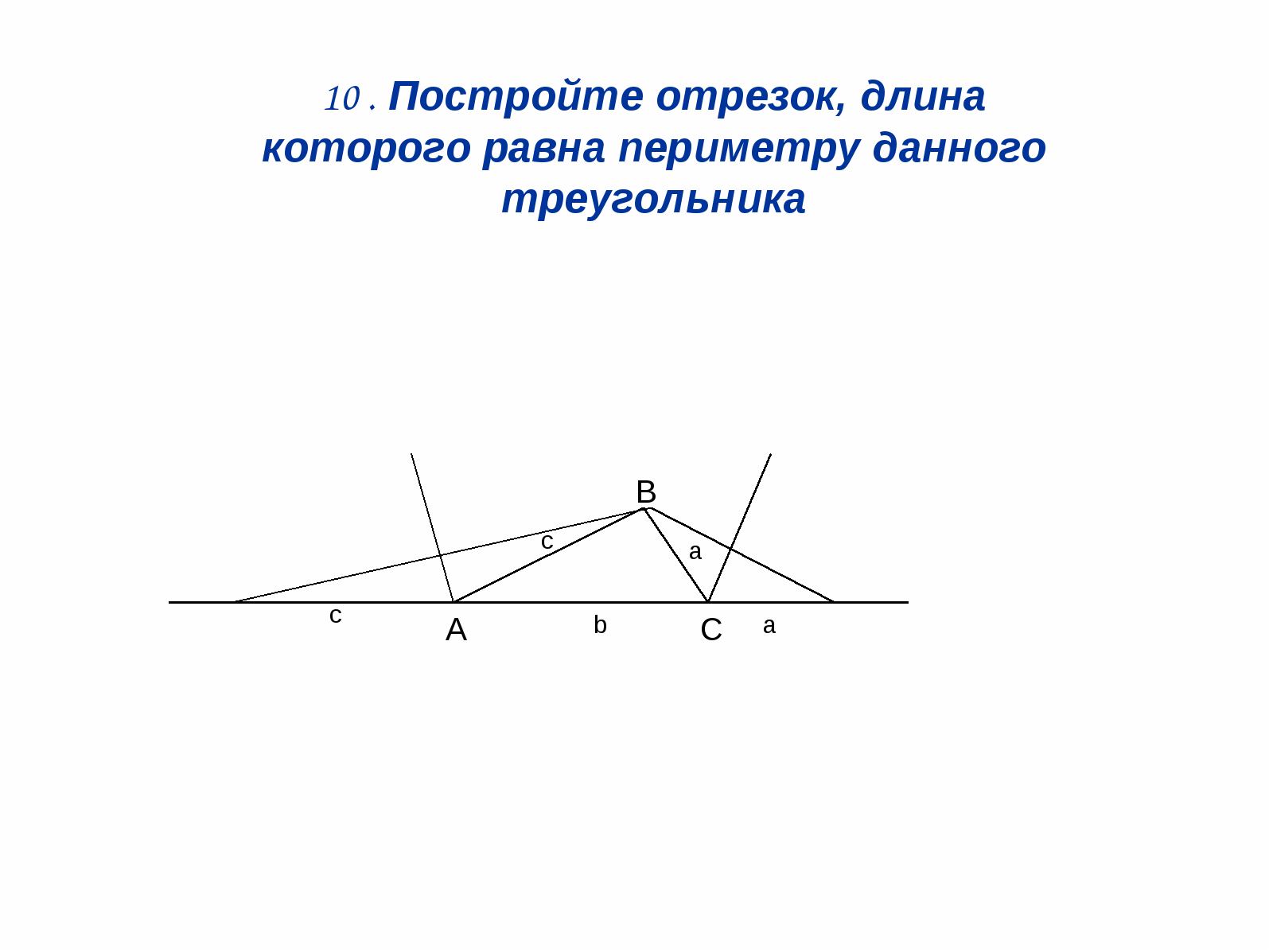egal cu perimetrul triunghiului dat.

Soluţie: (Fig. 12). Să construim bisectoare

două colțuri exterioare ale triunghiului și apoi

3 vârfuri ÎN să desenăm perpendiculare

la aceste bisectoare.

DE = a + b + s

Fig.12

4. Având în vedere un segment de lungime a. Construiți segmente de lungime 2a, 3a.

R soluţie: (Fig. 13)

1) (M N) || (AB) și (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

Direct;

2) (CA) și (CB) prin A și B.

Segmentele A 1 B 1 și A 2 B 2 sunt necesare.

O altă soluție la această problemă poate fi

obtinut din rezolvarea problemei 7.

Orez. 13

5. Două segmente sunt date pe o linie dreaptă, ale căror lungimi sunt a și b . Construiți segmente ale căror lungimi sunt egale cu a + b , b - A, ( o + b )/2 și ( b - o )/2 .

Soluţie: a) pentru o + b(Fig. 14, a)

Fig. 14, a

b) pentru ( o + b)/2 (Fig. 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) – direct;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1 ) = N, (M H) Ç (A 1 B 1 ) = P;

3) (PY) Ç (A 2 B 2) = L, (LZ ) Ç (A 1 B 1 ) = O,

Primim: N O = N.P. + P.O. =
.

Orez. 14, b

c) pentru b - A(Fig. 14, c)

Orez. 14,v

c) pentru ( b - o )/2 (Fig. 14,d)

Orez. 14,g

6
. Construiți centrul acestui cerc.

Soluţie : (Fig. 15) Să desenăm o linie dreaptă AB,

intersectarea cercului în punctele A și B;

Soare AB, unde C este punctul de intersecție

cu un cerc.

Prin punctul C tragem paralel cu AB

drept C D; CUDintersectează un cerc

la punctD.

ConectareDcu B și A cu C, obținem

punctul dorit este centrul cercului. Orez. 15

Soluția 2: (Fig. 16) Folosind o riglă cu două fețe, construiți două coarde paraleleAD ŞiB.C. . Obținem un trapez isoscelABCD. LasăK ŞiP - punctele de intersecție ale dreptelorA.C. ŞiBD , AB ŞiDC . Apoi dreptP K trece prin punctele medii ale bazelor trapezului perpendicular pe acestea, ceea ce înseamnă că trece prin centrul cercului dat. Construind în mod similar o altă astfel de linie dreaptă, găsim centrul cercului.

Orez. 16

7. Se dă un arc de cerc. Construiți centrul cercului

Soluţie . (Fig. 17) Marcați trei puncte A, B și C pe acest arc. Aplicați o riglă la capetele segmentului AB și conturați marginile acestuia. Obținem două drepte paralele. Schimbând poziția riglei, mai desenăm două linii paralele. Obținem un romb (un paralelogram cu înălțimi egale). Una dintre diagonalele unui romb este bisectoarea perpendiculară pe segmentAB , deoarece diagonala unui romb se află pe bisectoarea perpendiculară pe cealaltă diagonală. În mod similar, construim bisectoarea perpendiculară pe segmentA.C. . Punctul de intersecție al bisectoarelor construite este centrul cercului dorit.

Orez. 17

8. Având în vedere un segment AB, o dreaptă neparalelă l și un punct M pe acesta. Folosind o riglă cu două fețe, construiți punctele de intersecție ale dreptei l cu un cerc de rază AB cu centrul M.

Soluţie: (Fig.18)

Să completăm triunghiulA.B.M. la paralelogramABNM . Să construim bisectoarele MT șiDOMNIȘOARĂunghiuri întreMNși dreptl . Să tragem prin punctN drepte paralele cu aceste bisectoare:N.Q. || DOMNIȘOARĂ, NR || M.T.. MT│ DOMNIȘOARĂca bisectoare ale unghiurilor adiacente. Mijloace,N.Q. │ MT, adică într-un triunghiNMQbisectoarea este altitudinea, prin urmare triunghiul este isoscel:MQ = MN. De asemenea,DL. = MN. PuncteQŞiRcăutat.

Orez. 18

9. Având în vedere o dreaptă l şi un segment OA paralel cu l. Folosind o riglă cu două fețe, construiți punctele de intersecție ale dreptei l cu un cerc de rază OA cu centrul O.

Soluţie: (Fig. 19, a)

Să facem o directăl 1 , paralel cu liniaO.A. și departe de el la distanțăo . Să o luăm pe linie dreaptăl punct arbitrarB . LasăB 1 - punctul de intersecție a dreptelorO.B. Şil 1 . Să tragem prin punctB 1 drept, paralelAB ; această linie intersectează liniaO.A. la punctO 1 . Să tragem acum prin puncteO ŞiO 1 o pereche de linii paralele, distanța dintre ele esteo (pot exista două astfel de perechi de linii); lasaX ŞiX 1 - punctele de intersecție ale unei drepte care trece printr-un punctO , cu linii dreptel Şil 1 . DeoareceO.A. 1 = BOU 1 și ∆O.A. 1 X 1 ∆ OAX , apoi OA = OX, punctulX Căutat.

În mod similar, construim al doilea punct de intersecție al cercului și al dreptei - punctulY(Fig. 18, b).

Orez. 18,a

Orez. 18, b

I.6.Construcții cu riglă unilaterală

Z
hai sa ne uitam aici caz special: să fie date punctele P,Q, R 1 ŞiQ 1 . iar ele se află la vârfurile trapezului.

1. Împărțiți segmentul P Q în jumătate

Soluţie prezentat în figura 19

Datele puncte P,Q, R 1 ŞiQ 1 și linii paralele

RQ, R 1 Q 1 . Să realizăm RQ 1 QR 1 = B , RR 1 QQ 1 = A

Să conectăm punctele A și B. ABRQ = F– mijloc

segmentul PQ.

Orez. 19

2. Se dublează segmentul R 1 Q 1.

R
decizie prezentat în Figura 20. Să construim

punctF– mijlocul segmentului PQși conectați-l

CuQ 1. R 1 QFQ 1 = M. Să efectuăm RM. RMR 1 Q 1 = R

egalitateRQși P 1 Q 1 rezultă din asemănarea

triunghiuri RMFŞi RMQ 1 ,

FMQŞi R 1 MQ 1 , și egalitățile PFŞiFQ.

Orez. 20

3
. Construiți un segment de lungime n R 1 Q 1 .

m – 1 segmente egale PQ 2 , Q 2 Q 3, … Q m -1 Q m

Apoi construim (RR 1 ) ȘiQ m Q 1 și conectați

punctul lor de intersecție A cu punctele

Q 2 , Q 3, … Q m Primitm -1 direct

împărțițiR 1 Q 1 pem egal piese.

Pentrum = 4 soluția este prezentată în figura 22

Fig.22

I.7. Interschimbabilitatea riglei cu două fețe cu busolă și riglă

Să demonstrăm că o riglă cu două fețe este interschimbabilă cu o busolă și o riglă. Pentru a face acest lucru, demonstrăm următoarele afirmații:

Afirmația 1: toate construcțiile care se pot face cu busolă și riglă se pot face cu o riglă cu două fețe.

Deoarece atunci când construiește cu o busolă și o riglă, rigla trasează o linie prin două puncte, iar compasul construiește un cerc (găsește un set de puncte echidistante de unul dat), atunci toate construcțiile cu un compas și o riglă sunt reduse la construind intersecția a două drepte, două cercuri și un cerc cu o dreaptă.

Intersecția a două linii drepte poate fi construită folosind o riglă.

Intersecția unui cerc și a unei linii drepte (Fig. 23):

Constructie:Să fie dat segmentul AB - raza cercului, o linie dreaptăl , centrul cercului O, atunci:

1) Efectuăm OS ||l , OS = AB.

2) Efectuăm OS ||kși la distanță la a.

3) RealizamO.D., O.D.l = D; O.D.k) Prin corolar teoremei lui Thales

4) Conform legii tranzitivităţii egalităţilor

5) Luați în considerareOMQE. OMQEeste un paralelogram, deoarece OM ||EQși OE ||M.C.(laturile riglei sunt paralele). Să demonstrăm că acesta este un romb.

5.1) ConduitaQZO.C.ŞiQGPE, AtunciQG = QZ = o.

5.2) OMQ = RQM(întins în cruce); OS =PE, ceea ce trebuia dovedit.

Intersecția a două cercuri: asemănătoare.

Afirmația 2: toate construcțiile care se pot face cu o riglă cu două fețe se pot face cu busolă și dreptar.

Pentru a face acest lucru, vom efectua standardul de construcții pentru o riglă cu două fețe folosind o busolă și o riglă.

1) O linie dreaptă folosind două puncte este ușor de construit folosind o riglă.

2) Construirea unei drepte paralele cu una dată și la distanță de aceasta distanta data:

2.1) Să fie dată o linie dreaptăkși segment de lungimeo.

2.2) Construiți o dreaptă arbitrarăbk, lasăkb= B.

2.3) Pornitbpe ambele părți ale punctuluiBpe o linie dreaptăbpune deoparte o bucată de lungimeo, lasă puncteleCŞiD.

2.4) Printr-un punctCconstruiți o linie dreaptăck.

2.5) Printr-un punctDconstruiți o linie dreaptădk.

2.6) DirectcŞid-necesar, pentru căB.C.ŞiBDegaloprin construcție și sunt egale cu distanța dintre linia dreaptăkși drept

3) Construcția unor drepte paralele între ele și care trec prin două puncte date, iar distanța dintre ele este egală cu segmentul dat:

3.1) Lasă punctele să fie dateOŞiBși segment de lungimeo.

3.2) Construirea unui cerc cu un centru într-un punctOsi razao.

3.3) Construiți o tangentă la un cerc dat printr-un punctB; există două astfel de tangente dacăBse află în afara cercului (dacăAB> o), unul dacăBse află pe cerc (dacăAB= o), niciunul dacăBse află în interiorul cercului (AB< o). Această tangentă este una dintre liniile pe care le căutăm; rămâne să treacă prin punctOlinie dreaptă paralelă cu aceasta.

3.4) Deoarece una dintre drepte este perpendiculară pe raza cercului ca tangentă, a doua este și perpendiculară pe aceasta (deoarece sunt paralele), prin urmare, distanța dintre ele este egală cu raza, care prin construcție este egală cuo, care este ceea ce trebuia să fie obținut.

Astfel, am dovedit interschimbabilitatea unei rigle cu două fețe și a unei busole și a unei rigle.

Concluzie: o riglă cu două fețe este interschimbabilă cu o busolă și o riglă.

Concluzie

Deci, problema posibilității de a folosi o riglă pentru a rezolva problemele clasice de construcție folosind o busolă și o riglă a fost luată în considerare și rezolvată. Se pare că problemele de construcție pot fi rezolvate folosind doar o riglă cu margini paralele. Atunci când rezolvăm probleme mai complexe, ar trebui să se bazeze în continuare pe așa-numitele construcții de bază discutate în această lucrare.

Materialul prezentat poate avea aplicare directă nu doar în lecțiile de matematică, în orele de cerc de matematică, ci și în activități practice.

Lista literaturii folosite

    Aliev A.V. Construcții geometrice. Matematica la scoala. 1978 nr. 3

    Glazer G.I. Istoria matematicii la scoala. M., Iluminismul. 1981.

    Depman I.Ya. În spatele paginilor unui manual de matematică. M.. Iluminismul 1989.

    Elensky Shch. Pe urmele lui Pitagora. M., Detgiz. 1961.

    Dicționar enciclopedic al unui tânăr matematician. M., Pedagogie. 1985

În problemele de construcție vom lua în considerare construcția figură geometrică care se poate face folosind o riglă și o busolă.

Folosind o riglă puteți:

    linie dreaptă arbitrară;

    o dreaptă arbitrară care trece printr-un punct dat;

    o linie dreaptă care trece prin două puncte date.

Folosind o busolă, puteți descrie un cerc cu o rază dată de la un centru dat.

Folosind o busolă, puteți trasa un segment pe o linie dată dintr-un punct dat.

Să luăm în considerare principalele sarcini de construcție.

Sarcina 1. Construiți un triunghi cu laturile date a, b, c (Fig. 1).

Soluţie. Folosind o riglă, trageți o linie dreaptă arbitrară și luați un punct arbitrar B pe ea. Folosind o deschidere de busolă egală cu a, descriem un cerc cu centrul B și raza a. Fie C punctul de intersecție cu dreapta. Cu o deschidere de busolă egală cu c, descriem un cerc din centrul B, iar cu o deschidere de busolă egală cu b, descriem un cerc din centrul C. Fie A punctul de intersecție al acestor cercuri. Triunghiul ABC are laturile egale cu a, b, c.

Comentariu. Pentru ca trei segmente drepte să servească drept laturi ale unui triunghi, este necesar ca cel mai mare dintre ele să fie mai mic decât suma celorlalte două (și< b + с).

Sarcina 2.

Soluţie. Acest unghi cu vârful A și raza OM sunt prezentate în Figura 2.

Să desenăm un cerc arbitrar cu centrul său la vârful A al unghiului dat. Fie B și C punctele de intersecție ale cercului cu laturile unghiului (Fig. 3, a). Cu raza AB desenăm un cerc cu centrul în punctul O - punctul de plecare al acestei raze (Fig. 3, b). Să notăm punctul de intersecție al acestui cerc cu această rază ca C 1 . Să descriem un cerc cu centrul C 1 și raza BC. Punctul B 1 al intersecției a două cercuri se află pe partea unghiului dorit. Aceasta rezultă din egalitatea Δ ABC = Δ OB 1 C 1 (al treilea semn al egalității triunghiurilor).

Sarcina 3. Construiți bisectoarea acestui unghi (Fig. 4).

Soluţie. Din vârful A unui unghi dat, ca din centru, desenăm un cerc de rază arbitrară. Fie B și C punctele de intersecție cu laturile unghiului. Din punctele B și C descriem cercuri cu aceeași rază. Fie D punctul lor de intersecție, diferit de A. Raza AD bisectează unghiul A. Aceasta rezultă din egalitatea Δ ABD = Δ ACD (al treilea criteriu pentru egalitatea triunghiurilor).

Sarcina 4. Desenați o bisectoare perpendiculară pe acest segment (Fig. 5).

Soluţie. Folosind o deschidere de busolă arbitrară, dar identică (mai mare de 1/2 AB), descriem două arce cu centre în punctele A și B, care se vor intersecta în unele puncte C și D. Linia dreaptă CD va fi perpendiculara dorită. Într-adevăr, după cum se poate observa din construcție, fiecare dintre punctele C și D este la fel de îndepărtat de A și B; prin urmare, aceste puncte trebuie să se afle pe bisectoarea perpendiculară pe segmentul AB.

Sarcina 5.Împărțiți acest segment în jumătate. Se rezolvă în același mod ca problema 4 (vezi Fig. 5).

Sarcina 6. Printr-un punct dat trageți o dreaptă perpendiculară pe dreapta dată.

Soluţie. Există două cazuri posibile:

1) punct dat O se află pe o linie dreaptă dată a (Fig. 6).

Din punctul O desenăm un cerc cu o rază arbitrară care intersectează linia a în punctele A și B. Din punctele A și B desenăm cercuri cu aceeași rază. Fie O 1 punctul de intersectie al acestora, diferit de O. Se obtine OO 1 ⊥ AB. De fapt, punctele O și O 1 sunt echidistante de capetele segmentului AB și, prin urmare, se află pe bisectoarea perpendiculară pe acest segment.

Exemplu

Împărțirea unui segment în jumătate

Problema bisectiei. Folosiți o busolă și o riglă pentru a împărți acest segment ABîn două părți egale. Una dintre soluții este prezentată în figură:

  • Folosind o busolă, desenăm cercuri cu centre în puncte OŞi B rază AB.
  • Găsirea punctelor de intersecție PŞi Q două cercuri (arce) construite.
  • Folosind o riglă, trageți un segment sau o linie care trece prin puncte PŞi Q.
  • Găsirea punctului de mijloc dorit al segmentului AB- punctul de intersecție ABŞi PQ.

Definiție formală

În problemele de construcție, se ia în considerare mulțimea tuturor punctelor planului, mulțimea tuturor liniilor drepte ale planului și mulțimea tuturor cercurilor planului, pe care sunt permise următoarele operații:

  1. Selectați un punct din setul de toate punctele:
    1. punct arbitrar
    2. punct arbitrar pe o dreaptă dată
    3. punct arbitrar pe un cerc dat
    4. punctul de intersecție a două drepte date
    5. punctul de intersecție/tangență a unei drepte date și a unui cerc dat
    6. puncte de intersecție/tangență a două cercuri date
  2. „Prin folosirea conducători» selectați o linie din setul de toate liniile:
    1. linie dreaptă arbitrară
    2. o dreaptă arbitrară care trece printr-un punct dat
    3. o linie dreaptă care trece prin două puncte date
  3. „Prin folosirea busolă» selectați un cerc din setul de toate cercurile:
    1. cerc arbitrar
    2. un cerc arbitrar cu un centru într-un punct dat
    3. un cerc arbitrar cu o rază egală cu distanța dintre două puncte date
    4. un cerc cu un centru într-un punct dat și cu o rază egală cu distanța dintre două puncte date

În condițiile problemei, este specificat un anumit set de puncte. Este necesar, folosind un număr finit de operații dintre operațiile admisibile enumerate mai sus, pentru a construi un alt set de puncte care se află într-o relație dată cu mulțimea inițială.

Soluția la problema construcției conține trei părți esențiale:

  1. Descrierea metodei de construire a unei multimi date.
  2. Dovada că mulțimea construită în modul descris este într-adevăr într-o relație dată cu mulțimea inițială. De obicei, demonstrarea construcției se realizează ca o demonstrație obișnuită a teoremei, bazată pe axiome și alte teoreme dovedite.
  3. Analiza metodei de construcție descrise pentru aplicabilitatea acesteia la diferite versiuni ale condițiilor inițiale, precum și pentru unicitatea sau neunicitatea soluției obținute prin metoda descrisă.

Probleme cunoscute

  • Problema lui Apollonius de a construi un cerc tangent la trei cercuri date. Dacă niciunul dintre cercurile date nu se află în interiorul celuilalt, atunci această problemă are 8 soluții semnificativ diferite.
  • Problema lui Brahmagupta de a construi un patrulater înscris folosind cele patru laturi ale sale.

Construirea de poligoane regulate

Geometrii antici știau să construiască corect n-goni pentru , , și .

Construcții posibile și imposibile

Toate construcțiile nu sunt altceva decât soluții ale unei ecuații, iar coeficienții acestei ecuații sunt legați de lungimile segmentelor date. Prin urmare, este convenabil să vorbim despre construirea unui număr - o soluție grafică a unei ecuații de un anumit tip. În cadrul cerințelor de mai sus, sunt posibile următoarele construcții:

  • Construcția soluțiilor ecuațiilor liniare.
  • Construirea de soluții la ecuații pătratice.

Cu alte cuvinte, este posibil să se construiască numere egale cu expresii aritmetice numai folosind rădăcina pătrată a numerelor originale (lungimile segmentelor). De exemplu,

Variații și generalizări

  • Construcții folosind o singură busolă. Conform teoremei Mohr-Mascheroni, cu ajutorul unei busole puteți construi orice figură care poate fi construită cu un compas și o riglă. În acest caz, o linie dreaptă este considerată construită dacă pe ea sunt specificate două puncte.
  • Construcții folosind o singură riglă. Este ușor de observat că cu ajutorul unei rigle pot fi realizate numai construcții proiectiv-invariante. În special, este imposibil chiar să împărțiți un segment în două părți egale sau să găsiți centrul unui cerc desenat. Dar dacă există un cerc predesenat pe planul cu un centru marcat, folosind o riglă, puteți efectua aceleași construcții ca și cu busolele și o riglă (teorema Poncelet-Steiner ( engleză)), 1833. Dacă există două serife pe o riglă, atunci construcțiile care o folosesc sunt echivalente cu construcțiile care folosesc busole și o riglă (Napoleon a făcut un pas important în demonstrarea acestui lucru).
  • Construcții folosind instrumente cu capacități limitate.În problemele de acest gen, instrumentele (spre deosebire de formularea clasică a problemei) sunt considerate nu ideale, ci limitate: o linie dreaptă prin două puncte poate fi trasată folosind o riglă numai dacă distanța dintre aceste puncte nu depășește un anumit punct. valoare; raza cercurilor desenate folosind o busolă poate fi limitată de sus, de dedesubt sau atât deasupra cât și dedesubt.
  • Construcții folosind origami plat. vezi regulile Hujit

Vezi de asemenea

  • Programele de geometrie dinamică vă permit să efectuați construcții folosind o busolă și o riglă pe un computer.

Note

Literatură

  • A. Adler Teoria construcțiilor geometrice / Traducere din germană de G. M. Fikhtengolts. - Ediția a treia. - L.: Uchpedgiz, 1940. - 232 p.
  • I. I. Alexandrov Culegere de probleme de construcție geometrică. - Ediția a optsprezecea. - M.: Uchpedgiz, 1950. - 176 p.
  • B. I. Argunov, M. B. Balk. - Ediția a doua. - M.: Uchpedgiz, 1957. - 268 p.
  • A. M. Voroneţ Geometria busolei. - M.-L.: ONTI, 1934. - 40 p. - (Biblioteca populară de matematică sub editie generala L.A. Lyusternik).
  • V. A. Geiler Probleme de construcție de nerezolvat // lichid de răcire. - 1999. - Nr. 12. - P. 115-118.
  • V. A. Kirichenko Construcții cu busolă și riglă și teoria Galois // Scoala de vara„Matematică modernă”. - Dubna, 2005.
  • Yu. I. Manin Cartea a IV-a. Geometrie // Enciclopedia matematicii elementare. - M.: Fizmatgiz, 1963. - 568 p.
  • Y. Petersen Metode și teorii pentru rezolvarea problemelor de construcție geometrică. - M.: Tipografia lui E. Lissner și Y. Roman, 1892. - 114 p.
  • V. V. Prasolov Trei probleme clasice de construcție. Dublarea unui cub, trisecția unui unghi, pătrarea unui cerc. - M.: Nauka, 1992. - 80 p. - (Prelegeri populare despre matematică).
  • J. Steiner Construcții geometrice realizate folosind o dreaptă și un cerc fix. - M.: Uchpedgiz, 1939. - 80 p.
  • Curs optional de matematica. 7-9 / Comp. I. L. Nikolskaya. - M.: Educație, 1991. - P. 80. - 383 p. - ISBN 5-09-001287-3

Fundația Wikimedia.

2010.

    Vedeți ce înseamnă „Construcție folosind o busolă și o riglă” în alte dicționare:

    Rigle - obțineți un cupon de lucru pentru o reducere la AllInstruments la Akademika sau cumpărați rigle cu profit cu livrare gratuită la reducere la AllInstruments

    Construcțiile care folosesc busole și rigle sunt o ramură a geometriei euclidiene cunoscută încă din cele mai vechi timpuri. În sarcinile de construcție, sunt posibile următoarele operații: Marcați un punct arbitrar pe plan, un punct pe una dintre liniile construite sau un punct... ... Wikipedia

    Substantiv, s., folosit. comparaţie adesea Morfologie: (nu) ce? constructii, ce? construcție, (văd) ce? constructii, ce? construcție, despre ce? despre constructii; pl. Ce? construcție, (nu) ce? constructii, ce? construcții, (văd) ce? constructie, cu ce?... ... Dicţionar Dmitrieva

mob_info