, Concurs „Prezentare pentru lecție”

Prezentare pentru lecție

Înapoi Înainte

Atenţie! Previzualizările diapozitivelor au doar scop informativ și este posibil să nu reprezinte toate caracteristicile prezentării. Daca esti interesat această lucrare, vă rugăm să descărcați versiunea completă.

Obiectivele lecției:

Educațional: explorați decalajul graficului funcţie pătratică, determinați poziția graficului în funcție de valorile coeficienților b, c.

Educațional: capacitatea de a lucra în grup și de a fi organizat.

De dezvoltare: abilitati de cercetare, capacitatea de a formula ipoteze, de a analiza rezultatele obtinute, de a sistematiza datele obtinute.

Structura lecției

1. Moment organizatoric – 3 minute.
2. Munca de cercetare– 20 de minute.
3. Consolidarea materialului studiat – 15 minute.
4. Reflecție – 2 minute.
5. Rezumatul lecției: 3 minute.
6. Teme pentru acasă– 2 minute.

Progresul lecției

1. Moment organizatoric.

Scopul lecției este de a efectua lucrări de cercetare. Obiectul de studiu va fi funcțiile pătratice diferite tipuri. Trebuie să determinați modul în care coeficienții b, c afectează graficul funcțiilor de forma y=x 2 +c, y=(x-b) 2, y=(x-b) 2 +c.

Pentru a finaliza sarcina, trebuie să vă împărțiți în grupuri (4 grupuri de 5 persoane, un grup „experți” - cei mai pregătiți studenți).

Fiecare grup primește un plan de cercetare<Приложение>, Foaie A3 pentru înregistrarea rezultatelor.

2. Lucrări de cercetare

.

Două grupuri (nivelul A) studiază funcțiile de forma y= x 2 +c, o grupă (nivelul B) studiază o funcție de forma y=(x-b) 2, o grupă (nivelul C) studiază funcția y=(x-b) ) 2 +c. Un grup de „Experți” examinează toate funcțiile.

	Funcţie	Rezultat
1 grup	y=x2 +3;	<Рисунок 10>
a 2-a grupă	y=x2-5;	<Рисунок 11>
3 grupa	y=(x-4)2;	<Рисунок 12>
4 grupa	y=(x-2) 2 +3.	<Рисунок 13>

Plan de lucru

1. Pentru a formula o ipoteză, ghiciți cum ar putea arăta funcția dvs.
2. Construiți un grafic al funcțiilor studiate (determinați vârful parabolei (x 0, y 0), precizați 4 puncte în tabel).
3. Comparați graficul rezultat cu proba de control y=x 2 .
4. Trageți o concluzie (cum s-a schimbat poziția graficului funcției dumneavoastră în raport cu proba de control).
5. Întocmește rezultatele pe o foaie de hârtie A3 și prezintă-le grupului de „experți”.

Grupul „expert” își compară rezultatele cu rezultatele altor grupuri, sistematizează și rezumă rezultatele și vine cu concluzii. În caz de inexactități sau erori, profesorul face comentarii corective.

Reconcilierea rezultatelor obţinute cu diapozitivele nr. 2-5.

Orice funcție pătratică y=ax 2 +bx+c poate fi scrisă ca y=a(x-x 0) 2 +y 0, unde x 0 și y 0 sunt exprimate prin coeficienții a, b, c. Deci coeficienții tăi b=x 0 , c=y 0 sunt coordonatele vârfului parabolei.

3. Consolidarea materialului studiat.

Lucru frontal cu clasa.

1. Găsiți o eroare în graficele funcțiilor (Diapozitive nr. 6-9).

Coeficientul b	Nicio eroare
Figura 1	Figura 2
y=(x+5) 2 -1	y=(x-2) 2 +2
Coeficientul b și c	Coeficientul b
Figura 3	Figura 4

Rezultate

<Рисунок 7>

<Рисунок 2>

<Рисунок 8>

<Рисунок 9>

Ce coeficient te-a ajutat să găsești eroarea?

2. Potriviți graficele funcțiilor în funcție de culori (diapozitivul nr. 10).

Figura 5

4. Reflecție.

Un grup de „Experți” răspunde la întrebări:

– Ce greșeli au făcut grupurile?

– Scopul lecției a fost atins?

– Rezultatele cercetării corespund ipotezei enunţate?

5. Rezumatul lecției (diapozitivul nr. 11)

:

Poziția graficului funcției y=(x-b) 2 +c este influențată de coeficienții b și c,

„+b” parabola este deplasată spre dreapta de-a lungul axei absciselor cu b segmente de unitate,

„–b” parabola este deplasată spre stânga de-a lungul axei absciselor cu b segmente de unitate,

„+c” parabola este deplasată în sus de-a lungul axei ordonatelor cu c segmente unitare,

„-c” parabola este deplasată în jos de-a lungul axei ordonatelor cu c segmente unitare.

6. Tema pentru acasă

1. Construiți un grafic al unei funcții pătratice cu un vârf în punctul A(1;-2), coeficient a=1.
2. Gândește-te la domeniul în care poți folosi cunoștințele pe această temă (aplicație practică).

Convertirea graficelor de funcții

În acest articol vă voi prezenta transformările liniare ale graficelor de funcții și vă voi arăta cum să utilizați aceste transformări pentru a obține un grafic de funcție dintr-un grafic de funcție

O transformare liniară a unei funcții este o transformare a funcției în sine și/sau a argumentului acesteia la formă , precum și o transformare care conține un argument și/sau un modul de funcție.

Cele mai mari dificultăți la construirea graficelor folosind transformări liniare provoacă următoarele acțiuni:

1. Izolând funcția de bază, de fapt, graficul căruia îl transformăm.
2. Definiții ale ordinii transformărilor.

ŞI Tocmai asupra acestor puncte ne vom opri mai detaliat.

Să aruncăm o privire mai atentă asupra funcției

Se bazează pe funcție. Să o sunăm functie de baza.

La trasarea unei funcții efectuăm transformări pe graficul funcției de bază.

Dacă ar fi să realizăm transformări de funcţii în aceeași ordine în care s-a găsit valoarea lui pentru o anumită valoare a argumentului, atunci

Să luăm în considerare ce tipuri de transformări liniare ale argumentului și funcției există și cum să le efectuăm.

Transformări de argument.

1. f(x) f(x+b)

1. Construiți un grafic al funcției

2. Deplasați graficul funcției de-a lungul axei OX cu |b| unitati

• stânga dacă b>0
• corect dacă b<0

Să diagramăm funcția

1. Construiți un grafic al funcției

2. Deplasați-l cu 2 unități la dreapta:

2. f(x) f(kx)

1. Construiți un grafic al funcției

2. Împărțiți abscisele punctelor graficului cu k, lăsând neschimbate ordonatele punctelor.

Să construim un grafic al funcției.

1. Construiți un grafic al funcției

2. Împărțiți toate abscisele punctelor graficului cu 2, lăsând ordonatele neschimbate:

3. f(x) f(-x)

1. Construiți un grafic al funcției

2. Afișați-l simetric față de axa OY.

Să construim un grafic al funcției.

1. Construiți un grafic al funcției

2. Afișați-l simetric față de axa OY:

4. f(x) f(|x|)

1. Construiți un grafic al funcției

2. Partea graficului situată în stânga axei OY este ștearsă, partea din grafic situată în dreapta axei OY se completează simetric față de axa OY:

Graficul funcției arată astfel:

Să diagramăm funcția

1. Construim un grafic al funcției (acesta este un grafic al funcției, deplasat de-a lungul axei OX cu 2 unități la stânga):

2. O parte a graficului situată în stânga axei OY (x).<0) стираем:

3. Completam partea din grafic situata in dreapta axei OY (x>0) simetric fata de axa OY:

Important! Două reguli principale pentru transformarea unui argument.

1. Toate transformările argumentelor sunt efectuate de-a lungul axei OX

2. Toate transformările argumentului sunt efectuate „invers” și „în ordine inversă”.

De exemplu, într-o funcție, succesiunea transformărilor argumentelor este următoarea:

1. Luați modulul lui x.

2. Adăugați numărul 2 la modulo x.

Dar am construit graficul în ordine inversă:

Mai întâi, a fost efectuată transformarea 2 - graficul a fost deplasat cu 2 unități la stânga (adică abscisele punctelor au fost reduse cu 2, ca și cum „în sens invers”)

Apoi am efectuat transformarea f(x) f(|x|).

Pe scurt, succesiunea transformărilor este scrisă după cum urmează:

Acum să vorbim despre transformarea funcției . Au loc transformări

1. De-a lungul axei OY.

2. În aceeași succesiune în care sunt efectuate acțiunile.

Acestea sunt transformarile:

1. f(x)f(x)+D

2. Deplasați-l de-a lungul axei OY cu |D| unitati

• sus dacă D>0
• jos dacă D<0

Să diagramăm funcția

1. Construiți un grafic al funcției

2. Deplasați-l de-a lungul axei OY cu 2 unități în sus:

2. f(x)Af(x)

1. Construiți un grafic al funcției y=f(x)

2. Înmulțim ordonatele tuturor punctelor graficului cu A, lăsând abscisele neschimbate.

Să diagramăm funcția

1. Să construim un grafic al funcției

2. Înmulțiți ordonatele tuturor punctelor din grafic cu 2:

3.f(x)-f(x)

1. Construiți un grafic al funcției y=f(x)

Să construim un grafic al funcției.

1. Construiți un grafic al funcției.

2. Îl afișăm simetric față de axa OX.

4. f(x)|f(x)|

1. Construiți un grafic al funcției y=f(x)

2. Partea graficului situată deasupra axei OX este lăsată neschimbată, partea din grafic situată sub axa OX este afișată simetric față de această axă.

Să diagramăm funcția

1. Construiți un grafic al funcției. Se obține prin deplasarea graficului funcției de-a lungul axei OY cu 2 unități în jos:

2. Acum vom afișa partea din grafic situată sub axa OX simetric față de această axă:

Și ultima transformare, care, strict vorbind, nu poate fi numită transformare de funcție, deoarece rezultatul acestei transformări nu mai este o funcție:

|y|=f(x)

1. Construiți un grafic al funcției y=f(x)

2. Ștergem partea din grafic situată sub axa OX, apoi completăm partea din grafic situată deasupra axei OX simetric față de această axă.

Să tragem ecuația

1. Construim un grafic al funcției:

2. Ștergem partea din grafic situată sub axa OX:

3. Completam partea din grafic situata deasupra axei OX simetric fata de aceasta axa.

Și în sfârșit, vă sugerez să urmăriți un TUTORIAL VIDEO în care vă arăt un algoritm pas cu pas pentru construirea unui grafic al unei funcții

Graficul acestei funcții arată astfel:

Dependența formei +=

Programa ecuația dată este un cerc pe planul de coordonate x Oy cu centrul în punctul O(a;b) și raza r (r>0).

Graficul acestei ecuații nu poate fi numit grafic al unei funcții, deoarece se încalcă definiția funcției: fiecărei valori x îi corespunde o singură valoare y.

Mișcarea funcțiilor de-a lungul axelor de coordonate

unde l este un număr pozitiv dat, trebuie să mutați graficul funcției y=f(x) de-a lungul axei x cu unități de scară l spre stânga.

Pentru a reprezenta o funcție

unde l este un număr pozitiv dat, trebuie să mutați graficul funcției y=f(x) de-a lungul axei x cu unități de scară l spre dreapta.

Pentru a reprezenta o funcție

unde m este un număr pozitiv dat, trebuie să mutați graficul funcției y=f(x) de-a lungul axei y cu m unități de scară în sus.

Pentru a construi un grafic al funcției y=f(x)-m, unde m este un număr pozitiv dat, trebuie să mutați graficul funcției y=f(x) de-a lungul axei y cu m unități de scară în jos.

Algoritmul 1 pentru reprezentarea grafică a funcției y=f(x+l)+m:

• 1. Reprezentați grafic funcția y=f(x).
• 2. Efectuați un transfer paralel al graficului y=f(x) de-a lungul axei x cu unități de scară la stânga dacă l>0 și la dreapta dacă l
• 3. Efectuați un transfer paralel al graficului obținut în a doua etapă de-a lungul axei y cu unități de scară în sus, dacă

Algoritmul 2 pentru reprezentarea grafică a funcției y=f(x+l)+m:

• 1. Mergeți la sistemul de coordonate auxiliar desenând liniile drepte auxiliare x=-l, y=m cu o linie punctată, adică. alegand ca inceput sistem nou punct de coordonate (-l;m).
• 2. Legați graficul funcției y=f(x) de noul sistem de coordonate.

Funcțiile elementare de bază în forma lor pură fără transformare sunt rare, așa că cel mai adesea trebuie să lucrați cu acestea functii elementare, care au fost obținute din cele principale prin adăugarea de constante și coeficienți. Astfel de grafice sunt construite folosind transformări geometrice ale funcțiilor elementare date.

Să luăm în considerare exemplul unei funcții pătratice de forma y = - 1 3 x + 2 3 2 + 2, al cărei grafic este parabola y = x 2, care este comprimată de trei ori față de Oy și simetrică față de la Ox și deplasat cu 2 3 de-a lungul Ox la dreapta, în sus cu 2 unități de-a lungul Oy. Pe o linie de coordonate arată astfel:

Transformări geometrice ale graficului unei funcții

Aplicând transformări geometrice ale unui grafic dat, aflăm că graficul este reprezentat de o funcție de forma ± k 1 · f (± k 2 · (x + a)) + b, când k 1 > 0, k 2 > 0 sunt coeficienți de compresie la 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 de-a lungul O y și O x. Semnul din fața coeficienților k 1 și k 2 indică o afișare simetrică a graficului în raport cu axele, a și b îl deplasează de-a lungul O x și de-a lungul O y.

Definiția 1

Există 3 tipuri transformări geometrice ale graficului:

• Scalare de-a lungul O x și O y. Aceasta este influențată de coeficienții k 1 și k 2 cu condiția ca aceștia să nu fie egali cu 1 când 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, apoi graficul este întins de-a lungul O y și comprimat de-a lungul O x.
• Afișare simetrică față de axele de coordonate. Dacă există semnul „-” în fața lui k 1, simetria este relativă la O x, iar în fața lui k 2 este relativă la O y. Dacă „-” lipsește, atunci elementul este omis la rezolvare;
• Transfer paralel (deplasare) de-a lungul O x și O y. Transformarea se realizează dacă există coeficienți a și b inegali cu 0. Dacă a este pozitiv, graficul este deplasat la stânga cu | a | unități, dacă a este negativ, atunci la dreapta la aceeași distanță. Valoarea b determină mișcarea de-a lungul axei O y, ceea ce înseamnă că atunci când b este pozitiv, funcția se mișcă în sus, iar când b este negativ, se mișcă în jos.

Să ne uităm la soluții folosind exemple, începând cu o funcție de putere.

Exemplul 1

Transformați y = x 2 3 și reprezentați grafic funcția y = - 1 2 · 8 x - 4 2 3 + 3 .

Soluţie

Să reprezentăm funcțiile astfel:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Unde k 1 = 2, merită să acordați atenție prezenței „-”, a = - 1 2, b = 3. De aici obținem că transformările geometrice sunt efectuate prin întinderea de-a lungul O y de două ori, afișată simetric față de O x, deplasată la dreapta cu 1 2 și în sus cu 3 unități.

Dacă descriem funcția de putere inițială, obținem asta

când este întins de două ori de-a lungul O y avem asta

Maparea, simetrică față de O x, are forma

și deplasați-vă la dreapta cu 1 2

o mișcare de 3 unități în sus arată ca

Să ne uităm la transformările funcțiilor exponențiale folosind exemple.

Exemplul 2

Construiți un grafic al funcției exponențiale y = - 1 2 1 2 (2 - x) + 8.

Soluţie.

Să transformăm funcția pe baza proprietăților unei funcții de putere. Atunci obținem asta

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Din aceasta putem vedea că obținem un lanț de transformări y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Constatăm că originalul functie exponentiala arata ca

Strângerea de două ori de-a lungul O y dă

Întinderea de-a lungul O x

Maparea simetrică în raport cu O x

Maparea este simetrică în raport cu O y

Mutați în sus cu 8 unități

Să ne uităm la soluție folosind un exemplu funcţie logaritmică y = log(x) .

Exemplul 3

Construiți funcția y = ln e 2 · - 1 2 x 3 folosind transformarea y = ln (x) .

Soluţie

Pentru a rezolva este necesar să folosim proprietățile logaritmului, atunci obținem:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Transformările unei funcții logaritmice arată astfel:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Să diagramăm funcția logaritmică inițială

Comprimăm sistemul conform O y

Ne întindem de-a lungul O x

Efectuăm o mapare cu privire la O y

Trecem cu 2 unități, obținem

Pentru a transforma graficele unei funcții trigonometrice, este necesar să se potrivească schemei soluții de forma ± k 1 · f (± k 2 · (x + a)) + b. Este necesar ca k 2 să fie egal cu T k 2 . De aici obținem acel 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Să ne uităm la exemple de rezolvare a problemelor cu transformări y = sin x.

Exemplul 4

Construiți un grafic al lui y = - 3 sin 1 2 x - 3 2 - 2 folosind transformări ale funcției y=sinx.

Soluţie

Este necesar să se reducă funcția la forma ± k 1 · f ± k 2 · x + a + b. Pentru a face acest lucru:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Se poate observa că k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Deoarece există un „-” înainte de k 1, dar nu înainte de k 2, atunci obținem un lanț de transformări de forma:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Transformare detaliată a undei sinusoidale. Când trasăm sinusoida originală y = sin (x), aflăm că cea mai mică perioadă pozitivă este considerată a fi T = 2 π. Aflarea maximului în punctele π 2 + 2 π · k; 1, iar minimul - - π 2 + 2 π · k; - 1, k ∈ Z.

O y este întins de trei ori, ceea ce înseamnă că creșterea amplitudinii oscilațiilor va crește de 3 ori. T = 2 π este cea mai mică perioadă pozitivă. Maximele merg la π 2 + 2 π · k; 3, k ∈ Z, minime - - π 2 + 2 π · k; - 3, k ∈ Z.

Când se întinde de-a lungul O x la jumătate, constatăm că cea mai mică perioadă pozitivă crește de 2 ori și este egală cu T = 2 π k 2 = 4 π. Maximele merg la π + 4 π · k; 3, k ∈ Z, minime – în - π + 4 π · k; - 3, k ∈ Z.

Imaginea este produsă simetric în raport cu O x. Cea mai mică perioadă pozitivă în în acest caz, nu se modifică și este egal cu T = 2 π k 2 = 4 π . Tranziția maximă arată ca - π + 4 π · k; 3, k ∈ Z, iar minimul este π + 4 π · k; - 3, k ∈ Z.

Graficul este deplasat în jos cu 2 unități. Nu există nicio modificare a perioadei minime comune. Găsirea maximelor cu trecerea la puncte - π + 3 + 4 π · k; 1, k ∈ Z, minime - π + 3 + 4 π · k; - 5 , k ∈ Z .

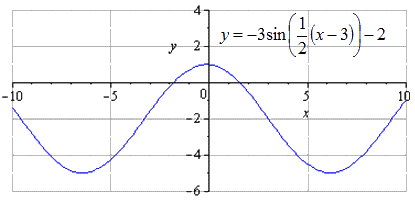
În această etapă, graficul funcției trigonometrice este considerat transformat.

Să considerăm o transformare detaliată a funcției y = cos x.

Exemplul 5

Construiți un grafic al funcției y = 3 2 cos 2 - 2 x + 1 folosind o transformare a funcției de forma y = cos x.

Soluţie

Conform algoritmului este necesar funcţie dată se reduce la forma ± k 1 · f ± k 2 · x + a + b. Atunci obținem asta

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Din condiție este clar că k 1 = 3 2, k 2 = 2, a = - 1, b = 1, unde k 2 are „-”, dar înainte de k 1 este absent.

Din aceasta vedem că obținem un grafic al unei funcții trigonometrice de forma:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

Transformare cosinus pas cu pas cu ilustrare grafică.

Având în vedere graficul y = cos(x), este clar că cea mai scurtă perioadă totală este T = 2π. Găsirea maximelor în 2 π · k ; 1, k ∈ Z, și există π + 2 π · k minime; - 1, k ∈ Z.

Când este întins de-a lungul Oy de 3 2 ori, amplitudinea oscilațiilor crește de 3 2 ori. T = 2 π este cea mai mică perioadă pozitivă. Găsirea maximelor în 2 π · k ; 3 2, k ∈ Z, minime în π + 2 π · k; - 3 2 , k ∈ Z .

Când este comprimată de-a lungul O x la jumătate, aflăm că cea mai mică perioadă pozitivă este numărul T = 2 π k 2 = π. Are loc trecerea maximelor la π · k; 3 2 , k ∈ Z , minime - π 2 + π · k ; - 3 2 , k ∈ Z .

Harta simetrica fata de Oy. Deoarece graficul este impar, nu se va schimba.

Când graficul este deplasat cu 1. Nu există modificări în cea mai mică perioadă pozitivă T = π. Găsirea maximelor în π · k + 1 ; 3 2, k ∈ Z, minime - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Când este deplasată cu 1, cea mai mică perioadă pozitivă este egală cu T = π și nu se modifică. Găsirea maximelor în π · k + 1 ; 5 2, k ∈ Z, minime în π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Transformarea funcției cosinus este completă.

Să luăm în considerare transformările folosind exemplul y = t g x.

Exemplul 6

Construiți un grafic al funcției y = - 1 2 t g π 3 - 2 3 x + π 3 folosind transformări ale funcției y = t g (x) .

Soluţie

Pentru început, este necesar să reducem funcția dată la forma ± k 1 · f ± k 2 · x + a + b, după care obținem că

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Este clar că k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, iar în fața coeficienților k 1 și k 2 există un „-”. Aceasta înseamnă că după transformarea tangentelor obținem

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Transformarea pas cu pas a tangentelor cu reprezentare grafică.

Avem că graficul original este y = t g (x) . Modificarea perioadei pozitive este egală cu T = π. Domeniul de definiție este considerat a fi - π 2 + π · k ; π 2 + π · k, k ∈ Z.

O comprimăm de 2 ori de-a lungul Oy. T = π este considerată cea mai mică perioadă pozitivă, unde domeniul de definiție are forma - π 2 + π · k; π 2 + π · k, k ∈ Z.

Întindeți de-a lungul O x 3 2 ori. Să calculăm cea mai mică perioadă pozitivă și a fost egală cu T = π k 2 = 3 2 π . Și domeniul de definire al funcției cu coordonate este 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, se modifică doar domeniul de definiție.

Simetria merge pe partea O x. Perioada nu se va schimba în acest moment.

Este necesar să afișați axele de coordonate simetric. Domeniul de definiție în acest caz este neschimbat. Programul coincide cu cel precedent. Aceasta sugerează că funcția tangentă este impară. Dacă să funcţie ciudată setați o mapare simetrică a O x și O y, apoi transformați la funcția originală.

Soluţie

Mai întâi trebuie să treceți de la arccosinus la arcsinus folosind inverse funcții trigonometrice a r c sin x + a r c o cos x = π 2 . Aceasta înseamnă că obținem că a r c sin x = π 2 - a r c cos x.

Se poate observa că y = a r c cos x → y = - a r c cos x → y = - a r c cos x + π 2 .

Transformarea arccosinusului pas cu pas și reprezentarea grafică.

Program dat de condiție

Efectuăm o mapare în raport cu O x

Ne deplasăm în sus cu π 2.

Astfel, se realizează trecerea de la arccosinus la cosinus. Este necesar să se efectueze transformări geometrice ale arcsinusului și ale graficului acestuia.

Se poate observa că k 1 = 2, k 2 = 1 3, a = - 1, b = 0, unde nu există semnul „-” pentru k 1 și k 2.

De aici rezultă că transformarea y = a r c sin x ia forma:

y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x - 1)

Transformarea pas cu pas a graficului arcsinus și reprezentarea grafică.

Graficul y = a r c sin x are un domeniu de forma x ∈ - 1 ; 1, atunci intervalul y ∈ - π 2; π 2 aparține domeniului de valori.

Este necesar să-l întindeți de două ori de-a lungul O y, iar domeniul de definiție va rămâne neschimbat x ∈ - 1; 1 și intervalul de valori y ∈ - π; π.

Întindere conform structurii Ox. Domeniul de definiție x ∈ - 3 este extins; 3, dar intervalul de valori rămâne neschimbat y ∈ - π; π.