Teorema lui Pitagora: istorie, dovezi, exemple de aplicare practică. Teoreme antice. Istoria teoremei lui Pitagora Ce a demonstrat Pitagora

Prividentsev Vladislav, Farafonova Ekaterina

Lucrări de proiect ale studenților pentru o conferință de matematică

Descărcați:

Previzualizare:

BOU TR OO „Școala Gimnazială Trosnyanskaya”

Conferință studențească de matematică dedicată marelui matematician Pitagora

(ca parte a Săptămânii Matematicii la școală)

Istoria teoremei lui Pitagora

(proiect)

Pregătit

elevi de clasa a IX-a

Farafonova Ekaterina și Prividentsev Vladislav

Profesorul Bilyk T.V.

ianuarie – 2016

Obiective:

1.Extindeți-vă cunoștințele despre istoria matematicii.
2.Faceți cunoștință fapte biografice din viaţa lui Pitagora legată de teoremă.
3. Studiază istoria teoremei lui Pitagora prin mituri și legende ale antichității.
4. Luați în considerare aplicarea teoremei lui Pitagora în rezolvarea problemelor din diverse ramuri ale geometriei.

Plan.

1.Introducere

2. Din istoria teoremei

3. Poezii despre Pitagora

4. Rezumat

5. Concluzie

Introducere.

Teorema lui Pitagora a fost mult timp folosită pe scară largă în diverse domenii ale științei, tehnologiei și viata practica. Arhitectul și inginerul roman Vitruvius, scriitorul moralist grec Plutarh și omul de știință grec în secolul al III-lea au scris despre asta în lucrările lor. Diogenes Laertius, matematician din secolul al V-lea Proclus și mulți alții. Legenda conform căreia, în cinstea descoperirii sale, Pitagora a sacrificat un taur, sau, după cum spun alții, o sută de tauri, a servit drept motiv de umor în poveștile scriitorilor și în poeziile poeților.

Poetul Heinrich Heine (1797-1856), cunoscut pentru opiniile sale antireligioase și ridicolul caustic al superstițiilor, într-una dintre lucrările sale ridiculizează „doctrina” transmigrării sufletelor după cum urmează:

"Cine ştie! Cine ştie! Sufletul lui Pitagora s-a așezat, poate, pe un candidat sărac care nu a putut dovedi teoremele lui Pitagora și, prin urmare, a picat examenul, în timp ce în examinatorii săi trăiesc chiar sufletele acelor tauri pe care Pitagora i-a sacrificat cândva zeilor nemuritori, încântat de descoperirea lui Pitagora. teorema lui.” Poveste Teorema lui Pitagoraîncepe cu mult înaintea lui Pitagora. De-a lungul secolelor au fost date numeroase dovezi diferite ale Teoremei lui Pitagora.

Din istoria teoremei

Să începem recenzia noastră istorică cu China antică. Aici cartea de matematică Chu-pei atrage o atenție deosebită. Acest eseu vorbește despre Triunghiul lui Pitagora cu laturile 3, 4 și 5: „Dacă un unghi drept este împărțit în părțile sale componente, atunci linia care leagă capetele laturilor sale va fi 5, când baza este 3 și înălțimea este 4”. În aceeași carte este propus un desen care coincide cu unul dintre desenele geometriei hinduse a lui Bashara.

Cantor (cel mai important istoric german al matematicii) crede că egalitatea 32 + 42 = 52 era deja cunoscut la egipteni încă în jurul anului 2300 î.Hr. e., pe vremea regelui Amenemhet I (conform papirusului 6619 al Muzeului din Berlin). Potrivit lui Cantor, harpedonapții, sau „trăgători de frânghii”, construiau unghiuri drepte folosind triunghiuri dreptunghiulare cu laturile 3, 4 și 5. Metoda lor de construcție poate fi reprodusă foarte ușor. Să luăm o frânghie de 12 m lungime și să legăm de ea o bandă colorată la o distanță de 3 m. de la un capăt și la 4 metri de celălalt. Unghiul drept va fi închis între laturile lungi de 3 și 4 metri. S-ar putea obiecta harpedonaptienilor că metoda lor de construcție devine de prisos dacă se folosește, de exemplu, un pătrat de lemn, care este folosit de toți dulgherii. Într-adevăr, se cunosc desene egiptene în care se găsește un astfel de instrument, de exemplu, desene înfățișând atelierul unui tâmplar.

Se știe puțin mai mult despre teorema lui Pitagora babilonienii . Într-un text legat de timp Hammurabi , adică până în 2000 î.Hr. e., se dă un calcul aproximativ al ipotenuzei unui triunghi dreptunghic. Din aceasta putem concluziona că în Mesopotamia au fost capabili să efectueze calcule cu triunghiuri dreptunghiulare, cel puțin în unele cazuri. Bazându-se, pe de o parte, pe nivelul actual de cunoștințe despre matematica egipteană și babiloniană, iar pe de altă parte, pe un studiu critic al surselor grecești, Van der Waerden (matematician olandez) a ajuns la următoarea concluzie:„Meritul primilor matematicieni greci, precum Thales, Pitagora și pitagoreenii, nu este descoperirea matematicii, ci sistematizarea și justificarea ei, în mâinile lor, rețetele de calcul bazate pe idei vagi s-au transformat într-o știință exactă.” Geometrie hindusă , ca și egiptenii și babilonienii, a fost strâns asociat cu cultul. Este foarte probabil ca teorema asupra pătratului ipotenuzei să fi fost deja cunoscută în India în jurul secolului al XVIII-lea î.Hr. e.

În prima traducere rusă a Elementelor euclidiene, realizată de F. I. Petrushevsky, teorema lui Pitagora este enunțată după cum urmează:"ÎN triunghi dreptunghic x pătrat al laturii opuse unghiului drept este egal cu suma pătratelor laturilor care conțin unghiul drept.”Acum se știe că această teoremă nu a fost descoperită de Pitagora. Cu toate acestea, unii cred că Pitagora a fost primul care a dat dovada completă, în timp ce alții îi neagă acest merit. Unii îi atribuie lui Pitagora dovada pe care Euclid o dă în prima carte a lui Elementele. Pe de altă parte, Proclu susține că demonstrația din Elemente îi aparține lui Euclid însuși. După cum vedem, istoria matematicii nu a păstrat aproape deloc date sigure despre viața lui Pitagora și activitățile sale matematice. Dar legenda ne spune chiar circumstanțele imediate care au însoțit descoperirea teoremei. Ei spun că în cinstea acestei descoperiri, Pitagora a sacrificat 100 de tauri.

Multă vreme s-a crezut că această teoremă nu era cunoscută înainte de Pitagora și, prin urmare, a fost numită „teorema lui Pitagora”. Acest nume a supraviețuit până în zilele noastre. Cu toate acestea, acum s-a stabilit că această teoremă cea mai importantă se găsește în textele babiloniene scrise cu 1200 de ani înainte de Pitagora.
Faptul că un triunghi cu laturile 3, 4 și 5 este dreptunghi era cunoscut în anul 2000 î.Hr. egiptenii, care probabil au folosit acest raport pentru a construi unghiuri drepte atunci când construiau clădiri. În China, propunerea pentru pătratul ipotenuzei era cunoscută cu cel puțin 500 de ani înainte de Pitagora. Această teoremă era cunoscută și în India antică; Acest lucru este dovedit de propozițiile conținute în Sutre.

Pitagora a făcut multe descoperiri importante, dar teorema pe care a demonstrat-o, care îi poartă acum numele, i-a adus cea mai mare faimă omului de știință. Într-adevăr, în manualele moderne teorema este formulată după cum urmează: „Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor.” - Cum se scrie teorema lui Pitagora pentru un triunghi dreptunghic ABC cu catetele a, b și ipotenuza c.

a 2 + b 2 = c 2

Se crede că pe vremea lui Pitagora teorema suna diferit: „Aria unui pătrat construit pe ipotenuza unui triunghi dreptunghic este egală cu suma ariilor pătratelor construite pe picioarele sale”. într-adevăr, Cu 2 – aria pătratului construit pe ipotenuză, a 2 și b 2 – zone de pătrate construite pe picioare.

Este probabil că faptul enunțat în teorema lui Pitagora a fost stabilit pentru prima dată pentru triunghiuri dreptunghiulare isoscele. Un pătrat construit pe ipotenuză conține patru triunghiuri. Și pe fiecare parte există un pătrat care conține două triunghiuri. Din figura 9 este clar că aria pătratului construit pe ipotenuză este egală cu suma ariilor pătratelor construite pe catete.

Poezii despre Pitagora.
Romancierul german A. Chamisso, care la începutul secolului al X-lea. A participat la o călătorie în jurul lumii pe nava rusă „Rurik” și a scris următoarele poezii:
Adevărul va rămâne etern, de îndată ce
O persoană slabă va ști!
Și acum teorema lui Pitagora
Adevărat, ca secolul lui îndepărtat.
Sacrificiul a fost abundent
Zeilor din Pitagora. O sută de tauri
A renunțat la el pentru a fi sacrificat și ars
În spatele luminii este o rază care a venit din nori.
Prin urmare, de atunci,
Adevărul este doar să te naști,
Taurii răcnesc, simțind-o, urmând-o.
Ei nu pot opri lumina,
Sau pot doar să închidă ochii și să tremure
Din frica pe care Pitagora le-a insuflat-o

Pentru a rezuma:
Dacă ni se dă un triunghi
Și, în plus, cu unghi drept,
Acesta este pătratul ipotenuzei
Întotdeauna putem găsi cu ușurință:
Îndreptăm picioarele,
Găsim suma puterilor
Și într-un mod atât de simplu
Vom ajunge la rezultat.

Se apropie un test de geometrie, iar în timpul testelor și examenelor există uneori cazuri când studenții, după ce au scos un bilet, își amintesc formularea teoremei, dar uită de unde să înceapă demonstrația. Pentru a preveni acest lucru, vă sugerez un desen - un semnal de referință. Cred că va rămâne în memoria ta multă vreme.

Ivan Tsarevich a tăiat capul balaurului și din el au crescut doi noi. În limbajul matematic, aceasta înseamnă: petrecut în Δ ABC înălțime CD , și s-au format două noi triunghiuri dreptunghiulare ADC și BDC.

Concluzie.

După ce am studiat materialul construit, putem concluziona că teorema lui Pitagora este una dintre cele mai importante teoreme ale geometriei deoarece cu ajutorul ei puteți demonstra multe alte teoreme și rezolva multe probleme.

Pitagora și școala pitagoreică au jucat un rol major în îmbunătățirea metodelor de rezolvare probleme științifice: poziția despre necesitatea demonstrațiilor riguroase a fost ferm stabilită în matematică, ceea ce i-a conferit semnificația unei științe speciale.

Introducere

Este dificil să găsești o persoană care să nu asocieze numele lui Pitagora cu teorema sa. Poate că chiar și cei care și-au luat rămas bun de la matematică pentru totdeauna în viața lor păstrează amintiri despre „pantaloni pitagoreici” - un pătrat pe ipotenuză, egal ca dimensiune cu două pătrate pe laturi.

Motivul pentru popularitatea teoremei lui Pitagora este triun: ea

simplitate - frumusețe - semnificație. Într-adevăr, teorema lui Pitagora este simplă, dar nu evidentă. Aceasta este o combinație a două contradictorii

a început să-i dea o forță de atracție deosebită, o face frumoasă.

În plus, teorema lui Pitagora este de mare importanță: este folosită în geometrie literalmente la fiecare pas, iar faptul că există aproximativ 500 de dovezi diferite ale acestei teoreme (geometrice, algebrice, mecanice etc.) indică un număr gigantic al acesteia. implementari specifice.

În manualele moderne, teorema este formulată după cum urmează: „Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor.”

Pe vremea lui Pitagora, suna așa: „Demonstrați că un pătrat construit pe ipotenuza unui triunghi dreptunghic este egal cu suma pătratelor construite pe picioarele sale” sau „Aria unui pătrat construit pe ipotenuză a unui triunghi dreptunghic este egală cu suma ariilor pătratelor construite pe picioarele sale.”

Scopuri și obiective

Scopul principal al lucrării a fost să arateimportanța teoremei lui Pitagora în dezvoltarea științei și tehnologiei multorațări și popoare ale lumii, precum și în cele mai simple și interesanteformă pentru a preda conținutul teoremei.

Metoda principală folosită în lucrare esteeste o metodă de organizare și prelucrare a datelor.

Atragerea tehnologia de informație, diversematerial zili cu diverse ilustrații colorate.

„VERSE DE AUR” ALE PITAGORUS

Fii corect atât în cuvintele tale, cât și în acțiunile tale... Pitagora (c. 570-c. 500 î.Hr.)

Filosof și matematician grec anticdezvoltat cu învăţătura sa despre armonia cosmică şitransmigrarea sufletelor. Tradiția îl creditează pe Pitagora pentru că a demonstrat teorema care îi poartă numele. Mult înÎnvățăturile lui Platon se întorc la Pitagora și succesorii săi tel.

Nu au mai rămas documente scrise despre Pitagora din Samos, fiul lui Mnesarchus, iar din dovezile ulterioare este dificil de reconstruit imaginea adevărată a vieții și realizărilor sale.(Enciclopedia electronică:SteaLume) Se știe că Pitagora și-a părăsit insula natală, Samos, în Marea Egee, la malguvernatorul Asiei Mici în semn de protest împotriva tiraniei domnitorului și deja la maturitatevârsta (conform legendei la 40 de ani) a apărut în orașul grecesc Crotone din sudul Italiei. Pitagora și adepții săi - pitagoreicii - au format o alianță secretă care a jucat un rol semnificativ în viață colonii greceștiîn ItaLii. Pitagoreii s-au recunoscut unul pe altul după un pentagon în formă de stea - o pentagramă. Dar Pitagora a trebuit să se retragă la Metapontum, unde ela murit. Mai târziu, în a doua jumătateVî.Hr e., ordinul lui a fost distrus.

Învățăturile lui Pitagora au fost foarte influențate de filozofie și religiegia a Estului. A călătorit mult în țările din Orient: a fost înEgipt și Babilon. Acolo Pitagora a întâlnit și matematica orientală tikoy.

Pitagorei credeau că secretele erau ascunse în modele numerice.asupra lumii. Lumea numerelor a trăit o viață specială pentru Pitagorapropriul său sens special de viață. Numerele egale cu suma divizorilor lor erau percepute ca perfecte (6, 28, 496, 8128); prietenosnumere perechi de numere, fiecare dintre ele egal cu suma divizorilor celuilaltgogo (de exemplu, 220 și 284). Pitagora a fost primul care a împărțit numerele în pare șiimpare, prime și compuse, a introdus conceptul de numere figurate. În a luișcoală, au fost examinate în detaliu tripletele pitagorice ale numerelor naturale, în care pătratul unuia era egal cu suma pătratelor celorlalte două ( mare teoremă Fermă).

Lui Pitagora i se atribuie faptul că a spus: „Totul este un număr”. La numere(și a vrut doar să spună numere naturale) a vrut să aducă lumea întreagă împreună, șimatematica in special. Dar chiar în școala lui Pitagora a fost făcută o descoperire care a încălcat această armonie. S-a dovedit că rădăcina lui 2 nu esteeste număr rațional, adică neexprimat prin natural numere.

Desigur, geometria lui Pitagora era subordonată aritmeticii.Acest lucru s-a manifestat clar în teorema care îi poartă numele și a devenit mai târziubaza de aplicare metode numerice geometrie. (Mai târziu, Euclid a adus din nou geometria în prim-plan, subordonându-i algebra.) Aparent, pitagoreicii cunoșteau solidele corecte: tetraedrul, cubul și dodecaedrul.

Lui Pitagora i se atribuie introducerea sistematică a demonstrațiilor în geometrie, crearea planimetriei figurilor rectilinii, doctrina lui bii.

Numele lui Pitagora este asociat cu doctrina proporțiilor aritmetice, geometrice și armonice.

Trebuie remarcat faptul că Pitagora considera că Pământul este o minge în mișcareîn jurul soarelui. Când înXVIsecolul biserica a început să fie persecutată aprigDacă luăm învățătura lui Copernic, această învățătură a fost numită cu insistență pitagoreică.(Dicționar enciclopedic al unui tânăr matematician: E-68. A. P. Savin.- M.: Pedagogie, 1989, p. 28.)

Unele concepte fundamentale aparțin, fără îndoialălui Pitagora însuși. Primul- ideea de spațiu ca matematicăun întreg ordonat tic. Pitagora a venit la el după ce a descoperit că intervalele armonice fundamentale, adică octava, quinta perfectă și patra perfectă, apar atunci când lungimile corzilor care vibrează sunt legate ca 2:1, 3:2 și 4:3 (legenda spune că descoperirea a fost făcută cândPitagora a trecut pe lângă o forjă: nicovale cu mase diferitea generat relațiile sonore corespunzătoare la impact). UsmotDezvăluind o analogie între ordinea în muzică, exprimată prin relațiile descoperite de aceasta, și ordinea lumii materiale, Pitagoraa ajuns la concluzia că este pătruns de relații matematiceîntregul spațiu. O încercare de a aplica descoperirile matematice ale lui Pitagora la construcții fizice speculative a dus la consecințe interesante.rezultate. Astfel, s-a presupus că fiecare planetă în timpul revoluției saleîn jurul Pământului emite când trece prin aerul superior limpede, sau „eter”,tonul unei anumite tonuri. Înălțimea sunetului se modifică în funcție de vitezăviteza de mișcare a planetei, viteza depinde de distanța până la Pământ. PrunăCând sunetele cerești se unesc, ele formează ceea ce se numește „armonia sferelor” sau „muzica sferelor”, referiri la care sunt frecvente în literatura europeană.

Primii pitagoreici credeau că Pământul este plat și în centruspaţiu. Mai târziu au început să creadă că Pământul are o formă sferică și, împreună cu alte planete (din care au inclus Soarele), are formăse învârte în jurul centrului spațiului, adică „vatră”.

În antichitate, Pitagora era cel mai bine cunoscut ca predicatorstil de viață retras. Esențial pentru învățătura lui a fost ideeavorbim despre reîncarnare (transmigrarea sufletelor), care, desigur, presupune capacitatea sufletului de a supraviețui morții trupului, și deci nemurirea lui. Întrucât într-o nouă încarnare sufletul se poate muta în corpul unui animal, Pitagora s-a opus uciderii animalelor, consumului de carne a acestora și chiar a afirmat că nu trebuie să avem de-a face cu cei care sacrifică animalele sau le măcelează cadavrele. Din câte se poate judeca din scrierile lui Empedocles, care a împărtășit vederi religioase Pitagora, vărsarea sângelui era considerată aici ca păcat originar, pentru care sufletul este izgonit în lumea muritorilor, unde rătăcește, fiind închis într-un trup sau altul. Sufletul dorește cu pasiune eliberarea, dar din ignoranță repetă invariabil actul păcătos.

Poate salva sufletul dintr-o serie nesfârșită de reîncarnăricuratare Cea mai simplă curățare constă în observarea anumitorinterdicții (de exemplu, abținerea de la intoxicare sau de a beaconsumul de fasole) și reguli de comportament (de exemplu, onorarea bătrânilor, respectarea legii și a nu fi supărat).

Pitagoreii apreciau foarte mult prietenia și, conform conceptelor lor, toate proprietățile prietenilor ar trebui să fie comune. Câțiva aleși li s-a oferit cea mai înaltă formă de purificare - filozofia, adică dragostea de înțelepciune și, prin urmare, dorința pentru aceasta (acest cuvânt, potrivit lui Cicero, a fost folosit pentru prima dată de Pitagora, care s-a numit nu un înțelept, ci un iubitor. de înțelepciune). Prin aceste mijloace sufletul intră în contact cu principiile ordine cosmicăși devine în ton cu ei, ea se eliberează de atașamentul față de corp, de dorințele sale fără de lege și dezordonate. Matematica este una dintre componentele religieiPitagorei, care au învățat că Dumnezeu a pus numărul la baza lumiicomanda.

Influența Frăției Pitagoreice în prima reprizăVV. î.Hr e. Nucrescut continuu. Dar dorința lui de a da putere celor „cei mai buni” a intrat în conflict cu creșterea sentimentului democratic în orașele grecești din sudul Italiei și la scurt timp după 450 î.Hr. e. a fost un focar la Crotoneo rebeliune împotriva pitagoreenilor care a dus la uciderea și expulzarea multor, dacă nu a tuturor, membri ai frăției. Cu toate acestea, încă înIVV. î.Hr e. pythagoReich-ul s-a bucurat de influență în sudul Italiei, iar în Tarentum, unde a locuit prietenul lui Platon, Archytas, a rămas și mai mult. Cu toate acestea, mult mai importantă pentru istoria filozofiei a fost crearea centrelor pitagoreice chiar în Grecia,de exemplu la Teba, în a doua jumătateVV. î.Hr e. De aici pitagoricaideile au pătruns până la Atena, unde, după dialogul lui PlatonPhaedo,au fost adoptate de Socrate și transformate într-o mișcare ideologică largă,început de Platon și studentul său Aristotel.

În secolele următoare, figura lui Pitagora însuși a fost înconjurată
multe legende: a fost considerat zeul reîncarnat Apollo,
se credea că avea o coapsă de aur și era capabil să predea în
în același timp în două locuri. Părinții Bisericii Creștine timpurii răspund
dacă Pitagora are un loc de cinste între Moise şi Platon. Înapoi înăuntruXVIV[
au existat frecvente referiri la autoritatea lui Pitagora în chestiuni nu numai de știință |.:
dar și magie.(Enciclopedia electronică:SteaLume.).

În spatele legendei se află adevărul

Descoperirea teoremei lui Pitagora este înconjurată de un halou legende frumoase OProclus, comentând ultima propozițieeucărți „Elemente” de Euclid,scrie: „Dacă îi asculți pe cei cărora le place să repete legende străvechi, atuncitrebuie să spunem că această teoremă se întoarce la Pitagora; spun eică a sacrificat un taur în cinstea asta”. Această legendă a crescut ferm împreunăcu teorema lui Pitagora și după 2000 de ani a continuat să provoace fierbinte clicuri. Astfel, optimistul Mihailo Lomonosov a scris: „Pitagora pentru inventarea unui geometricConform domniei lui Zeves, a sacrificat o sută de boi.Dar dacă pentru cele găsite în vremurile moderne dinmatematicienii duhovnici guvernează după superstițiosul săugelozie să acționeze, apoi abiadacă ar fi atât de mulţi în lumea întreagăau fost găsite vite”.

Dar ironicul Heinrich Heine a văzut evoluția aceleiași situații oarecum diferit : « Cine ştie ! Cine ştie ! Pot fi , sufletul lui Pithas muntele sa mutat în bietul candidat , care nu a putut demonstra teorema lui Pitagora şi a eşuat din - pentru asta la examene , în timp ce în examinatorii săi locuiesc sufletele acelor tauri , pe care Pitagora , încântat de descoperirea teoremei sale , sacrificat zeilor nemuritori ».

Istoria descoperirii teoremei

Descoperirea teoremei lui Pitagora este de obicei atribuită filozofului și matematicianului grec antic Pitagora (VIV. î.Hr e.). Dar un studiu al tabelelor cuneiforme babiloniene și al manuscriselor chinezești antice (copii ale manuscriselor și mai vechi) a arătat că această afirmație era cunoscută cu mult înaintea lui Pitagora, poate cu milenii înaintea lui. Meritul lui Pitagora a fost că a descoperit demonstrația acestei teoreme.

Să începem recenzia noastră istorică cu China antică. Există o notă specială aicimania este atrasă de cartea de matematică Chu-pei. Această lucrare vorbește despre triunghiul lui Pitagora cu laturile 3, 4 și 5:„Dacă un unghi drept este descompus în părțile sale componente, atunci linia care leagă capetele laturilor sale va fi 5, când baza este 3 și înălțimea este 4.”

În aceeași carte este propus un desen care coincide cu unul dintre desenele geometriei hinduse a lui Bashara.

De asemenea, teorema lui Pitagora a fost descoperită în vechiul tratat chinezesc „Zhou-bi suan jin” („Tratat de matematicădespre gnomon"), al cărui moment de creație este necunoscut cu exactitate, dar unde se precizează că înXVV. î.Hr e. chinezii cunoşteau proprietăţile triunghiului egiptean, iar înXVIV. î.Hr e. - și forma generală a teoremei.

Cantor (cel mai mare istoric german al matematicii) consideră că egalitatea 3 2 + 4 2 = 5 2 era deja cunoscută egiptenilor în jurul anului 2300 î.Hr. e. pe vremea regelui Amenemheteu(conform papirusului 6619 al Muzeului din Berlin).

Potrivit lui Cantor, harpedonaptes, sau „trăgători de frânghii”, au construit unghiuri drepte când

folosind triunghiuri dreptunghiulare cu laturi 3, 4 și 5.

Este foarte ușor să reproduci metoda lorconstrucție. Să luăm o frânghie de 12 m lungime și să legăm de ea o dungă colorată la distanță3 m de un capăt și 4 m de celălalt. Unghi dreptvor fi închise între laturile de 3 și 4 m lungime. S-ar putea obiecta la Harpedonaptes că metoda lor de construcție devine redundantă dacă se folosește, de exemplu, un pătrat de lemn, care este folosit de toți dulgherii. Într-adevăr, se cunosc desene egiptene în care se găsește un astfel de instrument, de exemplu, desene înfățișând atelierul unui tâmplar.Se știe ceva mai multe despreTeorema lui Pitagora la babilonieni.Într-un text datând din timpMeni Hammurabi, adică până în 2000î.Hr e., se dă direct un calcul aproximativ al ipotenuzeitriunghiul cărbunelui. De aiciputem concluziona că în Dvuracare știa să facă calculecu triunghiuri dreptunghiularemi, cel puțin în unelecazuri. Bazat pe unullaturi, la nivelul de azicunoștințe despre egiptean și babilonianmatematică, iar pe de altă parte - în criticăstudiu logic al surselor grecești, Van der Waerden (olandezămatematician rus) a făcut următoarea concluzie:

„Meritul primilor matematicieni greci, precum Thales, Pitagora și pitagoreenii, nu este descoperirea matematicii, ci ea sistematizare si justificare. Rețeta de calcul este în mâinile lor tu, pe baza unor idei vagi, te-ai transformat în precis nouă știință”.

Geometria hindușilor, la fel ca cea a egiptenilor și babilonienilor, era strânsăasociat cu un cult. Este foarte probabil ca teorema pătratului să fie hipotenuse era cunoscută în India de aproximativXVIIIsecolul î.Hr e., de asemeneaera cunoscut și în geometria indiană anticătratat teologicVII- Vsecole î.Hr e. „Sulva Sutra” („Regulifrânghii").

Dar, în ciuda tuturor acestor dovezi, numele lui Pitagora este așafuzionat ferm cu teorema lui Pitagora, ceea ce este pur și simplu imposibil acumse poate imagina că această frază se va destrama. La fel de lase referă și la legenda vrăjii taurilor lui Pitagora. Și este puțin probabiltrebuie disecat cu un bisturiu istorico-matematicprofunde legende antice.

Metode de demonstrare a teoremei

Dovada teoremei lui Pitagora de către studenții din Evul Mediuconsiderată foarte dificilă și a numit-oDons asinorum - podul măgarului, sauelefuga - fuga „săracilor”, întrucât au fugit niște elevi „săraci” care nu aveau o pregătire serioasă la matematicăfie din geometrie. Elevi slabi care au memorat teoremefără a înțelege și, prin urmare, supranumit „măgari”, nu au pututcapacitatea de a depăși teorema lui Pitagora, care părea să le serveascăpod depășibil. Datorită desenelor care însoțesc teoremaPitagora, studenții au numit-o și „moară de vânt”, cuau scris poezii precum „Pantalonii pitagoreici sunt egali din toate părțile” și au desenat desene animate.

O). Cea mai simplă dovadă

Probabil faptul enunțat în teorema lui Pitagora a fost un vischala este setat pentru dreptunghiuri isoscele. Uită-te doar la mozaicul de triunghiuri negre și deschise,pentru a verifica validitatea teoremei pentru triunghiurika ABC : un patrat construit pe ipotenuza contine patru triunghiuri, iar pe fiecare latura este construit un patrat continanddouă triunghiuri (Fig. 1, 2).

Dovezi bazate pe utilizarea conceptului de dimensiune egală a figurilor.

În acest caz, putem lua în considerare dovezi în care quadRath construit pe ipotenuza unui triunghi dreptunghiular datpătrat, „alcătuit” din aceleași figuri ca pătratele construite pe laturi. Pot fi luate în considerare și următoarele doveziva, în care permutarea cifrelor sumand șisunt luate în considerare o serie de idei noi.

În fig. 3 arată două pătrate egale. Lungimea laturilor fiecareegală cu pătratula + b. Fiecare dintre pătrate este împărțit în părți,format din pătrate și triunghiuri dreptunghiulare. Este clar că dacă scădeți de patru ori aria unui triunghi dreptunghic cu catete din aria unui pătrata, b, atunci vor rămâne egali ai milă, adică Cu 2 = a 2 + b 2 . Cu toate acestea, vechii hinduși, cărora le-a aparținutacest raționament minte, de obicei nu l-au notat, ci l-au însoțitdesen cu un singur cuvânt: „Uite!” Este foarte posibil ca eaPitagora a oferit și câteva dovezi.

b). Dovada prin metoda de completare.

Esența acestei metode este că la pătrate, construițipe picioare, iar la un pătrat construit pe ipotenuză, cuconectați cifre egale astfel încât să fie egalecifre noi.

În fig. 4 arată un Pythago obișnuitfigura de rând triunghi dreptunghicABCcu pătrate construite pe laturile sale. La această figură sunt atașate treipătratele 1 și 2, egale cu dreapta inițialătriunghiul cărbunelui.

Valabilitatea teoremei lui Pitagora rezultă din dimensiunea egală a hexagoanelorAEDFPBŞi ACBNMQ. Iată un EP direct dehexagon aprinsAEDFPBîn două patrulatere egale, linia CM împarte hexagonulACBNMQîn două patrulatere egale; rotind planul cu 90° în jurul centrului A mapează patrulaterul AERB pe un patrulaterACMQ.

(Această dovadă a fost dată pentru prima dată de Leonardînainte de da Vinci.)

Figura pitagoreică finalizatăla un dreptunghi ale cărui laturi sunt paralelealiniat cu laturile corespunzătoare ale quadracoms construite pe picioare. Să împărțim acest dreptunghi în triunghiuri și dreptepătrate. Din dreptunghiul rezultatMai întâi, scădem toate poligoanele 1, 2, 3, 4, 5, 6, 7, 8, 9, lăsând un pătrat construit pe ipotenuză. Apoi din același dreptunghi scădem dreptunghiuri 5, 6, 7 și umbrite dreptepătrate, obținem pătrate construite pe picioare.

Acum să demonstrăm că cifrele scăzute în primul caz suntsunt egale ca mărime cu cifrele scăzute în al doilea caz.

Aceasta ilustrează dovada,dat de Nassir-ed-Din (1594). Aici: P.L.- Drept;

KLOA = ACPF = ACED = o 2 ;

LGBO= SVMR = CBNQ = b 2 ;

AKGB = AKLO + LGBO= c 2 ;

deci cu 2 = o 2 + b 2 .

Orez. 7 ilustrează dovada,dat de Hoffmann (1821). AiciFigura pitagoreică este construită în așa fel încâtpătratele se află pe o parte a unei liniiAB. Aici:

OCLP = ACLF = ACED = b 2 ;

CBML=CBNQ= O 2 ;

OVMR =ABMF= Cu 2 ;

OVMR = OCLP + CBML;

Prin urmare c 2 = a 2 + b.

Aceasta ilustrează un alt ori mai multdovezile finale oferiteHoffman. Aici: triunghiABC cu dreptate unghi de spalare C; segmentB.F.perpendicularNE și egal cu acesta, segmentFIperpendicularAB și egal cu acesta, segmentAD perpendicular ren AC și egal cu acesta; puncteF, CU, D aparține culege o linie dreaptă; patrulatereADFBși ACVE sunt egale ca mărime, deoareceABF= ESV; triunghiuriADFŞi ACE-urile sunt egale ca mărime;

scade din ambele patrulatere egalenickurile au un triunghi comunABC, obținem ½ o* o + ½ b* b – ½ c* c

V). Metoda algebrică de demonstrare.

Figura ilustrează dovada marelui matematician indian Bhaskari (celemul autor al lui Li-lavati,XIIV.). Desenul a fost însoțit de un singur cuvânt: UITE! Dintre dovezile teoremei lui Pitagora metoda algebrică primul loc (posibil cel mai vechi) pentrupreia probe folosind subtext albina.

Istoricii cred că Bhaskara s-a născut zona intepaturii cu 2 pătrat construit peipotenuză, ca suma ariilor a patru triunghiuri 4(ab/2) și aria unui pătrat cu latura egală cu diferența catetelor.

Să prezentăm într-o prezentare modernă una dintre aceste dovezi:corpuri aparținând lui Pitagora.

eu "

În fig. 10 ABC - dreptunghiular, C - unghi drept, ( CM.L AB) b - proiecția piciorului b la ipotenuză, O - proiectia picioruluiO pe ipotenuză, h - altitudinea triunghiului trasat ipotenuză. Din faptul că ABC este similar cu AFM, rezultăb 2 = cb; (1) din faptul că ABC este similar cu VSM, rezultă că 2 = CA (2) Adunând egalitățile (1) și (2) termen cu termen, obținem a 2 + b 2 = cb + ca = = c (b + o) = c 2 .

Dacă Pitagora a oferit de fapt o asemenea dovadă,apoi a fost familiarizat cu o serie de teoreme geometrice importante,pe care istoricii moderni ai matematicii o atribuie de obicei Euclid.

Dovada lui Möhl- mană. Zona dată triunghi dreptunghicnika, pe de o parte, este egală 0,5 o* b, pe de alta 0,5* p*g, unde p - semiperimetrul unui triunghi,r - raza înscrisă în el este de cca.circumferinta (r = 0,5 - (a + b - c)).Avem: 0,5*a*b - 0,5*p*g - 0,5 (a + b + c) * 0,5-(a + b - c), de unde rezultă că c 2 = a 2 + b 2 .

d) Dovada lui Garfield.

În Figura 12 există trei dreptetriunghiurile formează un trapez. De aceea.zona acestei figuri este posibilă.\ găsiți folosind formula zoneidi trapez dreptunghiular,sau ca sumă de zonetrei triunghiuri. În bandăÎn acest caz, această zonă este egală cucu 0,5 (a + b) (a + b), în secundă rom - 0,5* o* b+ 0,5*a* b+ 0,5*s 2

Echivalând aceste expresii, obținem teorema lui Pitagora.

Există multe dovezi ale teoremei lui Pitagora, realizatefolosind atât fiecare dintre metodele descrise cât și folosind o combinațiementiunea diferitelor metode. Încheierea revizuirii exemplelor de diverse docurideclarații, iată mai multe desene care ilustrează cele opt moduribov, la care există referințe în „Elementele” lui Euclid (Fig. 13 - 20).În aceste desene figura lui Pitagora este reprezentată ca o linie continuăea, și construcții suplimentare - punctate.

După cum am menționat mai sus, egiptenii antici de mai bine de 2000 de aniîn urmă, am folosit practic proprietățile unui triunghi cu laturile 3, 4, 5 pentru a construi unghi drept, adică au aplicat de fapt teorema inversă teoremei lui Pitagora. Să prezentăm o demonstrație a acestei teoreme bazată pe criteriul de egalitate a triunghiurilor (adică unul care poate fi introdus foarte devreme în școalăpractică nouă). Deci, lăsați laturile triunghiuluiABC (Fig. 21) legate de 2 = a 2 + b 2 . (3)

Să demonstrăm că acest triunghi este dreptunghic.

Să construim un triunghi dreptunghicO B C pe doua laturi, ale căror lungimi sunt egale cu lungimileOŞi b catetele unui triunghi dat. Fie lungimea ipotenuzei triunghiului construit pe c . Deoarece triunghiul construit este dreptunghic, atunci prin teorieîn rema pitagoreică avemc = o + b (4)

Comparând relațiile (3) și (4), obținem căCu= cu sau c = c Astfel, triunghiurile - date și construite - sunt egale, deoarece au, respectiv, trei laturi egale. Unghiul Ceste drept, prin urmare unghiul C al acestui triunghi este de asemenea drept.

Dovezi aditive.

Aceste dovezi se bazează pe descompunerea pătratelor construite pe laturi în figuri din care se poate forma un quadrath construit pe ipotenuză.

dovada lui Einstein ( orez. 23) bazat pe descompunereun pătrat construit pe ipotenuză în 8 triunghiuri.

Aici: ABC- dreptunghiular triunghi cu unghi drept C;COMN; SK MN; P.O.|| MN; E.F.|| MN.

Demonstrează-l singuregalitatea triunghiurilor, jumătatecalculat prin împărțirea pătratelor dupăconstruit pe catete și ipotenuză.

b) Pe baza dovezii lui al-Nayriziyah, a fost efectuată o altă descompunere a pătratelor în cifre egale în perechi (aiciABC - triunghi dreptunghic cu unghi drept C).

Această dovadă se mai numește și „articulată” deoarececă aici doar două părți, egale cu triunghiul inițial, își schimbă poziția și sunt, parcă, atașate de restulfigura pe balamalele în jurul cărora se rotesc (Fig. 25).

c) O altă demonstrație prin metoda descompunerii pătratelor înpărți egale, numite „roată cu lame”, este prezentată în orez. 26. Aici: ABC - triunghi dreptunghic cu unghi drept resturi S, O - centrul unui pătrat construit pe o latură mare; linii punctate care trec printr-un punctDESPRE, perpendicular sauparalel cu ipotenuza.

Această descompunere a pătratelor este interesantă deoarece patrulaterele sale egale în perechi pot fi mapate unul pe celălalt prin translație paralelă.

„Pantaloni pitagoreici” (dovada lui Euclid).

De două mii de ania schimbat dovada inventatăEuclid, care este pus în al luicelebrele „Principii”. Euclid opusînălțimea cal VN de la vârful unui triunghi dreptunghic la ipotenuză și a demonstrat că continuarea sa împarte pătratul construit pe ipotenuză în două dreptunghiuri ale căror arii sunt egale

zonele pătratelor corespunzătoare construite pe laturi. Dovada lui Euclid în comparație cu vechiul chinez sau vechiul indian arată caexcesiv de complicat. Din acest motivel a fost adesea numit „stilted” și „articol”. Dar această păreresuperficial. Desenul folosit pentru a demonstra teorema se numește în glumă „pantaloni pitagoreici”. Pentrumultă vreme a fost considerat unul dintre simbolurile științei matematice.

Dovezi chineze antice.

Tratatele de matematică din China antică au ajuns la noi în edițiiIIV. î.Hr e. Cert este că în 213 î.Hr. e. împărat chinez

Shi Huangdi, încercând să elimine tradițiile anterioare, a ordonat ca toate cărțile antice să fie arse. ÎnIIV. î.Hr e. hârtia a fost inventată în China și în același timp a început și restaurareacărți antice. Așa a apărut „Matematica în nouă cărți” -principalele lucrări de matematică și astronomie care au supraviețuit ny.

În cartea a 9-a din „Matematică” există un desencare demonstrează teorema lui Pitagora.Cheia acestei dovezi nu este greu de găsit (Fig. 27).

De fapt, în chineza vecheaceleași patru triunghiuri dreptunghiulare egalepătrat cu picioarea, c si ipotenuza Cu aşezate astfel încât conturul lor exterior să fieexistă un pătrat cu o laturăa + b,și intern - un pătrat cu latura c, construit pe ipotenuză (Fig. 28).

Dacă un pătrat cu laturăCu tăiat și restul de 4 triunghiuri umbriteplasate în două dreptunghiuri, este clar că golul rezultat, pe de o parte,

egal cu Cu, iar pe de alta

a + b 2 , adică Cu 2 = a 2 + b

Teorema a fost demonstrată.

Rețineți că cu o astfel de dovadă

Construcții în interiorul pătratului pe ipotenvedem noi
dim în desenul chinez antic nu sunt folosite (Fig. 30). Aparent, matematicienii chinezi antici au avut ceva diferit înaintedovada si anume: daca la patrat cu
lateralCu două triunghiuri umbritetăiați nick-ul și atașați ipotenusele laalte două ipotenuze, atunci este ușor de găsitconfirmă că cifra rezultată, care numit uneori „scaunul miresei”, cueste format din două pătrate cu laturiO Şib, adică cu 2 = O 2 + b 2 .

Figura reproduce negrudin tratatul „Zhou-bi...”. AiciTeorema lui Pitagora luată în considerare pentruTriunghi egiptean cu picioare3, 4 și ipotenuza 5 unități de măsură.Pătratul de pe ipotenuză conține 25celule, iar pătratul înscris în el pe latura mai mare este 16. Este clar că partea rămasă conține 9 celule. Aceasta șiva fi un pătrat pe latura mai mică.

Teorema lui Pitagora spune:

Într-un triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei:

a 2 + b 2 = c 2,

oŞi b– picioarele formând un unghi drept.
Cu– ipotenuza triunghiului.

Formule ale teoremei lui Pitagora

a = \sqrt(c^(2) - b^(2))
b = \sqrt (c^(2) - a^(2))
c = \sqrt (a^(2) + b^(2))

Demonstrarea teoremei lui Pitagora

Aria unui triunghi dreptunghic se calculează cu formula:

S = \frac(1)(2)ab

Pentru a calcula aria unui triunghi arbitrar, formula ariei este:

p– semiperimetrul. p=\frac(1)(2)(a+b+c),
r– raza cercului înscris. Pentru un dreptunghi r=\frac(1)(2)(a+b-c).

Apoi echivalăm părțile drepte ale ambelor formule pentru aria triunghiului:

\frac(1)(2) ab = \frac(1)(2)(a+b+c) \frac(1)(2)(a+b-c)

2 ab = (a+b+c) (a+b-c)

2 ab = \left((a+b)^(2) -c^(2) \right)

2 ab = a^(2)+2ab+b^(2)-c^(2)

0=a^(2)+b^(2)-c^(2)

c^(2) = a^(2)+b^(2)

Teorema inversă Pitagora:

Dacă pătratul unei laturi a unui triunghi este egal cu suma pătratelor celorlalte două laturi, atunci triunghiul este dreptunghic. Adică pentru orice triplu de numere pozitive a, bŞi c, astfel încât

a 2 + b 2 = c 2,

există un triunghi dreptunghic cu catete oŞi b si ipotenuza c.

Teorema lui Pitagora- una dintre teoremele fundamentale ale geometriei euclidiene, stabilind relaţia dintre laturile unui triunghi dreptunghic. A fost dovedit de savantul matematician și filosof Pitagora.

Sensul teoremei faptul că cu ajutorul lui poți demonstra și alte teoreme și rezolva probleme.

Material suplimentar:

Un lucru de care poți fi sută la sută sigur este că, atunci când este întrebat care este pătratul ipotenuzei, orice adult va răspunde cu îndrăzneală: „Suma pătratelor picioarelor”. Această teoremă este ferm înrădăcinată în mintea tuturor. persoană educată, dar tot ce trebuie să faci este să ceri pe cineva să-l demonstreze și pot apărea dificultăți. Așa că să ne amintim și să luăm în considerare moduri diferite demonstrarea teoremei lui Pitagora.

Scurtă biografie

Teorema lui Pitagora este familiară aproape tuturor, dar din anumite motive biografia persoanei care a adus-o pe lume nu este atât de populară. Acest lucru poate fi reparat. Prin urmare, înainte de a explora diferitele modalități de a demonstra teorema lui Pitagora, trebuie să-i cunoști pe scurt personalitatea.

Pitagora - filozof, matematician, gânditor originar din Astăzi este foarte greu să-i deosebești biografia de legendele care s-au dezvoltat în memoria acestui mare om. Dar, după cum rezultă din lucrările adepților săi, Pitagora din Samos s-a născut pe insula Samos. Tatăl său era un tăietor de pietre obișnuit, dar mama lui provenea dintr-o familie nobilă.

Judecând după legendă, nașterea lui Pitagora a fost prezisă de o femeie pe nume Pythia, în cinstea căreia băiatul a fost numit. Conform predicției ei, băiatul născut trebuia să aducă multe beneficii și bine omenirii. Ceea ce a făcut exact.

Nașterea teoremei

În tinerețe, Pitagora s-a mutat în Egipt pentru a se întâlni acolo cu faimoși înțelepți egipteni. După întâlnirea cu ei, i s-a permis să studieze, unde a învățat toate marile realizări ale filozofiei, matematicii și medicinei egiptene.

Probabil în Egipt, Pitagora s-a inspirat din măreția și frumusețea piramidelor și a creat marea sa teorie. Acest lucru poate șoca cititorii, dar istoricii moderni cred că Pitagora nu și-a dovedit teoria. Dar el a transmis cunoștințele sale doar adepților săi, care ulterior au finalizat toate calculele matematice necesare.

Oricum ar fi, astăzi nu se cunoaște o singură metodă de demonstrare a acestei teoreme, ci mai multe deodată. Astăzi putem doar ghici cum exact grecii antici și-au efectuat calculele, așa că aici vom analiza diferite moduri de a demonstra teorema lui Pitagora.

Teorema lui Pitagora

Înainte de a începe orice calcul, trebuie să vă dați seama ce teorie doriți să demonstrați. Teorema lui Pitagora spune astfel: „Într-un triunghi în care unul dintre unghiuri este de 90°, suma pătratelor catetelor este egală cu pătratul ipotenuzei.”

Există un total de 15 moduri diferite de a demonstra teorema lui Pitagora. Este suficient număr mare, așa că să acordăm atenție celor mai populare dintre ele.

Metoda unu

Mai întâi, să definim ce ni s-a dat. Aceste date se vor aplica și altor metode de demonstrare a teoremei lui Pitagora, așa că merită să ne amintim imediat toate notațiile disponibile.

Să presupunem că ni se dă un triunghi dreptunghic cu catetele a, b și o ipotenuză egală cu c. Prima metodă de demonstrare se bazează pe faptul că trebuie să desenați un pătrat dintr-un triunghi dreptunghic.

Pentru a face acest lucru, trebuie să adăugați un segment egal cu piciorul b la lungimea piciorului a și invers. Acest lucru ar trebui să rezulte în două laturi egale ale pătratului. Tot ce rămâne este să desenezi două linii paralele, iar pătratul este gata.

În interiorul figurii rezultate, trebuie să desenați un alt pătrat cu o latură egală cu ipotenuza triunghiului original. Pentru a face acest lucru, din vârfurile ас și св trebuie să desenați două segmente paralele egale cu с. Astfel, obținem trei laturi ale pătratului, dintre care una este ipotenuza triunghiului dreptunghic inițial. Tot ce rămâne este să desenăm al patrulea segment.

Pe baza cifrei rezultate, putem concluziona că aria pătratului exterior este (a + b) 2. Dacă te uiți în interiorul figurii, poți vedea că, pe lângă pătratul interior, există patru triunghiuri dreptunghiulare. Suprafața fiecăruia este de 0,5 av.

Prin urmare, aria este egală cu: 4 * 0.5ab + c 2 = 2av + c 2

Prin urmare (a+c) 2 =2ab+c 2

Și, prin urmare, c 2 =a 2 +b 2

Teorema a fost demonstrată.

Metoda a doua: triunghiuri similare

Această formulă pentru demonstrarea teoremei lui Pitagora a fost derivată pe baza unei afirmații din secțiunea de geometrie despre triunghiuri similare. Afirmă că catetul unui triunghi dreptunghic este media proporțională cu ipotenuza sa și cu segmentul ipotenuzei care provine din vârful unghiului de 90°.

Datele inițiale rămân aceleași, așa că să începem imediat cu dovada. Să ducem la îndeplinire perpendicular pe lateral Segmentul AB CD. Pe baza afirmației de mai sus, laturile triunghiurilor sunt egale:

AC=√AB*AD, SV=√AB*DV.

Pentru a răspunde la întrebarea cum să demonstrăm teorema lui Pitagora, demonstrația trebuie completată prin pătrarea ambelor inegalități.

AC 2 = AB * AD și CB 2 = AB * DV

Acum trebuie să adunăm inegalitățile rezultate.

AC 2 + CB 2 = AB * (AD * DV), unde AD + DV = AB

Rezultă că:

AC2 + CB2 =AB*AB

Si prin urmare:

AC 2 + CB 2 = AB 2

Demonstrarea teoremei lui Pitagora și diverse metode de rezolvare a acesteia necesită o abordare versatilă a acestei probleme. Cu toate acestea, această opțiune este una dintre cele mai simple.

O altă metodă de calcul

Descrierile diferitelor metode de demonstrare a teoremei lui Pitagora pot să nu însemne nimic până când nu începeți să exersați pe cont propriu. Multe metode implică nu numai calcule matematice, dar și construcția de noi figuri din triunghiul original.

ÎN în acest caz, Este necesar să se completeze un alt triunghi dreptunghic VSD din latura BC. Astfel, acum există două triunghiuri cu catetă comună BC.

Știind că ariile figurilor similare au un raport ca pătratele dimensiunilor lor liniare similare, atunci:

S avs * c 2 - S avd * în 2 = S avd * a 2 - S vsd * a 2

S avs *(de la 2 - la 2) = a 2 *(S avd -S vsd)

de la 2 - la 2 =a 2

c 2 =a 2 +b 2

Deoarece dintre diferitele metode de demonstrare a teoremei lui Pitagora pentru clasa a 8-a, această opțiune nu este potrivită, puteți utiliza următoarea metodă.

Cel mai simplu mod de a demonstra teorema lui Pitagora. Recenzii

Potrivit istoricilor, această metodă a fost folosită pentru prima dată pentru a demonstra teorema din nou Grecia antică. Este cel mai simplu, deoarece nu necesită absolut niciun calcul. Dacă desenați corect imaginea, atunci dovada afirmației că a 2 + b 2 = c 2 va fi clar vizibilă.

Condițiile pentru această metodă vor fi ușor diferite de cea anterioară. Pentru a demonstra teorema, să presupunem că este dreptunghiulară triunghiul ABC- isoscel.

Luăm ipotenuza AC ca latură a pătratului și desenăm cele trei laturi ale acestuia. În plus, este necesar să desenați două linii diagonale în pătratul rezultat. Astfel încât în interiorul ei să obții patru triunghiuri isoscele.

De asemenea, trebuie să desenați un pătrat la picioarele AB și CB și să desenați o linie dreaptă diagonală în fiecare dintre ele. Desenăm prima linie de la vârful A, a doua de la C.

Acum trebuie să vă uitați cu atenție la desenul rezultat. Deoarece pe ipotenuza AC sunt patru triunghiuri egale cu cel inițial, iar pe laturi sunt două, aceasta indică veridicitatea acestei teoreme.

Apropo, datorită acestei metode de demonstrare a teoremei lui Pitagora, s-a născut celebra frază: „Pantalonii pitagoreici sunt egali în toate direcțiile”.

Dovada de J. Garfield

James Garfield este al douăzecilea președinte al Statelor Unite ale Americii. Pe lângă faptul că și-a pus amprenta asupra istoriei ca conducător al Statelor Unite, a fost și un autodidact talentat.

La începutul carierei a fost un profesor obișnuit într-o școală publică, dar în curând a devenit directorul uneia dintre cele mai înalte institutii de invatamant. Dorința de auto-dezvoltare i-a permis să ofere noua teorie demonstrarea teoremei lui Pitagora. Teorema și un exemplu de soluție sunt după cum urmează.

Mai întâi trebuie să desenați două triunghiuri dreptunghiulare pe o bucată de hârtie, astfel încât piciorul unuia dintre ele să fie o continuare a celui de-al doilea. Vârfurile acestor triunghiuri trebuie să fie conectate pentru a forma în cele din urmă un trapez.

După cum știți, aria unui trapez este egală cu produsul dintre jumătate din suma bazelor sale și înălțimea sa.

S=a+b/2 * (a+b)

Dacă considerăm trapezul rezultat ca o figură formată din trei triunghiuri, atunci aria sa poate fi găsită după cum urmează:

S=av/2 *2 + s2/2

Acum trebuie să egalăm cele două expresii originale

2ab/2 + c/2=(a+b) 2 /2

c 2 =a 2 +b 2

S-ar putea scrie mai mult de un volum despre teorema lui Pitagora și despre metodele de demonstrare a acesteia. ajutor didactic. Dar există vreun moment în care aceste cunoștințe nu pot fi aplicate în practică?

Aplicarea practică a teoremei lui Pitagora

Din păcate, în modern programe scolare Această teoremă este destinată a fi utilizată numai în probleme geometrice. Absolvenții vor părăsi în curând școala fără să știe cum își pot aplica cunoștințele și abilitățile în practică.

De fapt, utilizați teorema lui Pitagora în dvs viata de zi cu zi toată lumea poate. Și nu numai în activitate profesională, dar și în treburile casnice obișnuite. Să luăm în considerare câteva cazuri în care teorema lui Pitagora și metodele de demonstrare a acesteia pot fi extrem de necesare.

Relația dintre teoremă și astronomie

S-ar părea că stelele și triunghiurile de pe hârtie pot fi conectate. De fapt, astronomia este un domeniu științific în care teorema lui Pitagora este utilizată pe scară largă.

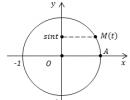
De exemplu, luați în considerare mișcarea unui fascicul de lumină în spațiu. Se știe că lumina se mișcă în ambele direcții cu aceeași viteză. Să numim traiectoria AB de-a lungul căreia se mișcă raza de lumină l. Și să numim jumătate din timpul necesar luminii pentru a ajunge din punctul A în punctul B t. Și viteza fasciculului - c. Rezultă că: c*t=l

Dacă te uiți la aceeași rază dintr-un alt plan, de exemplu, dintr-o linie spațială care se mișcă cu viteza v, atunci când observăm corpurile în acest fel, viteza lor se va schimba. În acest caz, chiar și elementele staționare vor începe să se miște cu viteza v în direcția opusă.

Să presupunem că linia de benzi desenate navighează spre dreapta. Apoi punctele A și B, între care fasciculul se repezi, vor începe să se miște spre stânga. Mai mult, atunci când fasciculul se deplasează din punctul A în punctul B, punctul A are timp să se miște și, în consecință, lumina va ajunge deja la punct nou C. Pentru a găsi jumătate din distanța cu care punctul A s-a deplasat, trebuie să înmulțiți viteza căptușelii cu jumătate din timpul de călătorie al fasciculului (t").

Și pentru a afla cât de departe ar putea călători o rază de lumină în acest timp, trebuie să marcați jumătatea drumului cu o nouă literă s și să obțineți următoarea expresie:

Dacă ne imaginăm că punctele de lumină C și B, precum și linia spațială, sunt vârfurile triunghi isoscel, atunci segmentul de la punctul A la linie îl va împărți în două triunghiuri dreptunghiulare. Prin urmare, datorită teoremei lui Pitagora, puteți afla distanța pe care o poate parcurge o rază de lumină.

Acest exemplu, desigur, nu este cel mai de succes, deoarece doar câțiva vor avea norocul să-l încerce în practică. Prin urmare, să luăm în considerare aplicații mai banale ale acestei teoreme.

Raza de transmisie a semnalului mobil

Viața modernă nu mai poate fi imaginată fără existența smartphone-urilor. Dar cât de mult le-ar folosi dacă nu ar putea conecta abonații prin comunicații mobile?!

Calitatea comunicațiilor mobile depinde direct de înălțimea la care se află antena operatorului de telefonie mobilă. Pentru a calcula cât de departe de un turn mobil un telefon poate primi un semnal, puteți aplica teorema lui Pitagora.

Să presupunem că trebuie să găsiți înălțimea aproximativă a unui turn staționar, astfel încât să poată distribui un semnal pe o rază de 200 de kilometri.

AB (înălțimea turnului) = x;

BC (raza transmisiei semnalului) = 200 km;

OS (raza glob) = 6380 km;

OB=OA+ABOB=r+x

Aplicând teorema lui Pitagora, aflăm că înălțimea minimă a turnului ar trebui să fie de 2,3 kilometri.

Teorema lui Pitagora în viața de zi cu zi

În mod ciudat, teorema lui Pitagora poate fi utilă chiar și în chestiuni de zi cu zi, cum ar fi determinarea înălțimii unui dulap, de exemplu. La prima vedere, nu este nevoie să folosiți astfel de lucruri calcule complexe, pentru că pur și simplu puteți lua măsurători folosind o bandă de măsurare. Dar mulți oameni se întreabă de ce apar anumite probleme în timpul procesului de asamblare dacă toate măsurătorile au fost luate mai mult decât corect.

Faptul este că dulapul este asamblat în poziție orizontală și abia apoi ridicat și instalat pe perete. Prin urmare, în timpul procesului de ridicare a structurii, partea laterală a dulapului trebuie să se miște liber atât de-a lungul înălțimii, cât și în diagonală a încăperii.

Să presupunem că există un dulap cu o adâncime de 800 mm. Distanța de la podea la tavan - 2600 mm. Un producător de mobilier cu experiență va spune că înălțimea dulapului ar trebui să fie cu 126 mm mai mică decât înălțimea camerei. Dar de ce exact 126 mm? Să ne uităm la un exemplu.

Cu dimensiunile ideale ale cabinetului, să verificăm funcționarea teoremei lui Pitagora:

AC =√AB 2 +√BC 2

AC=√2474 2 +800 2 =2600 mm - totul se potrivește.

Să presupunem că înălțimea dulapului nu este de 2474 mm, ci de 2505 mm. Apoi:

AC=√2505 2 +√800 2 =2629 mm.

Prin urmare, acest dulap nu este potrivit pentru instalarea în această cameră. Deoarece ridicarea acestuia într-o poziție verticală poate cauza deteriorarea corpului.

Poate, având în vedere diferite moduri de a demonstra teorema lui Pitagora de către diferiți oameni de știință, putem concluziona că este mai mult decât adevărată. Acum puteți folosi informațiile primite în viața de zi cu zi și puteți fi complet încrezător că toate calculele vor fi nu numai utile, ci și corecte.

Nu ar fi asociat cu teorema lui Pitagora. Chiar și cei care sunt departe de matematică în viața lor continuă să păstreze amintiri despre „pantalonii pitagoreici” - un pătrat pe ipotenuză, egal ca dimensiune cu două pătrate pe laturi. Motivul popularității teoremei lui Pitagora este clar: este simplitate - frumusețe - semnificație. Într-adevăr, teorema lui Pitagora este simplă, dar nu evidentă. Contradicția celor două principii îi conferă o forță de atracție deosebită și o face frumoasă. Dar, în plus, teorema lui Pitagora este de mare importanță. Este folosit în geometrie literalmente la fiecare pas. Există aproximativ cinci sute de dovezi diferite ale acestei teoreme, care indică un număr gigantic de implementări specifice ale acesteia.

Studiile istorice dau nașterea lui Pitagora la aproximativ 580 î.Hr. Fericitul tată Mnesarchus îl înconjoară cu grijă pe băiat. A avut ocazia să-i ofere fiului său o bună creștere și educație.

Viitorul mare matematician și filosof deja în copilărie a arătat abilități mari pentru știință. De la primul său profesor Hermodamas, Pitagora a învățat elementele de bază ale muzicii și picturii. Pentru a-și exercita memoria, Hermodamas l-a obligat să învețe cântece din Odiseea și Iliada. Primul profesor i-a insuflat tânărului Pitagora dragostea pentru natură și secretele ei.

Au trecut câțiva ani, iar la sfatul profesorului său, Pitagora decide să-și continue educația în Egipt. Cu ajutorul profesorului său, Pitagora reușește să părăsească insula Samos. Dar este încă departe de Egipt. Locuiește pe insula Lesbos împreună cu ruda lui Zoil. Acolo, Pitagora îl întâlnește pe filozoful Ferecyde, un prieten al lui Thales din Milet. De la Pherecydes, Pitagora a studiat astrologia, predicția eclipselor, secretele numerelor, medicina și alte științe necesare pentru acea vreme.

Apoi, în Milet, ascultă prelegeri ale lui Thales și ale colegului său mai tânăr și student Anaximandru, un geograf și astronom remarcabil. Pitagora a dobândit o mulțime de cunoștințe importante în timpul șederii sale la școala milesiană.

Înainte de Egipt, se oprește de ceva timp în Fenicia, unde, potrivit legendei, studiază cu celebrii preoți sidonieni.

Conform legendelor antice, în timp ce era în captivitate în Babilon, Pitagora s-a întâlnit cu magicieni persani, s-a familiarizat cu astrologia și misticismul răsăritean și s-a familiarizat cu învățăturile înțelepților caldeeni. Caldeii l-au introdus pe Pitagora în cunoștințele acumulate de popoarele răsăritene de-a lungul multor secole: astronomie și astrologie, medicină și aritmetică.

Pitagora a petrecut doisprezece ani în captivitatea babiloniană până a fost eliberat de regele persan Darius Hystaspes, care auzise despre faimosul grec. Pitagora are deja şaizeci de ani, se hotărăşte să se întoarcă în patria sa pentru a-i prezenta pe poporul său cunoştinţelor acumulate.

De când Pitagora a părăsit Grecia, acolo s-au produs mari schimbări. Cele mai bune minți, fugind de jugul persan, s-au mutat la Sudul Italiei, care se numea atunci Magna Graecia și a întemeiat acolo orașele-colonie Siracuza, Agrigentum și Croton. Aici Pitagora a decis să-și creeze propria școală filozofică.

Destul de repede câștigă o mare popularitate în rândul locuitorilor. Pitagora a folosit cu pricepere cunoștințele dobândite din călătoriile în jurul lumii. De-a lungul timpului, omul de știință încetează să mai performeze în biserici și pe străzi. Deja în casa lui, Pitagora a predat medicina, principiile activitate politică, astronomie, matematică, muzică, etică și multe altele. De la școala sa au venit oameni politici și de stat remarcabili, istorici, matematicieni și astronomi. Nu a fost doar profesor, ci și cercetător. Studenții săi au devenit și cercetători. Pitagora a dezvoltat teoria muzicii și acusticii, creând celebra „scara pitagoreică” și efectuând experimente fundamentale privind studiul tonurilor muzicale: el a exprimat relațiile pe care le-a găsit în limbajul matematicii. Școala lui Pitagora a sugerat pentru prima dată sfericitatea Pământului. Ideea că mișcarea corpuri cerești se supune anumitor relații matematice, ideile de „armonie a lumii” și „muzică a sferelor”, care au dus mai târziu la o revoluție în astronomie, au apărut pentru prima dată tocmai în Școala lui Pitagora.

Omul de știință a făcut multe și în geometrie. Proclus a apreciat contribuția savantului grec la geometrie în felul următor: „Pitagora a transformat geometria, dându-i forma unei științe libere, considerând principiile ei într-un mod pur abstract și explorând teoremele din punct de vedere imaterial, intelectual cel care a găsit teoria cantităților iraționale și proiectarea corpurilor cosmice.”

În școala lui Pitagora, geometria a fost pentru prima dată oficializată într-o disciplină științifică independentă. Pitagora și studenții săi au fost primii care au studiat geometria în mod sistematic - ca doctrină teoretică despre proprietățile abstractului. forme geometrice, și nu ca o colecție de rețete aplicate pentru topografie.

Cel mai important merit științific al lui Pitagora este considerat a fi introducerea sistematică a demonstrației în matematică și, mai ales, în geometrie. Strict vorbind, abia din acest moment matematica începe să existe ca știință, și nu ca o colecție de rețete practice egiptene antice și babiloniene antice. Odată cu nașterea matematicii, s-a născut știința în general, căci „nici o cercetare umană nu poate fi numită știință adevărată dacă nu a trecut prin dovezi matematice” (Leonardo da Vinci).

Deci, meritul lui Pitagora a fost că el, aparent, a fost primul care a ajuns la următorul gând: în geometrie, în primul rând, ar trebui luate în considerare obiectele ideale abstracte și, în al doilea rând, proprietățile acestor obiecte ideale nu ar trebui stabilite prin utilizarea măsurători pe un număr finit de obiecte, dar folosind un raționament care este valabil pentru un număr infinit de obiecte. Acest lanț de raționament, care, folosind legile logicii, reduce afirmațiile neevidente la adevăruri cunoscute sau evidente, este o demonstrație matematică.

Descoperirea teoremei de către Pitagora este înconjurată de o aură de legende frumoase. Proclus, comentând ultima propoziție a Cărții 1 a Elementelor, scrie: „Dacă îi asculți pe cei cărora le place să repete legende antice, va trebui să spui că această teoremă se întoarce la Pitagora ei spun că în cinstea acestei descoperiri; a sacrificat un taur.” Cu toate acestea, povestitorii mai generoși au transformat un taur într-un singur hecatomb, iar acesta este deja o sută întreagă. Și, deși Cicero a remarcat că orice vărsare de sânge era străină de carta ordinului pitagoreic, această legendă a fuzionat ferm cu teorema lui Pitagora și, două mii de ani mai târziu, a continuat să trezească răspunsuri arzătoare.