Sah mat așteaptă un proces aleatoriu. Variabile aleatorii. Variabilă aleatorie discretă. Legea distribuției unei variabile aleatoare discrete
Interferența în sistemele de comunicație este descrisă prin metode ale teoriei proceselor aleatorii.
O funcție se numește aleatorie dacă, în urma unui experiment, ia o formă sau alta și nu se știe dinainte care dintre ele. Un proces aleatoriu este o funcție aleatoare a timpului. Forma specifică pe care o ia un proces aleatoriu ca rezultat al unui experiment se numește implementarea unui proces aleatoriu.
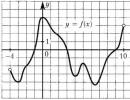
În fig. Figura 1.19 prezintă un set de câteva (trei) implementări ale procesului aleator , , . O astfel de colecție se numește ansamblu de realizări. Cu o valoare fixă a momentului de timp în primul experiment obținem o valoare specifică, în al doilea - , în al treilea - .
Procesul aleatoriu este de natură duală. Pe de o parte, în fiecare experiment specific este reprezentat de implementarea sa - o funcție non-aleatorie a timpului. Pe de altă parte, un proces aleatoriu este descris de un set de variabile aleatoare.
Într-adevăr, să luăm în considerare un proces aleatoriu la un moment fix în timp. Apoi, în fiecare experiment, acesta ia o valoare și nu se știe dinainte care. Astfel, un proces aleator considerat la un moment fix în timp este o variabilă aleatoare. Dacă se înregistrează două momente de timp și, atunci în fiecare experiment vom obține două valori ale lui și . În acest caz, luarea în considerare în comun a acestor valori duce la un sistem de două variabile aleatorii. Când analizăm procese aleatoare în N puncte în timp, ajungem la un set sau un sistem de N variabile aleatoare 
.
Funcția de așteptare, dispersie și corelație matematică a unui proces aleator Deoarece un proces aleator considerat la un moment fix în timp este o variabilă aleatorie, putem vorbi despre așteptarea și dispersia matematică a unui proces aleator:
, .
La fel ca pentru o variabilă aleatorie, dispersia caracterizează răspândirea valorilor unui proces aleatoriu în raport cu valoarea medie. Cu cât este mai mare, cu atât este mai mare probabilitatea unor valori de proces pozitive și negative foarte mari. O caracteristică mai convenabilă este deviația standard (MSD), care are aceeași dimensiune ca și procesul aleatoriu în sine.
Dacă un proces aleatoriu descrie, de exemplu, o modificare a distanței până la un obiect, atunci așteptarea matematică este intervalul mediu în metri; dispersia este măsurată în metri pătrați, iar Sco este măsurată în metri și caracterizează răspândirea posibilelor valori ale intervalului în raport cu medie.
Media și varianța sunt caracteristici foarte importante care ne permit să judecăm comportamentul unui proces aleatoriu la un moment fix în timp. Cu toate acestea, dacă este necesar să se estimeze „rata” schimbării într-un proces, atunci observațiile la un moment dat nu sunt suficiente. În acest scop, sunt utilizate două variabile aleatorii, considerate împreună. La fel ca și în cazul variabilelor aleatoare, se introduce o caracteristică a conexiunii sau dependenței dintre și. Pentru un proces aleator, această caracteristică depinde de două momente în timp și se numește funcție de corelație: .
Procese aleatoare staționare. Multe procese din sistemele de control au loc uniform în timp. Caracteristicile lor de bază nu se schimbă. Astfel de procese sunt numite staționare. Definiția exactă poate fi dată după cum urmează. Un proces aleatoriu se numește staționar dacă oricare dintre caracteristicile sale probabilistice nu depinde de schimbarea originii timpului. Pentru un proces aleator staționar, așteptările matematice, varianța și abaterea standard sunt constante: , .
Funcția de corelație a unui proces staționar nu depinde de originea t, adică. depinde doar de diferenta de timp:
Funcția de corelare a unui proces aleator staționar are următoarele proprietăți:
1) 
; 2) ; 3) .
Adesea funcțiile de corelare ale proceselor din sistemele de comunicație au forma prezentată în Fig. 1.20.
Orez. 1.20. Funcţiile de corelare a proceselor
Intervalul de timp în care funcția de corelare, de ex. magnitudinea conexiunii dintre valorile unui proces aleator scade de M ori, numit interval sau timp de corelare a procesului aleator. De obicei sau . Putem spune că valorile unui proces aleatoriu care diferă în timp prin intervalul de corelare sunt slab legate între ele.
Astfel, cunoașterea funcției de corelare permite să se judece rata de schimbare a unui proces aleatoriu.
O altă caracteristică importantă este spectrul energetic al unui proces aleatoriu. Este definită ca transformata Fourier a funcției de corelare:
.
Evident, transformarea inversă este de asemenea adevărată:
.
Spectrul de energie arată distribuția puterii unui proces aleatoriu, cum ar fi interferența, pe axa frecvenței.
Când se analizează un ACS, este foarte important să se determine caracteristicile unui proces aleatoriu la ieșirea unui sistem liniar cu caracteristici cunoscute ale procesului la intrarea ACS. Să presupunem că sistemul liniar este dat de un răspuns tranzitoriu la impuls. Atunci semnalul de ieșire în momentul de timp este determinat de integrala Duhamel:
,
unde este procesul la intrarea sistemului. Pentru a găsi funcția de corelare, scriem 
iar după înmulțire găsim așteptarea matematică
Aici, vom lua în considerare pe scurt principalele probleme ale sistematizării (clasificării) proceselor aleatorii.
Un proces aleator care are loc (trece) în orice sistem fizic reprezintă tranziții aleatorii ale sistemului de la o stare la alta. În funcție de varietatea acestor condiții 
din multi 
valorile argumentului 
toate procesele aleatoare sunt împărțite în clase (grupe):
1. Proces discret ( stare discretă) cu timp discret.
2. Proces discret cu timp continuu.
3. Proces continuu (stare continuă) cu timp discret.
4. Proces continuu cu timp continuu.
In prima
3 cazuri mult 
discret, adică argument 
ia valori discrete 
de obicei 
în primul caz
set de valori aleatorii ale funcției 
sunt definite de egalitățile:, este o mulțime discretă 
(set 
finit sau numărabil).
În al treilea caz, setul 
nenumărate, adică secţiune transversală a unui proces aleatoriu în orice moment 
este o variabilă aleatoare continuă.
În al 2-lea și al 4-lea caz sunt multe 
continuă, în al doilea caz setul de stări ale sistemului 
finit sau numărabil, iar în al patrulea caz o mulțime 
nenumărate.
Să dăm câteva exemple de procese aleatorii din clasele 1-4, respectiv:
1. Un jucător de hochei poate sau nu înscrie unul sau mai multe goluri în poarta adversarului în timpul meciurilor jucate în anumite momente (conform programului de joc) de timp. 
Proces aleatoriu 
este numărul de goluri marcate până la 
.
2. Proces aleatoriu 
- numărul de filme vizionate la cinematograful Zvezda
de la începutul cinematografului până la momentul actual 
.
3. În anumite momente în timp 
se măsoară temperatura 
pacient într-un centru de tratament. 
- este un proces aleator de tip continuu cu timp discret.
4. Indicator al nivelului de umiditate a aerului în timpul zilei în orașul A.
Pot fi luate în considerare și alte clase mai complexe de procese aleatorii. Pentru fiecare clasă de procese aleatorii sunt dezvoltate metode adecvate de studiere a acestora.
Puteți găsi o serie de exemple variate și interesante de fluxuri aleatorii în manuale [V. Feller, partea 1.2] și în monografie. Aici ne vom limita la asta.
Pentru procesele aleatorii se introduc și caracteristici funcționale simple, în funcție de parametru 
, similar cu caracteristicile numerice de bază ale variabilelor aleatoare.
Cunoașterea acestor caracteristici este suficientă pentru a rezolva multe probleme (amintim că o caracteristică completă a unui proces aleatoriu este dată de legea sa de distribuție multidimensională (finite-dimensională).
Spre deosebire de caracteristicile numerice ale variabilelor aleatoare, în cazul general caracteristicile funcționale sunt funcții specifice.
4. Așteptările matematice și varianța unui proces aleatoriu
Așteptarea matematică a unui proces aleatoriu 
definit pentru orice valoare de argument fix 
este egală cu așteptările matematice ale secțiunii corespunzătoare a procesului aleatoriu:
(12)
.
Pentru a desemna pe scurt așteptarea matematică a s.p. se foloseşte şi denumirea 
.
Funcţie 
caracterizează în medie comportamentul unui proces aleatoriu. Sensul geometric al așteptărilor matematice 
interpretată ca „curba medie”, în jurul căreia sunt situate curbele de implementare (vezi Fig. 60).
(vezi Fig. 60 Scrisori).
Pe baza proprietății așteptării matematice a unei variabile aleatoare și ținând cont de faptul că 
proces aleatoriu și 
funcție non-aleatorie, obținem proprietăți așteptări matematice proces aleatoriu:
1. Așteptările matematice ale unei funcții non-aleatoare sunt egale cu funcția în sine: 
.
2. Un multiplicator non-aleatoriu (funcție non-aleatoare) poate fi luat ca un semn al așteptării matematice a unui proces aleatoriu, i.e.
3. Așteptarea matematică a sumei (diferenței) a două procese aleatoare este egală cu suma
(diferențe) în așteptările matematice ale termenilor, i.e.
Rețineți că dacă reparăm argumentul (parametrul) 
, apoi trecem de la un proces aleator la o variabilă aleatoare (adică trecem la secțiunea transversală a unui proces aleator), putem găsi m.o. a acestui proces la acest fix 
Întrucât, dacă secțiunea s.p. 
pentru un dat 
există un r.v continuu. cu densitate 
atunci așteptarea sa matematică poate fi calculată folosind formula
(13)
.
Exemplul 2. Să s.p. este determinat de formula, i.e. 
s.v.,
Găsiți așteptările matematice ale unui proces aleatoriu 
Soluţie. Proprietatea 2. avem
deoarece 
si prin urmare, 
.
Exercita. Voi folosi egalități pentru a calcula așteptările matematice
,
,
apoi, pe baza formulei (13), calculați integrala și asigurați-vă că rezultatul este același.
Nota. Profită de egalitate
.
Varianta unui proces aleatoriu.
Varianta unui proces aleatoriu 
numită funcţie non-aleatorie
Dispersia 
s.p. este luată în considerare, caracterizați și răspândirea (dispersia) valorilor posibile ale r.p. raportat la așteptările sale matematice.
Odată cu dispersarea sp. se ia in considerare si abaterea standard 
(s.c.o. pe scurt), care este determinat de egalitate
(15)
Dimensiunea funcției 
egală cu dimensiunea s.p. 
.
Valorile de realizare ale s.p. la fiecare 
se abate de la așteptările matematice 
cu o sumă a comenzii 
(vezi Figura 60).
Să notăm cele mai simple proprietăți ale dispersiei proceselor aleatorii.
1. Varianta unei funcții non-aleatoare 
este egal cu zero, adică
2. Varianta unui proces aleatoriu 
nenegativ, adică
3. Varianța produsului unei funcții non-aleatoare 
la o funcție aleatorie 
este egal cu produsul dintre pătratul funcției non-aleatoare și varianța funcției aleatoare, i.e.
4. Dispersia sumei s.p. 
și funcție non-aleatorie 
egală cu dispersia sp., adică.
Exemplul 3. Să.p. este determinat de formula, i.e. 
s.v.
repartizat conform legii normale cu 
Aflați varianța și abaterea standard a s.p. 
.
Soluţie. Să calculăm varianța pe baza formulei din proprietatea 3. Avem
Dar 
, așadar, prin definiția dispersiei r.v. 
Prin urmare, 
aceste. 
Şi 
Ministerul Educației și Științei al Federației Ruse
Universitatea de Stat Cherepovets
Institutul de Inginerie și Economie
Conceptul de proces aleatoriu în matematică
Realizat de un student
Grupa 5 GMU-21
Ivanova Iulia
Cherepovets
Introducere
Partea principală
· Definirea unui proces aleator și a caracteristicilor acestuia
· Procese aleatoare Markov cu stări discrete
Procese aleatorii staționare
Proprietatea ergodică a proceselor aleatoare staționare
Literatură
Introducere
Conceptul de proces aleatoriu a fost introdus în secolul al XX-lea și este asociat cu numele lui A.N. Kolmogorov (1903-1987), A.Ya. Khinchin (1894-1959), E.E. Slutsky (1880-1948), N. Wiener (1894-1965).
Acest concept de astăzi este unul dintre cele centrale nu numai în teoria probabilității, ci și în știința naturii, inginerie, economie, organizarea producției și teoria comunicării. Teoria proceselor aleatoare aparține categoriei disciplinelor matematice cu cea mai rapidă creștere. Nu există nicio îndoială că această circumstanță este determinată în mare măsură de conexiunile ei profunde cu practica. Secolul al XX-lea nu a putut fi mulțumit de moștenirea ideologică primită din trecut. Într-adevăr, în timp ce fizicianul, biologul și inginerul erau interesați de proces, i.e. schimbarea în timp a fenomenului studiat, teoria probabilității le-a oferit ca un aparat matematic numai înseamnă că a studiat stările staționare.
Pentru a studia schimbările de-a lungul timpului, teoria probabilității de la sfârșitul secolului al XIX-lea - începutul secolului al XX-lea nu a dezvoltat scheme specifice, cu atât mai puțin tehnici generale. Iar nevoia de a le crea a bătut literalmente la ferestrele și ușile științei matematice. Studiul mișcării browniene în fizică a adus matematica în pragul creării unei teorii a proceselor aleatorii.
Consider că este necesar să menționez încă două grupe importante de studii, începute în momente diferite și din motive diferite.
În primul rând, această lucrare a lui A.A. Markov (1856-1922) privind studiul dependențelor în lanț. În al doilea rând, lucrările lui E.E. Slutsky (1880-1948) despre teoria funcțiilor aleatoare.
Ambele direcții au jucat un rol foarte important în formarea teoriei generale a proceselor aleatorii.
În acest scop, material inițial semnificativ fusese deja acumulat, iar nevoia de a construi o teorie părea să fie în aer.
A rămas să se efectueze o analiză profundă a lucrărilor existente, a ideilor și rezultatelor exprimate în acestea, iar pe baza acesteia să se realizeze sinteza necesară.
Definirea unui proces aleator și a caracteristicilor acestuia
Definiţie: Printr-un proces aleatoriu X(t) este un proces a cărui valoare, pentru orice valoare a argumentului t, este o variabilă aleatorie.
Cu alte cuvinte, un proces aleatoriu este o funcție care, în urma testării, poate lua una sau alta formă specifică, necunoscută dinainte. Pentru un t=t 0 fix X(t 0) este o variabilă aleatoare obișnuită, adică. secțiune proces aleatoriu la momentul t 0.
Exemple de procese aleatorii:
1. populația regiunii de-a lungul timpului;
2. numărul de solicitări primite de serviciul de reparații al companiei în timp.
Un proces aleator poate fi scris ca o funcție a două variabile X(t,ω), unde ω€Ω, t€T, X(t, ω) € ≡ și ω este un eveniment elementar, Ω este spațiul evenimentelor elementare , T este mulțimea valorilor argumentului t, ≡ este mulțimea valorilor posibile ale procesului aleator X(t, ω).
Implementarea procesul aleator X(t, ω) este funcția non-aleatoare x(t) în care se transformă procesul aleator X(t) ca rezultat al testării (pentru un ω fix), adică. forma specifică luată de procesul aleator X(t), sa traiectorie.
Astfel, proces aleatoriu X(t, ω) combină caracteristicile unei variabile aleatoare și ale unei funcții. Dacă fixăm valoarea argumentului t, procesul aleatoriu se transformă într-o variabilă aleatoare obișnuită dacă fixăm ω, atunci ca rezultat al fiecărui test se transformă într-o funcție obișnuită non-aleatoare; În discuția următoare vom omite argumentul ω, dar acesta va fi presupus implicit.
Figura 1 prezintă câteva implementări ale unui proces aleatoriu. Fie secțiunea transversală a acestui proces pentru un t dat o variabilă aleatoare continuă. Atunci procesul aleator X(t) pentru un t dat este determinat în întregime de probabilitatea φ(x‚ t). Este evident că densitatea φ(x, t) nu este o descriere exhaustivă a procesului aleator X(t), deoarece nu exprimă dependența dintre secțiunile sale în momente diferite.
Procesul aleator X(t) este o colecție de toate secțiunile pentru toate valorile posibile ale lui t, prin urmare, pentru a-l descrie este necesar să se ia în considerare o variabilă aleatoare multidimensională (X(t 1), X(t 2), . .., X(t n)), constând din toate combinațiile acestui proces. În principiu, există un număr infinit de astfel de combinații, dar pentru a descrie un proces aleatoriu este uneori posibil să se descurce cu un număr relativ mic de combinații.
Ei spun că un proces aleatoriu are comandan, dacă este complet determinată de densitatea distribuției îmbinării φ(x 1, x 2, ..., x n; t 1, t 2, ..., t n) n a secțiunilor arbitrare ale procesului, adică. densitatea unei variabile aleatoare n-dimensionale (X(t 1), X(t 2), ..., X(t n)), unde X(t i) este o combinație a procesului aleator X(t) la momentul t i , i=1, 2 , …, n.
Asemenea unei variabile aleatoare, un proces aleator poate fi descris prin caracteristici numerice. Dacă pentru o variabilă aleatorie aceste caracteristici sunt numere constante, atunci pentru un proces aleatoriu - funcții non-aleatoare.
Așteptări matematice procesul aleator X(t) este o funcție non-aleatoare a x (t), care pentru orice valoare a variabilei t este egală cu așteptarea matematică a secțiunii corespunzătoare a procesului aleator X(t), adică. a x (t)=M.
Varianta procesul aleator X(t) este o funcție non-aleatoare D x (t), pentru orice valoare a variabilei t egală cu dispersia combinației corespunzătoare a procesului aleator X(t), adică. D x (t) = D.
Abaterea standardσ x (t) al unui proces aleatoriu X(t) este valoarea aritmetică a rădăcinii pătrate a varianței sale, i.e. σ x (t)= D x (t).
Aşteptarea matematică a unui proces aleatoriu caracterizează medie traiectoria tuturor implementărilor sale posibile și dispersia sau deviația standard a acesteia - răspândire implementări relativ la traiectoria medie.
Caracteristicile unui proces aleatoriu introduse mai sus se dovedesc a fi insuficiente, deoarece sunt determinate doar de o lege de distribuție unidimensională. Dacă procesul aleator X 1 (t) se caracterizează printr-o modificare lentă a valorilor implementărilor cu o schimbare în t, atunci pentru procesul aleator X 2 (t) această schimbare are loc mult mai rapid. Cu alte cuvinte, procesul aleator X 1 (t) se caracterizează printr-o dependență probabilistică strânsă între cele două combinații ale sale X 1 (t 1) și X 1 (t 2), în timp ce pentru procesul aleator X 2 (t) această dependență între combinaţiile X 2 (t 1) şi X 2 (t 2) sunt practic absente. Dependența indicată între combinații este caracterizată printr-o funcție de corelare.
Definiţie: Funcția de corelare procesul aleator X(t) se numește funcție non-aleatoare
K x (t 1 , t 2) = M[(X(t 1) – a x (t 1))(X(t 2) – a x (t 2))] (1.)
două variabile t 1 și t 2, care pentru fiecare pereche de variabile t 1 și t 2 este egală cu covarianța combinațiilor corespunzătoare X(t 1) și X(t 2) ale procesului aleator.
Evident, pentru un proces aleator X(t 1) funcția de corelație K x 1 (t 1, t 2) scade pe măsură ce diferența t 2 - t 1 crește mult mai lent decât K x 2 (t 1, t 2) pentru o proces aleator X (t 2).
Funcția de corelație K x (t 1 , t 2) caracterizează nu numai gradul de apropiere a relației liniare dintre două combinații, ci și răspândirea acestor combinații în raport cu așteptarea matematică a x (t). Prin urmare, se ia în considerare și funcția de corelație normalizată a procesului aleator.
Funcția de corelare normalizată procesul aleator X(t) se numește funcția:
P x (t 1, t 2) = K x (t 1, t 2) / σ x (t 1)σ x (t 2) (2)
Exemplul #1
Un proces aleator este definit prin formula X(t) = X cosωt, unde X este o variabilă aleatoare. Găsiți principalele caracteristici ale acestui proces dacă M(X) = a, D(X) = σ 2.
SOLUŢIE:
Pe baza proprietăților așteptării și dispersiei matematice, avem:
a x (t) = M(X cosωt) = cosωt * M(X) = a cosωt,
D x (t) = D(X cosωt) = cos 2 ωt * D(X) = σ 2 cos 2 ωt.
Găsim funcția de corelare folosind formula (1.)
K x (t 1 , t 2) = M[(X cosωt 1 – a cosωt 1) (X cos ωt 2 – a cosωt 2)] =
Cosωt 1 cosωt 2 * M[(X – a)(X - a)] = cosωt 1 cosωt 2 * D(X) = σ 2 cosωt 1 cosωt 2 .
Găsim funcția de corelație normalizată folosind formula (2.):
P x (t 1, t 2) = σ 2 cosωt 1 cosωt 2 / (σ cosωt 1)(σ cosωt 2) ≡ 1.
Procesele aleatoare pot fi clasificate în funcție de dacă stările sistemului în care apar se modifică lin sau brusc, dacă mulțimea acestor stări este finită (numărabilă) sau infinită etc. Printre procesele aleatoare, un loc special aparține procesului aleator Markov.
Teorema. Un proces aleator X(t) este Hilbert dacă și numai dacă există R(t, t^) pentru toate (t, t^)€ T*T.
Teoria proceselor aleatoare Hilbert se numește teoria corelației.
Rețineți că mulțimea T poate fi discretă și continuă. În primul caz, procesul aleator X t se numește proces cu timp discret, în al doilea - cu timp continuu.
În consecință, combinațiile de X t pot fi variabile aleatoare discrete și continue.
Procesul aleator se numește X(t) selectiv neregulat, diferentiabil si integrabil intr-un punct ω€Ω daca realizarea lui x(t) = x(t, ω) este, respectiv, continua, diferentiabila si integrabila.
Procesul aleator X(t) se numește continuu: aproape, probabil Dacă
P(A)=1, A = (ω € Ω : lim x(t n) = x(t))
ÎN pătrat mediu, Dacă
Lim M[(X(t n) – X(t)) 2 ] = 0
După probabilitate, Dacă
Aδ ≥ 0: lim P[| X(t n) – X(t)| > δ] = 0
Convergența pătratică medie se notează și prin:
X(t) = lim X(t n)
Rezultă că din eșantion continuitatea urmează continuitatea aproape sigur, din continuitate aproape sigur și în pătratul mediu urmează continuitatea după probabilitate.
Teorema. Dacă X(t) este un proces aleator Hilbert, continuu în pătratul mediu, atunci m x (t) este o funcție continuă și relația este valabilă
Lim M = M = M .
Teorema. Un proces aleator Hilbert X(t) este mediu pătrat continuu dacă și numai dacă funcția sa de covarianță R(t, t^) în punctul (t, t) este continuă.
Un proces aleator Hilbert X(t) se numește pătrat mediu diferențiabil dacă există o funcție aleatoare X(t) = dX(t)/dt astfel încât
X(t) = dX(t)/ dt = lim X(t+∆t) – X(t) / ∆t
(t € T, t +∆t € T),
aceste. Când
Lim M [((X(t + ∆t) – X(t) / (∆t)) – X(t)) 2 ] = 0
Vom numi funcția aleatoare X(t) derivată pătrată medie proces aleatoriu X(t) în punctul t sau, respectiv, pe T.
Teorema. Procesul aleator Hilbert X(t) este diferențiabil în pătratul mediu în punctul t dacă și numai dacă există
δ 2 R(t, t^) / δtδt^ în punctul (t, t^). În acest caz:
R x (t, t^) = M = δ 2 R(t, t^) / δtδt^.
Dacă un proces aleator Hilbert este diferențiabil pe T, atunci derivata lui pătrată medie este, de asemenea, un proces aleator Hilbert; dacă traiectorii eșantionului unui proces sunt diferențiabile pe T cu probabilitatea 1, atunci cu probabilitatea 1 derivatele lor coincid cu derivatele pătratice medii pe T.
Teorema. Dacă X(t) este un proces aleator Hilbert, atunci
M = (d / dt) M = dm x (t) / dt.
Fie (0, t) un interval finit, 0
X(t) este un proces aleator Hilbert.
Y n = ∑ X(t i)(t i – t i-1) (n = 1,2, …).
Apoi variabila aleatoare
max (t i – t i -1)→0
Chemat integrală în pătrat mediu procesează X(t) pe (0, t) și este notat cu:
Y(t) = ∫ X(τ)dτ.
Teorema . Integrala pătratică medie Y(t) există dacă și numai dacă funcția de covarianță R(t, t^) a procesului Hilbert X(t) este continuă pe T×T și integrala există
R y (t, t^) = ∫ ∫ R(τ, τ^) dτdτ^
Dacă integrala pătratică medie a funcției X(t) există, atunci
M = ∫ Mdτ,
R Y (t, t^) = ∫ ∫ R(τ, τ^)dτdτ^
K y (t, t^) = ∫ ∫ K(τ, τ^)dτdτ^
Aici R y (t, t^) = M, K y (t, t^) = M sunt funcțiile de covarianță și corelație ale procesului aleator Y(t).
Teorema. Fie X(t) un proces aleator Hilbert cu funcția de covarianță R(t, t^), φ(t) o funcție reală și să existe o integrală
∫ ∫ φ(t)φ(t^)R(t, t^)dtdt^
Apoi există o integrală pătratică medie
∫ φ(t)X(t)dt.
procese aleatorii:
X i (t) = V i φ i (t) (i = 1n)
Unde φ i (t) sunt date funcții reale
Vi - variabile aleatoare cu caracteristici
Ele sunt numite elementare.
Extindere canonică procesul aleator X(t) se numește reprezentarea sa sub formă
Unde V i sunt coeficienții, iar φ i (t) sunt funcțiile de coordonate ale expansiunii canonice a procesului X(t).
Din relații:
M(V I = 0), D(V I) = D I, M(V i V j) = 0 (i ≠ j)
X(t) = m x (t) + ∑ V i φ i (t) (t € T)
K(t, t^) = ∑ D i φ i (t)φ i (t^)
Această formulă se numește expansiunea canonică funcția de corelare a unui proces aleatoriu.
În cazul ecuaţiei
X(t) = m x (t) + ∑ V i φ i (t) (t € T)
Se aplică următoarele formule:
X(t) = m x (t) + ∑ V i φ(t)
∫ x(τ)dt = ∫ m x (τ)dτ + ∑ V i ∫ φ i (t)dt.
Astfel, dacă un proces X(t) este reprezentat prin expansiunea sa canonică, atunci derivata și integrala sa pot fi reprezentate și ca expansiuni canonice.
Procese aleatoare Markov cu stări discrete
Un proces aleatoriu care are loc într-un anumit sistem S cu stări posibile S 1, S 2, S 3, ... se numește Markovsky, sau proces aleatoriu fără consecințe, dacă pentru orice moment t 0 caracteristicile probabile ale procesului în viitor (la t>t 0) depind doar de starea lui la momentul dat t 0 și nu depind de când și cum a ajuns sistemul în această stare; aceste. nu depind de comportamentul său în trecut (la t
Un exemplu de proces Markov: sistemul S este un taximetru. Starea sistemului la momentul t este caracterizată de numărul de kilometri (zecimi de kilometri) parcurși de mașină până în acest moment. Fie ca în momentul t 0 contorul să arate S 0 / Probabilitatea ca în momentul t>t 0 contorul să arate acest sau acel număr de kilometri (mai precis, numărul corespunzător de ruble) S 1 depinde de S 0, dar nu depinde de în ce momente, citirile contorului s-au schimbat până la momentul t 0.
Multe procese pot fi considerate aproximativ markoviene. De exemplu, procesul de a juca șah; sistemul S este un grup de piese de șah. Starea sistemului este caracterizată de numărul de piese inamice rămase pe tablă la momentul t 0 . Probabilitatea ca în momentul t>t 0 avantajul material să fie de partea unuia dintre adversari depinde în primul rând de starea sistemului la momentul t 0, și nu de când și în ce succesiune piesele cu scânduri până la timpul t 0 .
În unele cazuri, preistoria proceselor luate în considerare poate fi pur și simplu neglijată și modelele Markov pot fi folosite pentru a le studia.
Proces aleator Markov cu stări discrete și timp discret (sau lanț Markov ) se numește proces Markov, în care stările sale posibile S 1, S 2, S 3, ... pot fi enumerate în prealabil, iar trecerea de la stare la stare are loc instantaneu (salt), dar numai la anumite momente t 0, t 1, t 2, ..., numit trepte proces.
Să notăm p ij – probabilitatea de tranziție proces aleator (sistemul S) de la starea I la starea j. Dacă aceste probabilități nu depind de numărul etapei procesului, atunci un astfel de lanț Markov se numește omogen.
Fie numărul de stări ale sistemului finit și egal cu m. Apoi poate fi caracterizat matricea de tranziție P 1 , care conține toate probabilitățile de tranziție:
p 11 p 12 … p 1 min
p 21 p 22 … p 2m
P m1 p m2 … p mm
Desigur, pentru fiecare rând ∑ p ij = 1, I = 1, 2, …, m.
Să notăm p ij (n) ca probabilitatea ca, în urma a n pași, sistemul să se deplaseze din starea I în starea j. În acest caz, pentru I = 1 avem probabilități de tranziție care formează matricea P 1, adică. p ij (1) = p ij
Este necesar, cunoscând probabilitățile de tranziție p ij , să găsim p ij (n) – probabilitățile trecerii sistemului de la starea I la starea j în n trepte. În acest scop, vom considera o stare intermediară (între I și j) r, i.e. Vom presupune că din starea inițială I în k pași sistemul se va muta în starea intermediară r cu probabilitate p ir (k), după care în restul de n-k pași din starea intermediară r va trece în starea finală j cu probabilitatea p rj (n-k). Apoi, conform formulei probabilității totale
P ij (n) = ∑ p ir (k) p rj (n-k) – egalitate Markov.
Să ne asigurăm că, cunoscând toate probabilitățile de tranziție p ij = p ij (1), i.e. matricea P 1 de tranziție de la stare la stare într-un singur pas, puteți găsi probabilitatea p ij (2), adică. matricea P 2 de trecere de la stare la stare în două etape. Și cunoscând matricea P 2, găsiți matricea P 3 a trecerii de la stare la stare în trei pași etc.
Într-adevăr, punând n = 2 în formula P ij (n) = ∑ p ir (k) p rj (n-k), adică. k=1 (stare intermediară între pași), obținem
P ij (2) = ∑ p ir (1)p rj (2-1) = ∑ p ir p rj
Egalitatea rezultată înseamnă că P 2 = P 1 P 1 = P 2 1
Presupunând n = 3, k = 2, obținem în mod similar P 3 = P 1 P 2 = P 1 P 1 2 = P 1 3 , iar în cazul general P n = P 1 n
Exemplu
Totalitatea familiilor dintr-o anumită regiune poate fi împărțită în trei grupuri:
1. familiile care nu au mașină și nu intenționează să cumpere;
2. familiile care nu au mașină, dar intenționează să-și cumpere una;
3. familii cu mașină.
Ancheta statistică efectuată a arătat că matricea de tranziție pe un interval de un an are forma:
(În matricea P 1, elementul p 31 = 1 înseamnă probabilitatea ca o familie care are o mașină să aibă și una, iar, de exemplu, elementul p 23 = 0,3 este probabilitatea ca o familie care nu are un mașină, dar decide să cumpere, își va îndeplini intenția anul viitor etc.)
Găsiți probabilitatea ca:
1. o familie care nu avea mașină și nu plănuia să-și cumpere una va fi în aceeași situație peste doi ani;
2. o familie care nu avea mașină, dar intenționează să-și cumpere una, va avea o mașină în doi ani.
SOLUŢIE: Să găsim matricea de tranziție P 2 după doi ani:
0,8 0,1 0,1 0,8 0,1 0,1 0,64 0,15 0,21
0 0,7 0,3 0 0,7 0,3 0 0,49 0,51
0 0 1 0 0 1 0 0 1
Adică, probabilitățile căutate în exemplul 1) și, respectiv, 2) sunt egale
p 11 = 0,64, p 23 = 0,51
În continuare vom lua în considerare Proces aleator Markov cu stări discrete și timp continuu, în care, spre deosebire de lanțul Markov discutat mai sus, momentele posibilelor tranziții ale sistemului de la stat nu sunt fixate în prealabil, ci sunt aleatorii.
Când se analizează procese aleatorii cu stări discrete, este convenabil să se folosească o schemă geometrică - așa-numita programul evenimentelor. În mod obișnuit, stările sistemului sunt descrise prin dreptunghiuri (cercuri), iar posibilele tranziții de la stare la stare sunt descrise prin săgeți (arce orientate) care conectează stările.
Exemplu. Construiți un grafic de stare al următorului proces aleatoriu: dispozitivul S este format din două noduri, fiecare dintre ele putând eșua într-un moment aleator, după care începe imediat repararea nodului, continuând pentru un timp aleatoriu necunoscut anterior.
SOLUŢIE. Stări posibile ale sistemului: S 0 – ambele noduri sunt operaționale; S 1 – prima unitate este în reparație, a doua este în funcțiune; S 2 – a doua unitate este în reparație, prima este în funcțiune; S 3 – ambele unități sunt în curs de reparare.
O săgeată în direcția, de exemplu, de la S 0 la S 1, înseamnă o tranziție a sistemului în momentul defecțiunii primului nod, de la S 1 la S 0 - o tranziție în momentul finalizării reparației acestui nodul.
Nu există săgeți de la S 0 la S 3 și de la S 1 la S 2 pe grafic. Acest lucru se explică prin faptul că defecțiunile nodurilor sunt presupuse a fi independente unele de altele și, de exemplu, probabilitățile de defecțiune simultană a două noduri (tranziția de la S 0 la S 3) sau finalizarea simultană a reparațiilor a două noduri ( trecerea de la S 3 la S 0) poate fi neglijată.
Procese aleatorii staționare
staționar în sens restrâns, Dacă
F(x 1, …, x n; t 1, …, t n) = F(x 1, …, x n; t 1 +∆, …, t n +∆)
Pentru arbitrar
n≥1, x 1, …, x n, t 1, …, t n; ∆; t 1 € T, t i + ∆ € T.
Aici F(x 1, …, x n; t 1, …, t n) este funcția de distribuție n-dimensională a procesului aleator X(t).
Procesul aleator X(t) este numit staționar în sens larg, Dacă
Este evident că staționaritatea în sens restrâns implică staționaritate în sens larg.
Din formule:
m(t) = m(t + ∆), K(t, t^) = K(t + ∆, t^ + ∆)
(t € T, t^ € T, t + ∆€ T), t^ + ∆€ T)
Rezultă că pentru un proces care este staționar în sens larg, putem scrie
m (t) = m x (0) = const;
D (t) = K(t, t) = K(0,0) = const;
K(t, t^) = K(t – t^, 0) = K (0, t^ - t)
Astfel, pentru un proces care este staționar în sens larg, așteptarea și varianța matematică nu depind de timp, iar K(t, t^) este o funcție de forma:
Se poate observa că k(τ) este o funcție pară și
Aici D este dispersia procesului staționar
Х(t), α i (I = 1, n) – numere arbitrare.
Prima egalitate a sistemului
K(0) = B = σ 2 ; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0
rezultă din ecuaţia K(t, t^) = k(τ) = k(-τ), τ = t^ – t. Prima egalitate
K(0) = B = σ 2 ; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0 este o consecință simplă a inegalității Schwarz pentru secțiunile X(t), X(t^) ale procesului aleator staționar X(t). Ultima inegalitate:
K(0) = B = σ 2 ; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0
Obținut astfel:
∑ ∑ α i α j k(t i - t j) = ∑ ∑ K(t i , t j)α i α j = ∑ ∑ M[(α i X i)(α j X j)] = M[(∑ α i X i) 2] ≥0
Ținând cont de formula funcției de corelare a derivatei dX(t)/dt a unui proces aleator, pentru o funcție aleatoare staționară X(t) obținem
K 1 (t, t^) = M[(dX(t)/dt)*(dX(t^)/dt^)] = δ 2 K(t, t^) / δtδt^ = δ 2 k(t ^ - t) / δtδt^
Din moment ce
δk(t^ -t) / δt = (δk(τ) / δτ) * (δτ / δτ) = - δk(τ) / δτ,
δ 2 k(t^ - t) / δtδt^ = - (δ 2 k(τ) / δτ 2) * (δτ / δt^) = - (δ 2 k(τ) / δτ 2)
atunci K 1 (t, t^) = k 1 (τ) = - (δ 2 k(τ) / δτ 2), τ = t^ – t.
Aici K 1 (t, t^) și k 1 (τ) sunt funcția de corelație a derivatei întâi a procesului aleator staționar X(t).
Pentru derivata a n-a a unui proces aleator staționar, formula funcției de corelare are forma:
K n (τ) = (-1) n * (δ 2 n *k(τ) / δτ 2 n)
Teorema. Un proces aleator staționar X(t) cu funcție de corelație k(τ) este pătrat mediu continuu în punctul t € T dacă și numai dacă
Lim k(τ) = k(0)
Pentru a demonstra acest lucru, să scriem un lanț evident de egalități:
M [|X(t+τ)-X(T)| 2] = M[|X(t)| 2 ] – 2M[|X(t+τ)X(t)|] + M =
2D-2k(τ) = 2.
Prin urmare, este evident că condiția de continuitate în pătratul mediu al procesului X(t) în punctul t € T
Lim M[|X(t+τ) – X(t)| 2] = 0
Apare dacă și numai dacă Lim k(τ) = k(0)
Teorema. Dacă funcția de corelație k(τ) a unui proces aleator staționar X(t) este continuă în pătratul mediu în punctul τ=0, atunci este continuă în pătratul mediu în orice punct τ € R 1 .
Pentru a dovedi, notăm egalitățile evidente:
k(τ+∆τ)-k(τ) = M – M =
M(X(t))
Apoi, aplicând inegalitatea Schwartz factorilor din bretele și luând în considerare relațiile:
K(t, t^) = k(τ) = k(-τ), τ = t^ – t.
K(0) = B = σ 2 ; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0
0 ≤ 2 ≤ MM[|X(t+τ+∆τ)-X(t+τ)| 2] =
Trecând la limita la ∆τ→0 și ținând cont de condiția teoremei asupra continuității lui k(τ) în punctul τ=0, precum și de prima egalitate a sistemului
K(0) = B = σ 2 , găsim
Lim k(τ+∆τ) = k(τ)
Deoarece aici τ este un număr arbitrar, teorema ar trebui considerată dovedită.
Proprietatea ergodică a proceselor aleatoare staționare
Fie X(t) un proces aleator staționar pe o perioadă de timp cu caracteristici
τ = t^ – t, (t, t^) € T×T.
Proprietatea ergodică a unui proces aleator staționar este aceea că, pe baza unei implementări suficient de lungi a procesului, se poate judeca așteptările matematice, dispersia și funcția de corelare a acestuia.
Vom numi un proces aleator mai strict staționar X(t) ergodic în așteptările matematice, Dacă
Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0
Teorema
Proces aleator staționar X(t) cu caracteristici:
M = 0, K(t, t^) = M = k(τ),
τ = t^ – t, (t, t^) € T×T
este ergodic în așteptarea matematică dacă și numai dacă
Lim (2 / T) ∫ k(τ) (1 – τ/t)dτ = 0.
Pentru a dovedi, evident, este suficient să verificăm dacă egalitatea este adevărată
Să scriem relațiile evidente
C = M (|(1 / T)) ∫X(t)dt| 2 ) = (1 / T 2) ∫ ∫ k(t^ - t)dt^dt = (1/T) ∫ dt ∫ k(t^ - t)dt^.
Presupunând aici τ = t^ – t, dτ = dt^ și ținând cont de condițiile (t^ = T) → (τ = T - t),
(t^ = 0)→(τ = -t), obținem
С = (1/T 2) ∫ dt ∫ k(τ)dτ = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(τ)dτ =
= -(1/T 2) ∫ dt ∫ k(τ)dτ - (1/T 2) ∫ dt ∫ k(τ)dτ
Punând în primul și al doilea termen din partea dreaptă a acestei egalități, respectiv, τ = -τ^, dτ = -dτ^, τ = T-τ^, dτ = -dτ^, găsim
С = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(T - τ)dτ
Aplicând formula Dirichlet pentru integrale duble, scriem
С = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(T - τ)dτ = (1/T 2) ∫ (T - τ) k(τ) dτ + (1/T 2) ∫ τk (T – τ)dτ
În al doilea termen din partea dreaptă putem pune τ^ = T-τ, dτ = -dτ^, după care vom avea
Din aceasta și din definiția constantelor este clar că egalitatea
M((1 / T) ∫X(t)dt| 2 ) = (2 / T) ∫ k(τ) (1 – τ/t)dτ
Corect.
Teorema
Dacă funcția de corelație k(τ) a unui proces aleator staționar X(t) satisface condiția
Lim (1/T) ∫ |k(τ)| dt = 0
Atunci X(t) este ergodic în așteptările matematice.
Într-adevăr, având în vedere raportul
M((1 / T) ∫X(t)dt| 2 ) = (2 / T) ∫ k(τ) (1 – τ/t)dτ
Puteți nota
0 ≤ (2/T) ∫ (1 – τ/t) k(τ)dτ ≤ (2/T) ∫ (1- τ/t) |k(τ)|dτ ≤ (1/T) ∫ |k (τ)|dτ
Din aceasta este clar că dacă condiția este îndeplinită, atunci
Lim (2/T) ∫ (1 – τ/T) k(τ)dτ = 0
Acum, ținând cont de egalitate
C = (1/T 2) ∫ (T - τ) k(τ)dτ – (1/T 2) ∫ (T - τ) k(τ)dτ = 2/T ∫ (1- (τ/T) ) k(τ)dτ
Și condiția Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0
Ergodicitatea prin așteptarea matematică a procesului aleator staționar X(t), constatăm că necesarul este dovedit.
Teorema.
Dacă funcţia de corelaţie k(τ) a unui proces aleator staţionar
X(t) este integrabil și scade fără limită ca τ → ∞, adică. condiția este îndeplinită
Pentru ε > 0 arbitrar, atunci X(t) este un proces aleator staționar ergodic în așteptările matematice.
Într-adevăr, având în vedere expresia
Pentru T≥T 0 avem
(1/T) ∫ |k(τ)|dτ = (1/T)[ ∫ |k(τ)|dτ + ∫ |k(τ)|dτ ≤ (1/T) ∫ |k(τ)| dτ ε(1 – T 1 /T).
Trecând la limită ca Т → ∞, găsim
0 ≤ lim ∫ |k(τ)|dτ = ε.
Deoarece aici ε > 0 este o valoare arbitrară, arbitrar mică, atunci condiția ergodicității în termeni de așteptare matematică este îndeplinită. Din moment ce aceasta rezultă din condiție
La scăderea nelimitată a lui k(τ), atunci teorema ar trebui considerată dovedită.
Teoremele dovedite stabilesc criterii constructive pentru ergodicitatea proceselor aleatoare staţionare.
X(t) = m + X(t), m=const.
Atunci M = m, iar dacă X(t) este un proces aleator staționar ergodic, atunci condiția de ergodicitate Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0 după transformări simple poate fi reprezentată ca
Lim M([(1/T) ∫ X(t)dt – m] 2 ) = 0
Rezultă că dacă X(t) este un proces aleator staționar ergodic în așteptarea matematică, atunci așteptarea matematică a procesului X(t) = m + X(t) poate fi calculată aproximativ folosind formula
M = (1/T) ∫ x(t)dt
Aici T este o perioadă de timp destul de lungă;
x(t) – implementarea procesului X(t) pe intervalul de timp.
Putem considera ergodicitatea unui proces aleator staționar X(t) în raport cu funcția de corelație.
Se numește un proces aleator staționar X(t). ergodic în funcţie de corelaţie, Dacă
Lim M ([ (1/T) ∫ X(t) X(t + τ)dt – k(τ)] 2 ]) = 0
Rezultă că pentru un proces aleator staționar X(t) care este ergodic în funcția de corelare, putem seta
k (τ) = (1/T) ∫ x(t)x(t + τ)dt
la un T suficient de mare.
Se pare că starea
mărginirea lui k(τ) este suficientă pentru ca procesul staționar distribuit normal X(t) să fie ergodic în funcția de corelare.
Rețineți că procesul aleatoriu este numit distribuite normal, dacă oricare dintre funcțiile sale de distribuție finite-dimensională este normală.
O condiție necesară și suficientă pentru ergodicitatea unui proces aleator normal distribuit este relația
τ 0: lim (1/T) ∫ (1 – τ/T)dτ = 0
Literatură
1. N.Sh. Kremer „Teoria probabilității și statistica matematică” / UNITY / Moscova 2007.
2. Yu.V. Kozhevnikov „Teoria probabilității și statistica matematică” / Inginerie mecanică / Moscova 2002.
3. B.V. Gnedenko „Curs de teoria probabilității” / Redacția principală de literatură fizică și matematică / Moscova 1988.
