Eelnevalt tõestasime kindla integraali omadused, kasutades selle definitsiooni summade piirina. Täpselt samamoodi saab tõestada mitme integraali põhiomadusi. Lihtsuse huvides loeme kõik funktsioonid pidevateks, seega on nende integraalidel kindlasti mõte.

I. Konstantse teguri saab integraalimärgist välja võtta ja funktsioonide lõpliku summa integraal on võrdne terminite integraalide summaga:

II. Kui piirkond jaotatakse lõplikuks arvuks osadeks [näiteks kaheks osaks, siis on kogu piirkonna integraal võrdne kõigi osade integraalide summaga:

III. Kui piirkonnas, siis

Eriti :

IV. Kui piirkonna (a) märk säilib, kehtib valemiga väljendatud keskmise väärtuse teoreem

kus asub mingi punkt piirkonnas (a).

Eelkõige siis, kui saame

kus on piirkonna pindala.

Sarnased omadused kehtivad ka kolmikintegraali puhul. Pange tähele, et kahe- ja kolmikintegraali defineerimisel summa piiriks eeldatakse alati, et integratsioonipiirkond on lõplik ja integrandi funktsioon on igal juhul piiratud, see tähendab, et on olemas positiivne arv A, mis üldse integratsioonipiirkonna punktid N. Kui need tingimused ei ole täidetud, võib integraal eksisteerida ebaõige integraalina samamoodi nagu lihtsa kindla integraali puhul. Käsitleme valesid mitut integraali paragrahvis 8.

Ettevaatust. Kui arvutate integreerimisintervalli ainsuse punktidega valesid integraale, ei saa te Newtoni-Leibnizi valemit mehaaniliselt rakendada, kuna see võib põhjustada vigu.

Üldreegel: Newtoni-Leibnizi valem on õige, kui antiderivaat f(x) viimase ainsuse punktis on pidev.

Näide 2.11.

Vaatleme ebaõiget integraali ainsuse punktiga x = 0. Formaalselt rakendatud Newtoni-Leibnizi valem annab

Kuid üldreegel ei ole siin täidetud; kui f(x) = 1/x antiderivaat ln |x| ei ole defineeritud x = 0 juures ja on selles punktis lõpmatult suur, st. ei ole praegusel hetkel pidev. Integraali lahknemist on lihtne otsekontrolliga kontrollida. Tõesti,

Sellest tulenevat määramatust saab paljastada erineval viisil, kuna e ja d kipuvad nullima sõltumatult. Täpsemalt, seades e = d saame vale integraali põhiväärtuse, mis on võrdne 0-ga. Kui e = 1/n ja d =1/n 2, s.o. d kipub olema 0 kiiremini kui e, siis saame

millal ja vastupidi,

need. integraal lahkneb.n

Näide 2.12.

Vaatleme ebaõiget integraali ainsuse punktiga x = 0. Funktsiooni antituletisel on kuju ja see on pidev punktis x = 0. Seetõttu saame rakendada Newtoni–Leibnizi valemit:

Määratletud Riemanni integraali mõiste loomulik üldistus mitme muutuja funktsiooni korral on mitmekordse integraali mõiste. Kahe muutuja puhul nimetatakse selliseid integraale kahekordne.

Vaatleme kahemõõtmelises eukleidilises ruumis R´R, st. tasapinnal Descartes'i koordinaatsüsteemiga hulk E lõplik ala S.

Tähistame ( i = 1, …, k) seadke partitsioon E, st. selline selle alamhulkade süsteem E i, i = 1,. . ., k, et Ø i ¹ j ja (joonis 2.5). Siin tähistame alamhulka E i ilma selle piirita, st. alamhulga E i sisepunktid, mis koos selle piiriga Gr E ma moodustan suletud alamhulga E mina, . On selge, et ala S(E i) alamhulgad E i langeb kokku selle sisepinna pindalaga, kuna piiri pindala GrE i on võrdne nulliga.

Tähistagu d(E i). seatud läbimõõt E i, st. maksimaalne vahemaa selle kahe punkti vahel. Kutsutakse välja suurus l(t) = d(E i). vaheseina peenus t. Kui funktsioon f(x),x = (x, y), on defineeritud E-s kahe argumendi funktsioonina, siis vormi mis tahes summa

X i О E i , i = 1, . . . , k, x i = (x i , y i),

olenevalt nii funktsioonist f ja partitsioonist t kui ka punktide x i О E i М t valikust, nimetatakse funktsiooni f integraalsumma .

Kui funktsiooni f jaoks on olemas väärtus, mis ei sõltu ei partitsioonidest t ega punktide valikust (i = 1, ..., k), siis nimetatakse seda piiri topelt Riemanni integraal alates f(x,y) ja on tähistatud

Sel juhul kutsutakse välja funktsioon f ise Riemanni integreeritav.

Tuletame meelde, et funktsiooni puhul, millel on komplektina üks argument E mille üle integreerimine toimub, võetakse tavaliselt segment , ja selle partitsiooni t peetakse segmentidest koosnevaks partitsiooniks. Muidu, nagu on hästi näha, kordab Riemanni topeltintegraali definitsioon ühe argumendi funktsiooni jaoks kindla Riemanni integraali definitsiooni.

Kahe muutuja piiratud funktsioonide topelt-Riemanni integraalil on kindla integraali tavalised omadused ühe argumendi funktsioonide jaoks – lineaarsus, liitivus komplektide osas, mille kaudu integreerimine toimub, säilitamine integreerimisel mitte range ebavõrdsus, toote integreeritavus integreeritud funktsioonid jne.

Mitme Riemanni integraali arvutamine taandub arvutuseks itereeritud integraalid. Vaatleme topelt Riemanni integraali juhtumit. Laske funktsioonil f(x,y) on defineeritud hulgal E, mis asub hulkade X ´ Y, E М X ´ Y Descartes'i korrutis.

Korduva integraali abil funktsiooni f(x, y) nimetatakse integraaliks, milles integreerimine toimub järjestikku üle erinevate muutujate, st. vormi integraal

Määra E(y) = (x: О E) М X kutsutakse ristlõige seab antud y-le vastavad E, y О E y ; hulka E y nimetatakse - projektsioon seadke Y-teljele E.

Itereeritud integraali puhul kasutatakse ka järgmist tähistust:

mis, nagu ka eelmine, tähendab, et esiteks fikseeritud y, y О E y , funktsioon on integreeritud f(x, y) Kõrval x piki segmenti E(y), mis on komplekti osa E sellele vastav y. Selle tulemusena määratleb sisemine integraal ühe muutuja mõne funktsiooni - y. See funktsioon integreeritakse seejärel ühe muutuja funktsioonina, mida näitab väline integraalsümbol.

Integreerimise järjekorra muutmisel saame vormi korduva integraali

kus sisemine integratsioon viiakse läbi y, ja väline - poolt x. Kuidas on see itereeritud integraal seotud ülalmääratletud itereeritud integraaliga?

Kui funktsioonil on topeltintegraal f, st.

siis eksisteerivad mõlemad korduvad integraalid ja need on suuruselt identsed ja võrdsed kahekordsega, s.t.

Rõhutame, et selles avalduses sõnastatud tingimus integratsiooni järjekorra muutmise võimalusele itereeritud integraalides on ainult piisav, kuid mitte vajalik.

Muud piisavad tingimused itereeritud integraalide integreerimise järjekorra muutmise võimalused on sõnastatud järgmiselt:

kui vähemalt üks integraalidest on olemas

siis funktsioon f(x, y) Riemann võtteplatsil integreeritav E, on selle mõlemad korduvad integraalid olemas ja on võrdsed topeltintegraaliga. n

Täpsustame projektsioonide ja lõikude tähistust itereeritud integraalide tähistuses.

Kui hulk E on ristkülik

See E x = (x: a £ x £ b), E y = (y: c £ y £ d); kus E(y) = E x iga y, y О E y korral. , A E(x) = Ey mis tahes x jaoks , x О E x ..

Ametlik sissekanne: " y y О E yÞ E(y) = E xÙ" x x О E xÞ E(x) = Ey

Kui hulgal E on kumer ääris ja võimaldab esitusi

Sel juhul kirjutatakse korduvad integraalid järgmiselt:

Näide 2.13.

Arvutage ristkülikukujulise ala topeltintegraal, vähendades seda iteratiivseks.

Kuna tingimus sin 2 (x+ y) =| sin 2 (x + y)|, seejärel kontrollitakse topeltintegraali I olemasolu piisavate tingimuste täitmist mis tahes korduva integraali olemasolu kujul

seda pole vaja spetsiaalselt läbi viia ja saate kohe jätkata korduva integraali arvutamist

Kui see on olemas, siis on olemas ka topeltintegraal ja I = I 1 . Kuna

Seega I = .n

Näide 2.14.

Arvutage kolmnurkse piirkonna topeltintegraal (vt joonis 2.6), vähendades seda korduvaks

Gr(E) = ( : x = 0, y = 0, x + y = 2).

Esmalt kontrollime topeltintegraali I olemasolu. Selleks piisab korduva integraali olemasolu kontrollimisest.

need. integrandid on integreerimise intervallidel pidevad, kuna need kõik on võimsusfunktsioonid. Seetõttu on integraal I 1 olemas. Sel juhul eksisteerib ka topeltintegraal ja on võrdne mis tahes korduvaga, s.t.

Näide 2.15.

Topelt- ja itereeritud integraalide mõistete seose paremaks mõistmiseks vaatleme järgmist näidet, mille võib esimesel lugemisel ära jätta. Antakse kahe muutuja f(x, y) funktsioon

Pange tähele, et fikseeritud x puhul on see funktsioon y-s paaritu ja fikseeritud y puhul paaritu x-is. Hulgana E, mille üle see funktsioon on integreeritud, võtame ruudu E = ( : -1 £ x 1 £, -1 £ y £ 1).

Kõigepealt käsitleme itereeritud integraali

Sisemine integraal

on võetud fikseeritud y jaoks, -1 £ y £ 1. Kuna fikseeritud y integrand on x-is paaritu ja selle muutuja üle integreerimine toimub lõigu [-1, 1] üle, mis on punkti 0 suhtes sümmeetriline, siis sisemine integraal on võrdne 0-ga. Ilmselgelt on nullfunktsiooni muutuja y kohal olev välimine integraal samuti võrdne 0-ga, s.t.

Sarnased põhjendused teise itereeritud integraali kohta annavad sama tulemuse:

Seega on vaadeldava funktsiooni f(x, y) jaoks korduvad integraalid olemas ja need on üksteisega võrdsed. Funktsiooni f(x, y) topeltintegraali aga pole. Selle kontrollimiseks pöördume poole geomeetriline tunne itereeritud integraalide arvutused.

Itereeritud integraali arvutamiseks

kasutatakse ruudu E eritüüpi vaheseina, samuti integraalsummade spetsiaalset arvutamist. Nimelt on ruut E jagatud horisontaalseteks triipudeks (vt joonis 2.7), iga riba aga väikesteks ristkülikuteks. Iga riba vastab muutuja y teatud väärtusele; näiteks võib see olla riba horisontaaltelje ordinaat.

Integraalsummade arvutamine toimub järgmiselt: esiteks arvutatakse summad iga riba kohta eraldi, s.o. fikseeritud y juures erinevate x-ide jaoks ja siis need vahesummad summeeritakse erinevate ribade jaoks, st. erinevate y jaoks. Kui partitsiooni peenus kipub nulli, siis piirväärtuses saame ülalmainitud korduva integraali.

On selge, et teise itereeritud integraali puhul

hulk E on jagatud vertikaalseteks triipudeks, mis vastavad erinevatele x-dele. Vahesummad arvutatakse iga riba sees väikeste ristkülikutena, s.t. piki y-d ja seejärel summeeritakse need erinevate ribade kohta, st. x poolt. Piirväärtuses, kui partitsiooni peenus kipub olema null, saame vastava itereeritud integraali.

Tõestamaks, et topeltintegraali ei eksisteeri, piisab, kui tuua üks näide partitsioonist, mille integraalisummade arvutamine piiris, mil partitsiooni peenus kipub nulli, annab väärtusest erineva tulemuse. korduvatest integraalidest. Toome sellise polaarkoordinaatide süsteemile (r, j) vastava jaotuse näite (vt joonis 2.8).

Polaarkoordinaatide süsteemis määratakse raadiuse pikkusega r 0 mis tahes punkti asukoht tasapinnal M 0 (x 0, y 0), kus x 0, y 0 on punkti M 0 ristkoordinaadid. ühendades selle algpunktiga ja selle raadiusega moodustatud nurga j 0 positiivse x-telje suunaga (nurka loetakse vastupäeva). Seos Descartes'i ja polaarkoordinaatide vahel on ilmne:

y 0 = r 0 × sinj 0 .

Sektsioon on ehitatud järgmiselt. Esiteks jagatakse ruut E sektoriteks, mille raadiused lähtuvad koordinaatide keskpunktist, ja seejärel jagatakse iga sektor sektori teljega risti olevate joontega väikesteks trapetsideks. Integraalsummade arvutamine toimub järgmiselt: kõigepealt mööda väikeseid trapetse igas sektoris piki selle telge (piki r) ja seejärel kõigis sektorites (piki j). Iga sektori asukohta iseloomustab selle telje j nurk ja selle telje pikkus r(j) sõltub sellest nurgast:

kui või , siis ;

kui siis ;

kui siis

kui siis .

Minnes polaarsektsiooni integraalsummade piirini, kui partitsiooni peenus kipub olema null, saame topeltintegraali esituse polaarkoordinaatides. Sellise tähise võib saada puhtformaalsel viisil, asendades Descartes'i koordinaadid (x, y) polaarsetega (r, j).

Descartes'i koordinaatidelt polaarkoordinaatidele integraalide ülemineku reeglite kohaselt tuleks definitsiooni järgi kirjutada:

Polaarkoordinaatides kirjutatakse funktsioon f(x, y) järgmiselt:

Lõpuks ometi oleme

Sisemine integraal (vale) viimases valemis

kus ülal on näidatud funktsioon r(j), 0 £ j £ 2p võrdub +¥ mis tahes j korral, sest

Seetõttu ei ole j-ga hinnatud välise integraali integrand ühegi j jaoks määratletud. Aga siis ei ole väline integraal ise defineeritud, s.t. algne topeltintegraal ei ole defineeritud.

Pange tähele, et funktsioon f(x, y) ei täida piisavat tingimust topeltintegraali olemasoluks üle hulga E. Näitame, et integraal

ei eksisteeri. Tõesti,

Samamoodi määratakse integraali jaoks sama tulemus

Laadige alla saidist Depositfiles

Loengud 5-6

Teema2. Mitu integraali.

Kahekordne integraal.

Kontrollküsimused.

1. Topeltintegraal, selle geomeetriline ja füüsikaline tähendus

2. Topeltintegraali omadused.

3. Topeltintegraali arvutamine ristkoordinaatides.

4. Muutujate muutmine topeltintegraalis. Topeltintegraali arvutamine polaarkoordinaatides.

Laske funktsioonil z = f (x , y) määratletud piiratud suletud piirkonnas D lennuk. Jagame ala pooleks D juhuslikult sisse lülitatud n elementaarsed suletud alad  1 , … , n, millel on alad   1 , …,   n ja läbimõõdud d 1 , …, d n vastavalt. Tähistame d ala läbimõõtudest suurim  1 , … ,  n. Igal alal  k vali suvaline punkt P k (x k ,y k) ja koostage integraalsumma funktsioonid f(x,y)

S =
(1)

Definitsioon. Kahekordne integraal funktsioonid f(x,y) piirkondade kaupa D nimetatakse integraalsumma piiriks

, (2)

kui see on olemas.

kommenteerida. Kumulatiivne summa S oleneb sellest, kuidas ala on jagatud D ja punktide valimine P k (k=1, …, n). Siiski piir
, kui see on olemas, ei sõltu sellest, kuidas ala on jaotatud D ja punktide valimine P k .

Piisav seisukord topeltintegraali olemasolu. Topeltintegraal (1) on olemas, kui funktsioon f(x,y) pidev sisse D välja arvatud piiratud arv tükkhaaval sujuvaid kõveraid ja on piiratud D. Järgnevalt eeldame, et kõik vaadeldavad topeltintegraalid on olemas.

Topeltintegraali geomeetriline tähendus.

Kui f(x,y) ≥0 piirkonnas D, siis on topeltintegraal (1) võrdne joonisel näidatud silindrilise korpuse mahuga:

V =
(3)

Silindriline korpus on altpoolt piirkonnaga piiratud D, ülalt - osa pinnast z = f (x , y), külgedelt – selle pinna ja piirkonna piire ühendavate vertikaalsete sirgete segmentidega D.

Topeltintegraali füüsiline tähendus. Lameda plaadi mass.

Laske anda lame taldrik D teadaoleva tihedusfunktsiooniga γ( X,juures), seejärel purustage plaat D osadeks D i ja suvaliste punktide valimine
, saame plaadi massi kohta
või, võrreldes valemiga (2):

(4)

4. Topeltintegraali mõned omadused.

Lineaarsus. Kui KOOS on siis arvuline konstant

Aditiivsus. Kui piirkond D "murtud" piirkondadeks D 1 Ja D 2, siis

3) Piiratud ala pindala D võrdne

(5)

Topeltintegraali arvutamine ristkoordinaatides.

Olgu ala antud

1. pilt

D= { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Piirkond D ümbritsetud ribaga sirgjoonte vahel x = a , y = b, mis on vastavalt alt ja ülalt piiratud kõveratega y = φ 1 (x ) Ja y = φ 2 (x ) .

Topeltintegraal (1) üle piirkonna D(4) arvutatakse, edastades itereeritud integraalile:

(7)

See itereeritud integraal arvutatakse järgmiselt. Esiteks arvutatakse sisemine integraal

muutuja järgi y, kus x peetakse konstantseks. Tulemuseks on muutuja funktsioon x, ja seejärel arvutatakse selle funktsiooni "välimine" integraal üle muutuja x .

kommenteerida. Korduvale integraalile ülemineku protsessi vastavalt valemile (7) nimetatakse sageli integreerimispiiride paigutamiseks topeltintegraali. Integratsioonipiirangute seadmisel peate meeles pidama kahte punkti. Esiteks ei tohiks integreerimise alumine piir ületada ülemist ja teiseks peaksid välimise integraali piirid olema konstantsed ja sisemine peaks üldiselt sõltuma välimise integraali integreerimismuutujast.

Las nüüd ala D paistab nagu

D= { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Siis

. (9)

Oletame, et ala D saab esitada samaaegselt kui (6) ja (8). Siis kehtib võrdsus

(10)

Nimetatakse üleminekut ühelt itereeritud integraalilt teisele võrdsuses (10). lõimimise järjekorra muutmine topeltintegraalis.

Näited.

1) Muutke integraali integreerimise järjekorda

Lahendus. Kasutades itereeritud integraali vormi, leiame piirkonna

D= { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Kujutame piirkonda D. Jooniselt näeme, et see ala asub sirgjoonte vahel horisontaalsel ribal y =0, y=2 ja ridade vahel x =0 Ja x=D

Mõnikord tehakse arvutuste lihtsustamiseks muutujate muudatus:

,
(11)

Kui funktsioonid (11) on pidevalt diferentseeruvad ja determinant (Jacobian) on vaadeldavas domeenis nullist erinev:

(12)

Kahe muutuja funktsiooni jaoks, mis on määratud kui z = f(x, y) .

Topeltintegraal kirjutatakse järgmiselt:

Siin D– sirgetega piiratud tasapinnaline kujund, mille avaldised (võrdused) on toodud topeltintegraali arvutamise ülesandes. Vasak ja parem on võrdsused, milles on vasakpoolne muutuja x, ning üleval ja all – võrdustega, milles vasakpoolne muutuja on y. See koht on jätkuvalt üks tähtsamaid topeltintegraali arvutamise tehnika mõistmiseks.

Arvutage topeltintegraal - tähendab mainitud joonise pindalaga võrdse arvu leidmist D .

Kuni me puudutame topeltintegraali definitsioonid ja me õpime seda arvutama. Kahekordse integraali tähendusest on lihtsam aru saada, kui olete selle arvutamiseks lahendanud mitu ülesannet, seega leiate topeltintegraali definitsiooni selle õppetüki lõpust. Pisut ettepoole vaadates võib vaid märkida, et mainitud joonisega on seotud ka topeltintegraali definitsioon D .

Kui joonis D on ristkülik, kõik seda piiravad jooned on sirged. Kui joonis D- on kõverjooneline, siis vasakul ja paremal on see piiratud sirgjoontega ning ülalt ja alt kõverate joontega, mis on antud ülesandes toodud võrranditega. On ka juhtumeid, kui figuur D- kolmnurk, aga sellistest juhtumitest veidi kaugemal.

Topeltintegraali arvutamiseks on seetõttu vaja joonist ääristavaid jooni sorteerida D, millel on range nimi – integratsioonipiirkond. Sorteeri vasakule ja paremale ning ülemisele ja alla. Seda nõutakse siis, kui topeltintegraali taandamine itereeritud integraaliks – topeltintegraali arvutamise meetod.

Ristkülikukujulise ala juhtum:

Kumera piirkonna juhtum:

Ja see on meie tuttavate otsus kindlad integraalid, milles on täpsustatud integreerimise ülemine ja alumine piir. Figuuri piiritlevaid jooni määratlevad väljendid D, on tavapäraste kindlate integraalide integreerimise piirid, millele me juba läheneme.

Kahekordse integraali taandamine korduvaks integraaliks

Ristkülikukujulise piirkonna juhtum

Olgu sellise funktsiooni jaoks topeltintegraal

To hinda seda topeltintegraali , peame selle taandama itereeritud integraaliks, millel on vorm

.

Kõigepealt peate arvutama sisemise (paremal) kindel integraal, siis - välimine (vasak) kindel integraal.

Saate rolle vahetada x Ja y

.

Näide 1. Arvutage topeltintegraal

Arvutame sisemise (parempoolse) integraali, võttes y konstandiks. Saame aru.

.

Näide 2. Arvutage topeltintegraal

,

Lahendus. Me taandame selle topeltintegraali itereeritud integraaliks

Joonisel konstrueerime integratsioonipiirkonna:

Nüüd arvutame äsja arvutatud sisemise (parem) välimise (vasakpoolse) integraali:

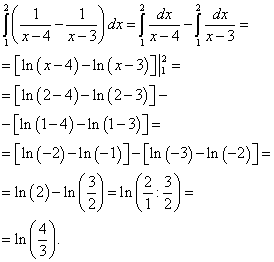
Tulemuseks on selle topeltintegraali lahendus.

Arvutage ise topeltintegraal ja seejärel vaadake lahendust

Kumera või kolmnurkse piirkonna juhtum

Olgu meile jälle antud kahe muutuja funktsioon f(x, y) ja piirangud D: juba veidi teist tüüpi:

See kirje tähendab, et joonis D vasak ja parem on piiratud, nagu sirgjoonelise piirkonna puhul - sirgjooned x = a Ja x = b, kuid allpool ja ülal on kõverad, mis on antud võrrandite ja . Teisisõnu ja on funktsioonid.

Olgu sellisel funktsioonil ka topeltintegraal

Selle topeltintegraali hindamiseks peame selle taandama itereeritud integraaliks, millel on vorm

.

Siin on integratsiooni piirid a Ja b- numbrid ja - funktsioonid. Kolmnurkse piirkonna puhul on üks funktsioonidest või sirgjoone võrrand. Seda juhtumit arutatakse näites 3.

Nagu sirgjoonelise piirkonna puhul, tuleb esmalt arvutada parempoolne kindel integraal, seejärel vasakpoolne kindel integraal.

Samamoodi saate rolle vahetada x Ja y. Siis saab korduv integraal vormi

.

Selline korduv integraal tuleb lahendada täpselt samamoodi: kõigepealt - sisemine (parem) integraal, seejärel - välimine (vasak).

Näide 5. Arvutage topeltintegraal

,

Lahendus. Me taandame selle topeltintegraali itereeritud integraaliks

.

Joonisel konstrueerime integratsioonipiirkonna ja näeme, et see on kolmnurkne:

Arvutame sisemise (parempoolse) integraali, pidades x-i konstandiks. Saame aru.

Nüüd arvutame välja äsja arvutatud sisemise (parem) välimise (vasakpoolse) integraali. Esmalt esitame selle integraali integraalide summana:

.

Arvutame esimese tähtaja:

Arvutame teise liikme:

Arvutame kolmanda liikme:

Saame summa, mis on selle topeltintegraali lahendus:

.

Näide 6. Arvutage topeltintegraal

Lahendus. Me taandame selle topeltintegraali itereeritud integraaliks

Joonisel konstrueerime integratsioonipiirkonna:

Arvutame sisemise (parempoolse) integraali, pidades x-i konstandiks. Saame aru.

.

Nüüd arvutame äsja arvutatud sisemise (parem) välimise (vasakpoolse) integraali:

Tulemuseks on selle topeltintegraali lahendus.

x- õige ja vale y-integratsiooni õiged ja valed domeenid

Juhtub, et topeltintegraali integratsioonipiirkond on piiratud selliste joontega, et tekib vajadus lõimimise valdkond osadeks jagada ja iga vastav korduv integraal eraldi lahendada. Need on juhtumid, kui:

1) integratsiooniala on kujund, millel on kaks või enam sirget või kõverat joont alumise või ülemise (vasak või parem) piiri kujul;

2) lõimimispiirkond on kujund, mille piirid ristuvad rohkem kui kahes punktis.

Kui ülaltoodu kehtib integratsioonidomeeni vasaku või parema piiri kohta, st piirangud, mis on määratletud joontega, mis on väljendatud x, siis nimetatakse integratsiooni domeeniks x- vale. Kui rida y = y0 lõikub vastava piiriga ainult ühes punktis ja kui piiriks on ainult üks sirge või kõver, siis integratsiooni valdkond nn. x- õige

Samamoodi, kui piir, mis on määratletud läbiva joontega y, sirge x = x0 lõikub rohkem kui ühes punktis või kui piiriks on rohkem kui üks sirgjoon või kõver, siis integratsiooni valdkonda nimetatakse y- vale. Nüüd kuvage märgid y- õige ala on arvatavasti üsna lihtne.

Siiani oleme vaadanud näiteid koos x-vale ja y-õiged integratsioonivaldkonnad. Nüüd kaaluge juhtumeid, kui korrektsuse tingimust rikutakse.

Näide 7. Arvutage topeltintegraal, mille integratsioonipiirkond on piiratud joontega y = x , xy = 1 , y = 2 .

Lahendus. Integratsiooni valdkond on y-vale, kuna selle alumist piiri ei saa ühe reaga määrata y = y(x) . Nagu ülaltoodud jooniselt näha, koosneb alumine piir y = x(tume Burgundia) ja xy= 1 (roheline). Seetõttu otse x= 1 (must) võime jagada integratsioonidomeeni kaheks osaks - ja .

See topeltintegraal arvutatakse järgmiselt:

Integreerimise järjekorra muutmine

Nagu eespool märgitud, saate pärast topeltintegraali redutseerimist itereeritud integraaliks muuta muutujaid x Ja y rollid, ehk teisisõnu muuta integratsiooni järjekorda.

Lõimumise järjekorra muutumist saab piltlikult kirjeldada järgmiste O'Henry sõnadega: „Nii käitub puuri sattudes džunglielanik – loom – ja nii käitub puurielanik – mees. käitub siis, kui ta kahtluste džunglisse ära eksib." Tulemus on O'Henry sõnul sama ja sama: "Chalmers rebis kirja tuhandeks pisikeseks viiludeks ja hakkas rebima oma kallist vaipa, kõndides tagasi ja sellest edasi." ( O. Henry. Madisoni väljaku Scheherazade.)

Siis, kui meie vasak integraal muutuja kohal x, ja õige – poolt y, siis pärast integreerimisjärjekorra muutmist on kõik vastupidi. Seejärel tuleb "uue" mängu integratsioonipiirid "laenata" "vanalt" X-lt ja integratsiooni piirid "uue" X jaoks saada kujul pöördfunktsioon, lahendades x jaoks võrrandi, mis määras y piirangu.

Näide 8.

.

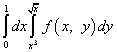Lahendus. Pärast integreerimise järjekorra muutmist muutub y kohal olev integraal vasakukäeliseks ja x-i kohal olev integraal parempoolseks. Laename “uue” mängu integreerimise piirid “vanalt” X-lt, see tähendab alampiirilt võrdne nulliga, ja ülemine – üks. Integratsiooni piirid “vana” mängu jaoks on antud võrranditega ja . Olles lahendanud need võrrandid x jaoks, saame x jaoks uued integreerimise piirid:

(alumine) ja (ülemine).

Seega, pärast integreerimise järjekorra muutmist, kirjutatakse korduv integraal järgmiselt:

.

Pärast integreerimise järjekorra muutmist topeltintegraalis muutub integreerimise domeen sageli ümber y-vale või x-vale (vt eelmist lõiku). Seejärel tuleb integreerimisdomeen osadeks jagada ja iga vastav itereeritud integraal eraldi lahendada.

Kuna lõiminguvaldkonna osadeks jagamine valmistab paljudele õpilastele teatud raskusi, ei piirdu me eelmises lõigus toodud näitega, vaid vaatame veel paari näidet.

Näide 9. Muutke itereeritud integraali integreerimise järjekorda

.

Lahendus. Niisiis on selle itereeritud integraali integreerimisala piiratud sirgjoontega y = 1 , y = 3 , x = 0 , x = 2y .

Erinevas järjekorras integreerimisel koosneb piirkonna alumine piir kahest sirgjoonest: AB Ja B.C., mis on antud võrranditega y= 1 ja y = x/2, nagu on näha alloleval joonisel.

Väljapääs sellisest ebakindlusest on jagada integratsioonivaldkond kaheks osaks. Integratsioonidomeeni jaotus on sirgjoon BM. Arvutame uued integratsiooni piirid leidmise teel pöördfunktsioon. Selle lahenduse kohaselt võrdub korduv integraal pärast integreerimisjärjekorra muutmist kahe integraali summaga:

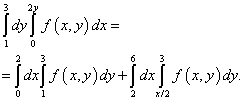
Loomulikult on sama lahendus ka topeltintegraalile, mis taandub selle näite tingimuses antud korduvaks integraaliks.

Näide 10. Muutke itereeritud integraali integreerimise järjekorda

.

Lahendus. Seega on itereeritud integraali integreerimise valdkond piiratud sirgjoontega x = 0 , x= 2 ja kõverad ja .

Nagu alloleval joonisel näha, teljega paralleelne sirgjoon 0x, lõikub integratsioonidomeeni alumise piiriga rohkem kui kahes punktis.

Seetõttu jagame integratsioonipiirkonna kolmeks osaks sirgjoontega, mis on joonisel mustaga tõmmatud. Arvutame integreerimise uued piirid, leides pöördfunktsiooni. Kolme uue integratsioonivaldkonna piirangud on järgmised.

Selle lahenduse kohaselt võrdub korduv integraal pärast integreerimisjärjekorra muutmist kolme integraali summaga:

Kolme integraali sama summa on võrdne topeltintegraaliga, mis taandub selle näite tingimuses antud korduvaks integraaliks.

Ja ometi segavad vääramatu jõu asjaolud õpilasi sageli juba eelmises etapis – lõimumise piiride seadmisel. Ärevus ja segadus pole aluseta: kui integratsioonipiirkonna osadeks jagamiseks piisab tavaliselt joonise tähelepanelikust vaatamisest ja korduva integraali - integraalide tabeli - lahendamisest, siis piirmäärade seadmisel on vaja mõningast koolituskogemust. integratsioonist. Toome läbi näite, milles keskendume ainult integratsiooni piiride seadmisele ja – peaaegu automaatselt – piirkonna partitsioonidele ja jätame lahenduse enda välja.

Näide 11. Leia topeltintegraali integreerimise piirid, kui integratsioonipiirkond D antud järgmiselt:

y - 2x ≤ 0;
2a - x ≥ 0;
xy ≤ 2.

Lahendus. Selgesõnaliselt (via x Ja y"ilma lisanditeta") integratsioonipiirkonda piiravaid jooni ei täpsustata. Kuna X puhul osutuvad need enamasti sirgjoonteks, mis ühes punktis puudutavad ülemist ja alumist piiri, väljendatuna i kaudu, siis läheme täpselt seda teed mööda. Veelgi enam, integreerimise järjekorra muutmisel saame sama alaga integratsioonipiirkonna. Lahendame mängu ebavõrdsused ja saame:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Saadud jooned ehitame joonisele. Integreerimise piirid üle x on tõepoolest jooned x= 0 ja x= 2. Kuid integratsiooni valdkond osutus selleks y-vale, kuna selle ülempiiri ei saa määrata ühe reaga y = y(x) .