Cauchy funktsiooni näidete limiit. Funktsiooni piiri universaalne definitsioon Heini ja Cauchy järgi. Lõpmatult väikesed ja lõpmata suured funktsioonid

Antakse funktsiooni piiri definitsioonid Heine (läbi jadade) ja Cauchy (läbi epsiloni ja delta naabruskonna) järgi. Definitsioonid on antud universaalsel kujul, mis on rakendatavad nii kahe- kui ka ühepoolsetele piiridele lõplikes ja lõpmatult kaugetes punktides. Arvestatakse määratlust, et punkt a ei ole funktsiooni piir. Heine ja Cauchy definitsioonide samaväärsuse tõestus.

Sisu

Vaata ka: Punkti naabruskond
Funktsiooni piiri määramine lõpp-punktis
Funktsiooni piiri määramine lõpmatuses

Funktsiooni piiri esimene määratlus (Heine järgi)

(x) punktis x 0 :
,
Kui
1) on selline punkti x torgatud naabruskond 0
2) mis tahes järjestuse jaoks (xn), lähenedes x-le 0 :
, mille elemendid kuuluvad naabrusse,
järeljada (f(xn)) koondub a:
.

Siin x 0 ja a võib olla kas lõplikud arvud või punktid lõpmatuses. Naabruskond võib olla nii kahe- kui ka ühepoolne.

Funktsiooni piiri teine määratlus (vastavalt Cauchyle)

Arvu a nimetatakse funktsiooni f piiriks (x) punktis x 0 :
,
Kui
1) on selline punkti x torgatud naabruskond 0 , millel funktsioon on määratletud;
2) iga positiivse arvu ε korral > 0 on selline arv δ ε > 0 , olenevalt ε-st, et kõigi punkteeritud δ ε-sse kuuluvate x jaoks on punkti x naabruskond 0 :
,
funktsiooni väärtused f (x) kuuluvad punkti a ε-naabrusse:
.

Punktid x 0 ja a võib olla kas lõplikud arvud või punktid lõpmatuses. Naabruskond võib olla ka kahe- või ühesuunaline.

Kirjutame selle definitsiooni olemasolu ja universaalsuse loogilisi sümboleid kasutades:
.

See definitsioon kasutab võrdsel kaugusel asuvate otstega linnaosasid. Samaväärse definitsiooni saab anda kasutades suvalisi punktide naabrusi.

Määratlus suvaliste naabruskondade abil
Arvu a nimetatakse funktsiooni f piiriks (x) punktis x 0 :
,
Kui
1) on selline punkti x torgatud naabruskond 0 , millel funktsioon on määratletud;
2) mis tahes naabruskonnas U (a) punktis a on selline punkti x punkteeritud naabruskond 0 et kõigi punkti x punkteeritud naabrusse kuuluvate x kohta 0 :
,
funktsiooni väärtused f (x) kuuluvad naabruskonda U (a) punktid a:
.

Kasutades olemasolu ja universaalsuse loogilisi sümboleid, saab selle määratluse kirjutada järgmiselt:
.

Ühe- ja kahepoolsed piirangud

Ülaltoodud määratlused on universaalsed selles mõttes, et neid saab kasutada mis tahes tüüpi naabruskonna jaoks. Kui kasutame lõpp-punkti vasakpoolset punkteeritud ümbrust, saame vasakpoolse piiri määratluse. Kui kasutame naabrusena lõpmatuspunkti naabrust, saame lõpmatuse piiri määratluse.

Heine piiri määramiseks taandub see asjaolule, et suvalisele järjestusele, mis koondub järjestusele , kehtestatakse täiendav piirang: selle elemendid peavad kuuluma punkti vastavasse punkteeritud naabrusse.

Cauchy piiri määramiseks on igal juhul vaja avaldised teisendada ebavõrdsusteks, kasutades punkti ümbruse sobivaid definitsioone.
Vt "Punkti naabruskond".

Selle punkti a määramine ei ole funktsiooni piir

Sageli osutub vajalikuks kasutada tingimust, et punkt a ei ole funktsiooni piiriks . Ehitame ülaltoodud definitsioonidele eitused. Nendes eeldame, et funktsioon f (x) on defineeritud punkti x mõnel torgatud naabruskonnal 0 . Punktid a ja x 0 võivad olla kas lõplikud arvud või lõpmatult kauged. Kõik allpool kirjeldatu kehtib nii kahepoolsete kui ka ühepoolsete piirangute kohta.

Heine sõnul.
Number a ei ole funktsiooni f piir (x) punktis x 0 : ,
kui selline jada on olemas (xn), lähenedes x-le 0 :
,
mille elemendid kuuluvad naabrusse,
milline on järjekord (f(xn)) ei ühti a :
.
.

Cauchy sõnul.
Number a ei ole funktsiooni f piir (x) punktis x 0 :
,
kui on selline positiivne arv ε > 0 , seega iga positiivse arvu δ korral > 0 , on olemas x, mis kuulub punkti x punkteeritud δ-naabrusse 0 :
,
et funktsiooni f väärtus (x) ei kuulu punkti a ε-naabrusse:
.
.

Muidugi, kui punkt a ei ole funktsiooni piiriks kohas , ei tähenda see, et sellel ei võiks olla piirmäära. Piirang võib olla, kuid see ei võrdu a-ga. Samuti on võimalik, et funktsioon on määratletud punkti punktsiooniga naabruses, kuid sellel pole piirangut .

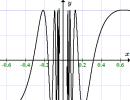
Funktsioon f(x) = sin(1/x) ei ole piirangut kui x → 0.

Näiteks funktsioon on defineeritud aadressil , kuid piirangut pole. Selle tõestamiseks võtame jada . See läheneb punktile 0 : . Sest siis.
Võtame järjestuse. See läheneb ka asjale 0 : . Aga sellest ajast peale.
Siis ei saa limiit olla võrdne ühegi arvuga a. Tõepoolest, , On jada, millega . Seetõttu ei ole nullist erinev arv piirang. Kuid see pole ka piir, kuna on olemas jada, millega .

Heine ja Cauchy piirimääratluste samaväärsus

Teoreem
Funktsiooni piiri Heine ja Cauchy definitsioonid on samaväärsed.

Tõestus

Tõestuses eeldame, et funktsioon on defineeritud punkti mingis punkteeritud ümbruses (lõpmatus või lõpmatuses). Punkt a võib olla ka lõplik või lõpmatus.

Heine tõestus ⇒ Cauchy oma

Olgu funktsioonil esimese definitsiooni järgi (Heine järgi) punktis piir a. See tähendab, et mis tahes jada jaoks, mis kuulub punkti punkteeritud naabrusse ja millel on piir
(1) ,
jada piirang on:
(2) .

Näitame, et funktsioonil on punktis Cauchy piir. See tähendab, et igaühe jaoks on midagi, mis sobib kõigile.

Oletame vastupidist. Olgu tingimused (1) ja (2) täidetud, kuid funktsioonil pole Cauchy limiiti. See tähendab, et igaühe jaoks on midagi olemas, nii et
.

Võtame , kus n on naturaalarv. Siis on , ja
.
Seega oleme konstrueerinud jada, mis läheneb , kuid jada piir ei ole võrdne a . See on vastuolus teoreemi tingimustega.

Esimene osa on tõestatud.

Cauchy tõestus ⇒ Heine oma

Olgu funktsioonil teise definitsiooni järgi (Cauchy järgi) punktis piir a. See tähendab, et igaühe jaoks on see olemas
(3) kõigi jaoks .

Näitame, et funktsioonil on Heine järgi punktis piir a.
Võtame suvalise arvu. Cauchy definitsiooni kohaselt on arv olemas, seega kehtib (3).

Võtame suvalise jada, mis kuulub punkteeritud naabruskonda ja läheneb . Konvergentse jada definitsiooni järgi on see olemas kõigi jaoks
aadressil .
Seejärel (3) järeldub, et
aadressil .
Kuna see kehtib kõigile, siis
.

Teoreem on tõestatud.

Viited:
L.D. Kudrjavtsev. Matemaatilise analüüsi kursus. 1. köide. Moskva, 2003.

Vaata ka:

Olgu funktsioon y = ƒ (x) defineeritud punkti x o mõnes naabruses, välja arvatud ehk punkt x o ise.

Sõnastame kaks samaväärset funktsiooni piiri definitsiooni punktis.

Definitsioon 1 (“jadade keeles” ehk Heine järgi).

Arvu A nimetatakse funktsiooni y=ƒ(x) piiriks ahjus x 0 (või punktis x® x o), kui argumendi x n mis tahes lubatud väärtuste jada korral n є N (x n ¹) x 0), lähenedes x-le, koondub funktsiooni ƒ(x n), n є N vastavate väärtuste jada arvule A

Sel juhul nad kirjutavad
või ƒ(x)->A punktis x→x o. Funktsiooni piiri geomeetriline tähendus: tähendab, et kõigi punktide x puhul, mis on punktile xo piisavalt lähedal, erinevad funktsiooni vastavad väärtused arvust A nii vähe kui soovitakse.

Definitsioon 2 ("ε keeles" või Cauchy järgi).

Arvu A nimetatakse funktsiooni piiriks punktis x o (või punktis x→x o), kui iga positiivse ε korral on positiivne arv δ, nii et kõigi x¹ x o korral, mis rahuldab võrratuse |x-x o |<δ, выполняется неравенство |ƒ(х)-А|<ε.

Funktsiooni piiri geomeetriline tähendus:

kui punkti A mis tahes ε-naabruses on punkti x o δ-naabrus, nii et kõigi selle δ-naabruse x1 xo jaoks asuvad funktsiooni ƒ(x) vastavad väärtused punkti ε-naabruses. punkt A. Teisisõnu, funktsiooni y = ƒ(x) graafiku punktid asuvad 2ε laiuse riba sees, mida piiravad sirged y=A+ ε, y=A-ε (vt joonis 110). Ilmselgelt sõltub δ väärtus ε valikust, seega kirjutame δ=δ(ε).

<< Пример 16.1

Tõesta seda

Lahendus: võtke suvaline ε>0, leidke δ=δ(ε)>0 nii, et kõigi x-de korral, mis rahuldavad võrratuse |x-3|< δ, выполняется неравенство |(2х-1)-5|<ε, т. е. |х-3|<ε.

Võttes δ=ε/2, näeme, et kõigi x puhul, mis rahuldavad ebavõrdsust |x-3|< δ, выполняется неравенство |(2х-1)-5|<ε. Следовательно, lim(2x-1)=5 при х –>3.

<< Пример 16.2

16.2. Ühepoolsed piirid

Funktsiooni piiri määratlemisel arvestatakse, et x kaldub igal viisil väärtusele x 0: jäädes väiksemaks kui x 0 (vasakul x 0), suurem kui x o (paremal x o-st) või võnkuma ümber punkt x 0.

On juhtumeid, kus argumendi x lähendamise meetod x o-le mõjutab oluliselt funktsioonipiirangu väärtust. Seetõttu võetakse kasutusele ühepoolsete piiride mõisted.

Arvu A 1 nimetatakse funktsiooni y=ƒ(x) piiriks vasakul punktis x o, kui mis tahes arvu ε>0 korral on arv δ=δ(ε)> 0, nii et punktis x є (x 0 -δ;x o), võrratus |ƒ(x)-A|<ε. Предел слева записывают так: limƒ(х)=А при х–>x 0 -0 või lühidalt: ƒ(x o- 0) = A 1 (Dirichlet' tähistus) (vt joonis 111).

Parempoolse funktsiooni piirang määratakse samamoodi, kasutades sümboleid:

Lühidalt, parempoolne piir on tähistatud ƒ(x o +0)=A.

Funktsiooni vasakut ja paremat piiri nimetatakse ühepoolseteks piirideks. Ilmselgelt, kui on olemas, siis eksisteerivad mõlemad ühepoolsed piirid ja A = A 1 = A 2.

Tõsi on ka vastupidine: kui mõlemad piirid ƒ(x 0 -0) ja ƒ(x 0 +0) on olemas ja need on võrdsed, siis on piir ja A = ƒ(x 0 -0).

Kui A 1 ¹ A 2, siis seda kabelit ei eksisteeri.

16.3. Funktsiooni piirväärtus x ® ∞

Olgu funktsioon y=ƒ(x) defineeritud intervallis (-∞;∞). Kutsutakse numbrit A funktsiooni piirƒ(x) juures x → ∞ , kui iga positiivse arvu ε korral on selline arv M=M()>0, et kõigi x-ide korral, mis rahuldavad võrratust |x|>M, on võrratus |ƒ(x)-A|<ε. Коротко это определение можно записать так:

Selle definitsiooni geomeetriline tähendus on järgmine: kui " ε>0 $ M>0, siis x є(-∞; -M) või x є(M; +∞) korral vastavad funktsiooni ƒ( x) langevad punkti A ε naabrusesse, see tähendab, et graafiku punktid asuvad 2ε laiusel ribal, mida piiravad sirged y=A+ε ja y=A-ε (vt joonis 112) .

16.4. Lõpmatult suur funktsioon (b.b.f.)

Funktsiooni y=ƒ(x) nimetatakse lõpmata suureks x→x 0 korral, kui suvalise arvu M>0 korral on arv δ=δ(M)>0, mis kõigi x-de korral, mis rahuldavad ebavõrdsust 0<|х-хо|<δ, выполняется неравенство |ƒ(х)|>M.

Näiteks funktsioon y=1/(x-2) on b.b.f. x->2 jaoks.

Kui ƒ(x) kaldub lõpmatusse kui x→x o ja võtab ainult positiivseid väärtusi, siis nad kirjutavad

kui ainult negatiivsed väärtused, siis

Funktsioon y=ƒ(x), mis on defineeritud tervel arvureal, nimetatakse lõpmatult suureks kui x→∞, kui mis tahes arvu M>0 korral on arv N=N(M)>0, nii et kõigi x-ide korral, mis rahuldavad võrratust |x|>N, kehtib võrratus |ƒ(x)|>M. Lühike:

Näiteks y=2x on b.b.f. nagu x→∞.

Pange tähele, et kui lõpmatusse kalduv argument x võtab ainult loomulikud väärtused, st xєN, siis vastav b.b.f. muutub lõpmatult suureks jadaks. Näiteks jada v n =n 2 +1, n є N on lõpmatult suur jada. Ilmselgelt iga b.b.f. punkti x o naabruses on selles naabruses piiramatu. Vastupidine pole tõsi: piiramata funktsioon ei pruugi olla b.b.f. (Näiteks y=xsinx.)

Kui aga limƒ(x)=A x→x 0, kus A on lõplik arv, siis funktsioon ƒ(x) on punkti x o läheduses piiratud.

Tõepoolest, funktsiooni piiri definitsioonist järeldub, et kui x→ x 0 on tingimus |ƒ(x)-A|<ε. Следовательно, А-ε<ƒ(х)<А+ε при х є (х о -ε; х о +ε), а это и означает, что функция ƒ (х) ограничена.

Antakse funktsiooni piiri põhiteoreemide ja omaduste sõnastus. Antud on lõplike ja lõpmatute piiride definitsioonid lõplikes punktides ja lõpmatuses (kahe- ja ühepoolsed) Cauchy ja Heine järgi. Aritmeetilisi omadusi arvestatakse; ebavõrdsustega seotud teoreemid; Cauchy konvergentsi kriteerium; kompleksfunktsiooni piir; lõpmata väikeste, lõpmata suurte ja monotoonsete funktsioonide omadused. Funktsiooni definitsioon on antud.

Sisu

Teine määratlus Cauchy järgi

Funktsiooni piir (Cauchy järgi) kui selle argumendi x kaldub x-le 0 on lõplik arv või punkt lõpmatuses a, mille jaoks on täidetud järgmised tingimused:
1) on selline punkti x torgatud naabruskond 0 , millel funktsioon f (x) kindlaks määratud;
2) punkti a mis tahes naabruses, kuhu kuulub , on selline punkti x punkteeritud naabruskond 0 , mille funktsiooni väärtused kuuluvad punkti a valitud naabrusesse:
aadressil .

Siin a ja x 0 võivad olla ka lõplikud arvud või punktid lõpmatuses. Kasutades olemasolu ja universaalsuse loogilisi sümboleid, saab selle määratluse kirjutada järgmiselt:
.

Kui võtame komplektina lõpp-punkti vasaku või parema naabruse, saame Cauchy piiri määratluse vasakul või paremal.

Teoreem
Funktsiooni piiri Cauchy ja Heine definitsioonid on samaväärsed.
Tõestus

Kohaldatavad punktide naabrused

Siis tegelikult tähendab Cauchy definitsioon järgmist.
Mis tahes positiivsete arvude jaoks on arvud , nii et kõigi x punktide punkt : naabrusesse kuuluvate funktsiooni väärtused kuuluvad punkti a naabrusesse: ,
Kus,.

Selle määratlusega pole eriti mugav töötada, kuna linnaosad on määratletud nelja numbriga. Kuid seda saab lihtsustada võrdsete otstega linnaosade tutvustamisega. See tähendab, et võite panna ,. Siis saame definitsiooni, mida on lihtsam kasutada teoreemide tõestamisel. Lisaks on see samaväärne määratlusega, milles kasutatakse suvalisi naabruskondi. Selle fakti tõestus on toodud jaotises “Funktsiooni piiri Cauchy definitsioonide ekvivalentsus”.

Siis saame anda funktsiooni piiri ühtse definitsiooni lõplikes ja lõpmata kaugetes punktides:
.
Siin on lõpp-punktid
; ;
.
Lõpmatuse punktide mis tahes ümbrus torgatakse:
; ; .

Funktsiooni lõplikud piirid lõpp-punktides

Arvu a nimetatakse funktsiooni f piiriks (x) punktis x 0 , Kui
1) funktsioon on määratletud lõpp-punkti mõnel läbitorgatud naabruskonnal;
2) iga on olemas selline, et olenevalt , Nii et kõigi x puhul, mille korral kehtib ebavõrdsus
.

Kasutades eksistentsi ja universaalsuse loogilisi sümboleid, saab funktsiooni piiri määratluse kirjutada järgmiselt:
.

Ühepoolsed piirid.
Vasakpoolne piir ühes punktis (vasakpoolne piir):
.
Parempoolne piir punktis (parempoolne piir):
.
Vasak- ja parempoolsed piirid on sageli tähistatud järgmiselt:
; .

Funktsiooni lõplikud piirid lõpmatuse punktides

Piirid lõpmatuse punktides määratakse kindlaks sarnasel viisil.
.
.
.

Lõpmatud funktsioonipiirangud

Võite tutvustada ka teatud märkide lõpmatute piiride määratlusi, mis on võrdsed ja :
.
.

Funktsiooni piiri omadused ja teoreemid

Lisaks eeldame, et vaadeldavad funktsioonid on määratletud punkti vastavas punkteeritud naabruses, mis on lõplik arv või üks sümbolitest: . See võib olla ka ühepoolne piirpunkt, st olla kujul või . Naabruskond on kahepoolse piirmäära jaoks kahepoolne ja ühepoolse piiri jaoks ühepoolne.

Põhiomadused

Kui funktsiooni f väärtused (x) muuta (või määramata) lõplikku arvu punkte x 1, x 2, x 3, ... x n, siis see muudatus ei mõjuta funktsiooni piiri olemasolu ja väärtust suvalises punktis x 0 .

Kui on olemas lõplik piir, siis on olemas punkti x punkteeritud ümbrus 0 , millel funktsioon f (x) piiratud:
.

Olgu funktsioonil punkt x 0 lõplik nullist erinev piir:
.
Siis on suvalise arvu c jaoks vahemikust punkt x selline punkteeritud naabruskond 0 milleks,
, Kui ;
, Kui.

Kui mõnel punkti naabruskonnal , , on konstant, siis .

Kui punkti x mõnel torgatud ümbruskonnal on lõplikud piirid ja ja 0
,
See .

Kui , Ja mõnel punkti naabruses
,
See .
Eelkõige siis, kui mõne punkti naabruses
,
siis kui , siis ja ;
kui , siis ja .

Kui punkti x mõnel torgatud naabruskonnal 0 :
,
ja on olemas lõplikud (või teatud märgi lõpmatud) võrdsed piirid:
, See
.

Peamiste omaduste tõendid on toodud lehel
"Funktsiooni piiri põhiomadused."

Olgu funktsioonid ja määratletud punkti mõnes punktsiooniga naabruses. Ja olgu piiratud piirid:
Ja .
Ja olgu C konstant, see tähendab etteantud arv. Siis
;
;
;
, Kui.

Kui siis.

Aritmeetiliste omaduste tõendid on toodud lehel
"Funktsiooni piiri aritmeetilised omadused".

Cauchy kriteerium funktsiooni piiri olemasoluks

Teoreem
Selleks, et funktsioon, mis on defineeritud lõpliku või lõpmatult kauge punkti x mingis punkteeritud ümbruses 0 , oli selles punktis lõplik piir, on vajalik ja piisav, et iga ε korral > 0 seal oli selline punkti x torgatud naabruskond 0 , et mis tahes punktide ja selle naabruskonna puhul kehtib järgmine ebavõrdsus:
.

Keerulise funktsiooni piir

Teoreem kompleksfunktsiooni piiri kohta
Laske funktsioonil olla piir ja kaardistada punkti läbimurtud naabruskond punkti punkteeritud ümbrusega. Olgu funktsioon sellel naabruskonnal määratletud ja sellel on piirang.
Siin on viimased või lõpmatult kauged punktid: . Naabruskonnad ja neile vastavad piirid võivad olla kas kahe- või ühepoolsed.
Siis on keerulise funktsiooni piirang ja see on võrdne:
.

Kompleksfunktsiooni piirteoreemi rakendatakse siis, kui funktsioon ei ole punktis defineeritud või selle väärtus erineb piirväärtusest. Selle teoreemi rakendamiseks peab punktis, kus funktsiooni väärtuste hulk punkti ei sisalda, olema punkteeritud naabrus:
.

Kui funktsioon on pidev punktis , saab pideva funktsiooni argumendile rakendada piirmärki:
.
Järgnev on sellele juhtumile vastav teoreem.

Teoreem funktsiooni pideva funktsiooni piiri kohta
Olgu funktsiooni g limiit (x) kui x → x 0 , ja see on võrdne t 0 :
.
Siin on punkt x 0 võib olla lõplik või lõpmatult kauge: .
Ja olgu funktsioon f (t) pidev punktis t 0 .
Siis on kompleksfunktsiooni f piir (g(x)), ja see on võrdne f-ga (t 0):
.

Teoreemide tõestused on toodud lehel
"Keerulise funktsiooni piir ja järjepidevus".

Lõpmatult väikesed ja lõpmata suured funktsioonid

Lõpmatult väikesed funktsioonid

Definitsioon
Funktsiooni kohta öeldakse, et see on lõpmatult väike, kui
.

Summa, vahe ja toode Lõpliku arvu lõpmatute väikeste funktsioonide juures on lõpmatult väike funktsioon juures .

Piiratud funktsiooni korrutis mõnel torgatud naabruses punkt , Et lõpmatu väike juures on lõpmatu funktsioon juures .

Selleks, et funktsioonil oleks lõplik piir, on vajalik ja piisav, et
,
kus on infinitesimal funktsioon juures .

"Lõpmata väikeste funktsioonide omadused".

Lõpmatult suured funktsioonid

Definitsioon
Funktsiooni nimetatakse lõpmatult suureks, kui
.

Piiratud funktsiooni summa või erinevus, mõnel punkti naabruses ja lõpmatult suur funktsioon juures on lõpmatult suur funktsioon .

Kui funktsioon on lõpmatult suur ja funktsioon on piiratud punkti mingi punktsiooniga naabruskonnaga, siis
.

Kui funktsioon , punkti mõnel torgatud naabruses, rahuldab ebavõrdsust:
,
ja funktsioon on lõpmatult väike:
, ja (punkti mõnel torgatud naabruskonnal), siis
.

Omaduste tõendid on esitatud jaotises
"Lõpmatult suurte funktsioonide omadused".

Lõpmatult suurte ja lõpmata väikeste funktsioonide vaheline seos

Kahest eelnevast omadusest tuleneb seos lõpmatult suurte ja lõpmata väikeste funktsioonide vahel.

Kui funktsioon on lõpmatult suur juures , siis funktsioon on lõpmatult väike juures .

Kui funktsioon on , ja jaoks lõpmatult väike, on funktsioon lõpmatult suur.

Lõpmatult väikese ja lõpmata suure funktsiooni suhet saab väljendada sümboolselt:
, .

Kui lõpmata väikesel funktsioonil on teatud märk punktis , see tähendab, et see on positiivne (või negatiivne) punkti mõnel punkteeritud naabruskonnal, siis saab seda fakti väljendada järgmiselt:
.
Samamoodi, kui lõpmata suurel funktsioonil on teatud märk kohas , kirjutavad nad:
.

Siis saab sümboolset seost lõpmatult väikeste ja lõpmatult suurte funktsioonide vahel täiendada järgmiste seostega:
, ,
, .

Täiendavad valemid lõpmatuse sümbolite kohta leiate lehelt
"Punktid lõpmatusele ja nende omadused."

Monotoonsete funktsioonide piirid

Definitsioon
Kutsutakse välja funktsioon, mis on defineeritud mõnel reaalarvude hulgal X rangelt suurenev, kui kõigi puhul kehtib järgmine ebavõrdsus:
.
Vastavalt sellele, jaoks rangelt vähenemas funktsioon kehtib järgmine ebavõrdsus:
.
Sest mitte-kahanev:
.
Sest mitte suurenev:
.

Sellest järeldub, et ka rangelt kasvav funktsioon ei ole kahanev. Rangelt kahanev funktsioon on ka mittekasv.

Funktsiooni kutsutakse üksluine, kui see ei vähene või ei suurene.

Teoreem
Las funktsioon ei vähene intervallil, kus .
Kui see on ülalt piiratud arvuga M: siis on olemas lõplik piir. Kui ülalt ei piirata, siis .
Kui see on altpoolt piiratud arvuga m: siis on olemas lõplik piir. Kui altpoolt ei piirdu, siis .

Kui punktid a ja b on lõpmatuses, siis avaldistes tähendavad piirmärgid, et .
Seda teoreemi saab sõnastada kompaktsemalt.

Las funktsioon ei vähene intervallil, kus . Siis on punktides a ja b ühepoolsed piirid:
;
.

Sarnane teoreem mittekasvava funktsiooni jaoks.

Las funktsioon ei suurene intervallil, kus . Siis on ühepoolsed piirangud:
;
.

Teoreemi tõestus on toodud lehel
"Monotoonsete funktsioonide piirid".

Funktsiooni definitsioon

Funktsioon y = f (x) on seadus (reegel), mille kohaselt on hulga X iga element x seotud hulga Y ühe ja ainult ühe elemendiga y.

Element x ∈ X helistas funktsiooni argument või sõltumatu muutuja.
Element y ∈ Y helistas funktsiooni väärtus või sõltuv muutuja.

Hulk X kutsutakse funktsiooni domeen.
Elementide hulk y ∈ Y, mille komplektis X on eelkujutised, kutsutakse ala või funktsiooni väärtuste komplekt.

Tegelikku funktsiooni nimetatakse ülalt piiratud (altpoolt), kui on olemas arv M, mille puhul ebavõrdsus kehtib kõigi kohta:
.
Kutsutakse numbrifunktsiooni piiratud, kui on olemas selline arv M, et kõigi jaoks:
.

Ülemine serv või täpne ülemine piir Tegelikku funktsiooni nimetatakse väikseimaks arvuks, mis piirab selle väärtuste vahemikku ülalt. See tähendab, et see on arv s, mille kõigi ja kõigi jaoks on argument, mille funktsiooni väärtus ületab s′: .
Funktsiooni ülemist piiri saab tähistada järgmiselt:
.

Vastavalt alumine serv või täpne alumine piir Reaalfunktsiooni nimetatakse suurimaks arvuks, mis piirab selle väärtuste vahemikku altpoolt. See tähendab, et see on arv i, mille kõigi ja kõigi jaoks on argument, mille funktsiooni väärtus on väiksem kui i′: .
Funktsiooni infimumi saab tähistada järgmiselt:
.

Viited:
L.D. Kudrjavtsev. Matemaatilise analüüsi kursus. 1. köide. Moskva, 2003.
CM. Nikolski. Matemaatilise analüüsi kursus. 1. köide. Moskva, 1983.

Vaata ka:

Järjestuse ja funktsiooni piiride määratlus, piiride omadused, esimene ja teine tähelepanuväärne piir, näited.

Püsiv number A helistas piir järjestused(x n), kui suvaliselt väikese positiivse arvu ε > 0 korral on arv N nii, et kõik väärtused x n, mille puhul n>N, rahuldavad ebavõrdsust

Kirjutage see üles järgmiselt: või x n → a.

Ebavõrdsus (6.1) on samaväärne topeltvõrdsusega

a - ε< x n < a + ε которое означает, что точки x n, alustades mingist arvust n>N, asuvad intervalli (a-ε , a+ε) sees, st. langevad punkti mis tahes väikesesse ε-naabrusse A.

Nimetatakse jada, millel on piir koonduv, muidu - lahknev.

Funktsiooni piirangu mõiste on jada piiri mõiste üldistus, kuna jada piiriks võib pidada täisarvu argumendi funktsiooni x n = f(n) piiri. n.

Olgu funktsioon f(x) antud ja olgu a - piirpunkt selle funktsiooni määratluspiirkond D(f), st. selline punkt, mille mis tahes naabrus sisaldab hulga D(f) muid punkte peale a. Punkt a võib või ei pruugi kuuluda hulka D(f).

Definitsioon 1. Nimetatakse konstantset arvu A piir funktsioonid f(x) juures x→ a, kui mis tahes argumentide väärtuste jada (x n ) puhul, mis kaldub sellele A, on vastavatel jadadel (f(x n)) sama piir A.

Seda määratlust nimetatakse funktsiooni piiri määramine Heine järgi, või " jadakeeles”.

2. definitsioon. Nimetatakse konstantset arvu A piir funktsioonid f(x) juures x→a, kui suvalise, suvaliselt väikese positiivse arvu ε korral on võimalik leida selline δ >0 (olenevalt ε-st), et kõigi x, mis asub arvu ε-naabruses A, st. Sest x, mis rahuldab ebavõrdsust
0 < x-a < ε , значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε

Seda määratlust nimetatakse defineerides funktsiooni piiri Cauchy järgi, või “keeles ε - δ"

Definitsioonid 1 ja 2 on samaväärsed. Kui funktsioonil f(x) as x → a on piir, võrdne A-ga, kirjutatakse see kujul

Juhul kui jada (f(x n)) suureneb (või väheneb) piiranguteta mis tahes lähendusmeetodi puhul x teie piirini A, siis ütleme, et funktsioonil f(x) on lõpmatu piir, ja kirjutage see kujule:

Kutsutakse muutujat (st jada või funktsiooni), mille piirväärtus on null lõputult väike.

Nimetatakse muutujat, mille piiriks on lõpmatus lõpmatult suur.

Praktikas piiri leidmiseks kasutatakse järgmisi teoreeme.

1. teoreem . Kui iga piir on olemas

(6.4)

(6.5)

(6.6)

Kommenteeri. Vormiga 0/0, ∞/∞, ∞-∞ 0*∞ avaldised on ebakindlad, näiteks kahe lõpmata väikese või lõpmata suure koguse suhe, ja seda tüüpi piiri leidmist nimetatakse "määramatuse avalikustamiseks".

2. teoreem.

need. piirini saab minna konstantse astendajaga võimsuse alusel, eelkõige

3. teoreem.

(6.11)

Kus e» 2,7 - naturaallogaritmi alus. Valemeid (6.10) ja (6.11) nimetatakse esimeseks tähelepanuväärseks piiriks ja teiseks tähelepanuväärseks piiriks.

Praktikas kasutatakse ka valemi (6.11) tagajärgi:

(6.12)

(6.13)

(6.14)

eelkõige piirmäär,

Kui x → a ja samal ajal x > a, siis kirjuta x →a + 0. Kui täpsemalt a = 0, siis sümboli 0+0 asemel kirjuta +0. Samamoodi, kui x→a ja samal ajal x ja neid kutsutakse vastavalt õige piir Ja vasak piir funktsioonid f(x) punktis A. Et funktsioonil f(x) oleks limiit kujul x→ a, on vajalik ja piisav, et . Kutsutakse funktsioon f(x). pidev punktis x 0, kui piirang

(6.15)

Tingimust (6.15) saab ümber kirjutada järgmiselt:

ehk funktsiooni märgi all oleva piirini üleminek on võimalik, kui see on antud punktis pidev.

Kui võrdsust (6.15) rikutakse, siis ütleme nii juures x = x o funktsiooni f(x) Sellel on lõhe Vaatleme funktsiooni y = 1/x. Selle funktsiooni määratluspiirkond on komplekt R, välja arvatud x = 0. Punkt x = 0 on hulga D(f) piirpunkt, kuna selle mis tahes naabruses, s.o. mis tahes avatud intervallis, mis sisaldab punkti 0, on punkte D(f), kuid see ise ei kuulu sellesse hulka. Väärtus f(x o)= f(0) on määratlemata, seega punktis x o = 0 on funktsioonil katkestus.

Kutsutakse funktsioon f(x). pidev paremal punktis x o kui piir

Ja pidev vasakul punktis x o, kui piir

Funktsiooni pidevus punktis x o on samaväärne selle järjepidevusega selles punktis nii paremal kui ka vasakul.

Selleks, et funktsioon oleks punktis pidev x o, näiteks paremal on vaja esiteks, et oleks lõplik piir, ja teiseks, et see piir oleks võrdne f(x o). Seega, kui vähemalt üks neist kahest tingimusest ei ole täidetud, tekib funktsioonil katkestus.

1. Kui piirmäär on olemas ja ei ole võrdne f(x o), siis nad ütlevad seda funktsiooni f(x) punktis x o on esimest tüüpi rebend, või hüpe.

2. Kui piir on +∞ või -∞ või seda ei ole olemas, siis öeldakse, et sisse punkt x o funktsioonil on katkestus teist liiki.

Näiteks funktsiooni y = ctg x as x → +0 piirväärtus on +∞, mis tähendab, et punktis x=0 on tal teist tüüpi katkestus. Funktsioon y = E(x) (täisarv osa x) on tervete abstsissidega punktides esimest tüüpi katkestusi ehk hüppeid.

Kutsutakse funktsiooni, mis on pidev intervalli igas punktis pidev V . Pidevat funktsiooni kujutab tahke kõver.

Paljud probleemid, mis on seotud mõne koguse pideva kasvuga, viivad teise tähelepanuväärse piirini. Selliste ülesannete hulka kuuluvad näiteks: hoiuste kasv liitintressi seaduse järgi, riigi rahvaarvu kasv, radioaktiivsete ainete lagunemine, bakterite vohamine jne.

Mõelgem näiteks Ya I. Perelman, mis annab numbri tõlgenduse e liitintressi probleemis. Number e on piir . Hoiukassades lisatakse põhikapitalile intressiraha igal aastal. Kui liituda sagedamini, siis kapital kasvab kiiremini, kuna intresside kujunemisse kaasatakse suurem summa. Võtame puhtalt teoreetilise, väga lihtsustatud näite. Panka hoiule 100 denjerit. ühikut põhineb 100% aastas. Kui intressiraha lisandub põhikapitalile alles aasta pärast, siis selleks perioodiks 100 den. ühikut muutub 200 rahaühikuks. Nüüd vaatame, milleks 100 denize muutub. ühikut, kui iga kuue kuu tagant lisatakse põhikapitalile intressiraha. Kuue kuu pärast 100 den. ühikut kasvab 100 × 1,5 = 150 ja veel kuue kuu pärast - 150 × 1,5 = 225 (den. ühikut). Kui liitumine toimub iga 1/3 aasta tagant, siis aasta pärast 100 den. ühikut muutub 100 × (1 +1/3) 3 ≈ 237 (den. ühikut). Tõstame intressiraha lisamise tähtajad 0,1 aastani, 0,01 aastani, 0,001 aastani jne. Siis 100 denist välja. ühikut aasta pärast on see:

100×(1 +1/10) 10 ≈ 259 (den. ühikut),

100×(1+1/100) 100 ≈ 270 (den. ühikut),

100×(1+1/1000) 1000 ≈271 (den. ühikut).

Intressi lisamise tingimuste piiramatu vähendamisega ei kasva kogunenud kapital lõputult, vaid läheneb teatud piirile, mis on ligikaudu 271. Aastas 100% hoiustatud kapital ei saa suureneda rohkem kui 2,71 korda, isegi kui kogunenud intress lisati pealinna iga sekund, sest limiit

Näide 3.1. Kasutades arvujada piiri definitsiooni, tõesta, et jada x n =(n-1)/n piirväärtus on võrdne 1-ga.

Lahendus. Peame tõestama, et olenemata sellest, millise ε > 0 me võtame, on selle jaoks olemas naturaalarv N, mille puhul kõigi n > N korral on võrratus |x n -1|< ε

Võtame suvalise ε > 0. Kuna x n -1 =(n+1)/n - 1= 1/n, siis N leidmiseks piisab võrratuse 1/n lahendamisest<ε. Отсюда n>1/ε ja seetõttu N võib olla 1/ε N = E(1/ε) täisarvuline osa. Oleme sellega tõestanud, et piir .

Näide 3.2. Leia ühise liikmega antud jada piir

Lahendus. Rakendame summateoreemi piirmäära ja leiame iga liikme piirmäära. Kuna n → ∞, kipuvad iga liikme lugeja ja nimetaja lõpmatuseni ning jagatispiiri teoreemi ei saa otseselt rakendada. Seetõttu muundame esmalt x n, jagades esimese liikme lugeja ja nimetaja arvuga n 2, ja teine sisse n. Seejärel, rakendades jagatise piiri ja summateoreemi piirmäära, leiame:

Näide 3.3. . Leia .

Lahendus.

Siin kasutasime astmeteoreemi piiri: astme piir on võrdne aluse piiri astmega.

Näide 3.4. Leia ( ).

Lahendus. Erinevusteoreemi on võimatu rakendada, kuna meil on kuju ∞-∞ määramatus. Teisendame üldtermini valemi:

Näide 3.5. Funktsioon f(x)=2 1/x on antud. Tõesta, et piire pole.

Lahendus. Kasutame funktsiooni piiri definitsiooni 1 jada kaudu. Võtame jada ( x n ), mis koondub 0-le, st. Näitame, et väärtus f(x n)= käitub erinevate jadade puhul erinevalt. Olgu x n = 1/n. Ilmselgelt siis piir Valime nüüd kui x n jada ühise liikmega x n = -1/n, mis kaldub samuti nulli. Seetõttu pole piirangut.

Näide 3.6. Tõesta, et piire pole.

Lahendus. Olgu x 1 , x 2 ,..., x n ,... jada, mille jaoks
. Kuidas jada (f(x n)) = (sin x n) käitub erinevate x n → ∞ korral

Kui x n = p n, siis sin x n = sin (lk n) = 0 kõigi jaoks n ja limiit Kui
x n =2 p n+ p /2, siis sin x n = sin(2 p n+ p /2) = sin p /2 = 1 kõigi jaoks n ja seega ka piir. Nii et seda pole olemas.

Mõelge funktsioonile %%f(x)%%, mis on määratletud vähemalt mõnes punktis %%\stackrel(\circ)(\text(U))(a)%% punktist %%a \in \overline( \) mathbb(R))%% laiendatud arvurida.

Cauchy piiri kontseptsioon

Arvu %%A \in \mathbb(R)%% kutsutakse funktsiooni piir%%f(x)%% punktis %%a \in \mathbb(R)%% (või %%x%% kaldudes %%a \in \mathbb(R)%%), kui, mis Olenemata positiivsest arvust %%\varepsilon%%, on positiivne arv %%\delta%%, nii et kõigi punktide puhul punkti %%\delta%% naabruses punkti %%a%% on funktsiooni väärtused kuuluvad %%\varepsilon %%-punkti %%A%% naabrusse või

$$ A = \lim\limits_(x \to a)(f(x)) \Leftright nool \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel(\circ)(\text (U))_\delta(a) \Paremnool f(x) \in \text(U)_\varepsilon (A) \big) $$

Seda määratlust nimetatakse %%\varepsilon%% ja %%\delta%% määratlusteks, mille pakkus välja prantsuse matemaatik Augustin Cauchy ja mida kasutati 19. sajandi algusest tänapäevani, kuna sellel on vajalik matemaatiline rangus ja täpsus.

Punkti %%a%% erinevate naabruste kombineerimine kujul %%\stackrel(\circ)(\text(U))_\delta(a), \text(U)_\delta (\infty), \ tekst(U) _\delta (-\infty), \text(U)_\delta (+\infty), \text(U)_\delta^+ (a), \text(U)_\delta^ - (a) %% ümbritsevaga %%\text(U)_\varepsilon (A), \text(U)_\varepsilon (\infty), \text(U)_\varepsilon (+\infty), \ text(U) _\varepsilon (-\infty)%%, saame 24 Cauchy piiri definitsiooni.

Geomeetriline tähendus

Funktsiooni piiri geomeetriline tähendus

Uurime välja, mis on funktsiooni piiri geomeetriline tähendus punktis. Koostame funktsiooni %%y = f(x)%% graafiku ja märgime sellele punktid %%x = a%% ja %%y = A%%.

Funktsiooni %%y = f(x)%% limiit punktis %%x \kuni a%% on olemas ja on võrdne A-ga, kui mis tahes %%\varepsilon%% naabruses punktist %%A%% saab määrata sellise %%\ delta%%-punkti %%a%% naabruskonna nii, et mis tahes %%x%% sellest %%\delta%%-st naabruskonnast on väärtus %%f(x)% % asub %%\varepsilon%%-naabruspunktides %%A%%.

Pange tähele, et funktsiooni limiidi definitsiooni järgi Cauchy järgi ei ole piirangu olemasolul %%x \kuni a%% vahet, mis väärtuse funktsioon võtab punktis %%a%%. Võib tuua näiteid, kus funktsioon ei ole määratletud, kui %%x = a%% või kui see võtab muu väärtuse kui %%A%%. Piirang võib siiski olla %%A%%.

Heine piiri määramine

Elementi %%A \in \overline(\mathbb(R))%% nimetatakse funktsiooni %%f(x)%% piiriks kohas %% x \to a, a \in \overline(\mathbb( R))%% , kui mis tahes järjestuse %%$x_n$ \kuni a%% definitsioonipiirkonnast, siis vastavate väärtuste jada %%\big$f(x_n)\big$% % kipub olema %%A%%.

Piirmäära definitsiooni Heine järgi on mugav kasutada siis, kui tekib kahtlus funktsiooni piiri olemasolus antud punktis. Kui on võimalik konstrueerida vähemalt üks jada %%$x_n$%% piiriga punktis %%a%%, nii et jada %%\big$f(x_n)\big$%% ei ole piirangut, siis võime järeldada, et funktsioonil %%f(x)%% pole praegu piirangut. Kui kahele mitmesugused jadad %%$x"_n$%% ja %%$x""_n$%%, millel on sama limiit %%a%%, järjestused %%\big$f(x"_n)\big$%% ja %%\big$f(x""_n)\big$%% on mitmesugused piirid, siis sel juhul pole ka funktsiooni %%f(x)%% limiiti.

Näide

Olgu %%f(x) = \sin(1/x)%%. Kontrollime, kas selle funktsiooni limiit eksisteerib punktis %%a = 0%%.

Esmalt valime jada $$ $x_n$ = \left$\frac((-1)^n)(n\pi)\right$, mis koondub sellesse punkti. $$

On selge, et %%x_n \ne 0~\forall~n \in \mathbb(N)%% ja %%\lim (x_n) = 0%%. Siis %%f(x_n) = \sin(\left((-1)^n n\pi\right)) \equiv 0%% ja %%\lim\big$f(x_n)\big$ = 0 %%.

Seejärel võtke jada $$ x"_n = \left$ \frac(2)((4n + 1)\pi) \right$, $$ koondub samasse punkti

mille puhul %%\lim(x"_n) = +0%%, %%f(x"_n) = \sin(\big((4n + 1)\pi/2\big)) \equiv 1%% ja %%\lim\big$f(x"_n)\big$ = 1%%. Samamoodi jada $$ x""_n = \left$-\frac(2)((4n + 1) puhul ) \pi) \right$, $$

samuti läheneb punktile %%x = 0%%, %%\lim\big$f(x""_n)\big$ = -1%%.

Kõik kolm järjestust andsid erinevaid tulemusi, mis on vastuolus Heine definitsioonitingimusega, s.t. sellel funktsioonil pole piirangut punktis %%x = 0%%.