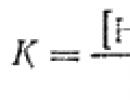Mittelineaarse võrrandi juurte leidmine

Kursusetöö

Arvutiteadus, küberneetika ja programmeerimine

Numbrilisi meetodeid rakendavad vooskeemid - dihhotoomiameetodi jaoks: Akordimeetodi vooskeemid: Newtoni meetodi vooskeemid: Programmide loendiüksus Unit1; interfce kasutab Windows Messges SysUtils Vrints Clsses Grphics Controls Vormid Diloogid TeEngine Series ExtCtrls TeeProcs Chrt Menüüd OleCtnrs StdCtrls xCtrls OleCtrls VCF1 Mth; tüüp TForm1 = clssTForm GroupBox1: TGroupBox; OleContiner2: TOleContiner; MinMenu1: TMinMenu; N1: TMenuItem; Chrt1: TChrt; 1. seeria:...

VENEMAA RIIKLIK ÕLI- JA GAASIÜLIKOOL. NEED. GUBKIN

Arvutiteaduse osakond

Kursuse töö

erialal "Informaatika".

Teema: " Mittelineaarse võrrandi juurte leidmine"

Lõpetanud: üliõpilane

Manepova A.M

rühmad: GI-12-05

Kontrollitud:

Moskva 2013

Kursusetöö ülesanne. Mittelineaarse võrrandi juurte leidmise teooria. Kasutatud numbriliste meetodite kirjeldus. 1. Poolitamise meetod (dihhotoomia) 2. Akordi meetod 3. Newtoni meetod Arvutused Mat lab matemaatilises paketis Aruanne võrrandi juure ligikaudse väärtuse arvutamise tulemuste kohta MS Excelis. Arvutustulemused parameetrite valiku abil Arvutustulemused lahenduste otsimise abil Delphi keskkonnas loodud rakenduse kirjeldus. Numbrilisi meetodeid rakendavad plokkskeemid Programmide loend Rakenduse akna pilt Saadud tulemuste analüüs Kirjandus.

Kursusetöö ülesanne.

1. arvutus , täidetakse matemaatilises paketis Matlab (Mathematica 5 .) (failifunktsioon mittelineaarse võrrandi, graafiku, lahenduse kirjeldamiseks sümboolsel ja numbrilisel kujul).
2. Leidmine mittelineaarse võrrandi juured arvutustabelites MS Excel (mittelineaarvõrrandi tüüp, mittelineaarvõrrandi juurte leidmise graafik, mittelineaarvõrrandi juure leidmine tingimusliku analüüsi vahenditega: “Parameetri valik”, “Lahendusotsing”).
3. Rakenduse loomine mittelineaarse võrrandi juurte leidmiseks Delphi keskkonnas (mittelineaarse võrrandi tüüp, graafik antud intervall, iga meetodi puhul: antud intervalli ja sammuga funktsiooni tabelite tabeldamise tulemused; numbrilise meetodi iga meetodi puhul kasutaja alamprogramm parameetrite ülekandega). Tulemused kuvatakse vormil tabeli ja faili kujul. Pakkuge ette väärtuse täpsuse muutmine (E<= 0 , 001).
4. võrrandi tüüp

Mittelineaarse võrrandi juurte leidmise teooria. Kasutatud numbriliste meetodite kirjeldus.

Olgu funktsioon antud , pidev koos selle mitmete tuletistega. Peate leidma kõik või mõned võrrandi tegelikud juured

.
See ülesanne on jagatud mitmeks alamülesandeks. Esiteks on vaja kindlaks määrata juurte arv ja neid uurida iseloomu ja asukoht. Teiseks leidke juurte ligikaudsed väärtused. Kolmandaks valige meid huvitavad juured ja arvutage need vajaliku täpsusega e. Esimene ja teine ​​ülesanne lahendatakse reeglina analüütiliste või graafiliste meetoditega. Juhul, kui otsitakse ainult võrrandi tegelikke juuri, on kasulik koostada väärtuste tabel funktsioonid . Kui kahes külgnevas sõlmes tabelid funktsioonil on erinevad märgid, siis nende sõlmede vahel asub paaritu arv võrrandi juuri (vähemalt üks). Kui need sõlmed on lähedal, on nende vahel tõenäoliselt ainult üks juur.
Leitud juurte ligikaudseid väärtusi saab täpsustada erinevate iteratiivsete meetodite abil.

Vaatleme kolme meetodit: 1) dihhotoomia meetod (ehk segmendi jagamine pooleks); 2) lihtsa iteratsiooni meetod ja 3) meetod Newton.

1. Poolitamise meetod (dihhotoomia)

Olgu lõigul antud pidev funktsioonKui funktsiooni väärtustel segmendi otstes on erinevad märgid, st.see tähendab, et selles segmendis on paaritu arv juuri. Kindluse mõttes olgu üks juur. Meetodi olemus seisneb selles, et iga iteratsiooni korral lõigatakse segmendi pikkus poole võrra. Leidke segmendi keskpunkt järgmise valemi abil:Arvutage funktsiooni väärtusja valige segment, millel funktsioon toimib muudab oma märki . Jagame uue segmendi uuesti pooleks. Ja see üks protsessi Jätkame seni, kuni segmendi pikkus on võrdne juure E arvutamise etteantud veaga.

2.Akordi meetod

Mittelineaarse võrrandi lahendamisel akordmeetodil määratakse intervallid, mille korral on ainult üks lahend, ja täpsus Ɛ. Seejärel joonistame läbi kahe punkti koordinaatidega (a,F(a)) ja (b,F(b)) sirgjoone lõigu (kõla) ja määrame selle sirge lõikepunkti abstsissteljega. Kui samal ajal F(a)*F(b)<0, то праву границу интервала пееносиим в точку x (b=x). Если указанное условие не выполняется, то в точку x nihutatakse intervalli vasak äär (a=x). Lahenduse otsimine peatub määratud täpsuse |F(x)|>Ɛ saavutamisel. Arvutused tehakse seni, kuni ebavõrdsus on täidetud:. Akordimeetodi iteratiivne valem on kujul:

3. Newtoni meetod

Võrrandi numbriliseks lahendamisekslihtsa iteratsioonimeetodi abil, tuleb see viia järgmisele kujule:, kus kokkusurutav kaardistamine.

Parima konvergentsi saavutamiseks meetod järgmise lähenduse punktistingimus peab olema täidetud. Selle võrrandi lahendust otsitakse vormis, Siis:

Eeldusel, et lähenemispunkt on juurele "piisavalt lähedal"., ja et antud funktsioon pidev , lõplik valem Kas see on:

Seda arvesse võttes funktsioon määratakse väljendiga:

See funktsioon teostab juure naabruses tihendavat kaardistamist, ja algoritm võrrandile numbrilise lahenduse leidmisekstaandub iteratiivseks arvutusprotseduuriks:

Arvutused matemaatilises paketis Mati labor

Matemaatilises paketis joonistati vastavalt ülesande tingimustele funktsiooni graafik ja leiti sümboolse lahendi abil võrrandi juur ( lahendada ) ja numbriliselt kasutades sisseehitatud funktsioone: fzero ja fsolve . Oma funktsiooni kirjeldamiseks kasutasin failifunktsiooni.

Järgmine joonis näitab funktsiooni graafikut:

Kasutasin käskude kirjutamiseks M-fail:

Käsuaknas saadi järgmised tulemused:

r 1 =

r 2 =

r 3 =

r 4 =

8.0000

r5 =

7.9979 -8.0000

Aruanne võrrandi juure ligikaudse väärtuse arvutamise tulemuste kohta MS Excelis.

MS Excel Võrrandi juure ligikaudne väärtus arvutati sisseehitatud võimaluste "Parameetrite valik" ja "Lahenduste otsimine" abil. Esialgse lähenduse valimiseks koostasin kõigepealt diagrammi.

Arvutustulemused parameetrite valiku abil

x =-9 (diagrammi alusel)

Parameetri valiku kasutamise tulemusena leiti juur x = -8,01.

Arvutustulemused lahenduste otsimise abil

Valiti esialgne lähendus x =-9 (diagrammi alusel)

Pärast teostamist saadi järgmine tulemus:

Lahenduse leidmine andis mulle tähenduse x = -8,00002

Delphi keskkonnas loodud rakenduse kirjeldus.

Rakenduse loomisel keskkonnas Delfi Liides kuvas funktsiooni tüübi ja graafiku. Mittelineaarse võrrandi juure leidmiseks kasutati kolme meetodit: dihhotoomia meetod, Hordi meetod ja Newtoni meetod. Erinevalt arvutusest sisse Excel kus juured leiti parameetrite valimise ja lahenduse otsimise teel, annab programm kasutajale võimaluse sisestada arvutuse täpsus. Arvutustulemusi kuvatakse nii rakenduse aknas kui ka tekstifailis.

Numbrilisi meetodeid rakendavad plokkskeemid

Dihhotoomia meetodi vooskeem:

Akordimeetodi plokkskeem:

Newtoni meetodi vooskeem:

Programmide loend

ühik Ühik1;

liides

kasutab

Windows, sõnumid, SysUtils, variandid, klassid, graafika, juhtnupud, vormid,

Dialoogid, TeEngine, seeria, ExtCtrl, TeeProcs, diagramm, menüüd, oleCtnrs,

StdCtrls, AxCtrls, OleCtrls, VCF1, Math;

tüüp

Tvorm1 = klass (Tvorm)

GroupBox1: TGroupbox;

OleContainer2: TOleContainer;

MainMenu1: TMainMenu;

N1: TMenuItem;

Diagramm1:Tdiagramm;

Series1: TPointSeries;

N2: TMenuItem;

N3: TMenuItem;

N4: TMenuItem;

N5: TMenuItem;

Silt1: Tsilt;

Edit1: TEdit;

GroupBox2: TGroupbox;

GroupBox3: TGroupbox;

GroupBox4: TGroupbox;

Silt2: Tsilt;

Silt3: TLabel;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Silt4: TLabel;

Edit5: TEdit;

Silt5: TLabel;

Edit7: TEdit;

Silt7: TLabel;

F1Book1: TF1Book;

F1Book2: TF1Book;

F1Book3: TF1Book;

F1Book4: TF1Book;

Protseduur N1Klõpsake(Saatja: TOobject);

Protseduur N3Click(Saatja: TOobject);

Protseduur FormCreate(Saatja: TObject);

Protseduur N4Click(Saatja: TOobject);

Protseduur N5Click(Saatja: TOobject);

Privaatne

(eraavaldused)

Avalik

(Avalikud deklaratsioonid)

Lõpp;

konst

xmin:real=-20;

xmax:real=20;

Vorm1: Tvorm1;

X,y,t,a,b,cor:real;

I,n:täisarv;

Ebaõnnestumine:tekstifail;

rakendamine

($R *.dfm)

funktsioon f(x:real):real;

alustada

f:=(8+x)/(x*sqrt(sqr(x)-4));

lõpp;

funktsioon f1(x:real):real;

alustada

f1:=(-võimsus(x,3)-16*x*x+32)/(x*X*sqrt(võimsus(x*x-4,3)));

lõpp;

protseduur metoddix(ta,tb,eps:real;var xk:real;var kolvo: integer);

alustada

kolvo:=0;

korda

xk:=(ta+tb)/2;

kolvo:=kolvo+1;

Vorm1.F1book1.NumberRC:=xk;

Vorm1.F1raamat1.ArvRC:=f(xk);

kui f(ta)*f(xk)<0 then tb:=xk

else ta:=xk;

kuni (abs(f(xk))<=eps);

lõpp;

protseduur metodhord(ta,tb,eps:real;var xk:real;var kolvo: integer);

alustada

kolvo:=0;

korda

xk:= ta-f(ta)*(ta-tb)/(f(ta)-f(tb));

kolvo:=kolvo+1;

Vorm1.F1book2.NumberRC:=xk;

Vorm1.F1raamat2.NumberRC:=f(xk);

kui f(ta)*f(xk)<0 then tb:=xk

else ta:=xk;

kuni (abs(f(xk))<=eps);

lõpp;

protseduur metodnyutona(ta,eps:real;var xk:real;var kolvo: integer);

alustada

kolvo:=0;

korda

xk:= ta-f(ta)/f1(ta);

ta:=xk;

kolvo:=kolvo+1;

Vorm1.F1book3.NumberRC:=xk;

Vorm1.F1raamat3.NumberRC:=f(xk);

kuni (abs(f(xk))<=eps);

lõpp;

protseduur TForm1.N1Click(Saatja: TObject);

alustada

x:=xmin;

i:=0;

samas kui x<=xmax do

alustada

kui abs(x)>5, siis

Alusta

I:=i+1;

Y:=f(x);

Seeria1.Addxy(x,y);

F1book4.NumberRC:=x;

F1book4.NumberRC:=y;

Lõpp;

x:=x+0,5;

lõpp;

lõpp;

protseduur TForm1.N3Click(Saatja: TObject); // Juure arvutamine poolitamise meetodil

alustada

F1book1.ClearRange(1;1;100;2;3);

t:=strtofloat(Redigeeri1.Tekst);

a:=strtofloat(Redigeeri2.Tekst);

b:=strtofloat(Redigeeri3.Tekst);

metoddix(a,b,t,cor,n);

F1book4.TextRC:="dihhotoomia";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" iteratsioonide arv = ";

F1book4.NumberRC:=n;

Lisa (ebaõnnestumine);

Writeln(ebaõnnestumine);

Writeln(ebaõnnestumine," Arvutamine dihhotoomia meetodil ");

sulgefail(ebaõnnestumine);

lõpp;

protseduur TForm1.FormCreate(Saatja: TObject);

alustada

Assignfile(ebaõnnestumine," raport .txt");

Rewrite (ebaõnnestus);

Sulgefail(ebaõnnestumine);

lõpp;

protseduur TForm1.N4Click(Saatja: TObject); // Juure arvutamine akordmeetodil

alustada

F1book2.ClearRange(1;1;100;2;3);

t:=strtofloat(Redigeeri1.Tekst);

a:=strtofloat(Redigeeri5.Tekst);

b:=strtofloat(Redigeeri4.Tekst);

metodhord(a,b,t,cor,n);

F1book4.TextRC:=" akordid ";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" iteratsioonide arv = ";

F1book4.NumberRC:=n;

Assignfile(ebaõnnestumine," raport .txt");

Lisa (ebaõnnestumine);

Writeln(ebaõnnestumine);

Writeln(fail," Arvutamine akordimeetodil ");

writeln(ebaõnnestus,"Arvutamise täpsus = ",t:10:7);

Writeln(ebaõnnestumine,"Esialgne lähendus:a = ",a:8:3," b = ",b:8:3);

writeln(fail, " Juur leiti : x = ",cor:8:3, " y=f(x)= ",f(cor):8:6);

writeln(fail, "Iteratsioonide arv = ",n);

sulgefail(ebaõnnestumine);

lõpp;

protseduur TForm1.N5Click(Saatja: TObject); // Juure arvutamine Newtoni meetodil

alustada

F1book3.ClearRange(1,1,100;2,3);

t:=strtofloat(Redigeeri1.Tekst);

a:=strtofloat(Redigeeri7.Tekst);

metodnyutona(a,t,cor,n);

F1book4.TextRC:="Newton";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" iteratsioonide arv = ";

F1book4.NumberRC:=n;

Assignfile(ebaõnnestumine," raport .txt");

Lisa (ebaõnnestumine);

Writeln(ebaõnnestumine);

Writeln(ebaõnnestumine," Arvutamine Newtoni meetodil ");

writeln(ebaõnnestus,"Arvutamise täpsus = ",t:10:7);

Writeln(ebaõnnestumine,"Esialgne lähendus:a = ",a:8:3," b = ",b:8:3);

writeln(fail, " Juur leiti : x = ",cor:8:3, " y=f(x)= ",f(cor):8:6);

writeln(fail, "Iteratsioonide arv = ",n);

Sulgefail(ebaõnnestumine);

lõpp;

lõpp.

Rakenduse akna pilt

Esialgne liides näeb välja selline:

Pärast arvutuste tegemist kl E<= 0,001:

Fail “Raport. txt.":

Saadud tulemuste analüüs

Vastavalt matemaatilise paketi kursusetöö ülesandele leidsin mittelineaarse võrrandi ( x =-8) ja koostati graafik.

Arvutustabelites leiti võrrandi juur, kasutades kahte sisseehitatud võimalust "Parameter Selection" ja "Solution Search", samas kui "Lahendusotsing" andis siiski täpsema väärtuse. Tulemused langesid praktiliselt kokku aasta tulemustega Matlab.

Et leida keskkonnast juur Delfi kasutajal on võimalus sisestada arvutuse täpsust klaviatuurilt. Programmi testimine näitas, et sama etteantud arvutustäpsuse korral leiab Newtoni meetod soovitud väärtuse väiksema arvu iteratsioonidega.

Seega näitasid arvutused, et mittelineaarset võrrandit saab lahendada erinevates meediumites. Kõige töömahukamaks arvutuseks osutus keskkond Delfi.

Kirjandus.

1. Amosov A.A. ja muud arvutusmeetodid inseneridele M., Higher School, 1994.
2. Faronov V.V. Delfi. Programmeerimine kõrgetasemelises keeles

3. Walkenbach D . Microsoft Office Excel 2007.Kasutaja Piibel

Volkov V.B. Selge õpetus Excel 2010 jaoks

Matemaatika kui teadus tekkis seoses vajadusega lahendada praktilisi probleeme: mõõtmised maapinnal, navigeerimine jne. Sellest tulenevalt oli matemaatika arvmatemaatika ja selle eesmärk oli saada lahendus arvu kujul. Rakendusülesannete numbriline lahendamine on matemaatikuid alati huvitanud. Mineviku suurimad esindajad ühendasid oma uurimistöös loodusnähtuste uurimist, saades nende matemaatilise kirjelduse, s.o. tema matemaatiline mudel ja uurimistöö. Keeruliste mudelite analüüs eeldas ülesannete lahendamiseks spetsiaalsete, tavaliselt numbriliste meetodite loomist. Mõnede nende meetodite nimed näitavad, et nende väljatöötamisse olid kaasatud oma aja suurimad teadlased. Need on Newtoni, Euleri, Lobatševski, Gaussi, Tšebõševi, Hermiidi meetodid.

Praegust aega iseloomustab matemaatika rakenduste järsk laienemine, mis on suuresti seotud arvutitehnoloogia loomise ja arendamisega. Arvutite tuleku tulemusena on vähem kui 40 aastaga operatsioonide kiirus kasvanud 0,1 toimingult sekundis käsitsi arvutamisel 10 toiminguni sekundis tänapäevastel arvutitel.

Laialt levinud arvamus kaasaegsete arvutite kõikvõimsusest jätab mulje, et matemaatikud on vabanenud kogu probleemide arvulise lahendamisega kaasnevast sekeldusest ning uute lahendusmeetodite väljatöötamine pole enam nii oluline. Tegelikkuses on olukord erinev, kuna evolutsiooni vajadused seavad teadusele reeglina ülesandeid, mis on selle võimekuse piiril. Matemaatika rakendusvõimaluste avardumine tõi kaasa erinevate teadusharude matematiseerimise: keemia, majandusteadus, bioloogia, geoloogia, geograafia, psühholoogia, meditsiin, tehnika jne.

Võib tuvastada kaks asjaolu, mis algselt määrasid soovi teaduste matematiseerimiseks:

esiteks, ainult matemaatiliste meetodite kasutamine võimaldab anda ühe või teise materiaalse maailma nähtuse uurimisele kvantitatiivse iseloomu;

teiseks, ja see on peamine, ainult matemaatiline mõtteviis teeb objekti. Seda uurimismeetodit nimetatakse arvutuslikuks eksperimendiks, täiesti objektiivseks uuringuks.

Viimasel ajal on esile kerkinud veel üks tegur, millel on tugev mõju teadmiste matematiseerimise protsessidele. See on arvutitehnoloogia kiire areng. Arvutite kasutamine teaduslike, inseneri- ja üldkasutatavate probleemide lahendamisel põhineb täielikult nende matematiseerimisel.

Matemaatilised mudelid.

Kaasaegne tehnoloogia keeruliste probleemide uurimiseks põhineb uuritava matemaatiliste mudelite konstrueerimisel ja analüüsil, tavaliselt arvuti abil. Tavaliselt koosneb arvutuskatse, nagu me juba nägime, mitmest etapist: ülesande püstitamine, matemaatilise mudeli konstrueerimine (probleemi matemaatiline formuleerimine), numbrilise meetodi väljatöötamine, algoritmi väljatöötamine selle rakendamiseks. numbriline meetod, programmi arendamine, programmi silumine, arvutuste tegemine, tulemuste analüüsimine.

Seega on arvuti kasutamine mis tahes teadusliku või inseneriprobleemi lahendamiseks paratamatult seotud üleminekuga reaalselt protsessilt või nähtuselt selle matemaatilisele mudelile. Seega on mudelite kasutamine teaduslikus uurimistöös ja inseneripraktikas matemaatilise modelleerimise kunst.

Tavaliselt nimetatakse mudeliks kujuteldavat või materiaalselt realiseeritavat süsteemi, mis taastoodab antud nähtuse põhilisi, kõige olulisemaid tunnuseid.

Peamised nõuded matemaatilisele mudelile on adekvaatsus vaadeldava nähtusega, s.o. see peab piisavalt kajastama nähtuse iseloomulikke jooni. Samas peaks see olema suhteliselt lihtne ja uurimiseks kättesaadav.

Matemaatiline mudel peegeldab seost uuritava nähtuse esinemise tingimuste ja selle tulemuste vahel teatud matemaatilistes struktuurides. Kõige sagedamini kasutatakse selliste konstruktsioonidena järgmisi matemaatilisi mõisteid: funktsioon, funktsionaal, operaator, arvvõrrand, tavaline diferentsiaalvõrrand, osadiferentsiaalvõrrand.

Matemaatilised mudelid võib liigitada erinevate kriteeriumide järgi: staatilised ja dünaamilised, kontsentreeritud ja hajutatud; deterministlik ja tõenäosuslik.

Mõelge mittelineaarse võrrandi juurte leidmise probleemile

Võrrandi (1) juured on need x väärtused, mis asendamisel muudavad selle identiteediks. Ainult kõige lihtsamatele võrranditele on võimalik leida lahendus valemite kujul, s.t. analüütiline vorm. Sagedamini on vaja võrrandeid lahendada ligikaudsete meetodite abil, millest kõige levinumad on arvutite tuleku tõttu arvulised meetodid.

Ligikaudsete meetodite abil juurte leidmise algoritmi saab jagada kaheks etapiks. Esimesel etapil uuritakse juurte asukohta ja viiakse läbi nende eraldamine. Leitakse piirkond, kus eksisteerib võrrandi juur või alglähendus juurele x 0. Lihtsaim viis selle ülesande lahendamiseks on uurida funktsiooni f(x) graafikut. Üldjuhul on selle lahendamiseks vaja kasutada kõiki matemaatilise analüüsi vahendeid.

Vähemalt ühe võrrandi (1) juur olemasolu leitud segmendis tuleneb Bolzano tingimusest:

f(a)*f(b)<0 (2)

See tähendab, et funktsioon f(x) on sellel intervallil pidev. See tingimus ei vasta aga küsimusele võrrandi juurte arvu kohta antud segmendil. Kui funktsiooni jätkuvuse nõuet täiendada selle monotoonsuse nõudega ja see tuleneb esimese tuletise märgi püsivusest, siis saame väita ühe juure olemasolu antud lõigul.

Juurte lokaliseerimisel on oluline teada ka seda tüüpi võrrandi põhiomadusi. Näiteks tuletame meelde mõningaid algebraliste võrrandite omadusi:

kus on tegelikud koefitsiendid.

• a) N-astme võrrandil on n juurt, mille hulgas võib olla nii reaal- kui ka kompleksvõrrand. Komplekssed juured moodustavad keerukaid konjugaatpaare ja seetõttu on võrrandis paarisarv selliseid juuri. Kui n on paaritu, on olemas vähemalt üks reaaljuur.
• b) Positiivsete reaaljuurte arv on väiksem või võrdne muutujamärkide arvuga koefitsientide jadas. X asendamine -x-ga võrrandis (3) võimaldab meil hinnata negatiivsete juurte arvu samal viisil.

Võrrandi (1) lahendamise teises etapis konstrueeritakse saadud esialgse lähenduse abil iteratiivne protsess, mis võimaldab täpsustada juure väärtust teatud etteantud täpsusega. Iteratiivne protsess koosneb esialgse lähenduse järjestikusest täpsustamisest. Iga sellist sammu nimetatakse iteratsiooniks. Iteratsiooniprotsessi tulemusena leitakse võrrandi juurte ligikaudsete väärtuste jada. Kui see jada läheneb n-i kasvades juure x tegelikule väärtusele, siis iteratiivne protsess läheneb. Väidetavalt läheneb iteratiivne protsess vähemalt järku m, kui on täidetud järgmine tingimus:

kus C>0 on mingi konstant. Kui m=1, siis räägime esimest järku konvergentsist; m=2 - umbes ruutkeskmine, m=3 - umbes kuupkonvergents.

Iteratiivsed tsüklid lõpevad, kui antud lubatud vea korral on täidetud absoluutsete või suhteliste hälvete kriteeriumid:

või väike lahknevus:

See töö on pühendatud Newtoni meetodi abil mittelineaarsete võrrandite lahendamise algoritmi uurimisele.

Mittelineaarsete võrrandite lahendamiseks on palju erinevaid meetodeid, mõned neist on toodud allpool:

• 1)Iteratsioonimeetod. Mittelineaarse võrrandi lahendamisel iteratsioonimeetodil kasutame võrrandit, mis on kirjutatud kujul x=f(x). Määratakse argumendi algväärtus x 0 ja täpsus e Lahenduse x 1 esimene lähendus leitakse avaldisest x 1 =f(x 0), teine ​​- x 2 =f(x 1) jne. . Üldjuhul leiame i+1 lähenduse valemi xi+1 =f(xi) abil. Kordame seda protseduuri kuni |f(xi)|>e. Iteratsioonimeetodi lähenemise tingimus |f"(x)|
• 2)Newtoni meetod. Mittelineaarse võrrandi lahendamisel Newtoni meetodil määratakse argumendi algväärtus x 0 ja täpsus e. Seejärel joonistame punktis (x 0 ,F(x 0)) graafiku F(x) puutuja ja määrake puutuja lõikepunkt abstsissteljega x 1 . Punktis (x 1 ,F(x 1)) konstrueerime uuesti puutuja, leiame soovitud lahendi x 2 järgmise lähenduse jne. Kordame seda protseduuri kuni |F(xi)| > e. X-telje puutuja lõikepunkti (i+1) määramiseks kasutame järgmist valemit

x i+1 =x i -F(x i) F"(x i).

Tingimus puutujameetodi F(x 0) F""(x)>0 konvergentsile jne.

3). Dihhotoomia meetod. Lahendustehnika taandub esialgse määramatuse intervalli järkjärgulisele jagamisele pooleks vastavalt valemile

C k = a k + b k /2.

Kahe saadud segmendi hulgast vajaliku valimiseks on vaja leida saadud segmentide otstest funktsiooni väärtus ja arvestada sellega, mille korral funktsioon märki muudab, st tingimust f ( a k) * f (in k) peab olema täidetud<0.

Segmendi jagamise protsess viiakse läbi seni, kuni praeguse mõõtemääramatuse intervalli pikkus on väiksem kui määratud täpsus, see tähendab k - a k< E. Тогда в качестве приближенного решения уравнения будет точка, соответствующая середине интервала неопределённости.

4). Akordi meetod. Meetodi idee seisneb selles, et lõigule konstrueeritakse kõõl, mis ühendab funktsiooni y=f(x) graafiku kaare otsad ja punkti c, kõõlu lõikepunkti x-ga. telg, peetakse juure ligikaudseks väärtuseks

c = a - (f(a)Х (a-b)) / (f(a) - f(b)),

c = b - (f(b)Х (a-b)) / (f(a) - f(b)).

Järgmist lähendust otsitakse intervalli järgi või sõltuvalt funktsiooni väärtuste märkidest punktides a, b, c

x*O, kui f(c)H f(a) > 0;

x* O, kui f(c)Х f(b)< 0 .

Kui f"(x) ei muuda märki , siis tähistades c=x 1 ja võttes esialgseks lähenduseks a või b, saame akordimeetodi iteratiivsed valemid fikseeritud parem- või vasakpoolse punktiga.

x 0 =a, x i+1 = x i - f(x i)(b-x i) / (f(b)-f(x i), kus f "(x)Х f "(x) > 0;

x 0 =b, x i+1 = x i - f(x i)(x i -a) / (f(x i)-f(a), kus f "(x)Х f "(x)< 0 .

Akordimeetodi lähenemine on lineaarne

Algebralised ja transtsendentaalsed võrrandid. Juurte lokaliseerimise meetodid.

Mittelineaarse võrrandi kõige üldisem vorm:

f(x)=0 (2.1)

kus on funktsioon f(x) defineeritud ja pidev lõplikul või lõpmatul intervallil [a, b].

Definitsioon 2.1. Mis tahes arv, mis inverteerib funktsiooni f(x) nullini nimetatakse võrrandi (2.1) juureks.

Definitsioon 2.2. Arvu nimetatakse kordsuse k-ndaks juureks koos funktsiooniga f(x) selle tuletised kuni (k-1) järku (kaasa arvatud) on võrdsed nulliga:

Definitsioon 2.3. Ühtset juurt nimetatakse lihtsaks.

Ühe muutujaga mittelineaarsed võrrandid jagunevad algebralisteks ja transtsendentaalseteks.

Definitsioon 2.4 . Võrrandit (2.1) nimetatakse algebraliseks, kui funktsioon F(x) on algebraline.

Algebraliste teisenduste abil saab mis tahes algebralisest võrrandist saada kanoonilise vormi võrrandi:

kus on võrrandi tegelikud koefitsiendid, x on tundmatu.

Algebrast on teada, et igal algebralisel võrrandil on vähemalt üks reaalne või kaks keerulist konjugaatjuurt.

Definitsioon 2.5. Võrrandit (2.1) nimetatakse transtsendentaalseks, kui funktsioon F(x) ei ole algebraline.

Võrrandi (2.1) lahendamine tähendab:

• 1. Määrake, kas võrrandil on juured.
• 2. Määrake võrrandi juurte arv.
• 3. Leidke võrrandi juurte väärtused etteantud täpsusega.

Praktikas esinevaid võrrandeid ei saa sageli analüütiliste meetoditega lahendada. Selliste võrrandite lahendamiseks kasutatakse numbrilisi meetodeid.

Algoritm võrrandi juure leidmiseks numbrilise meetodi abil koosneb kahest etapist:

• 1) osakond või lokaliseerimine juur, st. ühe juure sisaldava tühimiku loomine:
• 2) selgitus juurväärtused, kasutades järjestikuste lähenduste meetodit.

Juurte lokaliseerimise meetodid. Teoreetiline alus Juureeraldusalgoritm põhineb Cauchy teoreemil pideva funktsiooni vaheväärtuste kohta.

Teoreem 2.1. Kui funktsioon y = f(x) on pidev lõigul [a,b] ja f(a)=A, f(b)=B, siis iga punkti C jaoks, mis asub A ja B vahel, on punkt, mis .

Tagajärg. Kui funktsioon y = f(x) on lõigul [a,b] pidev ja omandab selle otstes erinevate märkide väärtused, siis on sellel vähemalt üks juur võrrandist f(x) = 0 segment.

Olgu funktsiooni määratluse ja pidevuse valdkond lõplik segment [a,b]. Jagage segment osadeks n osad: ,

Funktsiooni väärtusi punktides järjestikku arvutades leiame sellised segmendid, mille jaoks tingimus on täidetud:

need. , või, . Need segmendid sisaldavad vähemalt ühte juurt.

Teoreem 2.2. Kui funktsioon y = f(x) on pidev intervallil [a;b], siis f(a)f(b)<0 и f`(х) на интервале (а;b) сохраняет знак, то внутри отрезка [а;b] существует единственный корень уравнения f(х) = 0.

Juurte eraldamiseks saab kasutada ka funktsiooni graafikut juures=f (X). Võrrandi (2.1) juurteks on need väärtused X, mille juures funktsiooni y=f(x) graafik lõikub abstsissteljega. Funktsiooni graafiku joonistamine isegi madala täpsusega annab tavaliselt aimu võrrandi (2.1) juurte asukohast. Kui funktsiooni y=f(x) joonistamine on keeruline, tuleks algne võrrand (2.1) teisendada kujule ts1(x)= q2(x) nii et funktsioonide graafikud juures= ts1(x) Ja juures= q2(x) olid üsna lihtsad. Nende graafikute lõikepunktide abstsissid on võrrandi (2.1) juured.

Näide 1. Eraldage võrrandi x 2 -2cosx=0 juured.

Lahendus. Vaatame juurte eraldamiseks kahte võimalust.

• a) Graafiline meetod. Kirjutame võrrandi ümber kujul x 2 =2cosx ja joonistame funktsioonid y=x2 ja y=2cosx samasse koordinaatsüsteemi (joonis 5). kuna need graafikud ristuvad kahes punktis, on võrrandil kaks juurt, mis paiknevad intervallidel (-/2; 0) ja (0; /2) sümmeetriliselt alguspunkti suhtes.
• b) Analüütiline meetod. Lase f(x)= x 2-2cosx. Sest f(x) on paarisfunktsioon, siis piisab, kui arvestada ainult x mittenegatiivseid väärtusi. Ebavõrdsuse tõttu 2cosx2

Tuletis f"(x)=2(x+sinx). Intervallil (0; /2) f"(x)>0, seega f(x) siin suureneb see monotoonselt ja selle graafik võib ületada telje X mitte rohkem kui ühes punktis. Märka seda f(0)=- 2<0, аf(/2)=(/2) 2 > 0. Seega on võrrandil üks positiivne juur, lamades intervallil (0; /2). Funktsiooni paarsuse tõttu on võrrandil ka üks negatiivne juur, mis on sümmeetriline positiivsega. Liigume nüüd juure selgitamise juurde. Juurselgituse kombineeritud meetodi kasutamiseks peate selles veenduma f ""(x) on (0; /2) säilitab märgi ja vali tangensimeetodi rakendamiseks juure esialgne lähendus. See peab vastama tingimusele: f(x)f ""(x)>0. Sest f ""(x)=2(1+cosx) on positiivne , siis /2 võib võtta puutujameetodis juure esialgseks lähenduseks. Seetõttu võime panna x=/21,570796, x 1 =0 (vt algoritmi diagrammi). Meie puhul annab akordimeetod puudujäägiga juure ligikaudse väärtuse ja puutujameetod liigväärtuse.

Vaatleme juure täpsustamise üht iteratiivset sammu. Arvutame väärtused f(0), f(/2), f"(/2). Uued väärtused x 1 Ja x leiame vastavalt valemite abil:

|x-x 1 |=0,387680,4>10 -4 =.

Määratud täpsust ei saavutatud ja arvutusi tuleb jätkata.

Iteratsiooni number	x 1		f(x 1 )			|x-x 1 |

Järelikult leiti kolme iteratsiooni tulemusena vajaliku täpsusega juure ligikaudne väärtus ja see on ligikaudu võrdne 1,0217-ga.

Funktsiooni graafiku sümmeetria tõttu f(x) teise juure väärtus on ligikaudu võrdne -1,0217.

Juure selgitamine.

Probleemi sõnastamine . Oletame, et võrrandi (2.1) soovitud juur on eraldatud, s.o. leitud segment [a; b], millel on üks ja ainult üks võrrandi juur. Selle lõigu mis tahes punkti võib võtta juure ligikaudse väärtusena. Sellise lähenduse viga ei ületa pikkust [A; b]. Järelikult taandub antud täpsusega juure ligikaudse väärtuse leidmise ülesanne lõigu [a; b] (b - a<), содержащего только один корень уравнения (2.1). Эту задачу обычно называют задачей juure selgitamine.

Numbriliste meetodite kirjeldus. Numbrilised meetodid võimaldavad leida lahendusi teatud probleemidele, teades ette, et saadud tulemused arvutatakse teatud veaga, mistõttu on paljude numbriliste meetodite puhul vaja eelnevalt teada saada, millisele „täpsustaset“ saadud lahendus saavutab. vastama.

Sellega seoses on probleemiks vormi (3.1) polünoomi juurte leidmine

pakub erilist huvi, sest Isegi kuupvõrrandi juurte leidmise valemid on üsna keerulised. Kui teil on vaja leida polünoomi juured, mille aste on näiteks 5, siis ei saa te ilma numbriliste meetoditeta hakkama, eriti kuna sellisel polünoomil on tõenäosus, et sellel on looduslikud juured (kas täisarv või täpsed juured, millel on " lühike" murdosa) on üsna väike ja 4-st suurema astme võrrandi juurte leidmiseks pole valemeid. De facto vähendatakse kõiki edasisi toiminguid ainult juurte selgitamine, mille intervallid on ligikaudu ette teada. Lihtsaim viis nende "ligikaudsete" juurte leidmiseks on kasutada graafilisi meetodeid.

Polünoomi juurte leidmiseks on mitmeid arvulisi meetodeid: iteratsioonimeetod, akordide ja puutujate meetod, poolitamise meetod, sekantsi meetod.

Poolitamise meetod(tuntud ka kui “poolitamise meetod”) on samuti rekursiivne, s.t. näeb ette kordamise, võttes arvesse saadud tulemusi.

Poolitamise meetodi olemus on järgmine:

• - funktsioon F(x) on antud;
• - määratakse lubatud viga Q;
• - määratletakse teatud intervall [a, b], mis sisaldab täpselt võrrandi lahendit.

1) Arvutame E-koordinaadi väärtuse, võttes lõigu keskkoha, s.o.

E= (a + b) / 2 (3.2)

• 2) Arvutame F(a), F(b), F(E) väärtused ja teostame järgmise kontrolli: Kui F(E)>Q, siis on juur leitud määratud täpsusega. Kui F(E)
• 3) Mine punkti 1 juurde.

Lihtsate iteratsioonide meetod (järjestikuste lähenduste meetod). Asendame võrrandi (2.1) samaväärse võrrandiga

x=(x) (3.3)

saab teha näiteks mitmel viisil

x=x+сf(x), c0. (3.4)

Oletame, et on valitud võrrandi (3.3) juure algne lähendus. Määrame valemite abil numbrijada

X n+1 =(x n ), n=0,1,2,… (3.5)

Seda jada nimetatakse iteratiivseks.

Kui lõigul, mis sisaldab x 0 ja kõiki järgnevaid lähendusi x n, nN, on funktsioonil (x) pidev tuletis "(x) ja |"(x)|q<1, то итерационная последовательность (3.5) сходится к единственному на корню уравнения (3.3). Скорость сходимости определяется неравенством

Eelkõige sellest ebavõrdsusest järeldub, et lihtsa iteratsioonimeetodi konvergentsi kiirus sõltub q väärtusest: mida väiksem q, seda kiirem on konvergents.

Sellest tulenevalt on praktikas lihtsa iteratsioonimeetodi abil juurte leidmisel soovitav võrrand (2.1) esitada kujul (3.3) nii, et tuletis "(x) juure läheduses absoluutväärtuses on võib-olla väiksem. Selleks kasutatakse mõnikord valemi parameetrit c (3.4).

Newtoni meetod (tangentmeetod). Kui on teada piisavalt hea alglähendus, mille kohta ebavõrdsus kehtib:

siis saate Newtoni valemi abil arvutada võrrandi ainsa juure

Intervalli piire saab kasutada esialgse ligikaudsusena ja:

Kui sees.

Selle meetodi iga iteratsiooni korral on arvutuste arv suurem kui poolitamise ja iteratsiooni meetodite puhul, kuna lisaks funktsiooni väärtusele on vaja leida ka selle tuletis. Newtoni meetodi lähenemismäär on aga palju suurem.

Teoreem. Olgu võrrandi juur, st. , ja on pidev. Siis on juure naabrus, nii et kui esialgne lähendus kuulub sellesse naabrusse, siis Newtoni meetodi puhul läheneb väärtusjada at-le. Juurlähenduse viga saab hinnata järgmise valemi abil:

kus on segmendi teise tuletise mooduli suurim väärtus, on segmendi esimese tuletise mooduli väikseim väärtus.

Peatusreegel:

Akordide ja puutujate meetod (kombineeritud). See meetod põhineb funktsiooni skemaatilise graafiku koostamisel, selle abstsissteljega lõikumise intervallide määramisel ja selle intervalli järgneval "tihendamisel", kasutades selle funktsiooni graafiku konstrueeritud akorde ja puutujaid.

Tuleb märkida, et on olemas ka eraldi akordimeetodid (annab tüviväärtuse defitsiidiga) ja puutujameetod (ülejäägiga). Kombineeritud meetodi eeliseks on aga kõnealuse segmendi "kahepoolne kokkusurumine".

Mõelge järgmisele juhtumile:

• - antakse funktsioon F(x) ja joonistatakse selle graafik;
• - määratakse lubatud viga Q
• - graafiku põhjal määratakse segment, millel funktsiooni graafik lõikub abstsissteljega, seega on sellel lõigul kõnealuse polünoomi juur (tähistame seda A-ga)

Edasine algoritm taandub järgmistele etappidele:

• 1) konstrueerida punktis F(b) oleva funktsiooni graafiku puutuja
• 2) arvutab valemi (3.9) abil puutuja ja abstsisstelje lõikepunkti x-koordinaat ja tähistab seda tähega b"
• 3) konstrueerib punkte F(a) ja F(b) läbiva funktsiooni graafikule akord.
• 4) Arvutame valemi (2) abil kõõlu ja abstsisstelje lõikepunkti ja tähistame seda tähega a".

Seega saame uue lõigu, mis (akordi ja puutuja definitsioonide järgi) sisaldab veel võrrandi A lahendit.

Nüüd võtame lõigu uue lõiguna ja kordame samme 1-4, kuni erinevus F(b)-F(a) muutub väiksemaks kui algselt määratud viga Q. Samuti märgime, et pärast seda on soovitatav võtta aritmeetiline keskmine F kui soovitud lahendus (a) ja F (b).

Seega, kui akord (puutuja) annab juure väärtuse koos liiaga, siis võetakse see juur uueks parempoolseks piiriks ja kui puudujäägiga, siis vasakpoolseks. Mõlemal juhul asub täpne juur kõõlu ja x-telje puutuja lõikepunktide vahel.

Märkus akordide ja puutujate meetodi kohta. Kuna ülesande lahendamine eeldab funktsiooni F(x) tuletise leidmist, on akordide ja puutujate meetodit tarkvara tasemel üsna keeruline realiseerida, sest tuletisinstrumentide arvutamise reeglid üldkujul on arvutist “mõistmiseks” üsna tülikad; Polünoomi iga astme tuletise otse määramisel koormatakse tõsiselt arvuti mälu, mis aeglustab oluliselt tööd ning funktsiooni ja vastavalt ka selle tuletise määramine otse programmikoodis on vastuvõetamatu. Kuid seda meetodit kasutades toimub intervalli lähenemine juurele kõige kiiremini, eriti kui kombineerite akordide ja puutujate meetodit poolitusmeetodiga, sest uue segmendi keskpaik annab sageli täiesti rahuldava lahenduse.

Sekantne meetod. Sekantmeetodi saab Newtoni meetodist, asendades tuletise ligikaudse avaldisega - erinevuse valemiga:

Valem (3.8) kasutab kahte eelmist lähendust ja. Seetõttu on antud algväärtuse jaoks vaja arvutada järgmine lähendus, näiteks Newtoni meetodi abil tuletise ligikaudse asendamisega vastavalt valemile

Sekantse meetodi algoritm:

1) täpsustatakse algväärtus ja viga. Arvutame

2) eest n= 1,2, ..... kui tingimus on täidetud, arvutame selle valemi (3.8) abil.

Võrrandit nagu F(x)=0 või x=f(x) nimetatakse mittelineaarseks. Võrrandi lahendamine tähendab x leidmist nii, et võrrand muutub identiteediks. Üldiselt võib võrrandil olla 0; 1; 2;...∞ juured. Allpool käsitletud numbrilised meetodid mittelineaarsete võrrandite lahendamiseks võimaldavad leida antud intervallil ühe juure. Sel juhul peaks intervallil olema ainult üks juur. Vaatleme mitmeid mittelineaarsete võrrandite lahendamise meetodeid.

1. Toore jõu meetod. Mittelineaarse võrrandi lahendamisel toore jõu meetodil määratakse argumendi x=a algväärtus ja samm h, mis määrab ka mittelineaarvõrrandi juurte leidmise täpsuse. Kui tingimus F(x)*F(x+h)>0 on täidetud, suurendame argumenti x sammu h (x=x+h) võrra. Kui korrutis F(x)*F(x+h) muutub negatiivseks, siis on sellel intervallil võrrandi lahend. Meetodi struktuuriskeem on näidatud joonisel.

   
   

2. Pooljagamise meetod. Mittelineaarse võrrandi lahendamisel poolitamise meetodil määratakse intervall ε, milles on ainult üks lahend ja soovitud täpsus ε. Seejärel määratakse intervalli c=(a+b)/2 keskpunkt ja kontrollitakse tingimust F(a)∙F(c)<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=c). Если условие не выполняется, то в среднюю точку переносим левую границу(a=c). Деление отрезка пополам продолжается пока |b-a|>ε. Struktuuriskeem mittelineaarsete võrrandite lahendamiseks poolitamise meetodil on näidatud joonisel.

   Kuigi |b-a|>ε
   F(a)∙F(c)<0

   
   

   Riis. Struktogramm poolitamise meetodi jaoks

3. Akordi meetod. Mittelineaarse võrrandi lahendamisel akordmeetodil määratakse intervall , millel on ainult üks lahend, ja täpsus ε. Seejärel joonistame läbi kahe punkti koordinaatidega (a,F(a)) ja (b,F(b)) sirgjoone lõigu (kõla) ja määrame selle sirge lõikepunkti abstsissteljega (punkt c ). Kui sel juhul F(a)∙F(c)<0, то правую границу интервала переносим в точку с (b=c). Если указанное условие не выполняется, то в точку c intervalli vasak piir kantakse üle (a=c). Lahenduse otsimine peatub, kui määratud täpsus |F(c)|< ε. Для определения точки пересечения хорды с осью абсцисс воспользуемся следующей формулой (proovige valemit ise saada).Akordimeetodi struktuuriskeem on näidatud joonisel.

   Kuigi |F(c)|>ε
   F(a)∙F(c)<0

   
   

   Riis. Struktogramm akordimeetodi jaoks

4. Tangent meetod. Mittelineaarse võrrandi lahendamisel puutujameetodil määratakse argumendi algväärtus x 0 ja täpsus ε. Seejärel joonistame punktis (x 0 ,F(x 0)) graafikule F(x) puutuja ja määrame puutuja lõikepunkti x 1 teljega. Punktis (x 1 ,F(x 1)) konstrueerime uuesti puutuja, leiame soovitud lahendi x 2 järgmise lähenduse jne. Kordame seda protseduuri kuni |F(x i)| > ε. Puutuja ja abstsisstelje lõikepunkti (i+1) määramiseks kasutame järgmist valemit (hankige valem ise). Tangensimeetodi lähenemise tingimus on F(x 0)∙F""(x 0)>0. Struktuuriskeem mittelineaarsete võrrandite lahendamiseks puutujameetodiga on näidatud joonisel fig.

   
   

5. Akordi puutuja meetod. Kui puutujameetodis asendada funktsiooni F"(x i) tuletis lõplike sammude suhtega, siis saame akord-tangensi meetodi arvutusvalemi . Selle meetodi arvutuste tegemise protseduur on sarnane varem käsitletule.
6. Iteratsioonimeetod. Mittelineaarse võrrandi lahendamisel iteratsioonimeetodil kasutame võrrandit, mis on kirjutatud kujul x=f(x). Määratakse argumendi algväärtus x 0 ja täpsus ε. Lahenduse x 1 esimene lähendus leitakse avaldisest x 1 =f(x 0), teine ​​- x 2 =f(x 1) jne. Üldjuhul leiame i+1 lähenduse valemiga x i +1 =f(x i). Kordame seda protseduuri kuni |f(x i)|>ε. Iteratsioonimeetodi lähenemise tingimus |f"(x)|<1. Структограмма метода итераций показана на рис.

   
   

Testi ülesanne. Laboratoorsed tööd 4.

Mittelineaarsete võrrandite lahendamine.

Harjutus. Lahendage tabelis näidatud mittelineaarne võrrand. meetodid, olles eelnevalt kindlaks määranud intervalli, millel võrrandi lahendus eksisteerib. Kontrollige lahendust.

Võrrandite variandid ja nende lahendamise meetodid on toodud tabelis.

Võrrandite variandid ja nende lahendamise meetodid

	Võrrand	Lahendusmeetodid
		katkimine ja akordid
		Loendus ja puutujad
		Loendus- ja akordi puutujad
		Loendamine ja poolitamine
		katkimine ja akordid
		Loendus ja puutujad
		Loendus- ja akordi puutujad
		Loendamine ja poolitamine
		katkimine ja akordid
		Loendus ja puutujad
		Loendus- ja akordi puutujad
		Loendamine ja poolitamine
		katkimine ja akordid
		Loendus ja puutujad
		Loendus- ja akordi puutujad
		Loendamine ja poolitamine
		katkimine ja akordid
		Loendus ja puutujad
	x 2 =exp(-x 2)-1	Loendus- ja akordi puutujad
		Loendamine ja poolitamine
		katkimine ja akordid
		Loendus ja puutujad
		Loendus- ja akordi puutujad
		Loendamine ja poolitamine

1. Pealkiri, töö eesmärk ja ülesanne.
2. Matemaatiline kirjeldus, algoritm (struktogramm) ja programmi tekst.
3. Arvutustulemused, kontrollimine ja järeldused töö kohta.

Mõelge mittelineaarse võrrandi juurte leidmise probleemile

Võrrandi (1) juured on need x väärtused, mis asendamisel muudavad selle identiteediks. Ainult kõige lihtsamatele võrranditele on võimalik leida lahendus valemite kujul, s.t. analüütiline vorm. Sagedamini on vaja võrrandeid lahendada ligikaudsete meetodite abil, millest kõige levinumad on arvutite tuleku tõttu arvulised meetodid.

Ligikaudsete meetodite abil juurte leidmise algoritmi saab jagada kaheks etapiks. Esimesel etapil uuritakse juurte asukohta ja viiakse läbi nende eraldamine. Leitakse piirkond, kus eksisteerib võrrandi juur või alglähendus juurele x 0. Lihtsaim viis selle ülesande lahendamiseks on uurida funktsiooni f(x) graafikut. Üldjuhul on selle lahendamiseks vaja kasutada kõiki matemaatilise analüüsi vahendeid.

Vähemalt ühe võrrandi (1) juur olemasolu leitud segmendis tuleneb Bolzano tingimusest:

f(a)*f(b)<0 (2)

See tähendab, et funktsioon f(x) on sellel intervallil pidev. See tingimus ei vasta aga küsimusele võrrandi juurte arvu kohta antud segmendil. Kui funktsiooni jätkuvuse nõuet täiendada selle monotoonsuse nõudega ja see tuleneb esimese tuletise märgi püsivusest, siis saame väita ühe juure olemasolu antud lõigul.

Juurte lokaliseerimisel on oluline teada ka seda tüüpi võrrandi põhiomadusi. Näiteks tuletame meelde mõningaid algebraliste võrrandite omadusi:

kus on tegelikud koefitsiendid.

• a) N-astme võrrandil on n juurt, mille hulgas võib olla nii reaal- kui ka kompleksvõrrand. Komplekssed juured moodustavad keerukaid konjugaatpaare ja seetõttu on võrrandis paarisarv selliseid juuri. Kui n on paaritu, on olemas vähemalt üks reaaljuur.
• b) Positiivsete reaaljuurte arv on väiksem või võrdne muutujamärkide arvuga koefitsientide jadas. X asendamine -x-ga võrrandis (3) võimaldab meil hinnata negatiivsete juurte arvu samal viisil. iteratsioon Newtoni dihhotoomia mittelineaarne

Võrrandi (1) lahendamise teises etapis konstrueeritakse saadud esialgse lähenduse abil iteratiivne protsess, mis võimaldab täpsustada juure väärtust teatud etteantud täpsusega. Iteratiivne protsess koosneb esialgse lähenduse järjestikusest täpsustamisest. Iga sellist sammu nimetatakse iteratsiooniks. Iteratsiooniprotsessi tulemusena leitakse võrrandi juurte ligikaudsete väärtuste jada. Kui see jada läheneb n-i kasvades juure x tegelikule väärtusele, siis iteratiivne protsess läheneb. Väidetavalt läheneb iteratiivne protsess vähemalt järku m, kui on täidetud järgmine tingimus:

kus C>0 on mingi konstant. Kui m=1, siis räägime esimest järku konvergentsist; m=2 - umbes ruutkeskmine, m=3 - umbes kuupkonvergents.

Iteratiivsed tsüklid lõpevad, kui antud lubatud vea korral on täidetud absoluutsete või suhteliste hälvete kriteeriumid:

või väike lahknevus:

See töö on pühendatud Newtoni meetodi abil mittelineaarsete võrrandite lahendamise algoritmi uurimisele.