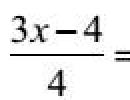When calculating a definite integral, we do not always obtain an exact solution. Representation in the form of an elementary function is not always possible. The Newton-Leibniz formula is not suitable for calculation, so numerical integration methods must be used. This method allows you to obtain data with high accuracy. Simpson's method is just that.

To do this, it is necessary to give a graphical representation of the derivation of the formula. The following is a record of the absolute error estimate using the Simpson method. In conclusion, we will compare three methods: Simpson, rectangles, trapezoids.

Parabola method - essence, formula, assessment, errors, illustrations

A function of the form y = f (x) is given, which has continuity on the interval [ a ; b ] , it is necessary to calculate the definite integral ∫ a b f (x) d x

It is necessary to split the segment [a; b ] into n segments of the form x 2 i - 2 ; x 2 i , i = 1 , 2 , . . . , n with length 2 h = b - a n and points a = x 0< x 2 < x 4 < . . . < x 2 π - 2 < x 2 π = b . Тогда точки x 2 i - 1 , i = 1 , 2 , . . . , n считаются серединами отрезков x 2 i - 2 ; x 2 i , i = 1 , 2 , . . . , n . Данный случай показывает, что определение узлов производится через x i = a + i · h , i = 0 , 1 , . . . , 2 n .

Each interval x 2 i - 2 ; x 2 i , i = 1 , 2 , . . . , n of the integrand is approximated using a parabola defined by y = a i x 2 + b i x + c i passing through points with coordinates x 2 i - 2 ; f (x 2 i - 2) , x 2 i - 1 ; x 2 i - 1 , x 2 i ; f (x 2 i) . That's why the method has this name.

These actions are performed in order to take the integral ∫ x 2 i - 2 x 2 i a i x 2 + b i x + c i d x as an approximate value ∫ x 2 i - 2 x 2 i f (x) d x . We can calculate using the Newton-Leibniz formula. This is the essence of the parabola method. Consider the figure below.

Graphic illustration of the parabola method (Simpson)

The red line shows the graph of the function y = f (x), and the blue line shows the approximation of the graph y = f (x) using quadratic parabolas.

Based on the fifth property of the definite integral, we obtain ∫ a b f (x) d x = ∑ i = 1 n ∫ x 2 i - 2 x 2 i f (x) d x ≈ ∑ i = 1 n ∫ x 2 i - 2 x 2 i (a i x 2 + b i x + c i) d x

In order to obtain the formula using the parabola method, it is necessary to perform the following calculation:

∫ x 2 i - 2 x 2 i (a i x 2 + b i x + c i) d x

Let x 2 i - 2 = 0 . Consider the figure below.

Let us depict that through the points with coordinates x 2 i - 2 ; f (x 2 i - 2) , x 2 i - 1 ; x 2 i - 1 , x 2 i ; f (x 2 i) can pass through one quadratic parabola of the form y = a i x 2 + b i x + c i . In other words, it is necessary to prove that the coefficients can only be determined in a single way.

We have that x 2 i - 2 ; f (x 2 i - 2) , x 2 i - 1 ; x 2 i - 1 , x 2 i ; f (x 2 i) are points of the parabola, then each of the presented equations is valid. We get that

a i (x 2 i - 2) 2 + b i x 2 i - 2 + c i = f (x 2 i - 2) a i (x 2 i - 1) 2 + b i x 2 i - 1 + c i = f ( x 2 i - 1) a i (x 2 i) 2 + b i x 2 i + c i = f (x 2 i)

The resulting system is resolved with respect to a i, b i, c i, where it is necessary to look for the determinant of the matrix according to Vandermonde. We get that

(x 2 i - 2) 2 x 2 i - 2 1 x 2 i - 1) 2 x 2 i - 1 1 (x 2 i) 2 x 2 i 1 , and it is considered non-zero and does not coincide with the points x 2 i - 2 , x 2 i - 1 , x 2 i . This is a sign that the equation has only one solution, then the selected coefficients a i ; b i ; c i can only be determined in a unique way, then through the points x 2 i - 2 ; f (x 2 i - 2) , x 2 i - 1 ; x 2 i - 1 , x 2 i ; f (x 2 i) only one parabola can pass through.

We can proceed to finding the integral ∫ x 2 i - 2 x 2 i (a i x 2 + b i x + c i) d x.

It's clear that

f (x 2 i - 2) = f (0) = a i 0 2 + b i 0 + c i = c i f (x 2 i - 1) = f (h) = a i h 2 + b i h + c i f ( x 2 i) = f (0) = 4 a i h 2 + 2 b i h + c i

To carry out the last transition, it is necessary to use an inequality of the form

∫ x 2 i - 2 x 2 i (a i x 2 + b i x + c i) d x = ∫ 0 2 h (a i x 2 + b i x + c i) d x = = a i x 3 3 + b i x 2 2 + c i x 0 2 h = 8 a i h 3 3 + 2 b i h 2 + 2 c i h = = h 3 8 a i h 2 + 6 b i h + 6 c i = h 3 f x 2 i - 2 + 4 f 2 2 i - 1 + f x 2 i

So, we get the formula using the parabola method:

∫ a b f (x) d x ≈ ∑ i = 1 n ∫ x 2 i - 2 x 2 i a i x 2 + b i x + c i d x = = ∑ i = 1 n h 3 (f (x 2 i - 2) + 4 f (x 2 i - 1) + f (x 2 i)) = = h 3 f (x 0) + 4 f (x 1) + f (x 2) + f (x 2) + 4 f (x 3) + f (x 4) + . . . + + f (x 2 n - 2) + 4 f (x 2 n - 1) + f (x 2 n) = = h 3 f (x 0) + 4 ∑ i = 1 n f (x 2 i - 1) + 2 ∑ i = 1 n - 1 f (x 2 i) + f (x 2 n)

Definition 1

The formula for Simpson's method is ∫ a b f (x) d x ≈ h 3 f (x 0) + 4 ∑ i = 1 n f (x 2 i - 1) + 2 ∑ i = 1 n - 1 f (x 2 i) + f (x 2 n) .

The formula for estimating the absolute error has the form δ n ≤ m a x [ a ; b ] f (4) (x) · (b - a) 5 2880 n 4 .

Examples of approximate calculation of definite integrals using the parabola method

Simpson's method involves the approximate calculation of definite integrals. Most often, there are two types of problems for which this method is applicable:

• in the approximate calculation of a definite integral;
• when finding an approximate value with an accuracy of δ n.

The accuracy of the calculation is affected by the value of n, the higher n, the more accurate the intermediate values.

Example 1

Calculate the definite integral ∫ 0 5 x d x x 4 + 4 using Simpson's method, dividing the integration segment into 5 parts.

Solution

By condition it is known that a = 0; b = 5 ; n = 5, f(x) = x x 4 + 4.

Then we write Simpson's formula in the form

∫ a b f (x) d x ≈ h 3 f (x 0) + 4 ∑ i = 1 n f (x 2 i - 1) + 2 ∑ i = 1 n - 1 f (x 2 i) + f (x 2 n)

To apply it fully, it is necessary to calculate the step using the formula h = b - a 2 n, determine the points x i = a + i · h, i = 0, 1, . . . , 2 n and find the values ​​of the integrand function f (x i) , i = 0 , 1 , . . . , 2 n .

Intermediate calculations must be rounded to 5 digits. Let's substitute the values ​​and get

h = b - a 2 n = 5 - 0 2 · 5 = 0 . 5

Let's find the value of the function at points

i = 0: x i = x 0 = a + i · h = 0 + 0 · 0 . 5 = 0 ⇒ f (x 0) = f (0) = 0 0 4 + 4 = 0 i = 1: x i = x 1 = a + i · h = 0 + 1 · 0. 5 = 0 . 5 ⇒ f (x 1) = f (0 . 5) = 0 . 50 . 5 4 + 4 ≈ 0. 12308. . . i = 10: x i = x 10 = a + i · h = 0 + 10 · 0. 5 = 5 ⇒ f (x 10) = f (5) = 5 5 4 + 4 ≈ 0. 00795

Clarity and convenience are presented in the table below

i	0	1	2	3	4	5
x i	0	0 . 5	1	1 . 5	2	2 . 5
f x i	0	0 . 12308	0 . 2	0 . 16552	0 . 1	0 . 05806

i	6	7	8	9	10
x i	3	3 . 5	4	4 . 5	5
f x i	0 . 03529	0 . 02272	0 . 01538	0 . 01087	0 . 00795

It is necessary to substitute the results into the formula of the parabola method:

∫ 0 5 x d x x 4 + 4 ≈ h 3 f (x 0) + 4 ∑ i = 1 n f (x 2 i - 1) + 2 ∑ i = 1 n - 1 f (x 2 i) + f (x 2 n ) = = 0 . 5 3 0 + 4 0 . 12308 + 0 . 16552 + 0 . 05806 + + 0 . 02272 + 0 . 01087 + 2 · 0 . 2 + 0 . 1 + + 0 . 03529 + 0 . 01538 + 0 . 00795 ≈ ≈ 0 . 37171

For the calculation, we chose a definite integral, which can be calculated using Newton-Leibniz. We get:

∫ 0 5 x d x x 4 + 4 = 1 2 ∫ 0 5 d (x 2) x 2 2 + 4 = 1 4 a r c t g x 2 2 0 5 = 1 4 a r c t g 25 2 ≈ 0 . 37274

Answer: The results match up to hundredths.

Example 2

Calculate the indefinite integral ∫ 0 π sin 3 x 2 + 1 2 d x using Simpson's method with an accuracy of 0.001.

Solution

By condition we have that a = 0, b = π, f (x) = sin 3 x 2 + 1 2, δ n ≤ 0. 001. The value of n needs to be determined. To do this, use a formula for estimating the absolute error of the Simpson method of the form δ n ≤ m a x [ a ; b ] f (4) (x) · (b - a) 5 2880 n 4 ≤ 0 . 001

When we find the value of n, then the inequality m a x [a; b ] f (4) (x) · (b - a) 5 2880 n 4 ≤ 0 . 001 will be executed. Then, using the parabola method, the error in the calculation will not exceed 0. 001. The last inequality takes the form

n 4 ≥ m a x [ a ; b ] f (4) (x) · (b - a) 5 2 . 88

Now we need to find out what is the largest value the modulus of the fourth derivative can take.

f " (x) = sin 3 x 2 + 1 2 " = 3 2 cos 3 x 2 ⇒ f "" (x) = 3 2 cos 3 x 2 " = - 9 4 sin 3 x 2 ⇒ f " " " ( x) = - 9 4 sin 3 x 2 " = - 27 8 cos 3 x 2 ⇒ f (4) (x) = - 27 8 cos 3 x 2 " = 81 16 sin 3 x 2

The domain of definition f (4) (x) = 81 16 sin 3 x 2 belongs to the interval - 81 16 ; 81 16, and the integration segment itself [0; π) has an extremum point, it follows that m a x [ 0 ; π ] f (4) (x) = 81 16 .

We make the substitution:

n 4 ≥ m a x [ a ; b ] f (4) (x) · (b - a) 5 2 . 88 ⇔ n 4 ≥ 81 16 · π - 0 5 2 . 88 ⇔ ⇔ n 4 > 537 . 9252 ⇔ n > 4 . 8159

We found that n is a natural number, then its value can be equal to n = 5, 6, 7... first you need to take the value n = 5.

Perform actions similar to the previous example. You need to calculate the step. For this

h = b - a 2 n = π - 0 2 5 = π 10

Let's find the nodes x i = a + i · h, i = 0, 1, . . . , 2 n , then the value of the integrand will have the form

i = 0: x i = x 0 = a + i · h = 0 + 0 · π 10 = 0 ⇒ f (x 0) = f (0) = sin 3 · 0 2 + 1 2 = 0 . 5 i = 1: x i = x 1 = a + i · h = 0 + 1 · π 10 = π 10 ⇒ f (x 1) = f (π 10) = sin 3 · π 10 2 + 1 2 ≈ 0. 953990. . . i = 10: x i = x 10 = a + i · h = 0 + 10 · π 10 = π ⇒ f (x 10) = f (π) = sin 3 · π 2 + 1 2 ≈ - 0. 5 7 π 10

4 π 5 9 π 10 π f (x i) 1 . 207107 0 . 809017 0 . 343566 - 0 . 087785 - 0 . 391007 - 0 . 5

It remains to substitute the values ​​into the solution formula using the parabola method and we get

∫ 0 π sin 3 x 2 + 1 2 ≈ h 3 f (x 0) + 4 ∑ i = 1 n f (x 2 i - 1) + 2 ∑ i = 1 n - 1 f (x 2 i) + f ( x 2 n) = = π 30 · 0, 5 + 4 · 0. 953990 + 1 . 487688 + 1 . 207107 + + 0 . 343566 - 0 . 391007 + 2 1 . 309017 + 1 . 451056 + + 0 . 809017 - 0 . 87785 - 0 . 5 = = 2 . 237650

Simpson's method allows us to obtain an approximate value of the definite integral ∫ 0 π sin 3 x 2 + 1 2 d x ≈ 2. 237 with an accuracy of 0.001.

When calculating using the Newton-Leibniz formula, we obtain as a result

∫ 0 π sin 3 x 2 + 1 2 d x = - 2 3 cos 3 x 2 + 1 2 x 0 π = = - 3 2 cos 3 π 2 + π 2 - - 2 3 cos 0 + 1 2 0 = π 2 + 2 3 ≈ 2. 237463

Answer:∫ 0 π sin 3 x 2 + 1 2 d x ≈ 2 . 237

Comment

In most cases, finding m a x [ a ; b ] f (4) (x) is problematic. Therefore, an alternative is used - the parabola method. Its principle is explained in detail in the section on the trapezoidal method. The parabola method is considered the preferred method for solving the integral. Computational error affects the result n. The smaller its value, the more accurate the approximate required number.

If you notice an error in the text, please highlight it and press Ctrl+Enter

To find the definite integral by the trapezoidal method, the area of ​​a curvilinear trapezoid is also divided into n rectangular trapezoids with heights h and bases 1, 2, 3,..у n, where n is the number of the rectangular trapezoid. The integral will be numerically equal to the sum of the areas of rectangular trapezoids (Figure 4).

Rice. 4

n - number of partitions

The error of the trapezoidal formula is estimated by the number

The error of the trapezoid formula decreases faster with growth than the error of the rectangle formula. Therefore, the trapezoidal formula allows for greater accuracy than the rectangle method.

Simpson's formula

If for each pair of segments we construct a polynomial of the second degree, then integrate it on the segment and use the additivity property of the integral, we obtain Simpson’s formula.

In Simpson's method, to calculate a definite integral, the entire integration interval is divided into subintervals of equal length h=(b-a)/n. The number of partition segments is an even number. Then, on each pair of adjacent subintervals, the integrand function f(x) is replaced by a Lagrange polynomial of the second degree (Figure 5).

Rice. 5 The function y=f(x) on the segment is replaced by a 2nd order polynomial

Let's consider the integrand on a segment. Let us replace this integrand with a Lagrange interpolation polynomial of the second degree, coinciding with y= at the points:

Let's integrate on the segment:

Let's introduce a change of variables:

Considering the replacement formulas,

After performing the integration, we obtain Simpson's formula:

The value obtained for the integral coincides with the area of ​​a curvilinear trapezoid bounded by an axis, straight lines, and a parabola passing through points. On a segment, Simpson's formula will look like:

In the parabola formula, the value of the function f(x) at odd points of the partition x 1, x 3, ..., x 2n-1 has a coefficient of 4, at even points x 2, x 4, ..., x 2n-2 - coefficient 2 and at two boundary points x 0 =a, x n =b - coefficient 1.

The geometric meaning of Simpson's formula: the area of ​​a curvilinear trapezoid under the graph of the function f(x) on a segment is approximately replaced by the sum of the areas of the figures lying under the parabolas.

If the function f(x) has a fourth-order continuous derivative, then the absolute value of the error of the Simpson formula is no more than

where M is the largest value on the segment. Since n 4 grows faster than n 2, the error of the Simpson formula decreases with increasing n much faster than the error of the trapezoidal formula.

Let's calculate the integral

This integral is easy to calculate:

Let's take n equal to 10, h=0.1, calculate the values ​​of the integrand at the partition points, as well as half-integer points.

Using the formula of average rectangles, we obtain I straight = 0.785606 (the error is 0.027%), using the trapezoid formula I trap = 0.784981 (the error is about 0.054. When using the method of right and left rectangles, the error is more than 3%.

To compare the accuracy of approximate formulas, let us calculate the integral again

but now according to Simpson's formula with n=4. Let's divide the segment into four equal parts by points x 0 =0, x 1 =1/4, x 2 =1/2, x 3 =3/4, x 4 =1 and calculate approximately the values ​​of the function f(x)=1/( 1+x) at these points: 0 =1.0000, 1 =0.8000, 2 =0.6667, 3 =0.5714, 4 =0.5000.

Using Simpson's formula we get

Let us estimate the error of the obtained result. For the integrand function f(x)=1/(1+x) we have: f (4) (x)=24/(1+x) 5, which means that on the segment . Therefore, we can take M=24, and the error of the result does not exceed 24/(2880 4 4)=0.0004. Comparing the approximate value with the exact one, we conclude that the absolute error of the result obtained using the Simpson formula is less than 0.00011. This is in accordance with the error estimate given above and, in addition, indicates that the Simpson formula is much more accurate than the trapezoidal formula. Therefore, Simpson's formula is used more often for approximate calculation of definite integrals than the trapezoidal formula.

Using three points to interpolate the integrand allows the use of a parabolic function (second degree polynomial). This leads to Simpson's formula for approximate calculation of the integral.

Consider an arbitrary integral

Let's use a change of variable in such a way that the boundaries of the integration segment become [-1,1] instead; for this we introduce the variable z:

Then

Let's consider the problem of interpolating an integrand with a polynomial of the second degree (parabola), using three equidistant nodal points as nodes - z = -1, z = 0, z = +1 (step is 1, length of the integration segment is 2). Let us denote the corresponding values ​​of the integrand at the interpolation nodes

System of equations for finding polynomial coefficients

Passing through three points, and

will take the form

or

Odds can be easily obtained

Let us now calculate the value of the integral of the interpolation polynomial

By inversely changing the variable, we return to the original integral. Let's take into account that

We obtain Simpson's formula for an arbitrary integration interval:

If necessary, the original integration segment can be divided into N double segments, to each of which the Simpson formula is applied. The interpolation step will be

For the first segment of integration, the interpolation nodes will be points a, a+h, a+2h, for the second - a+2h, a+3h, a+4h, for the third a+4h, a+5h, a+6h, etc. . The approximate value of the integral is obtained by summing N areas:

This sum includes identical terms (for internal nodes with an even index value - 2i). Therefore, we can rearrange the terms in this sum in this way

What is equivalent

Because

The error of this approximate method decreases in proportion to the length of the integration step to the fourth power, i.e. when the number of intervals is doubled, the error decreases by 16 times

Increased accuracy

Here we look at the so-called Aitken process. It makes it possible to estimate the error of the method and indicates an algorithm for refining the results. The calculation is carried out sequentially three times at different partition steps h 1 , h 2 , h 3 , and their ratios are constant: h 2 / h 1 = h 3 / h 2 = q (for example, when dividing the step in half q = 0.5). Let the values ​​of the integral I 1, I 2, I 3 be obtained as a result of numerical integration. Then the refined value of the integral is calculated using the formula

and the order of accuracy of the numerical integration method used is determined by the relation

.

The value of the integral can also be refined using the Runge-Romberg method.

From the analysis of errors in numerical integration methods, it follows that the accuracy of the results obtained depends both on the nature of the change in the integrand and on the integration step. We will assume that we set the step size. It is clear that in order to achieve comparable accuracy when integrating a weakly changing function, the step can be chosen larger than when integrating sharply changing functions.

In practice, there are often cases when the integrand function changes differently in individual sections of the integration segment. This circumstance requires such an organization of economical numerical algorithms in which they would automatically adapt to the nature of the change in the function. Such algorithms are called adaptive (adjusting). They allow you to enter different values ​​of the integration step in individual sections of the integration segment. This makes it possible to reduce machine time without losing the accuracy of the calculation results. We emphasize that this approach is usually used when specifying the integrand function y=f(x) in the form of a formula, and not in tabular form.

Let's consider the principle of operation of the adaptive algorithm. Initially, we divide the segment into n parts. In the future, we divide each such elementary segment successively in half. The final number of steps, their location and size depend on the integrand and permissible error e.

For each elementary segment we apply numerical integration formulas for two different partitions. We obtain approximations for the integral over this segment:

We compare the obtained values ​​and evaluate their error. If the error is within acceptable limits, then one of these approximations is taken as the value of the integral over this elementary segment. Otherwise, the segment is further divided and new approximations are calculated. To save time, the division points are positioned so that the calculated values ​​at the previous division points are used.

The process of dividing the segment in half and calculating the updated values ​​continues until their difference becomes no more than a certain specified value d i, depending on e and h:

.

A similar procedure is carried out for all n elementary segments. The quantity is accepted as the desired value of the integral. Conditions and the corresponding choice of values ​​d i ensure the fulfillment of the condition

Trapezoid method

Let's divide the segment into equal parts using points:

The trapezoidal method consists of replacing the integral with the sum:

The absolute error of the approximation obtained using the trapezoidal formula is estimated using the formula, where.

Parabola method (Simpson's method)

a) Only one parabola passes through any three points with coordinates.

b) Express the area under the parabola on the segment through:

Taking into account the values ​​and from point a) it follows:

c) Divide the segment into equal parts using points:

The parabola method involves replacing the integral with the sum:

For approximate practical calculations, the formula is used:

The absolute error of calculation according to formula (4) is estimated by the relation, where.

Estimation of the accuracy of calculating “untaken” integrals

In this work, the calculation of absolute and relative errors is carried out under the condition that the exact value of the definite integral is known. However, not every antiderivative, even when it exists, is expressed in its final form through elementary functions. These are antiderivatives expressed by integrals, etc. In all such cases, the antiderivative represents some new function that cannot be reduced to a combination of a finite number of elementary functions.

Definite integrals of such functions can only be calculated approximately. To assess the accuracy of calculations in such cases, for example, Runge's rule is used. In this case, the integral is calculated using the selected formula (rectangles, trapezoids, Simpson parabolas) with a number of steps equal to n, and then with a number of steps equal to. The error in calculating the value of the integral when the number of steps is equal is calculated using the Runge formula: for formulas of rectangles and trapezoids, and for Sipson's formula. Thus, the integral is calculated for successive values ​​of the number of steps, ..., where is the initial number of steps. The calculation process ends when the next value meets the condition where is the specified accuracy.

In order not to calculate the same integral several times for different partitions of the integration segment, you can calculate the integration step in advance.

Example. Select the integration step to calculate the integral with an accuracy of 0.01 using the quadrature formulas of rectangles, trapezoids, and Simpson.

Quadrature formula of rectangles.

Let's calculate at what step the error will be 0.01:

integrand trapezoid parabola unbreakable

Because, then.

During a step, the segment is divided into equally spaced nodes.

Quadrature formula of trapezoids.

Because the, .

During a step, the segment is divided into equally spaced nodes.

Simpson's quadrature formula.

Let's calculate at what step the error will be 0.01:

During a step, the segment is divided into equally spaced nodes.

As one would expect, the smallest number of equally spaced nodes is obtained when calculating the integral using Simpson's quadrature formula.

The student is offered work consisting of four stages:

• Stage 1 - exact calculation of a definite integral.
• Stage 2 - approximate calculation of a definite integral using one of the methods: rectangles or trapezoids.
• Stage 3 - approximate calculation of a definite integral using the parabola method.

Stage 4 - calculation and comparison of the absolute and relative errors of approximate methods: , where is the exact solution of the integral, is the value of the integral obtained using approximate methods.

Plotting the integrand function.

Options and a sample of performing RGR are given below.

Options

Option No.

Sample execution of RGR

Exercise. Calculate integral

1. Exact calculation:

2. Approximate calculation using rectangle formulas:

Let's make a table:

Using the first formula of rectangles we get:

0.1 = 0.1 3.062514 = 0.306251.

Using the second formula of rectangles we get:

0.1 = 0.1 4.802669 = 0.480267.

In this case, the first formula gives the value of the integral with a deficiency, the second - with an excess.

3. Approximate calculation using the trapezoidal formula:

In our case we get:

0.1 = =0.1 = 0.1·4.095562 = =0.409556.

Let's calculate the relative and absolute errors.

4. Approximate calculation using Simpson's formula:

In our case we get:

Let's calculate the relative and absolute errors.

In reality, = 0.40631714.

Thus, when dividing the segment into 10 parts using Simpson’s formula, we received 5 correct signs; according to the trapezoidal formula - three correct signs; According to the rectangle formula, we can only vouch for the first sign.