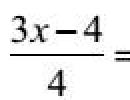An equation with one unknown, which, after opening the brackets and bringing similar terms, takes the form

ax + b = 0, where a and b are arbitrary numbers, is called linear equation with one unknown. Today we’ll figure out how to solve these linear equations.

For example, all equations:

2x + 3= 7 – 0.5x; 0.3x = 0; x/2 + 3 = 1/2 (x – 2) - linear.

The value of the unknown that turns the equation into a true equality is called decision or root of the equation .

For example, if in the equation 3x + 7 = 13 instead of the unknown x we ​​substitute the number 2, we obtain the correct equality 3 2 +7 = 13. This means that the value x = 2 is the solution or root of the equation.

And the value x = 3 does not turn the equation 3x + 7 = 13 into a true equality, since 3 2 +7 ≠ 13. This means that the value x = 3 is not a solution or a root of the equation.

Solving any linear equations reduces to solving equations of the form

ax + b = 0.

Let's move the free term from the left side of the equation to the right, changing the sign in front of b to the opposite, we get

If a ≠ 0, then x = ‒ b/a .

Example 1. Solve the equation 3x + 2 =11.

Let's move 2 from the left side of the equation to the right, changing the sign in front of 2 to the opposite, we get
3x = 11 – 2.

Let's do the subtraction, then
3x = 9.

To find x, you need to divide the product by a known factor, that is
x = 9:3.

This means that the value x = 3 is the solution or root of the equation.

Answer: x = 3.

If a = 0 and b = 0, then we get the equation 0x = 0. This equation has infinitely many solutions, since when we multiply any number by 0 we get 0, but b is also equal to 0. The solution to this equation is any number.

Example 2. Solve the equation 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.

Let's expand the brackets:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.

5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.

Here are some similar terms:
0x = 0.

Answer: x - any number.

If a = 0 and b ≠ 0, then we get the equation 0x = - b. This equation has no solutions, since when we multiply any number by 0 we get 0, but b ≠ 0.

Example 3. Solve the equation x + 8 = x + 5.

Let’s group terms containing unknowns on the left side, and free terms on the right side:
x – x = 5 – 8.

Here are some similar terms:
0х = ‒ 3.

Answer: no solutions.

On Figure 1 shows a diagram for solving a linear equation

Let's draw up a general scheme for solving equations with one variable. Let's consider the solution to Example 4.

Example 4. Suppose we need to solve the equation

1) Multiply all terms of the equation by the least common multiple of the denominators, equal to 12.

2) After reduction we get
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)

3) To separate terms containing unknown and free terms, open the brackets:
4x – 16 + 6x + 6 – 12 = 30x – 90 + 24x – 22x – 86.

4) Let us group in one part the terms containing unknowns, and in the other - free terms:
4x + 6x – 30x – 24x + 22x = ‒ 90 – 86 + 16 – 6 + 12.

5) Let us present similar terms:
- 22х = - 154.

6) Divide by – 22, We get
x = 7.

As you can see, the root of the equation is seven.

Generally such equations can be solved using the following scheme:

a) bring the equation to its integer form;

b) open the brackets;

c) group the terms containing the unknown in one part of the equation, and the free terms in the other;

d) bring similar members;

e) solve an equation of the form aх = b, which was obtained after bringing similar terms.

However, this scheme is not necessary for every equation. When solving many simpler equations, you have to start not from the first, but from the second ( Example. 2), third ( Example. 13) and even from the fifth stage, as in example 5.

Example 5. Solve the equation 2x = 1/4.

Find the unknown x = 1/4: 2,
x = 1/8 .

Let's look at solving some linear equations found in the main state exam.

Example 6. Solve the equation 2 (x + 3) = 5 – 6x.

2x + 6 = 5 – 6x

2x + 6x = 5 – 6

Answer: - 0.125

Example 7. Solve the equation – 6 (5 – 3x) = 8x – 7.

– 30 + 18x = 8x – 7

18x – 8x = – 7 +30

Answer: 2.3

Example 8. Solve the equation

3(3x – 4) = 4 7x + 24

9x – 12 = 28x + 24

9x – 28x = 24 + 12

Example 9. Find f(6) if f (x + 2) = 3 7's

Solution

Since we need to find f(6), and we know f (x + 2),
then x + 2 = 6.

We solve the linear equation x + 2 = 6,
we get x = 6 – 2, x = 4.

If x = 4 then
f(6) = 3 7-4 = 3 3 = 27

Answer: 27.

If you still have questions or want to understand solving equations more thoroughly, sign up for my lessons in the SCHEDULE. I will be glad to help you!

TutorOnline also recommends watching a new video lesson from our tutor Olga Alexandrovna, which will help you understand both linear equations and others.

website, when copying material in full or in part, a link to the source is required.

Class: 4

Target: Consider practical ways to solve equations that require more than one arithmetic operation.

Lesson equipment: computer presentation of mental arithmetic, cards with equations, cards of three levels for independent work on problems, feedback cube

During the classes

1. Organizational moment
Checking readiness for the lesson. The number is written in the notebooks, cool work.

2. Oral counting(computer presentation, slide No. 1)
Game "Snail Competition"
Your favorite dog Alik at the snail competition. Two snails must climb to the top of the mountain. Which one of them will come out first? Our snail is number 1 on the left. The snail takes a step only if we find the meaning of the expression correctly.
You are ready?
The signal to start has already sounded. We repeat the procedure and name the correct meanings of the expressions.

(122 + 18) : 70 = 2
(64: 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 (30 + 2) – 4 4 = 16
5 4 + 12 = 32
(400 – 300) – 36 = 64

We have a series of numbers.
2, 4, 8, 16, 32, 64
What pattern did you notice in the compilation of this series? (each subsequent number is doubled)
Continue this series of numbers and name at least the next three numbers. (128, 256, 512…)
Well done! We decided everything correctly, so our snail is on top of the mountain.
Each number has an encrypted letter. Let's turn them over and read the topic of today's lesson.

2 4 8 16 32 64 128 256 512
THE EQUATION

What is the equation called?
What is the root of an equation?
What does it mean to solve an equation?
We already know how to solve simple equations, and today we will get acquainted with solving complex equations where we need to perform several arithmetic operations.

3. Solving simple equations. Preparation for the introduction of new material.
On a magnetic board in random order there are cards with equations.
What groups can all these equations be divided into? (equations are distributed in 3 columns)

1) 7000 – x = 2489
7000 – x = 3489
7000 – x = 1689
Why did we put these equations in the first group? (simple equations With identically reduced) Can we solve them?
Find among them the equation with the largest root and solve it (one student at the board)

2) 71: x = 20 + 7
x: 3 = 16 + 11 ( these are equations on the right side of which the expression)
Can we solve the equations of the second column?
Solve any of the equations, but replace the sum on the right side with the difference. The root of the equation should remain the same. (two students at the blackboard)

3) (490 – x) – 250 = 70

Look at the remaining equation. Is it easy for us to solve it? Why?

4. Working on new material. (frontal conversation with the class, during which the solution to the equation is considered)

(490 – x) – 250 = 70
490 – x = 70 + 250
490 – x = 320
x = 490 – 320
x = 170
(490 – 170) – 250 = 70
70 = 70
Answer: 70

5. Consolidation.

1) Solving the equation (one of the strong students at the blackboard)
5 a + 500 = 4500: 5
5 a + 500 = 900
5 a = 900 – 500
5 a = 400
a = 400: 5
a = 80
5 80 + 500 = 900
900 = 900
Answer: 80

Solve the equations.
A+ 156 = 17 ∙ 20 (1604 – y) – 108 = 800
252: 36 ∙ x = 560 103300: (x + 297) = 25 ∙2

We solved two new complex equations. Look at the equations in front of you. Are they all complex? Which equation is the odd one out? Why? The rest are on the left side an expression in several actions. Find among them a sequence of actions that has already been encountered today.

(1604 – y) – 108 = 800
1604 – y = 800 + 108
1604 – y = 908
y = 1604 – 908
y = 696
(1604 – 696) – 108 = 800
800 = 800
Answer: 696
Solve the equation in pairs. One student turns the board around for later checking.

6. Solving the problem
Independent work using cards of 3 levels. Having completed the task of the first stage, the student proceeds to complete the task of the second stage, then the third. (Various methods of differentiated work)

Frontal check

1) 25700 – x = 12350
x = 25700 – 12350
x = 13350
25700 – 13350 = 12350
12350 = 12350
Answer: 13350 seedlings.

2) 25700 – x = 12000 + 350

3) 25700 – (x + 8580) = 12350
x + 8580 = 25700 – 12350
x + 8580 = 13350
x = 13350 – 8580
x = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
Answer: 4770 limes.
4) What other equation could be made?
(25700 – x) – 8580 = 12350

We solved three problems by composing three equations. Which equation is considered complex? Why?

7. Homework.
Consider how the equations were solved in the textbook on page 106 and solve the equation in the printed notebook No. 44 (a).
Solve problem No. 47. Additional task: what other questions can be asked about this problem?

8. Lesson summary.
What equations did you learn to solve in class?
Was it difficult?
Who had it easy?

LESSON SCRIPT

using a computer.

Educational institution - Municipal educational institution "Severskaya Gymnasium" ZATO Seversk.

Item - mathematics.

Class - third.

Subject: Solving equations in several steps.

Lesson type- discovery of new knowledge.

Lesson form – combined lesson with elements of problem-search learning.

Forms of organizing educational activities: collective activity to solve a problem, individual tasks of choice, work in pairs, independent work.

Lesson objectives:

Educational and methodological support – textbook for third grade in 3 parts “Mathematics”, part 2, L.G. Peterson.

Lesson duration- 45 minutes.

13 slides (Power Point, Word).

Necessary equipment and materials for the lesson:

Computer, media projector, screen.

Blackboard, textbook, workbooks, media product.

Methods:

Problem

Comparative

Observation

Using schematization ( drawing up an algorithm)

Forms of work:

Collective activities

Work on options, mutual verification

Performing an optional task

Independent work

Equation, components of actions, order of actions, algorithm.

Bibliography:

Textbook for third grade “Mathematics” by L.G. Peterson in 3 parts, part two, M.: Yuventa Publishing House, 2008.

L.G. Peterson “The activity-based approach and its implementation in mathematics lessons in elementary school,” article in the journal “Elementary School: Plus or Minus,” No. 5, 1999.

Internet resources: http:// www. cwer. ru/ files ( Pictures)

During the classes:

Lesson objectives: systematize knowledge about equations of various types;

To develop the skill of finding an unknown component, to train students in commenting on equations through action components;

Introduce the algorithm for solving compound equations;

Develop computational skills, practice solving problems of the types studied;

Develop correct mathematical speech and logical thinking;

Teach self-assessment of your activities, compare the results of your activities with a model.

Organizational moment (Slide No. 1).

Oral exercises (Slide No. 2).

Consider the expressions. Determine the order of actions, highlight the last action.

k m + n: 3 (5 + b): 16

a · 4 – 8 (15: x) · (8 – y)

Read the expressions based on the last action.

Introduction of new material.

(Slide No. 3)

Read the entries. Remember what each entry is called?

26 + 37 (D: expression)

236 – 21 = 215 (D: true equality)

48: x (D: variable expression)

At what values A inequality will be true?

What mathematical concept have we not named? (D: equation)

I suggest you solve several equations, but first we will repeat the rules for finding an unknown component:

Cards:

(Students repeat the rules for finding an unknown component using the cards).

Now write down the number in your notebooks and solve the following equations:

(Slide No. 4)

a – 86 = 9 56: c = 2 4 (4 b – 16) : 2 = 10

Who did the job?

How many equations did you solve? (D: two equations).

Let's check the solved equations. (Slide No. 4a).

What is the root of the first equation? (D: a = 95).

What is the root of the second equation? (D: c = 7).

What problem arose in solving the third equation?

(D: There is nothing to simplify on the right side).

Maybe someone can formulate the topic of the lesson?

(D: Solving equations in several steps).

Yes, that's right, today we will learn how to solve equations in several steps. (Slide No. 5)

Let's take a closer look at our equation again. Think about what you and I know well? What can we already do?

Children's answers (Slide No. 6):

We know how to determine the order of actions.

We can solve simple equations and find unknown components.

We know how to perform operations (direct and inverse).

Let's do what we know how to do, it should help us. And I will record our actions. (The teacher directs the activities of the students with an introductory dialogue; they pronounce the actions and solve the equation in their notebooks). Slide number 7

(4 ·b – 16) : 2 = 10 1. Determine the order of actions.

2. Select the last action.

3. Determine the unknown component.

4 · b – 16 = 10 · 2 4. Apply the rule.

4 ·b – 16 = 20 5. Simplify the right side.

6. We arrange the order of actions.

7. Select the last action.

8. Determine the unknown component.

4 · b = 20 + 16 9. Apply the rule.

4 · b = 36 10. Simplify the right side.

11. Determine the unknown component.

b = 36: 4 12. Apply the rule.

b = 9 13. Find the root.

Look carefully, what program of action have we come up with?

What interesting things did you notice?

Is it possible to shorten our program somehow?

Let's create an algorithm of actions:

(Slide No. 8)

Physical education minute (Slide No. 9).

Gymnastics for the eyes.

Primary consolidation (pronunciation).

(Slide number 10).

Now, using the algorithm, let's try to explain the following equation:

(2 + x: 7) · 8 = 72

2 + x: 7 = 72: 8

2 + X : 7 = 9 Students comment step by step

x: 7 = 9 – 2 solution to the equation.

Raise your hand, who clearly understands how to solve the equation in several steps? Tell us about your actions.

Who else is experiencing difficulties and needs help?

Self-control.

Check your solution, exchange notebooks, help your neighbor check.

Whoever thinks that the solution is correct, that he coped with the work, put “+” in the margin.

Check students' work. Who got the same root of the equation?

The result of the work.

Guys, what is the topic of today's lesson?

What problem did you encounter at the beginning of the lesson?

How did you cope with difficulties?

Repeat the algorithm of actions.

Do you think, while doing work now, is it only equations that we learn to solve? (D: we learn to plan our activities, practice counting, calculations, learn to complete tasks).

Can our knowledge and skills be useful in life? Where? When?

What keywords would you highlight in the lesson?

(D: Equation, procedure, unknown component, rule for finding the unknown component, expressions) – Slide number 11.

8. Self-assessment of your activities.

If it was easy in the lesson, you figured it all out – the color green. If there were difficulties, doubts - yellow. If you didn’t understand the topic, it was difficult - the color red. – Slide “12.

9. Homework (Slide No. 13)

Compose your example equation in several steps;

p. 36, No. 7 (according to options).

Slide number 14 – end of the lesson.

Equations

How to solve equations?

In this section we will recall (or study, depending on who you choose) the most elementary equations. So what is the equation? In human language, this is some kind of mathematical expression where there is an equal sign and an unknown. Which is usually denoted by the letter "X". Solve the equation- this is to find such values ​​of x that, when substituted into original expression will give us the correct identity. Let me remind you that identity is an expression that is beyond doubt even for a person who is absolutely not burdened with mathematical knowledge. Like 2=2, 0=0, ab=ab, etc. So how to solve equations? Let's figure it out.

There are all sorts of equations (I’m surprised, right?). But all their infinite variety can be divided into only four types.

4. Other.)

All the others, of course, most of all, yes...) This includes both cubic and demonstrative, And logarithmic, And trigonometric and all sorts of others. We will work closely with them in the appropriate sections.

I’ll say right away that sometimes the equations of the first three types are so screwed up that you won’t even recognize them... Nothing. We will learn how to unwind them.

And why do we need these four types? And then what linear equations solved in one way square others, fractional rationals - third, A rest They don’t dare at all! Well, it’s not that they can’t decide at all, it’s that I was wrong with mathematics.) It’s just that they have their own special techniques and methods.

But for any (I repeat - for any!) equations provide a reliable and fail-safe basis for solving. Works everywhere and always. This foundation - Sounds scary, but it's very simple. And very (Very!) important.

Actually, the solution to the equation consists of these very transformations. 99% Answer to the question: " How to solve equations?" lies precisely in these transformations. Is the hint clear?)

Identical transformations of equations.

IN any equations To find the unknown, you need to transform and simplify the original example. And so that when the appearance changes the essence of the equation has not changed. Such transformations are called identical or equivalent.

Note that these transformations apply specifically to the equations. In mathematics there are also identity transformations expressions. This is another topic.

Now we will repeat all, all, all basic identical transformations of equations.

Basic because they can be applied to any equations - linear, square, fractional trigonometric, indicative, logarithmic etc. and so on.

First identity transformation: you can add (subtract) to both sides of any equation any(but one and the same!) number or expression (including an expression with an unknown!). This does not change the essence of the equation.

By the way, you constantly used this transformation, you just thought that you were transferring some terms from one part of the equation to another with a change of sign. Type:

The case is familiar, we move the two to the right, and we get:

Actually you taken away from both sides of the equation is two. The result is the same:

x+2 - 2 = 3 - 2

Moving terms left and right with a change of sign is simply a shortened version of the first identity transformation. And why do we need such deep knowledge? - you ask. Nothing in the equations. For God's sake, bear it. Just don’t forget to change the sign. But in inequalities the habit of transference can lead to a dead end...

Second identity transformation: both sides of the equation can be multiplied (divided) by the same thing non-zero number or expression. Here an understandable limitation already appears: multiplying by zero is stupid, and dividing is completely impossible. This is the transformation you use when you solve something cool like

It's clear X= 2. How did you find it? By selection? Or did it just dawn on you? In order not to select and not wait for insight, you need to understand that you are just divided both sides of the equation by 5. When dividing the left side (5x), the five was reduced, leaving pure X. Which is exactly what we needed. And when dividing the right side of (10) by five, the result is, of course, two.

That's all.

It's funny, but these two (only two!) identical transformations are the basis of the solution all equations of mathematics. Wow! It makes sense to look at examples of what and how, right?)

Examples of identical transformations of equations. Main problems.

Let's start with first identity transformation. Transfer left-right.

An example for the younger ones.)

Let's say we need to solve the following equation:

3-2x=5-3x

Let's remember the spell: "with X's - to the left, without X's - to the right!" This spell is instructions for using the first identity transformation.) What expression with an X is on the right? 3x? The answer is incorrect! On our right - 3x! Minus three x! Therefore, when moving to the left, the sign will change to plus. It will turn out:

3-2x+3x=5

So, the X’s were collected in a pile. Let's get into the numbers. There is a three on the left. With what sign? The answer “with none” is not accepted!) In front of the three, indeed, nothing is drawn. And this means that before the three there is plus. So the mathematicians agreed. Nothing is written, which means plus. Therefore, the triple will be transferred to the right side with a minus. We get:

-2x+3x=5-3

There are mere trifles left. On the left - bring similar ones, on the right - count. The answer comes straight away:

In this example, one identity transformation was enough. The second one was not needed. Well, okay.)

An example for older children.)

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Let's learn - with interest!)

You can get acquainted with functions and derivatives.