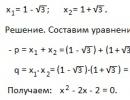On the application of Vieta's theorem in solving quadratic equations. Vieta's theorem for quadratic and other equations When Vieta's theorem applies

I. Vieta's theorem for the reduced quadratic equation.

Sum of roots of the reduced quadratic equation x 2 +px+q=0 is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term:

x 1 + x 2 = -p; x 1 ∙x 2 =q.

Find the roots of the given quadratic equation using Vieta's theorem.

Example 1) x 2 -x-30=0. This is the reduced quadratic equation ( x 2 +px+q=0), second coefficient p=-1, and the free member q=-30. First, let's make sure that this equation has roots, and that the roots (if any) will be expressed in integers. To do this, it is enough that the discriminant be a perfect square of an integer.

Finding the discriminant D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .

Now, according to Vieta’s theorem, the sum of the roots must be equal to the second coefficient taken with the opposite sign, i.e. ( -p), and the product is equal to the free term, i.e. ( q). Then:

x 1 +x 2 =1; x 1 ∙x 2 =-30. We need to choose two numbers such that their product is equal to -30 , and the amount is unit. These are numbers -5 And 6 . Answer: -5; 6.

Example 2) x 2 +6x+8=0. We have the reduced quadratic equation with the second coefficient p=6 and free member q=8. Let's make sure that there are integer roots. Let's find the discriminant D 1 D 1=3 2 -1∙8=9-8=1=1 2 . The discriminant D 1 is the perfect square of the number 1 , which means that the roots of this equation are integers. Let us select the roots using Vieta’s theorem: the sum of the roots is equal to –р=-6, and the product of the roots is equal to q=8. These are numbers -4 And -2 .

In fact: -4-2=-6=-р; -4∙(-2)=8=q. Answer: -4; -2.

Example 3) x 2 +2x-4=0. In this reduced quadratic equation, the second coefficient is p=2, and the free member q=-4. Let's find the discriminant D 1, since the second coefficient is an even number. D 1=1 2 -1∙(-4)=1+4=5. The discriminant is not a perfect square of the number, so we do conclusion: The roots of this equation are not integers and cannot be found using Vieta’s theorem. This means that we solve this equation, as usual, using the formulas (in this case, using the formulas). We get:

Example 4). Write a quadratic equation using its roots if x 1 =-7, x 2 =4.

Solution. The required equation will be written in the form: x 2 +px+q=0, and, based on Vieta’s theorem –p=x 1 +x 2=-7+4=-3 → p=3; q=x 1 ∙x 2=-7∙4=-28 . Then the equation will take the form: x 2 +3x-28=0.

Example 5). Write a quadratic equation using its roots if:

II. Vieta's theorem for a complete quadratic equation ax 2 +bx+c=0.

The sum of the roots is minus b, divided by A, the product of the roots is equal to With, divided by

In this lecture we will get acquainted with the curious relationships between the roots of a quadratic equation and its coefficients. These relationships were first discovered by the French mathematician François Viète (1540-1603).

For example, for the equation 3x 2 - 8x - 6 = 0, without finding its roots, you can, using Vieta’s theorem, immediately say that the sum of the roots is equal to , and the product of the roots is equal to
i.e. - 2. And for the equation x 2 - 6x + 8 = 0 we conclude: the sum of the roots is 6, the product of the roots is 8; By the way, it’s not difficult to guess what the roots are equal to: 4 and 2.
Proof of Vieta's theorem. The roots x 1 and x 2 of the quadratic equation ax 2 + bx + c = 0 are found by the formulas

Where D = b 2 - 4ac is the discriminant of the equation. Having put these roots together,
we get

Now let's calculate the product of the roots x 1 and x 2. We have

The second relation has been proven:
Comment. Vieta's theorem is also valid in the case when the quadratic equation has one root (that is, when D = 0), it is simply assumed in this case that the equation has two identical roots, to which the above relations are applied.
The proven relations for the reduced quadratic equation x 2 + px + q = 0 take a particularly simple form. In this case, we obtain:

x 1 = x 2 = -p, x 1 x 2 =q
those. the sum of the roots of the reduced quadratic equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term.
Using Vieta's theorem, you can obtain other relationships between the roots and coefficients of a quadratic equation. Let, for example, x 1 and x 2 be the roots of the reduced quadratic equation x 2 + px + q = 0. Then

However, the main purpose of Vieta's theorem is not that it expresses some relationships between the roots and coefficients of a quadratic equation. Much more important is that, using Vieta’s theorem, a formula for factoring a quadratic trinomial is derived, which we will not be able to do without in the future.

Proof. We have

Example 1. Factor the quadratic trinomial 3x 2 - 10x + 3.
Solution. Having solved the equation 3x 2 - 10x + 3 = 0, we find the roots of the square trinomial 3x 2 - 10x + 3: x 1 = 3, x2 = .
Using Theorem 2, we obtain

It makes sense to write 3x - 1 instead. Then we finally get 3x 2 - 10x + 3 = (x - 3)(3x - 1).
Note that a given quadratic trinomial can be factorized without applying Theorem 2, using the grouping method:

3x 2 - 10x + 3 = 3x 2 - 9x - x + 3 =
= 3x (x - 3) - (x - 3) = (x - 3) (3x - 1).

But, as you can see, with this method success depends on whether we are able to find a successful grouping or not, whereas with the first method success is guaranteed.
Example 1. Reduce a fraction

Solution. From the equation 2x 2 + 5x + 2 = 0 we find x 1 = - 2,

From the equation x2 - 4x - 12 = 0 we find x 1 = 6, x 2 = -2. That's why
x 2 - 4x - 12 = (x - 6) (x - (- 2)) = (x - 6) (x + 2).
Now let’s reduce the given fraction:

Example 3. Factor the expressions:
a)x4 + 5x 2 +6; b)2x+-3
Solution. a) Let's introduce a new variable y = x2. This will allow you to rewrite the given expression in the form of a quadratic trinomial with respect to the variable y, namely in the form y 2 + bу + 6.
Having solved the equation y 2 + bу + 6 = 0, we find the roots of the quadratic trinomial y 2 + 5у + 6: y 1 = - 2, y 2 = -3. Now let's use Theorem 2; we get

y 2 + 5y + 6 = (y + 2) (y + 3).
It remains to remember that y = x 2, i.e. return to the given expression. So,
x 4 + 5x 2 + 6 = (x 2 + 2)(x 2 + 3).
b) Let's introduce a new variable y = . This will allow you to rewrite the given expression in the form of a quadratic trinomial with respect to the variable y, namely in the form 2y 2 + y - 3. Having solved the equation
2y 2 + y - 3 = 0, find the roots of the square trinomial 2y 2 + y - 3:
y 1 = 1, y 2 = . Next, using Theorem 2, we obtain:

It remains to remember that y = , i.e. return to the given expression. So,

At the end of the section - some reasoning, again related to Vieta’s theorem, or rather, to the converse statement:
if the numbers x 1, x 2 are such that x 1 + x 2 = - p, x 1 x 2 = q, then these numbers are the roots of the equation
Using this statement, you can solve many quadratic equations orally, without using cumbersome root formulas, and also compose quadratic equations with given roots. Let's give examples.

1) x 2 - 11x + 24 = 0. Here x 1 + x 2 = 11, x 1 x 2 = 24. It’s easy to guess that x 1 = 8, x 2 = 3.

2) x 2 + 11x + 30 = 0. Here x 1 + x 2 = -11, x 1 x 2 = 30. It’s easy to guess that x 1 = -5, x 2 = -6.
Note that if the dummy term of the equation is a positive number, then both roots are either positive or negative; This is important to consider when selecting roots.

3) x 2 + x - 12 = 0. Here x 1 + x 2 = -1, x 1 x 2 = -12. It is easy to guess that x 1 = 3, x2 = -4.
Please note: if the free term of the equation is a negative number, then the roots have different signs; This is important to consider when selecting roots.

4) 5x 2 + 17x - 22 = 0. It is easy to see that x = 1 satisfies the equation, i.e. x 1 = 1 is the root of the equation. Since x 1 x 2 = -, and x 1 = 1, we obtain that x 2 = -.

5) x 2 - 293x + 2830 = 0. Here x 1 + x 2 = 293, x 1 x 2 = 2830. If you pay attention to the fact that 2830 = 283. 10, and 293 = 283 + 10, then it becomes clear that x 1 = 283, x 2 = 10 (now imagine what calculations would have to be performed to solve this quadratic equation using standard formulas).

6) Let's compose a quadratic equation so that its roots are the numbers x 1 = 8, x 2 = - 4. Usually in such cases we make up the reduced quadratic equation x 2 + px + q = 0.
We have x 1 + x 2 = -p, so 8 - 4 = -p, i.e. p = -4. Next, x 1 x 2 = q, i.e. 8 «(-4) = q, from where we get q = -32. So, p = -4, q = -32, which means the required quadratic equation has the form x 2 -4x-32 = 0.

One of the methods for solving a quadratic equation is to use VIET formulas, which was named after FRANCOIS VIETTE.

He was a famous lawyer who served the French king in the 16th century. In his spare time he studied astronomy and mathematics. He established a connection between the roots and coefficients of a quadratic equation.

Advantages of the formula:

1 . By applying the formula, you can quickly find a solution. Because there is no need to enter the second coefficient into the square, then subtract 4ac from it, find the discriminant, and substitute its value into the formula to find the roots.

2 . Without a solution, you can determine the signs of the roots and select the values ​​of the roots.

3 . Having solved a system of two records, it is not difficult to find the roots themselves. In the above quadratic equation, the sum of the roots is equal to the value of the second coefficient with a minus sign. The product of the roots in the above quadratic equation is equal to the value of the third coefficient.

4 . Using these roots, write down a quadratic equation, that is, solve the inverse problem. For example, this method is used when solving problems in theoretical mechanics.

5 . It is convenient to use the formula when the leading coefficient is equal to one.

Flaws:

1 . The formula is not universal.

Vieta's theorem 8th grade

Formula
If x 1 and x 2 are the roots of the reduced quadratic equation x 2 + px + q = 0, then:

Examples
x 1 = -1; x 2 = 3 - roots of the equation x 2 - 2x - 3 = 0.

P = -2, q = -3.

X 1 + x 2 = -1 + 3 = 2 = -p,

X 1 x 2 = -1 3 = -3 = q.

Converse theorem

Formula
If the numbers x 1, x 2, p, q are related by the conditions:

Then x 1 and x 2 are the roots of the equation x 2 + px + q = 0.

Example
Let's create a quadratic equation using its roots:

X 1 = 2 - ? 3 and x 2 = 2 + ? 3.

P = x 1 + x 2 = 4; p = -4; q = x 1 x 2 = (2 - ? 3 )(2 + ? 3 ) = 4 - 3 = 1.

The required equation has the form: x 2 - 4x + 1 = 0.

Vieta's theorem is often used to check roots that have already been found. If you have found the roots, you can use the formulas \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) to calculate the values ​​of \(p\) and \(q\ ). And if they turn out to be the same as in the original equation, then the roots are found correctly.

For example, let us, using , solve the equation \(x^2+x-56=0\) and get the roots: \(x_1=7\), \(x_2=-8\). Let's check if we made a mistake in the solution process. In our case, \(p=1\), and \(q=-56\). By Vieta's theorem we have:

\(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)7+(-8)=-1 \\7\cdot(-8)=-56\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)-1=-1\\-56=-56\end(cases)\ )

Both statements converged, which means we solved the equation correctly.

This check can be done orally. It will take 5 seconds and will save you from stupid mistakes.

Vieta's converse theorem

If \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\), then \(x_1\) and \(x_2\) are the roots of the quadratic equation \(x^ 2+px+q=0\).

Or in a simple way: if you have an equation of the form \(x^2+px+q=0\), then solving the system \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\ end(cases)\) you will find its roots.

Thanks to this theorem, you can quickly find the roots of a quadratic equation, especially if these roots are . This skill is important because it saves a lot of time.

Example . Solve the equation \(x^2-5x+6=0\).

Solution : Using Vieta’s inverse theorem, we find that the roots satisfy the conditions: \(\begin(cases)x_1+x_2=5 \\x_1 \cdot x_2=6\end(cases)\).
Look at the second equation of the system \(x_1 \cdot x_2=6\). What two can the number \(6\) be decomposed into? On \(2\) and \(3\), \(6\) and \(1\) or \(-2\) and \(-3\), and \(-6\) and \(- 1\). The first equation of the system will tell you which pair to choose: \(x_1+x_2=5\). \(2\) and \(3\) are similar, since \(2+3=5\).
Answer : \(x_1=2\), \(x_2=3\).

Examples . Using the converse of Vieta's theorem, find the roots of the quadratic equation:
a) \(x^2-15x+14=0\); b) \(x^2+3x-4=0\); c) \(x^2+9x+20=0\); d) \(x^2-88x+780=0\).

Solution :
a) \(x^2-15x+14=0\) – what factors does \(14\) decompose into? \(2\) and \(7\), \(-2\) and \(-7\), \(-1\) and \(-14\), \(1\) and \(14\ ). What pairs of numbers add up to \(15\)? Answer: \(1\) and \(14\).

b) \(x^2+3x-4=0\) – what factors does \(-4\) decompose into? \(-2\) and \(2\), \(4\) and \(-1\), \(1\) and \(-4\). What pairs of numbers add up to \(-3\)? Answer: \(1\) and \(-4\).

c) \(x^2+9x+20=0\) – what factors does \(20\) decompose into? \(4\) and \(5\), \(-4\) and \(-5\), \(2\) and \(10\), \(-2\) and \(-10\ ), \(-20\) and \(-1\), \(20\) and \(1\). What pairs of numbers add up to \(-9\)? Answer: \(-4\) and \(-5\).

d) \(x^2-88x+780=0\) – what factors does \(780\) decompose into? \(390\) and \(2\). Will they add up to \(88\)? No. What other multipliers does \(780\) have? \(78\) and \(10\). Will they add up to \(88\)? Yes. Answer: \(78\) and \(10\).

It is not necessary to expand the last term into all possible factors (as in the last example). You can immediately check whether their sum gives \(-p\).

Important! Vieta's theorem and the converse theorem only work with , that is, one for which the coefficient of \(x^2\) is equal to one. If we were initially given a non-reduced equation, then we can make it reduced by simply dividing by the coefficient in front of \(x^2\).

For example, let the equation \(2x^2-4x-6=0\) be given and we want to use one of Vieta’s theorems. But we can’t, since the coefficient of \(x^2\) is equal to \(2\). Let's get rid of it by dividing the entire equation by \(2\).

\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)

Ready. Now you can use both theorems.

Answers to frequently asked questions

Question: Using Vieta's theorem, you can solve any ?
Answer: Unfortunately no. If the equation does not contain integers or the equation has no roots at all, then Vieta’s theorem will not help. In this case you need to use discriminant . Fortunately, 80% of the equations in school mathematics have integer solutions.

Vieta's theorem (more precisely, the theorem inverse to Vieta's theorem) allows you to reduce the time for solving quadratic equations. You just need to know how to use it. How to learn to solve quadratic equations using Vieta's theorem? It's not difficult if you think about it a little.

Now we will only talk about solving the reduced quadratic equation using Vieta’s theorem. A reduced quadratic equation is an equation in which a, that is, the coefficient of x², is equal to one. It is also possible to solve quadratic equations that are not given using Vieta’s theorem, but at least one of the roots is not an integer. They are more difficult to guess.

The inverse theorem to Vieta's theorem states: if the numbers x1 and x2 are such that

then x1 and x2 are the roots of the quadratic equation

When solving a quadratic equation using Vieta's theorem, only 4 options are possible. If you remember the line of reasoning, you can learn to find whole roots very quickly.

I. If q is a positive number,

this means that the roots x1 and x2 are numbers of the same sign (since only multiplying numbers with the same signs produces a positive number).

I.a. If -p is a positive number, (respectively, p<0), то оба корня x1 и x2 — положительные числа (поскольку складывали числа одного знака и получили положительное число).

I.b. If -p is a negative number, (respectively, p>0), then both roots are negative numbers (we added numbers of the same sign and got a negative number).

II. If q is a negative number,

this means that the roots x1 and x2 have different signs (when multiplying numbers, a negative number is obtained only when the signs of the factors are different). In this case, x1 + x2 is no longer a sum, but a difference (after all, when adding numbers with different signs, we subtract the smaller from the larger in absolute value). Therefore, x1+x2 shows how much the roots x1 and x2 differ, that is, how much one root is greater than the other (in absolute value).

II.a. If -p is a positive number, (that is, p<0), то больший (по модулю) корень — положительное число.

II.b. If -p is a negative number, (p>0), then the larger (modulo) root is a negative number.

Let's consider solving quadratic equations using Vieta's theorem using examples.

Solve the given quadratic equation using Vieta’s theorem:

Here q=12>0, so the roots x1 and x2 are numbers of the same sign. Their sum is -p=7>0, so both roots are positive numbers. We select integers whose product is equal to 12. These are 1 and 12, 2 and 6, 3 and 4. The sum is 7 for the pair 3 and 4. This means that 3 and 4 are the roots of the equation.

In this example, q=16>0, which means that the roots x1 and x2 are numbers of the same sign. Their sum is -p=-10<0, поэтому оба корня — отрицательные числа. Подбираем числа, произведение которых равно 16. Это 1 и 16, 2 и 8, 4 и 4. Сумма 2 и 8 равна 10, а раз нужны отрицательные числа, то искомые корни — это -2 и -8.

Here q=-15<0, что означает, что корни x1 и x2 — числа разных знаков. Поэтому 2 — это уже не их сумма, а разность, то есть числа отличаются на 2. Подбираем числа, произведение которых равно 15, отличающиеся на 2. Произведение равно 15 у 1 и 15, 3 и 5. Отличаются на 2 числа в паре 3 и 5. Поскольку -p=2>0, then the larger number is positive. So the roots are 5 and -3.

q=-36<0, значит, корни x1 и x2 имеют разные знаки. Тогда 5 — это то, насколько отличаются x1 и x2 (по модулю, то есть пока что без учета знака). Среди чисел, произведение которых равно 36: 1 и 36, 2 и 18, 3 и 12, 4 и 9 — выбираем пару, в которой числа отличаются на 5. Это 4 и 9. Осталось определить их знаки. Поскольку -p=-5<0, бОльшее число имеет знак минус. Поэтому корни данного уравнения равны -9 и 4.