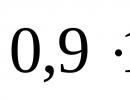Razvijanje prognoze metodom najmanjih kvadrata. Primjer rješavanja problema. Analiza linearne regresije para Izračunavanje najmanjih kvadrata
Aproksimacija eksperimentalnih podataka je metoda koja se temelji na zamjeni eksperimentalno dobivenih podataka analitičkom funkcijom koja najbliže prolazi ili se podudara u čvornim točkama s izvornim vrijednostima (podaci dobiveni tijekom eksperimenta ili eksperimenta). Trenutno postoje dva načina za definiranje analitičke funkcije:
Koristeći konstrukciju interpolacijski polinom n-stepen koji prolazi direktno kroz sve tačke dati niz podataka. IN u ovom slučaju aproksimirajuća funkcija je predstavljena kao: interpolacijski polinom u Lagrangeovom obliku ili interpolacijski polinom u Newtonovom obliku.
Konstruiranjem n-stepenog aproksimiranog polinoma koji prolazi u neposrednoj blizini tačaka iz datog niza podataka. Dakle, aproksimirajuća funkcija izglađuje sav slučajni šum (ili greške) koji se može pojaviti tijekom eksperimenta: izmjerene vrijednosti tijekom eksperimenta zavise od slučajnih faktora koji fluktuiraju u skladu sa svojim vlastitim slučajni zakoni(greške mjerenja ili instrumenta, nepreciznost ili eksperimentalne greške). U ovom slučaju, aproksimirajuća funkcija se određuje metodom najmanjih kvadrata.
Metoda najmanjeg kvadrata(u engleskoj književnosti Ordinary Least Squares, OLS) - matematička metoda, na osnovu definicije aproksimirajuće funkcije, koja je konstruisana u najbližoj blizini tačaka iz datog niza eksperimentalnih podataka. Bliskost izvorne i aproksimirajuće funkcije F(x) određena je numeričkom mjerom, odnosno: zbir kvadrata odstupanja eksperimentalnih podataka od aproksimirajuće krive F(x) treba da bude najmanji.
Aproksimirajuća kriva konstruirana metodom najmanjih kvadrata
Koristi se metoda najmanjih kvadrata:
Za rješavanje preodređenih sistema jednačina kada broj jednačina premašuje broj nepoznatih;
Za pronalaženje rješenja u slučaju običnog (ne poništenog) nelinearni sistemi jednadžbe;
Za aproksimaciju vrijednosti tačaka nekom aproksimirajućom funkcijom.
Aproksimirajuća funkcija metodom najmanjih kvadrata određena je iz uvjeta minimalnog zbira kvadrata odstupanja izračunate aproksimativne funkcije iz datog niza eksperimentalnih podataka. Ovaj kriterij metode najmanjih kvadrata zapisuje se kao sljedeći izraz:

Vrijednosti izračunate aproksimirajuće funkcije u čvornim točkama,
Dati niz eksperimentalnih podataka na čvornim tačkama.
Kvadratni kriterij ima niz “dobrih” svojstava, kao što je diferencijabilnost, pružajući jedinstveno rješenje problema aproksimacije sa polinomskim aproksimirajućim funkcijama.
U zavisnosti od uslova problema, aproksimirajuća funkcija je polinom stepena m
Stepen aproksimirajuće funkcije ne zavisi od broja čvornih tačaka, ali njena dimenzija uvek mora biti manja od dimenzije (broja tačaka) datog eksperimentalnog niza podataka.
![]()
∙ Ako je stepen aproksimirajuće funkcije m=1, tada tabelarnu funkciju aproksimiramo ravnom linijom (linearna regresija).
∙ Ako je stepen aproksimirajuće funkcije m=2, tada tabelu funkciju aproksimiramo kvadratnom parabolom (kvadratna aproksimacija).
∙ Ako je stepen aproksimirajuće funkcije m=3, tada tabelu funkciju aproksimiramo kubnom parabolom (kubična aproksimacija).
U opštem slučaju, kada je potrebno konstruisati aproksimativni polinom stepena m za date vrednosti tabele, uslov za minimum zbira kvadrata odstupanja po svim čvornim tačkama se prepisuje u sledećem obliku:
![]() - nepoznati koeficijenti aproksimirajućeg polinoma stepena m;
- nepoznati koeficijenti aproksimirajućeg polinoma stepena m;
Broj navedenih vrijednosti u tabeli.
Neophodan uslov za postojanje minimuma funkcije je jednakost sa nulom njenih parcijalnih izvoda u odnosu na nepoznate varijable ![]() . Kao rezultat dobijamo sledeći sistem jednačina:
. Kao rezultat dobijamo sledeći sistem jednačina:

Hajde da transformišemo rezultirajući linearni sistem jednačina: otvorimo zagrade i pomerimo slobodne članove na desnu stranu izraza. Kao rezultat, rezultujući sistem linearnih algebarskih izraza biće napisan u sledećem obliku:

Ovaj sistem linearnih algebarskih izraza može se prepisati u matričnom obliku:

Rezultat je bio sistem linearne jednačine dimenzija m+1, koja se sastoji od m+1 nepoznatih. Ovaj sistem se može riješiti bilo kojom metodom za rješavanje linearnih algebarskih jednadžbi (na primjer, Gausovom metodom). Kao rezultat rješenja naći će se nepoznati parametri aproksimirajuće funkcije koji daju minimalni zbir kvadrata odstupanja aproksimirajuće funkcije od izvornih podataka, tj. najbolja moguća kvadratna aproksimacija. Treba imati na umu da ako se promijeni čak i jedna vrijednost izvornih podataka, svi koeficijenti će promijeniti svoje vrijednosti, jer su u potpunosti određeni izvornim podacima.
Aproksimacija izvornih podataka linearnom zavisnošću
(linearna regresija)
Kao primjer, razmotrite tehniku za određivanje aproksimativne funkcije, koja je data u obliku linearna zavisnost. U skladu sa metodom najmanjih kvadrata, uslov za minimum zbira kvadrata odstupanja zapisuje se u sledećem obliku:
Koordinate čvorova tablice;
Nepoznati koeficijenti aproksimirajuće funkcije, koja je specificirana kao linearna ovisnost.
Neophodan uslov za postojanje minimuma funkcije je jednakost nuli njenih parcijalnih izvoda u odnosu na nepoznate varijable. Kao rezultat dobijamo sledeći sistem jednačina:

Hajde da transformišemo rezultujući linearni sistem jednačina.

Rešavamo rezultujući sistem linearnih jednačina. Koeficijenti aproksimirajuće funkcije u analitičkom obliku određuju se na sljedeći način (Cramerova metoda):

Ovi koeficijenti osiguravaju konstrukciju linearne aproksimirajuće funkcije u skladu s kriterijem minimiziranja sume kvadrata aproksimirajuće funkcije iz zadanih tabličnih vrijednosti (eksperimentalnih podataka).
Algoritam za implementaciju metode najmanjih kvadrata
1. Početni podaci:
Naveden je niz eksperimentalnih podataka sa brojem mjerenja N
Specificira se stepen aproksimirajućeg polinoma (m).
2. Algoritam proračuna:
2.1. Koeficijenti se određuju za konstruisanje sistema jednačina sa dimenzijama

Koeficijenti sistema jednadžbi (lijeva strana jednadžbe)
![]()
![]() - indeks broja kolone kvadratne matrice sistema jednačina
- indeks broja kolone kvadratne matrice sistema jednačina

Slobodni članovi sistema linearnih jednačina (desna strana jednačine)
![]() - indeks broja reda kvadratne matrice sistema jednačina
- indeks broja reda kvadratne matrice sistema jednačina
2.2. Formiranje sistema linearnih jednadžbi sa dimenzijom .

2.3. Rješavanje sistema linearnih jednadžbi za određivanje nepoznatih koeficijenata aproksimirajućeg polinoma stepena m.
2.4. Određivanje sume kvadrata odstupanja aproksimirajućeg polinoma od originalnih vrijednosti u svim čvornim točkama

Pronađena vrijednost zbira kvadrata odstupanja je najmanja moguća.
Aproksimacija pomoću drugih funkcija
Treba napomenuti da se prilikom aproksimacije izvornih podataka u skladu s metodom najmanjih kvadrata, ponekad kao aproksimirajuća funkcija koriste logaritamska funkcija, eksponencijalna funkcija i funkcija stepena.
Logaritamska aproksimacija
Razmotrimo slučaj kada je data aproksimirajuća funkcija logaritamska funkcija tip:
Suština metode najmanjih kvadrata je u pronalaženju parametara modela trenda koji najbolje opisuje tendenciju razvoja bilo koje slučajne pojave u vremenu ili prostoru (trend je linija koja karakteriše tendenciju ovog razvoja). Zadatak metode najmanjih kvadrata (LSM) svodi se na pronalaženje ne samo nekog trend modela, već na pronalaženje najboljeg ili optimalnog modela. Ovaj model će biti optimalan ako je zbroj kvadratnih odstupanja između uočenih stvarnih vrijednosti i odgovarajućih izračunatih vrijednosti trenda minimalan (najmanji):
gdje je kvadratna devijacija između uočene stvarne vrijednosti
i odgovarajuću izračunatu vrijednost trenda,
Stvarna (uočena) vrijednost fenomena koji se proučava,
Izračunata vrijednost modela trenda,
Broj zapažanja fenomena koji se proučava.
MNC se vrlo rijetko koristi samostalno. U pravilu se najčešće koristi samo kao neophodna tehnička tehnika u studijama korelacije. Treba imati na umu da informaciona osnova OLS-a može biti samo pouzdana statistička serija, a broj zapažanja ne bi trebao biti manji od 4, u suprotnom procedure izglađivanja OLS-a mogu izgubiti zdrav razum.
MNC komplet alata se svodi na sljedeće procedure:
Prva procedura. Ispostavlja se postoji li uopće tendencija promjene rezultantnog atributa kada se promijeni odabrani faktor-argument, ili drugim riječima, postoji li veza između “ at " i " X ».
Drugi postupak. Utvrđuje se koja linija (trajektorija) može najbolje opisati ili okarakterizirati ovaj trend.
Treći postupak.
Primjer. Recimo da imamo informacije o prosječnom prinosu suncokreta za farmu koja se proučava (Tabela 9.1).
Tabela 9.1
|
Broj zapažanja |
||||||||||
|
Produktivnost, c/ha |
Budući da je nivo tehnologije proizvodnje suncokreta u našoj zemlji ostao praktično nepromenjen u poslednjih 10 godina, to znači da su, očigledno, fluktuacije prinosa u analiziranom periodu u velikoj meri zavisile od fluktuacija vremenskih i klimatskih uslova. Da li je ovo zaista istina?
Prva OLS procedura. Ispituje se hipoteza o postojanju trenda promene prinosa suncokreta u zavisnosti od promena vremenskih i klimatskih uslova tokom analiziranih 10 godina.
U ovom primjeru, za " y " preporučljivo je uzeti prinos suncokreta, a za " x » – broj posmatrane godine u analiziranom periodu. Testiranje hipoteze o postojanju bilo kakvog odnosa između " x " i " y „može se uraditi na dva načina: ručno i korišćenjem kompjuterskih programa. Naravno, uz dostupnost kompjuterske tehnologije, ovaj problem se može riješiti sam od sebe. Ali da bismo bolje razumjeli MNC alate, preporučljivo je testirati hipotezu o postojanju veze između “ x " i " y » ručno, kada su pri ruci samo olovka i običan kalkulator. U takvim slučajevima, hipotezu o postojanju trenda najbolje je provjeriti vizualno prema lokaciji grafička slika analizirana serija dinamike - korelaciono polje:


Korelacijsko polje u našem primjeru nalazi se oko linije koja se polako povećava. To samo po sebi ukazuje na postojanje određenog trenda promjene prinosa suncokreta. Nemoguće je govoriti o prisutnosti bilo kakve tendencije samo kada korelacijsko polje izgleda kao krug, krug, strogo vertikalni ili striktno horizontalni oblak, ili se sastoji od haotično raštrkanih tačaka. U svim ostalim slučajevima, hipoteza o postojanju veze između “ x " i " y “, i nastaviti istraživanje.
Druga OLS procedura. Utvrđuje se koja linija (traktorija) najbolje može opisati ili okarakterizirati trend promjene prinosa suncokreta u analiziranom periodu.
Ako imate kompjutersku tehnologiju, odabir optimalnog trenda se dešava automatski. U "ručnoj" obradi odabir optimalne funkcije se po pravilu vrši vizualno - prema lokaciji korelacionog polja. Odnosno, na osnovu tipa grafa, bira se jednačina linije koja najbolje odgovara empirijskom trendu (stvarnoj putanji).
Kao što znate, u prirodi postoji ogromna raznolikost funkcionalne zavisnosti, stoga je vizuelno analizirati čak i mali dio njih izuzetno teško. Srećom, u realnoj ekonomskoj praksi većina odnosa može se prilično precizno opisati ili parabolom, ili hiperbolom, ili pravom linijom. S tim u vezi, uz “ručnu” opciju odabira najbolje funkcije, možete se ograničiti samo na ova tri modela.
|
hiperbola: |
||
|
|
|
Parabola drugog reda: ![]() :
:

Lako je uočiti da je u našem primjeru trend promjene prinosa suncokreta u analiziranih 10 godina najbolje okarakterisan ravnom linijom, pa će jednačina regresije biti jednačina prave linije.
Treći postupak. Izračunavaju se parametri regresione jednačine koja karakteriše ovu liniju, odnosno određuje se analitička formula koja opisuje najbolji model trenda.
Pronalaženje vrijednosti parametara jednadžbe regresije, u našem slučaju parametara i , je srž OLS-a. Ovaj proces svodi na rješavanje sistema normalnih jednačina.
 (9.2)
(9.2)
Ovaj sistem jednačina može se prilično lako riješiti Gaussovom metodom. Podsjetimo da su kao rezultat rješenja, u našem primjeru, pronađene vrijednosti parametara i. Dakle, pronađena jednačina regresije će imati sljedeći oblik: ![]()
Ekstrapolacija - ovo je metoda naučno istraživanje, koji se zasniva na diseminaciji prošlih i sadašnjih trendova, obrazaca, veza sa budućim razvojem objekta prognoze. Metode ekstrapolacije uključuju metoda pokretnog prosjeka, metoda eksponencijalnog izglađivanja, metoda najmanjih kvadrata.
Essence metoda najmanjih kvadrata sastoji se u minimiziranju sume kvadrata odstupanja između posmatranih i izračunatih vrednosti. Izračunate vrijednosti se nalaze pomoću odabrane jednadžbe - jednadžbe regresije. Što je manja udaljenost između stvarnih vrijednosti i izračunatih, to je preciznija prognoza zasnovana na jednadžbi regresije.
Teorijska analiza suštine fenomena koji se proučava, čija se promjena odražava kroz vremensku seriju, služi kao osnova za odabir krive. Ponekad se u obzir uzimaju razmatranja o prirodi povećanja nivoa serije. Dakle, ako se očekuje rast proizvodnje na aritmetička progresija, zatim se izravnavanje izvodi u pravoj liniji. Ako se ispostavi da je rast in geometrijska progresija, tada se izravnavanje mora obaviti korištenjem eksponencijalne funkcije.
Radna formula za metodu najmanjih kvadrata : Y t+1 = a*X + b, gdje je t + 1 – period prognoze; Ut+1 – predviđeni indikator; a i b su koeficijenti; X je simbol vremena.
Izračunavanje koeficijenata a i b vrši se pomoću sljedećih formula:
gdje je, Uf – stvarne vrijednosti serije dinamike; n – broj nivoa vremenske serije;
Izglađivanje vremenskih serija metodom najmanjih kvadrata služi da se odrazi obrazac razvoja fenomena koji se proučava. U analitičkom izražavanju trenda, vrijeme se smatra nezavisnom varijablom, a nivoi serije djeluju kao funkcija ove nezavisne varijable.
Razvoj neke pojave ne zavisi od toga koliko je godina prošlo od početne tačke, već od toga koji su faktori uticali na njen razvoj, u kom pravcu i kojim intenzitetom. Odavde je jasno da je razvoj neke pojave tokom vremena rezultat djelovanja ovih faktora.
Ispravno utvrđivanje tipa krive, tipa analitičke zavisnosti od vremena jedan je od najtežih zadataka prediktivne analize. .
Odabir tipa funkcije koja opisuje trend, čiji se parametri određuju metodom najmanjih kvadrata, u većini slučajeva provodi se empirijski, konstruiranjem većeg broja funkcija i međusobnom poređenjem prema vrijednosti srednja kvadratna greška, izračunata po formuli:
gdje su UV stvarne vrijednosti serije dinamike; Ur – izračunate (izglađene) vrijednosti serije dinamike; n – broj nivoa vremenske serije; p – broj parametara definisanih u formulama koje opisuju trend (trend razvoja).
Nedostaci metode najmanjih kvadrata :
- kada pokušavate da opišete ekonomski fenomen koji se proučava pomoću matematičke jednačine, prognoza će biti tačna za kratak vremenski period i regresionu jednačinu treba ponovo izračunati kako nove informacije postanu dostupne;
- složenost odabira jednadžbe regresije koja je rješiva korištenjem standardnih kompjuterskih programa.
Primjer korištenja metode najmanjih kvadrata za razvoj prognoze
Zadatak . Postoje podaci koji karakterišu stopu nezaposlenosti u regionu, %
- Konstruisati prognozu stope nezaposlenosti u regionu za novembar, decembar, januar koristeći sledeće metode: pokretni prosek, eksponencijalno izglađivanje, najmanji kvadrati.
- Izračunajte greške u rezultirajućim prognozama koristeći svaku metodu.
- Uporedite rezultate i izvucite zaključke.
Rješenje najmanjih kvadrata
Da bismo to riješili, sastavit ćemo tabelu u kojoj ćemo napraviti potrebne proračune:
Definišimo simbol vremena kao sekvencijalno numerisanje perioda baze prognoze (kolona 3). Izračunajmo kolone 4 i 5. Određujemo izračunate vrijednosti serije Ur koristeći formulu Y t+1 = a*X + b, gdje je t + 1 period prognoze; Ut+1 – predviđeni indikator; a i b su koeficijenti; X je simbol vremena.
Određujemo koeficijente a i b koristeći sljedeće formule:
gdje je, Uf – stvarne vrijednosti serije dinamike; n je broj nivoa vremenske serije.
a = / = - 0,17
b = 22,13/10 – (-0,17)*55/10 = 3,15
Izračunavamo prosječnu relativnu grešku koristeći formulu:
ε = 28,63/10 = 2,86% tačnost prognoze visoko.
Zaključak : Poređenje rezultata dobijenih iz proračuna metoda pokretnog prosjeka , metoda eksponencijalnog izglađivanja i metodom najmanjih kvadrata, možemo reći da se prosječna relativna greška pri izračunavanju korištenjem metode eksponencijalnog glađenja nalazi u rasponu od 20-50%. To znači da je tačnost prognoze u ovom slučaju samo zadovoljavajuća.
U prvom i trećem slučaju tačnost prognoze je visoka, jer je prosječna relativna greška manja od 10%. Ali metoda pokretnog proseka omogućila je dobijanje pouzdanijih rezultata (prognoza za novembar - 1,52%, prognoza za decembar - 1,53%, prognoza za januar - 1,49%), pošto je prosečna relativna greška pri upotrebi ove metode najmanja - 1 ,13%.
Široko se koristi u ekonometriji u obliku jasne ekonomske interpretacije njenih parametara.
Linearna regresija se svodi na pronalaženje jednačine oblika
ili
Jednačina oblika dozvoljava na osnovu specificiranih vrijednosti parametara X imaju teorijske vrijednosti rezultantne karakteristike, zamjenjujući stvarne vrijednosti faktora u nju X.
Konstrukcija linearne regresije svodi se na procjenu njenih parametara - A I V. Procjene parametara linearne regresije mogu se pronaći korištenjem različitih metoda.
Klasičan pristup procjeni parametara linearne regresije temelji se na metoda najmanjih kvadrata(MNC).
Metoda najmanjih kvadrata nam omogućava da dobijemo takve procjene parametara A I V, pri čemu je zbir kvadrata odstupanja stvarnih vrijednosti rezultantne karakteristike (y) od izračunatog (teorijskog) minimum:
Da biste pronašli minimum funkcije, morate izračunati parcijalne izvode za svaki od parametara A I b i postavite ih jednakima nuli.
Označimo sa S, tada:
Transformacijom formule dobijamo sledeći sistem normalnih jednačina za procenu parametara A I V:
Rješavajući sistem normalnih jednačina (3.5) bilo metodom sekvencijalne eliminacije varijabli ili metodom determinanti, nalazimo tražene procjene parametara A I V.
Parametar V naziva se koeficijent regresije. Njegova vrijednost pokazuje prosječnu promjenu rezultata sa promjenom faktora za jednu jedinicu.
Jednačina regresije je uvijek dopunjena indikatorom bliskosti veze. Kada se koristi linearna regresija, takav pokazatelj je koeficijent linearne korelacije. Postoje različite modifikacije formule koeficijenta linearne korelacije. Neki od njih su dati u nastavku:
Kao što je poznato, koeficijent linearne korelacije je u granicama: -1 ≤ ≤ 1.
Za procjenu kvaliteta selekcije linearna funkcija izračunava se kvadrat
Koeficijent linearne korelacije tzv koeficijent odlučnosti. Koeficijent determinacije karakterizira udio varijanse rezultirajuće karakteristike y, objašnjeno regresijom, u ukupnoj varijansi rezultirajuće osobine:
Shodno tome, vrijednost 1 karakterizira udio varijanse y, uzrokovane uticajem drugih faktora koji nisu uzeti u obzir u modelu.
Pitanja za samokontrolu
1. Suština metode najmanjih kvadrata?
2. Koliko varijabli pruža parna regresija?
3. Koji koeficijent određuje bliskost veze između promjena?
4. U kojim granicama se utvrđuje koeficijent determinacije?
5. Procjena parametra b u korelaciono-regresionoj analizi?
1. Christopher Dougherty. Uvod u ekonometriju. - M.: INFRA - M, 2001 - 402 str.
2. S.A. Borodich. Ekonometrija. Minsk DOO “Novo znanje” 2001.
3. R.U. Rakhmetova Kratki kurs u ekonometriji. Tutorial. Almaty. 2004. -78p.
4. I.I. Eliseeva Econometrics. - M.: “Finansije i statistika”, 2002
5. Mjesečni informativno-analitički časopis.
Nelinearni ekonomski modeli. Modeli nelinearne regresije. Transformacija varijabli.
Nelinearni ekonomski modeli..
Transformacija varijabli.
Koeficijent elastičnosti.
Ako postoje nelinearni odnosi između ekonomskih fenomena, onda se oni izražavaju pomoću odgovarajućih nelinearnih funkcija: na primjer, jednakostranična hiperbola , parabole drugog stepena itd.
Postoje dvije klase nelinearnih regresija:
1. Regresije koje su nelinearne u odnosu na objašnjavajuće varijable uključene u analizu, ali linearne u odnosu na procijenjene parametre, na primjer:
Polinomi različitih stupnjeva - , ;
Jednakostranična hiperbola - ;
Semilogaritamska funkcija - .
2. Regresije koje su nelinearne u parametrima koji se procjenjuju, na primjer:
Snaga - ;
Demonstrativna - ;
Eksponencijalno - .
Ukupan zbroj kvadrata odstupanja pojedinačnih vrijednosti rezultirajuće karakteristike at od prosječne vrijednosti uzrokovano je uticajem mnogih razloga. Uvjetno podijelimo cijeli niz razloga u dvije grupe: faktor koji se proučava x I drugi faktori.
Ako faktor ne utječe na rezultat, tada je linija regresije na grafu paralelna s osom Oh I
Tada je cijela varijansa rezultirajuće karakteristike posljedica utjecaja drugih faktora i ukupni zbir kvadrata odstupanja će se poklopiti sa ostatkom. Ako drugi faktori ne utiču na rezultat, onda y tied With X funkcionalno i rezidualni zbir kvadrata je nula. U ovom slučaju, zbir kvadrata odstupanja objašnjenih regresijom je isti kao i ukupni zbir kvadrata.
Budući da ne leže sve tačke korelacionog polja na regresijskoj liniji, njihovo rasipanje se uvek javlja kao rezultat uticaja faktora X, odnosno regresija at By X, i uzrokovane drugim uzrocima (neobjašnjive varijacije). Pogodnost linije regresije za predviđanje zavisi od toga koji deo ukupne varijacije osobine at objašnjava objašnjenu varijaciju
Očigledno, ako je zbir kvadrata odstupanja zbog regresije veći od preostalog zbira kvadrata, tada je jednadžba regresije statistički značajna i faktor X ima značajan uticaj na rezultat u.
, tj. sa brojem slobode nezavisne varijacije karakteristike. Broj stepeni slobode povezan je sa brojem jedinica populacije n i brojem konstanti koje se iz njega određuju. U odnosu na problem koji se proučava, broj stepeni slobode treba da pokaže koliko je nezavisnih odstupanja od P
Procjena značaja regresione jednačine u cjelini data je korištenjem F-Fišerov kriterijum. U ovom slučaju, postavlja se nulta hipoteza da je koeficijent regresije jednaka nuli, tj. b = 0, a samim tim i faktor X ne utiče na rezultat u.
Neposrednom izračunavanju F-testa prethodi analiza varijanse. Centralno mjesto u njemu zauzima dekompozicija ukupan iznos kvadratne devijacije varijable at od prosječne vrijednosti at na dva dijela - "objašnjeno" i "neobjašnjeno":
Ukupan zbroj kvadrata odstupanja;
Zbir kvadratnog odstupanja objašnjenog regresijom;
Preostali zbir kvadrata odstupanja.
Svaki zbir odstupanja na kvadrat povezan je sa brojem stepeni slobode , tj. sa brojem slobode nezavisne varijacije karakteristike. Broj stepena slobode povezan je sa brojem populacijskih jedinica n i sa brojem konstanti određenim iz njega. U odnosu na problem koji se proučava, broj stepeni slobode treba da pokaže koliko je nezavisnih odstupanja od P moguće potrebno za formiranje date sume kvadrata.
Disperzija po stepenu slobodeD.
F-odnosi (F-test):
Ako je nulta hipoteza tačna, tada se faktor i preostale varijanse ne razlikuju jedna od druge. Za H 0 potrebno je opovrgavanje kako bi disperzija faktora nekoliko puta premašila disperziju ostatka. Engleski statističar Snedekor razvio je tabele kritičnih vrednosti F- odnosi na različitim nivoima značaja nulte hipoteze i razni brojevi stepena slobode. Vrijednost tabele F-kriterijum je maksimalna vrijednost omjera varijansi koja se može pojaviti u slučaju slučajne divergencije za dati nivo vjerovatnoće prisustva nulte hipoteze. Izračunata vrijednost F-relacije se smatraju pouzdanim ako je o veće od tabele.
U ovom slučaju, nulta hipoteza o nepostojanju veze između znakova se odbacuje i izvodi se zaključak o značaju ovog odnosa: F činjenica > F tabela H 0 je odbijen.
Ako je vrijednost manja od prikazane u tabeli F činjenica ‹, F tabela, tada je vjerovatnoća nulte hipoteze veća od određenog nivoa i ne može se odbaciti bez ozbiljnog rizika od izvođenja pogrešnog zaključka o postojanju veze. U ovom slučaju, jednačina regresije se smatra statistički beznačajnom. Ali on ne odstupa.
Standardna greška koeficijenta regresije
Da bi se procijenila značajnost koeficijenta regresije, njegova vrijednost se upoređuje sa njegovom standardnom greškom, odnosno utvrđuje se stvarna vrijednost t-Studentov t-test: koji se zatim poredi sa tabelarnom vrednošću na određenom nivou značajnosti i broju stepeni slobode ( n- 2).
Standardna greška parametra A:
Značajnost koeficijenta linearne korelacije se provjerava na osnovu veličine greške koeficijent korelacije t r:
Ukupna varijansa osobina X:
Višestruka linearna regresija
Izgradnja modela
Višestruka regresija predstavlja regresiju rezultantnog znaka sa dva i veliki broj faktore, odnosno model forme
Regresija može dati dobre rezultate u modeliranju ako se zanemari uticaj drugih faktora koji utiču na predmet proučavanja. Ponašanje pojedinih ekonomskih varijabli ne može se kontrolisati, odnosno nije moguće osigurati jednakost svih ostalih uslova za procjenu uticaja jednog faktora koji se proučava. U ovom slučaju, trebali biste pokušati identificirati utjecaj drugih faktora tako što ćete ih uvesti u model, tj. konstruirati jednadžbu višestruke regresije: y = a+b 1 x 1 +b 2 +…+b p x p + .
Osnovni cilj višestruke regresije je da se izgradi model sa velikim brojem faktora, pri čemu se utvrđuje uticaj svakog od njih posebno, kao i njihov kombinovani uticaj na modelirani indikator. Specifikacija modela uključuje dva niza pitanja: izbor faktora i izbor vrste regresijske jednačine
Metoda najmanjeg kvadrata koristi se za procjenu parametara regresione jednadžbe.Jedna od metoda za proučavanje stohastičkih odnosa između karakteristika je regresiona analiza.
Regresiona analiza predstavlja izvođenje regresione jednačine, uz pomoć koje se pronalazi prosječna vrijednost slučajne varijable (atribut rezultata) ako je poznata vrijednost druge (ili druge) varijabli (faktor-atributa). Uključuje sljedeće korake:
- izbor oblika veze (vrsta analitičke regresione jednačine);
- procjena parametara jednadžbe;
- procjena kvaliteta analitičke regresione jednačine.
U slučaju linearne parne veze, jednačina regresije će imati oblik: y i =a+b·x i +u i . Opcije zadata jednačina a i b su procijenjeni iz podataka statističko posmatranje x i y. Rezultat takve procjene je jednadžba: , gdje su procjene parametara a i b , je vrijednost rezultirajućeg atributa (varijable) dobijene iz jednačine regresije (izračunata vrijednost).
Najčešće se koristi za procjenu parametara metoda najmanjih kvadrata (LSM).
Metoda najmanjih kvadrata daje najbolje (dosljedne, efikasne i nepristrasne) procjene parametara regresione jednačine. Ali samo ako su ispunjene određene pretpostavke u vezi sa slučajnim članom (u) i nezavisnom varijablom (x) (vidi OLS pretpostavke).
Problem procjene parametara jednadžbe linearnog para metodom najmanjih kvadrata je kako slijedi: da se dobiju takve procjene parametara , , kod kojih je zbroj kvadrata odstupanja stvarnih vrijednosti rezultujuće karakteristike - y i od izračunatih vrijednosti - minimalan.
Formalno OLS kriterijum može se napisati ovako:  .
.
Klasifikacija metoda najmanjih kvadrata
- Metoda najmanjeg kvadrata.
- Metoda maksimalne vjerovatnoće (za normalan klasični model linearne regresije, postulira se normalnost reziduala regresije).
- Generalizirana metoda najmanjih kvadrata OLS se koristi u slučaju autokorelacije grešaka iu slučaju heteroskedastičnosti.
- Metoda ponderiranih najmanjih kvadrata ( poseban slučaj OLS sa heteroskedastičnim rezidualima).
Hajde da ilustrujemo poentu klasična metoda najmanji kvadrati grafički. Da bismo to uradili, konstruisaćemo dijagram raspršenja na osnovu podataka posmatranja (x i, y i, i=1; n) u pravougaonom koordinatnom sistemu (takav dijagram raspršenja naziva se korelaciono polje). Pokušajmo odabrati pravu liniju koja je najbliža tačkama korelacionog polja. Prema metodi najmanjih kvadrata, linija se bira tako da zbir kvadrata vertikalnih udaljenosti između tačaka korelacionog polja i ove prave bude minimalan. 
Matematička notacija za ovaj problem:  .
.
Poznate su nam vrijednosti y i i x i =1...n; ovo su podaci opservacije. U S funkciji predstavljaju konstante. Varijable u ovoj funkciji su potrebne procjene parametara - , . Da bi se pronašao minimum funkcije dvije varijable, potrebno je izračunati parcijalne izvode ove funkcije za svaki od parametara i izjednačiti ih sa nulom, tj.  .
.
Kao rezultat, dobijamo sistem od 2 normalne linearne jednadžbe: 
Rješavajući ovaj sistem, nalazimo potrebne procjene parametara: 
Ispravnost proračuna parametara regresione jednačine može se provjeriti poređenjem iznosa (može doći do neslaganja zbog zaokruživanja proračuna).
Da biste izračunali procjene parametara, možete napraviti tabelu 1.
Znak koeficijenta regresije b ukazuje na smjer odnosa (ako je b >0, odnos je direktan, ako je b<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Formalno, vrijednost parametra a je prosječna vrijednost y sa x jednakim nuli. Ako faktor-atribut nema i ne može imati nultu vrijednost, onda gornja interpretacija parametra a nema smisla.
Procjena bliskosti odnosa između karakteristika
izvršeno korištenjem koeficijenta linearne parne korelacije - r x,y. Može se izračunati pomoću formule:  . Osim toga, koeficijent korelacije linearnog para može se odrediti preko koeficijenta regresije b:
. Osim toga, koeficijent korelacije linearnog para može se odrediti preko koeficijenta regresije b:  .
.
Raspon prihvatljivih vrijednosti koeficijenta linearne korelacije para je od –1 do +1. Znak koeficijenta korelacije ukazuje na smjer odnosa. Ako je r x, y >0, onda je veza direktna; ako je r x, y<0, то связь обратная.
Ako je ovaj koeficijent po veličini blizu jedinice, onda se odnos između karakteristika može tumačiti kao prilično blizak linearni. Ako je njegov modul jednak jednom ê r x , y ê =1, tada je odnos između karakteristika funkcionalno linearan. Ako su karakteristike x i y linearno nezavisne, tada je r x,y blizu 0.
Za izračunavanje r x,y možete koristiti i tabelu 1.
Da biste procijenili kvalitetu rezultirajuće regresione jednačine, izračunajte teoretski koeficijent determinacije - R 2 yx:  ,
,
gdje je d 2 varijansa y objašnjena jednadžbom regresije;
e 2 - rezidualna (neobjašnjena jednadžbom regresije) varijansa y;
s 2 y - ukupna (ukupna) varijansa y.
Koeficijent determinacije karakteriše udio varijacije (disperzije) rezultujućeg atributa y objašnjen regresijom (i, posljedično, faktorom x) u ukupnoj varijaciji (disperziji) y. Koeficijent determinacije R 2 yx ima vrijednosti od 0 do 1. Shodno tome, vrijednost 1-R 2 yx karakterizira udio varijanse y uzrokovane utjecajem drugih faktora koji nisu uzeti u obzir u modelu i greškama u specifikaciji.
Sa uparenom linearnom regresijom, R 2 yx =r 2 yx.