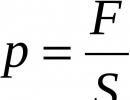Pronađi najmanji period u primjerima funkcije. Lekcija "Periodičnost funkcija y=sinx, y=cosx"
Cilj: sumirati i sistematizovati znanja učenika na temu „Periodičnost funkcija“; razviti vještine primjene svojstava periodične funkcije, pronalaženja najmanjeg pozitivnog perioda funkcije, konstruiranja grafova periodičnih funkcija; promovirati interesovanje za proučavanje matematike; neguju zapažanje i tačnost.
Oprema: kompjuter, multimedijalni projektor, kartice sa zadacima, slajdovi, satovi, tablice ukrasa, elementi narodnih zanata
“Matematika je ono što ljudi koriste da kontrolišu prirodu i sebe.”
A.N. Kolmogorov
Napredak lekcije
I. Organizaciona faza.
Provjera spremnosti učenika za čas. Izvijestite o temi i ciljevima lekcije.
II. Provjera domaćeg.
Provjeravamo domaće zadatke pomoću uzoraka i raspravljamo o najtežim točkama.
III. Generalizacija i sistematizacija znanja.
1. Oralni frontalni rad.
Teorijska pitanja.
1) Formirajte definiciju perioda funkcije
2) Imenujte najmanji pozitivni period funkcija y=sin(x), y=cos(x)
3). Koji je najmanji pozitivni period funkcija y=tg(x), y=ctg(x)
4) Koristeći krug dokažite ispravnost relacija:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z
5) Kako nacrtati periodičnu funkciju?
Oralne vježbe.
1) Dokažite sljedeće relacije
a) sin(740º) = sin(20º)
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º)
2. Dokazati da je ugao od 540º jedan od perioda funkcije y= cos(2x)
3. Dokazati da je ugao od 360º jedan od perioda funkcije y=tg(x)
4. Transformirajte ove izraze tako da uglovi uključeni u njih ne prelaze 90º u apsolutnoj vrijednosti.
a) tg375º
b)ctg530º
c) sin1268º
d)cos(-7363º)
5. Gdje ste naišli na riječi PERIOD, PERIODIČNOST?
Odgovor učenika: Period u muzici je struktura u kojoj je predstavljena manje ili više cjelovita muzička misao. Geološki period je deo jedne ere i podeljen je na epohe sa periodom od 35 do 90 miliona godina.
Poluživot radioaktivne supstance. Periodični razlomak. Periodične publikacije su štampane publikacije koje se pojavljuju u strogo određenim rokovima. Mendeljejevljev periodični sistem.
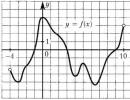
6. Slike prikazuju dijelove grafova periodičnih funkcija. Odredite period funkcije. Odredite period funkcije.

Odgovori: T=2; T=2; T=4; T=8.
7. Gdje ste se u životu susreli sa konstrukcijom ponavljajućih elemenata?
Odgovor učenika: Elementi ornamenta, narodna umjetnost.

IV. Kolektivno rješavanje problema.
(Rješavanje zadataka na slajdovima.)
Razmotrimo jedan od načina proučavanja funkcije za periodičnost.
Ova metoda izbjegava poteškoće povezane s dokazivanjem da je određeni period najmanji, a također eliminiše potrebu da se bavimo pitanjima o aritmetičkim operacijama nad periodičnim funkcijama i periodičnosti složene funkcije. Obrazloženje se zasniva samo na definiciji periodične funkcije i na sljedećoj činjenici: ako je T period funkcije, onda je nT(n?0) njen period.
Zadatak 1. Pronađite najmanji pozitivni period funkcije f(x)=1+3(x+q>5)
Rješenje: Pretpostavimo da je T-period ove funkcije. Tada je f(x+T)=f(x) za sve x € D(f), tj.
1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)
Stavimo x=-0.25 i dobijamo
(T)=0 T=n, n € Z
Dobili smo da su svi periodi dotične funkcije (ako postoje) među cijelim brojevima. Odaberimo najmanji pozitivan broj među ovim brojevima. Ovo je 1. Hajde da proverimo da li će to zaista biti period 1.
f(x+1) =3(x+1+0,25)+1
Kako je (T+1)=(T) za bilo koji T, onda je f(x+1)=3((x+0.25)+1)+1=3(x+0.25)+1=f(x), tj. 1 – tačka f. Kako je 1 najmanji od svih pozitivnih cijelih brojeva, onda je T=1.
Zadatak 2. Pokazati da je funkcija f(x)=cos 2 (x) periodična i pronaći njen glavni period.

Problem 3. Pronađite glavni period funkcije
f(x)=sin(1.5x)+5cos(0.75x)
Pretpostavimo T-period funkcije, tada je za bilo koje x relacija važeća
sin1.5(x+T)+5cos0.75(x+T)=sin(1.5x)+5cos(0.75x)
Ako je x=0, onda
sin(1.5T)+5cos(0.75T)=sin0+5cos0
sin(1.5T)+5cos(0.75T)=5
Ako je x=-T, onda
sin0+5cos0=sin(-1.5T)+5cos0.75(-T)
5= – sin(1.5T)+5cos(0.75T)
| sin(1.5T)+5cos(0.75T)=5 – sin(1.5T)+5cos(0.75T)=5 |
Zbrajanjem dobijamo:
10cos(0.75T)=10
2π n, n € Z
Odaberimo najmanji pozitivan broj od svih “sumnjivih” brojeva za period i provjerimo da li je to period za f. Ovaj broj
f(x+)=sin(1,5x+4π )+5cos(0,75x+2π)= sin(1,5x)+5cos(0,75x)=f(x)
To znači da je ovo glavni period funkcije f.
Problem 4. Provjerimo da li je funkcija f(x)=sin(x) periodična
Neka je T period funkcije f. Zatim za bilo koji x
sin|x+T|=sin|x|
Ako je x=0, onda sin|T|=sin0, sin|T|=0 T=π n, n € Z.
Pretpostavimo. Da je za neko n broj π n period
razmatrana funkcija π n>0. Tada sin|π n+x|=sin|x|

Ovo implicira da n mora biti i paran i neparan broj, ali to je nemoguće. Stoga ova funkcija nije periodična.
Zadatak 5. Provjerite je li funkcija periodična
f(x)= 
Neka je T onda period od f
 , dakle sinT=0, T=π n, n € Z. Pretpostavimo da je za neko n broj π n zaista period ove funkcije. Tada će broj 2π n biti period
, dakle sinT=0, T=π n, n € Z. Pretpostavimo da je za neko n broj π n zaista period ove funkcije. Tada će broj 2π n biti period

Pošto su brojnici jednaki, i imenioci su im, dakle, jednaki

To znači da funkcija f nije periodična.
Rad u grupama.
Zadaci za grupu 1.
Zadaci za grupu 2.
Provjerite je li funkcija f periodična i pronađite njenu osnovnu period (ako postoji).
f(x)=cos(2x)+2sin(2x)
Zadaci za grupu 3.
Na kraju rada grupe predstavljaju svoja rješenja.
VI. Sumiranje lekcije.
Refleksija.
Nastavnik daje učenicima kartice sa crtežima i traži od njih da dio prvog crteža obojaju u skladu sa stepenom u kojem misle da su savladali metode proučavanja funkcije za periodičnost, a dio drugog crteža - u skladu sa svojim doprinos radu na času.
VII. Domaći
1). Provjerite je li funkcija f periodična i pronađite njen osnovni period (ako postoji)
b). f(x)=x 2 -2x+4
c). f(x)=2tg(3x+5)
2). Funkcija y=f(x) ima period T=2 i f(x)=x 2 +2x za x € [-2; 0]. Pronađite vrijednost izraza -2f(-3)-4f(3.5)
književnost/
U julu 2020. NASA pokreće ekspediciju na Mars. Letelica će na Mars isporučiti elektronski medij sa imenima svih registrovanih učesnika ekspedicije.
Registracija učesnika je otvorena. Nabavite svoju kartu za Mars koristeći ovaj link.
Ako je ova objava riješila vaš problem ili vam se jednostavno svidjela, podijelite link do nje sa svojim prijateljima na društvenim mrežama.
Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kod vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake. Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako unesete prvi kod, morat ćete ga povremeno ažurirati. Ako umetnete drugi kod, stranice će se učitavati sporije, ali nećete morati stalno pratiti ažuriranja MathJaxa.
Najlakši način za povezivanje MathJax-a je u Blogger-u ili WordPress-u: na kontrolnoj ploči stranice dodajte widget dizajniran za umetanje JavaScript koda treće strane, u njega kopirajte prvu ili drugu verziju koda za preuzimanje prikazanog iznad i postavite widget bliže na početak šablona (usput, to uopće nije potrebno, pošto se MathJax skripta učitava asinhrono). To je to. Sada naučite sintaksu označavanja MathML-a, LaTeX-a i ASCIIMathML-a i spremni ste da umetnete matematičke formule u web stranice svoje web stranice.
Još jedna novogodišnja noć... mrazno vrijeme i pahulje na prozorskom staklu... Sve me to natjeralo da ponovo pišem o... fraktalima, i šta Wolfram Alpha zna o njima. Postoji zanimljiv članak o ovoj temi, koji sadrži primjere dvodimenzionalnih fraktalnih struktura. Ovdje ćemo pogledati složenije primjere trodimenzionalnih fraktala.
Fraktal se može vizualno predstaviti (opisati) kao geometrijska figura ili tijelo (što znači da su oboje skup, u ovom slučaju skup tačaka), čiji detalji imaju isti oblik kao i sama originalna figura. Odnosno, ovo je samoslična struktura, ispitujući detalje čije ćemo uvećanje vidjeti isti oblik kao bez povećanja. Dok u slučaju obične geometrijske figure (ne fraktala), nakon povećanja ćemo vidjeti detalje koji imaju jednostavniji oblik od same originalne figure. Na primjer, pri dovoljno velikom povećanju, dio elipse izgleda kao segment prave linije. To se ne dešava sa fraktalima: sa svakim njihovim povećanjem, ponovo ćemo videti isti složeni oblik, koji će se ponavljati iznova i iznova sa svakim povećanjem.
Benoit Mandelbrot, osnivač nauke o fraktalima, napisao je u svom članku Fraktali i umjetnost u ime nauke: „Fraktali su geometrijski oblici koji su složeni u svojim detaljima kao i po svom cjelokupnom obliku će biti uvećan na veličinu cjeline, izgledat će kao cjelina, ili tačno, ili možda s malom deformacijom."
Trigonometrijske funkcije su periodične, odnosno ponavljaju se nakon određenog perioda. Kao rezultat, dovoljno je proučiti funkciju na ovom intervalu i proširiti otkrivena svojstva na sve ostale periode.
Uputstva1. Ako vam je dat primitivan izraz u kojem postoji samo jedna trigonometrijska funkcija (sin, cos, tg, ctg, sec, cosec), a ugao unutar funkcije se ne množi ni sa jednim brojem, a sam se ne podiže u bilo kom stepenu - koristite definiciju. Za izraze koji sadrže sin, cos, sec, cosec, podebljano postavite period na 2P, a ako jednačina sadrži tg, ctg, onda P. Recimo, za funkciju y=2 sinx+5, period će biti jednak 2P.
2. Ako se ugao x pod znakom trigonometrijske funkcije pomnoži sa nekim brojem, tada, da bismo pronašli period ove funkcije, podijelimo tipični period ovim brojem. Recimo da vam je data funkcija y = sin 5x. Tipičan period za sinus je 2P ako ga podijelite sa 5, dobijete 2P/5 - ovo je željeni period ovog izraza.
3. Da biste pronašli period trigonometrijske funkcije podignute na stepen, procijenite paritet stepena. Za ravnomjeran stepen, smanjite tipični period za polovicu. Recimo, ako vam je data funkcija y = 3 cos^2x, tada će se tipični period 2P smanjiti za 2 puta, tako da će period biti jednak P. Imajte na umu da su funkcije tg, ctg periodične na P za svaki stepen.
4. Ako vam je data jednadžba koja sadrži proizvod ili količnik dvije trigonometrijske funkcije, prvo pronađite period za sve njih posebno. Nakon ovoga pronađite minimalni broj koji bi sadržavao cijeli broj oba perioda. Recimo da je data funkcija y=tgx*cos5x. Za tangentu period je P, za kosinus 5x period je 2P/5. Minimalni broj u kojem se mogu smjestiti oba ova perioda je 2P, tako da je željeni period 2P.
5. Ako vam je teško učiniti kako je predloženo ili sumnjate u rezultat, pokušajte to učiniti kako je definirano. Uzmite T kao period funkcije, veći je od nule. Zamijenite izraz (x + T) umjesto x u jednadžbu i riješite rezultirajuću jednakost kao da je T parametar ili broj. Kao rezultat, otkrit ćete vrijednost trigonometrijske funkcije i moći ćete pronaći najmanji period. Recimo, kao rezultat reljefa, dobijete identitet sin (T/2) = 0. Minimalna vrijednost T pri kojoj se izvodi je 2P, to će biti rezultat zadatka.
Periodična funkcija je funkcija koja ponavlja svoje vrijednosti nakon nekog perioda različitog od nule. Period funkcije je broj koji, kada se doda argumentu funkcije, ne mijenja vrijednost funkcije.

Trebaće ti
- Poznavanje elementarne matematike i osnovni pregled.
1. Označimo period funkcije f(x) brojem K. Naš zadatak je da otkrijemo ovu vrijednost K. Da bismo to učinili, zamislimo da funkcija f(x), koristeći definiciju periodične funkcije, izjednačavamo f(x+K)=f(x).
2. Rezultirajuću jednačinu u vezi s nepoznatim K rješavamo kao da je x konstanta. U zavisnosti od vrednosti K, biće nekoliko opcija.
3. Ako je K>0 – onda je ovo period vaše funkcije – onda funkcija f(x) nije periodična ne postoji za bilo koji K koji nije jednak nuli, onda se takva funkcija naziva aperiodična i također nema period.
Video na temu
Obratite pažnju!
Sve trigonometrijske funkcije su periodične, a sve polinomske funkcije sa stepenom većim od 2 su aperiodične.
Koristan savjet
Period funkcije koja se sastoji od 2 periodične funkcije je najmanji univerzalni višekratnik perioda ovih funkcija.
Trigonometrijske jednadžbe su jednadžbe koje sadrže trigonometrijske funkcije nepoznatog argumenta (na primjer: 5sinx-3cosx =7). Da biste naučili kako ih riješiti, morate znati neke načine kako to učiniti.

1. Rješenje takvih jednačina se sastoji od 2 faze. Najjednostavnije trigonometrijske jednadžbe su: Sinx=a; Cosx=a, itd.
2. Drugo je rješenje najjednostavnije dobivene trigonometrijske jednačine. Postoje osnovni načini za rješavanje jednačina ovog tipa: Rješavanje algebarski. Ova metoda je poznata iz škole, iz kursa algebre. Inače se naziva metoda zamjene i zamjene varijable. Koristeći formule redukcije, transformiramo, vršimo zamjenu, a zatim pronalazimo korijene.
3. Faktorovanje jednačine. Prvo, pomjerimo sve pojmove ulijevo i činimo ih.
4. Svođenje jednačine na homogenu. Jednačine se nazivaju homogenim ako su svi članovi istog stepena, a sinus i kosinus istog ugla. izbaci sve univerzalne faktore iz zagrada; izjednačiti faktore i zagrade na nulu; izjednačene zagrade daju homogenu jednačinu nižeg stepena, koju treba podeliti sa cos (ili sin) do najvišeg stepena; riješiti rezultirajuću algebarsku jednadžbu u vezi tan.
5. Sljedeća metoda je pomicanje na pola kuta. Recimo, riješite jednačinu: 3 sin x – 5 cos x = 7. Pređimo na polovinu ugla: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 sin ? (x / 2) = 7 sin ? (x / 2) + 7 cos ? (x/ 2) , nakon čega sve članove svedemo na jedan dio (najbolje desnu stranu) i rješavamo jednačinu.
6. Unos pomoćnog ugla. Kada zamijenimo cjelobrojnu vrijednost cos(a) ili sin(a). Znak "a" je pomoćni ugao.
7. Metoda pretvaranja proizvoda u zbir. Ovdje morate primijeniti odgovarajuće formule. Recimo dato: 2 sin x · sin 3x = cos 4x Riješimo lijevu stranu u zbir, odnosno: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p / 16 + pk / 8.
8. Konačna metoda se zove multifunkcionalna zamjena. Transformišemo izraz i izvršimo promjenu, recimo Cos(x/2)=u, a zatim riješimo jednačinu sa parametrom u. Prilikom kupovine ukupne vrijednosti pretvaramo vrijednost u suprotno.
Video na temu
Ako uzmemo u obzir tačke na kružnici, onda tačke x, x + 2π, x + 4π, itd. poklapaju jedno s drugim. Dakle, trigonometrijske funkcije na pravoj liniji periodično ponavljaju svoju vrijednost. Ako je poznat period funkcije, moguće je konstruisati funkciju na tom periodu i ponoviti je na drugim.

1. Period je broj T takav da je f(x) = f(x+T). Da biste pronašli period, riješite odgovarajuću jednačinu, zamjenjujući x i x+T kao argument. U ovom slučaju koriste već dobro poznate periode za funkcije. Za sinusne i kosinusne funkcije period je 2π, a za tangente i kotangense π.
2. Neka je data funkcija f(x) = sin^2(10x). Razmotrimo izraz sin^2(10x) = sin^2(10(x+T)). Koristite formulu da smanjite stepen: sin^2(x) = (1 – cos 2x)/2. Tada dobijate 1 – cos 20x = 1 – cos 20(x+T) ili cos 20x = cos (20x+20T). Znajući da je period kosinusa 2π, 20T = 2π. To znači T = π/10. T je minimalni ispravan period, a funkcija će se ponoviti nakon 2T, i nakon 3T, iu drugom smjeru duž ose: -T, -2T, itd.
Koristan savjet
Koristite formule da smanjite stepen funkcije. Ako već znate periode nekih funkcija, pokušajte svesti postojeću funkciju na poznate.
Ispitivanje funkcije na parnost i neparnost pomaže u izgradnji grafa funkcije i razumijevanju prirode njenog ponašanja. Za ovo istraživanje morate uporediti ovu funkciju napisanu za argument “x” i za argument “-x”.
1. Zapišite funkciju koju želite proučavati u obliku y=y(x).
2. Zamijenite argument funkcije sa “-x”. Zamijenite ovaj argument u funkcionalni izraz.
3. Pojednostavite izraz.
4. Dakle, imate istu funkciju napisanu za argumente “x” i “-x”. Pogledajte ove dvije stavke Ako je y(-x)=y(x), onda je to parna funkcija recimo za funkciju da je y (-x)=y(x) ili y(-x)=-y(x), onda je po svojstvu parnosti ovo funkcija univerzalnog oblika. Odnosno, nije ni paran ni neparan.
5. Zapišite svoje nalaze. Sada ih možete koristiti u izgradnji grafa funkcije ili u budućoj analitičkoj studiji svojstava funkcije.
6. Takođe je moguće govoriti o parnosti i neparnosti funkcije u slučaju kada je graf funkcije već dat. Recimo da je graf poslužio kao rezultat fizičkog eksperimenta. Ako je graf funkcije simetričan u odnosu na os ordinate, onda je y(x) parna funkcija x(y) je parna funkcija. x(y) je funkcija inverzna funkciji y(x) Ako je graf funkcije simetričan u odnosu na ishodište (0,0), onda je y(x) neparna funkcija. Inverzna funkcija x(y) će također biti neparna.
7. Važno je zapamtiti da ideja o parnosti i neparnosti funkcije ima direktnu vezu sa domenom definicije funkcije. Ako, recimo, parna ili neparna funkcija ne postoji na x=5, onda ne postoji na x=-5, što se ne može reći za funkciju univerzalnog oblika. Prilikom uspostavljanja parnog i neparnog pariteta obratite pažnju na domen funkcije.
8. Pronalaženje funkcije za parnost i neparnost korelira s pronalaženjem skupa vrijednosti funkcije. Da biste pronašli skup vrijednosti parne funkcije, dovoljno je pogledati polovicu funkcije, desno ili lijevo od nule. Ako pri x>0 parna funkcija y(x) uzima vrijednosti od A do B, tada će poprimiti iste vrijednosti, a pri x0 neparna funkcija y(x) preuzima raspon vrijednosti od A do B, tada na x sin^2 ? + cos^2 ? = 1. Treći i četvrti identitet se dobijaju dijeljenjem, respektivno, sa b^2 i a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/sin^ ? ili 1 + ctg^2 ? = 1/sin^2 ? Peti i šesti glavni identitet se dokazuju određivanjem sume oštrih uglova pravougaonog trougla, koji je jednak 90° ili?/2. Teži trigonometrijski identiteti: formule za sabiranje argumenata. dvostruki i trostruki uglovi, smanjenje stepena, reformisanje zbira ili proizvoda funkcija, kao i formule za trigonometrijsku supstituciju, odnosno izraze osnovnih trigonometrijskih funkcija u terminima tan poluugla: sin ?= (2*tg ?/2)/ (1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).
Potreba da se pronađe minimalna vrijednost matematičke funkcije je od stvarnog interesa za rješavanje primijenjenih problema, recimo, u ekonomiji. Minimiziranje gubitaka je od velikog značaja za poslovne aktivnosti.

1. Da bi se pronašla minimalna vrijednost funkcije, potrebno je odrediti pri kojoj vrijednosti argumenta x0 će biti zadovoljena nejednakost y(x0)? y(x), gdje je x? x0. Kao i obično, ovaj problem se rješava na određenom intervalu ili u svakom rasponu vrijednosti funkcije, ako nije naveden. Jedan aspekt rješenja je pronalaženje fiksnih tačaka.
2. Stacionarna tačka je vrijednost argumenta u kojoj derivacija funkcije postaje nula. Prema Fermatovoj teoremi, ako diferencijabilna funkcija u nekoj tački poprimi ekstremnu vrijednost (u ovom slučaju lokalni minimum), tada je ta tačka stacionarna.
3. Funkcija često uzima svoju minimalnu vrijednost upravo u ovoj tački, ali se ona ne može uvijek odrediti. Štaviše, nije uvijek moguće precizno reći čemu je jednak minimum funkcije ili uzima li beskonačno malu vrijednost. Zatim, kao i obično, pronalaze granicu kojoj teži kako se smanjuje.
4. Da bi se odredila minimalna vrijednost funkcije, potrebno je izvršiti niz radnji koji se sastoji od četiri faze: pronalaženje domene definicije funkcije, stjecanje fiksnih tačaka, pregled vrijednosti funkcije na ovim tačkama i na krajevima intervala, pronalaženje minimuma.
5. Ispostavilo se da je neka funkcija y(x) data na intervalu sa granicama u tačkama A i B. Pronađite domen njene definicije i saznajte da li je interval njen podskup.
6. Izračunajte derivaciju funkcije. Izjednačite rezultirajući izraz sa nulom i pronađite korijene jednadžbe. Provjerite da li ove stacionarne točke spadaju u jaz. Ako nisu, onda se ne uzimaju u obzir u daljoj fazi.
7. Ispitajte jaz za vrstu granica: otvorene, zatvorene, složene ili nemjerljive. Ovo određuje način na koji tražite minimalnu vrijednost. Recimo da je segment [A, B] zatvoreni interval. Uključite ih u funkciju i izračunajte vrijednosti. Uradite isto sa stacionarnom tačkom. Odaberite najmanji zbroj.
8. Sa otvorenim i nemjerljivim intervalima situacija je nešto teža. Ovdje ćete morati tražiti jednostrane granice koje ne daju uvijek nedvosmislen rezultat. Recimo, za interval sa jednom zatvorenom i jednom probušenom granicom [A, B) treba pronaći funkciju na x = A i jednostranu granicu lim y na x? B-0.
>> Periodičnost funkcija y = sin x, y = cos x
§ 11. Periodičnost funkcija y = sin x, y = cos x
U prethodnim paragrafima koristili smo sedam svojstava funkcija: domen definicije, paran ili neparan, monotonost, ograničenost, najveće i najmanje vrijednosti, kontinuitet, raspon vrijednosti funkcije. Koristili smo ova svojstva ili za konstruisanje grafika funkcije (to se desilo, na primer, u § 9), ili za čitanje konstruisanog grafa (to se desilo, na primer, u § 10). Sada je došao pravi trenutak da se uvede još jedno (osmo) svojstvo funkcija, koje je jasno vidljivo na grafovima funkcija y = sin x (vidi sliku 37), y = cos x (vidi sliku 41) koji su gore konstruisani.
Definicija. Funkcija se naziva periodičnom ako postoji broj T koji nije nula takav da za bilo koji x u skupovima vrijedi dvostruka jednakost:
![]() Broj T koji zadovoljava navedeni uvjet naziva se period funkcije y = f(x).
Broj T koji zadovoljava navedeni uvjet naziva se period funkcije y = f(x).
Iz toga slijedi da, pošto za bilo koje x vrijede jednakosti:
![]()
tada su funkcije y = sin x, y = cos x periodične i broj je 2 n služi kao period za obe funkcije.
Periodičnost funkcije je obećano osmo svojstvo funkcija.
Sada pogledajte grafik funkcije y = sin x (slika 37). Da bi se izgradio sinusni val, dovoljno je nacrtati jedan od njegovih valova (na segmentu, a zatim pomaknuti ovaj val duž x osi za. Kao rezultat, koristeći jedan talas ćemo izgraditi cijeli graf.
Pogledajmo sa iste tačke gledišta grafik funkcije y = cos x (slika 41). Vidimo da je ovdje, za crtanje grafika, dovoljno prvo nacrtati jedan val (na primjer, na segmentu
I onda ga pomaknite duž x ose
Sumirajući, donosimo sljedeći zaključak.
Ako funkcija y = f(x) ima period T, tada da biste izgradili graf funkcije prvo morate izgraditi granu (val, dio) grafa na bilo kojem intervalu dužine T (najčešće uzimaju interval sa završava u tačkama, a zatim ovu granu pomeriti duž x ose udesno i ulevo na T, 2T, ZT, itd.
Periodična funkcija ima beskonačno mnogo perioda: ako je T period, onda je 2T period, a ZT je period, a -T je period; Općenito, period je bilo koji broj oblika KT, gdje je k = ±1, ±2, ± 3... Obično pokušavaju, ako je moguće, izolovati najmanji pozitivni period, on se naziva glavnim periodom.
Dakle, bilo koji broj oblika 2pk, gdje je k = ±1, ± 2, ± 3, je period funkcija y = sinn x, y = cos x; 2n je glavni period obje funkcije.
Primjer. Pronađite glavni period funkcije:
![]()
a) Neka je T glavni period funkcije y = sin x. Hajde da stavimo
Da bi broj T bio period funkcije, identitet Ali, pošto govorimo o pronalaženju glavnog perioda, dobijamo
b) Neka je T glavni period funkcije y = cos 0,5x. Stavimo f(x)=cos 0.5x. Tada je f(x + T)=cos 0,5(x + T)=cos (0,5x + 0,5T).
Da bi broj T bio period funkcije, mora vrijediti identitet cos (0,5x + 0,5T) = cos 0,5x.
To znači 0,5t = 2pp. Ali, pošto govorimo o pronalaženju glavnog perioda, dobijamo 0,5T = 2 l, T = 4 l.
![]()
Generalizacija rezultata dobijenih u primjeru je sljedeća izjava: glavni period funkcije ![]()
A.G. Mordkovich algebra 10. razred
Sadržaj lekcije bilješke lekcija koje podržavaju okvir prezentacije lekcije metode ubrzanja interaktivne tehnologije Vježbajte zadaci i vježbe radionice za samotestiranje, treninzi, slučajevi, potrage domaća zadaća diskusija pitanja retorička pitanja učenika Ilustracije audio, video isječci i multimedijalne fotografije, slike, grafikoni, tabele, dijagrami, humor, anegdote, vicevi, stripovi, parabole, izreke, ukrštene riječi, citati Dodaci sažeci članci savjeti za radoznale jaslice listovi udžbenici osnovni i dodatni rječnik pojmova ostalo Poboljšanje udžbenika i lekcija ispravljanje grešaka u udžbeniku ažuriranje fragmenta u udžbeniku elementi inovacije u lekciji zamjena zastarjelog znanja novim Samo za nastavnike idealan kalendar časova plan za godinu metodološke preporuke programi diskusije Integrisane lekcije