Teorija trigonometrijskih nejednakosti. Trigonometrijske nejednakosti. Šema za rješavanje trigonometrijskih jednačina

Tokom praktične nastave ponovićemo glavne vrste zadataka iz teme „Trigonometrija“ i dodatno analizirati probleme povećana složenost i razmotriti primjere rješavanja raznih trigonometrijskih nejednačina i njihovih sistema.

Ova lekcija će vam pomoći da se pripremite za jednu od vrsta zadataka B5, B7, C1 i C3.

Počnimo s pregledom glavnih vrsta zadataka koje smo pokrili u temi "Trigonometrija" i riješimo nekoliko nestandardnih problema.

Zadatak br. 1. Pretvorite uglove u radijane i stepene: a) ; b) .

a) Koristimo formulu za pretvaranje stupnjeva u radijane

Zamijenimo navedenu vrijednost u njega.

b) Primijenite formulu za pretvaranje radijana u stupnjeve

Izvršimo zamjenu .

Odgovori. A) ; b) .

Zadatak br. 2. Izračunajte: a) ; b) .

a) Pošto ugao ide daleko izvan tabele, smanjićemo ga oduzimanjem perioda sinusa. Jer Ugao je naznačen u radijanima, tada ćemo period smatrati .

b) B u ovom slučaju situacija je slična. Pošto je ugao naznačen u stepenima, period tangente ćemo smatrati kao .

Rezultirajući ugao, iako manji od perioda, je veći, što znači da se više ne odnosi na glavni, već na prošireni dio tabele. Kako ne biste još jednom trenirali svoje pamćenje pamćenjem proširene tablice vrijednosti trigofunkcije, hajdemo ponovo oduzeti period tangente:

Iskoristili smo neparnost tangentne funkcije.

Odgovori. a) 1; b) .

Zadatak br. 3. Izračunati , Ako .

Svodimo cijeli izraz na tangente dijeljenjem brojnika i nazivnika razlomka sa . Istovremeno, toga se ne možemo bojati, jer u ovom slučaju tangentna vrijednost ne bi postojala.

Zadatak br. 4. Pojednostavite izraz.

Navedeni izrazi se konvertuju pomoću formula redukcije. Oni su samo neobično napisani pomoću stepeni. Prvi izraz općenito predstavlja broj. Pojednostavimo sve trigofunkcije jednu po jednu:

Jer , tada se funkcija mijenja u kofunkciju, tj. na kotangens, a ugao pada u drugu četvrtinu, u kojoj prvobitna tangenta ima negativan predznak.

Iz istih razloga kao u prethodnom izrazu, funkcija se mijenja u kofunkciju, tj. na kotangens, a ugao pada u prvu četvrtinu, u kojoj originalna tangenta ima pozitivan predznak.

Zamenimo sve u pojednostavljeni izraz:

Problem #5. Pojednostavite izraz.

Zapišimo tangentu dvostrukog ugla koristeći odgovarajuću formulu i pojednostavimo izraz:

Posljednji identitet je jedna od univerzalnih zamjenskih formula za kosinus.

Problem #6. Izračunati.

Glavna stvar je ne napraviti standardnu ​​grešku i ne dati odgovor da je izraz jednak . Ne možete koristiti osnovno svojstvo arktangensa sve dok pored njega postoji faktor u obliku dva. Da bismo ga se riješili, napisat ćemo izraz prema formuli za tangentu dvostrukog kuta, dok ćemo tretirati , kao običan argument.

Sada možemo primijeniti osnovno svojstvo arktangensa; zapamtite da nema ograničenja za njegov numerički rezultat.

Problem br. 7. Riješite jednačinu.

Prilikom rješavanja jednadžbe razlomaka koja je jednaka nuli, uvijek je naznačeno da je brojilac jednak nuli, ali imenilac nije, jer Ne možete dijeliti sa nulom.

Prva jednadžba je poseban slučaj najjednostavnije jednadžbe koja se može riješiti pomoću trigonometrijskog kruga. Zapamtite ovo rješenje i sami. Druga nejednakost je riješena kao najjednostavnija jednadžba koristeći opću formulu za korijene tangente, ali samo sa predznakom koji nije jednak.

Kao što vidimo, jedna porodica korijena isključuje drugu porodicu potpuno istog tipa korijena koji ne zadovoljavaju jednačinu. One. nema korena.

Odgovori. Nema korijena.

Problem br. 8. Riješite jednačinu.

Odmah primijetimo da možemo izvaditi zajednički faktor i uradimo to:

Jednačina je svedena na jedan od standardnih oblika, gdje je proizvod više faktora jednak nuli. Već znamo da je u ovom slučaju ili jedno od njih jednako nuli, ili drugo, ili treće. Zapišimo ovo u obliku skupa jednadžbi:

Prve dvije jednadžbe su posebni slučajevi najjednostavnijih, sa sličnim jednadžbama smo se već susreli mnogo puta, pa ćemo odmah navesti njihova rješenja. Treću jednačinu svodimo na jednu funkciju koristeći sinusnu formulu dvostrukog ugla.

Riješimo posljednju jednačinu posebno:

Ova jednadžba nema korijen, jer vrijednost sinusa ne može ići dalje .

Dakle, rješenje su samo prve dvije porodice korijena; oni se mogu kombinovati u jednu, što je lako prikazati na trigonometrijskom krugu:

Ovo je porodica svih polovina, tj.

Pređimo na rješavanje trigonometrijskih nejednačina. Prvo, pogledajmo pristup rješavanju primjera bez korištenja formula opšta rješenja, ali koristeći trigonometrijski krug.

Problem br. 9. Riješite nejednakost.

Nacrtajmo pomoćnu liniju na trigonometrijskoj kružnici koja odgovara vrijednosti sinusa jednakoj , i pokažimo raspon uglova koji zadovoljavaju nejednakost.

Vrlo je važno razumjeti kako tačno označiti rezultujući interval uglova, tj. šta je njegov početak, a šta kraj. Početak intervala će biti ugao koji odgovara tački u koju ćemo ući na samom početku intervala ako se krećemo suprotno od kazaljke na satu. U našem slučaju, ovo je tačka koja je sa leve strane, jer krećući se u smjeru suprotnom od kazaljke na satu i prolazeći pravu tačku, mi, naprotiv, ostavljamo traženi raspon uglova. Prava tačka će stoga odgovarati kraju jaza.

Sada moramo razumjeti uglove početka i kraja našeg intervala rješenja nejednakosti. Tipična greška je odmah naznačiti da desna tačka odgovara uglu, a lijeva i dati odgovor. Ovo nije istina! Napominjemo da smo upravo naznačili interval koji odgovara gornjem dijelu kruga, iako nas zanima donji dio, drugim riječima, pomiješali smo početak i kraj intervala rješenja koji nam je potreban.

Da bi interval počeo od ugla desne tačke i završio sa uglom lijeve tačke, potrebno je da prvi navedeni ugao bude manji od drugog. Da bismo to učinili, morat ćemo izmjeriti ugao desne tačke u negativnom smjeru reference, tj. u smjeru kazaljke na satu i to će biti jednako . Zatim, počevši se kretati od njega u pozitivnom smjeru kazaljke na satu, doći ćemo do desne točke nakon lijeve točke i dobiti vrijednost ugla za nju. Sada je početak intervala uglova manji od kraja i možemo napisati interval rješenja bez uzimanja u obzir perioda:

Uzimajući u obzir da će se takvi intervali ponavljati beskonačan broj puta nakon bilo kojeg cijelog broja rotacija, dobivamo opće rješenje uzimajući u obzir sinusni period:

Stavljamo zagrade jer je nejednakost stroga, a na kružnici biramo tačke koje odgovaraju krajevima intervala.

Odgovor koji dobijete uporedite sa formulom za opšte rešenje koje smo dali na predavanju.

Odgovori. .

Ova metoda je dobra za razumijevanje odakle dolaze formule za opšta rješenja najjednostavnijih nejednačina trigona. Osim toga, korisno je za one koji su previše lijeni da nauče sve ove glomazne formule. Međutim, sama metoda također nije laka; odaberite koji vam pristup rješenju najviše odgovara.

Za rješavanje trigonometrijskih nejednakosti možete koristiti i grafove funkcija na kojima je konstruirana pomoćna linija, slično prikazanoj metodi koristeći jedinični krug. Ako ste zainteresirani, pokušajte sami smisliti ovaj pristup rješenju. U nastavku ćemo koristiti opće formule za rješavanje jednostavnih trigonometrijskih nejednakosti.

Problem br. 10. Riješite nejednakost.

Koristimo formulu za opće rješenje, uzimajući u obzir činjenicu da nejednakost nije stroga:

U našem slučaju dobijamo:

Odgovori.

Problem br. 11. Riješite nejednakost.

Upotrijebimo opću formulu rješenja za odgovarajuću striktno nejednakost:

Odgovori. .

Problem br. 12. Riješite nejednačine: a) ; b) .

U ovim nejednačinama nema potrebe žuriti s korištenjem formula za opća rješenja ili trigonometrijskog kruga, dovoljno je jednostavno zapamtiti raspon vrijednosti sinusa i kosinusa.

a) Od , onda nejednakost nema smisla. Dakle, nema rješenja.

b) Zato što slično tome, sinus bilo kojeg argumenta uvijek zadovoljava nejednakost specificiranu u uvjetu. Dakle, sve realne vrijednosti argumenta zadovoljavaju nejednakost.

Odgovori. a) nema rješenja; b) .

Problem 13. Riješite nejednakost .

Ministarstvo obrazovanja Republike Bjelorusije

Obrazovne ustanove

„Gomeljski državni univerzitet

nazvan po Francisku Skarini"

Matematički fakultet

Odsjek za algebru i geometriju

Prihvaćeno za odbranu

Glava Odeljenje Šemetkov L.A.

Trigonometrijske jednačine i nejednačine

Rad na kursu

Izvršilac:

učenik grupe M-51

CM. Gorsky

Naučni rukovodilac dr.-mr.

viši predavač

V.G. Safonov

Gomel 2008

UVOD

OSNOVNE METODE ZA RJEŠAVANJE TRIGONOMETRIJSKIH JEDNAČINA

Faktorizacija

Rješavanje jednadžbi pretvaranjem proizvoda trigonometrijskih funkcija u zbir

Rješavanje jednadžbi pomoću formula trostrukog argumenta

Množenje nekom trigonometrijskom funkcijom

NESTANDARDNE TRIGONOMETRIJSKE JEDNAČINE

TRIGONOMETRIJSKE NEJEDNAKOSTI

ODABIR KORIJENA

ZADACI ZA SAMOSTALNO RJEŠENJE

ZAKLJUČAK

SPISAK KORIŠĆENIH IZVORA


U antičko doba, trigonometrija je nastala u vezi sa potrebama astronomije, geodezije i izgradnje, odnosno bila je čisto geometrijske prirode i predstavljala je uglavnom<<исчисление хорд>>. Vremenom su se u njega počeli ukrštati neki analitički momenti. U prvoj polovini 18. veka došlo je do nagle promene, nakon koje je trigonometrija dobila novi pravac i pomerila se ka matematička analiza. U to vrijeme su se trigonometrijski odnosi počeli smatrati funkcijama.

Trigonometrijske jednačine jedna su od najtežih tema u školskom kursu matematike. Trigonometrijske jednadžbe nastaju prilikom rješavanja zadataka iz planimetrije, stereometrije, astronomije, fizike i drugih oblasti. Trigonometrijske jednačine i nejednakosti nalaze se među zadacima centraliziranog testiranja iz godine u godinu.

Najvažnija razlika trigonometrijske jednačine od algebarskih je da u algebarskim jednadžbama postoji konačan broj korijena, a u trigonometrijskim je beskonačan broj, što uvelike otežava odabir korijena. Još jedna specifičnost trigonometrijskih jednačina je nejedinstven oblik pisanja odgovora.

Ovaj rad je posvećen metodama rješavanja trigonometrijskih jednačina i nejednačina.

Rad se sastoji od 6 dijelova.

Prvi dio daje osnovne teorijske informacije: definiciju i svojstva trigonometrijskih i inverznih trigonometrijskih funkcija; tablica vrijednosti trigonometrijskih funkcija za neke argumente; izražavanje trigonometrijskih funkcija u terminima drugih trigonometrijskih funkcija, što je vrlo važno za transformaciju trigonometrijskih izraza, posebno onih koji sadrže inverzne trigonometrijske funkcije; pored osnovnih trigonometrijskih formula, dobro poznatih iz školski kurs, date su formule koje pojednostavljuju izraze koji sadrže inverzne trigonometrijske funkcije.

U drugom dijelu su navedene osnovne metode za rješavanje trigonometrijskih jednačina. Razmatraju se rješenja elementarnih trigonometrijskih jednačina, metoda faktorizacije i metode svođenja trigonometrijskih jednačina na algebarske. Zbog činjenice da se rješenja trigonometrijskih jednačina mogu pisati na više načina, a oblik ovih rješenja ne omogućava da se odmah utvrdi da li su ova rješenja ista ili različita, što može<<сбить с толку>> prilikom rješavanja testova, uzeti u obzir opšta šema detaljno se razmatraju rješenja trigonometrijskih jednačina i transformacija grupa općih rješenja trigonometrijskih jednačina.

Treći dio ispituje nestandardne trigonometrijske jednačine, čija su rješenja zasnovana na funkcionalnom pristupu.

Četvrti dio razmatra trigonometrijske nejednakosti. Detaljno su obrađene metode rješavanja elementarnih trigonometrijskih nejednačina, kako na jediničnom krugu, tako i grafičkom metodom. Opisan je proces rješavanja neelementarnih trigonometrijskih nejednačina kroz elementarne nejednakosti i metoda intervala, već dobro poznata školarcima.

U petom dijelu predstavljeni su najteži zadaci: kada je potrebno ne samo riješiti trigonometrijsku jednačinu, već i od pronađenih korijena odabrati korijene koji zadovoljavaju neki uvjet. Ovaj odjeljak pruža rješenja za tipične zadatke odabira korijena. Neophodan teorijske informacije za odabir korijena: particioniranje skupa cijelih brojeva na disjunktne podskupove, rješavanje jednadžbi u cijelim brojevima (dijafantin).

Šesti dio predstavlja zadatke za nezavisna odluka, dizajniran u obliku testa. 20 testnih zadataka sadrži najteže zadatke koji se mogu susresti tokom centraliziranog testiranja.

Elementarne trigonometrijske jednadžbe

Elementarne trigonometrijske jednadžbe su jednačine oblika , gdje --- jedna od trigonometrijskih funkcija: , , , .

Elementarne trigonometrijske jednadžbe imaju beskonačan broj korijena. Na primjer, sljedeće vrijednosti zadovoljavaju jednadžbu: , , , itd. Opća formula duž koje se nalaze svi korijeni jednadžbe, gdje je ,

Ovdje može uzeti bilo koje cjelobrojne vrijednosti, svaka od njih odgovara određenom korijenu jednačine; u ovoj formuli (kao i u drugim formulama kojima se rješavaju elementarne trigonometrijske jednadžbe) nazivaju se parametar. Obično pišu , čime se naglašava da parametar može prihvatiti bilo koje cjelobrojne vrijednosti.

Rješenja jednadžbe , gdje , nalaze se po formuli

Jednačina se rješava pomoću formule

a jednačina je po formuli

Posebno napomenimo neke posebne slučajeve elementarnih trigonometrijskih jednadžbi, kada se rješenje može napisati bez korištenja općih formula:

Prilikom rješavanja trigonometrijskih jednačina važnu ulogu igra period trigonometrijskih funkcija. Stoga predstavljamo dvije korisne teoreme:

Teorema Ako --- glavni period funkcije, tada je broj glavni period funkcije.

Periodima funkcija i se kaže da su mjerljivi ako postoje prirodni brojevi i to .

Teorema Ako periodične funkcije i , imaju srazmjerno i , Tada imaju zajednički period, koji je period funkcija , , .

Teorema kaže da je period funkcije , , , i nije nužno glavni period. Na primjer, glavni period funkcija i --- , i glavni period njihovog proizvoda --- .

Uvođenje pomoćnog argumenta

Standardnim načinom transformacije izraza forme je sljedeća tehnika: neka --- ugao, dato jednakostima , . Za bilo koji, takav ugao postoji. Tako . Ako , ili , , , u drugim slučajevima.

Šema za rješavanje trigonometrijskih jednačina

Osnovna shema koju ćemo slijediti prilikom rješavanja trigonometrijskih jednačina je sljedeća:

rješenje zadata jednačina svodi se na rješavanje elementarnih jednačina. Rješenja --- konverzije, faktorizacija, zamjena nepoznatih. Vodeći princip je da ne izgubite svoje korijene. To znači da se pri prelasku na sljedeću jednadžbu(e) ne bojimo pojave dodatnih (stranih) korijena, već samo brinemo da svaka naredna jednadžba našeg „lanca“ (ili skup jednačina u slučaju grananja) ) je posljedica prethodnog. Jedna od mogućih metoda za odabir korijena je testiranje. Odmah da primijetimo da se u slučaju trigonometrijskih jednadžbi poteškoće povezane s odabirom korijena i provjerom, po pravilu, naglo povećavaju u odnosu na algebarske jednadžbe. Na kraju krajeva, moramo provjeriti nizove koji se sastoje od beskonačnog broja članova.

Posebno treba istaći zamjenu nepoznanica pri rješavanju trigonometrijskih jednačina. U većini slučajeva, nakon potrebne zamjene, dobije se algebarska jednadžba. Štaviše, jednadžbe nisu toliko rijetke, iako su trigonometrijske izgled, u suštini nisu, jer nakon prvog koraka --- zamjene varijable --- pretvaraju se u algebarske, a povratak na trigonometriju nastaje tek u fazi rješavanja elementarnih trigonometrijskih jednačina.

Podsjetimo još jednom: zamjenu nepoznate treba izvršiti prvom prilikom; rezultirajuća jednačina nakon zamjene mora se riješiti do kraja, uključujući fazu odabira korijena, pa tek onda vratiti na prvobitnu nepoznatu.

Jedna od karakteristika trigonometrijskih jednačina je da se odgovor u mnogim slučajevima može napisati na različite načine. Čak i za rješavanje jednačine odgovor se može napisati na sljedeći način:

1) u obliku dvije serije: , , ;

2) u standardnom obliku, koji predstavlja kombinaciju navedenih serija: , ;

3) jer , onda se odgovor može napisati u obliku , . (U nastavku, prisustvo parametra , ili parametra u zapisu odgovora automatski znači da ovaj parametar prihvata sve moguće vrijednosti cijelih brojeva. Izuzeci će biti specificirani.)

Očigledno, tri navedena slučaja ne iscrpljuju sve mogućnosti za pisanje odgovora na razmatranu jednačinu (ima ih beskonačno mnogo).

Na primjer, kada je jednakost istinita . Stoga, u prva dva slučaja, ako , možemo zamijeniti sa .

Obično se odgovor piše na osnovu tačke 2. Korisno je zapamtiti sljedeću preporuku: ako se rad ne završi rješavanjem jednadžbe, još uvijek je potrebno provesti istraživanje i odabrati korijene, tada je najpogodniji oblik snimanja je naznačeno u tački 1. (Sličnu preporuku treba dati i za jednačinu.)

Razmotrimo primjer koji ilustruje ono što je rečeno.

Primjer Riješite jednačinu.

Rješenje. Najočiglednije je sljedeći način. Ova se jednadžba rastavlja na dvije: i . Rješavajući svaki od njih i kombinirajući dobivene odgovore, nalazimo .

Drugi način. Budući da , Zatim, zamjenjujući i koristeći formule za smanjenje stupnja. Nakon malih transformacija dobijamo , odakle .

Na prvi pogled, druga formula nema nekih posebnih prednosti u odnosu na prvu. Međutim, ako uzmemo, na primjer, onda ispada da, tj. jednadžba ima rješenje, dok nas prvi metod vodi do odgovora . "Vidi" i dokazati jednakost nije tako lako.

Odgovori. .

Pretvaranje i kombinovanje grupa opštih rešenja trigonometrijskih jednačina

Mi ćemo razmotriti aritmetička progresija, koji se beskrajno proteže u oba smjera. Članovi ove progresije mogu se podijeliti u dvije grupe članova, smještene desno i lijevo od određenog člana koji se naziva centralni ili nulti član progresije.

Fiksiranjem jednog od članova beskonačne progresije sa nultim brojem, moraćemo da izvršimo dvostruko numerisanje za sve preostale članove: pozitivno za članove koji se nalaze desno, i negativno za članove koji se nalaze levo od nule.

Općenito, ako je razlika progresije nulti član, formula za bilo koji (ti) član beskonačne aritmetičke progresije je:

Transformacije formule za bilo koji član beskonačne aritmetičke progresije

1. Ako razliku progresije dodate ili oduzmete nultom članu, onda se progresija neće promijeniti, već će se samo nulti član pomicati, tj. Broj članova će se promijeniti.

2. Ako se koeficijent vrijednosti varijable pomnoži sa , onda će to rezultirati samo preuređivanjem desne i lijeve grupe članova.

3. Ako su uzastopni članovi beskonačne progresije

na primjer, , , ..., , čine središnje članove progresije s istom razlikom jednakom:

tada progresija i niz progresija izražavaju iste brojeve.

Primjer Red se može zamijeniti sa sljedeća tri reda: , , .

4. Ako beskonačne progresije sa istom razlikom imaju kao centralne članove brojeve koji čine aritmetičku progresiju sa razlikom, tada se ovi nizovi mogu zamijeniti jednom progresijom sa razlikom, i sa središnjim članom jednakim bilo kojem od centralnih članova ovih progresija, tj. Ako

onda se ove progresije kombinuju u jednu:

Primjer ... oba su kombinovana u jednu grupu, pošto .

Da bi se grupe koje imaju zajednička rješenja transformirale u grupe koje nemaju zajednička rješenja, te grupe se razlažu u grupe sa zajedničkim periodom, a zatim pokušavaju ujediniti rezultirajuće grupe, isključujući one koje se ponavljaju.

Faktorizacija

Metoda faktorizacije je sljedeća: ako

onda svako rješenje jednačine

je rješenje skupa jednačina

Obratna izjava je, općenito govoreći, netačna: nije svako rješenje populacije rješenje jednačine. Ovo se objašnjava činjenicom da rješenja pojedinačnih jednačina ne mogu biti uključena u domenu definicije funkcije.

Primjer Riješite jednačinu.

Rješenje. Koristeći osnovni trigonometrijski identitet, predstavljamo jednačinu u obliku

Odgovori. ; .

Pretvaranje sume trigonometrijskih funkcija u proizvod

Primjer Riješite jednačinu .

Rješenje. Primjenom formule dobijamo ekvivalentnu jednačinu

Odgovori. .

Primjer Riješite jednačinu.

Rješenje. U ovom slučaju, prije primjene formula za zbir trigonometrijskih funkcija, trebali biste koristiti formulu redukcije . Kao rezultat, dobijamo ekvivalentnu jednačinu

Odgovori. , .

Rješavanje jednadžbi pretvaranjem proizvoda trigonometrijskih funkcija u zbir

Prilikom rješavanja većeg broja jednačina koriste se formule.

Primjer Riješite jednačinu

Rješenje.

Odgovori. , .

Primjer Riješite jednačinu.

Rješenje. Primjenom formule dobijamo ekvivalentnu jednačinu:

Odgovori. .

Rješavanje jednadžbi pomoću redukcijskih formula

Prilikom rješavanja širokog spektra trigonometrijskih jednadžbi, formule igraju ključnu ulogu.

Primjer Riješite jednačinu.

Rješenje. Primjenom formule dobijamo ekvivalentnu jednačinu.


Odgovori. ; .

Rješavanje jednadžbi pomoću formula trostrukog argumenta

Primjer Riješite jednačinu.

Rješenje. Primjenom formule dobijamo jednačinu

Odgovori. ; .

Primjer Riješite jednačinu .

Rješenje. Primjenom formula za smanjenje stepena dobijamo: . Prijavom dobijamo:

Odgovori. ; .

Jednakost istoimenih trigonometrijskih funkcija

Primjer Riješite jednačinu.

Rješenje.

Odgovori. , .

Primjer Riješite jednačinu .

Rješenje. Hajde da transformišemo jednačinu.

Odgovori. .

Primjer Poznato je da i zadovoljiti jednačinu

Pronađite iznos.

Rješenje. Iz jednačine slijedi da

Odgovori. .


Hajde da razmotrimo zbrojeve forme

Ove količine se mogu pretvoriti u proizvod množenjem i dijeljenjem sa, a onda dobijemo

Ova tehnika se može koristiti za rješavanje nekih trigonometrijskih jednadžbi, ali treba imati na umu da se kao rezultat toga mogu pojaviti strani korijeni. Hajde da sumiramo ove formule:

Primjer Riješite jednačinu.

Rješenje. Može se vidjeti da je skup rješenje originalne jednačine. Stoga, množenje lijeve i desne strane jednadžbe sa neće dovesti do pojave dodatnih korijena.

Imamo .

Odgovori. ; .

Primjer Riješite jednačinu.

Rješenje. Pomnožimo lijevu i desnu stranu jednačine sa i primijenimo formule za pretvaranje proizvoda trigonometrijskih funkcija u zbir, dobićemo

Ova jednadžba je ekvivalentna kombinaciji dvije jednačine i , Odatle i .

Budući da korijeni jednadžbe nisu korijeni jednadžbe, trebali bismo isključiti . To znači da je u skupu potrebno isključiti .

Odgovori. I , .

Primjer Riješite jednačinu .

Rješenje. Transformirajmo izraz:

Jednačina će biti napisana kao:

Odgovori. .

Svođenje trigonometrijskih jednadžbi na algebarske

Svodi se na kvadrat

Ako je jednadžba oblika

onda ga zamjena vodi na kvadrat, jer () I.

Ako umjesto termina postoji , tada će potrebna zamjena biti .

Jednačina

svodi se na kvadratna jednačina

prezentacija kao . Lako je provjeriti da za koje , nisu korijeni jednadžbe, a zamjenom se jednačina svodi na kvadratnu.

Primjer Riješite jednačinu.

Rješenje. Pomaknimo ga na lijevu stranu, zamijenimo ga sa , i izrazimo ga kroz i .

Nakon pojednostavljenja dobijamo: . Podijelite termin po pojam i izvršite zamjenu:

Vraćajući se na , nalazimo .

Jednačine homogene s obzirom na ,

Razmotrimo jednačinu oblika

Gdje , , , ..., , --- validan brojevi. U svakom članu na lijevoj strani jednačine, stepeni monoma su jednaki, odnosno zbir stupnjeva sinusa i kosinusa je isti i jednak. Ova jednačina se zove homogena u odnosu na i , a broj se zove indikator homogenosti .

Jasno je da ako , tada će jednadžba poprimiti oblik:

čija su rješenja vrijednosti na kojima , tj. brojevi , . Druga jednačina napisana u zagradama je takođe homogena, ali su stepeni niži za 1.

Ako , onda ovi brojevi nisu korijeni jednadžbe.

Kada dobijemo: , a lijeva strana jednačine (1) uzima vrijednost .

Dakle, za , I , Stoga možemo podijeliti obje strane jednadžbe po . Kao rezultat, dobijamo jednačinu:

koji se zamjenom lako može svesti na algebarski:

Homogene jednadžbe sa indeksom homogenosti 1. Kada imamo jednačinu .

Ako , Tada je ova jednadžba ekvivalentna jednadžbi , , Otuda , .

Primjer Riješite jednačinu.

Rješenje. Ova jednačina je homogena prvog stepena. Podijelimo oba dijela sa dobivamo: , , , .

Odgovori. .

Primjer Kada dobijemo homogenu jednačinu oblika

Rješenje.

Ako , Zatim podijelite obje strane jednadžbe sa , Dobijamo jednačinu , koji se lako može svesti na kvadrat zamjenom: . Ako , tada jednadžba ima realne korijene , . Originalna jednačina će imati dvije grupe rješenja: , , .

Ako , tada jednačina nema rješenja.

Primjer Riješite jednačinu.

Rješenje. Ova jednačina je homogena drugog stepena. Podijelimo obje strane jednadžbe sa , dobivamo: . Neka , onda , , . , , ; .

Odgovori. .

Jednačina se svodi na jednačinu oblika

Da biste to učinili, dovoljno je koristiti identitet

Konkretno, jednačina se reducira na homogenu ako je zamijenimo sa , tada dobijamo ekvivalentnu jednačinu:

Primjer Riješite jednačinu.

Rješenje. Transformirajmo jednačinu u homogenu:

Podijelimo obje strane jednačine sa , dobijamo jednačinu:

Neka , tada dolazimo do kvadratne jednadžbe: , , , , .

Odgovori. .

Primjer Riješite jednačinu.

Rješenje. Kvadirajmo obje strane jednadžbe, uzimajući u obzir da imaju pozitivne vrijednosti: , ,

Neka bude, onda ćemo dobiti , , .

Odgovori. .

Jednačine rješavane korištenjem identiteta

Korisno je znati sljedeće formule:

Primjer Riješite jednačinu.

Rješenje. Koristeći, dobijamo

Odgovori.

Ne nudimo same formule, već metodu za njihovo izvođenje:

dakle,

Isto tako, .

Primjer Riješite jednačinu .

Rješenje. Transformirajmo izraz:

Jednačina će biti napisana kao:

Prihvatanjem primamo. , . Dakle

Odgovori. .

Univerzalna trigonometrijska supstitucija

Trigonometrijska jednadžba oblika

Gdje --- racionalno funkcija uz pomoć formula - , kao i uz pomoć formula - može se svesti na racionalnu jednadžbu s obzirom na argumente , , , , nakon čega se jednadžba može svesti na algebarsku racionalnu jednadžbu s obzirom na korištenje formule univerzalne trigonometrijske supstitucije

Treba napomenuti da upotreba formula može dovesti do sužavanja OD izvorne jednadžbe, budući da ona nije definirana u tačkama, pa je u takvim slučajevima potrebno provjeriti da li su uglovi korijeni izvorne jednadžbe. .

Primjer Riješite jednačinu.

Rješenje. Prema uslovima zadatka. Primjenjujući formule i vršeći zamjenu, dobijamo

odakle i stoga .

Jednačine oblika

Jednačine oblika , gdje --- polinom, rješavaju se zamjenama nepoznatih

Primjer Riješite jednačinu.

Rješenje. Izvršavajući zamjenu i uzimajući u obzir to, dobijamo

gdje , . --- vanjski korijen, jer . Korijeni jednadžbe su .

Korištenje ograničenja funkcija

U praksi centraliziranog testiranja nije tako rijetko naići na jednadžbe čije je rješenje zasnovano na ograničenim funkcijama i . Na primjer:

Primjer Riješite jednačinu.

Rješenje. Budući da , , Tada lijeva strana ne prelazi i jednaka je , Ako

Da bismo pronašli vrijednosti koje zadovoljavaju obje jednadžbe, postupimo na sljedeći način. Riješimo jednu od njih, pa ćemo među pronađenim vrijednostima odabrati one koje zadovoljavaju drugu.

Počnimo s drugim: , . onda , .

Jasno je da će samo za parne brojeve postojati .

Odgovori. .

Druga ideja se ostvaruje rješavanjem sljedeće jednačine:

Primjer Riješite jednačinu .

Rješenje. Iskoristimo imovinu eksponencijalna funkcija: , .

Zbrajanjem ovih nejednakosti pojam po član imamo:

Prema tome, lijeva strana ove jednadžbe je jednaka ako i samo ako su dvije jednakosti zadovoljene:

tj. može poprimiti vrijednosti , , , ili može poprimiti vrijednosti , .

Odgovori. , .

Primjer Riješite jednačinu .

Rješenje., . dakle, .

Odgovori. .

Primjer Riješite jednačinu

Rješenje. Označimo , Tada iz definicije inverzne trigonometrijske funkcije imamo I .

Pošto, onda nejednakost slijedi iz jednačine, tj. . Budući da i , onda i . Međutim, zato.

Ako i, onda. Pošto je ranije utvrđeno da je .

Odgovori. , .

Primjer Riješite jednačinu

Rješenje. Raspon prihvatljivih vrijednosti jednačine je .

Prvo ćemo pokazati da je funkcija

Za bilo koje, može imati samo pozitivne vrijednosti.

Zamislimo funkciju na sljedeći način: .

Od , tada se odvija, tj. .

Dakle, da bi se dokazala nejednakost, potrebno je to pokazati . U tu svrhu, onda kockirajmo obje strane ove nejednakosti

Rezultirajuća numerička nejednakost pokazuje da . Ako također uzmemo u obzir da , tada je lijeva strana jednadžbe nenegativna.

Pogledajmo sada desnu stranu jednačine.

Jer , To

Međutim, poznato je da . Iz toga slijedi da , tj. desna strana jednačine ne prelazi . Prethodno je dokazano da je lijeva strana jednadžbe nenegativna, pa se jednakost u može dogoditi samo ako su obje strane jednake, a to je moguće samo ako .

Odgovori. .

Primjer Riješite jednačinu

Rješenje. Označimo i . Primjenom nejednakosti Cauchy-Bunyakovsky dobivamo . Iz toga slijedi . S druge strane, postoji . Dakle, jednadžba nema korijen.

Odgovori. .

Primjer Riješite jednačinu:

Rješenje. Prepišimo jednačinu kao:

Odgovori. .

Funkcionalne metode za rješavanje trigonometrijskih i kombinovanih jednačina

Ne može se svaka jednadžba kao rezultat transformacija svesti na jednačinu jednog ili drugog standardnog oblika za koju postoji specifična metoda rješenja. U takvim slučajevima se pokazuje korisnim koristiti svojstva funkcija kao što su monotonost, ograničenost, parnost, periodičnost, itd. Dakle, ako jedna od funkcija opada, a druga raste na intervalu, onda ako jednačina ima korijen na ovom intervalu, ovaj korijen je jedinstven, a onda se, na primjer, može pronaći odabirom. Ako je funkcija ograničena iznad, i , i funkcija je ograničena ispod, i , tada je jednadžba ekvivalentna sistemu jednačina

Primjer Riješite jednačinu

Rješenje. Transformirajmo originalnu jednačinu u oblik

i riješiti ga kao kvadratni u odnosu na . onda dobijamo,

Rešimo prvu jednačinu populacije. Uzimajući u obzir ograničenu prirodu funkcije, dolazimo do zaključka da jednačina može imati korijen samo na segmentu. Na ovom intervalu funkcija raste, a funkcija smanjuje se. Stoga, ako ova jednadžba ima korijen, onda je jedinstvena. Nalazimo odabirom.

Odgovori. .

Primjer Riješite jednačinu

Rješenje. Neka i , onda se originalna jednačina može napisati kao funkcionalna jednačina. Budući da je funkcija neparna, onda . U ovom slučaju dobijamo jednačinu.

Budući da je , i monotona na , jednačina je ekvivalentna jednadžbi, tj. , koji ima jedan korijen.

Odgovori. .

Primjer Riješite jednačinu .

Rješenje. Na osnovu teoreme izvoda složena funkcija jasno je da je funkcija opadajuće (funkcija opada, raste, opada). Iz ovoga je jasno da je funkcija definiran na , opadajući. Dakle, ova jednadžba ima najviše jedan korijen. Jer , To

Odgovori. .

Primjer Riješite jednačinu.

Rješenje. Razmotrimo jednačinu na tri intervala.

a) Neka . Tada je na ovom skupu originalna jednadžba ekvivalentna jednadžbi . Koji nema rješenja na intervalu, jer , , A . Na intervalu, izvorna jednadžba također nema korijen, jer , A .

b) Neka . Tada je na ovom skupu originalna jednačina ekvivalentna jednačini

čiji su korijeni na intervalu brojevi , , , .

c) Neka . Tada je na ovom skupu originalna jednačina ekvivalentna jednačini

Koji nema rješenja na intervalu, jer , i . Na intervalu, jednadžba također nema rješenja, jer , , A .

Odgovori. , , , .

Metoda simetrije

Metoda simetrije je pogodna za korištenje kada formulacija zadatka zahtijeva jedinstveno rješenje jednačine, nejednakosti, sistema itd. ili tačnu indikaciju broja rješenja. U ovom slučaju treba detektovati bilo kakvu simetriju datih izraza.

Također je potrebno uzeti u obzir raznolikost različitih mogućih tipova simetrije.

Jednako je važno striktno pridržavanje logičkih faza u rasuđivanju sa simetrijom.

Tipično, simetrija omogućava samo uspostavljanje neophodne uslove, a zatim je potrebna provjera njihove dovoljnosti.

Primjer Pronađite sve vrijednosti parametra za koje jednačina ima jedinstveno rješenje.

Rješenje. Imajte na umu da i --- čak i funkcije, pa je lijeva strana jednadžbe parna funkcija.

Sta ako --- rešenje jednačine, odnosno i rješenje jednačine. Ako --- jedina stvar rješenje jednadžbe, onda neophodno , .

Mi ćemo izabrati moguće vrijednosti, zahtijevajući da to bude korijen jednačine.

Odmah da primijetimo da druge vrijednosti ne mogu zadovoljiti uslove problema.

Ali još nije poznato da li svi odabrani zaista zadovoljavaju uslove problema.

Adekvatnost.

1), jednačina će poprimiti oblik .

2), jednačina će imati oblik:

Očigledno je da za svakog i . Prema tome, posljednja jednačina je ekvivalentna sistemu:

Tako smo dokazali da za , jednačina ima jedinstveno rješenje.

Odgovori. .

Rješenje s istraživanjem funkcija

Primjer Dokažite da su sva rješenja jednadžbe

Cijeli brojevi.

Rješenje. Glavni period originalne jednadžbe je . Stoga prvo ispitujemo ovu jednačinu na intervalu.

Transformirajmo jednačinu u oblik:

Uz pomoć mikrokalkulatora dobijamo:

Ako je , tada iz prethodnih jednakosti dobijamo:

Nakon što smo riješili rezultirajuću jednačinu, dobijamo: .

Izvršeni proračuni omogućavaju pretpostavku da su korijeni jednadžbe koji pripadaju segmentu , i .

Direktno testiranje potvrđuje ovu hipotezu. Dakle, dokazano je da su korijeni jednadžbe samo cijeli brojevi , .

Primjer Riješite jednačinu .

Rješenje. Nađimo glavni period jednačine. Funkcija ima osnovni period jednak . Glavni period funkcije je . Najmanji zajednički višekratnik i jednak je . Dakle, glavni period jednačine je . Neka .

Očigledno, to je rješenje jednačine. Na intervalu. Funkcija je negativna. Stoga druge korijene jednačine treba tražiti samo na intervalima x i .

Pomoću mikrokalkulatora prvo pronalazimo približne vrijednosti korijena jednadžbe. Da bismo to učinili, sastavljamo tablicu vrijednosti funkcije na intervalima i ; tj. na intervalima i .

0 0 202,5 0,85355342
3 -0,00080306 207 0,6893642
6 -0,00119426 210 0,57635189
9 -0,00261932 213 0,4614465
12 -0,00448897 216 0,34549155
15 -0,00667995 219 0,22934931
18 -0,00903692 222 0,1138931
21 -0,01137519 225 0,00000002
24 -0,01312438 228 -0,11145712
27 -0,01512438 231 -0,21961736
30 -0,01604446 234 -0,32363903
33 -0,01597149 237 -0,42270819
36 -0,01462203 240 -0,5160445
39 -0,01170562 243 -0,60290965
42 -0,00692866 246 -0,65261345
45 0,00000002 249 -0,75452006
48 0,00936458 252 -0,81805397
51 0,02143757 255 -0,87270535
54 0,03647455 258 -0,91803444
57 0,0547098 261 -0,95367586
60 0,07635185 264 -0,97934187
63 0,10157893 267 -0,99482505
66 0,1305352 270 -1
67,5 0,14644661

Iz tabele se lako mogu uočiti sledeće hipoteze: koreni jednačine koja pripada segmentu su brojevi: ; ; . Direktno testiranje potvrđuje ovu hipotezu.

Odgovori. ; ; .

Rješavanje trigonometrijskih nejednačina pomoću jediničnog kruga

Prilikom rješavanja trigonometrijskih nejednačina oblika , gdje je jedna od trigonometrijskih funkcija, zgodno je koristiti trigonometrijski krug kako bi se što jasnije predstavila rješenja nejednačine i zapisali odgovor. Glavna metoda za rješavanje trigonometrijskih nejednačina je njihovo svođenje na najjednostavnije nejednačine tipa. Pogledajmo primjer kako riješiti takve nejednakosti.

Primjer Riješite nejednakost.

Rješenje. Nacrtajmo trigonometrijski krug i označimo na njemu točke za koje ordinata prelazi .

Rješenje ove nejednakosti će biti . Također je jasno da ako se određeni broj razlikuje od bilo kojeg broja iz navedenog intervala za , tada će također biti ne manji od . Stoga, trebate samo dodati na krajeve segmenta pronađenog rješenja. Konačno, nalazimo da će rješenja izvorne nejednakosti biti sva .

Odgovori. .

Za rješavanje nejednakosti s tangentom i kotangensom, koristan je koncept linije tangenta i kotangensa. To su prave i, respektivno (na slici (1) i (2)), tangente na trigonometrijski krug.

Lako je vidjeti da ako konstruiramo zrak sa svojim ishodištem u početku koordinata, čineći ugao s pozitivnim smjerom ose apscise, onda je dužina segmenta od tačke do tačke presjeka ovog zraka sa tangentna linija je tačno jednaka tangentu ugla koji ovaj zrak čini sa osom apscise. Slično se opaža za kotangens.

Primjer Riješite nejednakost.

Rješenje. Označimo , tada će nejednakost poprimiti najjednostavniji oblik: . Razmotrimo interval dužine jednak najmanjem pozitivnom periodu (LPP) tangente. Na ovom segmentu, koristeći liniju tangenti, utvrđujemo da . Prisjetimo se sada šta je potrebno dodati pošto NPP funkcioniše. dakle, . Vraćajući se na varijablu, dobijamo to.

Odgovori. .

Nejednakosti sa inverzima trigonometrijske funkcije zgodno je riješiti korištenjem grafova inverznih trigonometrijskih funkcija. Pokažimo kako se to radi na primjeru.

Grafičko rješavanje trigonometrijskih nejednačina

Imajte na umu da ako --- periodično funkciju, tada je za rješavanje nejednačine potrebno pronaći njeno rješenje na odsječku čija je dužina jednaka periodu funkcije. Sva rješenja izvorne nejednakosti sastojat će se od pronađenih vrijednosti, kao i svih onih koje se razlikuju od onih pronađenih za bilo koji cijeli broj perioda funkcije.

Razmotrimo rješenje nejednakosti ().

Budući da , Tada nejednakost nema rješenja. Ako , tada je skup rješenja nejednakosti --- gomila svi realni brojevi.

Neka . Sinusna funkcija ima najmanji pozitivni period, pa se nejednakost može prvo riješiti na segmentu dužine, na primjer, na segmentu. Gradimo grafove funkcija i (). date su nejednačinama oblika: i, odakle,

U ovom radu su razmatrane metode za rješavanje trigonometrijskih jednačina i nejednačina, kako jednostavnih tako i olimpijskih nivoa. Razmatrane su glavne metode za rješavanje trigonometrijskih jednadžbi i nejednačina, te, osim toga, kao specifične --- karakteristika samo za trigonometrijske jednačine i nejednačine, i opšte funkcionalne metode za rješavanje jednačina i nejednačina koje se primjenjuju na trigonometrijske jednačine.

U radu su date osnovne teorijske informacije: definicija i svojstva trigonometrijskih i inverznih trigonometrijskih funkcija; izražavanje trigonometrijskih funkcija u terminima drugih trigonometrijskih funkcija, što je vrlo važno za transformaciju trigonometrijskih izraza, posebno onih koji sadrže inverzne trigonometrijske funkcije; Pored osnovnih trigonometrijskih formula, dobro poznatih iz školskog predmeta, date su formule koje pojednostavljuju izraze koji sadrže inverzne trigonometrijske funkcije. Razmatraju se rješenja elementarnih trigonometrijskih jednačina, metoda faktorizacije i metode svođenja trigonometrijskih jednačina na algebarske. Zbog činjenice da se rješenja trigonometrijskih jednadžbi mogu pisati na više načina, a oblik ovih rješenja ne omogućava da se odmah utvrdi da li su ova rješenja ista ili različita, razmatra se opća shema za rješavanje trigonometrijskih jednačina i transformacija grupa općih rješenja trigonometrijskih jednačina je detaljno razmotrena. Detaljno su obrađene metode rješavanja elementarnih trigonometrijskih nejednačina, kako na jediničnom krugu, tako i grafičkom metodom. Opisan je proces rješavanja neelementarnih trigonometrijskih nejednačina kroz elementarne nejednakosti i metoda intervala, već dobro poznata školarcima. Daju se rješenja tipičnih zadataka za odabir korijena. Date su potrebne teorijske informacije za odabir korijena: particioniranje skupa cijelih brojeva na disjunktne podskupove, rješavanje jednadžbi u cijelim brojevima (dijafantin).

Rezultati ove teze mogu se koristiti kao edukativni materijal pri izradi nastavnih i diplomskih radova, pri sastavljanju izbornih predmeta za školarce, rad se može koristiti i za pripremu studenata za prijemne ispite i centralizovano testiranje.


Vygodsky Ya.Ya., Priručnik za osnovnu matematiku. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.

Igudisman O., Matematika na usmenom ispitu / Igudisman O. --- M.: Iris Press, Rolf, 2001.

Azarov A.I., jednadžbe/Azarov A.I., Gladun O.M., Fedosenko V.S. --- Mn.: Trivium, 1994.

Litvinenko V.N., Radionica o osnovnoj matematici / Litvinenko V.N. --- M.: Obrazovanje, 1991.

Sharygin I.F., Izborni predmet matematike: rješavanje problema / Sharygin I.F., Golubev V.I. --- M.: Obrazovanje, 1991.

Bardushkin V., Trigonometrijske jednadžbe. Odabir korijena/B. Barduškin, A. Prokofjev.// Matematika, br. 12, 2005. str. 23--27.

Vasilevsky A.B., Zadaci za vannastavni rad iz matematike/Vasilevsky A.B. --- Mn.: Narodna Asveta. 1988. --- 176 str.

Sapunov P. I., Transformacija i unija grupa općih rješenja trigonometrijskih jednadžbi / Sapunov P. I. // Matematičko obrazovanje, broj 3, 1935.

Borodin P., Trigonometrija. Materijali prijemni ispiti na Moskovskom državnom univerzitetu [tekst]/P. Borodin, V. Galkin, V. Panferov, I. Sergejev, V. Tarasov // Matematika br. 1, 2005. str. 36--48.

Samusenko A.V., Matematika: Tipične greške kandidata: Referentni priručnik / Samusenko A.V., Kazachenok V.V. --- Mn.: Viša škola, 1991.

Azarov A.I., Funkcionalne i grafičke metode za rješavanje ispitnih zadataka / Azarov A.I., Barvenov S.A., --- Mn.: Aversev, 2004.

Rješavanje jednostavnih trigonometrijskih jednadžbi

Prvo, prisjetimo se formula za rješavanje najjednostavnijih trigonometrijskih jednadžbi.

  1. $sinx=a$
  1. $cosx=a$
  1. $tgx=a$
  1. $ctgx=a$

Rješavanje jednostavnih trigonometrijskih nejednačina.

Da bismo riješili najjednostavnije trigonometrijske nejednačine, prvo trebamo riješiti odgovarajuću jednadžbu, a zatim pomoću trigonometrijskog kruga pronaći rješenje nejednačine. Razmotrimo rješenja najjednostavnijih trigonometrijskih nejednakosti na primjerima.

Primjer 1

$sinx\ge \frac(1)(2)$

Nađimo rješenje trigonometrijske nejednakosti $sinx=\frac(1)(2)$

\ \

Slika 1. Rješenje nejednakosti $sinx\ge \frac(1)(2)$.

Budući da nejednakost ima predznak „veće ili jednako“, rješenje leži na gornjem luku kružnice (u odnosu na rješenje jednadžbe).

Odgovor: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.

Primjer 2

Nađimo rješenje trigonometrijske nejednakosti $cosx=\frac(\sqrt(3))(2)$

\ \

Označimo rješenje na trigonometrijskom krugu

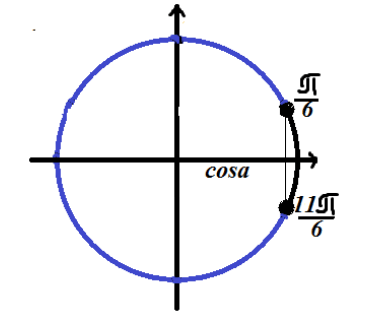
Budući da nejednakost ima predznak „manje od“, rješenje leži na luku kružnice koja se nalazi lijevo (u odnosu na rješenje jednadžbe).

Odgovor: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.

Primjer 3

$tgx\le \frac(\sqrt(3))(3)$

Nađimo rješenje trigonometrijske nejednakosti $tgx=\frac(\sqrt(3))(3)$

\ \

Ovdje nam je također potreban domen definicije. Kao što se sjećamo, tangentna funkcija $x\ne \frac(\pi )(2)+\pi n,n\in Z$

Označimo rješenje na trigonometrijskom krugu

Slika 3. Rješenje nejednakosti $tgx\le \frac(\sqrt(3))(3)$.

Budući da nejednakost ima predznak „manje ili jednako“, rješenje leži na kružnim lukovima označenim plavom bojom na slici 3.

Odgovor:$\ \left(-\frac(\pi )(2)+2\pi n\desno.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\desno.\lijevo.\frac(7\pi )(6)+2\pi n\right]$

Primjer 4

Nađimo rješenje trigonometrijske nejednakosti $ctgx=\sqrt(3)$

\ \

Ovdje nam je također potreban domen definicije. Kao što se sjećamo, tangentna funkcija $x\ne \pi n,n\in Z$

Označimo rješenje na trigonometrijskom krugu

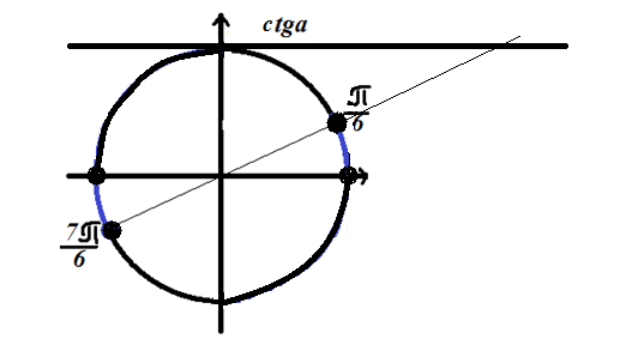
Slika 4. Rješenje nejednakosti $ctgx\le \sqrt(3)$.

Budući da nejednačina ima predznak „veće od“, rješenje leži na kružnim lukovima označenim plavom bojom na slici 4.

Odgovor:$\ \left(2\pi n,\frac(\pi )(6)+2\pi n\desno)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\desno)$

DEFINICIJA

Trigonometrijske nejednakosti su nejednakosti koje sadrže varijablu pod znakom trigonometrijske funkcije.

Rješavanje trigonometrijskih nejednačina

Rješavanje trigonometrijskih nejednačina često se svodi na rješavanje najjednostavnijih trigonometrijskih nejednačina oblika: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \), \(\ \ operatorname(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname(tg) x \leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)

Najjednostavnije trigonometrijske nejednakosti rješavaju se grafički ili pomoću jediničnog trigonometrijskog kruga.

Po definiciji, sinus ugla \(\\alpha \) je ordinata tačke \(\P_(\alpha)(x, y)\) jedinične kružnice (slika 1), a kosinus je apscisa ove tačke. Ova činjenica se koristi za rješavanje jednostavnih trigonometrijskih nejednakosti s kosinusom i sinusom koristeći jedinični krug.

Primjeri rješavanja trigonometrijskih nejednačina

  • Vježbajte

    Riješite nejednačinu \(\ \sin x \leq \frac(\sqrt(3))(2) \)

  • Rešeno

    Budući da \(\ \left|\frac(\sqrt(3))(2)\right| , onda ova nejednakost ima rješenje i može se riješiti na dva načina

    Prvi način. Rešimo ovu nejednačinu grafički. Da bismo to uradili, napravimo graf sinusa \(\ y=\sin x \) (slika 2) i prave linije \(\ y=\frac(\sqrt(3))(2) \) u jedan koordinatni sistem

    Istaknimo intervale na kojima se sinusoida nalazi ispod grafika prave linije \(\ y=\frac(\sqrt(3))(2) \) . Nađimo apscise \(\ x_(1) \) i \(\ x_(2) \) tačaka preseka ovih grafova: \(\ x_(1)=\pi-\arcsin \frac(\sqrt( 3))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+ 2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

    Dobili smo interval \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) ali pošto funkcija \(\ y=\sin x \) je periodičan i ima period \(\ 2 \pi \) , tada će odgovor biti unija intervala: \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac( 7 \pi)(3)+ 2 \pi k\desno]\), \(\k \in Z\)

    Drugi način. Konstruirajmo jediničnu kružnicu i pravu liniju \(\ y=\frac(\sqrt(3))(2) \, njihove točke presjeka će biti označene sa \(\ P_(x_(1)) \) i \ (\ P_(x_(2 )) \) (Sl. 3). Rješenje izvorne nejednakosti bit će skup ordinatnih tačaka, koje su manje od \(\ \frac(\sqrt(3))(2) \) . Nađimo vrijednost \(\ \boldsymbol(I)_(1) \) i \(\ \boldsymbol(I)_(2) \) vrteći se u smjeru suprotnom od kazaljke na satu, \(\ x_(1) Slika 3

    \(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)

    Uzimajući u obzir periodičnost sinusne funkcije, konačno dobijamo intervale \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\desno] \), \(\k\in Z\)

  • Odgovor\(\ x \in\left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \pi\right] \), \(\ k \u Z\)
  • Vježbajte

    Riješite nejednačinu \(\ \sin x>2\)

  • Rješenje

    Sinus je ograničena funkcija: \(\ |\sin x| \leq 1 \) , a desna strana ove nejednakosti je veća od jedan, tako da nema rješenja.

  • Odgovor: nema rješenja.
  • Vježbajte

    Riješite nejednačinu \(\ \cos x>\frac(1)(2) \)

  • Rješenje

    Ova nejednakost se može riješiti na dva načina: grafički i pomoću jediničnog kruga. Razmotrimo svaku od metoda.

    Prvi način. Opišimo u jednom koordinatnom sistemu funkcije koje opisuju lijevu i desnu stranu nejednakosti, odnosno \(\ y=\cos x \) i \(\ y=\frac(1)(2) \) . Istaknimo intervale u kojima se graf kosinusne funkcije \(\ y=\cos x \) nalazi iznad grafika prave linije \(\ y=\frac(1)(2) \) (Sl. 4 ).

    Nađimo apscise tačaka \(\ \boldsymbol(x)_(1) \) i \(\ x_(2) \) – tačke preseka grafova funkcija \(\ y=\cos x \) i \(\ y=\frac (1)(2) \) , koji su krajevi jednog od intervala na kojima vrijedi navedena nejednakost. \(\x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3)\); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)

    S obzirom da je kosinus periodična funkcija, sa periodom \(\ 2 \pi \) , odgovor će biti vrijednosti \(\ x \) iz intervala \(\ \left(-\frac(\pi) (3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\desno \), \(\ k \in Z \)

    Drugi način. Konstruirajmo jediničnu kružnicu i pravu liniju \(\x=\frac(1)(2)\) (pošto apscisa odgovara kosinusima na jediničnom krugu). Označimo \(\ P_(x_(1)) \) i \(\ P_(x_(2)) \) (Sl. 5) – tačke preseka prave i jedinične kružnice. Rješenje originalne jednadžbe će biti skup tačaka apscise, koje su manje od \(\ \frac(1)(2) \) . Nađimo vrijednost \(\ x_(1) \) i \(\ 2 \) obilazeći u smjeru suprotnom od kazaljke na satu tako da \(\ x_(1) Uzimajući u obzir periodičnost kosinusa, konačno dobijamo intervale \( \ \left(-\frac (\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \),\(\k \in Z\)

  • Odgovor: \(\ x \in\left(-\frac(\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k\in Z\)
  • Vježbajte

    Riješite nejednačinu \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)

  • Rješenje

    Konstruirajmo grafove funkcija \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) u jednom koordinatnom sistemu

    Istaknimo intervale u kojima se graf funkcije \(\ y=\operatorname(ctg) x \) nalazi ne više od grafika prave linije \(\ y=-\frac(\sqrt(3) )(3) \) (slika 6) .

    Nađimo apscisu tačke \(\ x_(0) \) , koja je kraj jednog od intervala na kojem je nejednakost \(\ x_(0)=\operatorname(arcctg)\left(-\frac( \sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)( 3)=\frac(2 \pi)(3)\)

    Drugi kraj ovog intervala je tačka \(\ \pi \) , a funkcija \(\ y=\operatorname(ctg) x \) u ovoj tački je nedefinisana. Dakle, jedno od rješenja ove nejednakosti je interval \(\ \frac(2 \pi)(3) \leq x

  • Odgovor:\(\x \in\left[\frac(2 \pi)(3)+\pi k ; \pi+\pi k\right) \), \(\k \in Z\)

    Trigonometrijske nejednakosti sa kompleksnim argumentom

    Trigonometrijske nejednakosti sa složenim argumentima mogu se svesti na jednostavne trigonometrijske nejednakosti primjenom zamjene. Nakon rješavanja, vrši se obrnuta zamjena i izražava se originalna nepoznata.

  • Vježbajte

    Riješite nejednačinu \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)

  • Rješenje

    Izrazimo kosinus na desnoj strani ove nejednakosti: \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)

    Napravimo zamjenu \(\ t=2 x+100^(\circ) \) , nakon čega se ova nejednakost transformira u najjednostavniju nejednačinu \(\ \cos t \leq-\frac(1)(2) \)

    Rešimo ga pomoću jediničnog kruga. Konstruirajmo jediničnu kružnicu i pravu liniju \(\ x=-\frac(1)(2) \) . Označimo \(\P_(1)\) i \(\P_(2)\) – tačke preseka prave i jedinične kružnice (slika 7).

    Rješenje izvorne nejednakosti bit će skup tačaka apscisa, kojih nema više od \(\ -\frac(1)(2)\). Tačka \(\ P_(1) \) odgovara uglu \(\ 120^(\circ) \) , a tačka \(\ P_(2) \) . Dakle, uzimajući u obzir period kosinusa, dobijamo \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \) ,\(\n\in Z\)

    Napravimo obrnutu promjenu \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n\), \(\n \u Z\)

    Izrazimo \(\ \mathbf(x) \), da prvo oduzmemo \(\ 100^(\circ) 120^(\circ)-100^(\circ)+360^(\circ) \ cdot n \ leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \n\ u Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)

    a zatim podijelite sa 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\n \u Z\); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \u Z \)

  • Odgovor\(\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\desno) \), \ (\ x \in\left(10^(\circ)+180^(\circ) \cdot n ; 10^(\circ)+180^(\circ) \cdot n\desno) \)

    Dvostruke trigonometrijske nejednakosti

  • Vježbajte

    Riješite dvostruku trigonometrijsku nejednačinu \(\ \frac(1)(2)

  • Rješenje

    Hajde da uvedemo zamjenu \(\ t=\frac(x)(2) \) , tada će originalna nejednakost poprimiti oblik \(\ \frac(1)(2)

    Rešimo ga pomoću jediničnog kruga. Budući da na jediničnom krugu sinus odgovara osi ordinata, na njemu biramo skup ordinata čije su ordinate veće od \(\ x=\frac(1)(2) \) i manje ili jednake \(\ \frac(\sqrt(2))(2) \) . Na slici 8, ove tačke će se nalaziti na lukovima \(\P_(t_(1))\), \(\P_(t_(2))\) i \(\P_(t_(3))\) , \( \P_(t_(4))\) . Nađimo vrijednost \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) vrteći se u smjeru suprotnom od kazaljke na satu i \ (\t_(1)\(\t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3\ pi)(4) \);\(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi) (6)\)

    Tako dobijamo dva intervala, koji se, uzimajući u obzir periodičnost sinusne funkcije, mogu zapisati na sljedeći način \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k Napravimo obrnutu promjenu \(\ t=\frac(x)(2) \frac(\pi)( 6)+2 \pi k \ leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \), \(\ \frac(3 \pi)(4)+2 \ pi k Izrazimo \(\ \mathbf( x) \), da bismo to uradili, pomnožimo sve strane obe nejednačine sa 2, dobićemo \(\ \frac(\pi)(3)+4 \pi k \leq x

  • Odgovor\(\ x \in\left(\frac(\pi)(3)+4 \pi k ; \frac(\pi)(2)+4 \pi k\desno] \cup\left[\frac( 3 \pi)(2)+4 \pi k ; \frac(5 \pi)(3)+4 \pi k\desno) \(\k \in Z \)

    • Nejednakosti su relacije oblika a › b, gdje su a i b izrazi koji sadrže barem jednu varijablu. Nejednakosti mogu biti stroge - ‹, › i nestroge - ≥, ≤.

    Trigonometrijske nejednakosti su izrazi oblika: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, u kojima je F(x) predstavljen jednom ili više trigonometrijskih funkcija .

    Primjer najjednostavnije trigonometrijske nejednakosti je: sin x ‹ 1/2. Uobičajeno je da se takvi problemi rješavaju grafički, za to su razvijene dvije metode.

    Metoda 1 - Rješavanje nejednačina grafičkim prikazom funkcije

    Da biste pronašli interval koji zadovoljava uslove nejednakosti sin x ‹ 1/2, morate izvršiti sljedeće korake:

    1. Na koordinatnoj osi konstruisati sinusoidu y = sin x.
    2. Na istoj osi nacrtajte grafik numeričkog argumenta nejednakosti, tj. pravu liniju koja prolazi kroz tačku ½ ordinate OY.
    3. Označite tačke preseka dva grafikona.
    4. Zasenčite segment koji je rješenje za primjer.

    Kada su u izrazu prisutni strogi znaci, tačke preseka nisu rešenja. Budući da je najmanji pozitivni period sinusoide 2π, odgovor pišemo na sljedeći način:

    Ako predznaci izraza nisu strogi, tada se interval rješenja mora staviti u uglaste zagrade - . Odgovor na problem se također može zapisati kao sljedeća nejednakost:

    Metoda 2 - Rješavanje trigonometrijskih nejednačina korištenjem jediničnog kruga

    Slični problemi se lako mogu riješiti korištenjem trigonometrijskog kruga. Algoritam za pronalaženje odgovora je vrlo jednostavan:

    1. Prvo morate nacrtati jedinični krug.
    2. Zatim morate zabilježiti vrijednost funkcije luka argumenta desne strane nejednakosti na luku kružnice.
    3. Potrebno je povući pravu liniju koja prolazi kroz vrijednost funkcije luka paralelno sa apscisnom osom (OX).
    4. Nakon toga, ostaje samo odabrati luk kružnice, koji je skup rješenja trigonometrijske nejednakosti.
    5. Zapišite odgovor u traženom obliku.

    Analizirajmo faze rješenja na primjeru nejednakosti sin x › 1/2. Na kružnici su označene tačke α i β - vrijednosti

    Tačke luka koje se nalaze iznad α i β su interval za rješavanje date nejednakosti.

    Ako trebate riješiti primjer za cos, tada će luk odgovora biti lociran simetrično na os OX, a ne na OY. Možete razmotriti razliku između intervala rješenja za sin i cos na dijagramima ispod u tekstu.

    Grafička rješenja za tangentne i kotangensne nejednakosti će se razlikovati i od sinusa i od kosinusa. To je zbog svojstava funkcija.

    Arktangens i arkotangens su tangente na trigonometrijski krug, a minimalni pozitivni period za obje funkcije je π. Da biste brzo i ispravno koristili drugu metodu, morate zapamtiti na kojoj su osi iscrtane vrijednosti sin, cos, tg i ctg.

    Tangentna tangenta ide paralelno sa OY osom. Ako vrijednost arktana a unesemo na jedinični krug, tada će se druga tražena točka nalaziti u dijagonalnoj četvrtini. Uglovi

    One su prijelomne tačke za funkciju, jer graf teži njima, ali ih nikada ne dostiže.

    U slučaju kotangensa, tangenta ide paralelno sa OX osom, a funkcija je prekinuta u tačkama π i 2π.

    Kompleksne trigonometrijske nejednakosti

    Ako je argument funkcije nejednakosti predstavljen ne samo promjenljivom, već cijelim izrazom koji sadrži nepoznanicu, onda govorimo o složenoj nejednakosti. Proces i postupak za njegovo rješavanje se donekle razlikuju od gore opisanih metoda. Pretpostavimo da moramo pronaći rješenje za sljedeću nejednakost:

    Grafičko rješenje uključuje konstruiranje obične sinusoide y = sin x koristeći proizvoljno odabrane vrijednosti x. Izračunajmo tabelu sa koordinatama za kontrolne tačke grafa:

    Rezultat bi trebao biti lijepa kriva.

    Da bismo lakše pronašli rješenje, zamijenimo složen argument funkcije

    Presjek dva grafika nam omogućava da odredimo površinu željenih vrijednosti na kojoj je uvjet nejednakosti zadovoljen.

    Pronađeni segment je rješenje za varijablu t:

    Međutim, cilj zadatka je pronaći sve moguće opcije nepoznato x:

    Rješavanje dvostruke nejednakosti je prilično jednostavno; potrebno je premjestiti π/3 na krajnje dijelove jednadžbe i izvršiti potrebne proračune:

    Odgovorite na zadatakće izgledati kao interval za strogu nejednakost:

    Takvi problemi će zahtijevati od učenika iskustvo i spretnost u rukovanju trigonometrijskim funkcijama. Što se više zadataka za obuku riješi tokom pripremnog procesa, to će student lakše i brže pronaći odgovor na ispitno pitanje Jedinstvenog državnog ispita.

    mob_info