rješenje nejednakosti u modu online rješenje skoro svaku datu nejednakost online. Matematički nejednakosti na mreži da rešavam matematiku. Pronađite brzo rješenje nejednakosti u modu online. Web stranica www.site vam omogućava da pronađete rješenje skoro svaki dat algebarski, trigonometrijski ili transcendentalna nejednakost na mreži. Kada proučavate gotovo bilo koju granu matematike u različitim fazama, morate odlučiti nejednakosti na mreži. Da biste odmah dobili odgovor, i što je najvažnije tačan, potreban vam je resurs koji vam to omogućava. Hvala sajtu www.site rješavanje nejednakosti na mreži trajat će nekoliko minuta. Glavna prednost www.site kod rješavanja matematičkih nejednakosti na mreži- ovo je brzina i tačnost pruženog odgovora. Stranica je u stanju riješiti bilo koje algebarske nejednakosti na mreži, trigonometrijske nejednakosti na mreži, transcendentalne nejednakosti na mreži, i nejednakosti sa nepoznatim parametrima u modu online. Nejednakosti služe kao moćan matematički aparat rješenja praktični problemi. Uz pomoć matematičke nejednakosti moguće je izraziti činjenice i odnose koji na prvi pogled mogu izgledati zbunjujuće i složene. Nepoznate količine nejednakosti može se naći formulisanjem problema u matematički jezik u formi nejednakosti I odlučiti primljen zadatak u modu online na web stranici www.site. Bilo koji algebarska nejednakost, trigonometrijske nejednakosti ili nejednakosti koji sadrži transcendentalno funkcije koje možete lako odlučiti online i dobiti tačan odgovor. Studiranje prirodne nauke, neizbježno se suočavate s potrebom rješenja nejednakosti. U ovom slučaju, odgovor mora biti tačan i mora se dobiti odmah u režimu online. Stoga za rješavanje matematičkih nejednakosti na mreži preporučujemo stranicu www.site, koja će postati vaš nezamjenjiv kalkulator rješavanje algebarskih nejednakosti online, trigonometrijske nejednakosti online, i transcendentalne nejednakosti na mreži ili nejednakosti sa nepoznatim parametrima. Za praktične probleme pronalaženja online rješenja za razna matematičke nejednakosti resurs www.. Rješavanje nejednakosti na mreži sami, korisno je provjeriti primljeni odgovor koristeći online rješenje nejednakosti na web stranici www.site. Trebate ispravno napisati nejednakost i odmah dobiti online rješenje, nakon čega ostaje samo da uporedite odgovor sa svojim rješenjem nejednakosti. Provjera odgovora neće trajati više od minute, dovoljno je rješavanje nejednakosti na mreži i uporedi odgovore. Ovo će vam pomoći da izbjegnete greške u odluka i ispraviti odgovor na vrijeme kada rješavanje nejednakosti na mreži bilo algebarski, trigonometrijski, transcendentalno ili nejednakost sa nepoznatim parametrima.

Modul brojeva sam taj broj naziva se ako nije negativan, ili isti broj sa suprotnim predznakom ako je negativan.

Na primjer, modul broja 6 je 6, a modul broja -6 je također 6.

To jest, modul broja se razumije kao apsolutna vrijednost, apsolutna vrijednost ovog broja bez uzimanja u obzir njegovog predznaka.

Označava se kako slijedi: |6|, | X|, |A| itd.

(Više detalja u odjeljku „Brojni modul“).

Jednačine sa modulom.

Primjer 1 . Riješite jednačinu|10 X - 5| = 15.

Rješenje.

Prema pravilu, jednadžba je ekvivalentna kombinaciji dvije jednačine:

10X - 5 = 15
10X - 5 = -15

Odlučujemo:

10X = 15 + 5 = 20
10X = -15 + 5 = -10

X = 20: 10
X = -10: 10

X = 2
X = -1

Odgovori: X 1 = 2, X 2 = -1.

Primjer 2 . Riješite jednačinu|2 X + 1| = X + 2.

Rješenje.

Pošto je modul nenegativan broj, onda X+ 2 ≥ 0. Prema tome:

X ≥ -2.

Napravimo dvije jednačine:

2X + 1 = X + 2
2X + 1 = -(X + 2)

Odlučujemo:

2X + 1 = X + 2
2X + 1 = -X - 2

2X - X = 2 - 1
2X + X = -2 - 1

X = 1
X = -1

Oba broja su veća od -2. Dakle, oba su korijeni jednadžbe.

Odgovori: X 1 = -1, X 2 = 1.

Primjer 3 . Riješite jednačinu

|X + 3| - 1
————— = 4
X - 1

Rješenje.

Jednačina ima smisla ako nazivnik nije jednaka nuli- znači ako X≠ 1. Uzmimo u obzir ovaj uslov. Naša prva akcija je jednostavna - ne samo da se riješimo razlomka, već ga transformiramo tako da dobijemo modul u njegovom čistom obliku:

|X+ 3| - 1 = 4 · ( X - 1),

|X + 3| - 1 = 4X - 4,

|X + 3| = 4X - 4 + 1,

|X + 3| = 4X - 3.

Sada imamo samo izraz ispod modula na lijevoj strani jednačine. Nastavi.
Modul broja je nenegativan broj - to jest, mora biti veći od nule ili jednak nuli. U skladu s tim rješavamo nejednakost:

4X - 3 ≥ 0

4X ≥ 3

X ≥ 3/4

Dakle, imamo drugi uslov: korijen jednadžbe mora biti najmanje 3/4.

U skladu s pravilom sastavljamo skup od dvije jednadžbe i rješavamo ih:

X + 3 = 4X - 3
X + 3 = -(4X - 3)

X + 3 = 4X - 3
X + 3 = -4X + 3

X - 4X = -3 - 3
X + 4X = 3 - 3

X = 2
X = 0

Dobili smo dva odgovora. Provjerimo jesu li korijeni originalne jednadžbe.

Imali smo dva uslova: koren jednačine ne može biti jednak 1 i mora biti najmanje 3/4. To je X ≠ 1, X≥ 3/4. Oba ova uslova odgovaraju samo jednom od dva dobijena odgovora - broju 2. To znači da je samo ovo koren originalne jednačine.

Odgovori: X = 2.

Nejednakosti sa modulom.

Primjer 1 . Riješite nejednakost| X - 3| < 4

Rješenje.

Pravilo modula kaže:

|A| = A, Ako A ≥ 0.

|A| = -A, Ako A < 0.

Modul može imati i ne-negativne i negativne brojeve. Dakle, moramo uzeti u obzir oba slučaja: X- 3 ≥ 0 i X - 3 < 0.

1) Kada X- 3 ≥ 0 naša prvobitna nejednakost ostaje onakva kakva jeste, samo bez predznaka modula:
X - 3 < 4.

2) Kada X - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

-(X - 3) < 4.

Otvaranjem zagrada dobijamo:

-X + 3 < 4.

Tako smo iz ova dva uslova došli do ujedinjenja dva sistema nejednakosti:

X - 3 ≥ 0
X - 3 < 4

X - 3 < 0
-X + 3 < 4

Hajde da ih rešimo:

X ≥ 3
X < 7

X < 3
X > -1

Dakle, naš odgovor je unija dva skupa:

3 ≤ X < 7 U -1 < X < 3.

Odrediti najmanji i najveća vrijednost. To su -1 i 7. Štaviše X veći od -1 ali manji od 7.
osim toga, X≥ 3. To znači da je rješenje nejednakosti cijeli skup brojeva od -1 do 7, isključujući ove ekstremne brojeve.

Odgovori: -1 < X < 7.

Ili: X ∈ (-1; 7).

Dodaci.

1) Postoji jednostavniji i kraći način za rješavanje naše nejednakosti - grafički. Da biste to učinili, morate nacrtati horizontalnu os (slika 1).

Izraz | X - 3| < 4 означает, что расстояние от точки X do tačke 3 je manje od četiri jedinice. Označavamo broj 3 na osi i brojimo 4 podjele lijevo i desno od nje. Lijevo dolazimo do tačke -1, desno - do tačke 7. Dakle, tačke X samo smo ih vidjeli bez da smo ih izračunali.

Štaviše, prema uslovu nejednakosti, sami -1 i 7 nisu uključeni u skup rješenja. Tako dobijamo odgovor:

1 < X < 7.

2) Ali postoji još jedno rješenje koje je jednostavnije čak i od grafičke metode. Da bismo to učinili, naša nejednakost mora biti predstavljena u sljedećem obliku:

4 < X - 3 < 4.

Uostalom, ovako je po pravilu modula. Nenegativni broj 4 i sličan negativni broj -4 su granice za rješavanje nejednakosti.

4 + 3 < X < 4 + 3

1 < X < 7.

Primjer 2 . Riješite nejednakost| X - 2| ≥ 5

Rješenje.

Ovaj primjer se značajno razlikuje od prethodnog. Lijeva strana je veća od 5 ili jednaka 5. C geometrijska tačka Sa stanovišta, rješenje nejednakosti su svi brojevi koji se nalaze na udaljenosti od 5 jedinica ili više od tačke 2 (slika 2). Grafikon pokazuje da su to svi brojevi koji su manji ili jednaki -3 i veći ili jednaki 7. To znači da smo već dobili odgovor.

Odgovori: -3 ≥ X ≥ 7.

Usput rješavamo istu nejednakost tako što ćemo slobodni član preurediti lijevo i desno sa suprotnim predznakom:

5 ≥ X - 2 ≥ 5

5 + 2 ≥ X ≥ 5 + 2

Odgovor je isti: -3 ≥ X ≥ 7.

Ili: X ∈ [-3; 7]

Primjer je riješen.

Primjer 3 . Riješite nejednakost 6 X 2 - | X| - 2 ≤ 0

Rješenje.

Broj X može biti pozitivan broj, negativan broj ili nula. Stoga moramo uzeti u obzir sve tri okolnosti. Kao što znate, oni se uzimaju u obzir u dvije nejednakosti: X≥ 0 i X < 0. При X≥ 0 jednostavno prepisujemo našu originalnu nejednakost kakva jeste, samo bez predznaka modula:

6x 2 - X - 2 ≤ 0.

Sada o drugom slučaju: ako X < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6X 2 - (-X) - 2 ≤ 0.

Proširivanje zagrada:

6X 2 + X - 2 ≤ 0.

Tako smo dobili dva sistema jednačina:

6X 2 - X - 2 ≤ 0
X ≥ 0

6X 2 + X - 2 ≤ 0
X < 0

Moramo riješiti nejednakosti u sistemima - a to znači da moramo pronaći korijene dvije kvadratne jednačine. Da bismo to uradili, izjednačavamo leve strane nejednakosti sa nulom.

Počnimo s prvim:

6X 2 - X - 2 = 0.

Kako riješiti kvadratnu jednačinu - pogledajte odjeljak “Kvadratna jednačina”. Odmah ćemo imenovati odgovor:

X 1 = -1/2, x 2 = 2/3.

Iz prvog sistema nejednačina dobijamo da je rješenje izvorne nejednakosti cijeli skup brojeva od -1/2 do 2/3. Zapisujemo uniju rješenja na X ≥ 0:
[-1/2; 2/3].

Sada da riješimo drugu kvadratnu jednačinu:

6X 2 + X - 2 = 0.

Njegovi koreni:

X 1 = -2/3, X 2 = 1/2.

Zaključak: kada X < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.

Kombinirajmo dva odgovora i dobijemo konačni odgovor: rješenje je cijeli skup brojeva od -2/3 do 2/3, uključujući ove ekstremne brojeve.

Odgovori: -2/3 ≤ X ≤ 2/3.

Ili: X ∈ [-2/3; 2/3].

REVIEWED

Pedagoško vijeće MOU

"Srednja škola Zashizhemskaya"

Protokol br. 1

DOGOVOREN

Zamjenik direktora za ljudske resurse

_______ /Sidorkina R.L./

ODOBRIO sam

Glavni učitelj:

A.P. Konakov

Naredba br. 63

Rješavanje jednadžbi i nejednačina s modulom

Istraživanja

Program je sastavio:

viši nastavnik matematike

Sidorkina R.L.

Selo Zashizhemye, 2014

Sadržaj

Uvod………………………………………………………………………………………………3

Najjednostavnije jednadžbe i nejednačine sa modulom…………5

Grafičko rješenje jednačina i nejednačina sa modulom………….8

Drugi načini rješavanja jednadžbi i nejednačina sa modulom.........10

Zaključak…………………………………………………………………..16

Reference…………………………………………………………18

1. Uvod

Koncept apsolutne vrijednosti (modula) je jedna od najvažnijih karakteristika broja, kako u oblasti realnih tako i kompleksnih brojeva.

Ovaj koncept se široko koristi ne samo u različitim dijelovima školskog kursa matematike, već iu predmetima višu matematiku, fiziku i tehničke nauke studirao na univerzitetima. Na primjer, u teoriji približnih proračuna koriste se koncepti apsolutne i relativne greške približnog broja. U mehanici i geometriji proučavaju se pojmovi vektora i njegove dužine (vektorski modul). IN matematička analiza koncept apsolutne vrijednosti broja sadržan je u definicijama takvih osnovnih pojmova kao što su granica, ograničena funkcija itd. Problemi vezani za apsolutne vrijednosti često se nalaze na matematičkim olimpijadama, prijemni ispiti na univerzitete i Jedinstveni državni ispit. I tako nam je postalo važno da proučimo neke aspekte ove teme.

Dom svrha Naš rad je proučavanje različitih metoda za rješavanje jednačina i nejednačina sa modulima.

Ovaj cilj se mora postići rješavanjem sljedećeg zadataka:

Proučite definiciju i neka svojstva modula.

Ovladati rješavanjem jednostavnih jednačina i nejednačina s modulom kroz ekvivalentne prijelaze

Razmotrite različite metode za rješavanje jednačina i nejednačina s modulom.

Objekat proučavaju se neke vrste jednačina i nejednačina sa modulom.

Stavka istraživanje - razne metode za rješavanje jednačina i nejednačina sa modulom i to: grafička metoda, metoda geometrijske interpretacije, upotreba identiteta, primjena teoreme znakova, metoda prijelaza na posljedicu, metoda intervala, metoda množenja pozitivnim faktorom, metoda otkrivanja modula.

Tokom istraživanja korišćene su metode kao što su proučavanje literature o ovoj problematici i praktična metoda.

U toku našeg rada ispitali smo izvore kao što su:

1. “Velika matematička enciklopedija” za školarce i studente;

Matematika. Jedinstveni državni ispit - 2011-2012. Tipične opcije ispita. / Uredio A.L. Semenova, I.V. Yashchenko.

Enciklopedija “Ja poznajem svijet” Matematika;

;

1. 1. Najjednostavnije jednadžbe i nejednačine s modulom

Najjednostavnijim jednadžbama smatrat ćemo one koje se rješavaju jednim od sljedećih ekvivalentnih prijelaza:

Primjeri rješavanja jednostavnih jednačina.

Primjer 1 Hajde da riješimo jednačinu
.

Rješenje.

Odgovori.
.

Primjer 2 Hajde da riješimo jednačinu.

Rješenje.

Odgovori.
.

Primjer 3 Hajde da riješimo jednačinu
.

Rješenje.

Odgovori.
.

Niz jednačina se rješava korištenjem sljedeće teoreme.

Teorema.4 Zbir modula jednak je algebarskom zbiru submodularnih veličina ako i samo ako svaka veličina ima predznak s kojim je uključena u algebarski zbir.

Primjer 5 Riješite jednačinu

Rješenje. Budući da , Tada imamo jednakost oblika , Gdje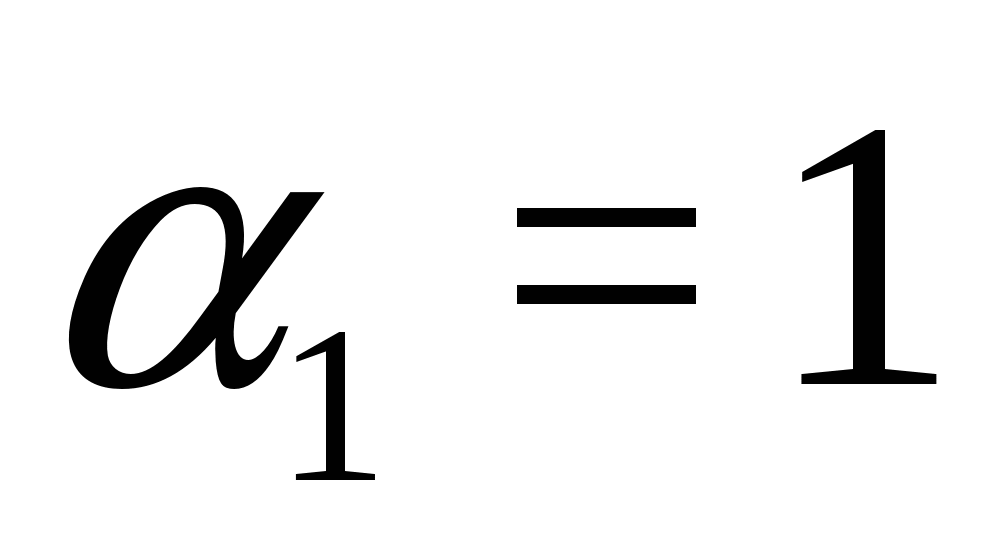
,
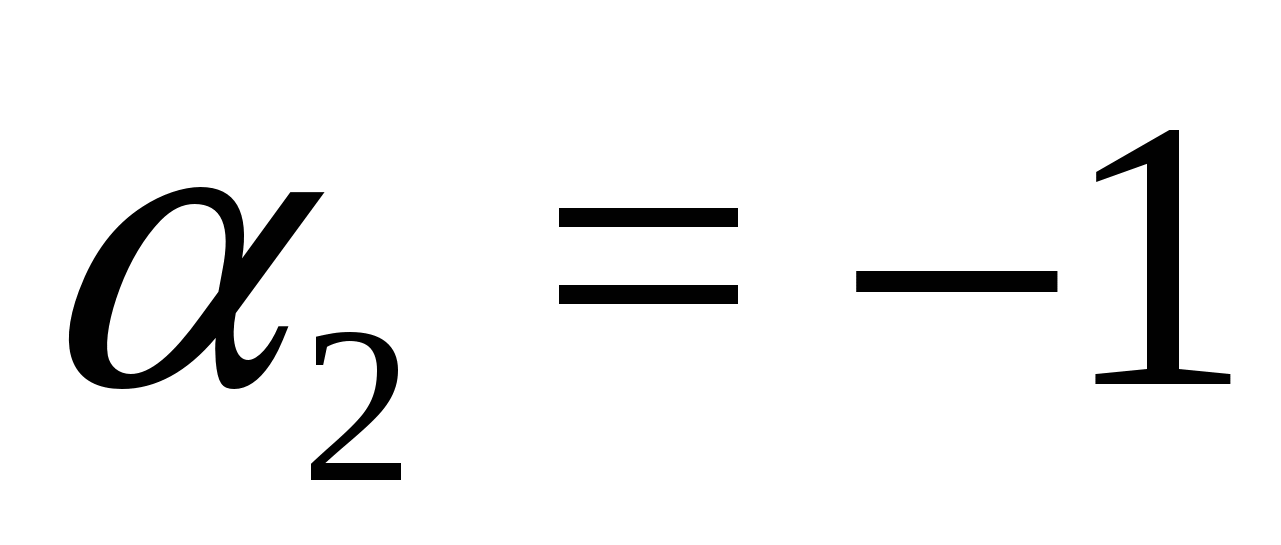. Prema tome, originalna jednačina je ekvivalentna sistemu:

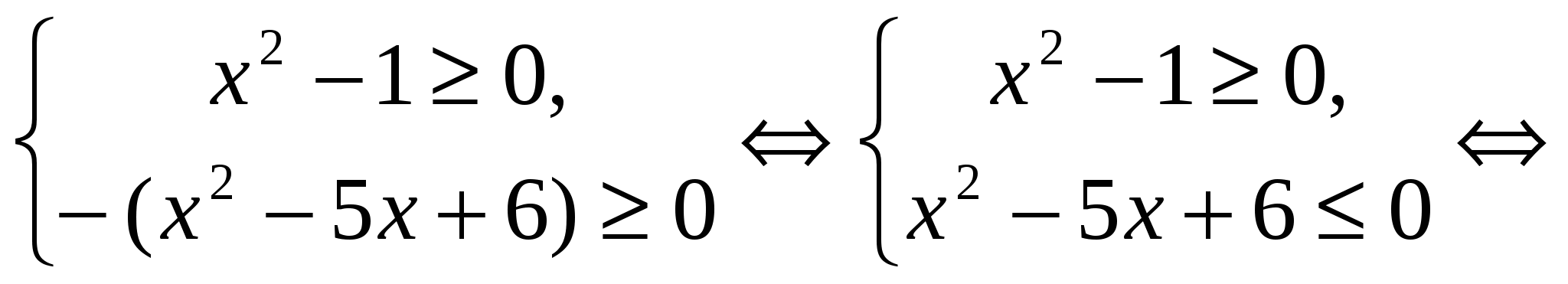
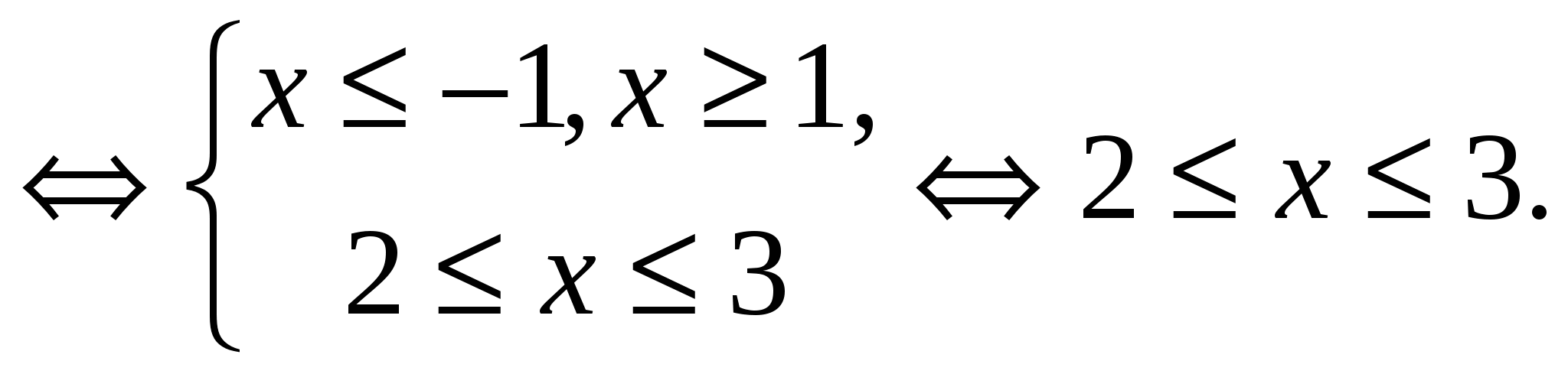
Odgovori.
.

Primjeri rješavanja jednostavnih nejednačina.

Primjer 6 Hajde da riješimo nejednakost
.

Rješenje.

Odgovori.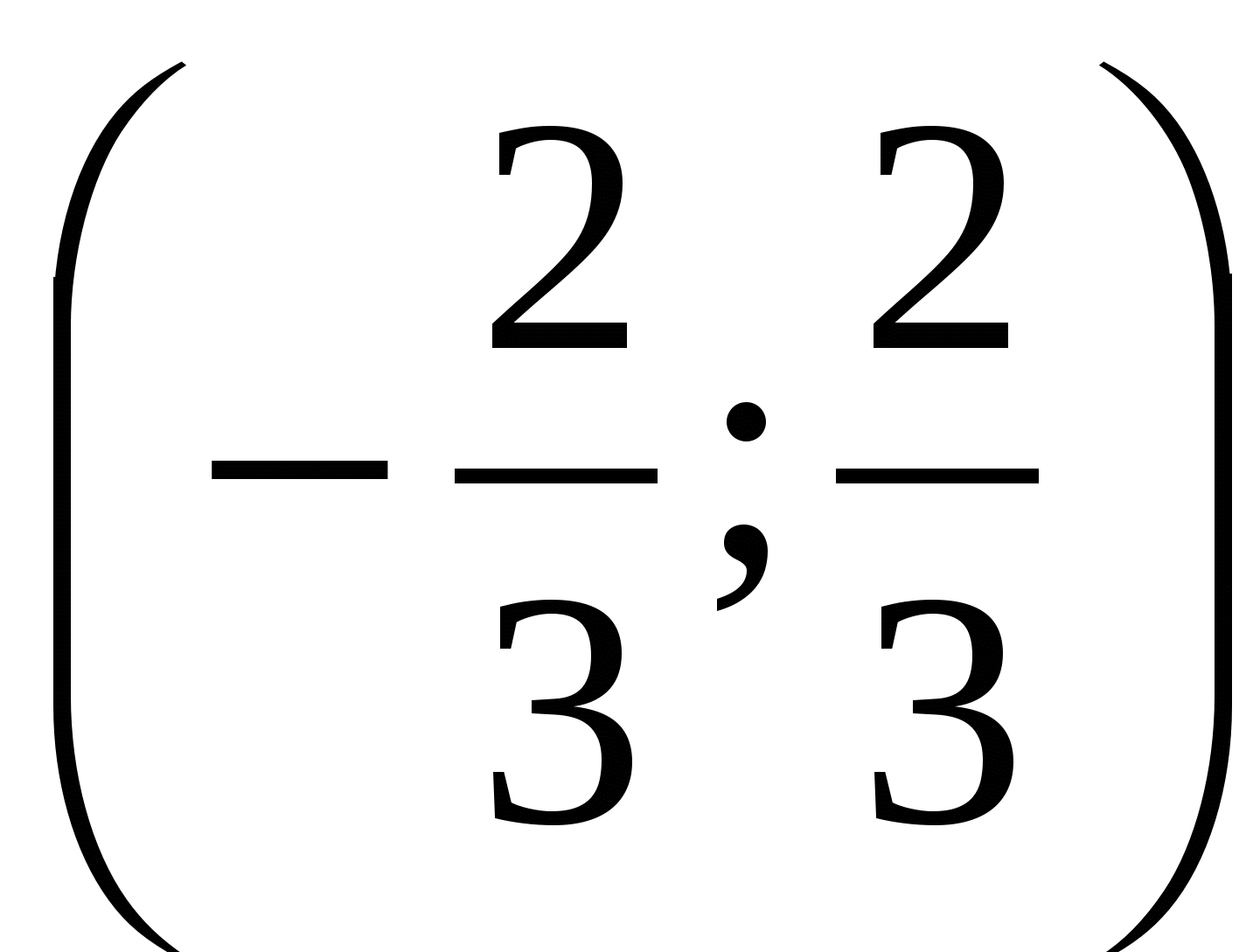
.

Primjer 7 Hajde da riješimo nejednakost
.

Rješenje.

Odgovori.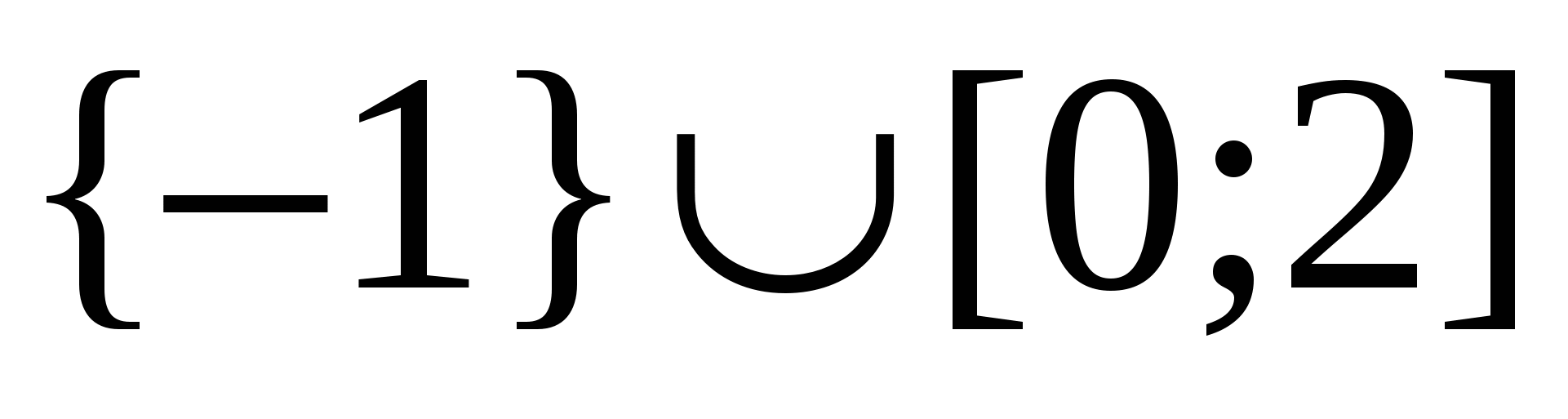
.

Čudno, ali
je dovoljno da se riješi predznaka modula u bilo kojoj nejednakosti.

Primjer 8 Riješite nejednakost

Rješenje.

Odgovori.
.

3. Grafičko rješenje jednačina i nejednačina sa modulom

Rješavanje jednačina koje sadrže predznak apsolutne vrijednosti često je mnogo pogodnije za rješavanje ne analitički, već grafički (posebno jednadžbe koje sadrže parametre).

Primjer 9(C5, Jedinstveni državni ispit - 2010.)

C5. Za svaku vrijednosta naznačiti broj rješenja jednačine

Rješenje.Nacrtajmo funkciju
. Da biste to učinili, odaberite cijeli kvadrat:

Broj presječnih tačaka grafa funkcije y =
sa horizontalnim linijama y = a jednako je broju rješenja jednadžbe.

O odgovor: Ako < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, onda postoje dva rješenja.

Drugi načini rješavanja jednačina i nejednačina s modulom

• Metoda proširenja modula

Pogledajmo metodu proširenja modula koristeći primjer:

Primjer 10 Riješite jednačinu

Rješenje. Ova jednadžba sadrži više od jednog modula.

Metoda za rješavanje jednačina koje sadrže varijable pod znakom dva ili više modula je sljedeća.

1. Pronađite vrijednosti varijable pri kojima svaki od modula postaje nula: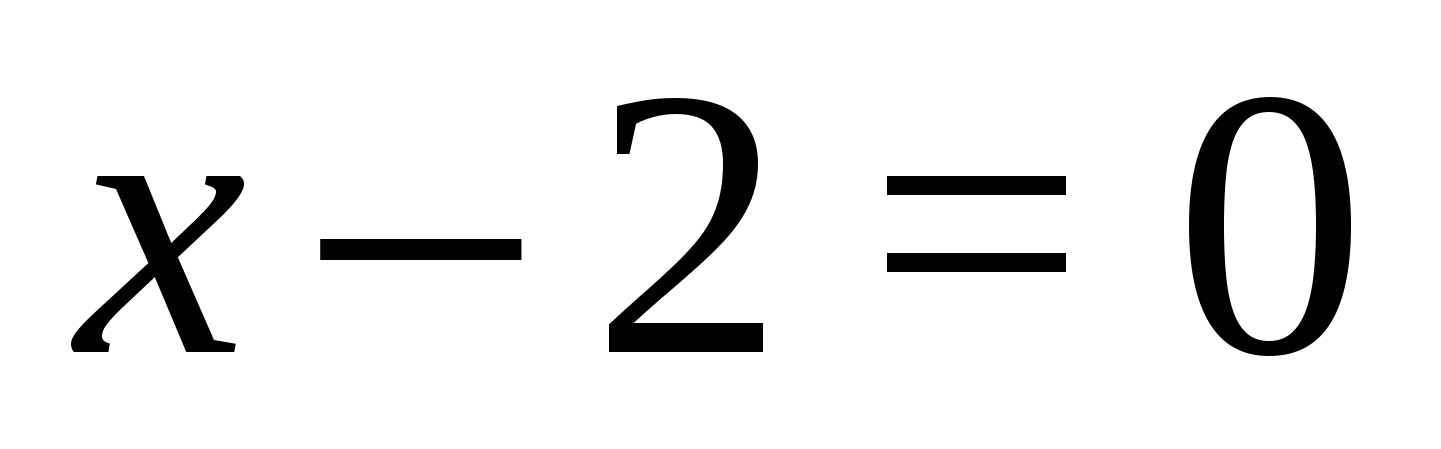
,
;
,
;
,
.

2. Označite ove tačke na brojevnoj pravoj.

3. Razmatramo jednačinu na svakom od intervala i postavljamo predznak izraza koji se nalaze ispod modula.

1) Kada
ili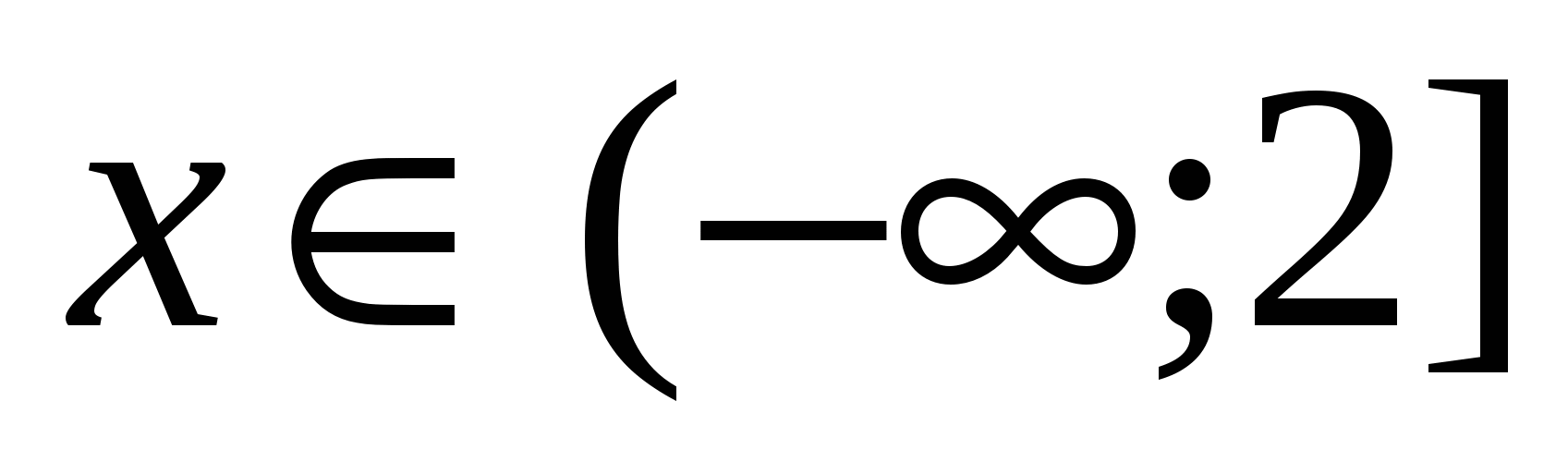
. Da bi se odredio predznak svakog od modulo izraza na ovom intervalu, dovoljno je uzeti bilo koju vrijednost iz ovog intervala i zamijenite ga u izraz. Ako je rezultirajuća vrijednost negativna, onda za sve iz ovog intervala izraz će biti negativan; ako je primljeno numerička vrijednost pozitivno, što znači za sve vrijednosti iz ovog intervala izraz će biti pozitivan.

Uzmimo vrijednost
između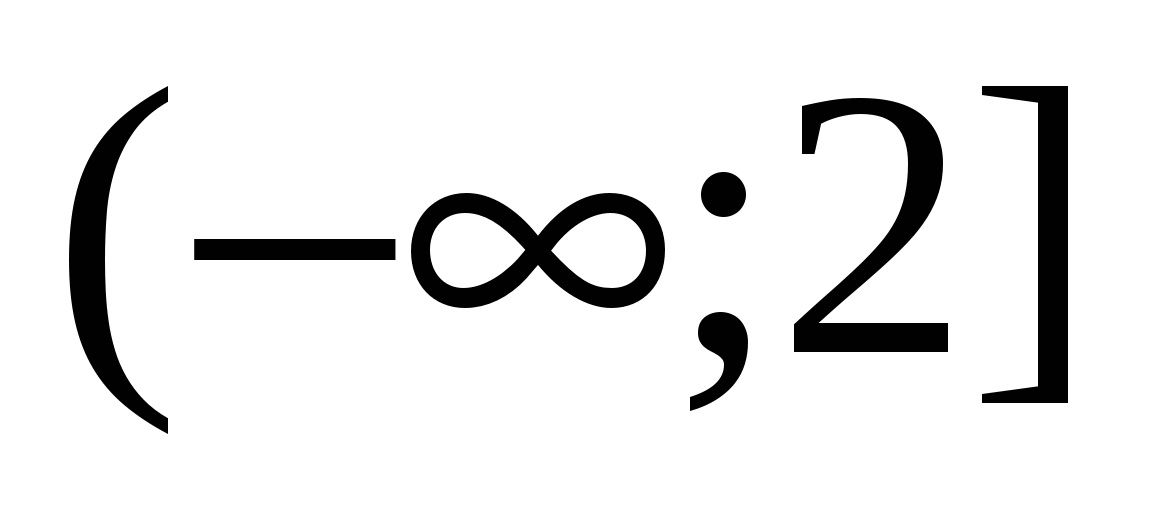
i zamijenite njegovu vrijednost u izraz
, dobijamo
, što znači u ovom intervalu
negativan, i stoga ``će izaći"" ispod modula sa znakom ``minus", dobijamo:
.

Na ovoj vrijednosti , izraz
dobiće vrednost
, što znači da je u intervalu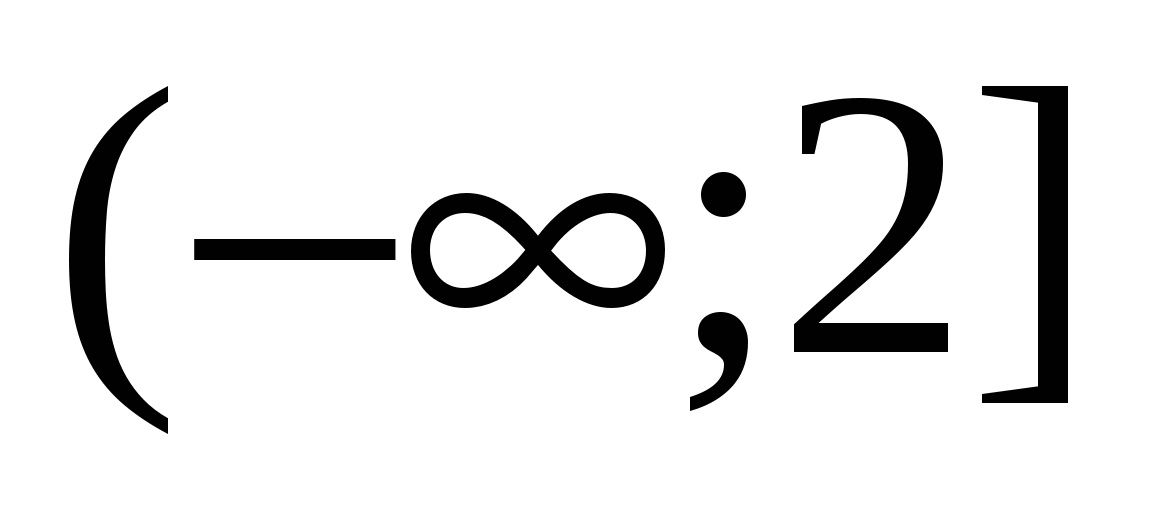
također uzima negativne vrijednosti i ``izići će"" iz modula sa znakom ``minus", dobijamo:
.

Izraz
dobiće vrednost
i "izaći" ispod modula sa znakom "minus":
.

Jednačina na ovom intervalu će ispasti ovako: rješavajući je, nalazimo:
.

Saznajemo da li je ova vrijednost uključena u interval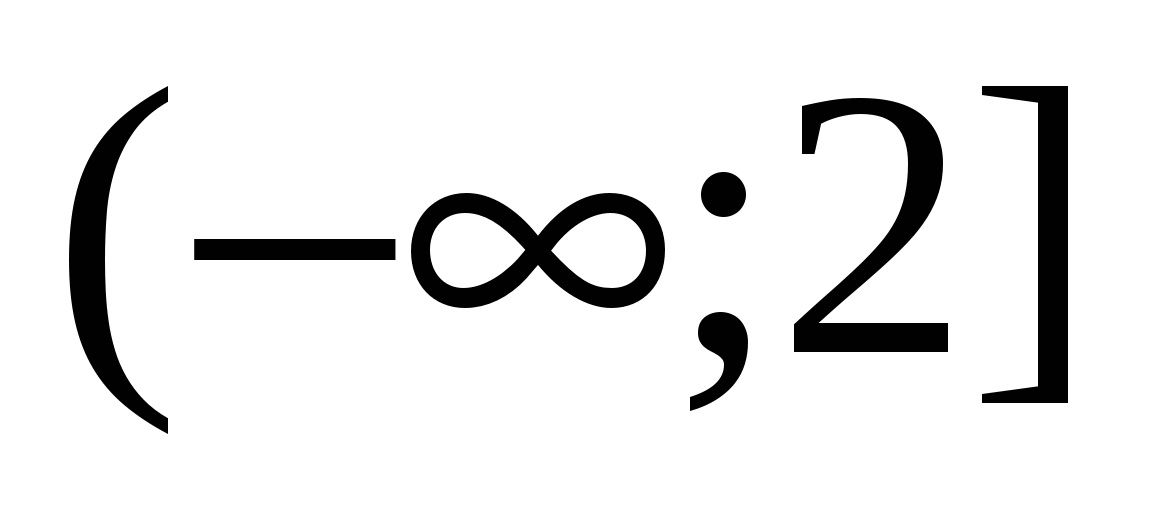
. Ispostavilo se da je uključen, što znači
je korijen jednadžbe.

2) Kada
. Odaberite bilo koju vrijednost iz ovog jaza. Neka
. Određujemo predznak svakog od izraza pod modulom na ovoj vrijednosti . Ispostavilo se da je izraz
pozitivna, a druga dva negativna.

Jednačina na ovom intervalu će imati oblik: . Rešavajući to, nalazimo
. Ova vrijednost nije uključena u raspon
, i stoga nije korijen jednadžbe.

3) Kada
. Odaberite proizvoljnu vrijednost iz ovog intervala, recimo
i zamijenite svaki od izraza. Nalazimo da su izrazi
I
su pozitivni i
- negativan. Dobijamo sljedeću jednačinu: .

Nakon transformacije dobijamo:
, što znači da jednačina nema korijen na ovom intervalu.

4) Kada
. Lako je ustanoviti da su svi izrazi na ovom intervalu pozitivni, što znači da dobijamo jednačinu: ,
,
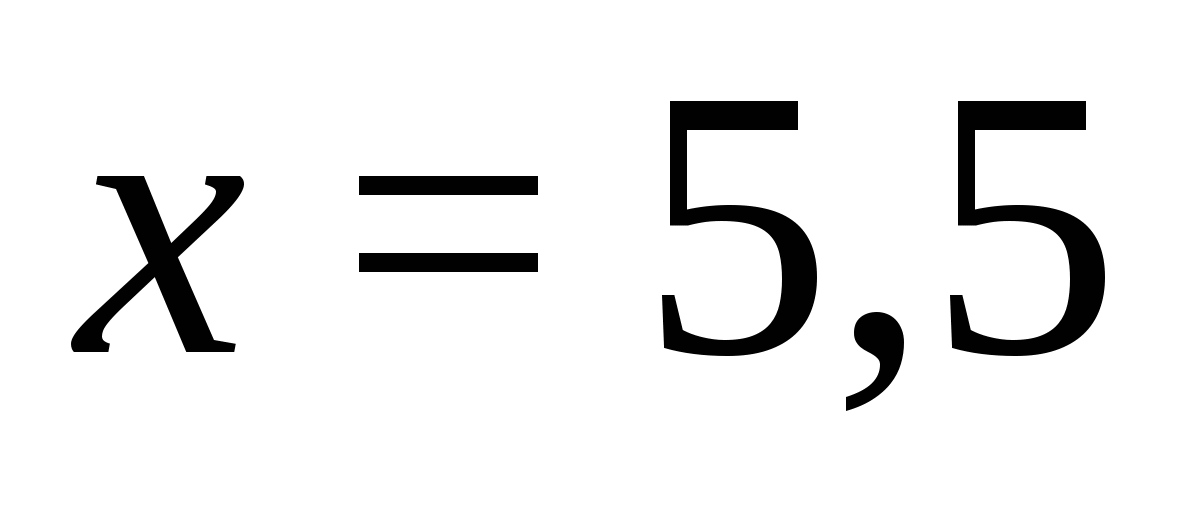koji je uključen u interval i korijen je jednačine.

Odgovori.
,
.

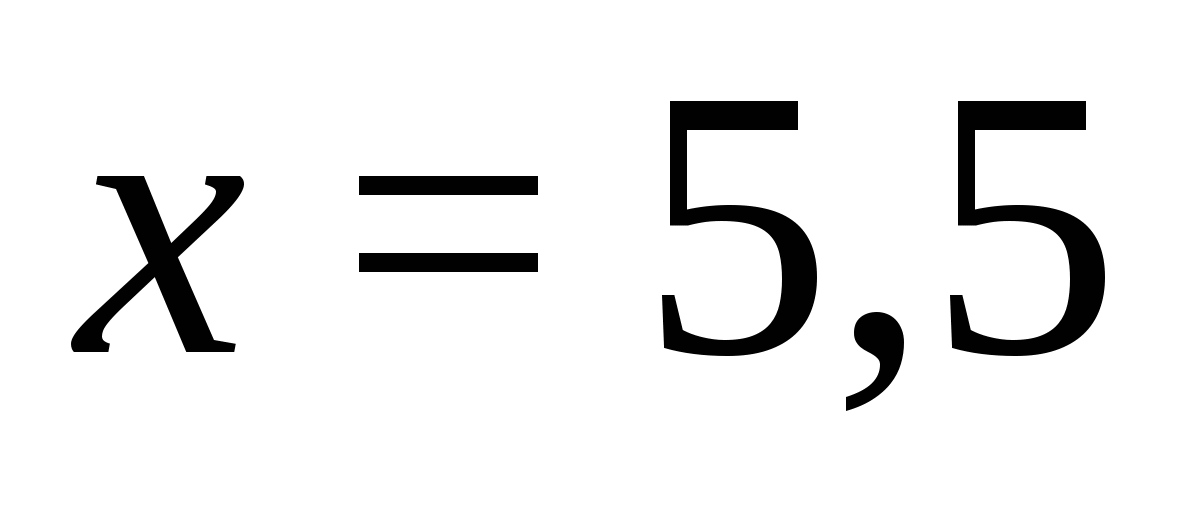• Rješavanje jednadžbi koje sadrže module nenegativnih izraza

Primjer 11 Koliki je zbir korijena jednadžbe (korijena, ako postoji) jednadžbe

Rješenje. Razmotrite izraz

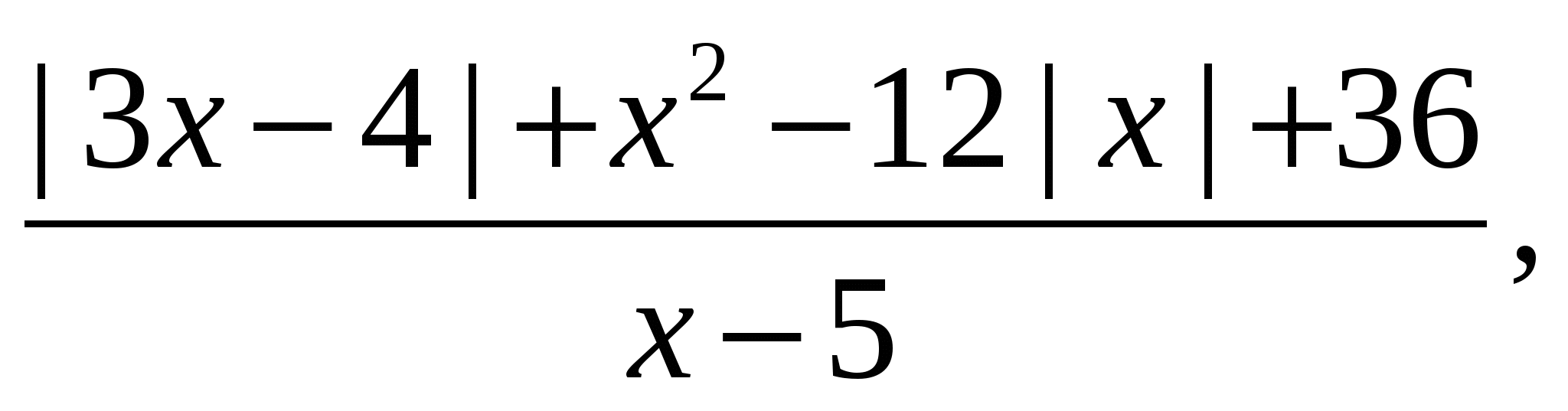i pretvoriti ga u formu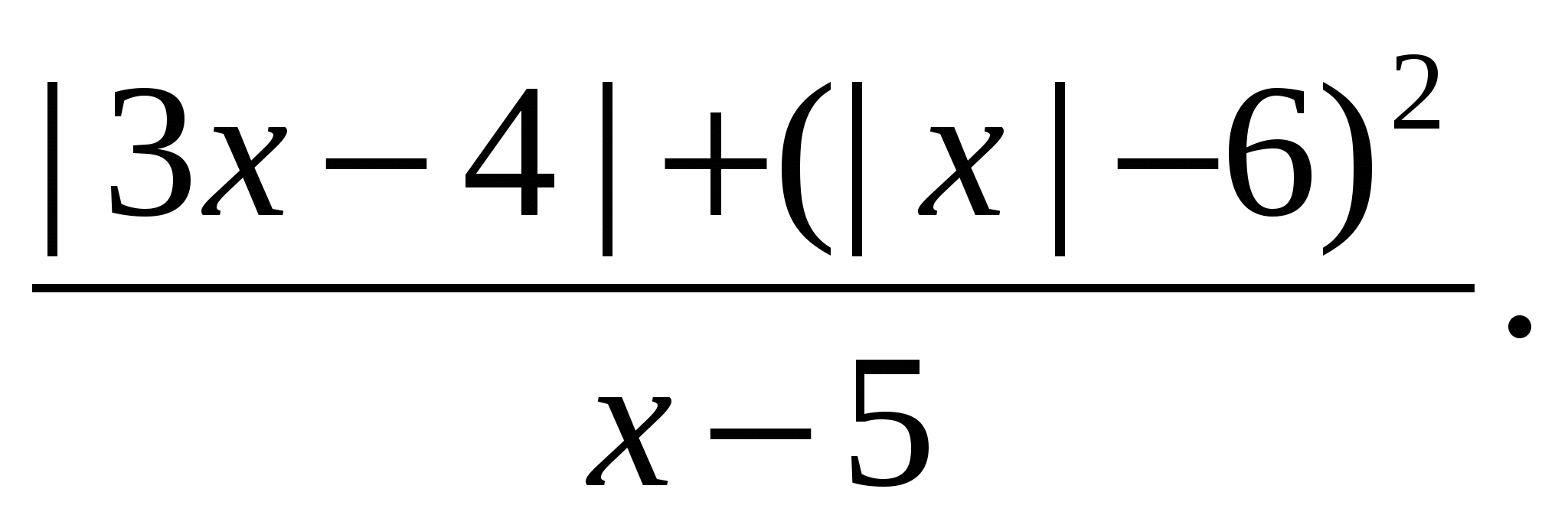

Očigledno je da je brojilac razlomka pozitivan broj za bilo koju vrijednost varijable. To znači da je frakcijski izraz pozitivan ako
(jer
). Dozvolite da transformišemo dobijeni izraz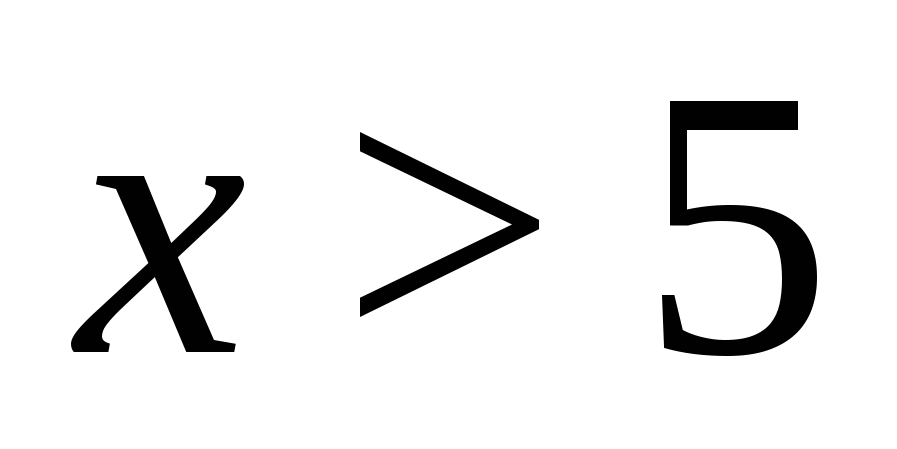
. Dobijamo jednačinu koja je ekvivalentna originalnoj:

Odgovori.
.

Primjer 12 Riješite jednačinu

Rješenje. Budući da je lijeva strana jednadžbe nenegativna, za sve dopuštene vrijednosti varijable, na skupu korijena jednadžbe i njena desna strana mora biti nenegativna, pa stoga uvjet
, na ovom intervalu su imenioci oba razlomka jednaki i ostaje da se reši jednačina
. Rješavanje i uzimanje u obzir ograničenja
, dobijamo

Odgovori.
.

• Rješavanje jednadžbi pomoću geometrijske interpretacije

Geometrijsko značenje izraza
- dužina segmenta koordinatne ose koji povezuje tačke sa apscisama I . Prevođenje algebarskog problema u geometrijski jezik često omogućava izbjegavanje glomaznih proračuna.

Primjer 13 Hajde da riješimo jednačinu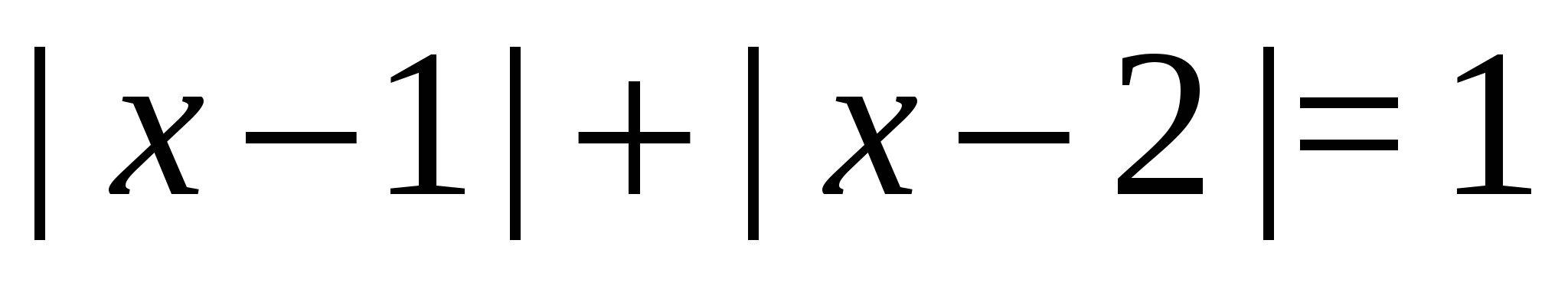
.

Rješenje. Rezonovaćemo na sledeći način: na osnovu geometrijske interpretacije modula, leva strana jednačine je zbir udaljenosti od određene tačke sa apscisom na dvije fiksne tačke sa apscisama 1 i 2. Zatim sve tačke sa apscisama iz segmenta
imaju traženo svojstvo, ali tačke koje se nalaze izvan ovog segmenta nemaju.

Odgovori.
.

Primjer 14 Riješite nejednakost
.

Rješenje. Opišimo tačke na koordinatnoj liniji, zbir udaljenosti od kojih do tačaka
I tačno jednako . Sve su to tačke segmenta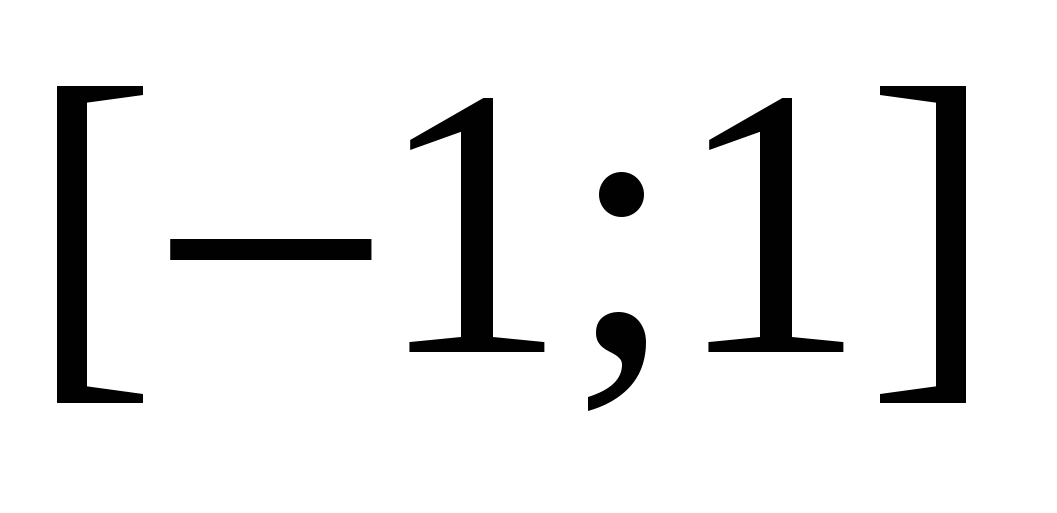
. Za sve vanjske brojeve ovog segmenta zbir udaljenosti će biti veći od dva.

Odgovori.
.

Primjer(C3, Jedinstveni državni ispit - 2010.) 15 Riješite jednačinu

Rješenje. Primjena identiteta dvaput
, dobijamo jednačinu

čije je rješenje interval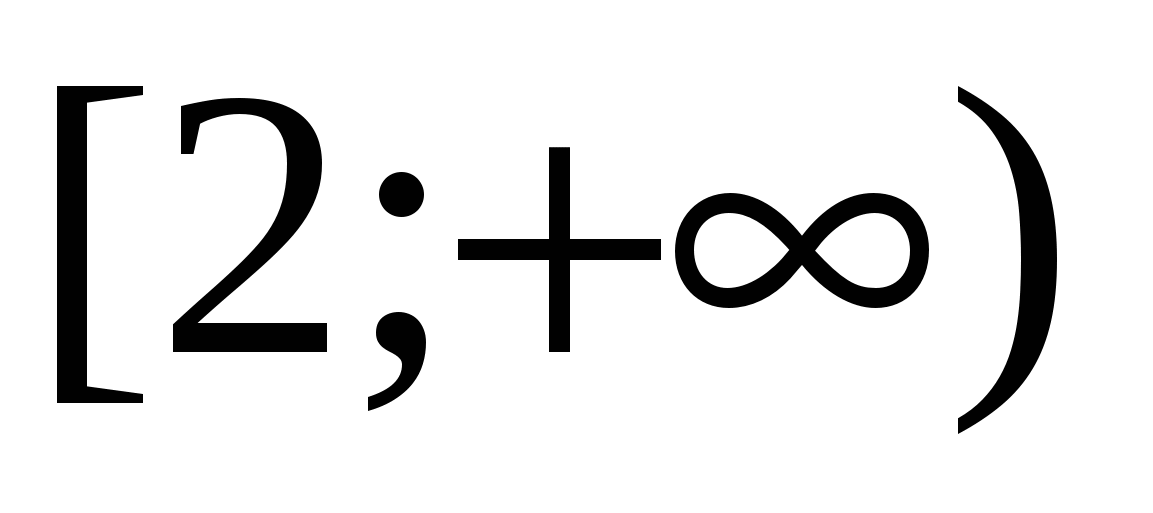
.

Odgovori.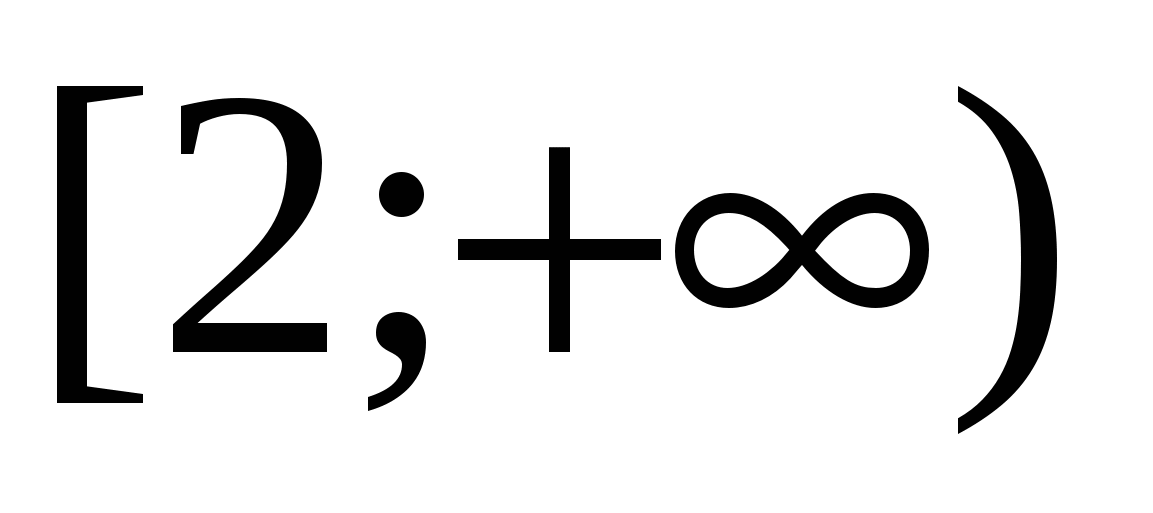
.

Primjer(C3, Jedinstveni državni ispit - 2011.) 16 17 Riješite jednačinu

Rješenje. .

Odgovori.
.

• Primjena teoreme predznaka na rješavanje jednačina

Formulirajmo teoremu pogodnu za rješavanje nejednakosti u pogledu proizvoda ili količnika razlika modula:

Teorema 18 Znak razlike između modula dvaju izraza poklapa se sa predznakom razlike kvadrata ovih izraza. ne nestaje ni za jednu vrijednost varijable. To znači da je u cijelom domenu definicije funkcija konstantnog predznaka. Računajući npr.
, nalazimo da funkcija uzima samo pozitivne vrijednosti.

Odgovori.
.

Metoda intervala omogućava rješavanje složenijih jednadžbi i nejednačina s modulima, ali u ovom slučaju ima nešto drugačiju svrhu. Stvar je u sljedećem. Pronalazimo korijene svih submodularnih izraza i dijelimo numeričku osu na intervale konstantnog predznaka ovih izraza. Ovo vam omogućava da se uzastopnim prolaskom kroz ove intervale istovremeno riješite svih modula i riješite običnu jednadžbu ili nejednačinu (provjeravajući da li je pronađeni odgovor uključen u ovaj interval).

• Rješavanje jednadžbi množenjem pozitivnim faktorom

Zaključak.

Da sumiramo naš rad, možemo reći sljedeće.

Cilj rada je bio proučavanje različitih metoda za rješavanje jednačina i nejednačina sa modulima.

Razmatraju se neke varijante najjednostavnijih jednadžbi i nejednačina sa modulom, rješivih pomoću ekvivalentnih prijelaza, kao i teorema o zbiru modula; grafički način rješavanja jednačina. Mora se reći da u školski kurs matematičari, to su metode rješenja koje se najčešće koriste. Grafička metoda je posebno relevantna pri rješavanju problema C 5 iz kontrole i mjerenja Materijali za Jedinstveni državni ispit.

Zatim smo, na nekoliko primjera, proučavali druge načine rješavanja jednačina i nejednačina sa modulima, i to: metodu otkrivanja modula; rješavanje jednadžbi koje sadrže module nenegativnih izraza; rješavanje jednadžbi pomoću geometrijske interpretacije; koristeći identitet
; primjena teoreme o znaku; rješavanje jednačina odlaskom na posljedice, množenje sa pozitivnim faktorom, kao i rješavanje nejednačina metodom intervala.

Tako smo tokom istraživanja došli do sljedećih zaključaka.

Smatramo da su metoda otkrivanja modula, grafička metoda i intervalna metoda najuniverzalnije i primjenjivo na najveći broj problema. Ovo uvjerenje je nastalo kao rezultat odluke veliki broj zadaci iz provjere i mjerenja materijala Jedinstvenog državnog ispita, predmetnih prvenstava, olimpijada, kao i proučavanje literature o ovoj problematici. Takođe smatramo da su poznavanje i primjena identiteta veoma važni
, budući da se koristi ne samo za rješavanje jednačina i nejednačina, već i za transformaciju mnogih izraza s radikalima. Preostale metode rješenja koje smo razmatrali svakako su od velikog interesa u smislu proširenja matematičkih horizonata i općenito matematički razvoj. Stoga planiramo da ih iskoristimo za pripremu za državnu završnu certifikaciju u Obrazac za jedinstveni državni ispit i priprema za studiranje na visokoškolskoj ustanovi.

Bibliografija.

“Velika matematička enciklopedija” za školarce i studente;

Matematika. Jedinstveni državni ispit - 2011, 2012. Mogućnosti modela ispita. / Uredio A.L. Semenova, I.V. Yashchenko.

M.Ya. Vygodsky. Priručnik za osnovnu matematiku

"Najnoviji školski priručnik";

Enciklopedija „Istražujem svijet. Matematika";

;

Ovaj članak je posvećen tehnikama rješavanja različitih jednadžbi i nejednačina koje sadrže
varijabla pod znakom modula.

Ako na ispitu naiđete na jednadžbu ili nejednačinu s modulom, možete je riješiti na taj način
bez poznavanja bilo kakvih posebnih metoda i korištenja samo definicije modula. Da li je istina,
Ovo može potrajati sat i po dragocjenog vremena ispita.

Zato vam želimo reći o tehnikama koje pojednostavljuju rješavanje takvih problema.

Prije svega, zapamtimo to

Hajde da razmotrimo Razne vrste jednačine sa modulom. (Kasnije ćemo prijeći na nejednakosti.)

Modul lijevo, broj desno

Ovo je najjednostavniji slučaj. Hajde da riješimo jednačinu

Postoje samo dva broja čiji su moduli jednaki četiri. To su 4 i −4. Stoga jednačina
je ekvivalentno kombinaciji dva jednostavna:

Druga jednačina nema rješenja. Rješenja prvog: x = 0 i x = 5.

Odgovor: 0; 5.

Varijabilna i ispod i izvan modula

Ovdje moramo proširiti modul po definiciji. . . ili razmisli!

Jednačina se dijeli na dva slučaja, ovisno o predznaku izraza pod modulom.
Drugim riječima, to je ekvivalentno kombinaciji dva sistema:

Rješenje prvog sistema: . Drugi sistem nema rješenja.
Odgovor: 1.

Prvi slučaj: x ≥ 3. Uklonite modul:

Broj, budući da je negativan, ne zadovoljava uvjet x ≥ 3 i stoga nije korijen originalne jednadžbe.

Hajde da saznamo da li zadovoljava ovo stanje broj . Da bismo to učinili, sastavljamo razliku i određujemo njen znak:

To znači da je veći od tri i stoga je korijen originalne jednadžbe

Drugi slučaj: x< 3. Снимаем модуль:

Broj . veći od , i stoga ne zadovoljava uvjet x< 3. Проверим :

Znači, . je korijen originalne jednadžbe.

Uklanjanje modula po definiciji? Strašno je i pomisliti na to, jer diskriminanta nije savršen kvadrat. Bolje iskoristimo sljedeće razmatranje: jednačina oblika |A| = B je ekvivalentno kombinaciji dva sistema:

Ista stvar, ali malo drugačija:

Drugim riječima, rješavamo dvije jednačine, A = B i A = −B, a zatim biramo korijene koji zadovoljavaju uvjet B ≥ 0.

Hajde da počnemo. Prvo rješavamo prvu jednačinu:

Zatim rješavamo drugu jednačinu:

Sada u svakom slučaju provjeravamo znak desne strane:

Stoga su samo i prikladni.

Kvadratne jednadžbe sa zamjenom |x| = t

Rešimo jednačinu:

Budući da je zgodno napraviti zamjenu |x| = t. Dobijamo:

Odgovor: ±1.

Modul jednak modulu

Govorimo o jednačinama oblika |A| = |B|. Ovo je dar sudbine. Nema otkrivanja modula po definiciji! jednostavno je:

Na primjer, razmotrite jednadžbu: . To je ekvivalentno sljedećem skupu:

Ostaje riješiti svaku od jednadžbi skupa i zapisati odgovor.

Dva ili više modula

Rešimo jednačinu:

Nemojmo se zamarati svakim modulom posebno i otvarati ga po definiciji - bit će previše opcija. Postoji racionalniji način - intervalna metoda.

Izrazi modula nestaju u tačkama x = 1, x = 2 i x = 3. Ove tačke dijele brojevnu pravu na četiri intervala (intervale). Označimo ove tačke na brojevnoj pravoj i stavimo znake za svaki od izraza ispod modula na rezultujućim intervalima. (Red predznaka se poklapa sa redosledom odgovarajućih modula u jednačini.)

Dakle, moramo razmotriti četiri slučaja - kada je x u svakom od intervala.

Slučaj 1: x ≥ 3. Svi moduli se uklanjaju „sa plusom“:

Rezultirajuća vrijednost x = 5 zadovoljava uvjet x ≥ 3 i stoga je korijen originalne jednadžbe.

Slučaj 2: 2 ≤ x ≤ 3. Posljednji modul je sada uklonjen "sa minusom":

Rezultirajuća vrijednost x je također prikladna - pripada intervalu koji se razmatra.

Slučaj 3: 1 ≤ x ≤ 2. Drugi i treći modul se uklanjaju "sa minusom":

Dobili smo tačnu numeričku jednakost za bilo koje x iz intervala koji se razmatra, oni služe kao rješenja ove jednačine.

Slučaj 4: x ≤ 1 ≤ 1. Drugi i treći modul se uklanjaju "sa minusom":

Ništa novo. Već znamo da je x = 1 rješenje.

Odgovor: ∪ (5).

Modul unutar modula

Rešimo jednačinu:

Počinjemo otvaranjem unutrašnjeg modula.

1) x ≤ 3. Dobijamo:

Izraz pod modulom nestaje na . Ova tačka pripada dotičnoj
između. Stoga moramo analizirati dva podslučaja.

1.1) U ovom slučaju dobijamo:

Ova vrijednost x nije prikladna jer ne pripada intervalu koji se razmatra.

1.2) . onda:

Ova vrijednost x također nije dobra.

Dakle, za x ≤ 3 nema rješenja. Pređimo na drugi slučaj.

2) x ≥ 3. Imamo:

Ovdje imamo sreće: izraz x + 2 je pozitivan u intervalu koji se razmatra! Stoga više neće biti podslučaja: modul se uklanja "sa plusom":

Ova vrijednost x je u intervalu koji se razmatra i stoga je korijen originalne jednadžbe.

Ovako se rješavaju svi problemi ovog tipa - otvaramo ugniježđene module jedan po jedan, počevši od internog.