Rješenje se zgodno može podijeliti u dvije točke:

1) Prvo provjeravamo da li postoje vertikalne asimptote. Imenilac ide na nulu u, i odmah je jasno da u ovoj tački funkcija trpi beskonačan diskontinuitet, a prava linija dato jednačinom, je vertikalna asimptota grafa funkcije. Ali, prije nego što se donese takav zaključak, potrebno je pronaći jednostrane granice:

Podsjećam vas na tehniku ​​izračunavanja na koju sam se na sličan način fokusirao u članku Kontinuitet funkcije. Prelomne tačke. Zamjenjujemo “X” u izrazu ispod znaka granice. Nema ništa zanimljivo u brojiocu:

Ali nazivnik rezultira beskonačno malim negativnim brojem:

Ono određuje sudbinu granice.

Lijeva granica je beskonačna i, u principu, već je moguće donijeti presudu o prisutnosti vertikalne asimptote. Ali jednostrane granice nisu potrebne samo za ovo - one POMAŽU DA RAZUMIJETE KAKO se nalazi graf funkcije i da ga ISPRAVNO konstruišete. Stoga moramo izračunati i granicu za desnu ruku:

Zaključak: jednostrane granice su beskonačne, što znači da je prava vertikalna asimptota grafa funkcije at.

Prva granica je konačna, što znači da moramo "nastaviti razgovor" i pronaći drugu granicu:

Druga granica je također konačna.

Dakle, naša asimptota je:

Zaključak: prava linija određena jednadžbom je horizontalna asimptota grafa funkcije at.

Da biste pronašli horizontalnu asimptotu, možete koristiti pojednostavljenu formulu:

Ako postoji konačna granica, tada je prava linija horizontalna asimptota grafa funkcije at.

Lako je uočiti da su brojnik i nazivnik funkcije istog reda rasta, što znači da će tražena granica biti konačna:

Prema uslovu, nema potrebe da se pravi crtež, ali ako smo u jeku istraživanja funkcije, onda odmah napravimo skicu na nacrtu:

Na osnovu tri pronađena ograničenja, pokušajte sami shvatiti kako bi se graf funkcije mogao nalaziti. Da li je to uopšte teško? Pronađite 5-6-7-8 bodova i označite ih na crtežu. Međutim, graf ove funkcije je konstruiran korištenjem transformacija grafa elementarne funkcije, a čitatelji koji su pažljivo ispitali primjer 21 gornjeg članka lako mogu pogoditi o kakvoj je krivulji riječ.

Ovo je primjer za nezavisna odluka. Da vas podsjetim da je proces zgodno podijeljen u dvije točke - vertikalne asimptote i kose asimptote. U rješenju uzorka, horizontalna asimptota se nalazi pomoću pojednostavljene sheme.

U praksi se najčešće susreću frakciono-racionalne funkcije, a nakon treninga na hiperbolama zakomplicirat ćemo zadatak:

Naći asimptote grafa funkcije

Rješenje: Jedan, dva i gotovo:

1) Vertikalne asimptote su u tačkama beskonačnog diskontinuiteta, tako da treba provjeriti da li imenilac ide na nulu. Hajde da odlučimo kvadratna jednačina:

Diskriminant je pozitivan, tako da jednačina ima dva realna korijena, a rad se značajno dodaje

U cilju daljeg pronalaženja jednostranih granica kvadratni trinom Zgodno je rastaviti na faktore:

(za kompaktnu notaciju, "minus" je uključen u prvu zagradu). Da budemo sigurni, provjerimo otvaranjem zagrada mentalno ili na propuhu.

Prepišimo funkciju u formu

Nađimo jednostrane granice u tački:

granica funkcije grafa asimptote

I u tački:

Dakle, prave su vertikalne asimptote grafa dotične funkcije.

2) Ako pogledate funkciju, sasvim je očito da će granica biti konačna i imamo horizontalnu asimptotu. Pokažimo njegovo prisustvo na kratak način:

Dakle, prava linija (os apscisa) je horizontalna asimptota grafa ove funkcije.

Pronađene granice i asimptote pružaju mnogo informacija o grafu funkcije. Pokušajte mentalno zamisliti crtež uzimajući u obzir sljedeće činjenice:

Skicirajte svoju verziju grafikona na nacrtu.

Naravno, pronađene granice ne određuju jasno izgled grafa i možete pogriješiti, ali sama vježba će vam pružiti neprocjenjivu pomoć u toku kompletnog proučavanja funkcije. Tačna slika je na kraju lekcije.

Naći asimptote grafa funkcije

Naći asimptote grafa funkcije

To su zadaci za samostalno rješavanje. Oba grafa opet imaju horizontalne asimptote, koje se odmah otkrivaju sljedećim karakteristikama: u primjeru 4, red rasta nazivnika je veći od reda rasta brojilaca, au primjeru 5 brojnik i imenilac su od isti red rasta. U rješenju uzorka, prva funkcija se ispituje na prisustvo kosih asimptota u potpunosti, a druga - kroz granicu.

Horizontalne asimptote, po mom subjektivnom dojmu, primjetno su češće od onih koje su “istinski nagnute”. Dugo očekivani opći slučaj:

Naći asimptote grafa funkcije

Rješenje: klasik žanra:

• 1) Pošto je nazivnik pozitivan, funkcija je kontinuirana duž cijele brojevne prave i nema vertikalnih asimptota. ...Je li ovo dobro? Nije prava riječ - odlično! Tačka br. 1 je zatvorena.
• 2) Provjerimo prisustvo kosih asimptota:

Druga granica je također konačna, stoga graf dotične funkcije ima kosu asimptotu:

Dakle, kada se graf funkcije približi pravoj liniji beskonačno blizu.

Imajte na umu da on siječe svoju kosu asimptotu u ishodištu, a takve točke presjeka su sasvim prihvatljive - važno je da je "sve normalno" u beskonačnosti (zapravo, ovdje je riječ o asimptotama).

Naći asimptote grafa funkcije

Rješenje: nema se šta posebno komentirati, pa ću nacrtati približan primjer konačnog rješenja:

1) Vertikalne asimptote. Hajde da istražimo poentu.

Prava linija je vertikalna asimptota za graf na.

2) Kose asimptote:

Prava linija je nagnuta asimptota za graf na.

Pronađene jednostrane granice i asimptote nam omogućavaju da sa velikom pouzdanošću predvidimo kako izgleda graf ove funkcije.

Naći asimptote grafa funkcije

Ovo je primjer za neovisno rješenje za praktičnost izračunavanja nekih granica, možete podijeliti brojilac po članu sa nazivnikom. Opet, kada analizirate svoje rezultate, pokušajte nacrtati graf ove funkcije.

Očigledno, vlasnici „stvarnih“ kosih asimptota su grafovi onih razlomaka racionalnih funkcija u kojima je najviši stepen brojila jedan veći od najvišeg stepena nazivnika. Ako je više, više neće postojati kosa asimptota (na primjer).

Ali druga čuda se dešavaju u životu.

Asimptote grafa funkcije

Duh asimptote dugo je lutao sajtom da bi se konačno materijalizovao u posebnom članku i doneo posebno oduševljenje zbunjenim čitaocima potpuno proučavanje funkcije. Pronalaženje asimptota grafa jedan je od rijetkih dijelova ovog zadatka koji je obuhvaćen školski kurs samo u pregledu, pošto se događaji vrte oko izračunavanja ograničenja funkcije, ali se i dalje odnose na višu matematiku. Za posetioce koji slabo razumeju matematičku analizu, mislim da je nagoveštaj jasan ;-) ...stani, stani, gde ćeš? Ograničenja- Lako je!

Primjeri asimptota susreli smo se odmah u prvoj lekciji o grafovi elementarnih funkcija, a tema se sada detaljno razmatra.

Dakle, šta je asimptota?

Zamislite varijabilna tačka, koji "putuje" duž grafa funkcije. Asimptota je ravno, na koji neograničeno blizu graf funkcije se približava dok se njena promenljiva tačka pomera ka beskonačnosti.

Napomena : definicija je smislena ako vam je potrebna formulacija u notaciji matematička analiza, pogledajte tutorijal.

Na ravni, asimptote su klasificirane prema njihovoj prirodnoj lokaciji:

1) Vertikalne asimptote, koje su date jednadžbom oblika , gdje je “alfa”. pravi broj. Popularni predstavnik definira samu ordinatnu osu,
uz blagi osjećaj mučnine prisjećamo se hiperbole.

2) Kose asimptote tradicionalno napisano jednačina prave linije sa ugaonim koeficijentom. Ponekad se identifikuje posebna grupa poseban slučaj – horizontalne asimptote. Na primjer, ista hiperbola sa asimptotom.

Idemo brzo, da pogodimo temu kratkim rafalom iz mitraljeza:

Koliko asimptota može imati graf funkcije?

Ne jedan, jedan, dva, tri,... ili beskonačno mnogo. Nećemo ići daleko za primjerima, prisjetimo se elementarne funkcije. Parabola, kubična parabola i sinusni val uopće nemaju asimptote. eksponencijalni graf, logaritamska funkcija ima jedinstvenu asimptotu. Arktangens i arkotangens imaju dva od njih, a tangenta i kotangens imaju beskonačno mnogo. Nije neuobičajeno da graf ima i horizontalne i vertikalne asimptote. Hiperbola, uvek će te voleti.

šta to znači?

Vertikalne asimptote grafa funkcije

Obično se nalazi vertikalna asimptota grafa na tački beskonačnog diskontinuiteta funkcije. Jednostavno je: ako u nekoj tački funkcija pretrpi beskonačan diskontinuitet, tada je prava linija određena jednadžbom vertikalna asimptota grafa.

Napomena : Imajte na umu da se unos koristi za upućivanje na dva potpuno različita koncepta. Da li se podrazumijeva tačka ili jednačina prave zavisi od konteksta.

Dakle, da bi se utvrdilo prisustvo vertikalne asimptote u tački, dovoljno je to pokazati barem jedan od jednostranih granica beskonačan. Najčešće je to tačka u kojoj je nazivnik funkcije jednaka nuli. U suštini, već smo pronašli vertikalne asimptote u posljednjim primjerima lekcije na kontinuitetu funkcije. Ali u nekim slučajevima postoji samo jedna jednostrana granica, a ako je beskonačna, onda opet - volite i favorizirajte vertikalnu asimptotu. Najjednostavnija ilustracija: i osa ordinate (vidi. Grafovi i svojstva elementarnih funkcija).

Iz navedenog proizilazi i očigledna činjenica: ako je funkcija kontinuirano uključena, tada nema vertikalnih asimptota. Iz nekog razloga mi je pala na pamet parabola. Zaista, gdje se ovdje može "zalijepiti" prava linija? ...da... razumijem... sljedbenici ujka Frojda su postali histerični =)

Obrnuti iskaz je općenito netačan: na primjer, funkcija nije definirana na cijeloj brojevnoj pravoj, ali je potpuno lišena asimptota.

Kose asimptote grafa funkcije

Kose (kao poseban slučaj - horizontalne) asimptote se mogu nacrtati ako argument funkcije teži ka “plus beskonačnost” ili “minus beskonačnost”. Zato graf funkcije ne može imati više od dvije kose asimptote. Na primjer, graf eksponencijalne funkcije ima jednu horizontalnu asimptotu na , a graf arktangensa na ima dvije takve asimptote, i to različite.

Kada se graf na oba mjesta približi jednoj kosoj asimptoti, tada se „beskonačnosti“ obično kombinuju pod jednim unosom. Na primjer, ... dobro ste pogodili: .

Opšte pravilo:

Ako postoje dva final limit , tada je prava linija kosa asimptota grafa funkcije na . Ako barem jedan od navedenih granica je beskonačan, onda ne postoji kosa asimptota.

Napomena : formule ostaju važeće ako “x” teži samo “plus beskonačnosti” ili samo “minus beskonačnosti”.

Pokažimo da parabola nema kosih asimptota:

Granica je beskonačna, što znači da ne postoji kosa asimptota. Imajte na umu da u pronalaženju granice potreba je nestala pošto je odgovor već primljen.

Napomena : Ako imate (ili ćete imati) poteškoća s razumijevanjem znakova plus-minus, minus-plus, pogledajte pomoć na početku lekcije
na infinitezimalnim funkcijama, gdje sam vam rekao kako pravilno protumačiti ove znakove.

Očigledno je da za bilo koju kvadratnu, kubičnu funkciju, polinom 4. i višim stepenima takođe nema kosih asimptota.

Sada se uvjerimo da graf također nema kosu asimptotu. Za otkrivanje neizvjesnosti koristimo se L'Hopitalovo pravilo:
, što je trebalo provjeriti.

Kada funkcija raste beskonačno, ali ne postoji prava linija kojoj bi se njen graf približio beskonačno blizu.

Pređimo na praktični dio lekcije:

Kako pronaći asimptote grafa funkcije?

Upravo je ovako formulisana tipičan zadatak, a uključuje pronalaženje SVIH asimptota grafa (vertikalne, nagnute/horizontalne). Mada, da budemo precizniji u postavljanju pitanja, govorimo o istraživanju prisutnosti asimptota (uostalom, možda ih uopće nema). Počnimo s nečim jednostavnim:

Primjer 1

Naći asimptote grafa funkcije

Rješenje Zgodno je to podijeliti na dvije tačke:

1) Prvo provjeravamo da li postoje vertikalne asimptote. Imenilac ide na nulu na , i odmah je jasno da u ovom trenutku funkcija pati beskrajni jaz, a ravna linija data jednadžbom je vertikalna asimptota grafa funkcije. Ali, prije nego što se donese takav zaključak, potrebno je pronaći jednostrane granice:

Podsjećam vas na tehniku ​​proračuna na koju sam se na sličan način fokusirao u članku Kontinuitet funkcije. Prelomne tačke. U izrazu pod graničnim znakom zamjenjujemo . Nema ništa zanimljivo u brojiocu:
.

Ali u nazivniku ispada beskonačno mali negativan broj:
, određuje sudbinu granice.

Lijeva granica je beskonačna i, u principu, već je moguće donijeti presudu o prisutnosti vertikalne asimptote. Ali jednostrana ograničenja nisu potrebna samo za ovo - ona POMAŽU DA SE RAZUMIJE KAKO locirati graf funkcije i izgraditi ga ISPRAVNO. Stoga moramo izračunati i granicu za desnu ruku:

Zaključak: jednostrane granice su beskonačne, što znači da je prava linija vertikalna asimptota grafa funkcije na .

Prva granica konačan, što znači da je potrebno "nastaviti razgovor" i pronaći drugu granicu:

Druga granica takođe konačan.

Dakle, naša asimptota je:

Zaključak: ravna linija data jednadžbom je horizontalna asimptota grafa funkcije na .

Da pronađemo horizontalnu asimptotu
možete koristiti pojednostavljenu formulu:

Ako postoji konačan granica, tada je prava linija horizontalna asimptota grafa funkcije na .

Lako je vidjeti da su brojnik i nazivnik funkcije isti red rasta, što znači da će tražena granica biti konačna:

Odgovori:

Prema uslovu, ne morate završiti crtež, ali ako je u punom jeku studija funkcije, onda na nacrtu odmah pravimo skicu:

Na osnovu tri pronađena ograničenja, pokušajte sami shvatiti kako bi se graf funkcije mogao nalaziti. Da li je to uopšte teško? Pronađite 5-6-7-8 bodova i označite ih na crtežu. Međutim, graf ove funkcije se konstruira pomoću transformacije grafa elementarne funkcije, a čitatelji koji su pažljivo ispitali primjer 21 gornjeg članka lako mogu pogoditi o kakvoj je krivulji riječ.

Primjer 2

Naći asimptote grafa funkcije

Ovo je primjer koji možete sami riješiti. Da vas podsjetim da je zgodno podijeliti proces na dvije tačke – vertikalne asimptote i kose asimptote. U rješenju uzorka, horizontalna asimptota se nalazi pomoću pojednostavljene sheme.

U praksi se najčešće susreću frakciono-racionalne funkcije, a nakon treninga na hiperbolama zakomplicirat ćemo zadatak:

Primjer 3

Naći asimptote grafa funkcije

Rješenje: Jedan, dva i gotovo:

1) Locirane su vertikalne asimptote u tačkama beskonačnog diskontinuiteta, pa morate provjeriti ide li imenilac na nulu. Hajde da odlučimo kvadratna jednačina:

Diskriminanta je pozitivna, tako da jednačina ima dva realna korijena, a rad je značajno povećan =)

Da bismo dalje pronašli jednostrane granice, zgodno je razložiti kvadratni trinom na faktore:
(za kompaktnu notaciju, "minus" je uključen u prvu zagradu). Da budemo sigurni, provjerimo otvaranjem zagrada mentalno ili na promaji.

Prepišimo funkciju u formu

Nađimo jednostrane granice u tački:

I u tački:

Dakle, prave su vertikalne asimptote grafa dotične funkcije.

2) Ako pogledate funkciju , onda je sasvim očito da će granica biti konačna i imamo horizontalnu asimptotu. Pokažimo njegovo prisustvo na kratak način:

Dakle, prava linija (os apscisa) je horizontalna asimptota grafa ove funkcije.

Odgovori:

Pronađene granice i asimptote pružaju mnogo informacija o grafu funkcije. Pokušajte mentalno zamisliti crtež uzimajući u obzir sljedeće činjenice:

Skicirajte svoju verziju grafikona na nacrtu.

Naravno, pronađene granice ne određuju jasno izgled grafikona i možete pogriješiti, ali sama vježba će vam pružiti neprocjenjivu pomoć tokom studija pune funkcije. Tačna slika je na kraju lekcije.

Primjer 4

Naći asimptote grafa funkcije

Primjer 5

Naći asimptote grafa funkcije

To su zadaci za samostalno rješavanje. Oba grafa ponovo imaju horizontalne asimptote, koje se odmah detektuju sledećim karakteristikama: u Primeru 4 redosled rasta imenilac više, nego redom rasta brojioca, a u primjeru 5 brojnik i imenilac isti red rasta. U rješenju uzorka, prva funkcija se ispituje na prisustvo kosih asimptota u potpunosti, a druga – kroz granicu.

Horizontalne asimptote, po mom subjektivnom dojmu, primjetno su češće od onih koje su “istinski nagnute”. Dugo očekivani opći slučaj:

Primjer 6

Naći asimptote grafa funkcije

Rješenje: klasik žanra:

1) Pošto je nazivnik pozitivan, onda je funkcija kontinuirano duž cijele brojevne prave i nema vertikalnih asimptota. ...Je li ovo dobro? To nije ta riječ - odlično! Tačka br. 1 je zatvorena.

2) Provjerimo prisustvo kosih asimptota:

Prva granica konačan, pa idemo dalje. Prilikom izračunavanja druge granice eliminisati neizvjesnost "beskonačnost minus beskonačnost" Dovodimo izraz do zajedničkog nazivnika: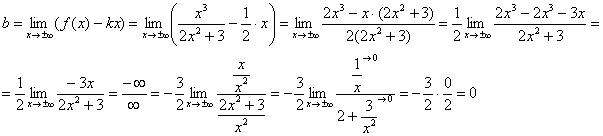

Druga granica takođe konačan Dakle, graf dotične funkcije ima kosu asimptotu:

Zaključak:

Dakle, kada je graf funkcije beskonačno blizu približava se pravoj liniji:

Imajte na umu da on siječe svoju kosu asimptotu u ishodištu, a takve točke presjeka su sasvim prihvatljive - važno je da je "sve normalno" u beskonačnosti (zapravo, ovdje je riječ o asimptotama).

Primjer 7

Naći asimptote grafa funkcije

Rješenje: Nemam šta posebno komentirati, pa ću nacrtati približan primjer čistog rješenja:

1) Vertikalne asimptote. Hajde da istražimo poentu.

Prava linija je vertikalna asimptota za graf na .

2) Kose asimptote:

Prava linija je nagnuta asimptota za graf na .

Odgovori:

Pronađene jednostrane granice i asimptote nam omogućavaju da sa velikom pouzdanošću predvidimo kako izgleda graf ove funkcije. Ispravno crtanje na kraju lekcije.

Primjer 8

Naći asimptote grafa funkcije

Ovo je primjer za neovisno rješenje za praktičnost izračunavanja nekih granica, možete podijeliti brojilac po članu sa nazivnikom. Opet, kada analizirate svoje rezultate, pokušajte nacrtati graf ove funkcije.

Očigledno, vlasnici “stvarnih” kosih asimptota su grafovi onih razlomaka racionalnih funkcija čiji je najviši stepen brojioca još jedan najviši stepen imenioca. Ako je više, neće biti kose asimptote (na primjer, ).

Ali druga čuda se dešavaju u životu:

Primjer 9

Primjer 11

Ispitajte graf funkcije za prisustvo asimptota

Rješenje: očigledno je da , stoga razmatramo samo desnu poluravninu, gdje postoji graf funkcije.

Dakle, prava linija (os ordinate) je vertikalna asimptota za graf funkcije na .

2) Studija o kosoj asimptoti može se provesti prema punoj shemi, ali u članku L'Hopitalova pravila saznali smo to linearna funkcija viši red rasta od logaritamskog, dakle: (Vidi primjer 1 iste lekcije).

Zaključak: x-osa je horizontalna asimptota grafa funkcije na .

Odgovori:
, Ako ;
, Ako .

Crtež radi jasnoće:

Zanimljivo je da naizgled slična funkcija uopće nema asimptote (ko žele, to mogu provjeriti).

Dva poslednja primera za samostalno učenje:

Primjer 12

Ispitajte graf funkcije za prisustvo asimptota

Postojaće i problemi koje ćete sami riješiti, na koje možete vidjeti odgovore.

Koncept asimptote

Ako prvo konstruirate asimptote krivulje, tada u mnogim slučajevima konstrukcija grafa funkcije postaje lakša.

Sudbina asimptote puna je tragedije. Zamislite kako je to provesti cijeli život krećući se u pravoj liniji cijenjeni cilj, približite mu se što je više moguće, ali ga nikada ne dođite. Na primjer, pokušajte povezati svoje životni put sa putanjom željene osobe, u nekom trenutku mu se približiti skoro izbliza, ali ga ni ne dodirnuti. Ili se trudite da zaradite milijardu, ali prije nego što postignete ovaj cilj i uđete u Ginisovu knjigu rekorda za vaš slučaj, nedostaju stoti dio centa. I slično. Tako je i sa asimptotom: stalno teži da dostigne krivulju grafa funkcije, približava joj se na najmanju moguću udaljenost, ali je nikada ne dodiruje.

Definicija 1. Asimptote su one prave linije kojima se graf funkcije približava koliko god se želi kada varijabla teži plus beskonačnosti ili minus beskonačnost.

Definicija 2. Prava linija se naziva asimptotom grafa funkcije ako je udaljenost od promjenljive tačke M grafik funkcije do ove linije teži nuli kako se tačka udaljava na neodređeno vrijeme M od početka duž bilo koje grane grafa funkcija.

Postoje tri vrste asimptota: vertikalne, horizontalne i kose.

Vertikalne asimptote

Prva stvar koju trebate znati o vertikalnim asimptotama je da su paralelne s osi Oy .

Definicija. Pravo x = a je vertikalna asimptota grafa funkcije , ako tačka x = a je tačka diskontinuiteta druge vrste za ovu funkciju.

Iz definicije proizilazi da je prava linija x = a je vertikalna asimptota grafa funkcije f(x) ako je ispunjen barem jedan od uslova:

U ovom slučaju, funkcija f(x) se uopšte ne može definisati, odnosno kada x ≥ a I x ≤ a .

komentar:

Primjer 1. Grafikon funkcije y=ln x ima vertikalnu asimptotu x= 0 (tj. poklapa se sa osom Oy) na granici domene definicije, budući da je granica funkcije kako x teži nuli s desne strane jednaka minus beskonačnost:

(slika iznad).

sami i onda vidite rješenja

Primjer 2. Pronađite asimptote grafa funkcije.

Primjer 3. Naći asimptote grafa funkcije

Horizontalne asimptote

Prva stvar koju trebate znati o horizontalnim asimptotama je da su paralelne s osi Ox .

If (granica funkcije kao argument teži plus ili minus beskonačnosti je jednaka određenoj vrijednosti b), To y = b – horizontalna asimptota krivo y = f(x ) (desno kada X teži plus beskonačnosti, lijevo kada X teži minus beskonačnosti i dvostrano ako su granice kako X teži plus ili minus beskonačnosti jednake).

Primjer 5. Grafikon funkcije

at a> 1 ima lijevu horizontalnu asimptotu y= 0 (tj. poklapa se sa osom Ox), budući da je granica funkcije kao “x” teži minus beskonačnosti nula:

Kriva nema desnu horizontalnu asimptotu, budući da je granica funkcije kako “x” teži plus beskonačnosti jednaka beskonačnosti:

Kose asimptote

Vertikalne i horizontalne asimptote koje smo prethodno ispitali su paralelne sa koordinatnim osa, pa nam je za njihovu konstruisanje bio potreban samo određeni broj - tačka na apscisi ili ordinatnoj osi kroz koju asimptota prolazi. Za kosu asimptotu potreban je veći nagib k, koji pokazuje ugao nagiba linije, i slobodni termin b, koji pokazuje koliko je linija iznad ili ispod ishodišta. Oni koji nisu zaboravili analitičku geometriju, a iz nje i jednačine prave, primijetit će da za kosu asimptotu nalaze jednadžba prave sa nagibom. Postojanje kose asimptote određeno je sljedećom teoremom na osnovu koje se nalaze upravo navedeni koeficijenti.

Teorema. Da napravimo krivu y = f(x) imala asimptotu y = kx + b , potrebno je i dovoljno da postoje konačne granice k I b funkcije koja se razmatra kako varijabla teži x na plus beskonačnost i minus beskonačnost:

(1)

(2)

Brojevi pronađeni na ovaj način k I b i koeficijenti kosih asimptota.

U prvom slučaju (kako x teži plus beskonačnosti) dobije se desna nagnuta asimptota, u drugom (kako x teži minus beskonačnosti) dobije se lijeva kosa asimptota. Desna kosa asimptota prikazana je na Sl. ispod.

Prilikom pronalaženja jednačine za kosu asimptotu potrebno je uzeti u obzir tendenciju X i plus beskonačnosti i minus beskonačnosti. Za neke funkcije, na primjer, razlomljene racionalne, ove granice se poklapaju, ali za mnoge funkcije su te granice različite i samo jedna od njih može postojati.

Ako se granice poklapaju i x teži plus beskonačnosti i minus beskonačnosti, prava linija y = kx + b je dvostrana asimptota krive.

Ako je barem jedna od granica koja definira asimptotu y = kx + b , ne postoji, onda graf funkcije nema kosu asimptotu (ali može imati vertikalnu).

Lako je vidjeti da je horizontalna asimptota y = b je poseban slučaj kosog y = kx + b at k = 0 .

Stoga, ako u bilo kojem smjeru kriva ima horizontalnu asimptotu, tada u ovom smjeru nema nagnute, i obrnuto.

Primjer 6. Naći asimptote grafa funkcije

Rješenje. Funkcija je definirana na cijeloj brojevnoj liniji osim x= 0, tj.

Dakle, na prelomnoj tački x= 0 kriva može imati vertikalnu asimptotu. Zaista, granica funkcije kako x teži nuli slijeva jednaka je plus beskonačno:

dakle, x= 0 – vertikalna asimptota grafa ove funkcije.

Graf ove funkcije nema horizontalnu asimptotu, jer je granica funkcije kako x teži plus beskonačnosti jednaka plus beskonačnosti:

Otkrijmo prisustvo kose asimptote:

Imamo konačne granice k= 2 i b= 0 . Pravo y = 2x je dvosmjerna nagnuta asimptota grafa ove funkcije (slika unutar primjera).

Primjer 7. Naći asimptote grafa funkcije

Rješenje. Funkcija ima jednu tačku prekida x= −1 . Izračunajmo jednostrane granice i odredimo vrstu diskontinuiteta:

zaključak: x= −1 je tačka diskontinuiteta druge vrste, dakle prava linija x= −1 je vertikalna asimptota grafa ove funkcije.

Tražimo kose asimptote. Pošto je ova funkcija razlomačno-racionalna, granice at i at će se poklapati. Tako nalazimo koeficijente za zamjenu ravne - kose asimptote u jednačinu:

Zamjenom pronađenih koeficijenata u jednadžbu prave linije sa koeficijentom nagiba, dobijamo jednačinu kose asimptote:

y = −3x + 5 .

Na slici je graf funkcije označen bordo, a asimptote crnom bojom.

Primjer 8. Naći asimptote grafa funkcije

Rješenje. Pošto je ova funkcija kontinuirana, njen graf nema vertikalne asimptote. Tražimo kose asimptote:

.

Dakle, graf ove funkcije ima asimptotu y= 0 at i nema asiptotu na .

Primjer 9. Naći asimptote grafa funkcije

Rješenje. Prvo tražimo vertikalne asimptote. Da bismo to učinili, nalazimo domenu definicije funkcije. Funkcija je definirana kada je nejednakost i . Znak varijable x odgovara znaku. Stoga, razmotrite ekvivalentnu nejednakost. Iz ovoga dobijamo domen definicije funkcije: . Vertikalna asimptota može biti samo na granici domene definicije funkcije. Ali x= 0 ne može biti vertikalna asimptota, jer je funkcija definirana na x = 0 .

Uzmite u obzir desnu granicu na (ne postoji granica na lijevoj strani):

.

Dot x= 2 je tačka diskontinuiteta druge vrste, dakle prava linija x= 2 - vertikalna asimptota grafa ove funkcije.

Tražimo kose asimptote:

dakle, y = x+ 1 - kosa asimptota grafa ove funkcije na . Mi tražimo kosu asimptotu na:

dakle, y = −x − 1 - kosa asimptota na .

Primjer 10. Naći asimptote grafa funkcije

Rješenje. Funkcija ima domenu definicije . Budući da vertikalna asimptota grafa ove funkcije može biti samo na granici domene definicije, nalazimo jednostrane granice funkcije na .

Koliko asimptota može imati graf funkcije?

Ne jedan, jedan, dva, tri,... ili beskonačno mnogo. Nećemo ići daleko za primjerima, prisjetimo se elementarne funkcije. Parabola, kubična parabola i sinusni val uopće nemaju asimptote. Graf eksponencijalne, logaritamske funkcije ima jednu asimptotu. Arktangens i arkotangens imaju dva od njih, a tangenta i kotangens imaju beskonačno mnogo. Nije neuobičajeno da graf ima i horizontalne i vertikalne asimptote. Hiperbola, uvek će te voleti.

Šta znači pronaći asimptote grafa funkcije?

To znači odgonetati njihove jednačine i crtati prave linije ako to problem zahtijeva. Proces uključuje pronalaženje granica funkcije.

Vertikalne asimptote grafa funkcije

Vertikalna asimptota grafa se po pravilu nalazi u tački beskonačnog diskontinuiteta funkcije. Jednostavno je: ako u nekoj tački funkcija pretrpi beskonačan diskontinuitet, tada je prava linija određena jednadžbom vertikalna asimptota grafa.

Napomena: Imajte na umu da se unos koristi za upućivanje na dva potpuno različita koncepta. Da li se podrazumijeva tačka ili jednačina prave zavisi od konteksta.

Dakle, da bi se utvrdilo prisustvo vertikalne asimptote u tački, dovoljno je pokazati da je barem jedna od jednostranih granica beskonačna. Najčešće je to tačka u kojoj je nazivnik funkcije nula. U suštini, vertikalne asimptote smo već pronašli u posljednjim primjerima lekcije o kontinuitetu funkcije. Ali u nekim slučajevima postoji samo jedna jednostrana granica, a ako je beskonačna, onda opet - volite i favorizirajte vertikalnu asimptotu. Najjednostavnija ilustracija: i ordinatna os.

Iz navedenog također slijedi očigledna činjenica: ako je funkcija kontinuirana, onda nema vertikalnih asimptota. Iz nekog razloga mi je pala na pamet parabola. Zaista, gdje se ovdje može "zalijepiti" prava linija? ...da... razumijem... sljedbenici ujka Frojda su postali histerični =)

Obrnuti iskaz je općenito netačan: na primjer, funkcija nije definirana na cijeloj brojevnoj pravoj, ali je potpuno lišena asimptota.

Kose asimptote grafa funkcije

Kose (kao poseban slučaj - horizontalne) asimptote se mogu nacrtati ako argument funkcije teži ka “plus beskonačnost” ili “minus beskonačnost”. Dakle, graf funkcije ne može imati više od 2 nagnute asimptote. Na primjer, graf eksponencijalne funkcije ima jednu horizontalnu asimptotu at, a graf arktangensa at ima dvije takve asimptote, i to različite.

Kada se graf na oba mjesta približi jednoj kosoj asimptoti, uobičajeno je kombinirati "beskonačnosti" pod jednim unosom. Na primjer, ... dobro ste pogodili: .

- (od grčkog negativan dio, i symptotos koji se poklapaju zajedno). Prava linija koja se stalno približava krivulji i sreće je samo u beskonačnosti. Rječnik strane reči, uključen u ruski jezik. Čudinov A.N., 1910. ASIMPTOTA iz ... ... Rečnik stranih reči ruskog jezika

ASIMPTOTA- (od grčkog asymptotos nepodudaranje), prava linija kojoj se beskonačna grana krive približava bez ograničenja, na primjer asimptota hiperbole ... Moderna enciklopedija

ASIMPTOTA- (od grčkog asymptotos koji se ne podudara) kriva s beskonačnom granom, ravna linija kojoj se ova grana približava bez ograničenja, na primjer, asimptota hiperbole ... Veliki enciklopedijski rječnik

asimptota- Prava linija sa krivinom koja joj se postepeno približava. asimptota Prava linija prema kojoj kriva neke funkcije, koja ima beskonačnu granu, teži (a da je nikada ne dosegne) kada se njen argument neograničeno povećava ili...

Vodič za tehnički prevodilac Asimptota - (od grčkog asymptotos nepodudaranje), prava linija kojoj se neograničeno približava beskonačna grana krive, na primjer asimptota hiperbole. ...

ASIMPTOTA Ilustrovani enciklopedijski rječnik - žensko, geom. prava linija, koja se uvijek približava krivulji (hiperbola), ali nikada ne konvergira s njom. Primjer koji objašnjava ovo: ako se bilo koji broj podijeli na pola, onda će se smanjiti do beskonačnosti, ali nikada neće postati nula...... Rječnik

asimptota Dahl - imenica, broj sinonima: 1 red (182) ASIS rječnik sinonima. V.N. Trishin. 2013…

Vodič za tehnički prevodilac- (od grčkih riječi: a, sunce, piptw) neusklađeno. Pod simptomom se podrazumijeva linija koja se, budući da je neograničeno produžena, približava datoj krivoj liniji ili nekom njenom dijelu tako da udaljenost između zajedničke linije manje urađeno...

Vodič za tehnički prevodilac- površina je prava linija koja siječe površinu u najmanje dvije tačke u beskonačnosti... Enciklopedija Brockhausa i Efrona

ASIMPTOTA- (asimptota) Vrijednost kojoj ova funkcija teži kada mijenja argument (argument), ali je ne postiže ni za jednu konačnu vrijednost argumenta. Na primjer, ako je ukupni trošak proizvodnje x dan funkcijom TC=a+bx, gdje su a i b konstante... Ekonomski rječnik

Vodič za tehnički prevodilac- prava linija kojoj teži kriva neke funkcije (a da je nikada ne dostigne), koja ima beskonačnu granu, kada se njen argument neograničeno povećava ili smanjuje. Na primjer, u funkciji: y = c + 1/x vrijednost y se približava sa ... ... Ekonomsko-matematički rječnik