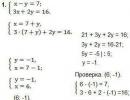Široko se koristi u e-trgovini. Algoritam se također koristi u rješavanju linearnih Diofantovih jednadžbi, u konstruiranju kontinuiranih razlomaka i u Sturmovoj metodi. Euklidov algoritam je glavni alat za dokazivanje teorema u modernoj teoriji brojeva, kao što je Lagrangeova teorema o zbiru četiri kvadrata i fundamentalna teorema aritmetike.

Enciklopedijski YouTube

1 / 5

✪ Matematika. Prirodni brojevi: Euklidov algoritam. Foxford Online Learning Center

✪Euklidski algoritam

✪ Euklidski algoritam, brz način nađi gcd

✪ Matematika 71. Najbolji zajednički djelitelj. Euklidov algoritam - Akademija zabavnih nauka

✪ 20 while petlja Python Euklidski algoritam

Titlovi

Priča

Drevni grčki matematičari nazvali su ovaj algoritam ἀνθυφαίρεσις ili ἀνταναίρεσις - “međusobno oduzimanje”. Ovaj algoritam nije otkrio Euklid, jer je već spomenut u Topeka Aristotel. U Euklidovim Elementima opisano je dva puta - u Knjizi VII za pronalaženje najvećeg zajedničkog djelitelja dva prirodni brojevi i u X knjizi za pronalaženje najveće zajedničke mjere za dvije homogene veličine. U oba slučaja dat je geometrijski opis algoritma za pronalaženje “zajedničke mjere” dva segmenta.

Opis

Euklidov algoritam za cijele brojeve

Neka a (\displaystyle a) I b (\displaystyle b)- cijeli brojevi koji u isto vrijeme nisu jednaki nuli i niz brojeva

a > b > r 1 > r 2 > r 3 > r 4 > … > r n (\displaystyle a>b>r_(1)>r_(2)>r_(3)>r_(4)>\ \dots \ >r_(n))

određeno činjenicom da svaki r k (\displaystyle r_(k))- ovo je ostatak od dijeljenja prethodnog broja sa prethodnim, a pretposljednji se dijeli s posljednjim u potpunosti, odnosno:

a = b q 0 + r 1 , (\displaystyle a=bq_(0)+r_(1),) b = r 1 q 1 + r 2 , (\displaystyle b=r_(1)q_(1)+r_(2),) r 1 = r 2 q 2 + r 3 , (\displaystyle r_(1)=r_(2)q_(2)+r_(3),) ⋯ (\displaystyle \cdots) r k − 2 = r k − 1 q k − 1 + r k , (\displaystyle r_(k-2)=r_(k-1)q_(k-1)+r_(k),) ⋯ (\displaystyle \cdots) r n − 2 = r n − 1 q n − 1 + r n , (\displaystyle r_(n-2)=r_(n-1)q_(n-1)+r_(n),) r n − 1 = r n q n . (\displaystyle r_(n-1)=r_(n)q_(n).)

Zatim GCD( a, b), najveći zajednički djelitelj a I b, je jednako r n, posljednji nenulti član ovog niza.

Postojanje takav r 1 , r 2 , ..., r n, odnosno mogućnost dijeljenja s ostatkom m on n za bilo koji cijeli broj m i cjelina n≠ 0, može se dokazati indukcijom na m.

Ispravnost Ovaj algoritam slijedi iz sljedeće dvije izjave:

• Neka a = b⋅q + r, tada je gcd (a, b) = gcd (b, r).

Dokaz

• GCD( r, 0) = r za bilo koji različit od nule r(pošto je 0 djeljiv s bilo kojim cijelim brojem osim nule).

Geometrijski euklidski algoritam

Neka su data dva segmenta dužine a I b. Oduzmite manji segment od većeg segmenta i zamenite veći segment rezultujućom razlikom. Ponavljamo ovu operaciju dok se segmenti ne izjednače. Ako se to dogodi, tada su originalni segmenti uporedivi, a posljednji rezultujući segment je njihova najveća zajednička mjera. Ako nema opće mjere, onda je proces beskonačan. U ovom obliku, algoritam je opisao Euklid i implementiran je pomoću šestara i ravnala.

Primjer

Za ilustraciju, Euklidski algoritam će se koristiti za pronalaženje gcd a= 1071 i b= 462. Prvo oduzmite višekratnik 462 od 1071 dok ne dobijemo razliku manju od 462. Moramo oduzeti 462 dvaput, ( q 0 = 2), ostavljajući ostatak od 147:

1071 = 2 × 462 + 147.

Zatim oduzimajte višekratnike 147 od 462 dok ne dobijemo razliku manju od 147. Moramo oduzeti 147 tri puta ( q 1 = 3), ostavljajući ostatak od 21:

462 = 3 × 147 + 21.

Zatim oduzimajte višekratnike 21 od 147 dok razlika ne bude manja od 21. Moramo oduzeti 21 sedam puta ( q 2 = 7), ne ostavljajući ostatak:

147 = 7 × 21 + 0.

Dakle, niz a > b > r 1 > r 2 > r 3 > … > r n u ovom konkretnom slučaju će izgledati ovako:

1071 > 462 > 147 > 21.

Od posljednjeg ostatka jednaka nuli, algoritam završava brojem 21 i gcd(1071, 462) = 21.

U tabelarnom obliku, koraci su bili sljedeći:

Prijave

Prošireni euklidski algoritam i Bezoutova relacija

Formule za r i (\displaystyle r_(i)) može se prepisati na sljedeći način:

r 1 = a + b (− q 0) (\displaystyle r_(1)=a+b(-q_(0))) r 2 = b − r 1 q 1 = a (− q 1) + b (1 + q 1 q 0) (\displaystyle r_(2)=b-r_(1)q_(1)=a(-q_( 1))+b(1+q_(1)q_(0))) ⋮ (\displaystyle \vdots) GCD (a, b) = r n = a s + b t (\displaystyle (a,b)=r_(n)=as+bt)

Evo s I t cijeli. Ovaj prikaz najvećeg zajedničkog djelitelja naziva se Bezoutova relacija i brojevi s I t- Bezout koeficijenti. Bezuova relacija je ključna u dokazu Euklidove leme i osnovne teoreme aritmetike.

Kontinuirani razlomci

Euklidov algoritam je usko povezan sa kontinuiranim razlomcima. Stav a/b može se predstaviti kao kontinuirani razlomak:

a b = [ q 0 ; q 1 , q 2 , ⋯ , q n ] (\displaystyle (\frac (a)(b))=).

U ovom slučaju, kontinuirani razlomak bez posljednjeg člana jednak je omjeru Bezoutovih koeficijenata t/s, snimljeno sa znakom minus:

[q 0 ; q 1 , q 2 , ⋯ , q n − 1 ] = − t s (\displaystyle =-(\frac (t)(s))).

Niz jednakosti koje definiraju Euklidski algoritam može se prepisati u obliku:

a b = q 0 + r 0 b b r 0 = q 1 + r 1 r 0 r 0 r 1 = q 2 + r 2 r 1 ⋮ r k − 2 r k − 1 = q k + r k r k − 1 ⋮ r − 2 r N 1 = q N (\displaystyle (\begin(aligned)(\frac (a)(b))&=q_(0)+(\frac (r_(0))(b))\\(\frac (b) )(r_(0)))&=q_(1)+(\frac (r_(1))(r_(0)))\\(\frac (r_(0))(r_(1)))& =q_(2)+(\frac (r_(2))(r_(1)))\\&()\ \vdots \\(\frac (r_(k-2))(r_(k-1) ))&=q_(k)+(\frac (r_(k))(r_(k-1)))\\&()\ \vdots \\(\frac (r_(N-2))(r_ (N-1)))&=q_(N)\end(poravnano)))

Posljednji član na desnoj strani jednačine uvijek je jednak inverznoj lijevoj strani sljedeće jednačine. Stoga se prve dvije jednadžbe mogu kombinirati u obliku:

a b = q 0 + 1 q 1 + r 1 r 0 (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\cfrac (r_( 1))(r_(0))))))

Treća jednakost se može koristiti za zamjenu nazivnika izraza r 1 /r 0 , dobijamo:

a b = q 0 + 1 q 1 + 1 q 2 + r 2 r 1 (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\ cfrac (1)(q_(2)+(\cfrac (r_(2))(r_(1)))))))

Zadnji preostali omjer r k /r k−1 se uvijek može zamijeniti sljedećom jednadžbom u nizu, i tako dalje do posljednje jednačine. Rezultat je kontinuirani razlomak:

a b = q 0 + 1 q 1 + 1 q 2 + 1 ⋱ + 1 q N = [ q 0 ; q 1 , q 2 , … , q N ] (\displaystyle (\frac (a)(b))=q_(0)+(\cfrac (1)(q_(1)+(\cfrac (1)(q_) (2)+(\cfrac (1)(\ddots +(\cfrac (1)(q_(N))))))))))=)

Generalizirani euklidski algoritam za polinome

Euklidski algoritam i prošireni Euklidski algoritam prirodno se generaliziraju na prsten polinoma k[x] iz jedne varijable preko proizvoljnog polja k, budući da je za takve polinome definirana operacija dijeljenja s ostatkom. Izvođenje Euklidovog algoritma za polinome na sličan način kao Euklidski algoritam za cijele brojeve proizvodi polinomski niz ostatka (PRS).

Primjer za prsten Z[x]

Neka je cont(f) po definiciji gcd koeficijenata polinoma f(x) iz Z[x] - sadržaj polinom. Poziva se količnik f(x) podijeljen sa cont(f). primitivni dio polinom f(x) i označava se sa primpart(f(x)). Ove definicije će biti potrebne za pronalaženje gcd dva polinoma p1(x) I p2(x) u prstenu Z[x]. Za polinome nad cijelim brojevima vrijedi sljedeće:

C o n t ((\displaystyle cont() NODNOD ( c o n t (p 1 (x)) , c o n t (p 2 (x)) , (\displaystyle \(nastavak(p_(1)(x)),nastavak(p_(2)(x))\),)

P r i m p a r t ((\displaystyle primpart() GCD ( p 1 (x) , p 2 (x) )) = (\displaystyle \(p_(1)(x),p_(2)(x)\))=) GCD ( p r i m p a r t (p 1 (x)), p r i m p a r t (p 2 (x)) . (\displaystyle \(primpart(p_(1)(x)),primpart(p_(2)(x))\).)

Dakle, problem nalaženja GCD dva proizvoljna polinoma se svodi na problem nalaženja GCD primitivnih polinoma.

Neka postoje dva primitivna polinoma p 1 (x) i p 2 (x) iz Z[x], za koje vrijedi relacija između njihovih potencija: deg(p 1 (x)) = m i deg(p 2 (x) ) = n, m > n. Dijeljenje polinoma sa ostatkom pretpostavlja tačnu djeljivost najvećeg koeficijenta dividende najvećim koeficijentom djelitelja, u opštem slučaju, dijeljenje s ostatkom se ne može izvršiti. Stoga se uvodi algoritam pseudo-podjele, koji i dalje omogućava da se dobije pseudo-količnik i pseudo-ostatak (prem), koji će i sami pripadati skupu polinoma nad cijelim brojevima.

Pod pseudo-dijeljenjem podrazumijevamo da samoj diobi prethodi množenje polinoma p 1 (x) (\displaystyle p_(1)(x)) on (l c (p 2 (x))) m − n + 1 (\displaystyle (lc(p_(2)(x)))^(m-n+1)), to je

L c (p 2 (x)) m − n + 1 p 1 (x) = p 2 (x) q (x) + r 2 (x) , deg ⁡ (r (x))< deg ⁡ (p 2 (x)) , {\displaystyle lc(p_{2}(x))^{m-n+1}p_{1}(x)=p_{2}(x)q(x)+r_{2}(x),\deg(r(x))<\deg(p_{2}(x)),}

Gdje q (x) (\displaystyle q(x)) I r (x) (\displaystyle r(x))- pseudo-količnik i pseudo-ostatak, respektivno.

dakle, p 1 (x) , p 2 (x) ∈ Z [ x ] (\displaystyle p_(1)(x),p_(2)(x)\in Z[x]), i stepen ⁡ (p 1) = n 1 ≥ stepen ⁡ (p 2) = n 2 (\displaystyle \deg(p_(1))=n_(1)\geq \deg(p_(2))=n_(2) ). Tada se Euklidski algoritam sastoji od sljedećih koraka:

1. Proračun sadržaja GCD:

C:= (\displaystyle c:=) GCD ( c o n t (p 1) , c o n t (p 2) ) (\displaystyle \(nastavak(p_(1)),nastavak(p_(2))\)).

2. Proračun primitivnih dijelova:

P 1 ′ (x) := p r i m p a r t (p 1 (x)) ; (\displaystyle p_(1)"(x):=primpart(p_(1)(x));)

P 2 ′ (x) := p r i m p a r t (p 2 (x)) . (\displaystyle p_(2)"(x):=primpart(p_(2)(x)).)

3. Konstrukcija niza polinomskih ostataka:

P 1 ′ (x) , (\displaystyle p_(1)"(x),)

P 2 ′ (x) , (\displaystyle p_(2)"(x),)

P 3 (x) := p r e m (p 1 ′ (x) , p 2 ′ (x)) , (\displaystyle p_(3)(x):=prem(p_(1)"(x),p_(2) )"(x)))

P 4 (x) := p r e m (p 2 ′ (x) , p 3 (x)) , (\displaystyle p_(4)(x):=prem(p_(2)"(x),p_(3) (x)))

P 5 (x) := p r e m (p 3 (x) , p 4 (x)) , (\displaystyle p_(5)(x):=prem(p_(3)(x),p_(4)(x) )))

. . . (\displaystyle ...)

P h (x) := p r e m (p h − 2 (x) , p h − 1 (x)) . (\displaystyle p_(h)(x):=prem(p_(h-2)(x),p_(h-1)(x)).)

• Uvesti koncept “Euklidovog algoritma”.
• Naučite pronaći najčešće djelitelje koristeći različite matematičke metode.

Tokom nastave

Koncept Euklidovog algoritma

Jedan je od najstarijih matematičkih, star više od 2000 godina.

Euklidov algoritam je izmišljen da pronađe najveći zajednički djelitelj parovi cijelih brojeva.

Najveći zajednički djelitelj

Najveći zajednički djelitelj(GCD) je broj koji dijeli dva broja bez ostatka i sam je djeljiv bez ostatka s bilo kojim drugim djeliteljem ovih brojeva.

Drugim riječima, ovo je najveći broj kojim se dva broja za koja se može naći zajednički djelitelj mogu podijeliti bez ostatka.

Algoritam za pronalaženje GCD po dijeljenju

Opis algoritma za pronalaženje najvećeg zajedničkog djelitelja dijeljenjem

Veći broj se dijeli manjim brojem

Ako je djeljiv bez ostatka, tada je manji broj najveći zajednički djelitelj. Sada moraš izaći ciklus

Ako postoji ostatak, onda zamijenite veći broj ostatkom dijeljenja

Idite na tačku 1.

primjer:

Pronađite najveći zajednički djelitelj za 300 i 180.

300/180 = 1 (ostatak 120)

180/120 = 1 (ostatak 60)

120/60 = 2 (ostatak 0).

kraj: Najveći zajednički djelitelj je 6.

IN ciklus“a” ili “b” fiksira ostatak podjele. Kada nema ostatka (ne znamo da li je u "a" ili "b", pa provjeravamo oba uslovima), tada se ciklus završava.

Na kraju se prikazuje zbir “a” i “b”, jer ne znamo koja varijabla sadrži najveći zajednički djelitelj, a u svakom slučaju jedna od njih sadrži 0, što ne utiče na rezultat zbira.

Algoritam za pronalaženje GCD oduzimanjem

Opis algoritma za pronalaženje najvećeg zajedničkog djelitelja oduzimanjem

Manji broj se oduzima od većeg broja

Ako je rezultat 0, tada su brojevi jednaki jedan drugom i najveći su zajednički djelitelj. Izlaz iz petlje

Ako rezultat oduzimanja nije 0, tada se veći broj zamjenjuje rezultatom oduzimanja

Idite na tačku 1.

primjer: Pronađite brojeve 300 i 180.

kraj: Najčešći djelitelj brojeva 300 i 180 je 60.

Pitagorejcima je bio poznat metod za pronalaženje najveće zajedničke mere dva segmenta (metoda naizmeničnog oduzimanja).

Prilikom pronalaženja najveće zajedničke mjere od dva segmentima postupite na isti način kao gore.

Operacija dijeljenja s ostatkom zamijenjena je svojim geometrijskim parnjakom: manje linijski segment odlažu na veći što više puta, a ostatak većeg segmenta (a to je ostatak podjele) odlažu na manji segment.

Ako segmenti a I b srazmjerno, tada će posljednji ostatak različit od nule dati najveću zajedničku mjeru segmenata.

Ako su nesamjerljivi, rezultirajući niz ostataka koji nisu nula bit će beskonačan.

primjer:

Kao segmente uzimamo stranice AB i AC jednakokračnog trougla ABC, u kojem je A=C = 72°, B= 36°.

Kao prvi ostatak dobićemo segment AD (CD-simetralu ugla C), a, kao što je lako videti, niz nultih ostataka će biti beskonačan.

To znači da segmenti AB i AC nisu uporedivi.

Pitanja

1. Šta je Euklidski algoritam?

2. Koji je najveći zajednički djelitelj?

Spisak korištenih izvora

1. Lekcija na temu: "Euklidski algoritam", P. I. Korchevoy, Lutsk

2. Shchetnikov A.I. Euklidski algoritam i kontinuirani razlomci. - Novosibirsk: ANT, 2003.

3. Countinho S. Uvod u teoriju brojeva. RSA algoritam, – M., 2001.

4. Kostrikin A.I. Uvod u algebru, - M., 2000.

Uredio i poslao nastavnik Kijevski nacionalni univerzitet nazvan po. Taras Shevchenko Solovjov M. S.

Radili smo na lekciji

Korchevoy P.I.

Solovjev M. S.

Možete postaviti pitanje o modernom obrazovanju, izraziti ideju ili riješiti gorući problem na Obrazovni forum

1.1 Primjena Euklidovog algoritma

Kao i svaki dobro obavljen posao, Euklidski algoritam proizvodi mnogo više nego što se prvobitno očekivalo. Iz njegovog ispitivanja je jasno, na primjer, da se skup djelitelja a i b poklapa sa skupom djelitelja (a, b). On također daje praktičan način pronalaženja brojeva u i v iz Z (ili, ako želite, iz teoreme u tački 2) tako da

r n = au + bv = (a, b).

Zaista, iz lanca jednakosti imamo:

r n = r n -2 - r n -1 q n = r n -2 - (r n -3 - r n -2 q n -1) q n =...

(idemo duž lanca jednakosti odozdo prema gore, izražavajući ostatak od svake sljedeće jednakosti i zamjenjujući ga u izraz koji se dobije u ovom trenutku)

Au + bv = (a, b).

Bez sumnje, postupak koji je opisao Euklid za određivanje zajedničke mjere dvije veličine u odnosu na brojeve (a zajednička mjera dva prirodna broja, očigledno je njihov najveći zajednički djelitelj) izmišljen je mnogo prije Euklida. Stari kineski matematičari su takođe pronašli GCD na isti način. I samo činjenica da je ovaj postupak postao poznat u renesansi upravo iz "Principa" dao mu je naziv "Euklidski algoritam"

Najvjerovatnije je proizašla iz komercijalne prakse drevnih trgovaca, kada su trebali upoređivati ​​različite omjere cijelih brojeva. Kako, na primjer, možemo uporediti omjere brojeva 3703700 i 1234567 i brojeva 22962965 i 7654321? Bilo je sasvim prirodno pokušati saznati koliko puta manji broj stane u veći. Lako je provjeriti da je 3703700 = 2 1234567 + 1234566 i 22962965 = 3 7654321 + 2. Sada je jasno da je omjer 3703700 prema 1234567 manji od omjera 3703700 prema 1234567 koji je sada manji od omjera 2666, 641, kao što je sada 652,661.

2,99999919 <= 3, 000000261,

Drevni kalkulatori objašnjeni u dugoj frazi.

Ako bismo morali uporediti bliže omjere brojeva, na primjer, i, onda bi proračuni bili složeniji:

71755875 = 61735500 + 10020375;

61735500 = 6 10020375 + 1613250;

10020375 = 6 1613250 + 340875;

1613250 = 4 340875 + 249750;

340875 = 249750 + 91125;

249750 = 2 91125 + 67500;

91125 = 67500 + 23625;

67500 = 2 23625 + 20250;

23625 = 20250 + 3375;

20250 = 6 3375.

Euklidski algoritam nam ovdje omogućava da odredimo gcd brojeva 71755875 i 61735500, koji je jednak 3375 i odgovara proširenju omjera 71755875 prema 61735500 u kontinuirani razlomak:

Pokazalo se da je Euklid algoritam ekvivalentan modernoj proceduri za razlaganje broja u kontinuirani razlomak i, osim toga, omogućava vam da „zaokružite“ omjere brojeva, tj. zamijeniti razlomak sa velikim imeniocem vrlo bliskim razlomkom sa manjim nazivnikom. U stvari, izraz

jednak razlomku, u modernoj matematici se naziva "prikladnim razlomkom" dekompozicije relacije b = na kontinuirani (ili kontinuirani) razlomak.

To je jasno

b=1+< 1 + и б=1 + > 1+ = ,

zbog

Gore navedeno poređenje je napravljeno u 3. vijeku. BC. Aristarh sa Samosa u svojoj raspravi “O udaljenosti i veličini Mjeseca i Sunca”.

Sada je poznato da su pogodni razlomci proširenja kontinuiranog razlomka bilo kojeg (racionalnog ili iracionalnog) broja najbolje racionalne aproksimacije tog broja.

Algoritmi sa polinomima

Euklidov algoritam je metoda za pronalaženje najvećeg zajedničkog djelitelja dva cijela broja, kao i dva polinoma iste varijable...

Jedan od najstarijih matematičkih algoritama je Euklid algoritam za pronalaženje najvećeg zajedničkog djelitelja dva pozitivna broja. Evo njegovog najjednostavnijeg oblika. Neka su data dva cijela broja. Ako su jednaki...

Analiza Euklidovog algoritma u Euklidskim prstenovima

Prije nego što počnemo s analizom Euklidovog algoritma, pogledajmo Fibonačijeve brojeve. Suština Fibonačijevog niza je da se počevši od 1.1, sljedeći broj dobije dodavanjem dva prethodna. 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 …...

Istorija formiranja koncepta "algoritma". Najpoznatiji algoritmi u istoriji matematike

Euklidski algoritam je univerzalna metoda koja vam omogućava da izračunate najveći zajednički djelitelj dva pozitivna cijela broja. Opis algoritma za pronalaženje GCD dijeljenjem: 1. Podijelite veći broj manjim 2. Ako se podijeli bez ostatka...

Gausov celobrojni prsten

Koristimo uobičajenu definiciju najvećeg zajedničkog djelitelja za prstenove. GCD dva Gausova broja je njihov zajednički djelitelj koji je djeljiv sa bilo kojim drugim zajedničkim djeliteljem. Kao u mnogim celim brojevima...

Matematičke osnove sistema rezidualnih klasa

Pogledajmo primjer. Neka je p = 6. Tada imamo šest klasa particije skupa cijelih brojeva po modulu 6: r = 0; r = 1; r = 2; r = 3; r = 4; r = 5; gdje r označava ostatak kada se cijeli broj podijeli sa 6...

Metode izučavanja polinoma u izbornoj nastavi u srednjoj školi

Neka je prsten polinoma gotov. Definicija 1: Neka i, ako postoji polinom, onda je ostatak dijeljenja nula, tada se naziva djelitelj polinoma i označava se: ()...

Glavne faze formiranja i strukture moderne matematike

U 3. veku pre nove ere, u Aleksandriji se pojavila istoimena Euklidova knjiga, u ruskom prevodu „Načela“. Termin "elementarna geometrija" dolazi od latinskog naziva "početci". Uprkos...

Na teritoriji određenog grada N nalaze se fabrike i prodavnice u koje se isporučuju proizvodi iz ovih fabrika. Kao rezultat razvoja, identifikovane su moguće rute za postavljanje komunikacija i procijenjena je cijena njihove izrade za svaku rutu...

Primjena metoda diskretne matematike u ekonomiji

Kompanija koja se bavi transportom kvarljive robe treba da isporuči robu iz Suifenhea do Habarovska, a postoji nekoliko ruta kojima se može izvršiti dostava. Udaljenost između Suifenhea i City 2 je 15 km...

Razvoj koncepta "prostora" i neeuklidske geometrije

Posebne metode za integraciju racionalnih izraza

Neka je potrebno pronaći gcd polinoma i. Bez gubitka opštosti, pretpostavićemo da stepen nije veći od stepena. Predstavimo polinom u obliku: gdje je ostatak dijeljenja sa. Tada je stepen manji od stepena delioca. Dalje...

Teorija ostataka

Teorija ostataka

Definicija. Broj d??Z, koji istovremeno dijeli brojeve a, b, c, ..., k??Z, naziva se zajednički djelitelj ovih brojeva. Najveći d sa ovim svojstvom naziva se najveći zajednički djelitelj. Oznaka: d = (a, b, c, ..., k). Teorema. Ako je (a, b) = d...

Teorija ostataka

Neka je potrebno riješiti linearnu Diofantovu jednačinu: ax + by = c, gdje je a, b, c ??Z; a i b nisu nule. Pokušajmo zaključiti gledajući ovu jednačinu. Neka (a, b) = d. Tada je a = a 1 d ; b = b 1 d i jednačina izgleda ovako: a 1 d x + b 1 d y = c, tj. d· (a 1 x + b 1 y) = c...

Euklidov algoritam je algoritam za pronalaženje najvećeg zajedničkog djelitelja (GCD) para cijelih brojeva.

Najveći zajednički djelitelj (GCD) je broj koji dijeli dva broja bez ostatka i sam je djeljiv bez ostatka s bilo kojim drugim djeliteljem data dva broja. Jednostavno rečeno, ovo je najveći broj kojim se dva broja za koja se traži gcd mogu podijeliti bez ostatka.

Algoritam za pronalaženje GCD po dijeljenju

1. Podijelite veći broj manjim brojem.
2. Ako se podijeli bez ostatka, tada je manji broj GCD (trebalo bi izaći iz ciklusa).
3. Ako postoji ostatak, onda zamijenite veći broj ostatkom dijeljenja.
4. Pređimo na tačku 1.

primjer:
Pronađite gcd za 30 i 18.
30 / 18 = 1 (ostatak 12)
18 / 12 = 1 (ostatak 6)
12 / 6 = 2 (ostatak 0)
Kraj: GCD je djelitelj od 6.
GCD(30, 18) = 6

a = 50 b = 130 dok je a != 0 i b != 0 : ako je a > b: a = a % b ostalo : b = b % a print (a + b)

U petlji, ostatak dijeljenja se upisuje u varijablu a ili b. Petlja se završava kada je barem jedna od varijabli nula. To znači da drugi sadrži gcd. Međutim, ne znamo koji tačno. Stoga, za GCD nalazimo zbir ovih varijabli. Pošto je jedna od varijabli nula, to nema utjecaja na rezultat.

Algoritam za pronalaženje GCD oduzimanjem

1. Oduzmite manji broj od većeg broja.
2. Ako je rezultat 0, to znači da su brojevi jednaki jedan drugom i da su GCD (trebalo bi izaći iz petlje).
3. Ako rezultat oduzimanja nije jednak 0, tada zamijenite veći broj rezultatom oduzimanja.
4. Pređimo na tačku 1.

primjer:
Pronađite gcd za 30 i 18.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 - 6 = 0
Kraj: GCD je minuend ili subtrahend.
GCD(30, 18) = 6

a = 50 b = 130 dok a != b: ako je a > b: a = a - b ostalo : b = b - otisak (a)

Razmotrimo dvije glavne metode za pronalaženje GCD na dva glavna načina: korištenjem Euklidovog algoritma i faktoringom u proste faktore. Primijenimo obje metode za dva, tri ili više brojeva.

Euklidski algoritam za pronalaženje GCD

Euklidski algoritam olakšava izračunavanje najvećeg zajedničkog faktora dva pozitivna broja. Formulacije i dokaz Euklidovog algoritma predstavili smo u odjeljku “Najveći zajednički djelitelj: determinanta, primjeri”.

Suština algoritma je da se uzastopno izvrši dijeljenje s ostatkom, pri čemu se dobija niz jednakosti oblika:

a = b q 1 + r 1 , 0< r 1 < b b = r 1 · q 2 + r 2 , 0 < r 2 < r 1 r 1 = r 2 · q 3 + r 3 , 0 < r 3 < r 2 r 2 = r 3 · q 4 + r 4 , 0 < r 4 < r 3 ⋮ r k - 2 = r k - 1 · q k + r k , 0 < r k < r k - 1 r k - 1 = r k · q k + 1

Možemo završiti podjelu kada r k + 1 = 0, pri čemu r k = gcd (a, b).

Primjer 1

64 I 48 .

Rješenje

Uvedemo sljedeće oznake: a = 64, b = 48.

Na osnovu Euklidovog algoritma izvršićemo podjelu 64 on 48 .

Dobijamo 1, a ostatak 16. Ispada da je q 1 = 1, r 1 = 16.

Drugi korak je podjela 48 do 16, dobijamo 3. To je q 2 = 3, A r 2 = 0 . Dakle, broj 16 je najveći zajednički djelitelj za brojeve iz uvjeta.

odgovor: GCD (64, 48) = 16.

Primjer 2

Šta je GCD brojeva? 111 I 432 ?

Rješenje

Mi se delimo 432 on 111 . Prema Euklidskom algoritmu dobijamo lanac jednakosti 432 = 111 · 3 + 99, 111 = 99 · 1 + 12, 99 = 12 · 8 + 3, 12 = 3 · 4.

Dakle, najveći zajednički djelitelj brojeva je 111 I 432 – ovo je 3.

odgovor: GCD (111, 432) = 3.

Primjer 3

Pronađite najveći zajednički djelitelj brojeva 661 i 113.

Rješenje

Podijelimo brojeve redom i dobijemo GCD (661 , 113) = 1 . To znači da su 661 i 113 relativno prosti brojevi. To bismo mogli shvatiti prije nego što započnemo računanje ako bismo konsultirali tabelu prostih brojeva.

odgovor: GCD (661, 113) = 1.

Pronalaženje GCD-a rastavljanjem brojeva u proste faktore

Da bi se metodom faktorizacije pronašao najveći zajednički djelitelj dva broja, potrebno je pomnožiti sve proste faktore koji se dobiju rastavljanjem ova dva broja na faktore i koji su im zajednički.

Primjer 4

Ako brojeve 220 i 600 razložimo u proste faktore, dobićemo dva proizvoda: 220 = 2 2 5 11 I 600 = 2 2 2 3 5 5. Zajednički faktori u ova dva proizvoda su 2, 2 i 5. To znači da je GCD (220, 600) = 2 2 5 = 20.

Primjer 5

Pronađite najveći zajednički djelitelj brojeva 72 I 96 .

Rješenje

Pronađite sve proste faktore brojeva 72 I 96 :

72 36 18 9 3 1 2 2 2 3 3

96 48 24 12 6 3 1 2 2 2 2 2 3

Uobičajeni prosti faktori za dva broja su 2, 2, 2 i 3. To znači da je GCD (72, 96) = 2 2 2 3 = 24.

odgovor: GCD (72, 96) = 24.

Pravilo za pronalaženje najvećeg zajedničkog djelitelja dva broja zasniva se na svojstvima najvećeg zajedničkog djelitelja, prema kojem je gcd (m a 1, m b 1) = m gcd (a 1, b 1), gdje je m bilo koji pozitivan cijeli broj .

Pronalaženje gcd tri ili više brojeva

Bez obzira na broj brojeva za koje trebamo pronaći GCD, slijedit ćemo isti algoritam koji se sastoji od uzastopnog pronalaženja GCD dva broja. Ovaj algoritam se zasniva na primeni sledeće teoreme: GCD više brojeva a 1 , a 2 , … , a k jednak broju dk, koji se nalazi sekvencijalnim izračunavanjem gcd (a 1 , a 2) = d 2, GCD (d 2 , a 3) = d 3 , GCD (d 3 , a 4) = d 4 , … , GCD (d k - 1 , a k) = d k .

Primjer 6

Pronađite najveći zajednički djelitelj četiri broja 78, 294, 570 i 36 .

Rješenje

Uvedemo oznaku: a 1 = 78, a 2 = 294, a 3 = 570, a 4 = 36.

Počnimo s pronalaženjem gcd brojeva 78 i 294: d 2 = GCD (78 , 294) = 6 .

Sada počnimo sa pronalaženjem d 3 = GCD (d 2 , a 3) = GCD (6, 570). Prema Euklidovom algoritmu 570 = 6 95. To znači da d 3 = GCD (6 , 570) = 6 .

Nađimo d 4 = GCD (d 3 , a 4) = GCD (6, 36). 36 djeljivo sa 6 bez ostatka. Ovo nam omogućava da dobijemo d 4 = GCD (6 , 36) = 6 .

d4 = 6, odnosno GCD (78 , 294 , 570 , 36) = 6 .

odgovor:

Pogledajmo sada drugi način izračunavanja GCD za te i više brojeva. Možemo pronaći gcd množenjem svih zajedničkih prostih faktora brojeva.

Primjer 7

Izračunajte GCD brojeva 78, 294, 570 i 36 .

Rješenje

Razložimo ove brojeve na proste faktore: 78 = 2 3 13, 294 = 2 3 7 7, 570 = 2 3 5 19, 36 = 2 2 3 3.

Za sva četiri broja, zajednički prosti činioci će biti brojevi 2 i 3.

Ispostavilo se da je GCD (78, 294, 570, 36) = 2 3 = 6.

odgovor: GCD (78, 294, 570, 36) = 6.

Pronalaženje GCD negativnih brojeva

Ako imamo posla s negativnim brojevima, onda možemo koristiti module ovih brojeva da pronađemo najveći zajednički djelitelj. To možemo učiniti, poznavajući svojstvo brojeva suprotnih predznaka: brojeva n I - n imaju iste djelitelje.

Primjer 8

Pronađite gcd negativnih cijelih brojeva − 231 I − 140 .

Rješenje

Za izvođenje proračuna uzimamo module brojeva datih u uvjetu. To će biti brojevi 231 i 140. Zapišimo to ukratko: GCD (− 231 , − 140) = GCD (231, 140) . Sada primjenjujemo Euklidov algoritam da pronađemo proste faktore dva broja: 231 = 140 · 1 + 91 ; 140 = 91 1 + 49 ; 91 = 49 · 1 + 42 ; 49 = 42 1 + 7 i 42 = 7 6. Dobijamo da je GCD (231, 140) = 7 .

I od GCD (− 231 , − 140) = GCD (231 , 140) , zatim gcd brojeva − 231 I − 140 jednaki 7 .

odgovor: GCD (− 231, − 140) = 7.

Primjer 9

Odrediti gcd tri broja − 585, 81 i − 189 .

Rješenje

Zamijenimo negativne brojeve u gornjoj listi njihovim apsolutnim vrijednostima, dobićemo GCD (− 585 , 81 , − 189) = GCD (585 , 81 , 189) . Zatim sve ove brojeve činimo u proste faktore: 585 = 3 3 5 13, 81 = 3 3 3 3 i 189 = 3 3 3 7. Zajednički za tri broja su prosti faktori 3 i 3. Ispada da je GCD (585, 81, 189) = GCD (− 585, 81, − 189) = 9.

odgovor: GCD (− 585, 81, − 189) = 9.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter