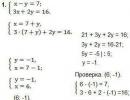Razlikovanje složenih i implicitnih funkcija nekoliko argumenata. §6 Parcijalni izvod kompleksnih funkcija nekoliko varijabli. Ekstremum funkcije dvije varijable

Naučit ćemo pronaći izvode funkcija specificiranih implicitno, odnosno specificiranih određenim jednadžbama koje povezuju varijable x I y. Primjeri funkcija navedenih implicitno:

Derivati funkcija specificiranih implicitno, ili derivati implicitnih funkcija, nalaze se prilično jednostavno. Pogledajmo sada odgovarajuće pravilo i primjer, a zatim otkrijemo zašto je to uopće potrebno.

Da biste pronašli izvod funkcije specificirane implicitno, morate razlikovati obje strane jednadžbe s obzirom na x. Oni termini u kojima je prisutan samo X pretvorit će se u uobičajeni derivat funkcije iz X. A termini s igrom moraju se razlikovati korištenjem pravila za diferenciranje složene funkcije, budući da je igra funkcija od X. Pojednostavljeno rečeno, rezultujuća derivacija pojma sa x treba da rezultira: derivacijom funkcije od y pomnoženom izvodom iz y. Na primjer, derivacija termina će biti napisana kao , derivacija pojma će biti napisana kao . Dalje, iz svega ovoga trebate izraziti ovaj "hod igre" i dobit će se željeni derivat funkcije specificirane implicitno. Pogledajmo ovo na primjeru.

Primjer 1.

Rješenje. Razlikujemo obje strane jednadžbe s obzirom na x, uz pretpostavku da je i funkcija od x:

Odavde dobijamo derivat koji je potreban u zadatku:

Sada nešto o dvosmislenom svojstvu funkcija specificiranih implicitno, i zašto su potrebna posebna pravila za njihovu diferencijaciju. U nekim slučajevima, možete se pobrinuti da zamjena izraza u terminima x u datu jednačinu (pogledajte primjere iznad) umjesto u igricu, dovodi do činjenice da se ova jednačina pretvara u identitet. Dakle. Gornja jednadžba implicitno definira sljedeće funkcije:

Nakon zamjene izraza za igru na kvadrat kroz x u originalnu jednačinu, dobivamo identitet:

Izrazi koje smo zamijenili dobijeni su rješavanjem jednadžbe za igru.

Ako bismo razlikovali odgovarajuću eksplicitnu funkciju

tada bismo dobili odgovor kao u primjeru 1 - iz funkcije specificirane implicitno:

Ali ne može svaka funkcija specificirana implicitno biti predstavljena u obliku y = f(x) . Tako, na primjer, implicitno specificirane funkcije

nisu izražene kroz elementarne funkcije, odnosno ove jednačine se ne mogu riješiti u odnosu na igru. Stoga postoji pravilo za diferenciranje funkcije specificirane implicitno, koje smo već proučavali i koje ćemo dalje dosljedno primjenjivati u drugim primjerima.

Primjer 2. Pronađite izvod funkcije date implicitno:

Izražavamo prost i - na izlazu - derivaciju navedene funkcije implicitno:

Primjer 3. Pronađite izvod funkcije date implicitno:

Rješenje. Razlikujemo obje strane jednadžbe s obzirom na x:

Primjer 4. Pronađite izvod funkcije date implicitno:

Rješenje. Razlikujemo obje strane jednadžbe s obzirom na x:

Izražavamo i dobijamo derivaciju:

Primjer 5. Pronađite izvod funkcije date implicitno:

Rješenje. Članove s desne strane jednačine pomjerimo na lijevu stranu i ostavimo nulu na desnoj strani. Razlikujemo obje strane jednadžbe s obzirom na x.

Funkcija Z= f(x; y) naziva se implicitnom ako je data jednačinom F(x,y,z)=0 nerazriješena u odnosu na Z. Nađimo parcijalne izvode funkcije Z date implicitno. Da bismo to učinili, zamjenom funkcije f(x;y) u jednačinu umjesto Z, dobijamo identitet F(x,y, f(x,y))=0. Parcijalni izvod funkcije identično jednak nuli u odnosu na x i y također je jednak nuli.

F(x,y, f (x, y)) =
=0 (smatra se konstanta)

F(x,y, f (x, y)) =
=0 (xsmatrana konstanta)

Gdje
I

Primjer: Pronađite parcijalne izvode funkcije Z date jednadžbom
.

Ovdje je F(x,y,z)=
;
;
;
. Prema gore navedenim formulama imamo:

Smjerni derivat

Neka je data funkcija dvije varijable Z= f(x; y) u određenom susjedstvu tačke M (x,y). Razmotrimo neki smjer definiran jediničnim vektorom
, Gdje
(vidi sliku).

Na pravoj liniji koja prolazi u ovom pravcu kroz tačku M, uzimamo tačku M 1 (
) tako da dužina
segmentMM 1 je jednak
. Prirast funkcije f(M) je određen relacijom gdje je
povezani odnosima. Granica omjera at
zvaće se derivacija funkcije
u tački
prema i biti određen .

Ako je funkcija Z diferencijabilna u točki
, zatim njegovo povećanje u ovoj tački uzimajući u obzir odnose za
može se napisati u sljedećem obliku.

dijeleći oba dijela sa

i prelazeći do granice na
dobijamo formulu za izvod funkcije Z= f(x; y) u pravcu:

Gradijent

Razmotrimo funkciju tri varijable
diferenciran u nekom trenutku
.

Gradijent ove funkcije
u tački M je vektor čije su koordinate jednake parcijalnim derivacijama
na ovom mjestu. Da biste označili gradijent, koristite simbol
.
=
.

.Gradijent pokazuje smjer najbržeg rasta funkcije u datoj tački.

Budući da je jedinični vektor ima koordinate (
), tada se derivacija smjera za slučaj funkcije tri varijable zapisuje u obliku, tj. ima formulu za skalarni proizvod vektora I
. Prepišimo posljednju formulu na sljedeći način:

, Gdje - ugao između vektora I
. Zbog
, onda slijedi da derivacija funkcije u smjeru uzima maksimalnu vrijednost na =0, tj. kada je smjer vektora I
podudaraju se. Gde
To jest, u stvari, gradijent funkcije karakterizira smjer i veličinu maksimalne brzine povećanja ove funkcije u nekoj tački.

Ekstremum funkcije dvije varijable

Koncepti max, min, ekstremuma funkcije dvije varijable slični su odgovarajućim konceptima funkcije jedne varijable. Neka je funkcija Z= f(x; y) definirana u nekom domenu D, itd. M
pripada ovom području. Tačka M
naziva se maksimalna tačka funkcije Z= f(x; y) ako postoji takvo δ-susjedstvo tačke
, da je za svaku tačku iz ove okoline nejednakost
. Tačka min se određuje na sličan način, samo će se promijeniti predznak nejednakosti
. Vrijednost funkcije u tački max(min) naziva se maksimum (minimum). Maksimum i minimum funkcije nazivaju se ekstremima.

Neophodni i dovoljni uslovi za ekstrem

Teorema:(Neophodni uslovi za ekstrem). Ako u tački M
diferencijabilna funkcija Z= f(x; y) ima ekstrem, tada su njeni parcijalni derivati u ovoj tački jednaki nuli:
,
.

dokaz: Nakon fiksiranja jedne od varijabli x ili y, transformiramo Z = f(x; y) u funkciju jedne varijable, za čiji ekstrem moraju biti ispunjeni gore navedeni uvjeti. Geometrijski jednakosti
I
znači da je u tački ekstrema funkcije Z= f(x; y), tangentna ravan na površinu koja predstavlja funkciju f(x,y)=Z paralelna sa ravninom OXY, jer jednadžba tangentne ravni je Z = Z 0. Tačka u kojoj su parcijalni izvodi prvog reda funkcije Z = f (x; y) jednaki nuli, tj.
,
, nazivaju se stacionarna točka funkcije. Funkcija može imati ekstrem u tačkama u kojima barem jedan od parcijalnih izvoda ne postoji. Na primjer Z=|-
| ima max u tački O(0,0), ali nema izvoda u ovoj tački.

Stacionarne tačke i tačke u kojima ne postoji barem jedan parcijalni izvod nazivaju se kritične tačke. U kritičnim tačkama, funkcija može, ali i ne mora imati ekstrem. Jednakost parcijalnih izvoda nuli je neophodan, ali ne i dovoljan uslov za postojanje ekstrema. Na primjer, kada je Z=xy, tačka O(0,0) je kritična. Međutim, funkcija Z=xy u sebi nema ekstrem. (Jer u kvartalima I i III Z>0, a u kvartalima II i IV – Z<0). Таким образом для нахождения экстремумов функции в данной области необходимо подвергнуть каждую критическую точку функции дополнительному исследованию.

Teorema: (dovoljno stanje za ekstreme). Neka u stacionarnoj tački
a u određenoj okolini funkcija f(x; y) ima kontinuirane parcijalne izvode do zaključno 2. reda. Izračunajmo u tački
vrijednosti
,
I
. Označimo

Ako
, ekstremum u tački
može i ne mora biti. Potrebno je više istraživanja.

Kao što je poznato, implicitno data funkcija jedne varijable definirana je na sljedeći način: funkcija y nezavisne varijable x naziva se implicitna ako je data jednadžbom koja nije riješena u odnosu na y:

Primjer 1.11.

Jednačina

implicitno specificira dvije funkcije:

I jednadžba

ne specificira nijednu funkciju.

Teorema 1.2 (postojanje implicitne funkcije).

Neka su funkcija z =f(x,y) i njene parcijalne derivacije f"x i f"y definirane i kontinuirane u nekom susjedstvu UM0 tačke M0(x0y0). Osim toga, f(x0,y0)=0 i f"(x0,y0)≠0, tada jednačina (1.33) definira u okolini UM0 implicitnu funkciju y= y(x), kontinuiranu i diferencijabilnu u nekom intervalu D sa centrom u tački x0, i y(x0)=y0.

Nema dokaza.

Iz teoreme 1.2 slijedi da je na ovom intervalu D:

odnosno postoji identitet u

gdje se "ukupni" derivat nalazi prema (1.31)

To jest, (1.35) daje formulu za pronalaženje izvoda implicitno date funkcije jedne varijable x.

Implicitna funkcija dvije ili više varijabli definirana je slično.

Na primjer, ako u nekom području V Oxyz prostora vrijedi jednačina:

onda pod određenim uvjetima na funkciji F implicitno definira funkciju

Štaviše, po analogiji sa (1.35), njeni parcijalni derivati se nalaze na sledeći način:

Primjer 1.12. Pod pretpostavkom da je jednadžba

implicitno definira funkciju

naći z"x, z"y.

dakle, prema (1.37), dobijamo odgovor.

11. Upotreba parcijalnih izvoda u geometriji.

12. Ekstremi funkcije dvije varijable.

Koncepti maksimuma, minimuma i ekstrema funkcije dvije varijable slični su odgovarajućim konceptima funkcije jedne nezavisne varijable (vidi odjeljak 25.4).

Neka je funkcija z = ƒ(x;y) definirana u nekom domenu D, tačka N(x0;y0) O D.

Tačka (x0;y0) se naziva maksimalnom tačkom funkcije z=ƒ(x;y) ako postoji d-okolina tačke (x0;y0) takva da je za svaku tačku (x;y) različita od (xo;yo), iz ove okoline vrijedi nejednakost ƒ(x;y).<ƒ(хо;уо).

A Minimalna tačka funkcije određena je na sličan način: za sve tačke (x; y) osim (x0; y0), iz d-okoline tačke (xo; yo) vrijedi sljedeća nejednakost: ƒ(x y)>ƒ(x0; y0).

Na slici 210: N1 je maksimalna tačka, a N2 je minimalna tačka funkcije z=ƒ(x;y).

Vrijednost funkcije u točki maksimuma (minimuma) naziva se maksimumom (minimumom) funkcije. Maksimum i minimum funkcije nazivaju se njenim ekstremima.

Imajte na umu da, po definiciji, tačka ekstrema funkcije leži unutar domena definicije funkcije; maksimum i minimum imaju lokalni (lokalni) karakter: vrijednost funkcije u tački (x0; y0) uspoređuje se s njenim vrijednostima u tačkama koje su dovoljno blizu (x0; y0). U regiji D, funkcija može imati nekoliko ekstrema ili nijedan.

46.2. Neophodni i dovoljni uslovi za ekstrem

Razmotrimo uslove za postojanje ekstrema funkcije.

Teorema 46.1 (neophodni uslovi za ekstrem). Ako u tački N(x0;y0) diferencijabilna funkcija z=ƒ(x;y) ima ekstrem, tada su njeni parcijalni derivati u ovoj tački jednaki nuli: ƒ"x(x0;y0)=0, ƒ" y(x0;y0 )=0.

Popravimo jednu od varijabli. Stavimo, na primjer, y=y0. Tada dobijamo funkciju ƒ(x;y0)=φ(x) jedne varijable, koja ima ekstrem na x = x0. Prema tome, prema potrebnom uslovu za ekstremum funkcije jedne varijable (vidi odjeljak 25.4), φ"(x0) = 0, tj. ƒ"x(x0;y0)=0.

Slično, može se pokazati da je ƒ"y(x0;y0) = 0.

Geometrijski, jednakosti ƒ"x(x0;y0)=0 i ƒ"y(x0;y0)=0 znače da u tački ekstrema funkcije z=ƒ(x;y) tangentna ravan na površinu koja predstavlja funkcija ƒ(x;y) ), paralelna je sa ravninom Oxy, pošto je jednadžba tangentne ravni z=z0 (vidi formulu (45.2)).

Z Bilješka. Funkcija može imati ekstrem u tačkama u kojima barem jedan od parcijalnih izvoda ne postoji. Na primjer, funkcija ima maksimum u tački O(0;0) (vidi sliku 211), ali nema parcijalne izvode u ovoj tački.

Tačka u kojoj su parcijalni izvodi prvog reda funkcije z ≈ ƒ(x; y) jednaki nuli, tj. f"x=0, f"y=0, naziva se stacionarna tačka funkcije z.

Stacionarne tačke i tačke u kojima ne postoji barem jedan parcijalni izvod nazivaju se kritične tačke.

U kritičnim tačkama, funkcija može, ali i ne mora imati ekstrem. Jednakost parcijalnih izvoda nuli je neophodan, ali ne i dovoljan uslov za postojanje ekstrema. Razmotrimo, na primjer, funkciju z = xy. Za njega je tačka O(0; 0) kritična (u njoj z"x=y i z"y - x nestaju). Međutim, funkcija z=xy u sebi nema ekstrem, jer u dovoljno maloj okolini tačke O(0; 0) postoje tačke za koje z>0 (tačke prve i treće četvrtine) i z< 0 (точки II и IV четвертей).

Dakle, da bi se pronašli ekstremi funkcije u datom području, potrebno je svaku kritičnu tačku funkcije podvrgnuti dodatnom istraživanju.

Teorema 46.2 (dovoljan uslov za ekstrem). Neka funkcija ƒ(x;y) u stacionarnoj tački (xo; y) i neka njena okolina imaju kontinuirane parcijalne izvode do zaključno drugog reda. Izračunajmo u tački (x0;y0) vrijednosti A=f""xx(x0;y0), B=ƒ""xy(x0;y0), C=ƒ""yy(x0;y0) . Označimo

1. ako je Δ > 0, tada funkcija ƒ(x;y) u tački (x0;y0) ima ekstrem: maksimum ako je A< 0; минимум, если А > 0;

2. ako je Δ< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

U slučaju Δ = 0, može postojati ili ne mora postojati ekstrem u tački (x0;y0). Potrebno je više istraživanja.

ZADACI

Primjer. Naći intervale rastuće i opadajuće funkcije. Rješenje. Prvi korak je pronalaženje domene definicije funkcije. U našem primjeru, izraz u nazivniku ne bi trebao ići na nulu, dakle, . Pređimo na derivirajuću funkciju: Za određivanje intervala povećanja i smanjenja funkcije na osnovu dovoljnog kriterija rješavamo nejednakosti u domeni definicije. Koristimo generalizaciju metode intervala. Jedini pravi korijen brojioca je x = 2, a imenilac ide na nulu u x = 0. Ove tačke dijele područje definicije na intervale u kojima derivacija funkcije zadržava svoj predznak. Označimo ove tačke na brojevnoj pravoj. Uobičajeno sa plusima i minusima označavamo intervale u kojima je derivacija pozitivna ili negativna. Strelice ispod šematski pokazuju povećanje ili smanjenje funkcije na odgovarajućem intervalu. dakle, I . U tački x = 2 funkcija je definirana i kontinuirana, pa je treba dodati i rastućim i opadajućim intervalima. U tački x = 0 funkcija nije definirana, tako da ovu tačku ne uključujemo u tražene intervale. Predstavljamo graf funkcije za upoređivanje rezultata dobivenih s njom. odgovor: funkcija se povećava sa , smanjuje se na intervalu (0; 2] .

Primjeri.

Postavite intervale konveksnosti i konkavnosti krive y = 2 – x 2 .

Naći ćemo y"" i odredite gdje je drugi izvod pozitivan, a gdje negativan. y" = –2x, y"" = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.

y = e x. Jer y"" = e x > 0 za bilo koji x, tada je kriva svuda konkavna.

y = x 3 . Jer y"" = 6x, To y"" < 0 при x < 0 и y"" > 0 at x> 0. Dakle, kada x < 0 кривая выпукла, а при x> 0 je konkavno.

4. Date su funkcije z=x^2-y^2+5x+4y, vektor l=3i-4j i tačka A(3,2). Pronađite dz/dl (kako ja razumijem, derivaciju funkcije u smjeru vektora), gradz(A), |gradz(A)|. Nađimo parcijalne izvode: z(u odnosu na x)=2x+5 z(u odnosu na y)=-2y+4 Nađimo vrijednosti izvoda u tački A(3,2): z(sa u odnosu na x)(3,2)=2*3+ 5=11 z(po y)(3,2)=-2*2+4=0 Odakle je gradz(A)=(11,0)= 11i |gradz(A)|=sqrt(11^2+0 ^2)=11 Derivat funkcije z u smjeru vektora l: dz/dl=z(in x)*cosa+z(in y) *cosb, a, b-uglovi vektora l sa koordinatnim osa. cosa=lx/|l|, cosb=ly/|l|, |l|=sqrt(lx^2+ly^2) lx=3, ly=-4, |l|=5. cosa=3/5, cosb=(-4)/5. dz/dl=11*3/5+0*(-4)/5=6,6.

Vrlo često se pri rješavanju praktičnih problema (na primjer, u višoj geodeziji ili analitičkoj fotogrametriji) pojavljuju složene funkcije više varijabli, tj. x, y, z jedna funkcija f(x,y,z) ) su same funkcije novih varijabli U, V, W ).

To se, na primjer, dešava kada se krećete iz fiksnog koordinatnog sistema Oxyz u mobilni sistem O 0 UVW i nazad. Istovremeno, važno je poznavati sve parcijalne derivacije u odnosu na varijable “fiksne” – “stare” i “pokretne” – “nove”, jer ove parcijalne derivacije obično karakteriziraju položaj objekta u ovim koordinatnim sistemima. , a posebno utiču na korespondenciju fotografija iz vazduha sa stvarnim objektom . U takvim slučajevima primjenjuju se sljedeće formule:

To jest, data je složena funkcija T tri "nove" varijable U, V, W kroz tri "stare" varijable x, y, z, onda:

Komentar. Može postojati varijacije u broju varijabli. Na primjer: ako

Konkretno, ako z = f(xy), y = y(x) , tada dobijamo takozvanu formulu "totalni derivat":

Ista formula za "ukupni derivat" u slučaju:

će poprimiti oblik:

Moguće su i druge varijacije formula (1.27) - (1.32).

Napomena: formula „totalni izvod” se koristi u predmetu fizike, odeljak „Hidrodinamika” kada se izvodi osnovni sistem jednačina kretanja fluida.

Primjer 1.10. Dato:

Prema (1.31):

§7 Parcijalni izvod implicitno date funkcije nekoliko varijabli

Kao što je poznato, implicitno specificirana funkcija jedne varijable definirana je na sljedeći način: funkcija nezavisne varijable x naziva se implicitnim ako je dat jednadžbom koja nije riješena u odnosu na y :

Primjer 1.11.

Jednačina

implicitno specificira dvije funkcije:

I jednadžba

ne specificira nijednu funkciju.

Teorema 1.2 (postojanje implicitne funkcije).

Neka funkcija z =f(x,y) i njegove parcijalne derivate f" x I f" y definiran i kontinuiran u nekom susjedstvu U M0 bodova M 0 (x 0 y 0 ) . osim toga, f(x 0 ,y 0 )=0 I f"(x 0 ,y 0 )≠0 , tada jednačina (1.33) definira u susjedstvu U M0 implicitna funkcija y=y(x) , kontinuirano i diferencibilno u određenom intervalu D centriran u tački x 0 , i y(x 0 )=y 0 .

Nema dokaza.

Iz teoreme 1.2 slijedi da na ovom intervalu D :

odnosno postoji identitet u

gdje se "ukupni" derivat nalazi prema (1.31)

To jest, (1.35) daje formulu za pronalaženje derivacije implicitno date funkcije jedne varijable x .

Implicitna funkcija dvije ili više varijabli definirana je slično.

Na primjer, ako u nekom području V prostor Oxyz vrijedi sljedeća jednačina:

onda pod nekim uslovima na funkciji F on implicitno definira funkciju

Štaviše, po analogiji sa (1.35), njeni parcijalni derivati se nalaze na sledeći način:

Primjer 1.12. Pod pretpostavkom da je jednadžba

implicitno definira funkciju

naći z" x , z" y .

dakle, prema (1.37), dobijamo odgovor.

§8 Parcijalni derivati drugog i višeg reda

Definicija 1.9 Parcijalni izvod funkcije drugog reda z=z(x,y) definisani su kako slijedi:

Bilo ih je četvoro. Štaviše, pod određenim uslovima na funkcije z(x,y) jednakost vrijedi:

Komentar. Parcijalni derivati drugog reda se također mogu označiti na sljedeći način:

Definicija 1.10 Parcijalne derivacije trećeg reda su osam (2 3).

Formula za izvod funkcije specificirane implicitno. Dokaz i primjeri primjene ove formule. Primjeri izračunavanja derivata prvog, drugog i trećeg reda.

Sadržaj

Izvod prvog reda

Neka funkcija bude specificirana implicitno koristeći jednadžbu
(1) .
I neka ova jednadžba, za neku vrijednost, ima jedinstveno rješenje. Neka je funkcija diferencijabilna funkcija u točki , i
.
Zatim, na ovoj vrijednosti, postoji izvod, koji je određen formulom:
(2) .

Dokaz

Da biste to dokazali, razmotrite funkciju kao kompleksnu funkciju varijable:
.
Primijenimo pravilo diferencijacije kompleksne funkcije i pronađemo derivaciju u odnosu na varijablu s lijeve i desne strane jednačine
(3) :
.
Budući da je derivacija konstante nula i , Onda
(4) ;
.

Formula je dokazana.

Derivati višeg reda

Prepišimo jednačinu (4) koristeći različite oznake:
(4) .
U isto vrijeme i složene su funkcije varijable:
;
.
Ovisnost je određena jednadžbom (1):
(1) .

Pronalazimo derivaciju u odnosu na varijablu s lijeve i desne strane jednačine (4).
Prema formuli za izvod kompleksne funkcije imamo:
;
.
Prema formuli derivata proizvoda:

.
Koristeći formulu izvedenog zbira:

.

Pošto je derivacija desne strane jednačine (4) jednaka nuli, onda
(5) .
Zamjenom izvoda ovdje dobijamo vrijednost izvoda drugog reda u implicitnom obliku.

Diferencirajući jednadžbu (5) na sličan način, dobijamo jednačinu koja sadrži izvod trećeg reda:
.
Zamjenjujući ovdje pronađene vrijednosti derivata prvog i drugog reda, nalazimo vrijednost derivata trećeg reda.

Nastavljajući diferencijaciju, može se pronaći derivat bilo kojeg reda.

Primjeri

Primjer 1

Pronađite izvod prvog reda funkcije date implicitno jednadžbom:
(P1) .

Rješenje po formuli 2

Izvod nalazimo pomoću formule (2):
(2) .

Pomerimo sve varijable na lijevu stranu tako da jednačina dobije oblik .
.
Odavde.

Nalazimo derivaciju u odnosu na , smatrajući je konstantnom.
;
;
;
.

Pronalazimo derivaciju u odnosu na varijablu, s obzirom na konstantu varijable.
;
;
;
.

Koristeći formulu (2) nalazimo:
.

Rezultat možemo pojednostaviti ako primijetimo da je prema izvornoj jednadžbi (A.1), . Zamenimo:
.
Pomnožite brojilac i imenilac sa:
.

Rešenje drugog načina

Riješimo ovaj primjer na drugi način. Da bismo to učinili, naći ćemo izvod u odnosu na varijablu lijeve i desne strane izvorne jednačine (A1).

Primjenjujemo:
.
Primjenjujemo formulu izvedenog razlomka:
;
.
Primjenjujemo formulu za izvod kompleksne funkcije:
.
Hajde da izdiferenciramo originalnu jednačinu (A1).
(P1) ;
;
.
Množimo i grupišemo pojmove.
;
.

Zamijenimo (iz jednačine (A1)):
.
pomnoži sa:
.

Primjer 2

Pronađite izvod drugog reda funkcije date implicitno koristeći jednadžbu:
(A2.1) .

Originalnu jednačinu razlikujemo s obzirom na varijablu, s obzirom da je ona funkcija:
;
.
Primjenjujemo formulu za izvod kompleksne funkcije.
.

Hajde da razlikujemo originalnu jednačinu (A2.1):
;
.
Iz originalne jednačine (A2.1) slijedi da . Zamenimo:
.
Otvorite zagrade i grupirajte članove:
;
(A2.2) .
Nalazimo izvod prvog reda:
(A2.3) .

Da bismo pronašli izvod drugog reda, diferenciramo jednačinu (A2.2).
;
;
;
.
Zamijenimo izraz za izvod prvog reda (A2.3):
.
pomnoži sa:

;
.
Odavde nalazimo derivat drugog reda.