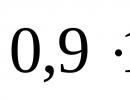Fermova teorema i teza. Hajde da razotkrijemo! Da li je Fermatova posljednja teorema dokazana? Kako su Taniyamina pretpostavka i Fermatova teorema povezani?
Nema mnogo ljudi na svijetu za koje nikada nisu čuli Fermatova posljednja teorema- možda je ovo jedini matematički problem koji je postao toliko poznat i postao prava legenda. Spominje se u mnogim knjigama i filmovima, a glavni kontekst gotovo svih referenci je nemogućnost dokazivanja teoreme.
Da, ova teorema je vrlo poznata i, na neki način, postala je “idol” kojeg obožavaju matematičari amateri i profesionalni matematičari, ali malo ljudi zna da je pronađen njen dokaz, a to se dogodilo davne 1995. godine. Ali prvo stvari.
Dakle, Fermatova posljednja teorema (često nazvana Fermatova posljednja teorema), koju je 1637. godine formulirao briljantni francuski matematičar Pierre Fermat, veoma je jednostavan u suštini i razumljiv svakome sa srednjom stručnom spremom. Kaže da formula a n + b n = c n nema prirodna (tj. ne frakciona) rješenja za n > 2. Sve izgleda jednostavno i jasno, ali najbolji matematičari i obični amateri već više od tri i po veka.
Sam Fermat je tvrdio da je izveo vrlo jednostavan i koncizan dokaz svoje teorije, ali još nije pronađen nijedan dokumentarni dokaz o ovoj činjenici. Stoga se sada vjeruje da Fermat nikada nije mogao da pronađe opšte rešenje za svoju teoremu, iako je poseban dokaz za n = 4 došao iz njegovog pera.
Nakon Ferma, tako veliki umovi kao Leonard Euler(1770. godine predložio je rješenje za n = 3), Adrien Legendre i Johann Dirichlet(ovi naučnici su zajedno pronašli dokaz za n = 5 1825. godine), Gabriel Lame(koji je našao dokaz za n = 7) i mnogi drugi. Sredinom 80-ih godina prošlog veka postalo je jasno da je naučni svet na putu konačnog rešenja
Fermatova posljednja teorema, međutim, tek 1993. godine matematičari su vidjeli i vjerovali da je trovjekovni ep o pronalaženju dokaza Fermatove posljednje teoreme praktično završen.
1993. godine engleski matematičar Andrew Wiles predstavio svetu svoje dokaz Fermatove posljednje teoreme, rad na kojem je trajao više od sedam godina. No, pokazalo se da ova odluka sadrži grubu grešku, iako je općenito ispravna. Wiles nije odustajao, pozvao je u pomoć čuvenog specijaliste za teoriju brojeva Richarda Taylora, a već 1994. godine objavili su ispravljeni i prošireni dokaz teoreme. Najnevjerovatnije je da je ovaj rad zauzeo čak 130 (!) stranica u matematičkom časopisu “Annals of Mathematics”. Ali ni tu se priča nije završila – konačna tačka je postignuta tek sljedeće, 1995. godine, kada je objavljena konačna i “idealna”, s matematičke tačke gledišta, verzija dokaza.
Od tog trenutka je prošlo dosta vremena, ali u društvu još uvijek postoji mišljenje da je Fermatova posljednja teorema nerješiva. Ali čak i oni koji znaju za pronađeni dokaz nastavljaju raditi u tom smjeru - malo je onih koji su zadovoljni da Velika teorema zahtijeva rješenje od 130 stranica! Stoga su sada napori mnogih matematičara (uglavnom amatera, a ne profesionalnih naučnika) bačeni u potragu za jednostavnim i konciznim dokazom, ali ovaj put, najvjerovatnije, neće voditi nikuda...
Pjer Ferma, čitajući „Aritmetiku“ Diofanta Aleksandrijskog i razmišljajući o njenim problemima, imao je običaj da zapisuje rezultate svojih razmišljanja u obliku kratkih komentara na marginama knjige. Protiv osmog Diofantovog problema na marginama knjige, Fermat je napisao: " Naprotiv, nemoguće je razložiti ni kocku na dvije kocke, ni bikvadrat na dva bikvadrata, i, općenito, nijednu snagu veću od kvadrata na dva stepena s istim eksponentom. Otkrio sam zaista divan dokaz za to, ali ova polja su preuska za to» / E.T. Bell "Kreatori matematike". M., 1979, str.69/. Predstavljam vam elementarni dokaz Fermatove teoreme, koji svaki srednjoškolac koji se zanima za matematiku može razumjeti.
Uporedimo Fermatov komentar na Diofantov problem sa modernom formulacijom poslednje Fermaove teoreme, koja ima oblik jednačine.
« Jednačina
x n + y n = z n(gdje je n cijeli broj veći od dva)
nema rješenja u pozitivnim cijelim brojevima»
Komentar je u logičkoj vezi sa zadatkom, slično logičkoj vezi predikata sa subjektom. Ono što tvrdi Diofantov problem, naprotiv, tvrdi Fermaov komentar.
Fermatov komentar može se protumačiti na sljedeći način: ako kvadratna jednadžba s tri nepoznate ima beskonačan broj rješenja na skupu svih trojki Pitagorinih brojeva, onda, naprotiv, jednačina sa tri nepoznanice na stepenu većoj od kvadrata
U jednačini njegove veze s Diofantovim problemom nema čak ni naznake. Njegov iskaz zahtijeva dokaz, ali ne postoji uvjet iz kojeg slijedi da nema rješenja u pozitivnim cijelim brojevima.
Opcije za dokazivanje meni poznate jednačine se svode na sljedeći algoritam.
- Kao zaključak uzima se jednadžba Fermatove teoreme, čija se valjanost potvrđuje dokazom.
- Ova ista jednadžba se zove original jednačina iz koje se mora polaziti njegov dokaz.
Kao rezultat toga, nastala je tautologija: “ Ako jednadžba nema rješenja u pozitivnim cijelim brojevima, onda nema rješenja u pozitivnim cijelim brojevima„Dokaz tautologije je očigledno netačan i lišen svakog značenja. Ali to se dokazuje kontradikcijom.
- Napravljena je pretpostavka koja je suprotna od onoga što je navedeno u jednačini koju treba dokazati. Ne bi trebalo da bude u suprotnosti sa originalnom jednačinom, ali jeste. Nema smisla dokazivati ono što je prihvaćeno bez dokaza, a prihvatati bez dokaza ono što treba dokazati.
- Na osnovu prihvaćene pretpostavke izvode se apsolutno ispravne matematičke operacije i radnje kako bi se dokazalo da je u suprotnosti sa izvornom jednačinom i da je netačna.
Stoga je već 370 godina dokazivanje jednačine Fermatove posljednje teoreme ostalo neostvariv san za specijaliste i zaljubljenike u matematiku.
Uzeo sam jednačinu kao zaključak teoreme, a osmi Diofantov problem i njegovu jednačinu kao uslov teoreme.
„Ako je jednačina x 2 + y 2 = z 2
(1) ima beskonačan broj rješenja na skupu svih trojki Pitagorinih brojeva, tada, obrnuto, jednačina x n + y n = z n
, Gdje n > 2
(2) nema rješenja na skupu pozitivnih cijelih brojeva.”
Dokaz.
A) Svi znaju da jednačina (1) ima beskonačan broj rješenja na skupu svih trojki Pitagorinih brojeva. Dokažimo da niti jedna trojka Pitagorinih brojeva koja je rješenje jednačine (1) nije rješenje jednačine (2).
Na osnovu zakona reverzibilnosti jednakosti, mijenjamo strane jednačine (1). Pitagorini brojevi (z, x, y) mogu se tumačiti kao dužine stranica pravouglog trougla i kvadrata (x 2 , y 2 , z 2) može se tumačiti kao površina kvadrata izgrađenih na njegovoj hipotenuzi i kracima.
Pomnožimo površine kvadrata jednačine (1) proizvoljnom visinom h :
z 2 h = x 2 h + y 2 h (3)
Jednačina (3) se može tumačiti kao jednakost zapremine paralelepipeda sa zbirom zapremina dva paralelepipeda.
Neka visina tri paralelepipeda h = z :
z 3 = x 2 z + y 2 z (4)
Zapremina kocke je razložena na dva volumena dva paralelepipeda. Ostavićemo volumen kocke nepromijenjen, a visinu prvog paralelepipeda smanjiti na x i smanjiti visinu drugog paralelepipeda na y . Zapremina kocke je veća od zbira zapremina dve kocke:
z 3 > x 3 + y 3 (5)
Na skupu trojki Pitagorinih brojeva ( x, y, z ) at n=3 ne može postojati nikakvo rješenje jednačine (2). Prema tome, na skupu svih trojki Pitagorinih brojeva nemoguće je rastaviti kocku na dvije kocke.
Neka u jednačini (3) bude visina tri paralelepipeda h = z 2 :
z 2 z 2 = x 2 z 2 + y 2 z 2 (6)
Zapremina paralelepipeda se rastavlja na zbir zapremina dva paralelepipeda.
Ostavljamo lijevu stranu jednačine (6) nepromijenjenom. Na njegovoj desnoj strani visina z 2
smanjiti na X
u prvom mandatu i ranije u 2
u drugom mandatu.
Jednačina (6) se pretvorila u nejednačinu:
Zapremina paralelepipeda se rastavlja na dva volumena po dva paralelepipeda.
Ostavljamo lijevu stranu jednačine (8) nepromijenjenom.
Na desnoj strani visina zn-2
smanjiti na xn-2
u prvom mandatu i svesti na y n-2
u drugom mandatu. Jednačina (8) postaje nejednakost:
| z n > x n + y n | (9) |
Na skupu trojki Pitagorinih brojeva ne može postojati jedno rješenje jednačine (2).
Shodno tome, na skupu svih trojki Pitagorinih brojeva za sve n > 2 jednačina (2) nema rješenja.
Dobijen je "zaista čudesan dokaz", ali samo za trojke Pitagorini brojevi. Ovo je nedostatak dokaza i razlog odbijanja P. Fermata od njega.
B) Dokažimo da jednačina (2) nema rješenja na skupu trojki nepitagorinih brojeva, koji predstavlja porodicu proizvoljne trojke pitagorinih brojeva z = 13, x = 12, y = 5 i porodica proizvoljne trojke pozitivnih cijelih brojeva z = 21, x = 19, y = 16
Obe trojke brojeva su članovi njihovih porodica:
| (13, 12, 12); (13, 12,11);…; (13, 12, 5) ;…; (13,7, 1);…; (13,1, 1) | (10) | |
| (21, 20, 20); (21, 20, 19);…;(21, 19, 16);…;(21, 1, 1) | (11) |
Broj članova porodice (10) i (11) jednak je polovini umnoška 13 sa 12 i 21 sa 20, odnosno 78 i 210.
Svaki član porodice (10) sadrži z = 13 i varijable X I at 13 > x > 0 , 13 > y > 0 1
Svaki član porodice (11) sadrži z = 21 i varijable X I at , koji uzimaju cjelobrojne vrijednosti 21 > x >0 , 21 > y > 0 . Varijable se sukcesivno smanjuju za 1 .
Trojke brojeva niza (10) i (11) mogu se predstaviti kao niz nejednakosti trećeg stepena:
| 13 3 < 12 3 + 12 3 ;13 3 < 12 3 + 11 3 ;…; 13 3 < 12 3 + 8 3 ; 13 3 > 12 3 + 7 3 ;…; 13 3 > 1 3 + 1 3 | ||
| 21 3 < 20 3 + 20 3 ; 21 3 < 20 3 + 19 3 ; …; 21 3 < 19 3 + 14 3 ; 21 3 > 19 3 + 13 3 ;…; 21 3 > 1 3 + 1 3 |
i u obliku nejednakosti četvrtog stepena:
| 13 4 < 12 4 + 12 4 ;…; 13 4 < 12 4 + 10 4 ; 13 4 > 12 4 + 9 4 ;…; 13 4 > 1 4 + 1 4 | ||
| 21 4 < 20 4 + 20 4 ; 21 4 < 20 4 + 19 4 ; …; 21 4 < 19 4 + 16 4 ;…; 21 4 > 1 4 + 1 4 |
Ispravnost svake nejednakosti potvrđuje se podizanjem brojeva na treći i četvrti stepen.
Kocka većeg broja ne može se rastaviti na dvije kocke manjih brojeva. On je ili manji ili veći od zbira kubova dva manja broja.
Bikvadrat većeg broja ne može se razložiti na dva bikvadrata manjih brojeva. On je ili manji ili veći od zbira bikvadrata manjih brojeva.
Kako eksponent raste, sve nejednakosti, osim lijeve krajnje nejednakosti, imaju isto značenje:
Svi imaju isto značenje: stepen većeg broja je veći od zbira potencija manja dva broja sa istim eksponentom:
| 13 n > 12 n + 12 n ; 13 n > 12 n + 11 n ;…; 13 n > 7 n + 4 n ;…; 13 n > 1 n + 1 n | (12) | |
| 21 n > 20 n + 20 n ; 21 n > 20 n + 19 n ;…; ;…; 21 n > 1 n + 1 n | (13) |
Lijevi ekstremni član nizova (12) (13) predstavlja najslabiju nejednakost. Njegova ispravnost određuje ispravnost svih narednih nejednakosti niza (12) za n > 8 i niz (13) na n > 14 .
Među njima ne može biti jednakosti. Proizvoljna trojka pozitivnih cijelih brojeva (21,19,16) nije rješenje jednadžbe (2) Fermatove posljednje teoreme. Ako proizvoljna trojka pozitivnih cijelih brojeva nije rješenje jednadžbe, onda jednačina nema rješenja na skupu pozitivnih cijelih brojeva, što je i trebalo dokazati.
SA) Fermatov komentar Diofantovog problema kaže da je nemoguće razgraditi" generalno, nema stepena većeg od kvadrata, dva stepena sa istim eksponentom».
Poljubac stepen veći od kvadrata ne može se stvarno razložiti na dva stepena sa istim eksponentom. Bez poljupca stepen veći od kvadrata može se razložiti na dva stepena sa istim eksponentom.
Bilo koja proizvoljna trojka pozitivnih cijelih brojeva (z, x, y) može pripadati porodici čiji se svaki član sastoji od konstantnog broja z i dva broja manji z . Svaki član porodice može se predstaviti u obliku nejednakosti, a sve rezultirajuće nejednakosti mogu se predstaviti u obliku niza nejednakosti:
| z n< (z — 1) n + (z — 1) n ; z n < (z — 1) n + (z — 2) n ; …; z n >1 n + 1 n | (14) |
Niz nejednačina (14) počinje nejednačinama kod kojih je lijeva strana manja od desne, a završava se nejednačinama kod kojih je desna strana manja od lijeve. Sa povećanjem eksponenta n > 2 broj nejednačina na desnoj strani niza (14) raste. Sa eksponentom n = k sve nejednačine na lijevoj strani niza mijenjaju svoje značenje i poprimaju značenje nejednačina na desnoj strani nejednakosti niza (14). Kao rezultat povećanja eksponenta svih nejednakosti, ispada da je lijeva strana veća od desne strane:
| z k > (z-1) k + (z-1) k ; z k > (z-1) k + (z-2) k ;…; z k > 2 k + 1 k ; z k > 1 k + 1 k | (15) |
Uz daljnje povećanje eksponenta n>k nijedna od nejednakosti ne mijenja svoje značenje i ne pretvara se u jednakost. Na osnovu toga, može se tvrditi da je bilo koja proizvoljno odabrana trojka pozitivnih cijelih brojeva (z, x, y) at n > 2 , z > x , z > y
U proizvoljno odabranoj trojci pozitivnih cijelih brojeva z može biti proizvoljno veliki prirodan broj. Za sve prirodne brojeve koji nisu veći od z , Fermatova posljednja teorema je dokazana.
D) Bez obzira koliko je veliki broj z , u prirodnom nizu brojeva postoji veliki, ali konačan skup cijelih brojeva prije njega, a nakon njega postoji beskonačan skup cijelih brojeva.
Dokažimo da je cijeli beskonačan skup prirodnih brojeva velik z , formiraju trojke brojeva koji nisu rješenja jednadžbe Fermatove posljednje teoreme, na primjer, proizvoljnu trojku pozitivnih cijelih brojeva (z + 1, x ,y) , pri čemu z + 1 > x I z + 1 > y za sve vrijednosti eksponenta n > 2 nije rješenje jednačine Fermaove posljednje teoreme.
Nasumično odabrana trojka pozitivnih cijelih brojeva (z + 1, x, y) može pripadati porodici trojki brojeva, od kojih se svaki član sastoji od konstantnog broja z+1 i dva broja X I at , poprima različite vrijednosti, manji z+1 . Članovi porodice mogu biti predstavljeni u obliku nejednakosti u kojima je konstantna leva strana manja ili veća od desne strane. Nejednakosti se mogu poredati u obliku niza nejednakosti:
Uz daljnje povećanje eksponenta n>k do beskonačnosti, nijedna od nejednakosti niza (17) ne mijenja svoje značenje i ne prelazi u jednakost. U nizu (16) nejednakost je formirana od proizvoljno odabrane trojke pozitivnih cijelih brojeva (z + 1, x, y) , može se nalaziti na njegovoj desnoj strani u obrascu (z + 1) n > x n + y n ili biti na njegovoj lijevoj strani u obrascu (z+1)n< x n + y n .
U svakom slučaju, trostruka pozitivnih cijelih brojeva (z + 1, x, y) at n > 2 , z + 1 > x , z + 1 > y u nizu (16) predstavlja nejednakost i ne može predstavljati jednakost, odnosno ne može predstavljati rješenje jednadžbe posljednje Fermatove teoreme.
Lako je i jednostavno razumjeti porijeklo niza nejednakosti snaga (16), u kojem su posljednja nejednakost na lijevoj strani i prva nejednakost na desnoj strani nejednakosti suprotnog značenja. Naprotiv, školarcima, srednjoškolcima i srednjoškolcima nije lako i teško da shvate kako se od niza nejednakosti (17) formira niz nejednakosti (17), u kojem sve nejednakosti imaju isto značenje. .
U nizu (16), povećanje cjelobrojnog stepena nejednakosti za 1 jedinicu pretvara posljednju nejednakost na lijevoj strani u prvu nejednakost suprotnog smisla na desnoj strani. Dakle, broj nejednačina na lijevoj strani niza opada, a broj nejednačina na desnoj strani raste. Između posljednje i prve nejednakosti moći suprotnog značenja nužno postoji jednakost moći. Njegov stepen ne može biti ceo broj, jer samo neceli brojevi leže između dva uzastopna prirodna broja. Jednakost stepena necijelog stepena, prema uslovima teoreme, ne može se smatrati rešenjem jednačine (1).
Ako u nizu (16) nastavimo povećavati stepen za 1 jedinicu, onda će se posljednja nejednakost njegove lijeve strane pretvoriti u prvu nejednakost suprotnog značenja desne strane. Kao rezultat, neće ostati nejednakosti lijeve strane i ostat će samo nejednakosti desne strane, što će biti niz rastućih nejednakosti snaga (17). Daljnje povećanje njihove cjelobrojne snage za 1 jedinicu samo pojačava njene nejednakosti snaga i kategorički isključuje mogućnost jednakosti u cjelobrojnom stepenu.
Slijedom toga, općenito, nijedna cjelobrojna potencija prirodnog broja (z+1) niza nejednakosti stepena (17) ne može se razložiti na dva cjelobrojna stepena s istim eksponentom. Dakle, jednadžba (1) nema rješenja na beskonačnom skupu prirodnih brojeva, što je i trebalo dokazati.
Prema tome, Fermatova posljednja teorema je dokazana u cijelosti:
- u dijelu A) za sve trojke (z, x, y) Pitagorini brojevi (Fermatovo otkriće je zaista divan dokaz),
- u odjeljku B) za sve članove porodice bilo koje trojke (z, x, y) Pitagorini brojevi,
- u dijelu C) za sve trojke brojeva (z, x, y) , ne veliki brojevi z
- u dijelu D) za sve trojke brojeva (z, x, y) prirodni niz brojeva.
|
Izmjene napravljene 09.05.2010 |
Koje se teoreme mogu, a koje ne mogu dokazati kontradikcijom?
Objašnjavajući rečnik matematičkih pojmova definiše dokaz kontradikcijom teoreme, suprotno od obrnutog teorema.
„Dokaz kontradikcijom je metoda dokazivanja teoreme (propozicije), koja se sastoji u dokazivanju ne same teoreme, već njene ekvivalentne (ekvivalentne) teoreme. Dokaz kontradikcijom se koristi kad god je direktnu teoremu teško dokazati, ali je suprotnu teoremu lakše dokazati. U dokazu kontradikcijom, zaključak teoreme zamjenjuje se njenom negacijom, a rasuđivanjem se dolazi do negacije uslova, tj. na kontradikciju, na suprotno (suprotno od onoga što je dato; ovo svođenje na apsurd dokazuje teoremu."
Dokaz kontradikcijom se vrlo često koristi u matematici. Dokaz kontradikcijom zasniva se na zakonu isključene sredine, koji se sastoji u tome da je od dva iskaza (tvrdnje) A i A (negacija A) jedan tačan, a drugi netačan.”/Objašnjavajući rečnik matematičkih pojmova: Priručnik za nastavnike/O. V. Manturov [i dr.]; uređeno od V. A. Ditkina.- M.: Obrazovanje, 1965.- 539 str.: ilustr.-C.112/.
Ne bi bilo bolje otvoreno izjaviti da metoda dokazivanja kontradikcijom nije matematička metoda, iako se koristi u matematici, da je logička metoda i da pripada logici. Da li je prihvatljivo reći da se dokaz kontradikcijom „koristi kad god je direktnu teoremu teško dokazati“, a zapravo se koristi kada i samo kada nema zamjene.
Karakterizacija međusobnog odnosa direktnih i inverznih teorema takođe zaslužuje posebnu pažnju. „Obrnuta teorema za datu teoremu (ili za datu teoremu) je teorema u kojoj je uvjet zaključak, a zaključak je uvjet date teoreme. Ova teorema u odnosu na obrnutu teoremu naziva se direktna teorema (originalna). U isto vrijeme, suprotna teorema obrnutoj teoremi će biti data teorema; stoga se direktna i konverzna teorema nazivaju međusobno inverzne. Ako je direktna (data) teorema tačna, onda obrnuta teorema nije uvijek tačna. Na primjer, ako je četverokut romb, tada su njegove dijagonale međusobno okomite (direktna teorema). Ako su u četvorouglu dijagonale međusobno okomite, onda je četvorougao romb - to je netačno, tj. obrnuti teorem je netačan.”/Objašnjavajući rečnik matematičkih pojmova: Priručnik za nastavnike/O. V. Manturov [i dr.]; uređeno od V. A. Ditkina.- M.: Obrazovanje, 1965.- 539 str.: ilustr.-C.261 /.
Ova karakteristika odnosa između direktne i inverzne teoreme ne uzima u obzir činjenicu da se uslov direktne teoreme prihvata kao dat, bez dokaza, pa se ne garantuje njegova ispravnost. Uslov inverzne teoreme se ne prihvata kao dat, jer je to zaključak dokazane direktne teoreme. Njegova ispravnost je potvrđena dokazom direktne teoreme. Ova suštinska logička razlika u uslovima direktne i inverzne teoreme pokazuje se kao odlučujuća u pitanju koje se teoreme mogu, a koje ne mogu dokazati logičkom metodom kontradikcijom.
Pretpostavimo da postoji direktna teorema na umu, koja se može dokazati uobičajenom matematičkom metodom, ali je teška. Formulirajmo ga općenito i ukratko na sljedeći način: od A trebalo bi E . Simbol A ima značenje datog uslova teoreme, prihvaćenog bez dokaza. Simbol E ono što je bitno je zaključak teoreme koji treba dokazati.
Direktnu teoremu ćemo dokazati kontradikcijom, logicno metoda. Logička metoda se koristi za dokazivanje teoreme koja ima nije matematički stanje, i logicno stanje. Može se dobiti ako je matematički uslov teoreme od A trebalo bi E , dopuniti sa potpuno suprotnim uslovom od A ne radi to E .
Rezultat je bio logički kontradiktorni uslov nove teoreme, koji sadrži dva dela: od A trebalo bi E I od A ne radi to E . Rezultirajući uslov nove teoreme odgovara logičkom zakonu isključene sredine i odgovara dokazu teoreme kontradikcijom.
Prema zakonu, jedan dio kontradiktornog stanja je netačan, drugi dio je istinit, a treći je isključen. Dokaz kontradikcijom ima zadatak i svrhu da utvrdi koji je tačno deo od dva dela uslova teoreme netačan. Kada se utvrdi netačan dio uvjeta, drugi dio se utvrđuje kao pravi dio, a treći se isključuje.
Prema objašnjenju matematičkih pojmova, „dokaz je rasuđivanje tokom kojeg se utvrđuje istinitost ili netačnost bilo koje tvrdnje (presude, izjave, teoreme)“. Dokaz kontradikcijom postoji obrazloženje tokom kojeg se to utvrđuje lažnost(apsurdnost) zaključka koji proizilazi iz false uslovi teoreme koju treba dokazati.
Dato: od A trebalo bi E i od A ne radi to E .
dokazati: od A trebalo bi E .
Dokaz: Logički uslov teoreme sadrži kontradikciju koja zahteva njeno razrešenje. Kontradikcija uvjeta mora naći svoje rješenje u dokazu i njegovom rezultatu. Rezultat se ispostavi da je lažan s besprijekornim rasuđivanjem bez greške. Razlog za lažan zaključak u logički ispravnom zaključivanju može biti samo kontradiktorni uslov: od A trebalo bi E I od A ne radi to E .
Nema sumnje da je jedan dio uvjeta netačan, a drugi u ovom slučaju tačan. Oba dijela uvjeta imaju isto porijeklo, prihvataju se kao podaci, pretpostavljeni, jednako mogući, jednako dopušteni itd. U toku logičkog zaključivanja nije otkrivena niti jedna logička karakteristika koja bi razlikovala jedan dio uvjeta od drugog. . Stoga, u istoj mjeri može biti od A trebalo bi E i možda od A ne radi to E . Izjava od A trebalo bi E Možda false, zatim izjava od A ne radi to E biće istina. Izjava od A ne radi to E može biti lažna, onda izjava od A trebalo bi E biće istina.
Prema tome, nemoguće je dokazati direktnu teoremu kontradikcijom.
Sada ćemo dokazati ovu istu direktnu teoremu koristeći uobičajenu matematičku metodu.
Dato: A .
dokazati: od A trebalo bi E .
Dokaz.
1. Od A trebalo bi B
2. Od B trebalo bi IN (prema prethodno dokazanoj teoremi)).
3. Od IN trebalo bi G (prema prethodno dokazanoj teoremi).
4. Od G trebalo bi D (prema prethodno dokazanoj teoremi).
5. Od D trebalo bi E (prema prethodno dokazanoj teoremi).
Na osnovu zakona tranzitivnosti, od A trebalo bi E . Direktna teorema se dokazuje uobičajenom metodom.
Neka dokazana direktna teorema ima tačnu inverznu teoremu: od E trebalo bi A .
Dokažimo to uobičajenim matematički metoda. Dokaz obrnute teoreme može se izraziti u simboličkom obliku kao algoritam matematičkih operacija.
Dato: E
dokazati: od E trebalo bi A .
Dokaz.
1. Od E trebalo bi D
2. Od D trebalo bi G (prema prethodno dokazanoj obrnutoj teoremi).
3. Od G trebalo bi IN (prema prethodno dokazanoj obrnutoj teoremi).
4. Od IN ne radi to B (obrnuta teorema nije tačna). Zbog toga od B ne radi to A .
U ovoj situaciji, nema smisla nastaviti matematički dokaz obrnutog teorema. Razlog za situaciju je logičan. Netačna obrnuta teorema ne može se ničim zamijeniti. Stoga je nemoguće dokazati ovu obrnutu teoremu korištenjem uobičajene matematičke metode. Sva nada je dokazati ovu inverznu teoremu kontradikcijom.
Da bismo ga dokazali kontradikcijom, potrebno je njegov matematički uslov zamijeniti logičkim kontradiktornim uvjetom, koji u svom značenju sadrži dva dijela - lažan i istinit.
Obratna teorema navodi: od E ne radi to A . Njeno stanje E , iz čega slijedi zaključak A , je rezultat dokazivanja direktne teoreme korištenjem uobičajene matematičke metode. Ovaj uslov se mora sačuvati i dopuniti izjavom od E trebalo bi A . Kao rezultat sabiranja, dobijamo kontradiktorni uslov nove inverzne teoreme: od E trebalo bi A I od E ne radi to A . Na osnovu ovoga logično kontradiktorni uslov, obrnuta teorema se može dokazati pomoću ispravnog logicno samo rezonovanje, i samo, logicno metodom kontradikcije. U kontradikciji, sve matematičke radnje i operacije su podređene logičkim i stoga se ne računaju.
U prvom dijelu kontradiktorne izjave od E trebalo bi A stanje E dokazano je dokazom direktne teoreme. U drugom dijelu od E ne radi to A stanje E je pretpostavljeno i prihvaćeno bez dokaza. Jedan od njih je lažan, a drugi je istinit. Morate dokazati koja je lažna.
Dokazujemo to tačno logicno rasuđivanja i otkriti da je njegov rezultat lažan, apsurdan zaključak. Razlog lažnog logičkog zaključka je kontradiktorni logički uslov teoreme, koji se sastoji od dva dijela - lažnog i istinitog. Lažni dio može biti samo izjava od E ne radi to A , u kojem E prihvaćen bez dokaza. To je ono po čemu se razlikuje E izjave od E trebalo bi A , što je dokazano dokazom direktne teoreme.
Dakle, tačna je izjava: od E trebalo bi A , što je trebalo dokazati.
Zaključak: logičkom metodom, kontradikcijom se dokazuje samo inverzna teorema, koja ima direktnu teoremu dokazanu matematičkom metodom, a koja se ne može dokazati matematičkom metodom.
Dobijeni zaključak dobija izuzetnu važnost u odnosu na metodu dokazivanja kontradiktorno Fermatovoj velikoj teoremi. Ogromna većina pokušaja da se to dokaže ne zasniva se na uobičajenoj matematičkoj metodi, već na logičkoj metodi dokaza kontradiktornošću. Wilesov dokaz Fermatove posljednje teoreme nije izuzetak.
Dmitrij Abrarov je u članku “Fermatova teorema: fenomen Wilesovih dokaza” objavio komentar na Wilesov dokaz Fermatove posljednje teoreme. Prema Abrarovu, Wiles dokazuje posljednju Fermatovu teoremu uz pomoć izvanrednog otkrića njemačkog matematičara Gerharda Freya (r. 1944.), koji je povezao potencijalno rješenje Fermatove jednačine x n + y n = z n
, Gdje n > 2
, s drugom, potpuno drugom jednadžbom. Ova nova jednačina je data posebnom krivom (nazvanom Freyeva eliptična kriva). Freyeva kriva je data vrlo jednostavnom jednadžbom:
.
“Frey je bio taj koji je upoređivao svaku odluku (a, b, c) Fermatova jednačina, odnosno brojevi koji zadovoljavaju relaciju a n + b n = c n, gornja kriva. U ovom slučaju slijedi Fermatova posljednja teorema.”(Citat iz: Abrarov D. “Fermatova teorema: fenomen Wilesovih dokaza”)
Drugim riječima, Gerhard Frey je predložio da jednačina Fermatove posljednje teoreme x n + y n = z n
, Gdje n > 2
, ima rješenja u pozitivnim cijelim brojevima. Ova ista rješenja su, prema Freyjevoj pretpostavci, rješenja njegove jednadžbe
y 2 + x (x - a n) (y + b n) = 0
, što je dato njegovom eliptičnom krivom.
Andrew Wiles je prihvatio ovo izvanredno Freyovo otkriće i, uz njegovu pomoć, matematički metodom je dokazano da ovo otkriće, odnosno Freyeva eliptična kriva, ne postoji. Dakle, ne postoji jednačina i njena rješenja koja su data nepostojećom eliptičnom krivom, pa je Wiles trebao prihvatiti zaključak da ne postoji jednačina posljednje Fermatove teoreme i same Fermatove teoreme. Međutim, on prihvata skromniji zaključak da jednačina Fermatove posljednje teoreme nema rješenja u pozitivnim cijelim brojevima.
Nepobitna činjenica može biti da je Wiles prihvatio pretpostavku koja je po značenju upravo suprotna od onoga što navodi Fermatova velika teorema. To obavezuje Wilesa da dokaže posljednju Fermatovu teoremu kontradikcijom. Slijedimo njegov primjer i vidimo šta je iz ovog primjera.
Fermatova posljednja teorema kaže da je jednadžba x n + y n = z n , Gdje n > 2 , nema rješenja u pozitivnim cijelim brojevima.
Prema logičkoj metodi dokazivanja kontradikcijom, ova tvrdnja se zadržava, prihvata kao datu bez dokaza, a zatim se dopunjava suprotnom tvrdnjom: jednačina x n + y n = z n , Gdje n > 2 , ima rješenja u pozitivnim cijelim brojevima.
Pretpostavljena izjava se takođe prihvata kao data, bez dokaza. Obe tvrdnje, posmatrane sa stanovišta osnovnih zakona logike, podjednako su validne, podjednako validne i podjednako moguće. Ispravnim rasuđivanjem potrebno je utvrditi koji je od njih netačan da bi se onda utvrdilo da je druga tvrdnja tačna.
Ispravno rezonovanje završava lažnim, apsurdnim zaključkom, čiji logički razlog može biti samo kontradiktorni uslov teoreme koja se dokazuje, a koja sadrži dva dijela direktno suprotnog značenja. Oni su bili logičan razlog za apsurdan zaključak, rezultat dokaza kontradikcijom.
Međutim, tokom logički ispravnog zaključivanja nije otkriven niti jedan znak po kojem bi se moglo utvrditi koja je konkretna tvrdnja lažna. To može biti izjava: jednačina x n + y n = z n , Gdje n > 2 , ima rješenja u pozitivnim cijelim brojevima. Na istoj osnovi, to bi mogla biti sljedeća izjava: jednačina x n + y n = z n , Gdje n > 2 , nema rješenja u pozitivnim cijelim brojevima.
Kao rezultat obrazloženja, može biti samo jedan zaključak: Fermatova posljednja teorema ne može se dokazati kontradikcijom.
Bila bi sasvim druga stvar da je Fermatova posljednja teorema inverzna teorema, koja ima direktnu teoremu dokazanu uobičajenom matematičkom metodom. U ovom slučaju, to bi se moglo dokazati kontradikcijom. A budući da je to direktna teorema, njen dokaz ne bi trebao biti zasnovan na logičkoj metodi dokazivanja kontradikcijom, već na običnoj matematičkoj metodi.
Prema D. Abrarovu, najpoznatiji savremeni ruski matematičar, akademik V. I. Arnold, reagovao je „aktivno skeptično“ na Wilesov dokaz. Akademik je izjavio: “ovo nije prava matematika – prava matematika je geometrijska i ima jake veze sa fizikom.” (Citat iz: Abrarov D. “Fermatova teorema: fenomen Wilesovih dokaza.” Akademikova izjava izražava samu suštinu Wilesov nematematički dokaz Fermatove posljednje teoreme.
Kontradikcijom je nemoguće dokazati da jednačina Fermaove posljednje teoreme nema rješenja ili da ima rješenja. Wilesova greška nije matematička, već logična - upotreba dokaza kontradiktornom gdje njegova upotreba nema smisla i Fermatova velika teorema ne dokazuje.
Fermatova posljednja teorema ne može se dokazati čak ni uobičajenom matematičkom metodom ako daje: jednadžbu x n + y n = z n , Gdje n > 2 , nema rješenja u pozitivnim cijelim brojevima, a ako želite u njemu dokazati: jednadžbu x n + y n = z n , Gdje n > 2 , nema rješenja u pozitivnim cijelim brojevima. U ovom obliku ne postoji teorema, već tautologija lišena značenja.
Bilješka. O mom BTF dokazu se raspravljalo na jednom od foruma. Jedan od učesnika Trotila, stručnjak za teoriju brojeva, dao je sljedeću autoritativnu izjavu pod naslovom: “Kratko prepričavanje onoga što je Mirgorodski uradio.” Citiram doslovno:
« A. Dokazao je da ako z 2 = x 2 + y , To z n > x n + y n . Ovo je dobro poznata i sasvim očigledna činjenica.
IN. Uzeo je dvije trojke - pitagorejsku i nepitagorejsku i jednostavnom pretragom pokazao da je za određenu, specifičnu porodicu trojki (78 i 210 komada) BTF zadovoljan (i samo za nju).
WITH. A onda je autor izostavio činjenicu da iz < kasnije se može ispostaviti da jeste = , ne samo > . Jednostavan kontraprimjer - tranzicija n=1 V n=2 u pitagorejskoj trojci.
D. Ova tačka ne doprinosi ničemu značajnom BTF dokazu. Zaključak: BTF nije dokazan.”
Razmotriću njegov zaključak tačku po tačku.
A. Dokazuje BTF za čitav beskonačan skup trojki Pitagorinih brojeva. Dokazano geometrijskom metodom, koju, kako vjerujem, nisam ja otkrio, nego ponovo otkrio. A otkrio ga je, vjerujem, lično P. Fermat. Fermat je to možda imao na umu kada je napisao:
“Otkrio sam zaista divan dokaz za ovo, ali ova polja su preuska za to.” Ova moja pretpostavka zasniva se na činjenici da se u Diofantovom problemu, protiv kojeg je Fermat pisao na marginama knjige, govori o rješenjima Diofantove jednačine, koja su trojke Pitagorinih brojeva.
Beskonačan skup trojki Pitagorinih brojeva su rješenja Diofateove jednačine, a u Fermatovoj teoremi, naprotiv, nijedno od rješenja ne može biti rješenje jednačine Fermatove teoreme. A Fermatov zaista divan dokaz direktno je povezan s ovom činjenicom. Fermat je kasnije mogao proširiti svoju teoremu na skup svih prirodnih brojeva. Na skupu svih prirodnih brojeva, BTF ne pripada "skupu izuzetno lijepih teorema". Ovo je moja pretpostavka, koja se ne može ni dokazati ni opovrgnuti. Može se prihvatiti ili odbiti.
IN. U ovom trenutku dokazujem da su i porodica proizvoljno uzete pitagorine trojke brojeva i porodica proizvoljno uzete nepitagorine trojke BTF brojeva zadovoljene. Ovo je neophodna, ali nedovoljna i srednja karika u mom dokazu BTF-a. . Primjeri koje sam uzeo o porodici trojke pitagorinih brojeva i porodici trojke nepitagorinih brojeva imaju značenje konkretnih primjera koji pretpostavljaju i ne isključuju postojanje sličnih drugih primjera.
Trotilova izjava da sam „jednostavnom pretragom pokazao da je za određenu, specifičnu porodicu trojki (78 i 210 komada) BTF zadovoljan (i samo za njega) je neosnovana. On ne može opovrgnuti činjenicu da isto tako lako mogu uzeti druge primjere pitagorinih i nepitagorinih trojki da bih dobio specifičnu definitivnu porodicu jedne i druge trojke.
Koji god par trojki da uzmem, provjera njihove podobnosti za rješavanje problema može se izvršiti, po mom mišljenju, samo metodom „jednostavnog nabrajanja“. Ne znam ni jednu drugu metodu i nije mi potrebna. Ako se Trotilu nije svidjelo, onda je trebao predložiti drugu metodu, koju on ne radi. Bez nuđenja bilo čega zauzvrat, pogrešno je osuđivati „jednostavno preterivanje“, koje je u ovom slučaju nezamjenjivo.
WITH. Izostavio sam = između< и < на основании того, что в доказательстве БТФ рассматривается уравнение z 2 = x 2 + y (1), u kojoj je stepen n > 2 — cijeli pozitivan broj. Iz jednakosti između nejednakosti slijedi obavezno razmatranje jednadžbe (1) za vrijednost stepena koji nije cijeli broj n > 2 . Trotil, odbrojavam obavezna razmatranje jednakosti između nejednakosti zapravo razmatra neophodno u BTF dokazu, razmatranje jednačine (1) sa nije cela vrijednost stepena n > 2 . Uradio sam ovo za sebe i našao tu jednačinu (1) sa nije cela vrijednost stepena n > 2 ima rješenje tri broja: z, (z-1), (z-1) za eksponent koji nije cijeli.
U 17. veku, advokat i honorarni matematičar Pjer Ferma živeo je u Francuskoj, koji je posvetio duge sate dokolice svom hobiju. Jedne zimske večeri, sjedeći kraj kamina, iznio je jednu vrlo radoznalu tvrdnju iz oblasti teorije brojeva - to je kasnije nazvana Fermatova velika teorema. Možda uzbuđenje ne bi bilo toliko značajno u matematičkim krugovima da se nije dogodio jedan događaj. Matematičar je često provodio večeri proučavajući svoju omiljenu knjigu „Aritmetika“ Diofanta Aleksandrijskog (3. vek), dok je na njene margine zapisivao važne misli - ovu retkost je njegov sin brižljivo čuvao za potomstvo. Dakle, na širokim marginama ove knjige, Fermatova ruka ostavila je sljedeći natpis: “Imam prilično upečatljiv dokaz, ali je prevelik da bi se stavio na margine.” Upravo je ovaj snimak izazvao zapanjujuće uzbuđenje oko teoreme. Matematičari nisu sumnjali da je veliki naučnik izjavio da je dokazao sopstvenu teoremu. Vjerovatno postavljate pitanje: „Da li je on to zaista dokazao, ili je to bila banalna laž, ili možda postoje druge verzije zašto je ova bilješka, koja matematičarima narednih generacija nije omogućila da mirno spavaju, završila na marginama knjiga?"
Suština Velike teoreme
Fermatova prilično poznata teorema je jednostavna u svojoj suštini i leži u činjenici da, pod uslovom da je n veći od dva, pozitivan broj, jednadžba X n + Y n = Z n neće imati rješenja nultog tipa unutar okvira prirodnih brojeva. Ova naizgled jednostavna formula maskirala je nevjerovatnu složenost, a za njen dokaz se borilo tri stoljeća. Postoji jedna čudna stvar - teorema je kasno rodila, pošto se njen specijalni slučaj sa n = 2 pojavio prije 2200 godina - ovo je ništa manje poznata Pitagorina teorema.
Treba napomenuti da je priča o Fermatovoj dobro poznatoj teoremi vrlo poučna i zabavna, i to ne samo za matematičare. Ono što je najzanimljivije jeste da nauka za naučnika nije bila posao, već običan hobi, što je farmeru zauzvrat pričinjalo veliko zadovoljstvo. Takođe je stalno bio u kontaktu sa matematičarem, a takođe i prijateljem, i delio ideje, ali začudo, nije težio objavljivanju sopstvenih radova.
Radovi matematičara Farmera
Što se tiče samih Farmerovih djela, ona su otkrivena upravo u obliku običnih slova. Na nekim mjestima nedostajale su cijele stranice, a sačuvani su samo fragmenti prepiske. Zanimljivija je činjenica da su naučnici tri vijeka tragali za teoremom koja je otkrivena u Farmerovim radovima.
Ali bez obzira ko se usudio da to dokaže, pokušaji su svedeni na "nulu". Čuveni matematičar Descartes je čak optužio naučnika da se hvali, ali sve se svelo samo na najobičniju zavist. Osim što ga je stvorio, Farmer je dokazao i vlastitu teoremu. Istina, rješenje je pronađeno za slučaj gdje je n=4. Što se tiče slučaja za n=3, otkrio ga je matematičar Euler.
Kako su pokušali dokazati Farmerovu teoremu
Na samom početku 19. veka ova teorema je nastavila da postoji. Matematičari su pronašli mnoge dokaze teorema koji su bili ograničeni na prirodne brojeve unutar dvije stotine.
A 1909. godine na kocku je stavljena prilično velika suma, jednaka sto hiljada maraka njemačkog porijekla - i sve to samo da bi se riješilo pitanje vezano za ovu teoremu. Sam nagradni fond je ostavio bogati zaljubljenik u matematiku, Paul Wolfskehl, porijeklom iz Njemačke; inače, on je bio taj koji je želio da se "ubije", ali je zahvaljujući takvoj uključenosti u Fermerovu teoremu želio živjeti. Uzbuđenje koje je rezultiralo izazvalo je gomilu „dokaza“ koji su punili njemačke univerzitete, a među matematičarima se rodio nadimak „farmist“, koji je napola prezrivo korišten da opiše svakog ambicioznog početnika koji nije bio u stanju pružiti jasne dokaze.
Pretpostavka japanskog matematičara Yutake Taniyame
Pomaci u istoriji Velike teoreme nisu primećeni sve do sredine 20. veka, ali se desio jedan zanimljiv događaj. Godine 1955. japanski matematičar Yutaka Taniyama, koji je imao 28 godina, pokazao je svijetu izjavu iz potpuno drugačijeg matematičkog područja - njegova hipoteza, za razliku od Fermatove, bila je ispred svog vremena. Kaže: "Svaka eliptična kriva odgovara određenom modularnom obliku." Čini se apsurdnim za svakog matematičara, poput ideje da se drvo sastoji od određenog metala! Paradoksalna hipoteza, kao i većina drugih zapanjujućih i genijalnih otkrića, nije prihvaćena, jer jednostavno još nisu dorasli do nje. I Yutaka Taniyama je izvršio samoubistvo tri godine kasnije - neobjašnjiv čin, ali je vjerovatno čast za istinskog samuraja genija bila iznad svega.
Hipoteza se nije pamtila čitavu deceniju, ali je sedamdesetih došla do vrhunca popularnosti - potvrdili su je svi koji su je mogli razumjeti, ali je, kao i Fermatova teorema, ostala nedokazana.
Kako su Taniyamina pretpostavka i Fermatova teorema povezani?
15 godina kasnije dogodio se ključni događaj u matematici, koji je ujedinio hipotezu čuvenog Japanca i Fermatovu teoremu. Gerhard Grey je izjavio da kada se dokaže Taniyamina pretpostavka, tada će postojati dokaz Fermatove teoreme. Odnosno, ovo drugo je posljedica Tanijamine pretpostavke, a za godinu i po dana Fermatov teorem je dokazao profesor Kalifornijskog univerziteta Kenneth Ribet.
Kako je vrijeme prolazilo, regresiju je zamijenio napredak, a nauka je brzo napredovala, posebno u oblasti kompjuterske tehnologije. Tako je vrijednost n počela sve više rasti.

Na samom kraju 20. vijeka najmoćniji kompjuteri su bili smješteni u vojnim laboratorijama, programiranjem je izvođeno rješenje dobro poznatog Fermatovog problema. Kao posljedica svih pokušaja, otkriveno je da je ova teorema tačna za mnoge vrijednosti n, x, y. Ali, nažalost, to nije postao konačan dokaz, jer nije bilo nikakvih specifičnosti kao takvih.
John Wiles je dokazao Fermatovu veliku teoremu
I konačno, tek krajem 1994. matematičar iz Engleske, John Wiles, pronašao je i demonstrirao tačan dokaz kontroverzne Fermerove teoreme. Zatim su, nakon mnogih modifikacija, rasprave o ovom pitanju došle do svog logičnog završetka.
Pobijanje je objavljeno na više od sto stranica jednog časopisa! Štaviše, teorema je dokazana korištenjem modernijeg aparata više matematike. I ono što je iznenađujuće je da u vrijeme kada je Farmer pisao svoje djelo, takav uređaj nije postojao u prirodi. Jednom riječju, čovjek je bio prepoznat kao genije u ovoj oblasti, s čime se niko nije mogao raspravljati. Uprkos svemu što se dogodilo, danas možemo biti sigurni da je iznesena teorema velikog naučnika Farmera opravdana i dokazana, a nijedan matematičar zdravog razuma neće pokrenuti raspravu o ovoj temi, s kojom se slažu čak i najokorjeliji skeptici čitavog čovječanstva. sa.
Puno ime čovjeka po kome je teorema predstavljena zvalo se Pierre de Fermer. Dao je doprinos u raznim oblastima matematike. Ali, nažalost, većina njegovih radova objavljena je tek nakon njegove smrti.
FERMA VELIKA TEOREMA - izjava Pierrea Fermata (francuskog pravnika i honorarnog matematičara) da Diofantova jednačina X n + Y n = Z n, sa eksponentom n>2, gdje je n = cijeli broj, nema rješenja u pozitivnim cijelim brojevima. Autorski tekst: “Nemoguće je rastaviti kocku na dvije kocke, ili bikvadrat na dva bikvadrata, ili općenito stepen veći od dva na dva stepena s istim eksponentom.”
"Fermat i njegova teorema", Amadeo Modigliani, 1920
Pjer je došao do ove teoreme 29. marta 1636. godine. I nekih 29 godina kasnije umro je. Ali tu je sve počelo. Na kraju krajeva, bogati njemački zaljubljenik u matematiku po imenu Wolfskehl zavještao je sto hiljada maraka onome koji bi pružio potpuni dokaz Fermatove teoreme! Ali uzbuđenje oko teoreme bilo je povezano ne samo s tim, već i sa profesionalnom matematičkom strašću. Sam Fermat je nagovijestio matematičku zajednicu da je znao dokaz – neposredno prije svoje smrti, 1665. godine, ostavio je sljedeću bilješku na marginama knjige Diofant Aleksandrijski Aritmetika: „Imam vrlo upečatljiv dokaz, ali on je prevelik za postaviti na polja."
Upravo je ovaj nagoveštaj (plus, naravno, novčani bonus) naterao matematičare da svoje najbolje godine provedu bezuspešno tražeći dokaz (prema američkim naučnicima, samo profesionalni matematičari su na to potrošili ukupno 543 godine).
U nekom trenutku (1901. godine), rad na Fermatovoj teoremi stekao je sumnjivu reputaciju „rada sličnog potrazi za vječnim motorom“ (pojavio se čak i pogrdni izraz – „fermatisti“). I iznenada, 23. juna 1993. godine, na matematičkoj konferenciji o teoriji brojeva u Kembridžu, engleski profesor matematike sa Univerziteta Princeton (New Jersey, SAD), Andrew Wiles, je objavio da je Fermat to konačno dokazao!
Dokaz, međutim, nije bio samo složen, već i očigledno pogrešan, kako su Wilesa istakle njegove kolege. Ali profesor Wiles je čitavog života sanjao o dokazivanju teoreme, pa nije iznenađujuće što je u maju 1994. predstavio novu, revidiranu verziju dokaza naučnoj zajednici. U njemu nije bilo harmonije ni ljepote, a i dalje je bilo vrlo složeno - činjenica da su matematičari proveli cijelu godinu (!) analizirajući ovaj dokaz kako bi shvatili da li je pogrešan govori sama za sebe!
Ali na kraju se pokazalo da je Wilesov dokaz tačan. Ali matematičari nisu oprostili Pierreu Fermau sam njegov nagovještaj u "Aritmetici", i, zapravo, počeli su ga smatrati lažovom. Zapravo, prva osoba koja je dovela u pitanje Fermatov moralni integritet bio je lično Andrew Wiles, koji je primijetio da "Fermat nije mogao imati takve dokaze. Ovo je dokaz iz dvadesetog vijeka." Tada se, među ostalim naučnicima, učvrstilo mišljenje da Fermat “ne može dokazati svoju teoremu na drugačiji način, a Fermat je nije mogao dokazati na način na koji je Wiles iz objektivnih razloga shvatio”.
Zapravo, Fermat bi to, naravno, mogao dokazati, a malo kasnije će ovaj dokaz ponovo kreirati analitičari Nove analitičke enciklopedije. Ali koji su to “objektivni razlozi”?
Postoji zapravo samo jedan takav razlog: u onim godinama kada je Fermat živeo, Taniyamina pretpostavka, na kojoj je Andrew Wiles zasnivao svoj dokaz, nije mogla da se pojavi, jer su modularne funkcije sa kojima Taniyamina pretpostavka operiše otkrivene tek krajem 19. veka.
Kako je sam Wiles dokazao teoremu? Pitanje nije prazno - važno je za razumijevanje kako bi sam Fermat mogao dokazati svoju teoremu. Wiles je svoj dokaz zasnovao na dokazu Taniyama pretpostavke, koju je 1955. iznio 28-godišnji japanski matematičar Yutaka Taniyama.
Hipoteza zvuči ovako: "svaka eliptična kriva odgovara određenom modularnom obliku." Odavno poznate eliptične krive imaju dvodimenzionalni oblik (nalaze se na ravni), dok modularne funkcije imaju četverodimenzionalni oblik. Odnosno, Taniyamina hipoteza kombinirala je potpuno različite koncepte - jednostavne ravne krivulje i nezamislive četverodimenzionalne oblike. Sama činjenica kombinovanja figura različitih dimenzija u hipotezi naučnicima se činila apsurdnom, zbog čega joj 1955. godine nije pridavan nikakav značaj.
Međutim, u jesen 1984. godine, „Tanijamina pretpostavka“ se iznenada ponovo prisjetila, i ne samo zapamćena, već je njen mogući dokaz povezan s dokazom Fermatove teoreme! To je uradio matematičar iz Saarbrikena Gerhard Frej, koji je obavestio naučnu zajednicu da „ako neko uspe da dokaže Tanijaminu pretpostavku, onda će biti dokazana i Fermatova poslednja teorema“.
Šta je Frey uradio? Transformirao je Fermatovu jednačinu u kubičnu, a zatim je primijetio da eliptična kriva dobivena korištenjem Fermatove jednadžbe transformirane u kubnu ne može biti modularna. Međutim, Tanijamina pretpostavka kaže da svaka eliptična kriva može biti modularna! U skladu s tim, eliptična kriva konstruirana iz Fermatove jednadžbe ne može postojati, što znači da ne može postojati cjelovita rješenja i Fermatov teorem, što znači da je istinit. Pa, 1993. godine, Andrew Wiles je jednostavno dokazao Taniyaminu pretpostavku, a time i Fermatov teorem.
Međutim, Fermatova teorema se može dokazati mnogo jednostavnije, na osnovu iste multidimenzionalnosti na kojoj su operirali i Taniyama i Frey.
Za početak, obratimo pažnju na uslov koji je naveo sam Pierre Fermat - n>2. Zašto je ovo stanje bilo potrebno? Da, samo zbog činjenice da sa n=2 poseban slučaj Fermatove teoreme postaje uobičajena Pitagorina teorema X 2 +Y 2 =Z 2, koja ima beskonačan broj cjelobrojnih rješenja - 3,4,5; 5,12,13; 7,24,25; 8,15,17; 12,16,20; 51,140,149 i tako dalje. Dakle, Pitagorina teorema je izuzetak od Fermaove teoreme.
Ali zašto se takav izuzetak javlja u slučaju n=2? Sve dolazi na svoje mjesto ako vidite odnos između stepena (n=2) i dimenzije same figure. Pitagorin trougao je dvodimenzionalna figura. Nije iznenađujuće da se Z (odnosno hipotenuza) može izraziti u terminima kateta (X i Y), koji mogu biti cijeli brojevi. Veličina ugla (90) omogućava da se hipotenuza smatra vektorom, a krakovi su vektori koji se nalaze na osi i dolaze iz početka. Prema tome, moguće je izraziti dvodimenzionalni vektor koji ne leži ni na jednoj osi u terminima vektora koji leže na njima.
Sada, ako pređemo na treću dimenziju, dakle na n=3, da bismo izrazili trodimenzionalni vektor, neće biti dovoljno informacija o dva vektora, pa će biti moguće izraziti Z u Fermatovoj jednadžbi kroz najmanje tri člana (tri vektora koji leže, respektivno, na tri ose koordinatnog sistema).
Ako je n=4, onda bi trebalo biti 4 člana, ako je n=5, onda bi trebalo biti 5 članova i tako dalje. U ovom slučaju će biti više nego dovoljno cjelovitih rješenja. Na primjer, 3 3 +4 3 +5 3 =6 3 i tako dalje (možete sami odabrati druge primjere za n=3, n=4 i tako dalje).
Šta iz svega toga slijedi? Iz ovoga proizilazi da Fermatova teorema zaista nema cjelobrojna rješenja za n>2 - ali samo zato što je sama jednadžba netačna! S istim uspjehom, mogao bi se pokušati izraziti volumen paralelepipeda u smislu dužina njegovih dvaju ivica - naravno, to je nemoguće (cijela rješenja nikada neće biti pronađena), ali samo zato da se pronađe volumen paralelepipeda morate znati dužine sve tri njegove ivice.
Kada su poznatog matematičara Dejvida Gilberta upitali šta je sada najvažniji problem nauke, on je odgovorio „uhvatiti muvu na suprotnoj strani meseca“. Na razumno pitanje "kome ovo treba?" odgovorio je: "Ovo nikome ne treba. Ali razmislite koliko je važnih, složenih problema potrebno riješiti da bi se ovo implementiralo."
Drugim riječima, Fermat je (prije svega pravnik!) odsvirao duhovitu pravnu šalu na cijeli matematički svijet, na osnovu netačne formulacije problema. On je, naime, predložio da matematičari pronađu odgovor zašto muva s druge strane Mjeseca ne može živjeti, a na marginama „Aritmetike“ želio je napisati samo da na Mjesecu jednostavno nema zraka, tj. Ne može postojati cjelovita rješenja njegove teoreme za n>2 samo zato što svaka vrijednost n mora odgovarati određenom broju članova na lijevoj strani njegove jednačine.
Ali je li to bila samo šala? Ne sve. Fermatov genij leži upravo u činjenici da je on zapravo prvi uvidio odnos između stepena i dimenzije matematičke figure – odnosno, što je apsolutno ekvivalentno broju članova na lijevoj strani jednačine. Smisao njegove čuvene teoreme je bio ne samo da gurne matematički svijet na ideju ovog odnosa, već i da pokrene dokaz postojanja ovog odnosa - intuitivno razumljivog, ali još uvijek matematički potkrijepljenog.
Fermat je, kao niko drugi, shvatio da je uspostavljanje odnosa između naizgled različitih objekata izuzetno plodonosno ne samo u matematici, već iu svakoj nauci. Ovaj odnos ukazuje na neki duboki princip koji leži u osnovi oba objekta i koji omogućava njihovo dublje razumijevanje.
Na primjer, fizičari su u početku gledali na elektricitet i magnetizam kao na potpuno nepovezane fenomene, ali su u 19. stoljeću teoretičari i eksperimentatori shvatili da su elektricitet i magnetizam usko povezani. Kao rezultat toga, postignuto je bolje razumijevanje i elektriciteta i magnetizma. Električne struje proizvode magnetna polja, a magneti mogu inducirati električnu energiju u provodnicima blizu magneta. To je dovelo do izuma dinamo i električnih motora. Na kraju je otkriveno da je svjetlost rezultat koordinisanih harmonijskih oscilacija magnetskog i električnog polja.
Matematika Fermatovog vremena sastojala se od ostrva znanja u moru neznanja. Na jednom ostrvu živeli su geometri koji su proučavali oblike, na drugom ostrvu matematičari teorije verovatnoće proučavali su rizike i slučajnost. Jezik geometrije bio je veoma različit od jezika teorije verovatnoće, a algebarska terminologija bila je strana onima koji su govorili samo o statistici. Nažalost, matematika našeg vremena se sastoji od približno istih ostrva.
Fermat je prvi shvatio da su sva ova ostrva međusobno povezana. I njegova poznata teorema - Fermatova posljednja teorema - odlična je potvrda toga.