Binomna distribucija: definicija, formula, primjeri. Binomna distribucija. Diskretne distribucije u EXCEL-u Binomna distribucija njeni ograničavajući oblici
Razmotrimo implementaciju Bernoullijeve šeme, tj. Izvodi se niz ponovljenih nezavisnih testova, u svakom od kojih dati događaj A ima istu vjerovatnoću, nezavisno od broja testa. A za svaki test postoje samo dva ishoda:
1) događaj A - uspeh;
2) događaj - neuspjeh,
sa konstantnim verovatnoćama
Hajde da uvedemo u razmatranje diskretnu slučajnu varijablu X - „broj pojavljivanja događaja A u P testovi" i pronađite zakon raspodjele ove slučajne varijable. Vrijednost X može imati sljedeće vrijednosti:
Vjerovatnoća 
da će slučajna varijabla X uzeti vrijednost x k pronađeno po Bernoullijevoj formuli
Zakon distribucije diskretne slučajne varijable, definisan Bernulijevom formulom (1), se zove zakon binomne distribucije. Trajno P I R (q=1-p), uključeni u formulu (1) se pozivaju parametri binomne distribucije.
Naziv „binomna distribucija“ nastao je zbog činjenice da je desna strana u jednakosti (1) opći pojam ekspanzije Newtonovog binoma, tj.
(2)
I od tada p+q=1, tada je desna strana jednakosti (2) jednaka 1
To znači da
(4)
U jednakosti (3) prvi član qn na desnoj strani znači vjerovatnoća da u P testovima, događaj A se neće pojaviti ni jednom, drugi termin 
vjerovatnoća da će se događaj A pojaviti jednom, treći član je vjerovatnoća da će se događaj A pojaviti dvaput, i na kraju posljednji član r p- vjerovatnoća da će se događaj A dogoditi tačno P jednom.
Binomni zakon distribucije diskretne slučajne varijable predstavljen je u obliku tabele:
| X | 0 | 1 | … | k | … | n |
| R | qn | … | 
|
… | r p |
Basic numeričke karakteristike binomna distribucija:
1) očekivanu vrijednost 
(5)
2) disperzija 
(6)
3) standardna devijacija 
(7)
4) najvjerovatniji broj pojavljivanja događaja k 0- ovo je broj koji za dati P odgovara maksimalnoj binomskoj vjerovatnoći
Za dato P I R ovaj broj je određen nejednačinama
(8)
ako broj pr+r onda nije cela k 0 jednako cijelom dijelu ovog broja, ako pr+r je onda cijeli broj k 0 ima dva značenja
Binomni zakon raspodjele vjerovatnoće koristi se u teoriji pucanja, u teoriji i praksi statističke kontrole kvaliteta proizvoda, u teoriji čekanja, u teoriji pouzdanosti itd. Ovaj zakon se može primijeniti u svim slučajevima gdje postoji niz nezavisnih testova.
Primjer 1: Testiranjem kvaliteta utvrđeno je da od svakih 100 uređaja 90 u prosjeku nema kvarova. Napravi binomni zakon distribucije vjerovatnoće broja nasumično kupljenih visokokvalitetnih uređaja 4.
Rješenje: Događaj A, čija se pojava provjerava, je “visokokvalitetni uređaj kupljen nasumično”. Prema uslovima problema, glavni parametri binomske distribucije su:
Slučajna varijabla X je broj visokokvalitetnih uređaja od 4 uzeta, što znači vrijednosti X - Hajde da pronađemo vjerovatnoće vrijednosti X koristeći formulu (1):
Dakle, zakon raspodjele vrijednosti X je broj visokokvalitetnih uređaja od 4 uzeta:
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Da bismo provjerili ispravnost konstrukcije distribucije, provjerimo koliko je jednak zbir vjerovatnoća
odgovor: Zakon o raspodjeli
| X | 0 | 1 | 2 | 3 | 4 |
| R | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Primjer 2: Korištena metoda liječenja dovodi do oporavka u 95% slučajeva. Pet pacijenata je koristilo ovu metodu. Pronađite najvjerovatniji broj oporavljenih osoba, kao i numeričke karakteristike slučajne varijable X - broj oporavljenih od 5 pacijenata koji su koristili ovu metodu.
Naravno, prilikom izračunavanja funkcije kumulativne distribucije treba koristiti spomenutu vezu između binomne i beta distribucije. Ova metoda je očigledno bolja od direktnog zbrajanja kada je n > 10.
U klasičnim udžbenicima iz statistike, za dobivanje vrijednosti binomne distribucije, često se preporučuje korištenje formula zasnovanih na graničnim teoremama (kao što je Moivre-Laplaceova formula). Treba napomenuti da sa čisto računske tačke gledišta vrijednost ovih teorema je blizu nule, posebno sada, kada skoro svaki stol ima moćan kompjuter. Glavni nedostatak gornjih aproksimacija je njihova potpuno nedovoljna tačnost za vrijednosti n karakteristične za većinu aplikacija. Ništa manji nedostatak je i nedostatak bilo kakvih jasnih preporuka o primjenjivosti ove ili one aproksimacije (standardni tekstovi daju samo asimptotske formulacije; nisu praćeni procjenama tačnosti i stoga su od male koristi). Rekao bih da su obje formule prikladne samo za n< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Ovdje ne razmatram problem nalaženja kvantila: za diskretne distribucije to je trivijalno, au onim problemima gdje se takve distribucije javljaju, po pravilu nije relevantno. Ako su kvantili i dalje potrebni, preporučujem da se problem preformuliše na takav način da radi sa p-vrijednostima (uočene značajnosti). Evo primjera: pri implementaciji nekih iscrpnih algoritama pretraživanja, u svakom koraku potrebno je testirati statističku hipotezu o binomnoj slučajnoj varijabli. Prema klasični pristup U svakom koraku morate izračunati statistiku kriterija i uporediti njegovu vrijednost sa granicom kritičnog skupa. Kako je, međutim, algoritam iscrpan, potrebno je svaki put iznova odrediti granicu kritičnog skupa (na kraju krajeva, veličina uzorka se mijenja iz koraka u korak), što neproduktivno povećava vremenske troškove. Moderan pristup preporučuje izračunavanje uočene važnosti i upoređivanje sa vjerovatnoćom pouzdanosti, štedeći na traženju kvantila.
Stoga u kodovima ispod nema izračunavanja inverzne funkcije, već je data funkcija rev_binomialDF, koja izračunava vjerovatnoću p uspjeha u pojedinačnom pokušaju s obzirom na zadani broj pokušaja n, broj m uspjeha u njima i vrijednost y vjerovatnoće za postizanje ovih m uspjeha. Ovo koristi gore spomenutu vezu između binomne i beta distribucije.
Zapravo, ova funkcija vam omogućava da dobijete granice intervala povjerenja. Zaista, pretpostavimo da u n binomnih pokušaja imamo m uspjeha. Kao što je poznato, lijeva granica dvostranog intervala povjerenja za parametar p sa nivoom povjerenja jednaka je 0 ako je m = 0, a za je rješenje jednadžbe 
. Slično, desna granica je 1 ako je m = n, a za je rješenje jednadžbe 
. Iz toga slijedi da da bismo pronašli lijevu granicu moramo riješiti relativnu jednačinu 
, a da pronađemo pravu – jednačinu 
. Oni se rješavaju u funkcijama binom_leftCI i binom_rightCI, koje vraćaju gornju i donju granicu dvostranog intervala povjerenja, respektivno.
Želio bih napomenuti da ako vam nije potrebna apsolutno nevjerojatna tačnost, onda za dovoljno veliko n možete koristiti sljedeću aproksimaciju [B.L. van der Waerden, Matematička statistika. M: IL, 1960, gl. 2, odjeljak 7]: 
, gdje je g kvantil normalne distribucije. Vrijednost ove aproksimacije je u tome što postoje vrlo jednostavne aproksimacije koje vam omogućavaju da izračunate kvantile normalne distribucije (pogledajte tekst o izračunavanju normalne distribucije i odgovarajući dio ovog priručnika). U mojoj praksi (uglavnom sa n > 100) ova aproksimacija je davala otprilike 3-4 cifre, što je po pravilu sasvim dovoljno.
Da biste izračunali koristeći sljedeće kodove, trebat će vam datoteke betaDF.h, betaDF.cpp (pogledajte odjeljak o beta distribuciji), kao i logGamma.h, logGamma.cpp (pogledajte Dodatak A). Također možete vidjeti primjer korištenja funkcija.
Datoteka binomialDF.h
| #ifndef __BINOMIAL_H__ #include "betaDF.h" dvostruki binomni DF (dvostruki pokušaji, dvostruki uspjesi, dvostruki p); /* * Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom. * Izračunajte vjerovatnoću B(uspjesi|pokusi,p) da se broj * uspjeha nalazi između 0 i "uspjeha" (uključivo). */ double rev_binomialDF(dvostruki pokušaji, dvostruki uspjesi, dvostruki y); /* * Neka je poznata vjerovatnoća y za najmanje m uspjeha * u pokušajima testiranja Bernoullijeve šeme. Funkcija pronalazi vjerovatnoću p* uspjeha u pojedinačnom pokušaju. * * U proračunima se koristi sljedeća relacija * * 1 - p = rev_Beta(pokušaji-uspjesi| uspjesi+1, y). */ double binom_leftCI(dvostruki pokušaji, dvostruki uspjesi, dvostruki nivo); /* Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom * i brojem uspjeha jednakim "uspjehu". * Lijeva granica dvostranog intervala povjerenja izračunava se * sa nivoom značaja. */ double binom_rightCI(dvostruki n, dvostruki uspjesi, dvostruki nivo); /* Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom * i brojem uspjeha jednakim "uspjehu". * Desna granica dvostranog intervala pouzdanosti izračunava se * sa nivoom značaja. */ #endif /* Završava #ifndef __BINOMIAL_H__ */ |
Datoteka binomialDF.cpp
| /************************************************** * *******/ /* Binomna distribucija */ /*********************************** * **************************/ #include |
Binomna distribucija je jedna od najvažnijih distribucija vjerovatnoće diskretno promjenjive slučajne varijable. Binomna distribucija je raspodjela vjerovatnoće broja m pojava događaja A V n međusobno nezavisna zapažanja. Često događaj A se naziva "uspjeh" zapažanja, a suprotan događaj se naziva "neuspjeh", ali ova oznaka je vrlo uslovna.
Binomni uslovi distribucije:
- ukupno sprovedeno n suđenja u kojima je događaj A može se dogoditi ili ne mora;
- događaj A u svakom ispitivanju može se dogoditi sa istom vjerovatnoćom str;
- testovi su međusobno nezavisni.
Verovatnoća da u n događaj testiranja A doći će tačno m puta, može se izračunati korištenjem Bernoullijeve formule:
Gdje str- vjerovatnoća da će se događaj dogoditi A;
q = 1 - str- vjerovatnoća da se dogodi suprotan događaj.
Hajde da to shvatimo zašto je binomna distribucija povezana s Bernoullijevom formulom na gore opisan način? . Događaj - broj uspjeha na n testovi su podijeljeni u više opcija, u svakoj od kojih se postiže uspjeh m testovi, a neuspjeh - u n - m testovi. Hajde da razmotrimo jednu od ovih opcija - B1 . Koristeći pravilo za sabiranje vjerovatnoća, množimo vjerovatnoće suprotnih događaja:
,
i ako označimo q = 1 - str, To
.
Bilo koja druga opcija u kojoj m uspjeh i n - m neuspjesi. Broj takvih opcija jednak je broju načina na koje se može n test get m uspjeh.
Zbir svih vjerovatnoća m brojevi pojavljivanja događaja A(brojevi od 0 do n) je jednako jedan:
gdje svaki član predstavlja pojam u Newtonovom binomu. Stoga se distribucija koja se razmatra naziva binomna distribucija.
U praksi je često potrebno izračunati vjerovatnoće „ne više od m uspjeh u n testovi" ili "barem m uspjeh u n testovi". Za to se koriste sljedeće formule.
Integralna funkcija, tj vjerovatnoća F(m) šta je unutra n posmatrački događaj A više neće doći m jednom, može se izračunati pomoću formule:
Zauzvrat vjerovatnoća F(≥m) šta je unutra n posmatrački događaj A neće doći ništa manje m jednom, izračunava se po formuli:
Ponekad je zgodnije izračunati vjerovatnoću da n posmatrački događaj A više neće doći m puta, kroz vjerovatnoću suprotnog događaja:
.
Koju formulu koristiti ovisi o tome koja od njih ima zbir koji sadrži manje članova.
Karakteristike binomne distribucije se izračunavaju korištenjem sljedećih formula .
Očekivana vrijednost: .
Disperzija: .
Standardna devijacija: .
Binomna distribucija i proračuni u MS Excel-u
Binomna vjerovatnoća P n ( m) i vrijednosti integralne funkcije F(m) može se izračunati pomoću MS Excel funkcije BINOM.DIST. Prozor za odgovarajući proračun je prikazan ispod (lijevi klik za povećanje).
MS Excel zahtijeva da unesete sljedeće podatke:
- broj uspjeha;
- broj testova;
- vjerovatnoća uspjeha;
- integral - logička vrijednost: 0 - ako treba izračunati vjerovatnoću P n ( m) i 1 - ako je vjerovatnoća F(m).
Primjer 1. Direktor kompanije sumirao je informacije o broju prodatih kamera u posljednjih 100 dana. Tabela sažima informacije i izračunava vjerovatnoće da će određeni broj kamera biti prodat dnevno.
Dan završava profitom ako se proda 13 ili više kamera. Verovatnoća da će dan biti odrađen profitabilno:
Verovatnoća da će se dan raditi bez profita:
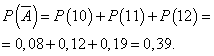
Neka je vjerovatnoća da se dan radi sa profitom konstantna i jednaka 0,61, a broj prodanih kamera dnevno ne zavisi od dana. Tada možemo koristiti binomnu distribuciju, gdje je događaj A- dan će se raditi sa profitom, - bez dobiti.
Verovatnoća da će svih 6 dana biti odrađeno sa profitom:
.
Isti rezultat dobijamo koristeći MS Excel funkciju BINOM.DIST (vrijednost integralne vrijednosti je 0):
P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.
Verovatnoća da će od 6 dana 4 ili više dana biti odrađeno sa profitom:
Gdje 
,
,
Koristeći MS Excel funkciju BINOM.DIST, izračunavamo vjerovatnoću da od 6 dana ne više od 3 dana bude završeno sa profitom (vrijednost integralne vrijednosti je 1):
P 6 (≤3 ) = BINOM.DIST(3; 6; 0,61; 1) = 0,435.
Verovatnoća da će svih 6 dana biti razrađeno sa gubicima:
,
Isti indikator možemo izračunati koristeći MS Excel funkciju BINOM.DIST:
P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.
Riješite problem sami, a zatim pogledajte rješenje
Primjer 2. U urni se nalaze 2 bijele i 3 crne kuglice. Iz urne se vadi kugla, postavlja se boja i vraća nazad. Pokušaj se ponavlja 5 puta. Broj pojavljivanja bijelih kuglica je diskretan slučajna vrijednost X, distribuiran prema binomskom zakonu. Nacrtajte zakon raspodjele slučajne varijable. Definirajte modus, matematičko očekivanje i disperziju.
Nastavimo zajedno rješavati probleme
Primjer 3. Iz kurirske službe smo otišli na lokacije n= 5 kurira. Svaki kurir je vjerovatno str= 0,3, bez obzira na druge, kasni za objekat. Diskretna slučajna varijabla X- broj kasnih kurira. Konstruirajte seriju distribucije za ovu slučajnu varijablu. Pronađite njegovo matematičko očekivanje, varijansu, standardnu devijaciju. Pronađite vjerovatnoću da će najmanje dva kurira zakasniti na objekte.
Poglavlje 7.
Specifični zakoni distribucije slučajnih varijabli
Vrste zakona raspodjele diskretnih slučajnih varijabli
Neka diskretna slučajna varijabla uzme vrijednosti X 1 , X 2 , …, x n,…. Vjerojatnosti ovih vrijednosti mogu se izračunati koristeći različite formule, na primjer, koristeći osnovne teoreme teorije vjerojatnosti, Bernoullijevu formulu ili neke druge formule. Za neke od ovih formula zakon raspodjele ima svoje ime.
Najčešći zakoni distribucije diskretne slučajne varijable su binomni, geometrijski, hipergeometrijski i Poissonov zakon raspodjele.
Zakon binomne distribucije
Neka se proizvede n nezavisna ispitivanja, u svakom od kojih se događaj može pojaviti ili ne mora A. Vjerovatnoća da se ovaj događaj dogodi u svakom pojedinačnom pokušaju je konstantna, ne ovisi o broju pokušaja i jednaka je R=R(A). Otuda je vjerovatnoća da se događaj ne dogodi A u svakom testu je takođe konstantan i jednak q=1–R. Uzmite u obzir slučajnu varijablu X jednak broju pojavljivanja događaja A V n testovi. Očigledno, vrijednosti ove količine su jednake
X 1 =0 – događaj A V n testovi se nisu pojavili;
X 2 =1 – događaj A V n pojavio se jednom u suđenjima;
X 3 =2 – događaj A V n testovi su se pojavili dva puta;
…………………………………………………………..
x n +1 = n- događaj A V n sve se pokazalo tokom testova n jednom.
Vjerojatnosti ovih vrijednosti mogu se izračunati korištenjem Bernoullijeve formule (4.1):
Gdje To=0, 1, 2, …,n .
Zakon binomne distribucije X, jednak broju uspjeh u n Bernulijevi testovi, sa vjerovatnoćom uspjeha R.
Dakle, diskretna slučajna varijabla ima binomnu distribuciju (ili je distribuirana prema binomskom zakonu) ako su njene moguće vrijednosti 0, 1, 2, ..., n, a odgovarajuće vjerovatnoće se izračunavaju pomoću formule (7.1).
Binomna distribucija zavisi od dva parametri R I n.
Red distribucije slučajne varijable raspoređene prema binomskom zakonu ima oblik:
| X | … | k | … | n | ||
| R |  | … | … |  |
Primjer 7.1 . Tri nezavisna hica se ispaljuju u metu. Vjerovatnoća da ćete pogoditi svaki metak je 0,4. Slučajna vrijednost X– broj pogodaka u metu. Konstruirajte njegovu distribucijsku seriju.
Rješenje. Moguće vrijednosti slučajne varijable X su X 1 =0; X 2 =1; X 3 =2; X 4 =3. Nađimo odgovarajuće vjerovatnoće koristeći Bernoullijevu formulu. Nije teško pokazati da je upotreba ove formule ovdje potpuno opravdana. Imajte na umu da će vjerovatnoća da jednim udarcem ne pogodite metu biti jednaka 1-0,4=0,6. Dobijamo
Serija distribucije ima sljedeći oblik:
| X | ||||
| R | 0,216 | 0,432 | 0,288 | 0,064 |
Lako je provjeriti da je zbir svih vjerovatnoća jednak 1. Sama slučajna varijabla X distribuiraju prema binomskom zakonu. ■
Nađimo matematičko očekivanje i varijansu slučajne varijable distribuirane prema binomskom zakonu.
Prilikom rješavanja primjera 6.5 pokazalo se da matematičko očekivanje broja pojavljivanja događaja A V n nezavisna ispitivanja, ako postoji vjerovatnoća pojave A u svakom testu je konstantan i jednak R, jednako n· R
U ovom primjeru korištena je slučajna varijabla distribuirana prema binomskom zakonu. Stoga je rješenje primjera 6.5 u suštini dokaz sljedeće teoreme.
Teorema 7.1. Matematičko očekivanje diskretne slučajne varijable raspoređene prema binomskom zakonu jednako je proizvodu broja pokušaja i vjerovatnoće “uspjeha”, tj. M(X)=n· R.
Teorema 7.2. Varijanca diskretne slučajne varijable raspoređene prema binomskom zakonu jednaka je proizvodu broja pokušaja sa vjerovatnoćom “uspjeha” i vjerovatnoćom “neuspjeha”, tj. D(X)=nrq.
Asimetrija i kurtozis slučajne varijable raspoređene prema binomskom zakonu određuju se formulama
Ove formule se mogu dobiti koristeći koncept početnih i centralnih momenata.
Zakon binomne distribucije je u osnovi mnogih situacija iz stvarnog života. Za velike vrijednosti n Binomna distribucija se može aproksimirati korištenjem drugih distribucija, posebno Poissonove distribucije.
Poissonova distribucija
Neka bude n Bernoulli testovi, sa brojem testova n dovoljno velik. Ranije je pokazano da u ovom slučaju (ako je, štaviše, vjerovatnoća R događaji A vrlo mala) da se pronađe vjerovatnoća da će događaj A da se pojavi T Kada ste u testovima, možete koristiti Poissonovu formulu (4.9). Ako je slučajna varijabla X znači broj pojavljivanja događaja A V n Bernulijevim testovima, onda vjerovatnoća da Xće uzeti vrijednost k može se izračunati pomoću formule
, (7.2)
Gdje λ = nr.
Poissonov zakon distribucije se naziva distribucija diskretne slučajne varijable X, za koje su moguće vrijednosti nenegativni cijeli brojevi i vjerovatnoće r t ove vrijednosti se nalaze pomoću formule (7.2).
Magnituda λ = nr pozvao parametar Poissonove distribucije.
Slučajna varijabla distribuirana prema Poissonovom zakonu može poprimiti beskonačan broj vrijednosti. Budući da je za ovu distribuciju vjerovatnoća R Pojava događaja u svakom ispitivanju je mala, tada se ova distribucija ponekad naziva zakonom rijetkih događaja.
Red raspodjele slučajne varijable raspoređene prema Poissonovom zakonu ima oblik
| X | … | T | … | ||||
| R | … | … |
Lako je provjeriti da je zbir vjerovatnoća drugog reda jednak 1. Da biste to učinili, morate zapamtiti da se funkcija može proširiti u Maclaurinov niz, koji konvergira za bilo koji X. IN u ovom slučaju imamo
. (7.3)
Kao što je navedeno, Poissonov zakon zamjenjuje binomni zakon u određenim ograničavajućim slučajevima. Primjer je slučajna varijabla X, čije su vrijednosti jednake broju kvarova u određenom vremenskom periodu tokom ponovljene upotrebe tehničkog uređaja. Pretpostavlja se da se radi o visoko pouzdanom uređaju, tj. Vjerovatnoća neuspjeha u jednoj aplikaciji je vrlo mala.
Pored ovakvih ograničavajućih slučajeva, u praksi postoje slučajne varijable raspoređene prema Poissonovom zakonu koje nisu povezane sa binomskom distribucijom. Na primjer, Poissonova distribucija se često koristi kada se radi o broju događaja koji se dešavaju u određenom vremenskom periodu (broj poziva primljenih na telefonskoj centrali tokom jednog sata, broj automobila koji stignu u autopraonicu tokom dana, broj zaustavljanja mašine sedmično, itd.). Svi ovi događaji bi trebali formirati takozvani tok događaja, što je jedan od osnovnih koncepata teorije čekanja. Parametar λ karakteriše prosečan intenzitet toka događaja.
Primjer 7.2 . Na fakultetu ima 500 studenata. Kolika je vjerovatnoća da je 1. septembar rođendan tri studenta ovog odjeljenja?
Rješenje . Od broja studenata n=500 je prilično veliko i R– vjerovatnoća da će se roditi 1. septembra za bilo kog od učenika jednaka je , tj. je dovoljno mala, onda možemo pretpostaviti da je slučajna varijabla X– broj učenika rođenih 1. septembra raspoređuje se prema Poissonovom zakonu sa parametrom λ = n.p.= =1,36986. Tada prema formuli (7.2) dobijamo
Teorema 7.3. Neka je slučajna varijabla X distribuiran prema Poissonovom zakonu. Tada su njegovo matematičko očekivanje i varijansa međusobno jednaki i jednaki vrijednosti parametra λ , tj. M(X) = D(X) = λ = n.p..
Dokaz. Po definiciji matematičkog očekivanja, koristeći formulu (7.3) i niz distribucije slučajne varijable distribuirane prema Poissonovom zakonu, dobijamo
Prije pronalaženja varijanse, prvo pronalazimo matematičko očekivanje kvadrata slučajne varijable koja se razmatra. Dobijamo
Odavde, po definiciji disperzije, dobijamo
Teorema je dokazana.
Koristeći koncepte početnih i centralnih momenata, može se pokazati da su za slučajnu varijablu distribuiranu prema Poissonovom zakonu, koeficijenti nagiba i kurtozisa određeni formulama
To nije teško razumjeti, budući da je semantički sadržaj parametra λ = n.p. je pozitivna, onda slučajna varijabla distribuirana prema Poissonovom zakonu uvijek ima pozitivnu asistenciju i eksces.
Ne mjere se svi fenomeni na kvantitativnoj skali kao što je 1, 2, 3... 100500... Pojava ne može uvijek poprimiti beskonačan ili veliki broj različitih stanja. Na primjer, spol osobe može biti ili M ili F. Strijelac ili pogađa metu ili promašuje. Možete glasati ili "za" ili "protiv" itd. i tako dalje. Drugim riječima, takvi podaci odražavaju stanje alternativnog atributa - ili "da" (događaj se dogodio) ili "ne" (događaj se nije dogodio). Događaj koji se dogodio (pozitivan ishod) naziva se i „uspjeh“.
Eksperimenti sa takvim podacima se nazivaju Bernoullijeva šema, u čast poznatog švajcarskog matematičara koji je utvrdio da kod velikog broja pokušaja odnos pozitivnih ishoda i ukupnog broja pokušaja teži verovatnoći nastanka ovog događaja.
Alternativna karakteristična varijabla
Da bi se u analizi koristio matematički aparat, rezultate takvih opažanja treba zapisati u numeričkom obliku. Da bi se to postiglo, pozitivnom ishodu se dodeljuje broj 1, negativnom - 0. Drugim rečima, radi se o promenljivoj koja može imati samo dve vrednosti: 0 ili 1.
Kakva korist se može izvući iz ovoga? Zapravo, ništa manje nego iz običnih podataka. Dakle, lako je izračunati broj pozitivnih ishoda - samo zbrojite sve vrijednosti, tj. sve 1 (uspjeh). Možete ići dalje, ali to će zahtijevati od vas da uvedete nekoliko oznaka.
Prva stvar koju treba primijetiti je da pozitivni ishodi (koji su jednaki 1) imaju izvjesnu vjerovatnoću da će se dogoditi. Na primjer, dobijanje glave prilikom bacanja novčića je ½ ili 0,5. Ova vjerovatnoća se tradicionalno označava latiničnim slovom str. Stoga je vjerovatnoća da se dogodi alternativni događaj jednaka 1 - str, što je takođe označeno sa q, to je q = 1 – str. Ove notacije se mogu jasno sistematizirati u obliku tablice varijabilne distribucije X.
Dobili smo listu mogućih vrijednosti i njihove vjerovatnoće. Može se izračunati očekivanu vrijednost I disperzija. Očekivanje je zbir proizvoda svih mogućih vrijednosti i njihovih odgovarajućih vjerovatnoća:
Izračunajmo očekivanje koristeći notaciju u gornjim tabelama.
Ispada da je matematičko očekivanje alternativnog znaka jednako vjerovatnoći ovog događaja - str.
Hajde sada da definišemo šta je varijansa alternativnog atributa. Disperzija je prosječni kvadrat odstupanja od matematičkog očekivanja. Opća formula(za diskretne podatke) ima oblik:
Otuda varijansa alternativnog atributa:
Lako je vidjeti da ova disperzija ima maksimum od 0,25 (sa p=0,5).
Standardna devijacija je korijen varijanse:
Maksimalna vrijednost ne prelazi 0,5.
Kao što možete vidjeti, i matematičko očekivanje i varijansa alternativnog atributa imaju vrlo kompaktan oblik.
Binomna distribucija slučajne varijable
Pogledajmo situaciju iz drugog ugla. Zaista, koga briga što je prosječan gubitak glava po bacanju 0,5? To je nemoguće ni zamisliti. Zanimljivije je postaviti pitanje o broju glava koje se javljaju za dati broj bacanja.
Drugim riječima, istraživača često zanima vjerovatnoća da će se desiti određeni broj uspješnih događaja. To može biti broj neispravnih proizvoda u testiranoj seriji (1 - neispravan, 0 - dobar) ili broj oporavljenih (1 - zdrav, 0 - bolestan) itd. Broj takvih "uspjeha" bit će jednak zbroju svih vrijednosti varijable X, tj. broj pojedinačnih ishoda.
Slučajna vrijednost B naziva se binom i uzima vrijednosti od 0 do n(kod B= 0 – svi dijelovi su prikladni, sa B = n– svi dijelovi su neispravni). Pretpostavlja se da su sve vrijednosti x nezavisni jedno od drugog. Razmotrimo glavne karakteristike binomske varijable, odnosno ustanovićemo njeno matematičko očekivanje, disperziju i distribuciju.
Očekivanje binomske varijable je vrlo lako dobiti. Matematičko očekivanje zbira količina je zbir matematičkih očekivanja svake dodane količine, i ono je isto za sve, stoga:
Na primjer, matematičko očekivanje broja ispuštenih glava u 100 bacanja je 100 × 0,5 = 50.
Sada izvodimo formulu za disperziju binomske varijable. Varijanca zbira nezavisnih slučajnih varijabli je zbir varijansi. Odavde
Standardna devijacija, respektivno
Za 100 bacanja novčića, standardna devijacija broja glava je
Konačno, razmotrite distribuciju binomne vrijednosti, tj. vjerovatnoća da je slučajna varijabla B poprimiće različite vrijednosti k, Gdje 0≤k≤n. Za novčić, ovaj problem može izgledati ovako: Kolika je vjerovatnoća da dobijete 40 grla na 100 bacanja?
Da biste razumjeli metodu izračuna, zamislite da se novčić baci samo 4 puta. Svaka strana može ispasti svaki put. Pitamo se: kolika je vjerovatnoća da dobijemo 2 glave od 4 bacanja. Svako bacanje je nezavisno jedno od drugog. To znači da će vjerovatnoća dobivanja bilo koje kombinacije biti jednaka proizvodu vjerovatnoće datog ishoda za svako pojedinačno bacanje. Neka su O glave, P repovi. Tada, na primjer, jedna od kombinacija koja nam odgovara može izgledati kao OOPP, odnosno:
Vjerovatnoća takve kombinacije jednaka je umnošku dvije vjerovatnoće da se dobiju glave i još dvije vjerovatnoće da se ne dobiju glave (obrnuti događaj, izračunat kao 1 - str), tj. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Ovo je vjerovatnoća jedne od kombinacija koja nam odgovara. Ali pitanje je bilo o ukupnom broju orlova, a ne o nekom konkretnom redu. Zatim morate sabrati vjerovatnoće svih kombinacija u kojima postoje tačno 2 glave. Jasno je da su svi isti (proizvod se ne mijenja kada se promijene faktori). Stoga morate izračunati njihov broj, a zatim pomnožiti s vjerovatnoćom bilo koje takve kombinacije. Izbrojimo sve kombinacije od 4 bacanja po 2 glave: RROO, RORO, ROOR, ORRO, OROR, OORR. Ukupno ima 6 opcija.
Dakle, željena vjerovatnoća da dobijete 2 glave nakon 4 bacanja je 6×0,0625=0,375.
Međutim, brojanje na ovaj način je zamorno. Već za 10 novčića bit će vrlo teško dobiti ukupan broj opcija grubom silom. Zbog toga pametni ljudi davno izmislio formulu pomoću koje se izračunava broj različitih kombinacija n elementi po k, Gdje n– ukupan broj elemenata, k– broj elemenata čije se opcije rasporeda broje. Kombinovana formula od n elementi po k je li ovo:
Slične stvari se dešavaju u sekciji kombinatorike. Saljem tamo sve koji zele da unaprede svoje znanje. Otuda, usput rečeno, naziv binomne distribucije (gornja formula je koeficijent u ekspanziji Newtonovog binoma).
Formula za određivanje vjerovatnoće može se lako generalizirati na bilo koju veličinu n I k. Kao rezultat, formula za binomnu distribuciju ima sljedeći oblik.
Broj kombinacija koje ispunjavaju uslov se množi sa verovatnoćom jedne od njih.
Za praktična upotreba Dovoljno je samo znati formulu za binomnu distribuciju. Ili možda čak i ne znate - u nastavku pokazujemo kako odrediti vjerovatnoću koristeći Excel. Ali bolje je znati.
Koristeći ovu formulu, izračunavamo vjerovatnoću da dobijemo 40 glava u 100 bacanja:
Ili samo 1,08%. Poređenja radi, vjerovatnoća matematičkog očekivanja ovog eksperimenta, odnosno 50 grla, iznosi 7,96%. Maksimalna vjerovatnoća binomske vrijednosti pripada vrijednosti koja odgovara matematičkom očekivanju.
Izračunavanje vjerovatnoće binomne distribucije u Excelu
Ako koristite samo papir i kalkulator, tada su izračuni pomoću formule binomne distribucije, unatoč odsustvu integrala, prilično teški. Na primjer, vrijednost je 100! – ima više od 150 karaktera. Ranije, pa čak i sada, za izračunavanje takvih količina korištene su približne formule. Trenutno je preporučljivo koristiti poseban softver, kao što je MS Excel. Dakle, svaki korisnik (čak i humanista po obrazovanju) može lako izračunati vjerovatnoću vrijednosti binomno raspoređene slučajne varijable.
Za konsolidaciju gradiva koristićemo za sada Excel kao običan kalkulator, tj. Izvršimo izračun korak po korak koristeći formulu binomne distribucije. Izračunajmo, na primjer, vjerovatnoću da dobijemo 50 grla. Ispod je slika sa koracima proračuna i konačnim rezultatom.
Kao što vidite, srednji rezultati su takve skale da se ne uklapaju u ćeliju, iako jednostavne funkcije poput FACTOR (izračunavanje faktorijala), POWER (podizanje broja na stepen), kao i operatori množenja i dijeljenja koriste se svuda. Štaviše, ovaj proračun je prilično glomazan, u svakom slučaju nije kompaktan, jer uključene su mnoge ćelije. Da, i malo je teško shvatiti odmah.
Općenito, Excel pruža gotovu funkciju za izračunavanje vjerovatnoće binomne distribucije. Funkcija se poziva BINOM.DIST.
Broj uspjeha – broj uspješnih testova. Imamo ih 50.
Broj testova – broj bacanja: 100 puta.
Vjerovatnoća uspjeha – vjerovatnoća dobijanja glave u jednom bacanju je 0,5.
Integral – naznačeno je ili 1 ili 0. Ako je 0, tada se izračunava vjerovatnoća P(B=k); ako je 1, tada će se izračunati funkcija binomne distribucije, tj. zbir svih vjerovatnoća iz B=0 prije B=k inkluzivno.
Kliknite OK i dobijete isti rezultat kao gore, samo što je sve izračunato pomoću jedne funkcije.
Vrlo udobno. Radi eksperimentiranja, umjesto posljednjeg parametra 0, stavljamo 1. Dobijamo 0,5398. To znači da je sa 100 bacanja novčića vjerovatnoća da dobijete glave između 0 i 50 skoro 54%. Ali u početku se činilo da bi trebalo da bude 50%. Općenito, proračuni se rade brzo i jednostavno.
Pravi analitičar mora razumjeti kako se funkcija ponaša (kakva je njena distribucija), pa ćemo izračunati vjerovatnoće za sve vrijednosti od 0 do 100. Odnosno, postavićemo pitanje: kolika je vjerovatnoća da nijedna glava pojaviće se 1 orao, 2, 3, 50, 90 ili 100. Izračun je prikazan na sljedećoj slici. Plava linija je sama binomna distribucija, crvena tačka je vjerovatnoća za određeni broj uspjeha k.
Moglo bi se zapitati da li je binomna distribucija slična... Da, vrlo slična. Čak je i Moivre (1733.) rekao da se binomna distribucija sa velikim uzorcima približava (ne znam kako se tada zvala), ali ga niko nije slušao. Tek su Gaus, a potom i Laplace 60-70 godina kasnije, ponovo otkrili i pažljivo proučili zakon normalne raspodjele. Gornji grafikon jasno pokazuje da maksimalna vjerovatnoća pada na matematičko očekivanje, a kako odstupa od njega, naglo opada. Baš kao i normalan zakon.
Binomna distribucija ima veliku praktični značaj, javlja se prilično često. Koristeći Excel, proračuni se rade brzo i jednostavno.
