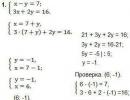Sistemi jednačina se široko koriste u ekonomskom sektoru za matematičko modeliranje različitih procesa. Na primjer, kod rješavanja problema upravljanja i planiranja proizvodnje, logističkih ruta (problem transporta) ili smještaja opreme.

Sistemi jednačina se koriste ne samo u matematici, već iu fizici, hemiji i biologiji, kada se rješavaju problemi određivanja veličine populacije.

Sistem linearnih jednačina su dvije ili više jednačina sa više varijabli za koje je potrebno pronaći zajedničko rješenje. Takav niz brojeva za koji sve jednačine postaju istinite jednakosti ili dokazuju da niz ne postoji.

Linearna jednadžba

Jednačine oblika ax+by=c nazivaju se linearne. Oznake x, y su nepoznanice čija se vrijednost mora pronaći, b, a su koeficijenti varijabli, c je slobodni član jednačine.
Rješavanje jednadžbe iscrtavanjem izgledat će kao prava linija, čije su sve točke rješenja polinoma.

Vrste sistema linearnih jednačina

Najjednostavnijim primjerima smatraju se sistemi linearnih jednadžbi s dvije varijable X i Y.

F1(x, y) = 0 i F2(x, y) = 0, gdje su F1,2 funkcije, a (x, y) funkcionalne varijable.

Riješiti sistem jednačina - to znači pronalaženje vrijednosti (x, y) pri kojima se sistem pretvara u pravu jednakost ili utvrđivanje da odgovarajuće vrijednosti x i y ne postoje.

Par vrijednosti (x, y), zapisan kao koordinate tačke, naziva se rješenjem sistema linearnih jednadžbi.

Ako sistemi imaju jedno zajedničko rješenje ili ne postoji rješenje, nazivaju se ekvivalentnim.

Homogeni sistemi linearnih jednačina su sistemi čija je desna strana jednaka nuli. Ako desni dio iza znaka jednakosti ima vrijednost ili je izražen funkcijom, takav sistem je heterogen.

Broj varijabli može biti mnogo veći od dvije, tada treba govoriti o primjeru sistema linearnih jednačina sa tri ili više varijabli.

Kada se suoče sa sistemima, školarci pretpostavljaju da se broj jednačina nužno mora podudarati s brojem nepoznanica, ali to nije slučaj. Broj jednačina u sistemu ne zavisi od varijabli, može ih biti koliko god želite.

Jednostavne i složene metode za rješavanje sistema jednačina

Ne postoji opšta analitička metoda za rešavanje ovakvih sistema, sve metode su zasnovane na numeričkim rešenjima. Školski predmet matematike detaljno opisuje metode kao što su permutacija, algebarsko sabiranje, supstitucija, kao i grafičke i matrične metode, rješenja Gaussovom metodom.

Glavni zadatak pri podučavanju metoda rješenja je naučiti kako pravilno analizirati sistem i pronaći optimalni algoritam rješenja za svaki primjer. Glavna stvar nije zapamtiti sistem pravila i radnji za svaku metodu, već razumjeti principe korištenja određene metode

Rješavanje primjera sistema linearnih jednačina u nastavnom planu i programu opšteg obrazovanja 7. razreda je prilično jednostavno i detaljno objašnjeno. U svakom udžbeniku matematike ovom dijelu se posvećuje dovoljno pažnje. Rješavanje primjera sistema linearnih jednačina Gauss-ovom i Cramerovom metodom detaljnije se proučava u prvim godinama visokog obrazovanja.

Rješavanje sistema metodom zamjene

Radnje metode zamjene imaju za cilj izražavanje vrijednosti jedne varijable u terminima druge. Izraz se zamjenjuje u preostalu jednačinu, a zatim se svodi na oblik s jednom promjenljivom. Akcija se ponavlja u zavisnosti od broja nepoznatih u sistemu

Dajemo rješenje za primjer sistema linearnih jednadžbi klase 7 koristeći metodu supstitucije:

Kao što se može vidjeti iz primjera, varijabla x je izražena kroz F(X) = 7 + Y. Rezultirajući izraz, zamijenjen u 2. jednačinu sistema umjesto X, pomogao je da se dobije jedna varijabla Y u 2. jednačini . Rješavanje ovog primjera je jednostavno i omogućava vam da dobijete vrijednost Y. Zadnji korak je provjera dobivenih vrijednosti.

Nije uvijek moguće riješiti primjer sistema linearnih jednačina zamjenom. Jednačine mogu biti složene i izražavanje varijable u terminima druge nepoznate biće previše glomazno za dalje proračune. Kada u sistemu ima više od 3 nepoznate, rješavanje zamjenom također nije prikladno.

Rješenje primjera sistema linearnih nehomogenih jednadžbi:

Rješenje korištenjem algebarskog sabiranja

Prilikom traženja rješenja sistema korištenjem metode sabiranja, jednačine se sabiraju pojam po član i množe različitim brojevima. Krajnji cilj matematičkih operacija je jednačina u jednoj varijabli.

Primena ove metode zahteva praksu i posmatranje. Rješavanje sistema linearnih jednadžbi metodom sabiranja kada postoje 3 ili više varijabli nije lako. Algebarsko sabiranje je pogodno za korištenje kada jednadžbe sadrže razlomke i decimale.

Algoritam rješenja:

1. Pomnožite obje strane jednačine određenim brojem. Kao rezultat aritmetičke operacije, jedan od koeficijenata varijable trebao bi postati jednak 1.
2. Dodajte rezultirajući izraz pojam po član i pronađite jednu od nepoznatih.
3. Zamijenite rezultirajuću vrijednost u 2. jednadžbu sistema da biste pronašli preostalu varijablu.

Metoda rješenja uvođenjem nove varijable

Nova varijabla se može uvesti ako sistem zahtijeva pronalaženje rješenja za ne više od dvije jednačine; broj nepoznatih također ne smije biti veći od dvije.

Metoda se koristi za pojednostavljenje jedne od jednadžbi uvođenjem nove varijable. Nova jednačina se rješava za uvedenu nepoznatu, a rezultirajuća vrijednost se koristi za određivanje originalne varijable.

Primjer pokazuje da je uvođenjem nove varijable t bilo moguće svesti 1. jednadžbu sistema na standardni kvadratni trinom. Polinom možete riješiti pronalaženjem diskriminanta.

Potrebno je pronaći vrijednost diskriminanta koristeći dobro poznatu formulu: D = b2 - 4*a*c, gdje je D željeni diskriminant, b, a, c su faktori polinoma. U datom primjeru, a=1, b=16, c=39, dakle D=100. Ako je diskriminanta veća od nule, tada postoje dva rješenja: t = -b±√D / 2*a, ako je diskriminanta manja od nule, postoji jedno rješenje: x = -b / 2*a.

Rješenje za rezultirajuće sisteme nalazi se metodom sabiranja.

Vizuelna metoda za rješavanje sistema

Pogodno za 3 sistema jednačina. Metoda se sastoji u konstruisanju grafova svake jednačine uključene u sistem na koordinatnoj osi. Koordinate presečnih tačaka krivih biće opšte rešenje sistema.

Grafička metoda ima niz nijansi. Pogledajmo nekoliko primjera rješavanja sistema linearnih jednačina na vizuelni način.

Kao što se može vidjeti iz primjera, za svaku liniju su konstruirane dvije tačke, a proizvoljno su odabrane vrijednosti varijable x: 0 i 3. Na osnovu vrijednosti x pronađene su vrijednosti za y: 3 i 0. Tačke sa koordinatama (0, 3) i (3, 0) označene su na grafikonu i povezane linijom.

Koraci se moraju ponoviti za drugu jednačinu. Tačka preseka pravih je rešenje sistema.

Sljedeći primjer zahtijeva pronalaženje grafičkog rješenja za sistem linearnih jednačina: 0,5x-y+2=0 i 0,5x-y-1=0.

Kao što se vidi iz primjera, sistem nema rješenja, jer su grafovi paralelni i ne seku se cijelom dužinom.

Sistemi iz primjera 2 i 3 su slični, ali kada se konstruišu postaje očigledno da su njihova rješenja različita. Treba imati na umu da nije uvijek moguće reći da li sistem ima rješenje ili ne; uvijek je potrebno konstruirati graf.

Matrica i njene varijante

Matrice se koriste za koncizno pisanje sistema linearnih jednačina. Matrica je posebna vrsta tabele ispunjene brojevima. n*m ima n - redova i m - kolona.

Matrica je kvadratna kada je broj kolona i redova jednak. Matrica-vektor je matrica od jednog stupca sa beskonačno mogućim brojem redova. Matrica s jedinicama duž jedne od dijagonala i drugim nultim elementima naziva se identitet.

Inverzna matrica je matrica kada se pomnoži s kojom se originalna matrica pretvara u jediničnu matricu; takva matrica postoji samo za originalnu kvadratnu matricu.

Pravila za pretvaranje sistema jednačina u matricu

U odnosu na sisteme jednačina, koeficijenti i slobodni članovi jednačina zapisuju se kao brojevi matrice, jedna jednačina je jedan red matrice.

Za red matrice se kaže da nije nula ako barem jedan element reda nije nula. Stoga, ako se u bilo kojoj od jednadžbi razlikuje broj varijabli, tada je potrebno unijeti nulu umjesto nepoznate koja nedostaje.

Kolone matrice moraju striktno odgovarati varijablama. To znači da se koeficijenti varijable x mogu upisati samo u jedan stupac, na primjer prvi, koeficijent nepoznate y - samo u drugi.

Prilikom množenja matrice, svi elementi matrice se sekvencijalno množe brojem.

Opcije za pronalaženje inverzne matrice

Formula za pronalaženje inverzne matrice je prilično jednostavna: K -1 = 1 / |K|, gdje je K -1 inverzna matrica, a |K| je determinanta matrice. |K| ne smije biti jednak nuli, tada sistem ima rješenje.

Determinanta se lako izračunava za matricu dva po dva; potrebno je samo pomnožiti dijagonalne elemente jedan s drugim. Za opciju “tri po tri” postoji formula |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Možete koristiti formulu, ili se možete sjetiti da morate uzeti po jedan element iz svakog reda i svake kolone kako se brojevi stupaca i redova elemenata ne bi ponavljali u radu.

Rješavanje primjera sistema linearnih jednadžbi matričnom metodom

Matrična metoda pronalaženja rješenja omogućava vam da smanjite glomazne unose pri rješavanju sistema s velikim brojem varijabli i jednačina.

U primjeru, a nm su koeficijenti jednadžbi, matrica je vektor x n su varijable, a b n su slobodni termini.

Rješavanje sistema Gausovom metodom

U višoj matematici Gaussova metoda se proučava zajedno sa Cramer metodom, a proces pronalaženja rješenja sistema naziva se Gauss-Cramerovom metodom rješenja. Ove metode se koriste za pronalaženje varijabli sistema sa velikim brojem linearnih jednačina.

Gaussova metoda je vrlo slična rješenjima zamjenom i algebarskim sabiranjem, ali je sistematičnija. U školskom predmetu se koristi rješenje Gaussove metode za sisteme od 3 i 4 jednačine. Svrha metode je da se sistem svede na oblik obrnutog trapeza. Pomoću algebarskih transformacija i supstitucija, vrijednost jedne varijable se nalazi u jednoj od jednačina sistema. Druga jednačina je izraz sa 2 nepoznate, dok su 3 i 4, respektivno, sa 3 i 4 varijable.

Nakon dovođenja sistema u opisani oblik, dalje rješenje se svodi na sekvencijalnu zamjenu poznatih varijabli u jednačine sistema.

U školskim udžbenicima za 7. razred primjer rješenja Gaussovom metodom opisan je na sljedeći način:

Kao što se može vidjeti iz primjera, u koraku (3) su dobijene dvije jednačine: 3x 3 -2x 4 =11 i 3x 3 +2x 4 =7. Rješavanje bilo koje od jednadžbi će vam omogućiti da saznate jednu od varijabli x n.

Teorema 5, koja se spominje u tekstu, kaže da ako se jedna od jednačina sistema zamijeni ekvivalentnom, onda će i rezultirajući sistem biti ekvivalentan izvornom.

Gaussovu metodu teško je razumjeti učenicima srednjih škola, ali je jedan od najzanimljivijih načina da se razvije domišljatost djece upisane u programe naprednog učenja na časovima matematike i fizike.

Radi lakšeg snimanja, proračuni se obično rade na sljedeći način:

Koeficijenti jednačina i slobodnih termina zapisani su u obliku matrice, pri čemu svaki red matrice odgovara jednoj od jednačina sistema. odvaja lijevu stranu jednačine od desne. Rimski brojevi označavaju brojeve jednačina u sistemu.

Prvo, zapišite matricu s kojom ćete raditi, a zatim sve radnje izvedene s jednim od redova. Rezultirajuća matrica se upisuje nakon znaka "strelica" i potrebne algebarske operacije se nastavljaju dok se ne postigne rezultat.

Rezultat bi trebao biti matrica u kojoj je jedna od dijagonala jednaka 1, a svi ostali koeficijenti jednaki nuli, odnosno matrica se svodi na jedinični oblik. Ne smijemo zaboraviti izvršiti proračune sa brojevima na obje strane jednačine.

Ova metoda snimanja je manje glomazna i omogućava vam da vas ne ometaju nabrajanje brojnih nepoznanica.

Besplatna upotreba bilo koje metode rješenja zahtijevat će brigu i određeno iskustvo. Nisu sve metode primijenjene prirode. Neke metode pronalaženja rješenja su poželjnije u određenom području ljudske djelatnosti, dok druge postoje u obrazovne svrhe.

Nastavni rad: Determinante i sistemi linearnih jednačina

1. Determinante drugog i trećeg reda i njihova svojstva

1.1. Pojam matrice i determinante drugog reda

Pravougaona tabela brojeva,

matrica. Da biste označili matricu, koristite bilo koju dvostruku vertikalu

crtice ili zagrade. Na primjer:

1 7 9.2 1 7 9.2

28 20 18 28 20 18

6 11 2 -6 11 2

Ako se broj redova matrice poklapa sa brojem njenih stupaca, tada se matrica naziva

kvadrat. Zovu ga brojevi koji čine matricu elementi.

Razmotrimo kvadratnu matricu koja se sastoji od četiri elementa:

Determinanta drugog reda koja odgovara matrici (3.1) je broj

i označeno simbolom

Dakle, po definiciji

Elementi koji čine matricu date determinante obično se nazivaju

elemente ove determinante.

Tačna je sljedeća izjava: kako bi determinanta drugog

poredak bio jednak nuli, potrebno je i dovoljno da elementi njegovih redova (ili

prema njegovim kolonama) bili su proporcionalni.

Da bismo dokazali ovu tvrdnju, dovoljno je napomenuti da svaki od

proporcije /

je ekvivalentno jednakosti

I posljednja jednakost, na osnovu (3.2), je ekvivalentna nestajanju determinante.

1.2. Sistem dvije linearne jednadžbe u dvije nepoznate

Pokazat ćemo kako se determinante drugog reda koriste za proučavanje i

pronalaženje rješenja za sistem od dvije linearne jednačine sa dvije nepoznate

(koeficijenti,

i besplatni članovi,

smatraju se datim). Podsjetimo da je to par brojeva

Called

rješenje sistema (3.3), ako postoji zamjena ovih brojeva

i u ovaj sistem

pretvara obje jednačine (3.3) u identitete.

Množenjem prve jednačine sistema (3.3) sa -

A drugi - na -i

zatim zbrajanjem rezultirajućih jednakosti dobijamo

Slično, množenjem jednadžbi (3.3) sa - i, respektivno, dobijamo:

Hajde da uvedemo sljedeću notaciju:

Koristeći ovu notaciju i izraz za determinantu drugog reda

jednačine (3.4) i (3.5) se mogu prepisati kao:

odrednica,

sastavljena od koeficijenata za nepoznanice sistema (3.3), obično se naziva

odrednica ovog sistema. Imajte na umu da su determinante

i dobijaju se od

sistemska determinanta

zamjenjujući njegovu prvu ili drugu kolonu slobodnim

Mogu se pojaviti dva slučaja: 1) determinanta sistema

različito od nule; 2) ova determinanta je jednaka nuli.

Hajde da prvo razmotrimo slučaj

0. Iz jednačina (3.7) odmah dobijamo formule za nepoznate,

pozvao Cramerove formule:

Rezultirajuće Cramerove formule (3.8) daju rješenje sistema (3.7) i stoga dokazuju

jedinstvenost rješenja za originalni sistem (3.3). Zaista, sistem (3.7)

je posljedica sistema (3.3), stoga svako rješenje sistema (3.3) (in

ako postoji!) mora biti rješenje za sistem (3.7). dakle,

do sada je dokazano da ako originalni sistem (3.3) postoji za

0, onda je ovo rješenje jednoznačno određeno Cramerovim formulama (3.8).

Lako je provjeriti postojanje rješenja, tj. o čemu

0 dva broja i

Definirano Cramerovim formulama (3.8). biti stavljen na mjesto nepoznatog u

jednadžbi (3.3), pretvoriti ove jednačine u identitete. (Pružamo čitaoca

sami zapišite izraze za odrednice

I uvjerite se da su navedeni identiteti tačni.)

Dolazimo do sljedećeg zaključka: ako je determinanta

sistem (3.3) je različit od nule, tada postoji i, štaviše, jedinstveno rješenje za ovo

sistem definisan Cramerovim formulama (3.8).

Razmotrimo sada slučaj kada je determinanta

sistem je jednak nula. Mogu se predstaviti dva podslučaja: Ili možda

bila bi jedna od odrednica

ili , različito od

nula; b) obe determinante

i jednaki su nuli. (Ako

odrednica i

jedan od dva kvalifikacija

i tada su jednaki nuli

druga od ove dvije determinante jednaka je nuli. U stvari, neka

na primjer = 0

Onda iz ovih proporcija dobijamo to

U podslučaju a) barem jedna od jednakosti (3.7) ispada nemoguća, tj.

sistem (3.7) nema rješenja, pa prema tome originalni sistem nema rješenja

(3.3) (čija je posljedica sistem (3.7)).

U podslučaju b) originalni sistem (3.3) ima beskonačan broj rješenja. IN

u stvari, iz jednakosti

0 i iz izjave na kraju odjeljka. 1.1 zaključujemo da je druga jednačina sistema

(3.3) je posljedica prvog i može se odbaciti. Ali jedna jednačina sa

dvije nepoznate

ima beskonačno mnogo rješenja (barem jedan od koeficijenata

Ili drugačije od

nula, a nepoznata vezana za nju može se odrediti iz jednačine (3.9)

kroz proizvoljno određenu vrijednost druge nepoznate).

Dakle, ako je determinanta

sistem (3.3) jednak nuli, tada sistem (3.3) ili nema rješenja (u

slučaju ako je barem jedna od determinanti

ili drugačije od

nula), ili ima beskonačan broj rješenja (u slučaju kada

0). U posljednjem

U slučaju da se dvije jednačine (3.3) mogu zamijeniti jednom, a prilikom njenog rješavanja jednom

nepoznato je postavljeno proizvoljno.

Komentar. U slučaju kada su slobodni članovi

i jednaki su nuli,

linearni sistem (3.3) naziva se homogena. Imajte na umu da je homogena

sistem uvek ima takozvano trivijalno rešenje:

0, = 0 (ova dva

brojevi pretvaraju obje homogene jednadžbe u identitete).

Ako je determinanta homogenog sistema

je različit od nule, onda ovaj sistem ima samo trivijalno rješenje. Ako

= 0, onda homogeni sistem ima beskonačan broj rješenja(zbog

za homogeni sistem mogućnost da nema rješenja je isključena). Dakle

način, homogeni sistem ima netrivijalno rješenje ako i samo ako

u slučaju kada je njegova determinanta jednaka nuli.

Sistemi linearnih jednačina. Predavanje 6.

Sistemi linearnih jednačina.

Osnovni koncepti.

Sistem pogleda

pozvao sistem - linearne jednadžbe sa nepoznanicama.

Zovu se brojevi , , sistemski koeficijenti.

Zovu se brojevi slobodni članovi sistema, – sistemske varijable. Matrix

pozvao glavna matrica sistema, i matrica

– prošireni matrični sistem. Matrice - kolone

I shodno tome matrice slobodnih termina i nepoznanica sistema. Tada se u matričnom obliku sistem jednačina može zapisati kao . Sistemsko rješenje naziva se vrijednosti varijabli, čijom zamjenom se sve jednačine sistema pretvaraju u ispravne numeričke jednakosti. Svako rješenje sistema može se predstaviti kao matrična kolona. Tada je matrična jednakost tačna.

Sistem jednačina se zove joint ako ima barem jedno rješenje i non-joint ako nema rješenja.

Rješavanje sistema linearnih jednačina znači utvrđivanje da li je konzistentan i, ako jeste, pronalaženje njegovog općeg rješenja.

Sistem se zove homogena ako su svi njeni slobodni članovi jednaki nuli. Homogeni sistem je uvijek konzistentan, jer ima rješenje

Kronecker-Copelli teorem.

Odgovor na pitanje postojanja rješenja linearnih sistema i njihove jedinstvenosti omogućava nam da dobijemo sljedeći rezultat, koji se može formulirati u obliku sljedećih tvrdnji o sistemu linearnih jednadžbi sa nepoznatim

(1)

Teorema 2. Sistem linearnih jednadžbi (1) je konzistentan ako i samo ako je rang glavne matrice jednak rangu proširene matrice (.

Teorema 3. Ako je rang glavne matrice simultanog sistema linearnih jednačina jednak broju nepoznatih, onda sistem ima jedinstveno rješenje.

Teorema 4. Ako je rang glavne matrice zajedničkog sistema manji od broja nepoznatih, onda sistem ima beskonačan broj rješenja.

Pravila za rješavanje sistema.

3. Naći izraze glavnih varijabli u terminima slobodnih i dobiti opšte rješenje sistema.

4. Davanjem proizvoljnih vrijednosti slobodnim varijablama dobijaju se sve vrijednosti glavnih varijabli.

Metode rješavanja sistema linearnih jednačina.

Metoda inverzne matrice.

i , tj. sistem ima jedinstveno rješenje. Zapišimo sistem u matričnom obliku

Gdje , , .

Pomnožimo obje strane matrične jednadžbe na lijevoj strani matricom

Od , Dobijamo , Od čega dobivamo jednakost za pronalaženje nepoznanica

Primjer 27. Rešiti sistem linearnih jednačina metodom inverzne matrice

Rješenje. Označimo sa glavnom matricom sistema

.

Neka, onda pronalazimo rješenje koristeći formulu.

Hajde da izračunamo.

Budući da , tada sistem ima jedinstveno rješenje. Nađimo sve algebarske komplemente

, ,

, ,

, ,

, ,

Dakle

.

Hajde da proverimo

.

Inverzna matrica je pronađena ispravno. Odavde, koristeći formulu, nalazimo matricu varijabli.

.

Upoređujući vrijednosti matrica, dobijamo odgovor: .

Cramerova metoda.

Neka je dat sistem linearnih jednačina sa nepoznatim

i , tj. sistem ima jedinstveno rješenje. Zapišimo rješenje sistema u matričnom obliku ili

Označimo

. . . . . . . . . . . . . . ,

Tako dobijamo formule za pronalaženje vrijednosti nepoznatih, koje se nazivaju Cramerove formule.

Primjer 28. Riješite sljedeći sistem linearnih jednačina koristeći Cramerovu metodu .

Rješenje. Nađimo determinantu glavne matrice sistema

.

Budući da , tada sistem ima jedinstveno rješenje.

Nađimo preostale determinante za Cramerove formule

,

,

.

Koristeći Cramerove formule nalazimo vrijednosti varijabli

Gaussova metoda.

Metoda se sastoji od sekvencijalne eliminacije varijabli.

Neka je dat sistem linearnih jednačina sa nepoznatim.

Proces Gausovog rješenja sastoji se od dvije faze:

U prvoj fazi, proširena matrica sistema se, koristeći elementarne transformacije, svodi na stepenasti oblik

,

gdje je , kojem sistem odgovara

Nakon toga varijable smatraju se slobodnim i prenose se na desnu stranu svake jednačine.

U drugoj fazi, varijabla se izražava iz posljednje jednačine, a rezultirajuća vrijednost se zamjenjuje u jednačinu. Iz ove jednačine

varijabla je izražena. Ovaj proces se nastavlja do prve jednačine. Rezultat je izraz glavnih varijabli kroz slobodne varijable .

Primjer 29. Riješite sljedeći sistem koristeći Gaussov metod

Rješenje. Hajde da ispišemo proširenu matricu sistema i dovedemo je u stepenasti oblik

.

Jer veći od broja nepoznatih, tada je sistem konzistentan i ima beskonačan broj rješenja. Napišimo sistem za matricu koraka

Determinanta proširene matrice ovog sistema, sastavljena od prva tri stupca, nije jednaka nuli, pa je smatramo osnovnom. Varijable

Oni će biti osnovni i varijabla će biti besplatna. Pomjerimo ga u svim jednadžbama na lijevu stranu

Iz posljednje jednačine koju izražavamo

Zamjenom ove vrijednosti u pretposljednju drugu jednačinu dobijamo

gdje . Zamjenom vrijednosti varijabli i u prvu jednačinu nalazimo . Napišimo odgovor u sljedećem obliku

Rješavanje sistema linearnih algebarskih jednačina jedan je od glavnih problema linearne algebre. Ovaj problem ima značajan primenjeni značaj u rešavanju naučnih i tehničkih problema, osim toga, pomoćni je u implementaciji mnogih algoritama u računarskoj matematici, matematičkoj fizici i obradi rezultata eksperimentalnih istraživanja.

Sistem linearnih algebarskih jednadžbi naziva se sistem jednačina oblika: (1)

Gdje – nepoznato; - besplatni članovi.

Rješavanje sistema jednačina(1) pozvati bilo koji skup brojeva koji, kada su postavljeni u sistem (1) umjesto nepoznatih pretvara sve jednačine sistema u tačne numeričke jednakosti.

Sistem jednačina se zove joint, ako ima barem jedno rješenje, i non-joint, ako nema rješenja.

Simultani sistem jednačina se naziva siguran, ako ima jedno jedinstveno rješenje, i neizvjesno, ako ima najmanje dva različita rješenja.

Zovu se dva sistema jednačina ekvivalentno ili ekvivalentno, ako imaju isti skup rješenja.

Sistem (1) se poziva homogena, ako su slobodni termini nula:

Homogeni sistem je uvijek konzistentan – ima rješenje (možda ne i jedino).

Ako je u sistemu (1), onda imamo sistem n linearne jednačine sa n nepoznato: gde – nepoznato; – koeficijenti za nepoznate, - besplatni članovi.

Linearni sistem može imati jedno rješenje, beskonačno mnogo rješenja ili uopće nema rješenja.

Razmotrimo sistem od dvije linearne jednačine sa dvije nepoznate

Ako tada sistem ima jedinstveno rješenje;

ako tada sistem nema rješenja;

ako tada sistem ima beskonačan broj rješenja.

Primjer. Sistem ima jedinstveno rješenje za par brojeva

Sistem ima beskonačan broj rješenja. Na primjer, rješenja za dati sistem su parovi brojeva itd.

Sistem nema rješenja, jer razlika dva broja ne može imati dvije različite vrijednosti.

Definicija. Odrednica drugog reda nazvan izrazom oblika:

Odrednica je označena simbolom D.

Brojevi A 11, …, A 22 se nazivaju elementi determinante.

Dijagonala formirana elementima A 11 ; A 22 su pozvani main dijagonala koju čine elementi A 12 ; A 21 − strana

Dakle, determinanta drugog reda jednaka je razlici između proizvoda elemenata glavne i sekundarne dijagonale.

Imajte na umu da je odgovor broj.

Primjer. Izračunajmo determinante:

Razmotrimo sistem od dvije linearne jednačine sa dvije nepoznate: gdje X 1, X 2 – nepoznato; A 11 , …, A 22 – koeficijenti za nepoznate, b 1 ,b 2 – besplatni članovi.

Ako sistem od dvije jednadžbe sa dvije nepoznate ima jedinstveno rješenje, onda se ono može naći pomoću determinanti drugog reda.

Definicija. Zove se determinanta sastavljena od koeficijenata za nepoznate determinanta sistema: D= .

Kolone determinante D sadrže koeficijente, odnosno za X 1 i at , X 2. Hajde da predstavimo dva dodatne kvalifikacije, koji se dobijaju iz determinante sistema zamenom jedne od kolona kolonom slobodnih pojmova: D 1 = D 2 = .

Teorema 14(Kramer, za slučaj n=2). Ako je determinanta D sistema različita od nule (D¹0), onda sistem ima jedinstveno rešenje, koje se nalazi pomoću formula:

Ove formule se nazivaju Cramerove formule.

Primjer. Rešimo sistem koristeći Cramerovo pravilo:

Rješenje. Hajde da nađemo brojeve

Odgovori.

Definicija. Odrednica trećeg reda nazvan izrazom oblika:

Elementi A 11; A 22 ; A 33 – čine glavnu dijagonalu.

Brojevi A 13; A 22 ; A 31 – formira bočnu dijagonalu.

Unos sa plusom uključuje: umnožak elemenata na glavnoj dijagonali, preostala dva člana su proizvod elemenata koji se nalaze u vrhovima trouglova sa bazama paralelnim sa glavnom dijagonalom. Minus članovi se formiraju prema istoj shemi u odnosu na sekundarnu dijagonalu.

Primjer. Izračunajmo determinante:

Razmotrimo sistem od tri linearne jednačine sa tri nepoznate: gdje – nepoznato; – koeficijenti za nepoznate, - besplatni članovi.

U slučaju jedinstvenog rješenja, sistem od 3 linearne jednadžbe sa tri nepoznate može se riješiti korištenjem determinanti trećeg reda.

Determinanta sistema D ima oblik:

Hajde da uvedemo tri dodatne determinante:

Teorema 15(Kramer, za slučaj n=3). Ako je determinanta D sistema različita od nule, onda sistem ima jedinstveno rješenje, koje se nalazi pomoću Cramerove formule:

Primjer. Rešimo sistem koristeći Cramerovo pravilo.

Rješenje. Hajde da nađemo brojeve

Koristimo Cramerove formule i pronađimo rješenje originalnog sistema:

Odgovori.

Imajte na umu da je Cramerova teorema primjenjiva kada je broj jednačina jednak broju nepoznatih i kada je determinanta sistema D različita od nule.

Ako je determinanta sistema jednaka nuli, onda u ovom slučaju sistem ili nema rješenja ili može imati beskonačan broj rješenja. Ovi slučajevi se proučavaju odvojeno.

Napomenimo samo jedan slučaj. Ako je determinanta sistema jednaka nuli (D=0), a barem jedna od dodatnih determinanti je različita od nule, onda sistem nema rješenja, odnosno nedosljedan je.

Cramerova teorema se može generalizirati na sistem n linearne jednačine sa n nepoznato: gde – nepoznato; – koeficijenti za nepoznate, - besplatni članovi.

Ako je determinanta sistema linearnih jednadžbi sa nepoznanicama, onda se jedino rešenje sistema nalazi pomoću Cramerovih formula:

Dodatna determinanta se dobija iz determinante D ako sadrži kolonu koeficijenata za nepoznatu x i zamijeniti kolonom slobodnih članova.

Imajte na umu da su determinante D, D 1 , … , D n imati reda n.

Gausova metoda za rješavanje sistema linearnih jednačina

Jedna od najčešćih metoda za rješavanje sistema linearnih algebarskih jednadžbi je metoda sekvencijalne eliminacije nepoznanica −Gaussova metoda. Ova metoda je generalizacija metode zamjene i sastoji se od uzastopnog eliminisanja nepoznatih sve dok ne ostane jedna jednačina sa jednom nepoznatom.

Metoda se zasniva na nekim transformacijama sistema linearnih jednačina, što rezultira sistemom ekvivalentnim originalnom sistemu. Algoritam metode se sastoji od dvije faze.

Prva faza se zove pravo naprijed Gaussova metoda. Sastoji se od sekvencijalnog eliminisanja nepoznatih iz jednačina. Da biste to učinili, u prvom koraku podijelite prvu jednačinu sistema sa (u suprotnom, preuredite jednačine sistema). Oni označavaju koeficijente rezultirajuće redukovane jednačine, množe je sa koeficijentom i oduzimaju od druge jednačine sistema, čime se eliminišu iz druge jednačine (nuliranje koeficijenta).

Učinite isto s preostalim jednadžbama i dobijete novi sistem, u čijim se jednačinama, počevši od druge, koeficijenti za , sadrže samo nule. Očigledno, rezultirajući novi sistem će biti ekvivalentan originalnom sistemu.

Ako novi koeficijenti, za , nisu svi jednaki nuli, mogu se na isti način isključiti iz treće i sljedećih jednačina. Nastavljajući ovu operaciju za sljedeće nepoznanice, sistem se dovodi u takozvani trokutni oblik:

Ovdje simboli označavaju numeričke koeficijente i slobodne termine koji su se promijenili kao rezultat transformacija.

Iz posljednje jednačine sistema preostale nepoznanice se određuju na jedinstven način, a zatim sekvencijalnom zamjenom.

Komentar. Ponekad se, kao rezultat transformacija, u bilo kojoj od jednadžbi svi koeficijenti i desna strana okreću na nulu, odnosno jednačina se pretvara u identičnost 0=0. Eliminacijom takve jednačine iz sistema, broj jednačina se smanjuje u odnosu na broj nepoznatih. Takav sistem ne može imati jedinstveno rješenje.

Ako se u procesu primjene Gaussove metode bilo koja jednačina pretvori u jednakost oblika 0 = 1 (koeficijenti za nepoznate se pretvaraju u 0, a desna strana poprima vrijednost različitu od nule), tada originalni sistem nema rješenja, jer je takva jednakost netačna za sve nepoznate vrijednosti.

Razmotrimo sistem od tri linearne jednadžbe sa tri nepoznate:

Gdje – nepoznato; – koeficijenti za nepoznate, - besplatni članovi. , zamjenjujući ono što je pronađeno

Rješenje. Primenom Gausove metode na ovaj sistem dobijamo

Gdje posljednja jednakost ne uspijeva za bilo koju vrijednost nepoznanica, dakle, sistem nema rješenja.

Odgovori. Sistem nema rješenja.

Imajte na umu da se prethodno razmatrana Cramerova metoda može koristiti za rješavanje samo onih sistema u kojima se broj jednačina poklapa sa brojem nepoznatih, a determinanta sistema mora biti različita od nule. Gaussova metoda je univerzalnija i pogodnija za sisteme s bilo kojim brojem jednačina.

Sistem linearnih jednačina je unija od n linearnih jednačina, od kojih svaka sadrži k varijabli. Napisano je ovako:

Mnogi, kada se prvi put susreću s višom algebrom, pogrešno vjeruju da se broj jednačina nužno mora podudarati s brojem varijabli. U školskoj algebri to se obično dešava, ali za višu algebru to generalno nije tačno.

Rješenje sistema jednačina je niz brojeva (k 1, k 2, ..., k n), koji je rješenje svake jednačine sistema, tj. pri zamjeni u ovu jednačinu umjesto varijabli x 1, x 2, ..., x n daje tačnu numeričku jednakost.

Prema tome, rješavanje sistema jednačina znači pronalaženje skupa svih njegovih rješenja ili dokazivanje da je ovaj skup prazan. Budući da se broj jednačina i broj nepoznatih možda ne poklapaju, moguća su tri slučaja:

1. Sistem je nekonzistentan, tj. skup svih rješenja je prazan. Prilično rijedak slučaj koji se lako otkriva bez obzira na to kojim se metodom rješava sistem.
2. Sistem je konzistentan i određen, tj. ima tačno jedno rešenje. Klasična verzija, poznata još od škole.
3. Sistem je konzistentan i nedefinisan, tj. ima beskonačno mnogo rješenja. Ovo je najteža opcija. Nije dovoljno naznačiti da “sistem ima beskonačan skup rješenja” – potrebno je opisati kako je ovaj skup strukturiran.

Varijabla x i se naziva dozvoljenom ako je uključena u samo jednu jednačinu sistema, i to sa koeficijentom 1. Drugim riječima, u drugim jednačinama koeficijent varijable x i mora biti jednak nuli.

Ako u svakoj jednačini odaberemo jednu dozvoljenu varijablu, dobićemo skup dozvoljenih varijabli za cijeli sistem jednačina. Sam sistem, napisan u ovom obliku, takođe će se zvati razriješenim. Uopšteno govoreći, jedan te isti izvorni sistem može se svesti na različite dozvoljene, ali nas to za sada ne brine. Evo primjera dozvoljenih sistema:

Oba sistema se rješavaju u odnosu na varijable x 1 , x 3 i x 4 . Međutim, sa istim uspjehom može se tvrditi da je drugi sistem razriješen u odnosu na x 1, x 3 i x 5. Dovoljno je prepisati poslednju jednačinu u obliku x 5 = x 4.

Hajde sada da razmotrimo opštiji slučaj. Neka imamo k varijabli ukupno, od kojih je r dozvoljeno. Tada su moguća dva slučaja:

1. Broj dozvoljenih varijabli r jednak je ukupnom broju varijabli k: r = k. Dobijamo sistem od k jednačina u kojem je r = k dozvoljenih varijabli. Takav sistem je zajednički i određen, jer x 1 = b 1, x 2 = b 2, ..., x k = b k;
2. Broj dozvoljenih varijabli r manji je od ukupnog broja varijabli k: r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Dakle, u gornjim sistemima varijable x 2, x 5, x 6 (za prvi sistem) i x 2, x 5 (za drugi) su slobodne. Slučaj kada postoje slobodne varijable bolje je formulirati kao teorem:

Imajte na umu: ovo je veoma važna tačka! U zavisnosti od toga kako pišete rezultujući sistem, ista varijabla može biti dozvoljena ili slobodna. Većina nastavnika više matematike preporučuje ispisivanje varijabli leksikografskim redom, tj. rastući indeks. Međutim, niste u obavezi da slijedite ovaj savjet.

Teorema. Ako su u sistemu od n jednačina dozvoljene varijable x 1, x 2, ..., x r, a x r + 1, x r + 2, ..., x k su slobodne, tada:

1. Ako postavimo vrijednosti slobodnih varijabli (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), a zatim pronađemo vrijednosti x 1, x 2, ..., x r, dobijamo jednu od odluka.
2. Ako se u dva rješenja poklapaju vrijednosti slobodnih varijabli, onda se poklapaju i vrijednosti dozvoljenih varijabli, tj. rješenja su jednaka.

Šta je značenje ove teoreme? Da bi se dobila sva rješenja riješenog sistema jednačina, dovoljno je izolovati slobodne varijable. Zatim, dodjeljujući različite vrijednosti slobodnim varijablama, dobit ćemo gotova rješenja. To je sve - na ovaj način možete dobiti sva rješenja sistema. Drugih rješenja nema.

Zaključak: riješeni sistem jednačina je uvijek konzistentan. Ako je broj jednačina u razriješenom sistemu jednak broju varijabli, sistem će biti definitivan; ako je manji, bit će neodređen.

I sve bi bilo u redu, ali postavlja se pitanje: kako dobiti riješeno iz originalnog sistema jednačina? Za ovo postoji