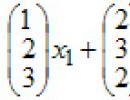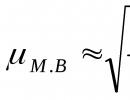Za karakterizaciju brzine kretanja uvodi se pojam brzine.

definicija: Prosječna brzina kretanja tačke u vremenskom intervalu od do
je vektorska veličina jednaka omjeru prirasta radijus vektora tačke tokom ovog vremenskog perioda i njenog trajanja
.

- prosječna brzina.

definicija: Brzina (ili trenutna brzina) tačke naziva se vektorska veličina jednaka prvom izvodu u odnosu na vrijeme radijus vektora.

Vektor brzine karakteriše kretanje, i po veličini i po pravcu. Vektor brzine je uvijek usmjeren tangencijalno na putanju u smjeru kretanja.

definicija: Modul brzine jednak je prvom izvodu s obzirom na vrijeme prijeđenog puta.

Proširimo vektor brzine prema osnovi pravougaonog kartezijanskog koordinatnog sistema:

, gdje su V x , V y , V z projekcije vektora brzine na odgovarajuću osu, koje su respektivno jednake:

Gdje
je rendgenska projekcija radijus vektora materijalne tačke.

U koordinatnoj reprezentaciji, vektor brzine ima oblik:

Modul vektora brzine u koordinatnom prikazu:

Obrnuti odnos.

Hajde da predstavimo vektor brzine radijusa koristeći određeni i neodređeni integral:

gdje je t, t 0 – početno i konačno vrijeme.

Predstavljanje pređenog puta kroz modul brzine pomoću određenog i neodređenog integrala.

§4. Vektor ubrzanja.

Da bi se okarakterizirala brzina promjene vektora brzine tačke, u mehanici se uvodi koncept ubrzanja.

definicija: Prosječno ubrzanje u vremenskom intervalu od prije
naziva se vektorska veličina jednaka omjeru prirasta vektora brzine tačke u datom vremenskom intervalu prema njenoj veličini.

definicija: Ubrzanje (ili trenutno ubrzanje) tačke naziva se vektorska veličina koja je brojčano jednaka prvom izvodu s obzirom na vrijeme brzine dotične tačke ili, što je isto, drugom izvodu u odnosu na vrijeme radijus vektor ove tačke:

Ubrzanje se može unijeti kroz ograničenje od prosječnog ubrzanja:

Dva unesena unosa ubrzanja su ekvivalentna.

Proširimo vektor ubrzanja prema bazi pravokutnog kartezijanskog koordinatnog sistema:

gdje su a x, a y, a z projekcije vektora ubrzanja na osu.

Koordinatni prikaz modula vektora ubrzanja:

Inverzni omjeri:

;

Razmotrimo kretanje materijalne tačke duž ravne krive. Ubrzanje je uvijek usmjereno prema udubljenosti krive ili putanje. Hajde da predstavimo dva jedinična vektora: , koji je usmjeren tangencijalno na putanju i - usmjeren okomito na putanju do centra krivine.

;

Proširimo vektor ubrzanja u datim smjerovima.

- tangencijalno ubrzanje.

definicija: Tangencijalno ubrzanje je vektorska veličina koja karakterizira brzinu promjene vektora brzine u veličini.

- vektorsko predstavljanje.

- skalarno predstavljanje.

- normalno ubrzanje.

definicija: Normalno ubrzanje karakterizira brzinu promjene vektora brzine u smjeru i izračunava se po formuli:

-gdje je R polumjer zakrivljenosti putanje u tački M

Ako je putanja kružnica, tada je R polumjer kružnice.

U skalarnom predstavljanju:

Iz svojstava komponenti ukupnog ubrzanja proizlazi da je ukupno ubrzanje usmjereno prema udubljenosti putanje.

Ukupni modul ubrzanja je jednak:

Slično za vektor ukupnog ubrzanja:

U ovoj temi ćemo se osvrnuti na jedan vrlo poseban tip neravnomerno kretanje. Na osnovu suprotnosti ravnomjernom kretanju, neravnomjerno kretanje je kretanje nejednakom brzinom duž bilo koje putanje. Koja je posebnost ravnomjerno ubrzanog kretanja? Ovo je neujednačen pokret, ali koji "jednako ubrzano". Ubrzanje povezujemo sa povećanjem brzine. Prisjetimo se riječi "jednako", dobijamo jednako povećanje brzine. Kako razumijemo „jednako povećanje brzine“, kako možemo procijeniti da li se brzina povećava jednako ili ne? Da bismo to učinili, potrebno je zabilježiti vrijeme i procijeniti brzinu u istom vremenskom intervalu. Na primjer, automobil počinje da se kreće, u prve dvije sekunde razvija brzinu do 10 m/s, u naredne dvije sekunde dostiže 20 m/s, a nakon još dvije sekunde već se kreće brzinom od 30 m/s. Svake dvije sekunde brzina se povećava i svaki put za 10 m/s. Ovo je jednoliko ubrzano kretanje.

Fizička veličina koja karakteriše koliko se brzina povećava svaki put naziva se ubrzanje.

Može li se smatrati da je kretanje bicikliste jednoliko ubrzano ako je nakon zaustavljanja u prvoj minuti njegova brzina 7 km/h, u drugoj - 9 km/h, u trećoj - 12 km/h? Zabranjeno je! Biciklista ubrzava, ali ne podjednako, prvo je ubrzao za 7 km/h (7-0), zatim za 2 km/h (9-7), pa za 3 km/h (12-9).

Obično se kretanje sa povećanjem brzine naziva ubrzano kretanje. Kretanje sa smanjenjem brzine je usporeno. Ali fizičari svako kretanje sa promjenjivom brzinom nazivaju ubrzanim kretanjem. Bilo da se auto kreće (brzina se povećava!) ili koči (brzina se smanjuje!), u svakom slučaju kreće se ubrzano.

Ravnomjerno ubrzano kretanje- ovo je kretanje tijela u kojem je njegova brzina za bilo koje jednake intervale vremena promjene(može povećati ili smanjiti) isto

Ubrzanje tijela

Ubrzanje karakterizira brzinu promjene brzine. Ovo je broj za koji se brzina mijenja svake sekunde. Ako je ubrzanje nekog tijela veliko, to znači da tijelo brzo dobija brzinu (kada ubrzava) ili je brzo gubi (pri kočenju). Ubrzanje je fizička vektorska veličina, numerički jednaka omjeru promjene brzine i vremenskog perioda tokom kojeg se ta promjena dogodila.

Odredimo ubrzanje u sljedećem zadatku. U početnom trenutku, brzina broda je bila 3 m/s, na kraju prve sekunde brzina broda je postala 5 m/s, na kraju druge - 7 m/s, na kraj trećeg 9 m/s itd. Očigledno, . Ali kako smo utvrdili? Gledamo razliku u brzini preko jedne sekunde. U prvoj sekundi 5-3=2, u drugoj drugoj 7-5=2, u trećoj 9-7=2. Ali šta ako brzine nisu date za svaku sekundu? Ovo je zadatak: startna brzina motorni brod 3 m/s, na kraju druge sekunde - 7 m/s, na kraju četvrte 11 m/s.U ovom slučaju potrebno je 11-7 = 4, zatim 4/2 = 2. Razliku u brzini dijelimo s vremenskim periodom.

Ova formula se najčešće koristi u modificiranom obliku pri rješavanju problema:

Formula nije napisana u vektorskom obliku, tako da pišemo znak “+” kada tijelo ubrzava, znak “-” kada usporava.

Smjer vektora ubrzanja

Smjer vektora ubrzanja prikazan je na slikama

Na ovoj slici, automobil se kreće u pozitivnom smjeru duž ose Ox, vektor brzine se uvijek poklapa sa smjerom kretanja (usmjeren udesno). Kada se vektor ubrzanja poklopi sa smjerom brzine, to znači da automobil ubrzava. Ubrzanje je pozitivno.

Prilikom ubrzanja, smjer ubrzanja se poklapa sa smjerom brzine. Ubrzanje je pozitivno.

Na ovoj slici automobil se kreće u pozitivnom smjeru duž ose Ox, vektor brzine se poklapa sa smjerom kretanja (usmjeren udesno), ubrzanje se NE poklapa sa smjerom brzine, to znači da automobil koči. Ubrzanje je negativno.

Prilikom kočenja, smjer ubrzanja je suprotan smjeru brzine. Ubrzanje je negativno.

Hajde da shvatimo zašto je ubrzanje negativno pri kočenju. Na primjer, u prvoj sekundi motorni brod je smanjio brzinu sa 9m/s na 7m/s, u drugoj sekundi na 5m/s, u trećoj na 3m/s. Brzina se mijenja na "-2m/s". 3-5=-2; 5-7=-2; 7-9=-2m/s. Odatle dolazi negativna vrijednost ubrzanja.

Prilikom rješavanja problema, ako tijelo usporava, ubrzanje se zamjenjuje u formule sa predznakom minus!!!

Kretanje tokom ravnomjerno ubrzanog kretanja

Dodatna formula tzv bezvremenski

Formula u koordinatama

Komunikacija srednje brzine

At ravnomerno ubrzano kretanje prosječna brzina se može izračunati kao aritmetička sredina početne i konačne brzine

Iz ovog pravila slijedi formula koja je vrlo zgodna za korištenje pri rješavanju mnogih problema

Omjer putanje

Ako se tijelo kreće ravnomjerno ubrzano, početna brzina je nula, tada se putevi prijeđeni u uzastopnim jednakim vremenskim intervalima odnose kao uzastopni niz neparnih brojeva.

Glavna stvar koju treba zapamtiti

1) Šta je jednoliko ubrzano kretanje;
2) Šta karakteriše ubrzanje;
3) Ubrzanje je vektor. Ako tijelo ubrzava, ubrzanje je pozitivno, ako usporava, ubrzanje je negativno;
3) Smjer vektora ubrzanja;
4) Formule, mjerne jedinice u SI

Vježbe

Dva voza se kreću jedan prema drugom: jedan ubrzano ide na sjever, drugi polako na jug. Kako se usmjeravaju ubrzanja voza?

Jednako na sjeveru. Zato što se ubrzanje prvog voza poklapa u pravcu kretanja, a ubrzanje drugog voza suprotno kretanju (usporava).

Trajektorija kretanja materijalne tačke kroz radijus vektor

Pošto sam pomalo zaboravio ovaj dio matematike, u mom sjećanju su jednačine kretanja materijalne točke uvijek bile predstavljene korištenjem zavisnosti koja je svima nama poznata y(x), i gledajući tekst problema, bio sam malo zatečen kada sam vidio vektore. Pokazalo se da postoji prikaz putanje materijalne tačke pomoću radijus vektor— vektor koji specificira položaj tačke u prostoru u odnosu na neku unapred fiksiranu tačku, koja se naziva ishodište.

Formula za putanju materijalne tačke, pored radijus vektora, opisana je na isti način orts— jedinični vektori i, j, k u našem slučaju, poklapa se sa osama koordinatnog sistema. I na kraju, razmotrimo primjer jednadžbe za putanju materijalne točke (u dvodimenzionalnom prostoru):

Šta je zanimljivo u ovom primjeru? Putanja tačke je data sinusima i kosinusima Šta mislite kako će graf izgledati u poznatom prikazu y(x)? “Vjerovatno nešto jezivo”, pomislili ste, ali nije sve tako komplikovano kako se čini! Pokušajmo konstruirati putanju materijalne točke y(x), ako se kreće prema gore predstavljenom zakonu:

Ovdje sam primijetio kvadrat kosinusa, ako u bilo kojem primjeru vidite kvadrat sinusa ili kosinusa, to znači da trebate primijeniti osnovni trigonometrijski identitet, što sam i uradio (druga formula) i transformirao koordinatnu formulu y, tako da umjesto sinusa u njega ubacite formulu promjene x:

Kao rezultat toga, strašni zakon kretanja tačke pokazao se običnim parabola, čije su grane usmjerene prema dolje. Nadam se da razumete približni algoritam za konstruisanje zavisnosti y(x) iz reprezentacije kretanja kroz vektor radijusa. Sada pređimo na naše glavno pitanje: kako pronaći vektor brzine i ubrzanja materijalne tačke, kao i njihove module.

Vektor brzine materijalne tačke

Svima je poznato da je brzina materijalne tačke količina puta koju tačka prijeđe u jedinici vremena, odnosno izvod formule za zakon kretanja. Da biste pronašli vektor brzine, morate uzeti derivaciju u odnosu na vrijeme. hajde da razmotrimo konkretan primjer pronalaženje vektora brzine.

Primjer pronalaženja vektora brzine

Imamo zakon kretanja materijalne tačke:

Sada morate uzeti derivaciju ovog polinoma, ako ste zaboravili kako se to radi, evo ga. Kao rezultat toga, vektor brzine će imati sljedeći oblik:

Ispostavilo se da je sve jednostavnije nego što ste mislili, sada pronađite vektor ubrzanja materijalne tačke koristeći isti zakon koji je gore prikazan.

Kako pronaći vektor ubrzanja materijalne tačke

Vektor ubrzanja tačke ovo je vektorska veličina koja karakteriše promenu tokom vremena u veličini i smeru brzine tačke. Da biste pronašli vektor ubrzanja materijalne tačke u našem primjeru, trebate uzeti derivaciju, ali iz formule vektora brzine predstavljene malo iznad:

Modul vektora brzine tačke

Sada pronađimo veličinu vektora brzine materijalne tačke. Kao što znate iz 9. razreda, modul vektora je njegova dužina, u pravokutnim dekartovskim koordinatama jednak je kvadratni korijen iz zbira kvadrata njegovih koordinata. A gdje možemo dobiti njegove koordinate iz vektora brzine koji smo dobili gore, pitate se? Sve je vrlo jednostavno:

Sada samo trebate zamijeniti vrijeme navedeno u problemu i dobiti određenu numeričku vrijednost.

Modul vektora ubrzanja

Kao što ste shvatili iz gore napisanog (i od 9. razreda), pronalaženje modula vektora ubrzanja odvija se na isti način kao i modula vektora brzine: uzimamo kvadratni korijen zbira kvadrata vektorskih koordinata , jednostavno je! Pa evo primjera za vas, naravno:

Kao što vidite, ubrzanje materijalne tačke prema gore datom zakonu ne zavisi od vremena i ima konstantnu veličinu i pravac.

Više primjera rješenja za problem nalaženja vektora brzine i ubrzanja

I ovdje možete pronaći primjere rješenja drugih problema iz fizike. A za one koji baš i ne razumiju kako pronaći vektor brzine i ubrzanja, evo još par primjera iz mreže bez suvišnih objašnjenja, nadam se da će vam pomoći.

Ako imate bilo kakvih pitanja, možete ih postaviti u komentarima.

Brzina je vektorska veličina koja karakterizira ne samo brzinu kretanja čestice duž putanje, već i smjer u kojem se čestica kreće u svakom trenutku vremena.

Prosječna brzina tokom vremena od t 1 prije t 2 jednak je omjeru kretanja za to vrijeme i vremenskog perioda tokom kojeg se ovo kretanje dogodilo:

Zabilježit ćemo činjenicu da je ovo prosječna brzina zatvaranjem prosječne vrijednosti u ugaone zagrade:<...>, kao što je gore urađeno.

Gornja formula za vektor prosječne brzine je direktna posljedica opšteg matematička definicija prosječna vrijednost<f(x)> proizvoljna funkcija f(x) na intervalu [ a,b]:

Zaista

Prosječna brzina može biti pregruba mjera kretanja. Na primjer, prosječna brzina tokom perioda osciliranja je uvijek nula, bez obzira na prirodu ovih oscilacija, iz jednostavnog razloga što će se tokom nekog perioda - po definiciji perioda - oscilirajuće tijelo vratiti na svoju početnu tačku i, prema tome, , pomak tokom perioda je uvijek nula. Iz ovog i niza drugih razloga uvodi se trenutna brzina - brzina ulaska ovog trenutka vrijeme. U budućnosti, što znači trenutnu brzinu, pisaćemo jednostavno: "brzina", izostavljajući riječi "trenutačno" ili "u datom trenutku u vremenu" kad god to ne može dovesti do nesporazuma. Da biste dobili brzinu u trenutku u vremenu t mora biti urađeno očigledna stvar: izračunajte granicu omjera kako vremenski interval teži t 2 – t 1 na nulu. Napravimo neke redizajniranja: t 1 = t I t 2 = t + i prepiši gornju relaciju kao:

Brzina na vreme t jednaka granici odnosa kretanja tokom vremena i vremenskog perioda tokom kojeg se ovo kretanje odvijalo, pošto potonje teži nuli

Rice. 2.5. Ka definiciji trenutne brzine.

U ovom trenutku ne razmatramo pitanje postojanja ove granice, pod pretpostavkom da ona postoji. Imajte na umu da ako postoji konačan pomak i konačan vremenski period, tada su i njihove granične vrijednosti: beskonačno mali pomak i infinitezimalni vremenski period. Dakle, desna strana definicije brzine

nije ništa više od razlomka - količnik dijeljenja sa, stoga se posljednja relacija može prepisati i vrlo često se koristi u obliku

By geometrijskog smisla derivacije, vektor brzine u svakoj tački putanje je usmjeren tangentno na putanju u ovoj tački u smjeru njenog kretanja.

Video 2.1. Vektor brzine je usmjeren tangencijalno na putanju. Eksperimentirajte s oštrilom.

Bilo koji vektor se može proširiti u bazu (za jedinične vektore baze, drugim riječima, jedinične vektore koji definiraju pozitivne smjerove osa OX,OY,OZ koristimo notaciju , , ili , respektivno). Koeficijenti ove ekspanzije su projekcije vektora na odgovarajuće ose. Važno je sljedeće: u vektorskoj algebri je dokazano da je proširenje u odnosu na bazu jedinstveno. Proširimo radijus vektor neke pokretne materijalne tačke u bazu

Uzimajući u obzir konstantnost kartezijanskih jediničnih vektora , , , razlikujemo ovaj izraz s obzirom na vrijeme

S druge strane, ekspanzija u smislu baze vektora brzine ima oblik

suprotstavljanje posljednja dva izraza, uzimajući u obzir jedinstvenost ekspanzije bilo kojeg vektora u odnosu na bazu, daje sljedeći rezultat: projekcije vektora brzine na kartezijanske ose jednake su vremenskim derivatima odgovarajućih koordinata, tj. je

Veličina vektora brzine je jednaka

Dobijmo još jedan, važan izraz za veličinu vektora brzine.

Već je napomenuto da kada vrijednost || se sve manje razlikuje od odgovarajućeg puta (vidi sliku 2). Zbog toga

i u granici (>0)

Drugim riječima, modul brzine je derivacija prijeđene udaljenosti u odnosu na vrijeme.

Konačno imamo:

Prosječna veličina vektora brzine, definira se na sljedeći način:

Prosječna vrijednost modula vektora brzine jednaka je omjeru prijeđenog puta i vremena za koje je ovaj put pređen:

Evo s(t 1, t 2)- put u vremenu od t 1 prije t 2 i shodno tome, s(t 0 , t 2)- put u vremenu od t 0 prije t 2 I s(t 0 , t 2)- put u vremenu od t 0 prije t 1.

Vektor prosječne brzine ili jednostavno prosječna brzina kao što je gore navedeno je

Imajte na umu da je, prije svega, ovo vektor, njegov modul - modul srednjeg vektora brzine ne treba brkati sa prosječnom vrijednošću modula vektora brzine. U opštem slučaju, oni nisu jednaki: modul prosječnog vektora uopće nije jednak srednjem modulu ovog vektora. Dvije operacije: izračunavanje modula i izračunavanje prosjeka, u opštem slučaju, ne mogu se zamijeniti.

Pogledajmo primjer. Neka se tačka kreće u jednom smjeru. Na sl. 2.6. pokazuje grafik putanje koju je prešla s u od vremena (tokom vremena od 0 prije t). Koristeći fizičko značenje brzinu, koristite ovaj grafikon da pronađete trenutak u vremenu u kojem je trenutna brzina jednaka prosječnoj brzini tla za prve sekunde kretanja točke.

Rice. 2.6. Određivanje trenutne i prosječne brzine tijela

Modul brzine u datom trenutku

budući da je derivacija putanje u odnosu na vrijeme, jednaka je ugaonom koeficijentu zamaha prema grafu zavisnosti tačke koja odgovara trenutku vremena t*. Prosječni modul brzine u vremenskom periodu od 0 prije t* je ugaoni koeficijent sekante koja prolazi kroz tačke istog grafa koji odgovaraju početku t = 0 i kraj t = t* vremenski interval. Moramo da pronađemo takav trenutak na vreme t*, kada se oba nagiba poklapaju. Da biste to učinili, povucite ravnu liniju kroz ishodište, tangentu na putanju. Kao što se može vidjeti sa slike, tačka tangente ovog pravog grafa je s(t) i daje t*. U našem primjeru ispada

Brzina je jedna od glavnih karakteristika. Ona izražava samu suštinu pokreta, tj. određuje razliku koja postoji između tijela koje miruje i tijela koje se kreće.

SI jedinica za brzinu je gospođa.

Važno je zapamtiti da je brzina vektorska veličina. Smjer vektora brzine određen je kretanjem. Vektor brzine je uvijek usmjeren tangencijalno na putanju u tački kroz koju prolazi tijelo koje se kreće (slika 1).

Na primjer, razmotrite točak automobila u pokretu. Točak se rotira i sve tačke točka se kreću u krug. Prskanje koje lete iz točka će letjeti duž tangenta na ove kružnice, ukazujući na smjerove vektora brzina pojedinih tačaka točka.

Dakle, brzina karakterizira smjer kretanja tijela (smjer vektora brzine) i brzinu njegovog kretanja (modul vektora brzine).

Negativna brzina

Može li brzina tijela biti negativna? Da možda. Ako je brzina nekog tijela negativna, to znači da se tijelo kreće u smjeru suprotnom od smjera koordinatne ose u odabranom referentnom sistemu. Slika 2 prikazuje kretanje autobusa i automobila. Brzina automobila je negativna, a brzina autobusa pozitivna. Treba imati na umu da kada govorimo o predznaku brzine, mislimo na projekciju vektora brzine na koordinatnu osu.

Ujednačeno i neravnomjerno kretanje

Općenito, brzina ovisi o vremenu. Prema prirodi ovisnosti brzine o vremenu, kretanje može biti ravnomjerno ili neravnomjerno.

DEFINICIJA

Ujednačeno kretanje– ovo je kretanje sa konstantnim modulom brzine.

U slučaju neravnomjernog kretanja govorimo o:

Primjeri rješavanja problema na temu "Brzina"

PRIMJER 1

Vježbajte	Automobil je prošao prvu polovinu puta između njih dvojice naselja brzinom od 90 km/h, a drugu polovinu brzinom od 54 km/h. Odredite prosječnu brzinu automobila.
Rješenje	Bilo bi pogrešno izračunati prosječnu brzinu automobila kao aritmetičku sredinu dvije navedene brzine. Koristimo definiciju prosječne brzine: Pošto se pretpostavlja pravolinijsko ravnomjerno kretanje, predznaci vektora se mogu izostaviti. Vrijeme provedeno autom za prelazak cijele udaljenosti: gdje je vrijeme potrošeno na završetak prve polovine puta, a vrijeme potrošeno na završetak druge polovine puta. Ukupno kretanje je jednako udaljenosti između naseljenih područja, tj. . Zamjenom ovih omjera u formulu za prosječnu brzinu, dobijamo: Pretvorimo brzine u pojedinačnim sekcijama u SI sistem: Tada je prosječna brzina automobila: (gospođa)
Odgovori	Prosječna brzina automobila je 18,8 m/s

PRIMJER 2

Vježbajte	Automobil putuje 10 sekundi brzinom od 10 m/s, a zatim vozi još 2 minuta brzinom od 25 m/s. Odredite prosječnu brzinu automobila.
Rješenje	Hajde da napravimo crtež.