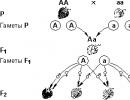
Dokazati da je funkcija neparna. Osnovna svojstva funkcije: parnost, neparnost, periodičnost, ograničenost. Dovoljni uslovi za postojanje ekstremuma
Nazad napred
Pažnja! Pregledi slajdova služe samo u informativne svrhe i možda ne predstavljaju sve karakteristike prezentacije. Ako ste zainteresovani za ovaj rad, preuzmite punu verziju.
Ciljevi:
- formiraju koncept parnosti i neparnosti funkcije, podučavaju sposobnost određivanja i upotrebe ovih svojstava kada istraživanje funkcije, crtanje;
- razvijati kreativnu aktivnost učenika, logičko razmišljanje, sposobnost poređenja, generalizacije;
- neguju marljiv rad i matematičku kulturu; razviti komunikacijske vještine .
Oprema: multimedijalna instalacija, interaktivna tabla, materijali.
Oblici rada: frontalni i grupni sa elementima aktivnosti pretraživanja i istraživanja.
Izvori informacija:
1. Algebra 9. razred A.G. Mordkovich. Udžbenik.
2. Algebra 9. razred A.G. Mordkovich. Knjiga problema.
3. Algebra 9. razred. Zadaci za učenje i razvoj učenika. Belenkova E.Yu. Lebedintseva E.A.
TOKOM NASTAVE
1. Organizacioni momenat
Postavljanje ciljeva i zadataka za lekciju.
2. Provjera domaćeg
br. 10.17 (knjiga zadataka 9. razreda. A.G. Mordkovich).
A) at = f(X), f(X) = 
b) f (–2) = –3; f (0) = –1; f(5) = 69;
c) 1. D( f) = [– 2; + ∞)
2. E( f) = [– 3; + ∞)
3. f(X) = 0 at X ~ 0,4
4. f(X) >0 at X > 0,4 ; f(X)
< 0 при – 2 <
X <
0,4.
5. Funkcija se povećava sa X € [– 2; + ∞)
6. Funkcija je ograničena odozdo.
7. at naim = – 3, at naib ne postoji
8. Funkcija je kontinuirana.
(Jeste li koristili algoritam za istraživanje funkcija?) Slajd.
2. Provjerimo tabelu koja vam je postavljena sa slajda.
| Popunite tabelu | |||||
Domain |
Funkcija nule |
Intervali konstantnosti znaka |
Koordinate tačaka preseka grafa sa Oy | ||
x = –5, |
x € (–5;3) U |
x € (–∞;–5) U |
|||
x ∞ –5, |
x € (–5;3) U |
x € (–∞;–5) U |
|||
x ≠ –5, |
x € (–∞; –5) U |
x € (–5; 2) |
|||
3. Ažuriranje znanja
– Funkcije su date.
– Odredite opseg definicije za svaku funkciju.
– Usporedite vrijednost svake funkcije za svaki par vrijednosti argumenata: 1 i – 1; 2 i – 2.
– Za koju od ovih funkcija u domenu definicije vrijede jednakosti f(– X)
= f(X), f(– X) = – f(X)? (unesite dobijene podatke u tabelu) Slajd
| f(1) i f(– 1) | f(2) i f(– 2) | grafovi | f(– X) = –f(X) | f(– X) = f(X) | ||
| 1. f(X) = | ||||||
| 2. f(X) = X 3 | ||||||
| 3. f(X) = | X | | ||||||
| 4.f(X) = 2X – 3 | ||||||
| 5. f(X) = | X ≠ 0 |
|||||
| 6. f(X)= | X > –1 | i nije definisano |
– Dok smo radili ovaj posao, momci, identifikovali smo još jedno svojstvo funkcije, vama nepoznato, ali ništa manje važno od ostalih – to je parnost i neparnost funkcije. Zapišite temu lekcije: "Parne i neparne funkcije", naš zadatak je naučiti odrediti parnost i neparnost funkcije, saznati značaj ove osobine u proučavanju funkcija i crtanju grafova.
Dakle, pronađimo definicije u udžbeniku i pročitajmo (str. 110) . Slajd
Def. 1 Funkcija at = f (X), definisan na skupu X se poziva čak, ako za bilo koju vrijednost XÊ X se izvršava jednakost f(–x)= f(x). Navedite primjere.
Def. 2 Funkcija y = f(x), definisan na skupu X se poziva odd, ako za bilo koju vrijednost XÊ X važi jednakost f(–h)= –f(h). Navedite primjere.
Gdje smo se susreli s pojmovima „parno“ i „neparno“?
Šta mislite koja će od ovih funkcija biti parna? Zašto? Koji su čudni? Zašto?
Za bilo koju funkciju obrasca at= x n, Gdje n– cijeli broj, može se tvrditi da je funkcija neparna kada n– neparan i funkcija je parna kada n– čak.
– Pregledajte funkcije at= i at = 2X– 3 nisu ni parne ni neparne, jer jednakosti nisu zadovoljene f(– X) = – f(X), f(–
X) = f(X)
Studija o tome da li je funkcija parna ili neparna naziva se proučavanjem parnosti funkcije. Slajd
U definicijama 1 i 2 govorili smo o vrijednostima funkcije na x i – x, pri čemu se pretpostavlja da je funkcija također definirana na vrijednosti X, i na – X.
Def 3. Ako numerički skup, zajedno sa svakim svojim elementom x, sadrži i suprotni element –x, tada skup X nazvan simetričnim skupom.
primjeri:
(–2;2), [–5;5]; (∞;∞) su simetrični skupovi, a , [–5;4] su asimetrični.
– Imaju li parne funkcije domen definicije koji je simetričan skup? Oni čudni?
– Ako je D( f) je asimetričan skup, koja je onda funkcija?
– Dakle, ako je funkcija at = f(X) – paran ili neparan, tada je njegov domen definicije D( f) je simetričan skup. Da li je istinita suprotna izjava: ako je domen definicije funkcije simetričan skup, da li je onda paran ili neparan?
– To znači da je prisustvo simetričnog skupa domena definicije neophodan uslov, ali ne i dovoljan.
– Dakle, kako ispitati funkciju na paritet? Pokušajmo napraviti algoritam.
Slajd
Algoritam za proučavanje funkcije za paritet
1. Odrediti da li je domen definicije funkcije simetričan. Ako nije, onda funkcija nije ni parna ni neparna. Ako jeste, onda idite na korak 2 algoritma.
2. Napišite izraz za f(–X).
3. Uporedite f(–X).I f(X):
- Ako f(–X).= f(X), tada je funkcija parna;
- Ako f(–X).= – f(X), tada je funkcija neparna;
- Ako f(–X) ≠ f(X) I f(–X) ≠ –f(X), tada funkcija nije ni parna ni neparna.
primjeri:
Ispitati funkciju a) radi pariteta at= x 5 +; b) at= ; V) at= .
Rješenje.
a) h(x) = x 5 +,
1) D(h) = (–∞; 0) U (0; +∞), simetričan skup.
2) h (– x) = (–x) 5 + – x5 –= – (x 5 +),
3) h(– x) = – h (x) => funkcija h(x)= x 5 + neparan.
b) y =,
at = f(X), D(f) = (–∞; –9)? (–9; +∞), asimetričan skup, što znači da funkcija nije ni parna ni neparna.
V) f(X) = , y = f (x),
1) D( f) = (–∞; 3] ≠ ; b) (∞; –2), (–4; 4]?
Opcija 2
1. Da li je dati skup simetričan: a) [–2;2]; b) (∞; 0], (0; 7) ?
A); b) y = x (5 – x 2).
a) y = x 2 (2x – x 3), b) y =
Grafikujte funkciju at = f(X), Ako at = f(X) je parna funkcija.

Grafikujte funkciju at = f(X), Ako at = f(X) je neparna funkcija.

Međusobna provjera slajd.
6. Domaći zadatak: №11.11, 11.21,11.22;
Dokaz geometrijskog značenja svojstva parnosti.
***(Dodjela opcije Jedinstvenog državnog ispita).
1. Neparna funkcija y = f(x) definirana je na cijeloj brojevnoj pravoj. Za bilo koju nenegativnu vrijednost varijable x, vrijednost ove funkcije poklapa se s vrijednošću funkcije g( X) = X(X + 1)(X + 3)(X– 7). Pronađite vrijednost funkcije h( X) = at X = 3.
7. Sumiranje
Zavisnost varijable y od varijable x, u kojoj svaka vrijednost x odgovara jednoj vrijednosti y, naziva se funkcija. Za označavanje koristite oznaku y=f(x). Svaka funkcija ima niz osnovnih svojstava, kao što su monotonost, parnost, periodičnost i druga.
Pogledajte bliže svojstvo pariteta.
Funkcija y=f(x) se poziva čak i ako zadovoljava sljedeća dva uslova:
2. Vrijednost funkcije u tački x, koja pripada domeni definicije funkcije, mora biti jednaka vrijednosti funkcije u tački -x. To jest, za bilo koju tačku x mora biti zadovoljena sljedeća jednakost iz domena definicije funkcije: f(x) = f(-x).
Grafikon parne funkcije
Ako nacrtate graf parne funkcije, on će biti simetričan u odnosu na Oy os.
Na primjer, funkcija y=x^2 je parna. Hajde da to proverimo. Domen definicije je cijela numerička osa, što znači da je simetrična oko tačke O.
Uzmimo proizvoljan x=3. f(x)=3^2=9.
f(-x)=(-3)^2=9. Stoga je f(x) = f(-x). Dakle, oba uslova su ispunjena, što znači da je funkcija parna. Ispod je graf funkcije y=x^2.
Slika pokazuje da je graf simetričan u odnosu na Oy os.
Grafikon neparne funkcije
Funkcija y=f(x) naziva se neparnom ako zadovoljava sljedeća dva uslova:
1. Područje definicije date funkcije mora biti simetrično u odnosu na tačku O. To jest, ako neka tačka a pripada domeni definicije funkcije, tada odgovarajuća tačka -a također mora pripadati domeni definicije date funkcije.
2. Za bilo koju tačku x, iz domena definicije funkcije mora biti zadovoljena sljedeća jednakost: f(x) = -f(x).
Graf neparne funkcije je simetričan u odnosu na tačku O - ishodište koordinata. Na primjer, funkcija y=x^3 je neparna. Hajde da to proverimo. Domen definicije je cijela numerička osa, što znači da je simetrična oko tačke O.
Uzmimo proizvoljan x=2. f(x)=2^3=8.
f(-x)=(-2)^3=-8. Stoga je f(x) = -f(x). Dakle, oba uslova su ispunjena, što znači da je funkcija neparna. Ispod je graf funkcije y=x^3.

Slika jasno pokazuje da je neparna funkcija y=x^3 simetrična u odnosu na ishodište.
Koje su vam bile poznate u ovom ili onom stepenu. Tamo je također napomenuto da će se zaliha svojstava funkcije postepeno popunjavati. U ovom odjeljku će se raspravljati o dvije nove nekretnine.
Definicija 1.
Funkcija y = f(x), x ê X, zove se čak i ako za bilo koju vrijednost x iz skupa X vrijedi jednakost f (-x) = f (x).
Definicija 2.
Funkcija y = f(x), x ê X, naziva se neparnom ako za bilo koju vrijednost x iz skupa X vrijedi jednakost f (-x) = -f (x).
Dokažite da je y = x 4 parna funkcija.
Rješenje. Imamo: f(x) = x 4, f(-x) = (-x) 4. Ali (-x) 4 = x 4. To znači da za bilo koji x vrijedi jednakost f(-x) = f(x), tj. funkcija je parna.
Slično, može se dokazati da su funkcije y - x 2, y = x 6, y - x 8 parne.
Dokaži da je y = x 3 ~ neparna funkcija.
Rješenje. Imamo: f(x) = x 3, f(-x) = (-x) 3. Ali (-x) 3 = -x 3. To znači da za bilo koje x vrijedi jednakost f (-x) = -f (x), tj. funkcija je neparna.
Slično, može se dokazati da su funkcije y = x, y = x 5, y = x 7 neparne.
Vi i ja smo se već više puta uvjerili da novi pojmovi u matematici najčešće imaju „zemaljsko“ porijeklo, tj. mogu se nekako objasniti. To je slučaj i sa parnim i neparnim funkcijama. Vidite: y - x 3, y = x 5, y = x 7 - ne čak i funkcije, dok su y = x 2, y = x 4, y = x 6 parne funkcije. I općenito, za bilo koju funkciju oblika y = x" (u nastavku ćemo posebno proučavati ove funkcije), gdje je n prirodan broj, možemo zaključiti: ako je n neparan broj, onda je funkcija y = x" odd; ako je n paran broj, tada je funkcija y = xn paran.
Postoje i funkcije koje nisu ni parne ni neparne. Takva je, na primjer, funkcija y = 2x + 3. Zaista, f(1) = 5, a f (-1) = 1. Kao što vidite, ovdje, dakle, ni identitet f(-x) = f ( x), niti identitet f(-x) = -f(x).
Dakle, funkcija može biti parna, neparna ili nijedna.
Proučavanje pitanja da li datu funkciju parno ili neparno se obično naziva proučavanjem funkcije za paritet.
Definicije 1 i 2 odnose se na vrijednosti funkcije u tačkama x i -x. Ovo pretpostavlja da je funkcija definirana i u tački x i u tački -x. To znači da tačka -x pripada domenu definicije funkcije istovremeno sa tačkom x. Ako numerički skup X, zajedno sa svakim svojim elementom x, sadrži i suprotni element -x, tada se X naziva simetričnim skupom. Recimo, (-2, 2), [-5, 5], (-oo, +oo) su simetrični skupovi, dok \).
Budući da je \(x^2\geqslant 0\) , tada je lijeva strana jednačine (*) veća ili jednaka \(0+ \mathrm(tg)^2\,1\) .
Dakle, jednakost (*) može biti istinita samo kada su obje strane jednačine jednake \(\mathrm(tg)^2\,1\) . A to znači to \[\begin(cases) 2x^2+\mathrm(tg)^2\,1=\mathrm(tg)^2\,1 \\ \mathrm(tg)\,1\cdot \mathrm(tg)\ ,(\cos x)=\mathrm(tg)^2\,1 \end(cases) \quad\Leftrightarrow\quad \begin(cases) x=0\\ \mathrm(tg)\,(\cos x) =\mathrm(tg)\,1 \end(case)\quad\Leftrightarrow\quad x=0\] Stoga nam odgovara vrijednost \(a=-\mathrm(tg)\,1\).
odgovor:
\(a\in \(-\mathrm(tg)\,1;0\)\)
Zadatak 2 #3923
Nivo zadatka: jednak Jedinstvenom državnom ispitu
Pronađite sve vrijednosti parametra \(a\) , za svaku od kojih je graf funkcije \
simetrično u odnosu na porijeklo.
Ako je graf funkcije simetričan u odnosu na ishodište, onda je takva funkcija neparna, to jest, \(f(-x)=-f(x)\) vrijedi za bilo koje \(x\) iz domene definicije funkcije. Dakle, potrebno je pronaći one vrijednosti parametara za koje je \(f(-x)=-f(x).\)
\[\begin(poravnano) &3\mathrm(tg)\,\left(-\dfrac(ax)5\desno)+2\sin \dfrac(8\pi a+3x)4= -\left(3\ mathrm(tg)\,\left(\dfrac(ax)5\desno)+2\sin \dfrac(8\pi a-3x)4\desno)\quad \Rightarrow\quad -3\mathrm(tg)\ ,\dfrac(ax)5+2\sin \dfrac(8\pi a+3x)4= -\left(3\mathrm(tg)\,\left(\dfrac(ax)5\right)+2\ sin \dfrac(8\pi a-3x)4\desno) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac(8\pi a+3x)4+\sin \dfrac(8\pi a- 3x)4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac(8\pi a+3x)4+\dfrac(8\pi a-3x)4\desno)\cdot \cos \dfrac12 \left(\dfrac(8\pi a+3x)4-\dfrac(8\pi a-3x)4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \ frac34 x=0 \end(poravnano)\]
Posljednja jednadžba mora biti zadovoljena za sve \(x\) iz domene \(f(x)\), dakle, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb(Z)\).
odgovor:
\(\dfrac n2, n\in\mathbb(Z)\)
Zadatak 3 #3069
Nivo zadatka: jednak Jedinstvenom državnom ispitu
Pronađite sve vrijednosti parametra \(a\) , za svaku od kojih jednačina \ ima 4 rješenja, gdje je \(f\) parna periodična funkcija s periodom \(T=\dfrac(16)3\) definiran na cijeloj brojevnoj pravoj , i \(f(x)=ax^2\) za \(0\leqslant x\leqslant \dfrac83.\)
(Zadatak od pretplatnika)
Zadatak 4 #3072
Nivo zadatka: jednak Jedinstvenom državnom ispitu
Pronađite sve vrijednosti \(a\) , za svaku od njih jednadžba \
ima barem jedan korijen.
(Zadatak od pretplatnika)
Prepišimo jednačinu u formu \
i razmotrite dvije funkcije: \(g(x)=7\sqrt(2x^2+49)\) i \(f(x)=3|x-7a|-6|x|-a^2+7a\ ) .
Funkcija \(g(x)\) je parna i ima minimalnu tačku \(x=0\) (i \(g(0)=49\) ).
Funkcija \(f(x)\) za \(x>0\) je opadajuća, a za \(x<0\)
– возрастающей, следовательно, \(x=0\)
– точка максимума.
Zaista, kada će se \(x>0\) drugi modul otvoriti pozitivno (\(|x|=x\) ), dakle, bez obzira na to kako će se prvi modul otvoriti, \(f(x)\) će biti jednak do \( kx+A\) , gdje je \(A\) izraz za \(a\) i \(k\) je jednako ili \(-9\) ili \(-3\) . Kada je \(x<0\)
наоборот: второй модуль раскроется отрицательно и \(f(x)=kx+A\)
, где \(k\)
равно либо \(3\)
, либо \(9\)
.
Nađimo vrijednost \(f\) na maksimalnoj tački: \ 
Da bi jednadžba imala barem jedno rješenje, potrebno je da grafovi funkcija \(f\) i \(g\) imaju barem jednu presječnu točku. Stoga vam je potrebno: \ Rešavanjem ovog skupa sistema dobijamo odgovor: \\]
odgovor:
\(a\u \(-7\)\šolja\)
Zadatak 5 #3912
Nivo zadatka: jednak Jedinstvenom državnom ispitu
Pronađite sve vrijednosti parametra \(a\) , za svaku od kojih je jednadžba \
ima šest različitih rješenja.
Napravimo zamjenu \((\sqrt2)^(x^3-3x^2+4)=t\) , \(t>0\) . Tada će jednačina poprimiti oblik \
Postepeno ćemo ispisivati uslove pod kojima će originalna jednačina imati šest rješenja.
primeti, to kvadratna jednačina\((*)\) može imati najviše dva rješenja. Bilo koja kubna jednačina \(Ax^3+Bx^2+Cx+D=0\) može imati najviše tri rješenja. Stoga, ako jednačina \((*)\) ima dva razna rješenja(pozitivno!, budući da \(t\) mora biti veći od nule) \(t_1\) i \(t_2\), tada izvođenjem obrnute zamjene dobijamo: \[\left[\begin(sakupljeno)\begin(poravnano) &(\sqrt2)^(x^3-3x^2+4)=t_1\\ &(\sqrt2)^(x^3-3x^2 +4)=t_2\end(poravnano)\end(sakupljeno)\desno.\] Budući da se bilo koji pozitivan broj može predstaviti kao \(\sqrt2\) u određenoj mjeri, npr. \(t_1=(\sqrt2)^(\log_(\sqrt2) t_1)\), tada će prva jednačina skupa biti prepisana u obliku \
Kao što smo već rekli, svaka kubična jednadžba nema više od tri rješenja, dakle, svaka jednačina u skupu neće imati više od tri rješenja. To znači da cijeli set neće imati više od šest rješenja.
To znači da da bi originalna jednadžba imala šest rješenja, kvadratna jednačina \((*)\) mora imati dva različita rješenja, a svaka rezultirajuća kubična jednačina (iz skupa) mora imati tri različita rješenja (a ne jedno rješenje jedna jednačina treba da se poklapa sa bilo kojom - odlukom druge!)
Očigledno, ako kvadratna jednadžba \((*)\) ima jedno rješenje, tada nećemo dobiti šest rješenja izvorne jednačine.
Dakle, plan rješenja postaje jasan. Hajde da zapišemo uslove koji moraju biti ispunjeni tačku po tačku.
1) Da bi jednačina \((*)\) imala dva različita rješenja, njen diskriminanta mora biti pozitivna: \
2) Također je potrebno da oba korijena budu pozitivna (pošto \(t>0\) ). Ako je proizvod dva korijena pozitivan, a njihov zbir pozitivan, tada će i sami korijeni biti pozitivni. Stoga vam je potrebno: \[\begin(cases) 12-a>0\\-(a-10)>0\end(cases)\quad\Leftrightarrow\quad a<10\]
Dakle, već smo si dali dva različita pozitivna korijena \(t_1\) i \(t_2\) .
3)
Pogledajmo ovu jednačinu \
Za koji \(t\) će imati tri različita rješenja? Dakle, utvrdili smo da oba korijena jednačine \((*)\) moraju ležati u intervalu \((1;4)\) . Kako napisati ovo stanje? Dakle, trebamo presjeći vrijednosti parametra \(a\) koji se nalaze u 1., 2. i 3. tački i dobićemo odgovor: \[\begin(cases) a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\\ a<10\\
4
Razmotrimo funkciju \(f(x)=x^3-3x^2+4\) .
Može se faktorizirati: \
Prema tome, njegove nule su: \(x=-1;2\) .
Ako nađemo derivaciju \(f"(x)=3x^2-6x\) , tada ćemo dobiti dvije tačke ekstrema \(x_(max)=0, x_(min)=2\) .
Stoga graf izgleda ovako: 
Vidimo da je bilo koja horizontalna linija \(y=k\) , gdje je \(0
Dakle, potrebno vam je: \[\početak(slučajevi) 0<\log_{\sqrt2}t_1<4\\ 0<\log_{\sqrt2}t_2<4\end{cases}\qquad (**)\]
Također odmah primijetimo da ako su brojevi \(t_1\) i \(t_2\) različiti, tada će brojevi \(\log_(\sqrt2)t_1\) i \(\log_(\sqrt2)t_2\) biti različite, što znači jednačine \(x^3-3x^2+4=\log_(\sqrt2) t_1\) I \(x^3-3x^2+4=\log_(\sqrt2) t_2\) imaće različite korene.
Sistem \((**)\) se može prepisati na sljedeći način: \[\početak(slučajevi) 1
Nećemo eksplicitno zapisivati korijene.
Razmotrimo funkciju \(g(t)=t^2+(a-10)t+12-a\) . Njegov graf je parabola sa granama nagore, koja ima dve tačke preseka sa x-osom (ovaj uslov smo zapisali u paragrafu 1)). Kako bi trebao izgledati njegov graf tako da su tačke presjeka sa x-osom u intervalu \((1;4)\)? dakle: 
Prvo, vrijednosti \(g(1)\) i \(g(4)\) funkcije u tačkama \(1\) i \(4\) moraju biti pozitivne, a drugo, vrh parabola \(t_0\ ) također mora biti u intervalu \((1;4)\) . Stoga možemo napisati sistem: \[\begin(slučajevi) 1+a-10+12-a>0\\ 4^2+(a-10)\cdot 4+12-a>0\\ 1<\dfrac{-(a-10)}2<4\end{cases}\quad\Leftrightarrow\quad 4