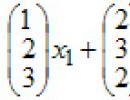Probabilističke statističke metode istraživanja ukratko. Probabilističko-statističke metode istraživanja i metoda sistemske analize. Opštenaučne metode naučnog istraživanja
Grupa metoda koja se razmatra je najvažnija u sociološkim istraživanjima, te metode se koriste u gotovo svim sociološkim studijama koje se mogu smatrati istinski naučnim. Oni su uglavnom usmjereni na identifikaciju statističkih obrazaca u empirijskim informacijama, tj. obrasci koji su ispunjeni “u prosjeku”. Zapravo, sociologija se bavi proučavanjem “prosječne osobe”. Osim toga, još jedna važna svrha korištenja probabilističkih i statističkih metoda u sociologiji je procjena pouzdanosti uzorka. Koliko je povjerenja da uzorak daje manje ili više tačne rezultate i koja je greška statističkih zaključaka?
Glavni predmet proučavanja pri primjeni probabilističkih i statističkih metoda je slučajne varijable. Uzimanje slučajne varijable na neku vrijednost je slučajni događaj– događaj koji, ako su ovi uslovi ispunjeni, može, ali i ne mora nastupiti. Na primjer, ako sociolog provodi ankete u oblasti političkih preferencija na gradskoj ulici, onda je događaj „ispostavilo se da je sljedeći ispitanik pristalica stranke na vlasti“ slučajan ako ništa od ispitanika ranije nije otkrilo njegove političke preferencije. . Ako je sociolog intervjuisao ispitanika u blizini zgrade Regionalne Dume, onda događaj više nije slučajan. Karakteriziran je slučajni događaj vjerovatnoća njegova ofanziva. Za razliku od klasičnih problema koji uključuju kombinacije kockica i karata koji se uče na kursevima vjerovatnoće, u sociološkim istraživanjima izračunavanje vjerovatnoće nije tako jednostavno.
Najvažnija osnova za empirijsku procjenu vjerovatnoće je tendencija frekvencije prema vjerovatnoći, ako pod učestalošću podrazumijevamo omjer koliko se puta događaj dogodio i koliko puta se teoretski mogao dogoditi. Na primjer, ako se od 500 nasumično odabranih na ulicama grada njih 220 ispostavi da su pristalice stranke na vlasti, onda je učestalost pojavljivanja takvih ispitanika 0,44. Kada reprezentativni uzorak dovoljno velike veličine dobićemo približnu vjerovatnoću događaja ili približan udio ljudi koji posjeduju datu osobinu. U našem primjeru, na dobro odabranom uzorku, nalazimo da je oko 44% građana pristalice stranke na vlasti. Naravno, pošto nisu svi građani anketirani, a neki su možda i lagali tokom ankete, postoji greška.
Razmotrimo neke probleme koji se javljaju u statističkoj analizi empirijskih podataka.
Procjena distribucije magnitude
Ako se određena karakteristika može kvantitativno izraziti (na primjer, politička aktivnost građanina kao vrijednost koja pokazuje koliko je puta u proteklih pet godina učestvovao na izborima na različitim nivoima), onda se može postaviti zadatak da se ocijeni zakon o raspodjeli. ove karakteristike kao slučajne varijable. Drugim riječima, zakon raspodjele pokazuje koje vrijednosti neka veličina uzima češće, a koje rjeđe, i koliko često/rjeđe. Najčešće se nalazi kako u tehnologiji i prirodi, tako iu društvu zakon normalne distribucije. Njegova formula i svojstva navedeni su u bilo kojem udžbeniku statistike, a na Sl. 10.1 prikazuje izgled grafikona - to je krivulja u obliku zvona, koja se može više "rastegnuti" prema gore ili više "razmazati" duž ose vrijednosti slučajne varijable. Suština normalnog zakona je da najčešće slučajna varijabla poprima vrijednosti blizu neke „centralne“ vrijednosti, tzv. matematičko očekivanje, i što je dalje od njega, to rjeđe vrijednost „dolazi“ tamo.
Postoji mnogo primjera distribucija koje se mogu prihvatiti kao normalne uz malu grešku. Još u 19. veku. Belgijski naučnik A. Quetelet i Englez F. Galton dokazali su da je distribucija frekvencija bilo kojeg demografskog ili antropometrijskog pokazatelja (očekivano trajanje života, visina, dob u braku, itd.) karakteristična po „zvonastoj“ distribuciji. Isti F. Galton i njegovi sljedbenici dokazali su da se psihološke karakteristike, na primjer, sposobnosti, pokoravaju normalnom zakonu.
Rice. 10.1.
Primjer
Najupečatljiviji primjer normalne distribucije u sociologiji tiče se društvene aktivnosti ljudi. Prema zakonu normalne distribucije, ispada da je društveno aktivnih ljudi u društvu obično oko 5-7%. Svi ti društveno aktivni ljudi idu na skupove, konferencije, seminare itd. Otprilike isti broj je potpuno isključen iz učešća u društvenom životu. Čini se da je većina ljudi (80–90%) indiferentna prema politici i javnom životu, ali prate procese koji ih zanimaju, iako općenito imaju distancirani odnos prema politici i društvu i ne pokazuju značajnu aktivnost. Takvi ljudi propuštaju većinu političkih događaja, ali povremeno gledaju vijesti na televiziji ili internetu. Idu glasati i na najvažnije izbore, pogotovo ako im se “prijeti štapom” ili “ohrabruje šargarepu”. Pripadnici ovih 80–90% pojedinačno su gotovo beskorisni sa društveno-političkog gledišta, ali su sociološki istraživački centri poprilično zainteresovani za te ljude, jer ih ima dosta i njihove preferencije se ne mogu zanemariti. Isto se odnosi i na pseudonaučne organizacije koje provode istraživanja po nalogu političara ili trgovačkih korporacija. A mišljenje “sive mase” o ključnim pitanjima vezanim za predviđanje ponašanja mnogih hiljada i miliona ljudi na izborima, kao i tokom akutnih političkih događaja, tokom raskola u društvu i sukoba između različitih političkih snaga, nije ravnodušno. u ove centre.
Naravno, nisu sve vrijednosti raspoređene prema normalnoj distribuciji. Osim toga, najvažnije u matematičkoj statistici su binomna i eksponencijalna raspodjela, Fisher-Snedecor, Hi-kvadrat i Student raspodjela.
Evaluacija odnosa karakteristika
Najjednostavniji slučaj je kada jednostavno trebate utvrditi prisutnost/odsustvo veze. Najpopularnija metoda u ovom pogledu je hi-kvadrat metoda. Ova metoda je fokusirana na rad sa kategorijalnim podacima. Na primjer, to su jasno spol i bračni status. Neki podaci na prvi pogled izgledaju numerički, ali se mogu "pretvoriti" u kategoričke podatke dijeljenjem raspona vrijednosti u nekoliko malih intervala. Na primjer, tvorničko iskustvo može se kategorizirati kao manje od jedne godine, jedne do tri godine, tri do šest godina i više od šest godina.
Neka parametar X dostupan P moguće vrijednosti: (x1,..., X r1), i parametar Y–t moguće vrijednosti: (y1,..., at T) , q ij je opažena učestalost pojavljivanja para ( x ja, at j), tj. broj otkrivenih pojavljivanja takvog para. Izračunavamo teorijske frekvencije, tj. koliko puta bi se svaki par vrijednosti trebao pojaviti za apsolutno nepovezane količine:

Na osnovu uočenih i teoretskih frekvencija izračunavamo vrijednost
![]()
Takođe morate izračunati iznos stepena slobode prema formuli
![]()
Gdje m, n– broj kategorija u tabeli. Osim toga, mi biramo nivo značajnosti. Što više pouzdanost koji želimo da dobijemo, treba uzeti niži nivo značaja. Obično se bira vrijednost od 0,05, što znači da možemo vjerovati rezultatima s vjerovatnoćom od 0,95. Zatim u referentnim tabelama nalazimo kritičnu vrijednost po broju stupnjeva slobode i nivou značajnosti. Ako je , onda parametri X I Y smatraju se nezavisnim. Ako je , onda parametri X I Y – zavisan. Ako, onda je opasno donositi zaključke o zavisnosti ili nezavisnosti parametara. U potonjem slučaju, preporučljivo je provesti dodatna istraživanja.
Imajte na umu da se Hi-kvadrat test može koristiti sa vrlo visokim povjerenjem samo kada sve teorijske frekvencije nisu ispod datog praga, koji se obično smatra 5. Neka je v minimalna teorijska frekvencija. Za v > 5, Hi-kvadrat test se može pouzdano koristiti. Na v< 5 использование критерия становится нежелательным. При v ≥ 5 вопрос остается открытым, требуется дополнительное исследование о применимости критерия "Хи-квадрат".
Dajemo primjer korištenja hi-kvadrat metode. Neka je, na primjer, u nekom gradu sprovedeno istraživanje među mladim navijačima lokalnih fudbalskih reprezentacija i dobijeni su sljedeći rezultati (tabela 10.1).
Hajde da iznesemo hipotezu o nezavisnosti fudbalskih preferencija omladine grada N od pola ispitanika na standardnom nivou značajnosti od 0,05. Izračunavamo teorijske frekvencije (tabela 10.2).
Tabela 10.1
Rezultati ankete navijača
Tabela 10.2
Teoretske preferencijalne frekvencije
Na primer, teorijska frekvencija za omladinske navijače Zvezde dobija se kao
slično - druge teorijske frekvencije. Zatim izračunavamo hi-kvadrat vrijednost:

Određujemo broj stupnjeva slobode. Za i nivo značajnosti od 0,05 tražimo kritičnu vrijednost:
Budući da je, a superiornost je značajna, gotovo sigurno možemo reći da su fudbalske preferencije gradskih dječaka i djevojčica N uvelike variraju, osim u slučaju nereprezentativnog uzorka, na primjer, ako istraživač nije dobio uzorak iz različitih dijelova grada, ograničavajući se na intervjuisanje ispitanika u svom bloku.
Teža situacija je kada je potrebno kvantificirati snagu veze. U ovom slučaju često se koriste metode korelacione analize. O ovim metodama se obično govori u naprednim kursevima matematičke statistike.
Aproksimacija zavisnosti korišćenjem podataka o tačkama
Neka postoji skup tačaka - empirijski podaci ( X ja, Yi), i = 1, ..., P. Potrebno je aproksimirati stvarnu zavisnost parametra at iz parametra X, te također razviti pravilo za izračunavanje vrijednosti y, Kada X nalazi se između dva "čvora" Xi.
Postoje dva fundamentalno različita pristupa rješavanju problema. Prvi je da se među funkcijama date porodice (na primjer, polinomi) bira funkcija čiji graf prolazi kroz postojeće tačke. Drugi pristup ne "prisiljava" graf funkcije da prolazi kroz tačke. Najpopularnija metoda u sociologiji i nizu drugih nauka je metoda najmanjeg kvadrata– spada u drugu grupu metoda.
Suština metode najmanjih kvadrata je sljedeća. S obzirom na porodicu funkcija at(x, a 1, ..., A t) sa m neizvesni koeficijenti. Potrebno je odabrati nesigurne koeficijente rješavanjem optimizacijskog problema
Minimalna vrijednost funkcije d može djelovati kao mjera tačnosti aproksimacije. Ako je ova vrijednost previsoka, treba odabrati drugu klasu funkcije at ili proširite korištenu klasu. Na primjer, ako klasa „polinomi stepena ne višeg od 3” nije dala prihvatljivu tačnost, uzimamo klasu „polinomi stepena ne višeg od 4” ili čak „polinomi stepena ne višeg od 5”.
Najčešće se metoda koristi za porodicu „polinoma stepena ne višeg od N":
Na primjer, kada N= 1 je porodica linearnih funkcija, sa N = 2 – porodica linearnih i kvadratnih funkcija, sa N = 3 – porodica linearnih, kvadratnih i kubnih funkcija. Neka
Tada su koeficijenti linearne funkcije ( N= 1) traže se kao rješenje sistema linearnih jednačina
Koeficijenti funkcije oblika A 0 + a 1x + a 2X 2 (N= 2) traže se kao rješenje sistema

![]()

Oni koji žele primijeniti ovu metodu na proizvoljnu vrijednost N može to učiniti tako što će vidjeti obrazac prema kojem su dati sistemi jednačina sastavljeni.
Dajemo primjer korištenja metode najmanjih kvadrata. Neka se broj određene političke stranke promijeni na sljedeći način:
Može se primijetiti da promjene veličine stranke u različitim godinama nisu mnogo različite, što nam omogućava da aproksimiramo ovisnost linearnom funkcijom. Da bi bilo lakše izračunati, umjesto varijable X– godina – uvesti varijablu t = x – 2010, tj. Uzmimo prvu godinu računanja kao “nula”. Računamo M 1; M 2:
Sada izračunavamo M", M*:
Odds a 0, a 1 funkcije y = a 0t + A 1 su izračunate kao rješenje sistema jednačina
![]()
Rješavajući ovaj sistem, na primjer, koristeći Cramerovo pravilo ili metodu zamjene, dobijamo: A 0 = 11,12; A 1 = 3,03. Tako dobijamo aproksimaciju
što vam omogućava ne samo da radite s jednom funkcijom umjesto skupom empirijskih točaka, već i da izračunate vrijednosti funkcije koje prelaze granice početnih podataka - "predvidjeti budućnost".
Također imajte na umu da se metoda najmanjih kvadrata može koristiti ne samo za polinome, već i za druge porodice funkcija, na primjer, za logaritme i eksponencijale:
Stepen pouzdanosti modela konstruiranog metodom najmanjih kvadrata može se odrediti na osnovu mjere R-kvadrata, odnosno koeficijenta determinacije. Izračunava se kao
![]()
Evo ![]() . Što bliže R 2 prema 1, što je model adekvatniji.
. Što bliže R 2 prema 1, što je model adekvatniji.
Detekcija odstupanja
Izuzetak serije podataka je anomalna vrijednost koja se oštro ističe u općem uzorku ili općoj seriji. Na primjer, neka bude postotak građana jedne zemlje koji imaju pozitivan stav prema određenom političaru 2008–2013. odnosno 15, 16, 12, 30, 14 i 12%. Lako je primijetiti da se jedna od vrijednosti oštro razlikuje od svih ostalih. Godine 2011. rejting političara je iz nekog razloga naglo premašio uobičajene vrijednosti, koje su bile u rasponu od 12-16%. Prisustvo emisija može biti uzrokovano različitim razlozima:
- 1)greške mjerenja;
- 2) neobična priroda ulaznih podataka(na primjer, kada se analizira prosječan procenat glasova koje je dobio političar; ova vrijednost na biračkom mjestu u vojnoj jedinici može se značajno razlikovati od prosječne vrijednosti u gradu);
- 3) posledica zakona(vrijednosti koje se oštro razlikuju od ostalih mogu biti posljedica matematičkog zakona - na primjer, u slučaju normalne distribucije, u uzorak može biti uključen objekt čija se vrijednost oštro razlikuje od prosjeka);
- 4) katastrofe(na primjer, u periodu kratke, ali akutne političke konfrontacije, nivo političke aktivnosti stanovništva može se dramatično promijeniti, kao što se dogodilo tokom „revolucija u boji“ 2000–2005. i „arapskog proljeća“ 2011.);
- 5) kontrolne radnje(na primjer, ako je u godini prije studije neki političar donio vrlo popularnu odluku, onda bi ove godine njegov rejting mogao biti znatno viši nego u drugim godinama).
Mnoge metode analize podataka nisu robustne za vanredne vrednosti, tako da se da bi se efikasno koristile, podaci moraju biti očišćeni od odstupanja. Upečatljiv primjer nestabilne metode je gore spomenuta metoda najmanjih kvadrata. Najjednostavniji metod za traženje outliera bazira se na tzv interkvartilna udaljenost. Određivanje dometa
Gdje Q m – značenje T- th kvartil. Ako neki član serije ne spada u raspon, onda se smatra da je izvan granica.
Objasnimo na primjeru. Značenje kvartila je da dijele niz u četiri jednake ili približno jednake grupe: prvi kvartil "odvaja" lijevu četvrtinu serije, sortiran uzlaznim redoslijedom, treći kvartil odvaja desnu četvrtinu serije, drugi kvartil trči u sredini. Hajde da objasnimo kako pretraživati Q 1, i Q 3. Ostavite niz brojeva sortiran uzlaznim redoslijedom P vrijednosti. Ako n + 1 je dakle djeljiv sa 4 bez ostatka Q k essence k(P+ 1)/4. član serije. Na primjer, s obzirom na niz: 1, 2, 5, 6, 7, 8, 10, 11, 13, 15, 20, evo broja pojmova n = 11. Zatim ( P+ 1)/4 = 3, tj. prvi kvartil Q 1 = 5 – treći član niza; 3( n + 1)/4 = 9, tj. treći kvartil Q:i= 13 – deveti član serije.
Slučaj je malo komplikovaniji kada n + 1 nije višekratnik 4. Na primjer, s obzirom na nizove 2, 3, 5, 6, 7, 8, 9, 30, 32, 100, gdje je broj članova P= 10. Tada ( P + 1)/4 = 2,75 -
položaj između drugog člana serije (v2 = 3) i trećeg člana serije (v3 = 5). Zatim uzimamo vrijednost 0,75v2 + 0,25v3 = 0,75 3 + 0,25 5 = 3,5 - to će biti Q 1. 3(P+ 1)/4 = 8,25 – pozicija između osmog člana serije (v8= 30) i devetog člana serije (v9=32). Uzimamo vrijednost 0,25v8 + 0,75v9 = 0,25 30 + + 0,75 32 = 31,5 - ovo će biti Q 3. Postoje i druge opcije proračuna Q 1 i Q 3, ali se preporučuje korištenje opcije predstavljene ovdje.
- Strogo govoreći, u praksi se obično susreće "približno" normalan zakon - budući da je normalni zakon definiran za kontinuiranu veličinu duž cijele realne ose, mnoge realne veličine ne mogu striktno zadovoljiti svojstva normalno raspoređenih veličina.
- Nasledov A. D. Matematičke metode psihološkog istraživanja. Analiza i interpretacija podataka: udžbenik, priručnik. Sankt Peterburg: Reč, 2004. str. 49–51.
- Za najvažnije distribucije slučajnih varijabli, pogledajte, na primjer: Orlov A.I. Matematika slučaja: vjerovatnoća i statistika - osnovne činjenice: udžbenik. dodatak. M.: MZ-Press, 2004.
Prilikom izvođenja psihološko-pedagoških istraživanja značajna uloga se pridaje matematičkim metodama modeliranja procesa i obrade eksperimentalnih podataka. Ove metode uključuju, prije svega, takozvane vjerovatno-statističke metode istraživanja. To je zbog činjenice da na ponašanje pojedinca u procesu njegove aktivnosti i osobe u timu značajno utiču mnogi slučajni faktori. Slučajnost nam ne dozvoljava da opišemo pojave u okviru determinističkih modela, jer se manifestuje kao nedovoljna pravilnost u masovnim pojavama i stoga ne omogućava pouzdano predviđanje nastanka određenih događaja. Međutim, kada se proučavaju takvi fenomeni, otkrivaju se određeni obrasci. Nepravilnost svojstvena slučajnim događajima, sa velikim brojem testova, obično se nadoknađuje pojavom statističkog obrasca, stabilizacijom učestalosti pojavljivanja slučajnih događaja. Stoga, ovi slučajni događaji imaju određenu vjerovatnoću. Postoje dvije fundamentalno različite probabilističko-statističke metode psihološkog i pedagoškog istraživanja: klasična i neklasična. Hajde da izvršimo komparativnu analizu ovih metoda.
Klasična probabilističko-statistička metoda. Klasična probabilističko-statistička metoda istraživanja zasniva se na teoriji vjerovatnoće i matematičkoj statistici. Ova metoda se koristi u proučavanju masovnih pojava slučajne prirode, uključuje nekoliko faza, od kojih su glavne sljedeće.
1. Izgradnja vjerovatnog modela stvarnosti na osnovu analize statističkih podataka (određivanje zakona raspodjele slučajne varijable). Naravno, obrasci masovnih nasumičnih pojava su izraženiji jasnije što je veći obim statističkog materijala. Podaci uzorka dobijeni tokom eksperimenta uvijek su ograničeni i, strogo govoreći, slučajne prirode. U tom smislu, značajna uloga se daje generalizaciji uzoraka dobijenih iz uzorka i njihovom proširenju na cjelokupnu populaciju objekata. Da bi se riješio ovaj problem, prihvaća se određena hipoteza o prirodi statističkog obrasca koji se manifestira u fenomenu koji se proučava, na primjer, hipoteza da se proučavani fenomen pokorava zakonu normalne distribucije. Ova hipoteza se naziva nultom hipotezom, koja se može pokazati lažnom, pa se uz nultu hipotezu postavlja i alternativna ili konkurentska hipoteza. Provjera koliko dobro dobiveni eksperimentalni podaci odgovaraju određenoj statističkoj hipotezi provodi se korištenjem takozvanih neparametarskih statističkih testova ili testova dobrosti. Trenutno se široko koriste kriterijumi dobrog uklapanja Kolmogorov, Smirnov, omega-kvadrat itd. Osnovna ideja ovih testova je mjerenje udaljenosti između empirijske funkcije distribucije i potpuno poznate teorijske funkcije distribucije. Metodologija testiranja statističke hipoteze je rigorozno razvijena i predstavljena u velikom broju radova o matematičkoj statistici.
2. Izvođenje potrebnih proračuna korištenjem matematičkih sredstava u okviru vjerovatnog modela. U skladu sa utvrđenim probabilističkim modelom pojave, vrše se proračuni karakterističnih parametara, na primjer, kao što su matematičko očekivanje ili srednja vrijednost, disperzija, standardna devijacija, mod, medijan, indeks asimetrije itd.
3. Interpretacija probabilističkih i statističkih zaključaka u odnosu na realno stanje.
Trenutno je klasična probabilističko-statistička metoda dobro razvijena i široko se koristi u istraživanjima u različitim oblastima prirodnih, tehničkih i društvenih nauka. Detaljan opis suštine ove metode i njene primjene na rješavanje konkretnih problema može se naći u velikom broju književnih izvora, na primjer u.
Neklasična probabilističko-statistička metoda. Neklasična probabilističko-statistička metoda istraživanja razlikuje se od klasične po tome što se primjenjuje ne samo na masovne događaje, već i na pojedinačne događaje koji su u osnovi slučajni po prirodi. Ova metoda se može efikasno koristiti u analizi ponašanja pojedinca u procesu obavljanja određene aktivnosti, na primjer, u procesu asimilacije znanja od strane učenika. Razmotrićemo karakteristike neklasične probabilističko-statističke metode psihološko-pedagoškog istraživanja na primjeru ponašanja učenika u procesu sticanja znanja.
U radu je po prvi put predložen probabilističko-statistički model ponašanja učenika u procesu sticanja znanja. U radu je izvršen dalji razvoj ovog modela. Nastava kao vrsta aktivnosti, čija je svrha sticanje znanja, vještina i sposobnosti od strane osobe, zavisi od stepena razvoja svijesti učenika. Struktura svijesti uključuje kognitivne procese kao što su osjet, percepcija, pamćenje, mišljenje, mašta. Analiza ovih procesa pokazuje da ih karakterišu elementi slučajnosti, zbog nasumične prirode psihičkih i somatskih stanja pojedinca, kao i fiziološke, psihološke i informacione buke tokom rada mozga. Potonje je dovelo, kada se opisuju misaoni procesi, do napuštanja upotrebe determinističkog modela dinamičkog sistema u korist modela slučajnog dinamičkog sistema. To znači da se determinizam svijesti ostvaruje kroz slučaj. Iz ovoga možemo zaključiti da ljudsko znanje, koje je zapravo proizvod svijesti, ima i slučajnu prirodu, te se stoga vjerovatno-statističkom metodom može opisati ponašanje svakog pojedinog učenika u procesu sticanja znanja.
U skladu sa ovom metodom, student se identifikuje pomoću funkcije distribucije (gustine verovatnoće), koja određuje verovatnoću da se nađe u jednom delu informacionog prostora. Tokom procesa učenja, funkcija distribucije sa kojom se učenik identifikuje kreće se u informacionom prostoru kako se razvija. Svaki student ima individualna svojstva i dozvoljena je nezavisna lokalizacija (prostorna i kinematička) pojedinaca u odnosu na druge.
Na osnovu zakona održanja vjerovatnoće napisan je sistem diferencijalnih jednadžbi, koje su jednačine kontinuiteta koje povezuju promjenu gustine vjerovatnoće po jedinici vremena u faznom prostoru (prostor koordinata, brzina i ubrzanja različitog reda) sa divergencijom. protoka gustoće vjerovatnoće u faznom prostoru koji se razmatra. Provedena je analiza analitičkih rješenja niza jednačina kontinuiteta (funkcija distribucije) koje karakteriziraju ponašanje pojedinih učenika u procesu učenja.
Prilikom izvođenja eksperimentalnih studija ponašanja učenika u procesu sticanja znanja koristi se vjerovatno-statističko skaliranje prema kojem je mjerna skala uređeni sistem.
1. Pronalaženje eksperimentalnih funkcija raspodjele na osnovu rezultata kontrolnog događaja, na primjer, ispita. Tipičan oblik pojedinačnih funkcija distribucije pronađen na skali od dvadeset tačaka prikazan je na Sl. 1. Metoda za pronalaženje takvih funkcija je opisana u.
2. Preslikavanje funkcija distribucije u brojevni prostor. U tu svrhu izračunavaju se momenti pojedinih funkcija raspodjele. U praksi je, po pravilu, dovoljno da se ograničimo na određivanje momenata prvog reda (matematičko očekivanje), drugog reda (varijansa) i trećeg reda, koji karakterišu asimetriju funkcije raspodele.
3. Rangiranje učenika po nivou znanja na osnovu poređenja momenata različitih redova njihovih pojedinačnih funkcija raspodele.
Rice. 1. Tipični oblik individualnih funkcija raspodjele učenika koji su dobili različite ocjene na ispitu iz opšte fizike: 1 - tradicionalna ocjena “2”; 2 - tradicionalna ocjena “3”; 3 - tradicionalna ocjena “4”; 4 - tradicionalna ocjena “5”
Na osnovu aditivnosti pojedinačnih funkcija raspodjele, pronađene su eksperimentalne funkcije raspodjele za protok studenata (slika 2).

Rice. 2. Evolucija kompletne funkcije distribucije studentskog toka, aproksimirana glatkim linijama: 1 - nakon prve godine; 2 - nakon druge godine; 3 - nakon treće godine; 4 - nakon četvrte godine; 5 - nakon pete godine
Analiza podataka prikazanih na sl. 2 pokazuje da kako se krećemo kroz informacijski prostor, funkcije distribucije postaju zamagljene. To se događa zbog činjenice da se matematička očekivanja funkcija distribucije pojedinaca kreću različitim brzinama, a same funkcije zamagljuju zbog disperzije. Dalja analiza ovih funkcija distribucije može se izvršiti u okviru klasične probabilističko-statističke metode.
Diskusija o rezultatima. Analiza klasičnih i neklasičnih probabilističko-statističkih metoda psiholoških i pedagoških istraživanja pokazala je da između njih postoji značajna razlika. Kao što se iz navedenog može shvatiti, klasična metoda je primjenjiva samo na analizu masovnih događaja, a neklasična metoda je primjenjiva i na analizu masovnih i pojedinačnih događaja. S tim u vezi, klasična metoda se uslovno može nazvati masovnom vjerovatnoćom-statističkom metodom (MPSM), a neklasična metoda - individualnom vjerovatnoćom-statističkom metodom (IPSM). U 4] je pokazano da se nijedna od klasičnih metoda za procjenu znanja studenata u okviru vjerovatno-statističkog modela pojedinca ne može primijeniti u ove svrhe.
Razmotrimo karakteristike MVSM i IVSM metoda na primjeru mjerenja potpunosti znanja učenika. U tu svrhu, izvršimo misaoni eksperiment. Pretpostavimo da postoji veliki broj učenika koji su apsolutno identični po psihičkim i fizičkim karakteristikama i imaju istu pozadinu, i neka, bez interakcije jedni s drugima, istovremeno učestvuju u istom kognitivnom procesu, doživljavajući apsolutno isto striktno određeno uticaj. Zatim, u skladu sa klasičnim idejama o objektima merenja, svi učenici treba da dobiju iste ocene o potpunosti znanja sa bilo kojom tačnošću merenja. Međutim, u stvarnosti, uz dovoljno visoku tačnost mjerenja, ocjene kompletnosti znanja učenika će se razlikovati. Ovaj rezultat mjerenja nije moguće objasniti u okviru MVSM-a, jer se inicijalno pretpostavlja da je utjecaj na apsolutno identične učenike koji nisu u interakciji jedni s drugima strogo determinističke prirode. Klasična probabilističko-statistička metoda ne uzima u obzir činjenicu da se determinizam procesa spoznaje ostvaruje kroz slučajnost, koja je svojstvena svakom pojedincu koji spoznaje svijet oko sebe.
Nasumična priroda ponašanja učenika u procesu sticanja znanja uzima u obzir IVSM. Upotreba individualne probabilističko-statističke metode za analizu ponašanja idealizovane grupe učenika koja se razmatra pokazala bi da je nemoguće naznačiti tačan položaj svakog studenta u informacionom prostoru, već se može reći samo verovatnoća da se on nađe u jedno ili drugo područje informacionog prostora. Zapravo, svaki učenik je identificiran individualnom funkcijom distribucije, a njeni parametri, kao što su matematičko očekivanje, varijansa, itd., individualni su za svakog učenika. To znači da će pojedinačne funkcije distribucije biti locirane u različitim područjima informacionog prostora. Razlog ovakvog ponašanja učenika leži u nasumičnoj prirodi procesa učenja.
Međutim, u određenom broju slučajeva rezultati istraživanja dobijeni u okviru IVSM mogu se tumačiti u okviru IVSM. Pretpostavimo da nastavnik koristi petostepenu skalu kada ocjenjuje znanje učenika. U ovom slučaju greška u ocjenjivanju znanja iznosi ±0,5 bodova. Dakle, kada student dobije ocjenu od, na primjer, 4 boda, to znači da je njegovo znanje u rasponu od 3,5 do 4,5 bodova. Naime, položaj pojedinca u informacionom prostoru u ovom slučaju je određen pravokutnom funkcijom raspodjele, čija je širina jednaka mjernoj grešci od ±0,5 bodova, a procjena je matematičko očekivanje. Ova greška je toliko velika da nam ne dozvoljava da uočimo pravi oblik funkcije distribucije. Međutim, uprkos ovako gruboj aproksimaciji funkcije distribucije, proučavanje njene evolucije nam omogućava da dobijemo važne informacije kako o ponašanju pojedinca tako i o grupi učenika u cjelini.
Na rezultat mjerenja kompletnosti znanja učenika direktno ili indirektno utiče svijest nastavnika (mjeritelja), koju također karakteriše slučajnost. U procesu pedagoških mjerenja zapravo dolazi do interakcije između dva slučajna dinamička sistema koji identifikuju ponašanje učenika i nastavnika u ovom procesu. Razmatra se interakcija studentskog podsistema sa nastavnim podsistemom i pokazuje da je brzina kretanja matematičkog očekivanja pojedinih funkcija distribucije učenika u informacionom prostoru proporcionalna funkciji uticaja nastavnog osoblja i obrnuto. proporcionalno funkciji inercije, koja karakteriše neuhvatljivost promjene položaja matematičkog očekivanja u prostoru (analog Aristotelovog zakona u mehanici).
U ovom trenutku, uprkos značajnim dostignućima u razvoju teorijskih i praktičnih osnova za mjerenja pri izvođenju psihološko-pedagoških istraživanja, problem mjerenja u cjelini još uvijek je daleko od rješenja. To je prije svega zbog činjenice da još uvijek nema dovoljno informacija o utjecaju svijesti na proces mjerenja. Slična situacija je nastala i pri rješavanju mjernog problema u kvantnoj mehanici. Tako se u radu, kada se razmatraju konceptualni problemi kvantne teorije mjerenja, kaže da je rješavanje nekih paradoksa mjerenja u kvantnoj mehanici „... teško moguće bez direktnog uključivanja svijesti posmatrača u teorijski opis kvantno mjerenje.” Dalje se kaže da „... dosljedno je pretpostaviti da svijest može učiniti neki događaj vjerovatnim, čak i ako je, prema zakonima fizike (kvantne mehanike), vjerovatnoća ovog događaja mala. Napravimo važno pojašnjenje formulacije: svest datog posmatrača može učiniti verovatnim da će on videti ovaj događaj.”
Pošaljite svoj dobar rad u bazu znanja je jednostavno. Koristite obrazac ispod
Studenti, postdiplomci, mladi naučnici koji koriste bazu znanja u svom studiranju i radu biće vam veoma zahvalni.
Objavljeno na http://www.allbest.ru/
Objavljeno na http://www.allbest.ru/
Uvod
1. Hi-kvadrat raspodjela
Zaključak
Aplikacija
Uvod
Kako se pristupi, ideje i rezultati teorije vjerovatnoće koriste u našim životima? matematička teorija kvadrata
Osnova je probabilistički model realne pojave ili procesa, tj. matematički model u kojem se objektivni odnosi izražavaju u terminima teorije vjerovatnoće. Vjerovatnoće se prvenstveno koriste za opisivanje neizvjesnosti koje se moraju uzeti u obzir prilikom donošenja odluka. To se odnosi i na nepoželjne prilike (rizici) i na one atraktivne („sretna prilika“). Ponekad se slučajnost namjerno uvodi u situaciju, na primjer, prilikom izvlačenja ždrijeba, nasumičnog odabira jedinica za kontrolu, provođenja lutrije ili provođenja anketa potrošača.
Teorija vjerovatnoće dozvoljava da se jedna vjerovatnoća koristi za izračunavanje drugih od interesa za istraživača.
Vjerovatni model pojave ili procesa je osnova matematičke statistike. Koriste se dvije paralelne serije koncepata - oni koji se odnose na teoriju (vjerovatni model) i oni koji se odnose na praksu (uzorkovanje rezultata posmatranja). Na primjer, teorijska vjerovatnoća odgovara frekvenciji pronađenoj iz uzorka. Matematičko očekivanje (teorijski niz) odgovara uzorku aritmetičke sredine (praktične serije). Po pravilu, karakteristike uzorka su procjene teorijskih. Istovremeno, količine koje se odnose na teorijske serije „su u glavama istraživača“, odnose se na svijet ideja (prema starogrčkom filozofu Platonu) i nisu dostupne za direktno mjerenje. Istraživači imaju samo uzorke podataka pomoću kojih pokušavaju utvrditi svojstva teorijskog vjerojatnosnog modela koji ih zanimaju.
Zašto nam je potreban probabilistički model? Činjenica je da se samo uz njegovu pomoć svojstva utvrđena analizom konkretnog uzorka mogu prenijeti na druge uzorke, kao i na cjelokupnu tzv. opštu populaciju. Termin "populacija" se koristi kada se odnosi na veliku, ali konačnu kolekciju jedinica koje se proučavaju. Na primjer, o ukupnosti svih stanovnika Rusije ili ukupnosti svih potrošača instant kafe u Moskvi. Cilj marketinških ili socioloških istraživanja je prenošenje izjava dobijenih sa uzorka od stotina ili hiljada ljudi na populaciju od nekoliko miliona ljudi. U kontroli kvaliteta, serija proizvoda djeluje kao opća populacija.
Za prenošenje zaključaka sa uzorka na veću populaciju potrebne su neke pretpostavke o odnosu karakteristika uzorka sa karakteristikama ove veće populacije. Ove pretpostavke su zasnovane na odgovarajućem vjerovatnostnom modelu.
Naravno, moguće je obraditi podatke uzorka bez korištenja jednog ili drugog vjerovatnostnog modela. Na primjer, možete izračunati uzorak aritmetičke sredine, izbrojati učestalost ispunjenja određenih uslova itd. Međutim, rezultati proračuna odnosit će se samo na određeni uzorak, a prenošenje zaključaka dobivenih uz njihovu pomoć na bilo koju drugu populaciju nije ispravno. Ova aktivnost se ponekad naziva "analiza podataka". U poređenju sa probabilističko-statističkim metodama, analiza podataka ima ograničenu edukativnu vrijednost.
Dakle, upotreba probabilističkih modela zasnovanih na procjeni i testiranju hipoteza korištenjem karakteristika uzorka predstavlja suštinu vjerovatno-statističkih metoda donošenja odluka.
1. Hi-kvadrat raspodjela
Koristeći normalnu distribuciju, definirane su tri distribucije koje se danas često koriste u statističkoj obradi podataka. To su Pirsonova („hi-kvadrat”), Studentova i Fišerova distribucija.
Fokusiraćemo se na distribuciju („hi-kvadrat“). Ovu distribuciju prvi je proučavao astronom F. Helmert 1876. godine. U vezi sa teorijom Gaussove greške, proučavao je sume kvadrata n nezavisnih standardno normalno distribuiranih slučajnih varijabli. Kasnije je Karl Pearson ovoj funkciji distribucije dao naziv "hi-kvadrat". I sada distribucija nosi njegovo ime.
Zbog svoje bliske veze sa normalnom distribucijom, distribucija h2 igra važnu ulogu u teoriji vjerovatnoće i matematičkoj statistici. Distribucija h2 i mnoge druge distribucije koje su određene distribucijom h2 (na primjer, Studentova raspodjela), opisuju uzorke distribucije različitih funkcija iz normalno raspoređenih rezultata posmatranja i koriste se za konstruiranje intervala povjerenja i statističkih testova.
Pirsonova distribucija (chi - kvadrat) - raspodela slučajne varijable, gde su X1, X2,..., Xn normalne nezavisne slučajne varijable, a matematičko očekivanje svake od njih je nula, a standardna devijacija jedan.
Zbir kvadrata
distribuiraju u skladu sa zakonom (“chi - kvadrat”).
U ovom slučaju, broj pojmova, tj. n se naziva "broj stepeni slobode" hi-kvadrat distribucije. Kako se broj stupnjeva slobode povećava, distribucija se polako približava normalnoj.
Gustina ove distribucije
Dakle, distribucija h2 zavisi od jednog parametra n - broja stepeni slobode.
Funkcija distribucije h2 ima oblik:
ako je h2?0. (2.7.)
Na slici 1 prikazan je graf gustoće vjerovatnoće i funkcija raspodjele h2 za različite stupnjeve slobode.
Slika 1. Zavisnost gustine vjerovatnoće q (x) u distribuciji h2 (hi - kvadrat) za različite brojeve stupnjeva slobode
Trenuci distribucije hi-kvadrat:
Hi-kvadrat distribucija se koristi u procjeni varijanse (koristeći interval povjerenja), testiranju hipoteza slaganja, homogenosti, nezavisnosti, prvenstveno za kvalitativne (kategorizirane) varijable koje uzimaju konačan broj vrijednosti, te u mnogim drugim zadacima statističke analize podataka. .
2. "Hi-kvadrat" u problemima statističke analize podataka
Statističke metode analize podataka koriste se u gotovo svim područjima ljudske djelatnosti. Koriste se kad god je potrebno dobiti i opravdati bilo kakve prosudbe o grupi (objekti ili subjekti) s nekom unutrašnjom heterogenošću.
Savremeni stupanj razvoja statističkih metoda može se računati od 1900. godine, kada je Englez K. Pearson osnovao časopis "Biometrika". Prva trećina dvadesetog veka. prošla pod znakom parametarske statistike. Metode su proučavane na osnovu analize podataka iz parametarskih porodica distribucija opisanih krivuljama Pearsonove porodice. Najpopularnija je bila normalna distribucija. Za testiranje hipoteza korišćeni su Pirsonov, Studentov i Fišerov test. Predložena je metoda maksimalne vjerovatnoće i analiza varijanse, te su formulirane osnovne ideje planiranja eksperimenta.
Hi-kvadrat distribucija je jedna od najčešće korištenih u statistici za testiranje statističkih hipoteza. Na osnovu hi-kvadrat distribucije, konstruisan je jedan od najmoćnijih testova dobrote uklapanja - Pirsonov hi-kvadrat test.
Kriterijum slaganja je kriterijum za proveru hipoteze o pretpostavljenom zakonu nepoznate raspodele.
Test h2 ("hi-kvadrat") se koristi za testiranje hipoteze različitih distribucija. Ovo je njegovo dostojanstvo.
Proračunska formula kriterija je jednaka
gdje su m i m" empirijske i teorijske frekvencije, respektivno
dotična distribucija;
n je broj stepeni slobode.
Da bismo provjerili, moramo uporediti empirijske (opažene) i teorijske (izračunate pod pretpostavkom normalne distribucije) frekvencije.
Ako se empirijske frekvencije u potpunosti poklapaju sa frekvencijama izračunatim ili očekivanim, S (E - T) = 0 i kriterij h2 će također biti jednak nuli. Ako S (E - T) nije jednako nuli, to će ukazati na neslaganje između izračunatih frekvencija i empirijskih frekvencija serije. U takvim slučajevima potrebno je procijeniti značajnost kriterija h2, koji teoretski može varirati od nule do beskonačnosti. Ovo se radi upoređivanjem stvarne vrijednosti h2f sa njegovom kritičnom vrijednošću (h2st).Nulta hipoteza, tj. pretpostavka da je neslaganje između empirijske i teorijske ili očekivane frekvencije nasumično, pobija se ako je h2f veći ili jednak h2st za prihvaćeni nivo značajnosti (a) i broj stepena slobode (n).
Distribucija vjerojatnih vrijednosti slučajne varijable h2 je kontinuirana i asimetrična. Zavisi od broja stupnjeva slobode (n) i približava se normalnoj raspodjeli kako se broj opažanja povećava. Stoga je primjena h2 kriterija na procjenu diskretnih distribucija povezana sa nekim greškama koje utiču na njegovu vrijednost, posebno na malim uzorcima. Da bi se dobile preciznije procjene, uzorak raspoređen u niz varijacija mora imati najmanje 50 opcija. Pravilna primjena kriterija h2 također zahtijeva da frekvencije varijanti u ekstremnim klasama ne budu manje od 5; ako ih je manje od 5, onda se kombinuju sa frekvencijama susjednih klasa tako da je ukupan iznos veći ili jednak 5. U skladu sa kombinacijom frekvencija, broj klasa (N) se smanjuje. Broj stupnjeva slobode utvrđuje se sekundarnim brojem klasa, uzimajući u obzir broj ograničenja slobode varijacije.
Budući da tačnost određivanja h2 kriterija u velikoj mjeri zavisi od tačnosti izračunavanja teoretskih frekvencija (T), za dobijanje razlike između empirijske i izračunate frekvencije treba koristiti nezaokružene teorijske frekvencije.
Kao primjer, uzmimo studiju objavljenu na web stranici posvećenoj primjeni statističkih metoda u humanističkim naukama.
Hi-kvadrat test vam omogućava da uporedite distribuciju frekvencija bez obzira na to da li su normalno raspoređene ili ne.
Učestalost se odnosi na broj pojavljivanja događaja. Obično se učestalost pojavljivanja događaja bavi kada se varijable mjere na skali imena i njihove druge karakteristike, osim učestalosti, nije moguće ili problematično odabrati. Drugim riječima, kada varijabla ima kvalitativne karakteristike. Takođe, mnogi istraživači imaju tendenciju da konvertuju rezultate testova u nivoe (visoki, prosečni, niski) i prave tabele distribucije rezultata kako bi saznali broj ljudi na ovim nivoima. Da bi se dokazalo da je na jednom od nivoa (u jednoj od kategorija) broj ljudi zaista veći (manji) koristi se i hi-kvadrat koeficijent.
Pogledajmo najjednostavniji primjer.
Proveden je test među mlađim adolescentima kako bi se utvrdilo samopoštovanje. Rezultati testova su konvertovani u tri nivoa: visok, srednji, nizak. Frekvencije su raspoređene na sljedeći način:
Visoka (B) 27 osoba.
Prosjek (C) 12 osoba.
Niska (L) 11 osoba
Očigledno je da većina djece ima visoko samopoštovanje, ali to treba statistički dokazati. Da bismo to učinili, koristimo Hi-kvadrat test.
Naš zadatak je provjeriti da li se dobijeni empirijski podaci razlikuju od teorijski jednako vjerovatnih. Da biste to učinili, morate pronaći teorijske frekvencije. U našem slučaju, teorijske frekvencije su jednako vjerovatne frekvencije, koje se nalaze sabiranjem svih frekvencija i dijeljenjem sa brojem kategorija.
u našem slučaju:
(B + C + H)/3 = (27+12+11)/3 = 16,6
Formula za izračunavanje hi-kvadrat testa:
h2 = ?(E - T)I / T
Izrađujemo sto:
|
Empirijski (E) |
Teorijski (T) |
(E - T)I / T |
||
Pronađite zbir zadnje kolone:
Sada morate pronaći kritičnu vrijednost kriterija koristeći tablicu kritičnih vrijednosti (Tablica 1 u Dodatku). Za to nam je potreban broj stupnjeva slobode (n).
n = (R - 1) * (C - 1)
gdje je R broj redova u tabeli, C je broj kolona.
U našem slučaju postoji samo jedna kolona (što znači originalne empirijske frekvencije) i tri reda (kategorije), pa se formula mijenja - izuzimamo kolone.
n = (R - 1) = 3-1 = 2
Za vjerovatnoću greške p?0,05 i n = 2, kritična vrijednost je h2 = 5,99.
Dobijena empirijska vrijednost je veća od kritične vrijednosti – razlike u frekvencijama su značajne (h2 = 9,64; p? 0,05).
Kao što vidite, izračunavanje kriterija je vrlo jednostavno i ne oduzima puno vremena. Praktična vrijednost hi-kvadrat testa je ogromna. Ova metoda je najvrednija kada se analiziraju odgovori na upitnike.
Pogledajmo složeniji primjer.
Na primjer, psiholog želi da zna da li je istina da su nastavnici pristrasniji prema dječacima nego prema djevojčicama. One. verovatnije je da hvali devojke. Da bi to uradila, psiholog je analizirao karakteristike učenika koje su napisali nastavnici na učestalost pojavljivanja tri reči: „aktivan“, „marljiv“, „disciplinovan“, a takođe su prebrojani i sinonimi reči.
Podaci o učestalosti pojavljivanja riječi uneseni su u tabelu:
Za obradu dobijenih podataka koristimo hi-kvadrat test.
Da bismo to uradili, napravićemo tabelu raspodele empirijskih frekvencija, tj. one frekvencije koje opažamo:
Teoretski, očekujemo da će frekvencije biti podjednako raspoređene, tj. učestalost će biti raspoređena proporcionalno između dječaka i djevojčica. Napravimo tabelu teoretskih frekvencija. Da biste to učinili, pomnožite zbir reda sa zbirom kolone i podijelite rezultirajući broj sa ukupnim zbrojem (s).
Konačna tabela za proračun će izgledati ovako:
|
Empirijski (E) |
Teorijski (T) |
(E - T)I / T |
|||
|
Momci |
"aktivan" |
||||
|
"Marljiv" |
|||||
|
"disciplinovan" |
|||||
|
"aktivan" |
|||||
|
"Marljiv" |
|||||
|
"disciplinovan" |
|||||
|
Iznos: 4.21 |
h2 = ?(E - T)I / T
gdje je R broj redova u tabeli.
U našem slučaju, hi-kvadrat = 4,21; n = 2.
Koristeći tablicu kritičnih vrijednosti kriterija, nalazimo: sa n = 2 i nivoom greške od 0,05, kritična vrijednost h2 = 5,99.
Rezultirajuća vrijednost je manja od kritične vrijednosti, što znači da je nulta hipoteza prihvaćena.
Zaključak: nastavnici ne pridaju značaj polu djeteta kada mu pišu karakteristike.
Zaključak
Studenti gotovo svih specijalnosti na kraju kursa više matematike izučavaju sekciju „teorija vjerovatnoće i matematička statistika“, a u stvarnosti se upoznaju samo sa nekim osnovnim pojmovima i rezultatima, koji očigledno nisu dovoljni za praktičan rad. Studenti se u posebnim predmetima upoznaju sa nekim matematičkim metodama istraživanja (npr. „Prognoziranje i tehničko-ekonomsko planiranje“, „Tehnička i ekonomska analiza“, „Kontrola kvaliteta proizvoda“, „Marketing“, „Kontroliranje“, „Matematičke metode predviđanja“. ”) “, „Statistika” itd. - u slučaju studenata ekonomskih specijalnosti), međutim, prikaz je u većini slučajeva vrlo štur i formularne prirode. Kao rezultat toga, znanje stručnjaka za primijenjenu statistiku je nedovoljno.
Stoga je od velike važnosti predmet „Primijenjena statistika“ na tehničkim fakultetima, a predmet „Ekonometrija“ na ekonomskim fakultetima, jer je ekonometrija, kao što je poznato, statistička analiza konkretnih ekonomskih podataka.
Teorija vjerovatnoće i matematička statistika pružaju osnovna znanja za primijenjenu statistiku i ekonometriju.
Potrebni su specijalistima za praktičan rad.
Pogledao sam kontinuirani probabilistički model i pokušao na primjerima pokazati njegovu upotrebu.
I na kraju svog rada došao sam do zaključka da je kompetentna implementacija osnovnih postupaka matematičko-statičke analize podataka i statičkog testiranja hipoteza nemoguća bez poznavanja hi-kvadrat modela, kao i sposobnosti korištenja njegovog sto.
Bibliografija
1. Orlov A.I. Primijenjena statistika. M.: Izdavačka kuća "Ispit", 2004.
2. Gmurman V.E. Teorija vjerojatnosti i matematička statistika. M.: Viša škola, 1999. - 479 str.
3. Ayvozyan S.A. Teorija vjerovatnoće i primijenjena statistika, tom 1. M.: Jedinstvo, 2001. - 656 str.
4. Khamitov G.P., Vedernikova T.I. Vjerovatnoće i statistika. Irkutsk: BGUEP, 2006 - 272 str.
5. Ezhova L.N. Ekonometrija. Irkutsk: BGUEP, 2002. - 314 str.
6. Mosteller F. Pedeset zabavnih probabilističkih problema s rješenjima. M.: Nauka, 1975. - 111 str.
7. Mosteller F. Vjerovatnoća. M.: Mir, 1969. - 428 str.
8. Yaglom A.M. Vjerovatnoća i informacija. M.: Nauka, 1973. - 511 str.
9. Čistjakov V.P. Kurs teorije vjerovatnoće. M.: Nauka, 1982. - 256 str.
10. Kremer N.Sh. Teorija vjerojatnosti i matematička statistika. M.: JEDINSTVO, 2000. - 543 str.
11. Matematička enciklopedija, vol.1. M.: Sovjetska enciklopedija, 1976. - 655 str.
12. http://psystat.at.ua/ - Statistika u psihologiji i pedagogiji. Članak Hi-kvadrat test.
Aplikacija
Kritične tačke distribucije h2
Tabela 1
Objavljeno na Allbest.ru
...Slični dokumenti
Vjerovatni model i aksiomatika A.N. Kolmogorov. Slučajne varijable i vektori, klasični granični problem teorije vjerovatnoće. Primarna obrada statističkih podataka. Tačkaste procjene numeričkih karakteristika. Statističko testiranje hipoteza.
priručnik za obuku, dodan 03.02.2010
Pravila za izvođenje i ispunjavanje testova za dopisni odjel. Zadaci i primjeri rješavanja zadataka iz matematičke statistike i teorije vjerojatnosti. Tabele referentnih podataka distribucija, gustina standardne normalne distribucije.
priručnik za obuku, dodan 29.11.2009
Osnovne metode formalizovanog opisa i analize slučajnih pojava, obrada i analiza rezultata fizičkih i numeričkih eksperimenata u teoriji verovatnoće. Osnovni pojmovi i aksiomi teorije vjerovatnoće. Osnovni pojmovi matematičke statistike.
kurs predavanja, dodato 08.04.2011
Određivanje zakona distribucije vjerovatnoća rezultata mjerenja u matematičkoj statistici. Provjera usklađenosti empirijske distribucije sa teoretskom. Određivanje intervala pouzdanosti u kojem se nalazi vrijednost mjerene veličine.
kurs, dodan 02.11.2012
Konvergencija nizova slučajnih varijabli i distribucije vjerovatnoće. Metoda karakterističnih funkcija. Testiranje statističkih hipoteza i izvođenje središnje granične teoreme za date nizove nezavisnih slučajnih varijabli.
kurs, dodan 13.11.2012
Glavne faze obrade podataka iz prirodnih posmatranja metodom matematičke statistike. Vrednovanje dobijenih rezultata, njihova upotreba u donošenju upravljačkih odluka u oblasti zaštite prirode i upravljanja životnom sredinom. Testiranje statističkih hipoteza.
praktični rad, dodato 24.05.2013
Suština zakona distribucije i njegova praktična primjena za rješavanje statističkih problema. Određivanje varijanse slučajne varijable, matematičko očekivanje i standardna devijacija. Osobine jednosmjerne analize varijanse.
test, dodano 12.07.2013
Vjerovatnoća i njena opšta definicija. Teoreme sabiranja i množenja vjerojatnosti. Diskretne slučajne varijable i njihove numeričke karakteristike. Zakon velikih brojeva. Statistička distribucija uzorka. Elementi korelacione i regresione analize.
kurs predavanja, dodato 13.06.2015
Program predmeta, osnovni pojmovi i formule teorije vjerovatnoće, njihovo obrazloženje i značaj. Mjesto i uloga matematičke statistike u disciplini. Primjeri i objašnjenja za rješavanje najčešćih problema na različite teme u ovim akademskim disciplinama.
priručnik za obuku, dodan 15.01.2010
Teorija vjerovatnoće i matematička statistika su nauke o metodama kvantitativne analize masovnih slučajnih pojava. Skup vrijednosti slučajne varijable naziva se uzorak, a elementi skupa se nazivaju vrijednosti uzorka slučajne varijable.
Od posebnog interesa je kvantitativna procjena poslovnog rizika korištenjem metoda matematičke statistike. Glavni alati ove metode procjene su:
§ vjerovatnoća pojave slučajne varijable,
§ matematičko očekivanje ili prosječna vrijednost slučajne varijable koja se proučava,
§ disperzija,
§ standardna (srednja kvadratna) devijacija,
§ koeficijent varijacije,
§ raspodjela vjerovatnoće slučajne varijable koja se proučava.
Da biste doneli odluku, morate znati veličinu (stepen) rizika koji se meri pomoću dva kriterijuma:
1) prosječna očekivana vrijednost (matematičko očekivanje),
2) fluktuacije (varijabilnost) mogućeg rezultata.
Prosječna očekivana vrijednost ![]() ovo je ponderisani prosjek slučajne varijable, koja je povezana s neizvjesnošću situacije:
ovo je ponderisani prosjek slučajne varijable, koja je povezana s neizvjesnošću situacije:
![]() ,
,
gdje je vrijednost slučajne varijable.
Prosječna očekivana vrijednost mjeri rezultat koji u prosjeku očekujemo.
Prosječna vrijednost je generalizirana kvalitativna karakteristika i ne dozvoljava da se donese odluka u korist bilo koje posebne vrijednosti slučajne varijable.
Za donošenje odluke potrebno je izmjeriti fluktuacije indikatora, odnosno odrediti mjeru varijabilnosti mogućeg rezultata.
Varijacija u mogućem ishodu je stepen do kojeg očekivana vrijednost odstupa od prosječne vrijednosti.
U tu svrhu se u praksi obično koriste dva blisko povezana kriterija: „disperzija“ i „standardna devijacija“.
Disperzija – ponderisani prosek kvadrata stvarnih rezultata od očekivanog proseka:
Standardna devijacija je kvadratni korijen varijanse. To je dimenzionalna veličina i mjeri se u istim jedinicama u kojima se mjeri slučajna varijabla koja se proučava:
![]() .
.
Varijanca i standardna devijacija daju mjeru apsolutne varijacije. Za analizu se obično koristi koeficijent varijacije.
Koeficijent varijacije predstavlja omjer standardne devijacije i prosječne očekivane vrijednosti, pomnožen sa 100%
![]() ili
ili  .
.
Apsolutne vrijednosti proučavanog indikatora ne utiču na koeficijent varijacije.
Koristeći koeficijent varijacije, možete čak uporediti fluktuacije karakteristika izraženih u različitim mjernim jedinicama. Koeficijent varijacije može varirati od 0 do 100%. Što je veći koeficijent, to su veće fluktuacije.
U ekonomskoj statistici utvrđuje se sljedeća procjena različitih vrijednosti koeficijenta varijacije:
do 10% - slaba fluktuacija, 10 – 25% - umjerena, preko 25% - visoka.
Shodno tome, što su fluktuacije veće, to je veći rizik.
Primjer. Vlasnik male radnje na početku svakog dana kupuje neki kvarljivi proizvod za prodaju. Jedinica ovog proizvoda košta 200 UAH. Prodajna cijena – 300 UAH. za jedinicu. Iz zapažanja je poznato da potražnja za ovim proizvodom tokom dana može biti 4, 5, 6 ili 7 jedinica sa odgovarajućom vjerovatnoćom od 0,1; 0,3; 0,5; 0.1. Ako se proizvod ne proda tokom dana, onda će se na kraju dana uvijek kupiti po cijeni od 150 UAH. za jedinicu. Koliko jedinica ovog proizvoda bi vlasnik trgovine trebao kupiti na početku dana?
Rješenje. Hajde da napravimo matricu profita za vlasnika prodavnice. Izračunajmo dobit koju će vlasnik dobiti ako, na primjer, kupi 7 jedinica proizvoda, a proda jednu jedinicu tokom 6. dana i na kraju dana. Svaka jedinica prodanog proizvoda tijekom dana daje dobit od 100 UAH, a na kraju dana - gubitak od 200 - 150 = 50 UAH. Dakle, dobit će u ovom slučaju biti:
Proračuni se vrše na sličan način za druge kombinacije ponude i potražnje.
Očekivani profit se izračunava kao matematičko očekivanje mogućih vrednosti profita za svaki red konstruisane matrice, uzimajući u obzir odgovarajuće verovatnoće. Kao što vidite, među očekivanim profitom najveći je 525 UAH. Odgovara kupovini predmetnog proizvoda u količini od 6 jedinica.
Da bismo opravdali konačnu preporuku za kupovinu potrebnog broja jedinica proizvoda, izračunavamo varijansu, standardnu devijaciju i koeficijent varijacije za svaku moguću kombinaciju ponude i potražnje za proizvodom (svaki red matrice profita):
| 400 | 0,1 | 40 | 16000 |
| 400 | 0,3 | 120 | 48000 |
| 400 | 0,5 | 200 | 80000 |
| 400 | 0,1 | 40 | 16000 |
| 1,0 | 400 | 160000 |
| 350 | 0,1 | 35 | 12250 |
| 500 | 0,3 | 150 | 75000 |
| 500 | 0,5 | 250 | 125000 |
| 500 | 0,1 | 50 | 25000 |
| 1,0 | 485 | 2372500 |
| 300 | 0,1 | 30 | 9000 |
| 450 | 0,3 | 135 | 60750 |
| 600 | 0,5 | 300 | 180000 |
| 600 | 0,1 | 60 | 36000 |
| 1,0 | 525 | 285750 |
Što se tiče vlasnika prodavnice koji kupuje 6 jedinica proizvoda u odnosu na 5 i 4 jedinice, to nije očigledno, jer je rizik pri kupovini 6 jedinica proizvoda (19,2%) veći nego kod kupovine 5 jedinica (9,3%) i još više nego pri kupovini 4 jedinice (0%).
Tako imamo sve informacije o očekivanim profitima i rizicima. A vlasnik prodavnice odlučuje koliko jedinica proizvoda treba da kupi svakog jutra, uzimajući u obzir svoje iskustvo i apetit za rizikom.
Po našem mišljenju, vlasniku radnje treba preporučiti da kupi 5 jedinica proizvoda svakog jutra i njegov prosječni očekivani profit će biti 485 UAH. a ako to uporedite sa kupovinom 6 jedinica proizvoda, pri čemu je prosječna očekivana dobit 525 UAH, što je 40 UAH. više, ali će rizik u ovom slučaju biti 2,06 puta veći.
Probabilističke i statističke metode za modeliranje ekonomskih sistema
Uvod
Problem identifikacije zakona distribucije posmatrane slučajne varijable (strukturno-parametrijska identifikacija), po pravilu, shvata se kao problem izbora parametarskog modela zakona raspodele verovatnoće koji najbolje odgovara rezultatima eksperimentalnih posmatranja. Slučajne greške u mjernim instrumentima često se ne pridržavaju normalnog zakona, tačnije, nisu tako često dobro opisane modelom normalnog zakona. Merni instrumenti i sistemi zasnovani su na različitim fizičkim principima, različitim metodama merenja i različitim konverzijama mernih signala. Greške mjerenja kao veličine posljedica su utjecaja mnogih faktora, slučajnih i neslučajnih, koji djeluju stalno ili epizodično. Stoga je jasno da samo ako su ispunjeni određeni preduslovi (teorijski i tehnički), greške mjerenja su prilično dobro opisane modelom normalnog zakona.
Uopšteno govoreći, treba shvatiti da pravi zakon raspodele (ako postoji, naravno), koji opisuje greške određenog mernog sistema, ostaje (ostaće) nepoznat, uprkos svim našim pokušajima da ga identifikujemo. Na osnovu podataka mjerenja i teorijskih razmatranja, možemo odabrati samo vjerojatnostni model koji, u nekom smislu, najbolje aproksimira ovaj pravi zakon. Ukoliko je konstruisani model adekvatan, odnosno primenjeni kriterijumi ne daju osnovu za njegovo odbacivanje, onda na osnovu ovog modela možemo izračunati sve verovatnoće karakteristike slučajne komponente greške mernog instrumenta koje su od interesa. nama, koje će se razlikovati od pravih vrijednosti samo zbog moguće sistematske (neuočljive ili neregistrirane) komponente greške mjerenja. Njegova malenkost karakteriše ispravnost mjerenja. Skup mogućih zakona raspodjele vjerovatnoće koji se mogu koristiti za opisivanje posmatranih slučajnih varijabli je neograničen. Nema smisla postavljati cilj problema identifikacije da se pronađe pravi zakon raspodjele posmatrane veličine. Možemo samo riješiti problem odabira najboljeg modela iz određenog skupa. Na primjer, iz tog skupa parametarskih zakona i porodice distribucija koje se koriste u aplikacijama, a reference na koje se mogu naći u literaturi.
Klasični pristup strukturno-parametarskoj identifikaciji zakona raspodjele. Pod klasičnim pristupom podrazumijevamo algoritam za izbor zakona raspodjele, u potpunosti zasnovan na aparatu matematičke statistike.
1. Elementarni pojmovi o slučajnim događajima, količinama i funkcijama
Već smo vidjeli da za mnoge eksperimente nema razlika u izračunavanju vjerovatnoća događaja, dok su elementarni ishodi u ovim eksperimentima veoma različiti. Ali treba da nas zanimaju upravo verovatnoće događaja, a ne struktura prostora elementarnih ishoda. Stoga je vrijeme da se u svim takvim „sličnim“ eksperimentima umjesto raznih elementarnih ishoda koriste, na primjer, brojevi. Drugim riječima, svaki elementarni ishod dodijelite određenom realnom broju i radite samo s brojevima.
Neka je dat prostor vjerovatnoće.
Definicija 26.Funkcija pozvao slučajna varijabla, ako za bilo koji Borelov skup gomila je događaj, tj. pripada - algebra .
Gomila , koji se sastoji od tih elementarnih ishoda , za koji pripada , naziva se kompletna predslika skupa.
Napomena 9 . Općenito, neka funkcija djeluje iz seta u mnoštvo , i dato -algebre I podskupovi I respektivno. Funkcija pozvao mjerljivo, ako za bilo koji set njegov kompletan prototip pripada .
Napomena 10. Čitalac koji ne želi da se zamara apstrakcijama koje se povezuju sa -algebre događaja i sa mjerljivošću, može sa sigurnošću pretpostaviti da je bilo koji skup elementarnih ishoda događaj, pa je, prema tome, slučajna varijabla besplatnofunkcija od V . U praksi to ne dovodi do problema, tako da možete preskočiti sve dalje u ovom odeljku.
Sada, nakon što smo se riješili radoznalih čitatelja, pokušajmo razumjeti zašto je slučajnoj varijabli potrebna mjerljivost.
Ako je data slučajna varijabla , možda ćemo morati izračunati vjerovatnoće oblika , , , (i općenito vrlo različite vjerovatnoće ulaska u Borel skupove na liniji). To je moguće samo ako su skupovi pod znakom vjerovatnoće događaji – ipak vjerovatnoćapostoji funkcija definirana samo na -algebra događaja. Zahtjev mjerljivosti je ekvivalentan činjenici da za bilo koji Borelov skup vjerovatnoća je određena.
Možete zahtijevati nešto drugo u definiciji 26. Na primjer, da bi događaj bio pogodak u bilo kojem intervalu: , ili u bilo kojem poluintervalu: .
Uvjerimo se, na primjer, da su definicije 26 i 27 ekvivalentne:
Definicija 27. Funkcija naziva se slučajna varijabla ako je za bilo koju realnu gomila pripada -algebri .
Dokaz ekvivalencija definicija 26, 27.
Ako je slučajna varijabla u smislu Definicije 26, onda će to biti slučajna varijabla u smislu Definicije 27, budući da svaki interval je Borelov set.
Dokažimo da je tačno i suprotno. Neka za bilo koji interval urađeno . Moramo dokazati da isto vrijedi za sve Borelove skupove.
Skupljajmo u izobilju svi podskupovi realne linije čiji su prototipovi događaji. Gomila već sadrži sve intervale . Pokažimo sada da je skup je -algebra. A-priorat, ako i samo ako je skup pripada .
1. Hajde da se uverimo u to . Ali i zbog toga .
2. Hajde da se uverimo u to za bilo koga . Neka . Onda , jer - -algebra.
3. Hajde da se uverimo u to za bilo koji . Neka za sve . Ali - -algebra, dakle
To smo dokazali - -algebra i sadrži sve intervale na pravoj. Ali - najmanji od -algebre koje sadrže sve intervale na pravoj. dakle, sadrži: .
Navedimo primjere mjerljivih i nemjerljivih funkcija.
Primjer 25. Baci kocku. Neka , i dvije funkcije iz V dati su ovako: , . Još nije navedeno -algebra , ne možemo govoriti o mjerljivosti. Funkcija mjerljiva u odnosu na neke -algebre možda neće biti isto za drugog.
Ako postoji skup svih podskupova , To I su slučajne varijable, pošto bilo koji skup elementarnih ishoda pripada , uključujući ili . Možete zapisati korespondenciju između vrijednosti slučajnih varijabli I a vjerovatnoće uzimaju ove vrijednosti u obliku "tabele raspodjele vjerovatnoće"ili, ukratko, "tablice distribucije":
Evo.
2. Neka -algebra događaja sastoji se od četiri seta:
one. Događaj je, pored pouzdanih i nemogućih događaja, gubitak parnog ili neparnog broja bodova. Uvjerimo se u to sa takvim relativno siromašnim -algebra ili , niti nisu slučajne varijable jer su nemjerljive. Recimo, . Vidimo to
2. Numeričke karakteristike slučajnih varijabli
Očekivana vrijednost.Matematičko očekivanje diskretne slučajne varijable X, koja uzima konačan broj vrijednosti xi sa vjerovatnoćama pi, je zbir:
(6a)
Matematičko očekivanje kontinuirane slučajne varijable X je integral proizvoda njenih vrijednosti x i gustine distribucije vjerovatnoće f(x):
(6b)
Pretpostavlja se da je nepravilan integral (6b) apsolutno konvergentan (inače kažemo da matematičko očekivanje M(X) ne postoji). Matematičko očekivanje karakteriše prosečnu vrednost slučajne varijable X. Njena dimenzija se poklapa sa dimenzijom slučajne varijable. Svojstva matematičkog očekivanja:
Disperzija.Varijanca slučajne varijable X je broj:
Disperzija je karakteristika disperzije vrijednosti slučajne varijable X u odnosu na njenu prosječnu vrijednost M (X). Dimenzija varijanse jednaka je kvadratu dimenzije slučajne varijable. Na osnovu definicija varijanse (8) i matematičkog očekivanja (5) za diskretnu slučajnu varijablu i (6) za kontinuiranu slučajnu varijablu, dobijamo slične izraze za varijansu:
Ovdje je m = M (X).
Svojstva disperzije:
(10)
Standardna devijacija:
(11)
Budući da standardna devijacija ima istu dimenziju kao slučajna varijabla, češće se koristi kao mjera disperzije nego varijanse.
Trenuci distribucije.Koncepti matematičkog očekivanja i disperzije su posebni slučajevi općenitijeg koncepta za numeričke karakteristike slučajnih varijabli - trenutaka distribucije. Trenuci distribucije slučajne varijable su predstavljeni kao matematička očekivanja nekih jednostavnih funkcija slučajne varijable. Dakle, trenutak reda k u odnosu na tačku x0 naziva se matematičko očekivanje M (X - x0) k. Momenti u odnosu na ishodište x = 0 nazivaju se početni momenti i označavaju se:
(12)
Početni trenutak prvog reda je centar distribucije slučajne varijable koja se razmatra:
(13)
Momenti u odnosu na centar distribucije x = m nazivaju se centralni momenti i označavaju se:
(14)
Iz (7) slijedi da je centralni moment prvog reda uvijek jednak nuli:
(15)
Centralni momenti ne ovise o porijeklu vrijednosti slučajne varijable, jer kada se pomakne za konstantnu vrijednost C, njen centar distribucije se pomiče na istu vrijednost C, a odstupanje od centra se ne mijenja:
X - m = (X - C) - (m - C).
Sada je jasno da je varijansa centralni moment drugog reda:
(16)
Asimetrija.Centralni trenutak trećeg reda:
(17)
služi za procjenu asimetrije distribucije. Ako je raspodjela simetrična u odnosu na tačku x = m, tada će središnji moment trećeg reda biti jednak nuli (kao i svi centralni momenti neparnog reda). Stoga, ako je centralni moment trećeg reda različit od nule, tada raspodjela ne može biti simetrična. Veličina asimetrije se procjenjuje korištenjem bezdimenzionalnog koeficijenta asimetrije:
(18)
Znak koeficijenta asimetrije (18) ukazuje na desnu ili lijevu asimetriju (slika 2).
Rice. 1. Vrste asimetrije distribucije
Višak.Centralni trenutak četvrtog reda:
(19)
služi za procjenu takozvanog kurtosisa, koji određuje stepen strmine (vrhovitosti) krivulje distribucije blizu centra distribucije u odnosu na krivu normalne distribucije. Pošto za normalnu distribuciju , tada je vrijednost uzeta kao eksces:
(20)
Na sl. Slika 3 prikazuje primjere krivulja distribucije s različitim vrijednostima ekscesa. Za normalnu distribuciju, E = 0. Krive koje su više vršne od normalne imaju pozitivnu ekscesiju, one sa ravnijim vrhom imaju negativnu ekscesiju.
Rice. 2. Krive distribucije sa različitim stepenom strmine (kurtozis)
Momenti višeg reda se obično ne koriste u inženjerskim aplikacijama matematičke statistike.
Modadiskretne slučajne varijable je njena najvjerovatnija vrijednost. Mod kontinuirane slučajne varijable je njena vrijednost pri kojoj je gustina vjerovatnoće maksimalna (slika 2). Ako kriva distribucije ima jedan maksimum, tada se raspodjela naziva unimodalna. Ako kriva distribucije ima više od jednog maksimuma, tada se distribucija naziva multimodalnom. Ponekad postoje distribucije čije krive imaju minimum, a ne maksimum. Takve distribucije se nazivaju antimodalne. U opštem slučaju, mod i matematičko očekivanje slučajne varijable se ne poklapaju. U konkretnom slučaju, za modalni, tj. imaju mod, simetričnu distribuciju i pod uslovom da postoji matematičko očekivanje, potonje se poklapa sa modom i centrom simetrije distribucije.
Medijanslučajna varijabla X je njena vrijednost Me, za koju vrijedi jednakost: one. Jednako je vjerovatno da će slučajna varijabla X biti manja ili veća od Me. Geometrijski, medijana je apscisa tačke u kojoj je površina ispod krivulje raspodjele podijeljena na pola. U slučaju simetrične modalne distribucije, medijan, mod i matematičko očekivanje su isti.
. Statistička procjena zakona raspodjele slučajnih varijabli
Opšta populacija je ukupnost svih objekata koji se proučavaju ili mogući rezultati svih opservacija izvršenih pod istim uslovima na jednom objektu.
Populacija uzorka ili uzorak je kolekcija objekata ili rezultata posmatranja objekta, nasumično odabranih iz opće populacije.
Veličina uzorkaje broj objekata ili zapažanja u uzorku.
Specifične vrijednosti uzorka nazivaju se opažene vrijednosti slučajne varijable X. Uočene vrijednosti se bilježe u protokolu. Protokol je tabela. Sastavljeni protokol je primarni oblik evidentiranja obrade primljenog materijala. Da bi se dobili pouzdani, pouzdani zaključci, uzorak mora biti dovoljno reprezentativan po veličini. Veliki uzorak je neuređen skup brojeva. Za istraživanje, uzorak se dovodi u vizuelno uređen oblik. Da bi to učinio, protokol pronalazi najveću i najmanju vrijednost slučajne varijable. Uzorak, sortiran uzlaznim redom, prikazan je u tabeli 1.
Tabela 1. Protokol
8,66-5,49-4,11-3,48-2,9-2,32-1,82-1,09-0,440,64-8,31-4,71-3,92-3,41-2,85-2,31-1,82-1,01-0,430,71-8,23-4,68-3,85-3,33-2,83-2,29-1,8-0,99-0,430,73-7,67-4,6-3,85-3,25-2,77-2,27-1,77-0,95-0,310,99-6,64-4,43-3,81-3,08-2,72-2,25-1,73-0,89-0,31,03-6,6-4,38-3,8-3,07-2,67-2,19-1,38-0,70,041,05-6,22-4,38-3,77-3,01-2,6-2,15-1,32-0,560,081,13-5,87-4,25-3,73-3,01-2,49-2,09-1,3-0,510,151,76-5,74-4,18-3,59-2,99-2,37-2,01-1,28-0,490,262,95-5,68-4,14-3,49-2,98-2,33-1,91-1,24-0,480,534,42
Raspon uzorkaje razlika između najveće i najmanje vrijednosti slučajne varijable X:
Opseg uzorka je podijeljen na k intervala - cifara. Broj cifara se postavlja u zavisnosti od raspona uzorka od 8 do 25; u ovom kursu ćemo uzeti k = 10.
Tada će dužina intervala biti jednaka:
U protokolu brojimo broj uočenih vrijednosti koje spadaju u svaki interval, označavajući ih m1, m2,…, m10. .
Pozovimo mi frekvencija udaraslučajna varijabla u intervalu i. Ako se bilo koja uočena vrijednost slučajne varijable poklapa sa krajem intervala, tada se ta vrijednost slučajne varijable pripisuje jednom od intervala po dogovoru.
Nakon što smo odredili frekvencije mi, odredimo frekvencijeslučajna varijabla, tj. Nađimo omjer frekvencija mi prema ukupnom broju uočenih vrijednosti n.
Učestalost, stanje kompletnosti -
Nađimo sredinu svakog intervala: .
Napravimo tabelu 2
Tabela vrijednosti granica intervala i odgovarajuće frekvencije , gdje je i = 1, 2, 3, …, k, naziva se statistički niz. Grafički prikaz statističke serije naziva se histogram. Konstruira se na sljedeći način: intervali se crtaju duž apscisne ose i na svakom takvom intervalu, kao na bazi, konstruiše se pravokutnik čija je površina jednaka odgovarajućoj frekvenciji.
, - visina pravougaonika, .
tabela 2
Broj intervala Lijeva granica intervala Desna granica intervala Interval Srednja intervala Interval frekvencija Intervalna frekvencija Visina pravokutnika1-8.66-7.352(-8.66; -7.352)-8.00640.040.03062-7.352-6.044 (3.064) 0,02293-6,044-4,736 (-6.044; -4.736)-5.3940.040.03064-4.736-3.428(-4.736; -3.428)-4.082200.20.15295-3.428-2.12(- 2.41286); .12-0.812(-2.12; - 0.812)-1.466180.180.13767-0.8120.496(-0.812; 0.496) -0.158140.140.107080.4961.804(0.496; 1.804)1.804)1.812.10.496. 804; 3.112)2.45810.010.0076103.1124.42(3.112; 4.42)3.76610.010.0076 Iznos1001
Slika 3
Funkcija statističke distribucije je frekvencija slučajne varijable koja ne prelazi datu vrijednost X:
Za diskretnu slučajnu varijablu X, statistička funkcija distribucije se nalazi po formuli:
Zapišimo funkciju statističke distribucije u proširenom obliku:
Gdje je sredina intervala i, i su odgovarajuće frekvencije, gdje je i=1, 2,…, k.
Grafikon funkcije statističke distribucije je stepenasta linija, čije su tačke prekida sredine intervala, a konačni skokovi su jednaki odgovarajućim frekvencijama.
Slika 3
Proračun numeričkih karakteristika statističke serije
Statističko matematičko očekivanje,
Statistička varijansa,
Statistička standardna devijacija.
Statističko matematičko očekivanjeili statistički prosjeknaziva se aritmetička sredina posmatranih vrednosti slučajne varijable X.
Statistička varijansanaziva se aritmetička srednja vrijednost veličine ili
Uz veliku veličinu uzorka, proračuni pomoću formula dovode do glomaznih proračuna. Da biste pojednostavili proračune, koristite statističku seriju s granicama i frekvencije , gdje je i = 1, 2, 3, …, k, pronađite sredine intervala a zatim i sve elemente selekcije , koji je upao u interval , zamijenjen jednom vrijednošću , onda će postojati takve vrijednosti u svakom intervalu.
Gdje - prosječna vrijednost odgovarajućeg intervala ;- frekvencija intervala
Tabela 4. Numeričke karakteristike
Frekvencija PiXiPi(Xi-m)^2(Xi-m)^2*Pi1-8.0060.04-0.320231.486911.25952-6.6980.03-0.200918.518560.555023.555023.5.5.39.5 -8.394 .0820.20-0.81642.847050.56945 -2.7740.26-0.72120.143880.03746-1.4660.18-0.26390.862450.15527 -0.1580.14-0.02215.002740.700481.016.30.481.01.15.30.15.15 4580.010.024623.548500.2355103.7660.010.037737.953980.3795Statističko matematičko očekivanje -2,3947Statistička varijansa 5,3822 Statistička standardna devijacija 2,3200
Određuje poziciju centra grupiranja posmatranih vrednosti slučajne varijable.
, karakteriziraju raspršivanje promatranih vrijednosti slučajne varijable okolo
Svaka statistička distribucija neizbježno sadrži elemente slučajnosti. Međutim, sa veoma velikim brojem zapažanja, ove nasumice se izglađuju, a slučajni fenomeni otkrivaju inherentni obrazac.
Prilikom obrade statističkog materijala potrebno je odlučiti o tome kako odabrati teorijsku krivu za datu statističku seriju. Ova teorijska kriva distribucije treba da izrazi bitne karakteristike statističke distribucije - ovaj zadatak se zove problem izravnavanja ili nivelisanja statističke serije.
Ponekad opći oblik distribucije slučajne varijable X slijedi iz same prirode ove slučajne varijable.
Neka je slučajna varijabla X rezultat mjerenja neke fizičke veličine uređaja.
X = tačna vrijednost fizičke veličine + greška instrumenta.
Slučajna greška uređaja tokom merenja ima totalnu prirodu i raspoređuje se prema normalnom zakonu. Prema tome, slučajna varijabla X ima istu distribuciju, tj. normalna distribucija sa gustinom verovatnoće:
gdje, , .
Opcije I određuju se tako da su numeričke karakteristike teorijske distribucije jednake odgovarajućim numeričkim karakteristikama statističke distribucije. Uz normalnu distribuciju pretpostavlja se da ,,, tada će funkcija normalne distribucije imati oblik:
Tabela 5. Kriva niveliranja
Broj intervala Srednja tačka intervala Xi Tabelarna funkcija Normalna kriva 1-8.0060-2.41870.02140.00922-6.6980-1.85490.07140.03083-5.3900-1.29110.17340.07474-4.0820-0.32673-0.326734 50,39360,1697M-2,394700,39890,17206-1,46600, 40030,36820,15877-0,15800,96410,25070,108081,15001,52790,12420,0535 92.45802, 09170.04480.0196600.051510.051510.
Iz tačaka konstruišemo teorijsku normalnu krivu na istom grafikonu sa histogramom statističke serije (Greška! Referentni izvor nije pronađen).
Slika 6
Usklađivanje funkcije statističke distribucije
Statistička funkcija raspodjele usklađeno s normalnom funkcijom distribucije:
Gdje ,,- Laplaceova funkcija.
Tabela 7. Funkcija distribucije
Broj intervala Srednja tačka intervala Xi Laplaceova funkcija Funkcija distribucije 1-8.0060-2.4187-0.49220.00782-6.6980-1.8549-0.46820.03183-5.3900-1.2911-0.40170.09834-4.0820-30,3020-30,3020-30,3020-30,30-30-30-30-30-30-30-30-25 .1635-0.06490,4351m-2.3947000,50006-1.46600, 40030,15550,65557-0.15800,96410,33250,832581,15001, 52790,43670,936792,45802,09170,48180,9818606,9818604
Gradimo graf teorijske funkcije distribucije u tačkama / zajedno sa grafikom funkcije statističke distribucije.
Slika 6
Hajde da proučavamo slučajnu varijablu X sa matematičkim očekivanjem i varijansu , oba parametra su nepoznata.
Neka je x1, x2, x3, …, xn uzorak dobijen kao rezultat n nezavisnih opažanja slučajne varijable X. Da bismo naglasili slučajnu prirodu veličina x1, x2, x3, …, xn, prepisujemo ih u oblik:
X1, X2, X3, …, Xn, gdje je Xi vrijednost slučajne varijable X u i-tom eksperimentu.
Na osnovu ovih eksperimentalnih podataka potrebno je procijeniti matematičko očekivanje i disperziju slučajne varijable. Takve procjene se nazivaju tačkaste procjene; statističko očekivanje se može uzeti kao procjena m i D i statistička varijansa, gdje
Prije eksperimenta, uzorak X1, X2, X3, ..., Xn je skup nezavisnih slučajnih varijabli koje imaju matematičko očekivanje i varijansu, što znači da je distribucija vjerovatnoće ista kao i sama slučajna varijabla X. Dakle:
Gdje je i = 1, 2, 3, …, n.
Na osnovu toga nalazimo matematičko očekivanje i varijansu slučajne varijable (koristeći svojstva matematičkog očekivanja).
Dakle, matematičko očekivanje statističkog prosjeka jednaka je tačnoj vrijednosti matematičkog očekivanja m izmjerene vrijednosti, a disperzija statističkog prosjeka n puta manje od varijanse pojedinačnih rezultata mjerenja.
at
To znači da je sa velikom veličinom uzorka N statistički prosjek je gotovo neslučajna veličina; samo malo odstupa od tačne vrijednosti slučajne varijable m. Ovaj zakon se naziva Čebiševljev zakon velikih brojeva.
Tačkaste procjene nepoznatih vrijednosti matematičkog očekivanja i varijanse su od velike važnosti u početnoj fazi obrade statičkih podataka. Njihov nedostatak je što se ne zna sa kojom tačnošću daju procenjeni parametar.
Neka se dobiju tačne statističke procjene za dati uzorak X1, X2, X3, …, Xn I , tada će numeričke karakteristike slučajne varijable X biti približno jednake . Za malu veličinu uzorka, pitanje tačnosti procjene je značajno, jer između m i , D i odstupanja neće biti dovoljno velika. Osim toga, prilikom rješavanja praktičnih problema potrebno je ne samo pronaći približne vrijednosti m i D, već i procijeniti njihovu točnost i pouzdanost. Neka , tj. je tačka procjene za m. Očigledno je da što je m preciznije određeno, to je manji modul razlike . Neka , Gdje ?>0, onda manje ?, što je tačnija procjena m. dakle, ?>0 karakterizira tačnost procjene parametara. Međutim, statističke metode nam ne dozvoljavaju da kategorički tvrdimo da procjena prave vrijednosti m zadovoljava , možemo govoriti samo o vjerovatnoći ?, s kojom vrijedi ova nejednakost:
dakle, ?- Ovo verovatnoća poverenjaili pouzdanost procjene, značenje ? se biraju unapred u zavisnosti od problema koji se rešava. Pouzdanost ? uobičajeno je odabrati 0,9; 0,95; 0,99; 0.999. Događaji sa takvom vjerovatnoćom su praktično izvjesni. Koristeći datu vjerovatnoću pouzdanosti, možete pronaći broj ?>0 od .
Tada dobijamo interval , koji pokriva sa vjerovatnoćom ? prava vrijednost matematičkog očekivanja m, dužina ovog intervala je 2 ?. Ovaj interval se zove interval povjerenja. A ova metoda procjene nepoznatog parametra m je interval.
Neka je dat uzorak X1, X2, X3, ..., Xn, i neka se nađe iz ovog uzorka, ,.
Moramo pronaći interval povjerenja za matematičko očekivanje m sa pouzdanom vjerovatnoćom ?. Magnituda je slučajna veličina sa matematičkim očekivanjem, .
Slučajna vrijednost ima sumarnu prirodu; sa velikom veličinom uzorka, distribuira se prema zakonu bliskom normalnom. Tada će vjerovatnoća da će slučajna varijabla pasti u interval biti jednaka:
Gdje
Gdje - Laplaceova funkcija.
Iz formule (3) i tabela Laplaceove funkcije nalazimo broj ?>0 i zapišite interval pouzdanosti za tačnu vrijednost slučajna varijabla X sa pouzdanošću ?.
U ovom predmetnom radu značenje ? mi ćemo zameniti , i tada će formula (3) poprimiti oblik:
Nađimo interval povjerenja , koji sadrži matematičko očekivanje. At ? = 0,99, n = 100, ,.
Koristeći Laplaceove tablice nalazimo:
Odavde? = 0,5986.
Interval pouzdanosti u kojem se sa vjerovatnoćom od 99% nalazi tačna vrijednost matematičkog očekivanja.
Zaključak
distribucija slučajne varijable ekonomska
Rješavanje problema strukturno-parametarske identifikacije uz ograničene veličine uzorka, koje metrolozi obično imaju, pogoršava problem. U ovom slučaju je još važnija pravilna primjena statističkih metoda analize, korištenje korištenje procjena koje imaju najbolja statistička svojstva i kriterija koji imaju najveću snagu.
Prilikom rješavanja problema identifikacije poželjno je osloniti se na klasičan pristup. Prilikom identifikacije, preporučuje se razmatranje šireg spektra zakona distribucije, uključujući modele u obliku mješavine zakona. U ovom slučaju, za bilo koju empirijsku distribuciju uvijek možemo izgraditi adekvatan, statistički značajno opravdaniji matematički model.
Treba se fokusirati na upotrebu i razvoj softverskih sistema koji pružaju rješenja za probleme strukturalne i parametarske identifikacije zakona distribucije za bilo koji oblik zabilježenih opservacija (mjerenja), uključujući savremene statističke metode. analitičke analize, fokusiranje na široko rasprostranjenu, ali ispravnu upotrebu metoda kompjuterskog modeliranja u istraživanju. Već smo vidjeli da za mnoge eksperimente nema razlika u izračunavanju vjerovatnoća događaja, dok su elementarni ishodi u ovim eksperimentima veoma različiti. Ali treba da nas zanimaju upravo verovatnoće događaja, a ne struktura prostora elementarnih ishoda. Stoga je vrijeme da se u svim takvim „sličnim“ eksperimentima umjesto raznih elementarnih ishoda koriste, na primjer, brojevi. Drugim riječima, svaki elementarni ishod dodijelite određenom realnom broju i radite samo s brojevima.