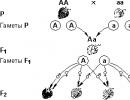
Pomicanje sinusoida duž x-ose. Transformacija funkcijskih grafova. Prikupljanje i korištenje ličnih podataka
, Takmičenje "Prezentacija za čas"
Prezentacija za lekciju









 Nazad napred
Nazad napred
Pažnja! Pregledi slajdova služe samo u informativne svrhe i možda ne predstavljaju sve karakteristike prezentacije. Ako ste zainteresovani za ovaj rad, preuzmite punu verziju.
Ciljevi lekcije:
edukativni: istražiti pomak grafa kvadratne funkcije, odrediti položaj grafa ovisno o vrijednostima koeficijenata b, c.
edukativni: sposobnost grupnog rada i organizovanosti.
Razvojni: istraživačke sposobnosti, sposobnost postavljanja hipoteza, analize dobijenih rezultata, sistematizacije dobijenih podataka.
Struktura lekcije
- Organizacioni trenutak – 3 minuta.
- Istraživački rad – 20 minuta.
- Konsolidacija proučenog materijala – 15 minuta.
- Refleksija – 2 minute.
- Sažetak lekcije: 3 minute.
- Domaći zadatak – 2 minute.
Tokom nastave
1. Organizacioni momenat.
Svrha časa je izvođenje istraživačkog rada. Predmet proučavanja bit će kvadratne funkcije različitih tipova. Morate odrediti kako koeficijenti b, c utiču na graf funkcija oblika y=x 2 +c, y=(x-b) 2, y=(x-b) 2 +c.
Da biste izvršili zadatak, morate se podijeliti u grupe (4 grupe po 5 ljudi, jedna grupa „stručnjaci” - najspremniji učenici).
Svaka grupa dobija plan istraživanja<Приложение>, A3 list za bilježenje rezultata.
2. Istraživački rad
.Dvije grupe (nivo A) proučavaju funkcije oblika y= x 2 +c, jedna grupa (nivo B) proučava funkciju oblika y=(x-b) 2, jedna grupa (nivo C) proučava funkciju y=(x-b) ) 2 +c. Grupa “stručnjaka” ispituje sve funkcije.
| Funkcija | Rezultat | ||
| 1 grupa | y=x 2 +3; | <Рисунок 10> |  |
| 2. grupa | y=x 2 -5; | <Рисунок 11> |  |
| 3 grupa | y=(x-4) 2; | <Рисунок 12> |  |
| 4 grupa | y=(x-2) 2 +3. | <Рисунок 13> |  |
Plan rada
- Da biste formulirali hipotezu, pretpostavite kako bi vaša funkcija mogla izgledati.
- Konstruisati graf proučavanih funkcija (odrediti vrh parabole (x 0, y 0), navesti 4 tačke u tabeli).
- Uporedite rezultujući graf sa kontrolnim uzorkom y=x 2 .
- Izvucite zaključak (kako se promijenila pozicija grafa vaše funkcije u odnosu na kontrolni uzorak).
- Nacrtajte rezultate na A3 list papira i predočite ih grupi „stručnjaka“.
„Stručna“ grupa upoređuje svoje rezultate sa rezultatima drugih grupa, sistematizuje i sumira rezultate i donosi zaključke. U slučaju netačnosti ili grešaka, nastavnik daje korektivne komentare.
Usklađivanje dobijenih rezultata sa slajdovi br. 2-5.
Bilo koja kvadratna funkcija y=ax 2 +bx+c može se napisati kao y=a(x-x 0) 2 +y 0, gdje su x 0 i y 0 izraženi kroz koeficijente a, b, c. Dakle, vaši koeficijenti b=x 0 , c=y 0 su koordinate vrha parabole.
3. Konsolidacija proučenog gradiva.
Frontalni rad sa razredom.
1. Pronađite grešku u grafovima funkcija (Slajdovi br. 6-9).
Koeficijent b |
Nema greške |
Slika 1 |
Slika 2 |
 |
 |
| y=(x+5) 2 -1 | y=(x-2) 2 +2 |
| Koeficijent b i c | Koeficijent b |
| Slika 3 | Slika 4 |
 |
 |
rezultate
<Рисунок 7>

<Рисунок 2>

<Рисунок 8>

<Рисунок 9>

Koji vam je koeficijent pomogao da pronađete grešku?
2. Uparite grafove funkcija prema bojama (slajd br. 10).

Slika 5
4. Refleksija.
Grupa "eksperata" odgovara na pitanja:
– Koje su greške napravile grupe?
– Da li je cilj lekcije postignut?
– Da li rezultati istraživanja odgovaraju izrečenoj hipotezi?
5. Sažetak lekcije (slajd br. 11)
:Na položaj grafika funkcije y=(x-b) 2 +c utiču koeficijenti b i c,
“+b” parabola je pomaknuta udesno duž x-ose za b jedinične segmente,
“–b” parabola je pomaknuta ulijevo duž ose apscise za b jedinične segmente,
“+c” parabola je pomaknuta prema gore duž ordinatne ose za c jedinične segmente,
“-c” parabola je pomaknuta prema dolje duž ordinatne ose za c jedinične segmente.
6. Domaći
- Konstruisati graf kvadratne funkcije sa vrhom u tački A(1;-2), koeficijent a=1.
- Razmislite o području u kojem možete koristiti znanje o ovoj temi (praktična primjena).
Pretvaranje grafova funkcija
U ovom članku ću vas upoznati s linearnim transformacijama grafova funkcija i pokazati vam kako koristiti ove transformacije da dobijete graf funkcije iz grafa funkcija ![]()
Linearna transformacija funkcije je transformacija same funkcije i/ili njenog argumenta u formu ![]() , kao i transformacija koja sadrži argument i/ili funkcijski modul.
, kao i transformacija koja sadrži argument i/ili funkcijski modul.
Najveće poteškoće pri konstruiranju grafova pomoću linearnih transformacija uzrokuju sljedeće radnje:
- Izolacija osnovne funkcije, zapravo, grafa koji transformiramo.
- Definicije reda transformacija.
I Upravo na ovim tačkama ćemo se detaljnije zadržati.
Pogledajmo detaljnije funkciju
![]()
Zasnovan je na funkciji . Pozovimo je osnovna funkcija.
Prilikom crtanja funkcije ![]() vršimo transformacije na grafu osnovne funkcije.
vršimo transformacije na grafu osnovne funkcije.
Ako bismo izvršili transformacije funkcija ![]() istim redoslijedom kojim je pronađena njegova vrijednost za određenu vrijednost argumenta
istim redoslijedom kojim je pronađena njegova vrijednost za određenu vrijednost argumenta
Razmotrimo koje vrste linearnih transformacija argumenta i funkcije postoje i kako ih izvesti.
Transformacije argumenata.
1. f(x) f(x+b)
1. Izgradite graf funkcije
2. Pomaknite grafik funkcije duž ose OX za |b| jedinice
- lijevo ako je b>0
- tačno ako b<0
Nacrtajmo funkciju
1. Izgradite graf funkcije
2. Pomaknite ga 2 jedinice udesno:

2. f(x) f(kx)
1. Izgradite graf funkcije
2. Podijelite apscise tačaka grafa sa k, ostavljajući ordinate tačaka nepromijenjene.
Napravimo graf funkcije.
1. Izgradite graf funkcije
2. Podijelite sve apscise tačaka grafikona sa 2, ostavljajući ordinate nepromijenjene:

3. f(x) f(-x)
1. Izgradite graf funkcije
2. Prikažite ga simetrično u odnosu na osu OY.
Napravimo graf funkcije.
1. Izgradite graf funkcije
2. Prikažite ga simetrično u odnosu na osu OY:

4. f(x) f(|x|)
1. Izgradite graf funkcije
2. Dio grafikona koji se nalazi lijevo od ose OY se briše, dio grafa koji se nalazi desno od ose OY se završava simetrično u odnosu na os OY:
Grafikon funkcije izgleda ovako:

Nacrtajmo funkciju
1. Gradimo graf funkcije (ovo je grafik funkcije, pomaknut duž ose OX za 2 jedinice ulijevo):

2. Dio grafikona koji se nalazi lijevo od ose OY (x).<0) стираем:
3. Završavamo dio grafa koji se nalazi desno od ose OY (x>0) simetrično u odnosu na osu OY:

Bitan! Dva glavna pravila za transformaciju argumenta.
1. Sve transformacije argumenata se izvode duž ose OX
2. Sve transformacije argumenta se izvode “obrnuto” i “obrnutim redoslijedom”.
Na primjer, u funkciji slijed transformacija argumenata je sljedeći:
1. Uzmimo modul od x.
2. Dodajte broj 2 modulu x.
Ali graf smo konstruisali obrnutim redoslijedom:
Prvo je izvršena transformacija 2 - graf je pomaknut za 2 jedinice ulijevo (to jest, apscise tačaka su smanjene za 2, kao da je "obrnuto")
Zatim smo izvršili transformaciju f(x) f(|x|).
Ukratko, redoslijed transformacija je napisan na sljedeći način:

Hajde sada da pričamo o tome transformacija funkcije . Transformacije se dešavaju
1. Duž ose OY.
2. U istom redoslijedu u kojem se radnje izvode.
Ovo su transformacije:
1. f(x)f(x)+D
2. Pomaknite ga duž ose OY za |D| jedinice
- gore ako je D>0
- dolje ako D<0
Nacrtajmo funkciju
1. Izgradite graf funkcije
2. Pomaknite ga duž ose OY 2 jedinice gore:

2. f(x)Af(x)
1. Napravite graf funkcije y=f(x)
2. Pomnožimo ordinate svih tačaka grafa sa A, ostavljajući apscise nepromenjene.
Nacrtajmo funkciju
1. Napravimo graf funkcije
2. Pomnožite ordinate svih tačaka na grafu sa 2:

3.f(x)-f(x)
1. Napravite graf funkcije y=f(x)
Napravimo graf funkcije.
1. Izgradite graf funkcije.
2. Prikazujemo ga simetrično u odnosu na osu OX.

4. f(x)|f(x)|
1. Napravite graf funkcije y=f(x)
2. Dio grafikona koji se nalazi iznad ose OX ostaje nepromenjen, deo grafikona koji se nalazi ispod ose OX prikazuje se simetrično u odnosu na ovu osu.
Nacrtajmo funkciju
1. Izgradite graf funkcije. Dobiva se pomicanjem grafa funkcije duž ose OY za 2 jedinice prema dolje:

2. Sada ćemo prikazati dio grafikona koji se nalazi ispod ose OX simetrično u odnosu na ovu osu:

I posljednja transformacija, koja se, strogo govoreći, ne može nazvati transformacijom funkcije, budući da rezultat ove transformacije više nije funkcija:
|y|=f(x)
1. Napravite graf funkcije y=f(x)
2. Brišemo dio grafikona koji se nalazi ispod ose OX, a zatim kompletiramo dio grafa koji se nalazi iznad ose OX simetrično u odnosu na ovu os.
Nacrtajmo jednačinu
1. Gradimo graf funkcije:

2. Brišemo dio grafikona koji se nalazi ispod OX ose:

3. Dio grafa koji se nalazi iznad ose OX završavamo simetrično u odnosu na ovu osu.
I na kraju, predlažem vam da pogledate VIDEO TUTORIAL u kojem pokazujem korak po korak algoritam za konstruiranje grafa funkcije
![]()
Grafikon ove funkcije izgleda ovako:

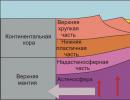
Zavisnost oblika +=
Grafikon ove jednačine je kružnica na koordinatnoj ravni x Oy sa centrom u tački O(a;b) i poluprečnikom r (r>0).
Graf ove jednadžbe ne može se nazvati grafom funkcije, jer definicija funkcije je prekršena: svaka vrijednost x odgovara jednoj vrijednosti y.
Kretanje funkcija duž koordinatnih osa
gdje je l dati pozitivan broj, trebate pomaknuti grafik funkcije y=f(x) duž x-ose za l jedinica skale ulijevo.
Za crtanje funkcije
gdje je l dati pozitivan broj, trebate pomaknuti grafik funkcije y=f(x) duž x-ose za l jedinica skale udesno.
Za crtanje funkcije
gdje je m dati pozitivan broj, trebate pomaknuti grafik funkcije y=f(x) duž y-ose za m jedinica skale prema gore.
Da biste napravili grafik funkcije y=f(x)-m, gdje je m dati pozitivan broj, trebate pomaknuti graf funkcije y=f(x) duž y-ose za m jedinica skale prema dolje.
Algoritam 1 za crtanje funkcije y=f(x+l)+m:
- 1. Konstruirajte graf funkcije y=f(x).
- 2. Izvršiti paralelni prijenos grafika y=f(x) duž x ose po jedinicama skale lijevo ako je l>0, i desno ako je l
- 3. Izvršite paralelni prijenos grafa dobivenog u drugom koraku duž y-ose po jedinicama skale prema gore, ako
Algoritam 2 za crtanje funkcije y=f(x+l)+m:
- 1. Idite na pomoćni koordinatni sistem tako što ćete isprekidanom linijom nacrtati pomoćne linije x=-l, y=m, tj. odabirom tačke (-l;m) kao ishodišta novog koordinatnog sistema.
- 2. Povežite graf funkcije y=f(x) sa novim koordinatnim sistemom.
Osnovne elementarne funkcije u svom čistom obliku bez transformacije su rijetke, pa najčešće morate raditi s elementarnim funkcijama koje su dobivene iz glavnih dodavanjem konstanti i koeficijenata. Takvi grafovi se konstruiraju korištenjem geometrijskih transformacija zadanih elementarnih funkcija.
Razmotrimo primjer kvadratne funkcije oblika y = - 1 3 x + 2 3 2 + 2, čiji je graf parabola y = x 2, koja je komprimirana tri puta u odnosu na Oy i simetrična u odnosu na na Ox, i pomaknut za 2 3 duž Ox udesno, gore 2 jedinice duž Oy. Na koordinatnoj liniji to izgleda ovako:
Geometrijske transformacije grafa funkcije
Primenom geometrijskih transformacija datog grafa dobijamo da je graf prikazan funkcijom oblika ± k 1 · f (± k 2 · (x + a)) + b, kada je k 1 > 0, k 2 > 0 su koeficijenti kompresije na 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 duž O y i O x. Znak ispred koeficijenata k 1 i k 2 označava simetričan prikaz grafika u odnosu na ose, a i b ga pomeraju duž O x i duž O y.
Definicija 1
Postoje 3 vrste geometrijske transformacije grafa:
- Skaliranje duž O x i O y. Na to utiču koeficijenti k 1 i k 2 pod uslovom da nisu jednaki 1 kada je 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, tada se graf rasteže duž O y i kompresuje duž O x.
- Simetričan prikaz u odnosu na koordinatne ose. Ako postoji znak “-” ispred k 1, simetrija je relativna u odnosu na O x, a ispred k 2 je u odnosu na O y. Ako nedostaje “-”, tada se stavka preskače prilikom rješavanja;
- Paralelni prijenos (smjena) duž O x i O y. Transformacija se vrši ako postoje koeficijenti a i b koji nisu jednaki 0. Ako je a pozitivan, graf se pomiče ulijevo za | a | jedinica, ako je a negativan, onda udesno na istoj udaljenosti. Vrijednost b određuje kretanje duž ose O y, što znači da kada je b pozitivan, funkcija se pomiče gore, a kada je b negativan, pomiče se dolje.
Pogledajmo rješenja koristeći primjere, počevši od funkcije snage.
Primjer 1
Transformirajte y = x 2 3 i nacrtajte funkciju y = - 1 2 · 8 x - 4 2 3 + 3 .
Rješenje
Predstavite funkcije na ovaj način:
y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3
Gdje je k 1 = 2, vrijedi obratiti pažnju na prisustvo "-", a = - 1 2, b = 3. Odavde dobijamo da se geometrijske transformacije izvode rastezanjem duž O y dvaput, prikazano simetrično u odnosu na O x, pomaknuto udesno za 1 2 i nagore za 3 jedinice.
Ako prikažemo izvornu funkciju snage, to ćemo dobiti

kada se dvaput razvuče duž O y imamo to

Preslikavanje, simetrično u odnosu na O x, ima oblik

i pomerite se udesno za 12

izgleda kretanje od 3 jedinice gore

Pogledajmo transformacije eksponencijalnih funkcija koristeći primjere.
Primjer 2
Napravi graf eksponencijalne funkcije y = - 1 2 1 2 (2 - x) + 8.
Rješenje.
Hajde da transformišemo funkciju na osnovu svojstava funkcije stepena. Onda to shvatamo
y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8
Iz ovoga možemo vidjeti da dobijamo lanac transformacija y = 1 2 x:
y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8
Nalazimo da originalna eksponencijalna funkcija ima oblik

Stiskanje dvaput duž O y daje

Istezanje duž O x

Simetrično preslikavanje u odnosu na O x

Preslikavanje je simetrično u odnosu na O y

Pomaknite se za 8 jedinica gore

Razmotrimo rješenje na primjeru logaritamske funkcije y = ln (x).
Primjer 3
Konstruirajte funkciju y = ln e 2 · - 1 2 x 3 koristeći transformaciju y = ln (x) .
Rješenje
Za rješavanje potrebno je koristiti svojstva logaritma, tada dobijamo:
y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2
Transformacije logaritamske funkcije izgledaju ovako:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2
Nacrtajmo originalnu logaritamsku funkciju

Sistem komprimujemo prema O y

Protežemo se duž O x

Izvodimo preslikavanje u odnosu na O y

Pomjerimo se za 2 jedinice, dobijamo

Za transformaciju grafova trigonometrijske funkcije potrebno je u shemu uklopiti rješenja oblika ± k 1 · f (± k 2 · (x + a)) + b. Potrebno je da k 2 bude jednak T k 2 . Odavde dobijamo to 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.
Pogledajmo primjere rješavanja problema s transformacijama y = sin x.
Primjer 4
Konstruirajte graf y = - 3 sin 1 2 x - 3 2 - 2 koristeći transformacije funkcije y=sinx.
Rješenje
Funkciju je potrebno svesti na oblik ± k 1 · f ± k 2 · x + a + b. Za ovo:
y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2
Može se vidjeti da je k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Pošto postoji "-" ispred k 1, ali ne i ispred k 2, onda dobijamo lanac transformacija oblika:
y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2
Detaljna transformacija sinusnog vala. Kada se crta originalna sinusoida y = sin (x), nalazimo da se smatra da je najmanji pozitivni period T = 2 π. Pronalaženje maksimuma u tačkama π 2 + 2 π · k; 1, a minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y je trostruko rastegnut, što znači da će se povećanje amplitude oscilacija povećati za 3 puta. T = 2 π je najmanji pozitivni period. Maksimumi idu na π 2 + 2 π · k; 3, k ∈ Z, minimumi - - π 2 + 2 π · k; - 3, k ∈ Z.

Kada se polovično rasteže duž O x, nalazimo da se najmanji pozitivni period povećava za 2 puta i jednak je T = 2 π k 2 = 4 π. Maksimumi idu na π + 4 π · k; 3, k ∈ Z, minimumi – in - π + 4 π · k; - 3, k ∈ Z.

Slika se proizvodi simetrično u odnosu na O x. Najmanji pozitivni period u ovom slučaju se ne mijenja i jednak je T = 2 π k 2 = 4 π. Maksimalni prelaz izgleda kao - π + 4 π · k; 3, k ∈ Z, a minimum je π + 4 π · k; - 3, k ∈ Z.

Grafikon je pomaknut naniže za 2 jedinice. Minimalni zajednički period se ne mijenja. Pronalaženje maksimuma sa prelazom u tačke - π + 3 + 4 π · k; 1, k ∈ Z, minimumi - π + 3 + 4 π · k; - 5 , k ∈ Z .
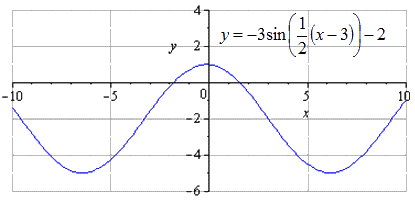
U ovoj fazi, graf trigonometrijske funkcije se smatra transformiranim.
Razmotrimo detaljnu transformaciju funkcije y = cos x.
Primjer 5
Konstruirajte graf funkcije y = 3 2 cos 2 - 2 x + 1 koristeći transformaciju funkcije oblika y = cos x.
Rješenje
Prema algoritmu, potrebno je datu funkciju svesti na oblik ± k 1 · f ± k 2 · x + a + b. Onda to shvatamo
y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1
Iz uslova je jasno da je k 1 = 3 2, k 2 = 2, a = - 1, b = 1, gdje k 2 ima “-”, ali prije k 1 nema.
Iz ovoga vidimo da dobijamo graf trigonometrijske funkcije oblika:
y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1
Korak po korak kosinusna transformacija sa grafičkom ilustracijom.
S obzirom na grafik y = cos(x), jasno je da je najkraći ukupni period T = 2π. Pronalaženje maksimuma u 2 π · k ; 1, k ∈ Z, i postoji π + 2 π · k minimuma; - 1, k ∈ Z.

Kada se rastegne duž Oy za 3 2 puta, amplituda oscilacija se povećava za 3 2 puta. T = 2 π je najmanji pozitivni period. Pronalaženje maksimuma u 2 π · k ; 3 2, k ∈ Z, minimumi u π + 2 π · k; - 3 2 , k ∈ Z .

Kada se kompresuje duž O x na pola, nalazimo da je najmanji pozitivni period broj T = 2 π k 2 = π. Dolazi do prijelaza maksimuma na π · k; 3 2 , k ∈ Z , minimumi - π 2 + π · k ; - 3 2 , k ∈ Z .

Simetrično preslikavanje u odnosu na Oy. Pošto je graf neparan, neće se promijeniti.

Kada se graf pomakne za 1. U najmanjem pozitivnom periodu T = π nema promjena. Pronalaženje maksimuma u π · k + 1 ; 3 2, k ∈ Z, minimumi - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Kada se pomakne za 1, najmanji pozitivni period je jednak T = π i ne mijenja se. Pronalaženje maksimuma u π · k + 1 ; 5 2, k ∈ Z, minimumi u π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Transformacija kosinusne funkcije je završena.
Razmotrimo transformacije koristeći primjer y = t g x.
Primjer 6
Konstruirajte graf funkcije y = - 1 2 t g π 3 - 2 3 x + π 3 koristeći transformacije funkcije y = t g (x) .
Rješenje
Za početak je potrebno datu funkciju svesti na oblik ± k 1 · f ± k 2 · x + a + b, nakon čega dobijamo da
y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3
Jasno je vidljivo da je k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, a ispred koeficijenata k 1 i k 2 stoji “-”. To znači da nakon transformacije tangentoida dobijemo
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3
Korak po korak transformacija tangenta sa grafičkim prikazom.
Imamo da je originalni graf y = t g (x) . Promjena pozitivnog perioda jednaka je T = π. Domen definicije se smatra - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Komprimujemo ga 2 puta duž Oy. T = π se smatra najmanjim pozitivnim periodom, pri čemu domen definicije ima oblik - π 2 + π · k; π 2 + π · k, k ∈ Z.

Rastegnite duž O x 3 2 puta. Izračunajmo najmanji pozitivni period, a on je bio jednak T = π k 2 = 3 2 π . A domen definicije funkcije sa koordinatama je 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, mijenja se samo domen definicije.

Simetrija ide na O x stranu. Period se u ovom trenutku neće mijenjati.

Koordinatne ose je potrebno prikazati simetrično. Domen definicije u ovom slučaju je nepromijenjen. Raspored se poklapa sa prethodnim. Ovo sugerira da je tangentna funkcija neparna. Ako neparnoj funkciji dodijelimo simetrično preslikavanje O x i O y, onda je transformiramo u originalnu funkciju.
Rješenje
Prvo, morate prijeći od arc kosinusa do arc sinusa koristeći inverzne trigonometrijske funkcije a r c sin x + a r c o cos x = π 2. To znači da dobijamo da je a r c sin x = π 2 - a r c cos x.
Može se vidjeti da je y = a r c cos x → y = - a r c cos x → y = - a r c cos x + π 2.
Korak po korak transformacija arkosinusa i grafički prikaz.
Raspored dat prema uslovima

Izvodimo preslikavanje u odnosu na O x

Krećemo se prema gore za π 2.

Tako se vrši prijelaz iz arc kosinusa u kosinus. Potrebno je izvršiti geometrijske transformacije arksinusa i njegovog grafa.
Može se vidjeti da je k 1 = 2, k 2 = 1 3, a = - 1, b = 0, gdje nedostaje znak “-” za k 1 i k 2.
Odavde dobijamo da transformacija y = a r c sin x poprima oblik:
y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x - 1)
Korak po korak transformacija arcsinusnog grafa i grafički prikaz.
Graf y = a r c sin x ima domenu oblika x ∈ - 1 ; 1, tada interval y ∈ - π 2; π 2 pripada rasponu vrijednosti.

Potrebno ga je dvaput rastegnuti duž O y, a domen definicije će ostati nepromijenjen x ∈ - 1; 1, i raspon vrijednosti y ∈ - π; π.

Istezanje prema strukturi Oxa. Domen definicije x ∈ - 3 je proširen; 3, ali raspon vrijednosti ostaje nepromijenjen y ∈ - π; π.