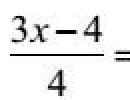Pronalaženje korijena nelinearne jednadžbe

Kurs

Računarstvo, kibernetika i programiranje

Dijagrami toka implementacije numeričkih metoda - za metodu dihotomije: Dijagram toka za metodu akorda: Dijagram toka za Newtonovu metodu: Jedinica liste programa Jedinica1; interfce koristi Windows Messges SysUtils Vrints Clsses Grafičke kontrole Forms Dilogs TeEngine Series ExtCtrls TeeProcs Chrt meniji OleCtnrs StdCtrls xCtrls OleCtrls VCF1 Mth; tip TForm1 = clssTForm GroupBox1: TGroupBox; OleContiner2: TOleContiner; MinMenu1: TMinMenu; N1: TMenuItem; Chrt1: TChrt; Serija 1:...

RUSKI DRŽAVNI UNIVERZITET ZA NAFTU I GAS. NJIH. GUBKIN

Odsjek za kompjuterske nauke

Rad na kursu

u disciplini "Informatika".

Predmet: " Pronalaženje korijena nelinearne jednačine"

Završio: student

Manepova A. M

grupe: GI-12-05

Provjereno:

Moskva 2013

Zadatak za kurs. Teorija pronalaženja korijena nelinearne jednadžbe. Opis korištenih numeričkih metoda. 1. Metoda polovina (dihotomija) 2. Metoda akorda 3. Newtonova metoda Proračuni u matematičkom paketu Mat lab Izveštaj o rezultatima izračunavanja približne vrednosti korena jednačine u MS Excel-u. Rezultati proračuna korištenjem Parameter Selection Rezultati proračuna korištenjem Search for Solutions Opis aplikacije kreirane u Delphi okruženju. Blok šeme koje implementiraju numeričke metode Lista programa Slika prozora aplikacije Analiza dobijenih rezultata Književnost.

Zadatak za kurs.

1. proračun , izveden u matematičkom paketu Matlab (Mathematica 5 .) (funkcija datoteke za opisivanje nelinearne jednadžbe, grafa, rješenja u simboličkom i numeričkom obliku).
2. Pronalaženje korijeni nelinearne jednadžbe u tabelama MS Excel (vrsta nelinearne jednačine, graf nalaženja korena nelinearne jednačine, pronalaženje korena nelinearne jednačine pomoću alata za uslovnu analizu: „Izbor parametra“, „Traženje rešenja“).
3. Kreiranje aplikacije da nađemo korene nelinearne jednačine u Delphi okruženju (tip nelinearne jednačine, graf na dati interval, za svaku metodu: rezultati tabele funkcija na datom intervalu sa datim korakom, za svaku metodu numeričke metode, korisnička potprograma sa prenosom parametara). Rezultati se prikazuju na obrascu u obliku tabele i u fajlu. Predvidjeti promjenu tačnosti vrijednosti (E<= 0 , 001).
4. tip jednadžbe

Teorija pronalaženja korijena nelinearne jednadžbe. Opis korištenih numeričkih metoda.

Neka je funkcija data , kontinuirano zajedno sa nekoliko njegovih derivata. Morate pronaći sve ili neke stvarne korijene jednadžbe

.
Ovaj zadatak je podijeljen na nekoliko podzadataka. Prvo je potrebno odrediti broj korijena i ispitati ih karakter i lokacija. Drugo, pronađite približne vrijednosti korijena. Treće, odaberite korijene koji nas zanimaju i izračunajte ih sa potrebnom preciznošću e. Prvi i drugi problem rješavaju se, po pravilu, analitičkim ili grafičkim metodama. U slučaju kada se traže samo realni korijeni jednadžbe, korisno je napraviti tablicu vrijednosti funkcije . Ako u dva susjedna čvora stolovi funkcija ima različite predznake, tada između ovih čvorova leži neparan broj korijena jednadžbe (barem jedan). Ako su ovi čvorovi blizu, najvjerovatnije postoji samo jedan korijen između njih.
Pronađene približne vrijednosti korijena mogu se precizirati različitim iterativnim metodama.

Razmotrimo tri metode: 1) metod dihotomije (ili dijeljenje segmenta na pola); 2) metoda jednostavne iteracije i 3) metoda Newton.

1. Metoda polovina (dihotomija)

Neka je na segmentu data kontinuirana funkcijaAko vrijednosti funkcije na krajevima segmenta imaju različite predznake, tj.to znači da postoji neparan broj korijena unutar ovog segmenta. Za određenost, neka postoji jedan korijen. Suština metode je prepoloviti dužinu segmenta pri svakoj iteraciji. Pronađite sredinu segmenta koristeći formulu:Izračunajte vrijednost funkcijei odaberite segment na kojem je funkcija menja svoj predznak . Ponovo dijelimo novi segment na pola. I ovaj proces Nastavljamo sve dok dužina segmenta ne bude jednaka unaprijed određenoj grešci u izračunavanju korijena E.

2. Metoda akorda

Kod rješavanja nelinearne jednadžbe metodom akorda određuju se intervali u kojima postoji samo jedno rješenje, a tačnost Ɛ. Zatim kroz dvije tačke sa koordinatama (a,F(a)) i (b,F(b)) povučemo pravi odsječak (tetivu) i odredimo točku presjeka ove prave sa osom apscise. Ako u isto vrijeme F(a)*F(b)<0, то праву границу интервала пееносиим в точку x (b=x). Если указанное условие не выполняется, то в точку x lijeva granica intervala se pomjera (a=x). Potraga za rješenjem se zaustavlja kada se postigne specificirana tačnost |F(x)|>Ɛ. Proračuni se provode dok se ne ispuni nejednakost:. Iterativna formula metode akorda ima oblik:

3. Newtonova metoda

Za numerički rješavanje jednačinejednostavnom metodom iteracije, mora biti doveden u sljedeći oblik:, gdje kompresivno mapiranje.

Za najbolju konvergenciju metoda u tački sljedeće aproksimacijeuslov mora biti ispunjen. Rješenje ove jednačine traži se u obliku, Zatim:

Pod pretpostavkom da je pristupna tačka "dovoljno blizu" korijenu, te da je data funkcija kontinuirano , konačna formula za je li ovo:

Uzimajući to u obzir, funkcija određuje se izrazom:

Ova funkcija vrši kompresivno preslikavanje u susjedstvu korijena, i algoritam za pronalaženje numeričkog rješenja jednačinesvodi na iterativni postupak izračunavanja:

Proračuni u matematičkom paketu Mat lab

U matematičkom paketu, prema uslovima zadatka, iscrtan je graf funkcije i pronađen je korijen jednadžbe pomoću simboličkog rješenja ( riješiti ) i numerički koristeći ugrađene funkcije: fzero i fsolve . Da opišem svoju funkciju koristio sam funkciju datoteke.

Sljedeća slika prikazuje graf funkcije:

Za pisanje naredbi koje sam koristio M-fajl:

U komandnom prozoru dobijeni su sljedeći rezultati:

r 1 =

r 2 =

r 3 =

r 4 =

8.0000

r5 =

7.9979 -8.0000

Izveštaj o rezultatima izračunavanja približne vrednosti korena jednačine u MS Excel-u.

MS Excel Približna vrijednost korijena jednadžbe izračunata je korištenjem ugrađenih mogućnosti “Izbor parametara” i “Traženje rješenja”. Da bih izabrao početnu aproksimaciju, prvo sam napravio dijagram.

Rezultati proračuna korištenjem Parameter Selection

x =-9 (na osnovu grafikona)

Kao rezultat korištenja odabira parametara, korijen je pronađen x = -8,01.

Rezultati proračuna korištenjem Search for Solutions

Odabrana je početna aproksimacija x =-9 (na osnovu grafikona)

Nakon izvršenja dobijen je sljedeći rezultat:

Pronalaženje rješenja dalo mi je smisao x = -8,00002

Opis aplikacije kreirane u Delphi okruženju.

Prilikom kreiranja aplikacije u okruženju Delphi Interfejs je pružao prikaz tipa funkcije i grafikona. Pronalaženje korijena nelinearne jednačine provedeno je korištenjem tri metode: Dihotomijska metoda, Hordova metoda i Newtonova metoda. Za razliku od kalkulacije u Excel gdje su korijeni pronađeni odabirom parametara i traženjem rješenja, program omogućava korisniku da unese tačnost proračuna. Rezultati proračuna se prikazuju u prozoru aplikacije iu tekstualnoj datoteci.

Blok šeme koje implementiraju numeričke metode

Dijagram toka za metodu dihotomije:

Blok dijagram za metodu akorda:

Dijagram toka za Newtonovu metodu:

Lista programa

jedinica Unit1;

interfejs

koristi

Windows, poruke, SysUtils, varijante, klase, grafika, kontrole, obrasci,

Dijalozi, TeEngine, Series, ExtCtrls, TeeProcs, Chart, Menus, OleCtnrs,

StdCtrls, AxCtrls, OleCtrls, VCF1, Math;

tip

TForm1 = klasa(TForm)

GroupBox1: TGroupBox;

OleContainer2: TOleContainer;

MainMenu1: TMainMenu;

N1: TMenuItem;

Chart1:TChart;

Serija1: TPointSeries;

N2: TMenuItem;

N3: TMenuItem;

N4: TMenuItem;

N5: TMenuItem;

Oznaka1: TLabel;

Edit1: TEdit;

GroupBox2: TGroupBox;

GroupBox3: TGroupBox;

GroupBox4: TGroupBox;

Label2: TLabel;

Label3: TLabel;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Label4: TLabel;

Edit5: TEdit;

Label5: TLabel;

Edit7: TEdit;

Oznaka7: TLabel;

F1Book1: TF1Book;

F1Book2: TF1Book;

F1Book3: TF1Book;

F1Book4: TF1Book;

Procedura N1Klik (Pošiljalac: TObject);

Procedura N3Click(Pošiljalac: TObject);

Procedura FormCreate(Pošiljalac: TObject);

Procedura N4Click(Pošiljalac: TObject);

Procedura N5Klik (Pošiljalac: TObject);

Privatno

(privatne izjave)

Javno

(Javne izjave)

End;

konst

xmin:real=-20;

xmax:real=20;

Form1: TForm1;

X,y,t,a,b,cor:real;

I,n:ceo broj;

Fail:textfile;

implementacija

($R *.dfm)

funkcija f(x:real):real;

početi

f:=(8+x)/(x*sqrt(sqr(x)-4));

kraj;

funkcija f1(x:real):real;

početi

f1:=(-power(x,3)-16*x*x+32)/(x*X*sqrt(power(x*x-4,3)));

kraj;

procedure metoddix(ta,tb,eps:real;var xk:real;var kolvo: integer);

početi

kolvo:=0;

ponovi

xk:=(ta+tb)/2;

kolvo:=kolvo+1;

Form1.F1book1.NumberRC:=xk;

Form1.F1book1.NumberRC:=f(xk);

ako je f(ta)*f(xk)<0 then tb:=xk

ostalo ta:=xk;

do (abs(f(xk))<=eps);

kraj;

procedure metodhord(ta,tb,eps:real;var xk:real;var kolvo: integer);

početi

kolvo:=0;

ponovi

xk:= ta-f(ta)*(ta-tb)/(f(ta)-f(tb));

kolvo:=kolvo+1;

Form1.F1book2.NumberRC:=xk;

Form1.F1book2.NumberRC:=f(xk);

ako je f(ta)*f(xk)<0 then tb:=xk

ostalo ta:=xk;

do (abs(f(xk))<=eps);

kraj;

procedura metodnyutona(ta,eps:real;var xk:real;var kolvo: integer);

početi

kolvo:=0;

ponovi

xk:= ta-f(ta)/f1(ta);

ta:=xk;

kolvo:=kolvo+1;

Form1.F1book3.NumberRC:=xk;

Form1.F1book3.NumberRC:=f(xk);

do (abs(f(xk))<=eps);

kraj;

procedura TForm1.N1Click(Pošiljalac: TObject);

početi

x:=xmin;

i:=0;

dok je x<=xmax do

početi

ako je abs(x)>5 onda

Počni

I:=i+1;

Y:=f(x);

Serija1.Addxy(x,y);

F1book4.NumberRC:=x;

F1book4.NumberRC:=y;

End;

x:=x+0,5;

kraj;

kraj;

procedura TForm1.N3Click(Pošiljalac: TObject); // Izračunavanje korijena metodom prepolovljenja

početi

F1book1.ClearRange(1,1,100,2,3);

t:=strtofloat(Edit1.Text);

a:=strtofloat(Edit2.Text);

b:=strtofloat(Edit3.Text);

metoddix(a,b,t,cor,n);

F1book4.TextRC:="dihotomija";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" broj iteracija = ";

F1book4.NumberRC:=n;

Dodati(neuspjeh);

Writen(fail);

Writeln(fail," Izračunavanje metodom dihotomije ");

closefile(fail);

kraj;

procedura TForm1.FormCreate(Pošiljalac: TObject);

početi

Assignfile(fail," report .txt");

Rewrite(fail);

Closefile(fail);

kraj;

procedura TForm1.N4Click(Pošiljalac: TObject); // Izračunavanje korijena metodom akorda

početi

F1book2.ClearRange(1,1,100,2,3);

t:=strtofloat(Edit1.Text);

a:=strtofloat(Edit5.Text);

b:=strtofloat(Edit4.Text);

metodhord(a,b,t,cor,n);

F1book4.TextRC:=" akordi ";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" broj iteracija = ";

F1book4.NumberRC:=n;

Assignfile(fail," report .txt");

Dodati(neuspjeh);

Writen(fail);

Writeln(fail," Izračunavanje pomoću metode akorda ");

writeln(fail,"Preciznost izračuna = ",t:10:7);

Writeln(fail,"Inicijalna aproksimacija:a = ",a:8:3," b = ",b:8:3);

writeln(fail, " Root pronađen : x = ",cor:8:3, " y=f(x)= ",f(cor):8:6);

writeln(fail, "Broj iteracija = ",n);

closefile(fail);

kraj;

procedura TForm1.N5Click(Pošiljalac: TObject); // Izračunavanje korijena pomoću Newtonove metode

početi

F1book3.ClearRange(1,1,100,2,3);

t:=strtofloat(Edit1.Text);

a:=strtofloat(Edit7.Text);

metodnyutona(a,t,cor,n);

F1book4.TextRC:="Njutn";

F1book4.TextRC:=" root = ";

F1book4.NumberRC:=cor;

F1book4.TextRC:="y=";

F1book4.NumberRC:=f(cor);

F1book4.TextRC:=" broj iteracija = ";

F1book4.NumberRC:=n;

Assignfile(fail," report .txt");

Dodati(neuspjeh);

Writen(fail);

Writeln(fail," Izračunavanje Newtonovom metodom ");

writeln(fail,"Preciznost izračuna = ",t:10:7);

Writeln(fail,"Inicijalna aproksimacija:a = ",a:8:3," b = ",b:8:3);

writeln(fail, " Root pronađen : x = ",cor:8:3, " y=f(x)= ",f(cor):8:6);

writeln(fail, "Broj iteracija = ",n);

Closefile(fail);

kraj;

kraj.

Slika prozora aplikacije

Početni interfejs izgleda ovako:

Nakon izvršenih proračuna na E<= 0,001:

Datoteka “Izvještaj. poruka.":

Analiza dobijenih rezultata

U skladu sa zadatkom za nastavni rad u matematičkom paketu, pronašao sam korijen nelinearne jednačine ( x =-8) i napravljen je graf.

U tabelama, korijen jednadžbe je pronađen pomoću dvije ugrađene mogućnosti “Odabir parametara” i “Traženje rješenja”, dok je “Traženje rješenja” ipak dalo precizniju vrijednost. Rezultati su se praktično poklopili sa rezultatima u Matlab.

Da pronađemo koren u okruženju Delphi korisnik ima mogućnost da unese preciznost proračuna sa tastature. Testiranje programa pokazalo je da za istu zadatu tačnost proračuna Newtonova metoda pronalazi željenu vrijednost u manjem broju iteracija.

Dakle, proračuni su pokazali da se nelinearna jednačina može riješiti u različitim medijima. Pokazalo se da je najintenzivniji proračun bio u okruženju Delphi.

Književnost.

1. Amosov A.A. i druge računske metode za inženjere M., Viša škola, 1994.
2. Faronov V.V. Delphi. Programiranje na jeziku visokog nivoa

3. Walkenbach D . Microsoft Office Excel 2007.Korisnička Biblija

Volkov V.B. Jasan vodič za Excel 2010

Matematika kao nauka nastala je u vezi sa potrebom rješavanja praktičnih problema: mjerenja na tlu, navigacije itd. Zbog toga je matematika bila numerička matematika i cilj joj je bio da dobije rješenje u obliku broja. Numeričko rješavanje primijenjenih problema uvijek je zanimalo matematičare. Najveći predstavnici prošlosti kombinovali su u svojim istraživanjima proučavanje prirodnih pojava, dobijajući njihov matematički opis, tj. njegov matematički model i njegova istraživanja. Analiza složenih modela zahtijevala je stvaranje posebnih, najčešće numeričkih metoda za rješavanje problema. Nazivi nekih od ovih metoda ukazuju da su u njihov razvoj bili uključeni najveći naučnici svog vremena. To su metode Njutna, Ojlera, Lobačevskog, Gausa, Čebiševa, Ermita.

Sadašnje vrijeme karakterizira naglo širenje primjene matematike, koje se u velikoj mjeri odnosi na stvaranje i razvoj računarske tehnologije. Kao rezultat pojave računara, za manje od 40 godina, brzina operacija se povećala sa 0,1 operacija u sekundi sa ručnim proračunom na 10 operacija u sekundi na modernim računarima.

Rašireno mišljenje o svemoći modernih kompjutera stvara utisak da su se matematičari riješili svih muka vezanih za numeričko rješavanje problema, a razvoj novih metoda za njihovo rješavanje više nije toliko važan. U stvarnosti je situacija drugačija, jer potrebe evolucije po pravilu postavljaju pred nauku zadatke koji su na granici njenih mogućnosti. Proširenje mogućnosti primjene matematike dovelo je do matematizacije različitih grana nauke: hemije, ekonomije, biologije, geologije, geografije, psihologije, medicine, tehnologije itd.

Mogu se identificirati dvije okolnosti koje su u početku odredile želju za matematiziranjem nauka:

prvo, samo korištenje matematičkih metoda omogućuje davanje kvantitativnog karaktera proučavanju jednog ili drugog fenomena materijalnog svijeta;

drugo, i to je glavna stvar, samo matematički način razmišljanja čini objekat. Ova metoda istraživanja se naziva kompjuterski eksperiment, potpuno objektivna studija.

Nedavno se pojavio još jedan faktor koji snažno utiče na procese matematizacije znanja. Ovo je brzi razvoj kompjuterske tehnologije. Upotreba računara za rešavanje naučnih, inženjerskih i opšteprimenjenih problema u potpunosti se zasniva na njihovoj matematiizaciji.

Matematički modeli.

Savremena tehnologija za proučavanje složenih problema zasniva se na konstrukciji i analizi, obično uz pomoć kompjutera, matematičkih modela onoga što se proučava. Tipično, računarski eksperiment, kao što smo već vidjeli, sastoji se od više faza: postavljanje problema, konstrukcija matematičkog modela (matematička formulacija problema), razvoj numeričke metode, razvoj algoritma za implementaciju numerička metoda, izrada programa, otklanjanje grešaka u programu, izvođenje proračuna, analiza rezultata.

Dakle, upotreba kompjutera za rešavanje bilo kog naučnog ili inženjerskog problema neizbežno je povezana sa prelaskom sa realnog procesa ili fenomena na njegov matematički model. Stoga je upotreba modela u naučnoistraživačkoj i inženjerskoj praksi umjetnost matematičkog modeliranja.

Model se obično naziva zamislivi ili materijalno ostvarivi sistem koji reproducira glavne, najbitnije karakteristike date pojave.

Glavni zahtjevi za matematički model su adekvatnost fenomena koji se razmatra, tj. mora dovoljno odražavati karakteristične karakteristike fenomena. Istovremeno, trebalo bi da bude relativno jednostavno i pristupačno za istraživanje.

Matematički model odražava odnos između uslova za pojavu fenomena koji se proučava i njegovih rezultata u određenim matematičkim strukturama. Najčešće se kao takve konstrukcije koriste sljedeći matematički koncepti: funkcija, funkcional, operator, numerička jednačina, obična diferencijalna jednačina, parcijalna diferencijalna jednačina.

Matematički modeli se mogu klasifikovati prema različitim kriterijumima: statički i dinamički, koncentrirani i distribuirani; deterministički i probabilistički.

Razmotrimo problem nalaženja korijena nelinearne jednačine

Korijeni jednadžbe (1) su one vrijednosti x koje ga, kada se zamijene, pretvaraju u identitet. Samo za najjednostavnije jednačine moguće je naći rješenje u obliku formula, tj. analitički oblik. Češće je potrebno rješavati jednadžbe aproksimativnim metodama, među kojima su, zbog pojave kompjutera, najraširenije numeričke metode.

Algoritam za pronalaženje korijena pomoću aproksimativnih metoda može se podijeliti u dvije faze. U prvoj fazi proučava se lokacija korijena i vrši se njihovo odvajanje. Pronađeno je područje u kojem postoji korijen jednadžbe ili početna aproksimacija korijenu x 0. Najjednostavniji način za rješavanje ovog problema je ispitivanje grafa funkcije f(x) . U opštem slučaju, za njegovo rešavanje potrebno je koristiti sva sredstva matematičke analize.

Postojanje barem jednog korijena jednadžbe (1) na pronađenom segmentu proizlazi iz Bolzanovog uvjeta:

f(a)*f(b)<0 (2)

To implicira da je funkcija f(x) kontinuirana na ovom intervalu. Međutim, ovaj uvjet ne daje odgovor na pitanje o broju korijena jednadžbe na datom intervalu. Ako se zahtjevu kontinuiteta funkcije dopuni i zahtjev njene monotonosti, a to proizilazi iz konstantnosti predznaka prvog izvoda, onda možemo tvrditi postojanje jednog korijena na datom segmentu.

Prilikom lokalizacije korijena također je važno poznavati osnovna svojstva ove vrste jednadžbi. Na primjer, prisjetimo se nekih svojstava algebarskih jednadžbi:

gdje su realni koeficijenti.

• a) Jednačina stepena n ima n korijena, među kojima može biti i realnih i kompleksnih. Kompleksni korijeni formiraju kompleksne konjugirane parove i, stoga, jednadžba ima paran broj takvih korijena. Ako je n neparno, postoji barem jedan pravi korijen.
• b) Broj pozitivnih realnih korijena manji je ili jednak broju promjenljivih predznaka u nizu koeficijenata. Zamjena x sa -x u jednačini (3) omogućava nam da procijenimo broj negativnih korijena na isti način.

U drugoj fazi rješavanja jednadžbe (1), koristeći dobijenu početnu aproksimaciju, konstruiše se iterativni proces koji omogućava da se vrijednost korijena precizira sa određenom unaprijed određenom točnošću. Iterativni proces se sastoji od sekvencijalnog preciziranja početne aproksimacije. Svaki takav korak naziva se iteracija. Kao rezultat procesa iteracije, nalazi se niz približnih vrijednosti korijena jednadžbe. Ako se ovaj niz približava pravoj vrijednosti korijena x kako n raste, tada se iterativni proces konvergira. Za iterativni proces se kaže da konvergira najmanje na red m ako je ispunjen sljedeći uvjet:

gdje je C>0 neka konstanta. Ako je m=1, onda govorimo o konvergenciji prvog reda; m=2 - oko kvadratne, m=3 - oko kubične konvergencije.

Iterativni ciklus se završava ako su za datu dozvoljenu grešku ispunjeni kriterijumi za apsolutna ili relativna odstupanja:

ili mala neslaganja:

Ovaj rad je posvećen proučavanju algoritma za rješavanje nelinearnih jednačina korištenjem Newtonove metode.

Postoji mnogo različitih metoda za rješavanje nelinearnih jednadžbi, neke od njih su predstavljene u nastavku:

• 1)Metoda iteracije. Prilikom rješavanja nelinearne jednačine metodom iteracije koristit ćemo jednačinu napisanu u obliku x=f(x). Navedena je početna vrijednost argumenta x 0 i tačnost e. Prva aproksimacija rješenja x 1 nalazi se iz izraza x 1 =f(x 0), druga - x 2 =f(x 1) itd. . U opštem slučaju, nalazimo i+1 aproksimaciju koristeći formulu xi+1 =f(xi). Ponavljamo ovaj postupak dok |f(xi)|>e. Uvjet za konvergenciju iteracijske metode |f"(x)|
• 2)Newtonova metoda. Prilikom rješavanja nelinearne jednadžbe Newtonovom metodom specificira se početna vrijednost argumenta x 0 i tačnost e. Zatim u tački (x 0 ,F(x 0)) povlačimo tangentu na graf F(x) i odredimo točku presjeka tangente sa osom apscise x 1 . U tački (x 1 ,F(x 1)) ponovo konstruišemo tangentu, nađemo sledeću aproksimaciju željenog rešenja x 2, itd. Ponavljamo ovaj postupak do |F(xi)| > e. Da bismo odredili tačku preseka (i+1) tangente sa x-osom, koristimo sledeću formulu

x i+1 =x i -F(x i) F"(x i).

Uslov za konvergenciju tangentne metode F(x 0) F""(x)>0, itd.

3). Metoda dihotomije. Tehnika rješenja se svodi na postepeno dijeljenje početnog intervala nesigurnosti na pola prema formuli

C k = a k + b k /2.

Da bismo od dva rezultujuća segmenta odabrali traženi, potrebno je na krajevima rezultujućih segmenata pronaći vrijednost funkcije i uzeti u obzir onaj na kojem će funkcija promijeniti predznak, odnosno uvjet f ( a k) * f (u k) mora biti zadovoljeno<0.

Proces dijeljenja segmenta se izvodi sve dok dužina trenutnog intervala nesigurnosti ne bude manja od navedene tačnosti, odnosno u k - a k< E. Тогда в качестве приближенного решения уравнения будет точка, соответствующая середине интервала неопределённости.

4). Metoda akorda. Ideja metode je da se na segmentu konstruiše tetiva, koja spaja krajeve luka grafa funkcije y=f(x), i tačku c, presek tetive sa x- os, smatra se približnom vrijednošću korijena

c = a - (f(a)H (a-b)) / (f(a) - f(b)),

c = b - (f(b)H (a-b)) / (f(a) - f(b)).

Sljedeća aproksimacija se traži na intervalu ili ovisno o predznacima vrijednosti funkcije ​​u tačkama a, b, c

x* O, ako je f(c)H f(a) > 0;

x* O ako je f(c)H f(b)< 0 .

Ako f"(x) ne promijeni predznak u , tada označavajući c=x 1 i uzimajući u obzir a ili b kao početnu aproksimaciju, dobijamo iterativne formule metode tetiva sa fiksnom desnom ili lijevom tačkom.

x 0 =a, x i+1 = x i - f(x i)(b-x i) / (f(b)-f(x i), pri čemu je f "(x)H f "(x) > 0;

x 0 =b, x i+1 = x i - f(x i)(x i -a) / (f(x i)-f(a), sa f "(x)H f "(x)< 0 .

Konvergencija metode akorda je linearna

Algebarske i transcendentalne jednadžbe. Metode lokalizacije korijena.

Najopštiji oblik nelinearne jednačine:

f(x)=0 (2.1)

gdje je funkcija f(x) definiran i kontinuiran na konačnom ili beskonačnom intervalu [a, b].

Definicija 2.1. Bilo koji broj koji invertuje funkciju f(x) na nulu naziva se korijenom jednačine (2.1).

Definicija 2.2. Broj se naziva k-tim korijenom višestrukosti ako, zajedno sa funkcijom f(x) njegovi derivati ​​do (k-1)-og reda, uključujući, jednaki su nuli:

Definicija 2.3. Jedan korijen se naziva jednostavnim.

Nelinearne jednačine sa jednom promenljivom dele se na algebarske i transcendentalne.

Definicija 2.4 . Jednačina (2.1) se naziva algebarskom ako je funkcija F(x) algebarska.

Pomoću algebarskih transformacija, iz bilo koje algebarske jednadžbe može se dobiti jednačina u kanonskom obliku:

gdje su realni koeficijenti jednačine, x je nepoznata.

Iz algebre je poznato da svaka algebarska jednadžba ima barem jedan realan ili dva kompleksna konjugirana korijena.

Definicija 2.5. Jednačina (2.1) se naziva transcendentnom ako funkcija F(x) nije algebarska.

Rješavanje jednadžbe (2.1) znači:

• 1. Odredite da li jednačina ima korijen.
• 2. Odrediti broj korijena jednadžbe.
• 3. Nađite vrijednosti korijena jednadžbe sa zadatom tačnošću.

Jednačine koje se susreću u praksi često se ne mogu riješiti analitičkim metodama. Za rješavanje takvih jednadžbi koriste se numeričke metode.

Algoritam za pronalaženje korijena jednadžbe pomoću numeričke metode sastoji se od dvije faze:

• 1) odjelu ili lokalizacija root, tj. uspostavljanje jaza koji sadrži jedan korijen:
• 2) pojašnjenje korijenske vrijednosti koristeći metodu uzastopnih aproksimacija.

Metode lokalizacije korijena. Teorijska osnova Algoritam razdvajanja korijena temelji se na Cauchyjevoj teoremi o srednjim vrijednostima kontinuirane funkcije.

Teorema 2.1. Ako je funkcija y = f(x) kontinuirana na segmentu [a,b] i f(a)=A, f(b)=B, tada za bilo koju tačku C koja leži između A i B postoji tačka koja .

Posljedica. Ako je funkcija y = f(x) kontinuirana na segmentu [a,b] i poprima vrijednosti različitih predznaka na svojim krajevima, tada postoji barem jedan korijen jednadžbe f(x) = 0 na ovom segment.

Neka je domen definicije i kontinuiteta funkcije konačan segment [a,b]. Podijelite segment na n dijelovi: ,

Uzastopnim izračunavanjem vrijednosti funkcije u tačkama, nalazimo takve segmente za koje je uvjet zadovoljen:

one. , ili, . Ovi segmenti sadrže najmanje jedan korijen.

Teorema 2.2. Ako je funkcija y = f(x) kontinuirana na intervalu [a;b], f(a)f(b)<0 и f`(х) на интервале (а;b) сохраняет знак, то внутри отрезка [а;b] существует единственный корень уравнения f(х) = 0.

Da biste razdvojili korijene, možete koristiti i graf funkcije at= f (X). Korijeni jednačine (2.1) su te vrijednosti X, na kojoj graf funkcije y=f(x) siječe osu apscise. Iscrtavanje grafa funkcije, čak i sa malom preciznošću, obično daje ideju o lokaciji korijena jednadžbe (2.1). Ako je crtanje funkcije y=f(x) teško, tada bi originalnu jednačinu (2.1) trebalo transformirati u oblik ts1(x)= q2(x) tako da grafovi funkcija at= ts1(x) I at= q2(x) bile prilično jednostavne. Apscise presječnih tačaka ovih grafova bit će korijeni jednačine (2.1).

Primjer 1. Odvojite korijene jednačine x 2 -2cosx=0.

Rješenje. Pogledajmo dva načina razdvajanja korijena.

• a) Grafička metoda. Prepišimo jednačinu u obliku x 2 =2cosx i ucrtajmo funkcije y=x2 i y=2cosx u isti koordinatni sistem (slika 5). pošto se ovi grafovi seku u dve tačke, jednačina ima dva korena koja se nalaze simetrično u odnosu na ishodište na intervalima (-/2; 0) i (0; /2).
• b) Analitička metoda. Neka f(x)= x 2 -2cosx. Jer f(x) je parna funkcija, onda je dovoljno uzeti u obzir samo nenegativne vrijednosti x. Zbog nejednakosti 2cosx2

Derivat f"(x)=2(x+sinx). Na intervalu (0; /2) f"(x)>0, dakle, f(x) ovdje se monotono povećava i njegov graf može prelaziti os X ne više od jedne tačke. primeti, to f(0)=- 2<0, аf(/2)=(/2) 2 >0. Dakle, jednačina ima jedan pozitivan korijen, koji leži na intervalu (0; /2). Zbog parnosti funkcije, jednadžba ima i jedan negativan korijen, simetričan pozitivnom. Sada pređimo na razjašnjavanje korijena. Da biste koristili kombiniranu metodu pojašnjenja korijena, morate to biti sigurni f ""(x) na (0; /2) zadržava predznak i bira početnu aproksimaciju korijena za primjenu metode tangente. Mora zadovoljiti uslov: f(x)f ""(x)>0. Jer f ""(x)=2(1+cosx) je pozitivan na , tada se /2 može uzeti kao početna aproksimacija korijena u tangentnoj metodi. Stoga, možemo staviti x=/21,570796, x 1 =0 (vidi dijagram algoritma). U našem slučaju, metoda akorda će dati približnu vrijednost korijena s nedostatkom, a tangentna metoda će dati višak.

Razmotrimo jedan iterativni korak rafiniranja korijena. Izračunajmo vrijednosti f(0), f(/2), f"(/2). Nove vrijednosti x 1 I x nalazimo u skladu s tim koristeći formule:

|x-x 1 |=0,387680.4>10 -4 =.

Navedena tačnost nije postignuta i proračuni se moraju nastaviti.

Broj iteracije	x 1		f(x 1 )			|x-x 1 |

Posljedično, približna vrijednost korijena sa traženom tačnošću pronađena je kao rezultat tri iteracije i približno je jednaka 1,0217.

Zbog simetrije grafa funkcije f(x) vrijednost drugog korijena je približno jednaka -1,0217.

Pojašnjenje korijena.

Formulacija problema . Pretpostavimo da je željeni korijen jednačine (2.1) odvojen, tj. pronađeni segment [a; b], na kojem postoji jedan i samo jedan korijen jednačine. Bilo koja tačka na ovom segmentu može se uzeti kao približna vrijednost korijena. Greška takve aproksimacije ne prelazi dužinu [A; b]. Shodno tome, zadatak pronalaženja približne vrijednosti korijena sa datom tačnošću svodi se na pronalaženje segmenta [a; b] (b - a<), содержащего только один корень уравнения (2.1). Эту задачу обычно называют задачей pojašnjenje korijena.

Opis numeričkih metoda. Numeričke metode vam omogućavaju da pronađete rješenja za određene probleme, znajući unaprijed da će se dobiveni rezultati izračunati sa određenom greškom, tako da je za mnoge numeričke metode potrebno unaprijed znati “nivo tačnosti” do kojeg će rezultirajuće rješenje dopisivati ​​se.

S tim u vezi, problem pronalaženja korijena polinoma oblika (3.1)

je od posebnog interesa jer Formule za pronalaženje korijena čak i kubične jednadžbe su prilično složene. Ako trebate pronaći korijene polinoma čiji je stepen, na primjer, 5, onda ne možete bez pomoći numeričkih metoda, pogotovo jer je vjerovatnoća da takav polinom ima prirodne korijene (bilo cijeli broj ili tačan korijen sa " kratki” razlomak) je prilično mali i ne postoje formule za pronalaženje korijena jednadžbe stepena većeg od 4. De facto, sve dalje operacije će se svesti samo na razjašnjavanje korena, čiji su intervali približno unaprijed poznati. Najlakši način da pronađete ove "približne" korijene je korištenje grafičkih metoda.

Postoji nekoliko numeričkih metoda za pronalaženje korijena polinoma: metoda iteracije, metoda tetiva i tangenta, metoda bisekcije, metoda sekanti.

Metoda bisekcije(također poznat kao “metoda bisekcije”) je također rekurzivan, tj. predviđa ponavljanje uzimajući u obzir dobijene rezultate.

Suština metode prepolovljenja je sljedeća:

• - data je funkcija F(x);
• - utvrđuje se dozvoljena greška Q;
• - definiran je određeni interval [a, b] koji tačno sadrži rješenje jednačine.

1) Izračunavamo vrijednost E koordinate, uzimajući sredinu segmenta, tj.

E= (a + b) / 2 (3.2)

• 2) Izračunavamo vrednosti F(a), F(b), F(E) i vršimo sledeću proveru: Ako je F(E)>Q, koren je pronađen sa navedenom tačnošću. Ako je F(E)
• 3) Idite na tačku 1.

Metoda jednostavnih iteracija (metoda uzastopnih aproksimacija). Zamenimo jednačinu (2.1) ekvivalentnom jednačinom

x=(x) (3.3)

može se izvesti na razne načine, npr

x=x+sf(x), c0. (3.4)

Pretpostavimo da je odabrana neka početna aproksimacija korijena jednadžbe (3.3). Odredimo niz brojeva koristeći formule

X n+1 =(x n ), n=0,1,2,… (3.5)

Ovaj niz se naziva iterativnim.

Ako na segmentu koji sadrži x 0 i sve naredne aproksimacije x n, nN, funkcija (x) ima kontinuirani izvod "(x) i |"(x)|q<1, то итерационная последовательность (3.5) сходится к единственному на корню уравнения (3.3). Скорость сходимости определяется неравенством

Iz ove nejednakosti, posebno, slijedi da stopa konvergencije jednostavne iteracijske metode ovisi o vrijednosti q: što je q manji, to je konvergencija brža.

Slijedom toga, u praksi, pri pronalaženju korijena metodom jednostavne iteracije, poželjno je jednadžbu (2.1) prikazati u obliku (3.3) na način da izvod "(x) u blizini korijena u apsolutnoj vrijednosti je moguće manji.Za to se ponekad koristi parametar c iz formule (3.4).

Newtonova metoda (tangentna metoda). Ako je poznata dovoljno dobra početna aproksimacija za koju vrijedi nejednakost:

tada možete izračunati jedini korijen jednadžbe koristeći Newtonovu formulu

Granice intervala se mogu koristiti kao početna aproksimacija i:

Ako je uključeno.

Pri svakoj iteraciji ove metode količina proračuna je veća nego u metodama bisekcije i iteracije, jer je potrebno pronaći ne samo vrijednost funkcije, već i njenu derivaciju. Međutim, stopa konvergencije Newtonove metode je mnogo veća.

Teorema. Neka je korijen jednadžbe, tj. , i kontinuirano je. Tada postoji susjedstvo korijena takvo da ako početna aproksimacija pripada ovom susjedstvu, tada za Newtonov metod niz vrijednosti konvergira na at. Greška aproksimacije th korijena može se procijeniti pomoću formule:

gdje je najveća vrijednost modula drugog izvoda na segmentu, je najmanja vrijednost modula prvog izvoda na segmentu.

Zaustavi pravilo:

Metoda akorda i tangenta (kombinovani). Ova metoda se zasniva na konstruisanju šematskog grafa funkcije, određivanju intervala njenog preseka sa apscisnom osom i naknadnom „komprimovanju“ ovog intervala korišćenjem konstruisanih tetiva i tangenti na graf ove funkcije.

Treba napomenuti da postoje i odvojene metode akorda (daje vrijednost korijena s nedostatkom) i metoda tangente (sa viškom). Međutim, prednost kombinovane metode leži u „bilateralnoj kompresiji“ dotičnog segmenta.

Razmotrite sljedeći slučaj:

• - data je funkcija F(x) i njen graf je ucrtan;
• - utvrđuje se dozvoljena greška Q
• - na osnovu grafa definira se segment na kojem graf funkcije siječe osu apscise, dakle na ovom segmentu se nalazi korijen polinoma o kojem je riječ (označavamo ga sa A)

Dalji algoritam se svodi na sljedeće korake:

• 1) konstruisati tangentu na graf funkcije u tački F(b)
• 2) izračunajte x koordinatu presjeka tangente sa osom apscise koristeći formulu (3.9) i označite je sa b"
• 3) konstruisati tetivu na grafu funkcije koja prolazi kroz tačke F(a) i F(b).
• 4) Tačku presjeka tetive sa osom apscise izračunavamo pomoću formule (2) i označavamo je sa a".

Tako dobijamo novi segment, koji (prema definicijama tetive i tangente) još uvijek sadrži rješenje jednačine A.

Sada uzimamo segment kao novi segment i ponavljamo korake 1-4 sve dok razlika F(b)-F(a) ne postane manja od početno utvrđene greške Q. Također napominjemo da se nakon toga preporučuje da se uzme aritmetička sredina F kao željeno rješenje (a) i F(b).

Dakle, ako tetiva (tangenta) daje vrijednost korijena s viškom, tada se ovaj korijen uzima kao nova desna granica, a ako je s nedostatkom, onda lijeva. U oba slučaja, tačan korijen leži između točaka presjeka tetive i tangente sa x-osom.

Napomena o metodi tetiva i tangenta. Budući da je za rješavanje problema potrebno pronaći derivaciju funkcije F(x), metodu tetiva i tangenta je prilično teško implementirati na softverskom nivou, jer pravila za izračunavanje izvedenica u opštem obliku prilično su glomazna za „razumevanje“ računara; Prilikom direktnog specificiranja izvoda za svaki stepen polinoma, memorija računara je ozbiljno opterećena, što uveliko usporava rad, a specificiranje funkcije i, shodno tome, njenog izvoda direktno u programskom kodu je neprihvatljivo. Međutim, primjenom ove metode najbrže dolazi do konvergencije intervala do korijena, posebno ako se kombinira metoda tetiva i tangenta s metodom bisekcije, jer sredina novog segmenta često daje potpuno zadovoljavajuće rješenje.

Sekantna metoda. Metoda sekante može se dobiti iz Newtonove metode zamjenom izvoda s približnim izrazom - formulom razlike:

Formula (3.8) koristi dvije prethodne aproksimacije i. Stoga je za datu početnu vrijednost potrebno izračunati sljedeću aproksimaciju, na primjer, Newtonovom metodom sa približnom zamjenom derivacije prema formuli

Algoritam za metodu sekante:

1) početna vrijednost i greška su navedene. Hajde da izračunamo

2) za n= 1.2, ..... dok je uslov ispunjen, izračunavamo ga pomoću formule (3.8).

Jednačina kao što je F(x)=0 ili x=f(x) naziva se nelinearna. Rješavanje jednadžbe znači pronalaženje x takvog da se jednačina pretvara u identitet. Uopšteno govoreći, jednačina može imati 0; 1; 2;...∞ korijenje. Numeričke metode za rješavanje nelinearnih jednačina o kojima se govori u nastavku omogućavaju pronalaženje jednog korijena na datom intervalu. U ovom slučaju, na intervalu bi trebao biti samo jedan korijen. Razmotrimo nekoliko metoda za rješavanje nelinearnih jednačina.

1. Metoda grube sile. Prilikom rješavanja nelinearne jednadžbe metodom grube sile specificira se početna vrijednost argumenta x=a i korak h, koji također određuje tačnost pronalaženja korijena nelinearne jednačine. Dok je uslov F(x)*F(x+h)>0 zadovoljen, povećavamo argument x za korak h (x=x+h). Ako proizvod F(x)*F(x+h) postane negativan, tada na intervalu postoji rješenje jednadžbe. Strukturni dijagram metode prikazan je na slici.

   
   

2. Metoda polovičnog dijeljenja. Prilikom rješavanja nelinearne jednadžbe metodom bisekcije specificira se interval ε u kojem postoji samo jedno rješenje i željena tačnost ε. Tada se određuje sredina intervala c=(a+b)/2 i provjerava se uvjet F(a)∙F(c).<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=c). Если условие не выполняется, то в среднюю точку переносим левую границу(a=c). Деление отрезка пополам продолжается пока |b-a|>ε. Strukturni dijagram za rješavanje nelinearnih jednadžbi metodom bisekcije prikazan je na slici.

   Dok je |b-a|>ε
   F(a)∙F(c)<0

   
   

   Rice. Strukturogram za metodu bisekcije

3. Metoda akorda. Prilikom rješavanja nelinearne jednadžbe metodom tetive specificira se interval , na kojem postoji samo jedno rješenje, i tačnost ε. Zatim, kroz dvije tačke sa koordinatama (a,F(a)) i (b,F(b)) povučemo odsječak prave (tetivu) i odredimo tačku presjeka ove prave sa osom apscise (tačka c ). Ako u ovom slučaju F(a)∙F(c)<0, то правую границу интервала переносим в точку с (b=c). Если указанное условие не выполняется, то в точку c prenosi se lijeva granica intervala (a=c). Potraga za rješenjem se zaustavlja kada je specificirana tačnost |F(c)|< ε. Для определения точки пересечения хорды с осью абсцисс воспользуемся следующей формулой (pokušajte sami dobiti formulu). Strukturni dijagram metode akorda je prikazan na slici.

   Dok je |F(c)|>ε
   F(a)∙F(c)<0

   
   

   Rice. Strukturogram za metodu akorda

4. Metoda tangente. Prilikom rješavanja nelinearne jednadžbe tangentnom metodom specificira se početna vrijednost argumenta x 0 i tačnost ε. Zatim u tački (x 0 ,F(x 0)) nacrtamo tangentu na graf F(x) i odredimo tačku preseka tangente sa x 1 osom. U tački (x 1 ,F(x 1)) ponovo konstruišemo tangentu, nađemo sledeću aproksimaciju željenog rešenja x 2, itd. Ponavljamo ovaj postupak do |F(x i)| > ε. Da bismo odredili točku presjeka (i+1) tangente sa osom apscise, koristimo sljedeću formulu (nabavite formulu sami). Uslov konvergencije za tangentnu metodu je F(x 0)∙F""(x 0)>0. Strukturni dijagram za rješavanje nelinearnih jednačina tangentnom metodom prikazan je na Sl.

   
   

5. Metoda akord-tangente. Ako se u metodi tangente derivacija funkcije F"(x i) zamijeni omjerom konačnih priraštaja, tada dobijamo formulu za proračun za metodu tangente tetive . Procedura za izvođenje proračuna u ovoj metodi je slična onoj o kojoj smo ranije govorili.
6. Metoda iteracije. Prilikom rješavanja nelinearne jednačine metodom iteracije koristimo jednačinu napisanu u obliku x=f(x). Navedena je početna vrijednost argumenta x 0 i tačnost ε. Prva aproksimacija rješenja x 1 nalazi se iz izraza x 1 =f(x 0), druga - x 2 =f(x 1), itd. U opštem slučaju, nalazimo i+1 aproksimaciju koristeći formulu x i +1 =f(x i). Ponavljamo ovaj postupak dok |f(x i)|>ε. Uvjet za konvergenciju iteracijske metode |f"(x)|<1. Структограмма метода итераций показана на рис.

   
   

Test zadatak. Laboratorijski rad 4.

Rješavanje nelinearnih jednadžbi.

Vježbajte. Riješite nelinearnu jednačinu navedenu u tabeli. metode, nakon što su prethodno odredili interval na kojem postoji rješenje jednačine. Provjerite rješenje.

Varijante jednadžbi i metode za njihovo rješavanje date su u tabeli.

Varijante jednadžbi i metode za njihovo rješavanje

	Jednačina	Metode rješenja
		busting i akordi
		Nabrajanje i tangente
		Nabrajanje i tangente akorda
		Nabrajanje i polovice
		busting i akordi
		Nabrajanje i tangente
		Nabrajanje i tangente akorda
		Nabrajanje i polovice
		busting i akordi
		Nabrajanje i tangente
		Nabrajanje i tangente akorda
		Nabrajanje i polovice
		busting i akordi
		Nabrajanje i tangente
		Nabrajanje i tangente akorda
		Nabrajanje i polovice
		busting i akordi
		Nabrajanje i tangente
	x 2 =exp(-x 2)-1	Nabrajanje i tangente akorda
		Nabrajanje i polovice
		busting i akordi
		Nabrajanje i tangente
		Nabrajanje i tangente akorda
		Nabrajanje i polovice

1. Naziv, svrha rada i zadatak.
2. Matematički opis, algoritam (strukturogram) i tekst programa.
3. Rezultati proračuna, verifikacija i zaključci o radu.

Razmotrimo problem nalaženja korijena nelinearne jednačine

Korijeni jednadžbe (1) su one vrijednosti x koje ga, kada se zamijene, pretvaraju u identitet. Samo za najjednostavnije jednačine moguće je naći rješenje u obliku formula, tj. analitički oblik. Češće je potrebno rješavati jednadžbe aproksimativnim metodama, među kojima su, zbog pojave kompjutera, najraširenije numeričke metode.

Algoritam za pronalaženje korijena pomoću aproksimativnih metoda može se podijeliti u dvije faze. U prvoj fazi proučava se lokacija korijena i vrši se njihovo odvajanje. Pronađeno je područje u kojem postoji korijen jednadžbe ili početna aproksimacija korijenu x 0. Najjednostavniji način za rješavanje ovog problema je ispitivanje grafa funkcije f(x) . U opštem slučaju, za njegovo rešavanje potrebno je koristiti sva sredstva matematičke analize.

Postojanje barem jednog korijena jednadžbe (1) na pronađenom segmentu proizlazi iz Bolzanovog uvjeta:

f(a)*f(b)<0 (2)

To implicira da je funkcija f(x) kontinuirana na ovom intervalu. Međutim, ovaj uvjet ne daje odgovor na pitanje o broju korijena jednadžbe na datom intervalu. Ako se zahtjevu kontinuiteta funkcije dopuni i zahtjev njene monotonosti, a to proizilazi iz konstantnosti predznaka prvog izvoda, onda možemo tvrditi postojanje jednog korijena na datom segmentu.

Prilikom lokalizacije korijena također je važno poznavati osnovna svojstva ove vrste jednadžbi. Na primjer, prisjetimo se nekih svojstava algebarskih jednadžbi:

gdje su realni koeficijenti.

• a) Jednačina stepena n ima n korijena, među kojima može biti i realnih i kompleksnih. Kompleksni korijeni formiraju kompleksne konjugirane parove i, stoga, jednadžba ima paran broj takvih korijena. Ako je n neparno, postoji barem jedan pravi korijen.
• b) Broj pozitivnih realnih korijena manji je ili jednak broju promjenljivih predznaka u nizu koeficijenata. Zamjena x sa -x u jednačini (3) omogućava nam da procijenimo broj negativnih korijena na isti način. iteracija Newtonova dihotomija nelinearna

U drugoj fazi rješavanja jednadžbe (1), koristeći dobijenu početnu aproksimaciju, konstruiše se iterativni proces koji omogućava da se vrijednost korijena precizira sa određenom unaprijed određenom točnošću. Iterativni proces se sastoji od sekvencijalnog preciziranja početne aproksimacije. Svaki takav korak naziva se iteracija. Kao rezultat procesa iteracije, nalazi se niz približnih vrijednosti korijena jednadžbe. Ako se ovaj niz približava pravoj vrijednosti korijena x kako n raste, tada se iterativni proces konvergira. Za iterativni proces se kaže da konvergira najmanje na red m ako je ispunjen sljedeći uvjet:

gdje je C>0 neka konstanta. Ako je m=1, onda govorimo o konvergenciji prvog reda; m=2 - oko kvadratne, m=3 - oko kubične konvergencije.

Iterativni ciklus se završava ako su za datu dozvoljenu grešku ispunjeni kriterijumi za apsolutna ili relativna odstupanja:

ili mala neslaganja:

Ovaj rad je posvećen proučavanju algoritma za rješavanje nelinearnih jednačina korištenjem Newtonove metode.