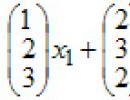Pronađite ugao između ravnih sistema jednačina. Najjednostavniji problemi sa pravom linijom na ravni. Relativni položaj linija. Ugao između pravih linija. Udaljenost od tačke do linije

Definicija. Ako su date dvije prave y = k 1 x + b 1, y = k 2 x + b 2, tada oštri ugao između ovih pravih će se definirati kao

Dvije prave su paralelne ako je k 1 = k 2. Dvije prave su okomite ako je k 1 = -1/ k 2.

Teorema. Prave Ax + Bu + C = 0 i A 1 x + B 1 y + C 1 = 0 su paralelne kada su koeficijenti A 1 = λA, B 1 = λB proporcionalni. Ako je i C 1 = λC, tada se linije poklapaju. Koordinate tačke preseka dve prave nalaze se kao rešenje sistema jednačina ovih pravih.

Jednačina prave koja prolazi ovu tačku

Okomito na datu pravu

Definicija. Prava linija koja prolazi kroz tačku M 1 (x 1, y 1) i okomita na pravu liniju y = kx + b predstavljena je jednadžbom:

Udaljenost od tačke do linije

Teorema. Ako je data tačka M(x 0, y 0), tada se udaljenost do prave Ax + Bu + C = 0 određuje kao

Dokaz. Neka je tačka M 1 (x 1, y 1) osnova okomice spuštene iz tačke M na datu pravu liniju. Tada je rastojanje između tačaka M i M 1:

(1)

Koordinate x 1 i y 1 se mogu naći rješavanjem sistema jednadžbi:

Druga jednačina sistema je jednačina prave koja prolazi kroz datu tačku M 0 okomito na datu pravu. Ako transformišemo prvu jednačinu sistema u oblik:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

tada, rješavanjem, dobijamo:

Zamjenom ovih izraza u jednačinu (1) nalazimo:

Teorema je dokazana.

Primjer. Odrediti ugao između pravih: y = -3 x + 7; y = 2 x + 1.

k 1 = -3; k 2 = 2; tgφ = ; φ= p /4.

Primjer. Pokažite da su prave 3x – 5y + 7 = 0 i 10x + 6y – 3 = 0 okomite.

Rješenje. Nalazimo: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, dakle, prave su okomite.

Primjer. Dati su vrhovi trougla A(0; 1), B (6; 5), C (12; -1). Naći jednadžbu visine povučene iz vrha C.

Rješenje. Pronalazimo jednačinu stranice AB: ; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;

Tražena jednačina visine ima oblik: Ax + By + C = 0 ili y = kx + b. k = . Tada je y = . Jer visina prolazi kroz tačku C, tada njene koordinate zadovoljavaju ovu jednačinu: odakle je b = 17. Ukupno: .

Odgovor: 3 x + 2 y – 34 = 0.

Jednačina prave koja prolazi kroz datu tačku u u ovom pravcu. Jednačina prave koja prolazi kroz dvije date tačke. Ugao između dvije prave linije. Uslov paralelnosti i okomitosti dvije prave. Određivanje tačke preseka dve prave

1. Jednačina prave koja prolazi kroz datu tačku A(x 1 , y 1) u datom pravcu, određenom nagibom k,

y - y 1 = k(x - x 1). (1)

Ova jednačina definira olovku linija koje prolaze kroz tačku A(x 1 , y 1), koji se naziva centar snopa.

2. Jednačina prave koja prolazi kroz dvije tačke: A(x 1 , y 1) i B(x 2 , y 2), napisano ovako:

Ugaoni koeficijent prave linije koja prolazi kroz dvije date tačke određuje se formulom

3. Ugao između pravih linija A I B je ugao za koji se prva prava linija mora rotirati A oko tačke preseka ovih linija u smeru suprotnom od kazaljke na satu dok se ne poklopi sa drugom linijom B. Ako su dvije prave date jednadžbama sa nagibom

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

tada je ugao između njih određen formulom

Treba napomenuti da se u brojiocu razlomka nagib prve linije oduzima od nagiba druge linije.

Ako su jednadžbe prave date u opštem obliku

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

ugao između njih određen je formulom

4. Uslovi za paralelizam dve prave:

a) Ako su linije date jednadžbama (4) sa ugaonim koeficijentom, tada su potrebne i dovoljno stanje njihov paralelizam se sastoji u jednakosti njihovih ugaonih koeficijenata:

k 1 = k 2 . (8)

b) Za slučaj kada su prave date jednačinama u opštem obliku (6), neophodan i dovoljan uslov za njihov paralelizam je da su koeficijenti za odgovarajuće strujne koordinate u njihovim jednačinama proporcionalni, tj.

5. Uslovi za okomitost dvije prave:

a) U slučaju kada su linije date jednačinama (4) sa ugaonim koeficijentom, neophodan i dovoljan uslov za njihovu okomitost je da su njihovi ugaoni koeficijenti inverzni po veličini i suprotni po predznaku, tj.

Ovaj uslov se takođe može napisati u obliku

k 1 k 2 = -1. (11)

b) Ako su jednadžbe pravih date u opštem obliku (6), onda je uslov za njihovu okomitost (neophodan i dovoljan) da zadovolji jednakost

A 1 A 2 + B 1 B 2 = 0. (12)

6. Koordinate tačke preseka dve prave nalaze se rešavanjem sistema jednačina (6). Prave (6) se sijeku ako i samo ako

1. Napišite jednadžbe pravih koje prolaze kroz tačku M, od kojih je jedna paralelna, a druga okomita na datu pravu l.

Uz pomoć ovoga online kalkulator možete pronaći ugao između pravih linija. Dato je detaljno rješenje sa objašnjenjima. Da biste izračunali ugao između pravih linija, postavite dimenziju (2 ako se smatra ravna linija na ravni, 3 ako se razmatra prava linija u prostoru), unesite elemente jednadžbe u ćelije i kliknite na "Riješi" dugme. Pogledajte teoretski dio u nastavku.

Upozorenje

Obrisati sve ćelije?

Zatvori Clear

Instrukcije za unos podataka. Brojevi se unose kao cijeli brojevi (primjeri: 487, 5, -7623, itd.), decimale (npr. 67., 102.54, itd.) ili razlomci. Razlomak se mora unijeti u obliku a/b, gdje su a i b (b>0) cijeli brojevi ili decimalni brojevi. Primjeri 45/5, 6.6/76.4, -7/6.7, itd.

1. Ugao između pravih linija na ravni

Prave su definirane kanonskim jednadžbama

1.1. Određivanje ugla između pravih linija

Neka su linije u dvodimenzionalnom prostoru L 1 i L

Dakle, iz formule (1.4) možemo pronaći ugao između pravih linija L 1 i L 2. Kao što se može vidjeti na slici 1, linije koje se seku formiraju susjedne uglove φ I φ 1 . Ako je pronađeni ugao veći od 90°, tada možete pronaći minimalni ugao između pravih linija L 1 i L 2: φ 1 =180-φ .

Iz formule (1.4) možemo izvesti uslove za paralelnost i okomitost dve prave.

Primjer 1. Odrediti ugao između linija

Pojednostavimo i riješimo:

1.2. Uslov za paralelne prave

Neka φ =0. Onda cosφ=1. U ovom slučaju, izraz (1.4) će poprimiti sljedeći oblik:

Primjer 2: Odredite da li su prave paralelne

Jednakost (1.9) je zadovoljena, pa su prave (1.10) i (1.11) paralelne.

Odgovori. Prave (1.10) i (1.11) su paralelne.

1.3. Uslov za okomitost linija

Neka φ =90°. Onda cosφ=0. U ovom slučaju, izraz (1.4) će poprimiti sljedeći oblik:

Primjer 3. Odrediti da li su prave okomite

Uslov (1.13) je zadovoljen, pa su prave (1.14) i (1.15) okomite.

Odgovori. Prave (1.14) i (1.15) su okomite.

Prave su definirane općim jednačinama

1.4. Određivanje ugla između pravih linija

Neka dvije ravne linije L 1 i L 2 su date općim jednačinama

Iz definicije skalarnog proizvoda dva vektora, imamo:

Primjer 4. Pronađite ugao između linija

Zamjenjivanje vrijednosti A 1 , B 1 , A 2 , B 2 in (1.23), dobijamo:

Ovaj ugao je veći od 90°. Nađimo minimalni ugao između pravih linija. Da biste to učinili, oduzmite ovaj ugao od 180:

S druge strane, uvjet paralelnih pravih L 1 i L 2 je ekvivalentno uslovu kolinearnosti vektora n 1 i n 2 i može se predstaviti ovako:

Jednakost (1.24) je zadovoljena, pa su prave (1.26) i (1.27) paralelne.

Odgovori. Prave (1.26) i (1.27) su paralelne.

1.6. Uslov za okomitost linija

Uslov za okomitost linija L 1 i L 2 se može izdvojiti iz formule (1.20) zamjenom cos(φ )=0. Zatim skalarni proizvod ( n 1 ,n 2)=0. Gdje

Jednakost (1.28) je zadovoljena, pa su prave (1.29) i (1.30) okomite.

Odgovori. Prave (1.29) i (1.30) su okomite.

2. Ugao između pravih linija u prostoru

2.1. Određivanje ugla između pravih linija

Neka postoje prave linije u prostoru L 1 i L 2 su date kanonskim jednačinama

gdje | q 1 | i | q 2 | moduli vektora smjera q 1 i q 2 odnosno φ -ugao između vektora q 1 i q 2 .

Iz izraza (2.3) dobijamo:

Pojednostavimo i riješimo:

Nađimo ugao φ

Problem 1

Pronađite kosinus ugla između pravih $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $ i $\left\( \begin(niz )(c) (x=2\cdot t-3) \\ (y=-t+1) \\ (z=3\cdot t+5) \end(niz)\desno. $.

Neka su u prostoru date dvije linije: $\frac(x-x_(1) )(m_(1) ) =\frac(y-y_(1) )(n_(1) ) =\frac(z-z_( 1 ) )(p_(1) ) $ i $\frac(x-x_(2) )(m_(2) ) =\frac(y-y_(2) )(n_(2) ) =\frac(z - z_(2) )(p_(2) ) $. Odaberimo proizvoljnu tačku u prostoru i povučemo kroz nju dvije pomoćne linije paralelne sa podacima. Ugao između ovih linija je bilo koji od dva susjedna ugla formirana od pomoćnih linija. Kosinus jednog od uglova između pravih može se naći pomoću dobro poznate formule $\cos \phi =\frac(m_(1) \cdot m_(2) +n_(1) \cdot n_(2) + p_(1) \cdot p_( 2) )(\sqrt(m_(1)^(2) +n_(1)^(2) +p_(1)^(2) ) \cdot \sqrt(m_(2) )^(2) +n_( 2)^(2) +p_(2)^(2) ) ) $. Ako je vrijednost $\cos \phi >0$, onda se dobija oštar ugao između linija, ako je $\cos \phi

Kanonske jednadžbe prvog reda: $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $.

Kanonske jednadžbe druge linije mogu se dobiti iz parametarskih:

\ \ \

Dakle, kanonske jednadžbe ove linije su: $\frac(x+3)(2) =\frac(y-1)(-1) =\frac(z-5)(3) $.

Računamo:

\[\cos \phi =\frac(5\cdot 2+\left(-3\right)\cdot \left(-1\right)+4\cdot 3)(\sqrt(5^(2) +\ lijevo(-3\desno)^(2) +4^(2) ) \cdot \sqrt(2^(2) +\left(-1\desno)^(2) +3^(2) ) = \ frac(25)(\sqrt(50) \cdot \sqrt(14) ) \približno 0,9449.\]

Problem 2

Prva linija prolazi kroz date tačke $A\left(2,-4,-1\right)$ i $B\left(-3,5,6\right)$, druga prava prolazi kroz date tačke $ C\levo (1,-2,8\desno)$ i $D\left(6,7,-2\desno)$. Pronađite udaljenost između ovih linija.

Neka je određena prava okomita na prave $AB$ i $CD$ i siječe ih u tačkama $M$ i $N$, redom. Pod ovim uslovima, dužina segmenta $MN$ jednaka je udaljenosti između pravih $AB$ i $CD$.

Konstruišemo vektor $\overline(AB)$:

\[\overline(AB)=\left(-3-2\right)\cdot \bar(i)+\left(5-\left(-4\right)\right)\cdot \bar(j)+ \left(6-\left(-1\right)\right)\cdot \bar(k)=-5\cdot \bar(i)+9\cdot \bar(j)+7\cdot \bar(k ).\]

Neka segment koji prikazuje rastojanje između pravih prolazi kroz tačku $M\left(x_(M) ,y_(M) ,z_(M) \right)$ na pravoj $AB$.

Konstruišemo vektor $\overline(AM)$:

\[\overline(AM)=\left(x_(M) -2\desno)\cdot \bar(i)+\left(y_(M) -\left(-4\right)\desno)\cdot \ bar(j)+\left(z_(M) -\left(-1\desno)\desno)\cdot \bar(k)=\] \[=\left(x_(M) -2\desno)\ cdot \bar(i)+\left(y_(M) +4\desno)\cdot \bar(j)+\left(z_(M) +1\desno)\cdot \bar(k).\]

Vektori $\overline(AB)$ i $\overline(AM)$ su isti, stoga su kolinearni.

Poznato je da ako su vektori $\overline(a)=x_(1) \cdot \overline(i)+y_(1) \cdot \overline(j)+z_(1) \cdot \overline(k)$ i $ \overline(b)=x_(2) \cdot \overline(i)+y_(2) \cdot \overline(j)+z_(2) \cdot \overline(k)$ su kolinearni, tada su njihove koordinate su proporcionalni, onda postoji $\frac(x_((\it 2)) )((\it x)_((\it 1)) ) =\frac(y_((\it 2)) )((\ it y)_( (\it 1)) ) =\frac(z_((\it 2)) )((\it z)_((\it 1)) ) $.

$\frac(x_(M) -2)(-5) =\frac(y_(M) +4)(9) =\frac(z_(M) +1)(7) =m$, gdje je $m $ je rezultat dijeljenja.

Odavde dobijamo: $x_(M) -2=-5\cdot m$; $y_(M) +4=9\cdot m$; $z_(M) +1=7\cdot m$.

Konačno dobijamo izraze za koordinate tačke $M$:

Konstruišemo vektor $\overline(CD)$:

\[\overline(CD)=\left(6-1\desno)\cdot \bar(i)+\left(7-\left(-2\right)\right)\cdot \bar(j)+\ lijevo(-2-8\desno)\cdot \bar(k)=5\cdot \bar(i)+9\cdot \bar(j)-10\cdot \bar(k).\]

Neka segment koji predstavlja rastojanje između pravih prolazi kroz tačku $N\left(x_(N) ,y_(N) ,z_(N) \right)$ na pravoj $CD$.

Konstruišemo vektor $\overline(CN)$:

\[\overline(CN)=\left(x_(N) -1\desno)\cdot \bar(i)+\left(y_(N) -\left(-2\right)\right)\cdot \ bar(j)+\left(z_(N) -8\desno)\cdot \bar(k)=\] \[=\left(x_(N) -1\desno)\cdot \bar(i)+ \left(y_(N) +2\desno)\cdot \bar(j)+\left(z_(N) -8\desno)\cdot \bar(k).\]

Vektori $\overline(CD)$ i $\overline(CN)$ se poklapaju, stoga su kolinearni. Primjenjujemo uvjet kolinearnosti vektora:

$\frac(x_(N) -1)(5) =\frac(y_(N) +2)(9) =\frac(z_(N) -8)(-10) =n$, gdje je $n $ je rezultat dijeljenja.

Odavde dobijamo: $x_(N) -1=5\cdot n$; $y_(N) +2=9\cdot n$; $z_(N) -8=-10\cdot n$.

Konačno dobijamo izraze za koordinate tačke $N$:

Konstruišemo vektor $\overline(MN)$:

\[\overline(MN)=\left(x_(N) -x_(M) \desno)\cdot \bar(i)+\left(y_(N) -y_(M) \desno)\cdot \bar (j)+\levo(z_(N) -z_(M) \desno)\cdot \bar(k).\]

Zamijenjujemo izraze za koordinate tačaka $M$ i $N$:

\[\overline(MN)=\left(1+5\cdot n-\left(2-5\cdot m\desno)\desno)\cdot \bar(i)+\] \[+\left(- 2+9\cdot n-\left(-4+9\cdot m\desno)\desno)\cdot \bar(j)+\left(8-10\cdot n-\left(-1+7\cdot) m\desno)\desno)\cdot \bar(k).\]

Po završetku koraka dobijamo:

\[\overline(MN)=\left(-1+5\cdot n+5\cdot m\desno)\cdot \bar(i)+\left(2+9\cdot n-9\cdot m\desno )\cdot \bar(j)+\left(9-10\cdot n-7\cdot m\desno)\cdot \bar(k).\]

Pošto su prave $AB$ i $MN$ okomite, skalarni proizvod odgovarajućih vektora jednak je nuli, odnosno $\overline(AB)\cdot \overline(MN)=0$:

\[-5\cdot \left(-1+5\cdot n+5\cdot m\desno)+9\cdot \left(2+9\cdot n-9\cdot m\desno)+7\cdot \ lijevo(9-10\cdot n-7\cdot m\desno)=0;\] \

Po završetku koraka dobijamo prvu jednačinu za određivanje $m$ i $n$: $155\cdot m+14\cdot n=86$.

Pošto su prave $CD$ i $MN$ okomite, skalarni proizvod odgovarajućih vektora jednak je nuli, odnosno $\overline(CD)\cdot \overline(MN)=0$:

\ \[-5+25\cdot n+25\cdot m+18+81\cdot n-81\cdot m-90+100\cdot n+70\cdot m=0.\]

Po završetku koraka dobijamo drugu jednačinu za određivanje $m$ i $n$: $14\cdot m+206\cdot n=77$.

$m$ i $n$ pronalazimo rješavanjem sistema jednačina $\left\(\begin(array)(c) (155\cdot m+14\cdot n=86) \\ (14\cdot m+206) \cdot n =77)\end(niz)\right.$.

Primjenjujemo Cramerovu metodu:

Pronađite koordinate tačaka $M$ i $N$:

\ \

konačno:

Konačno, pišemo vektor $\overline(MN)$:

$\overline(MN)=\left(2.691-\left(-0.6215\right)\right)\cdot \bar(i)+\left(1.0438-0.7187\right)\cdot \bar (j)+\left (4.618-2.6701\desno)\cdot \bar(k)$ ili $\overline(MN)=3,3125\cdot \bar(i)+0,3251\cdot \bar(j)+1,9479\cdot \bar(k)$ .

Udaljenost između linija $AB$ i $CD$ je dužina vektora $\overline(MN)$:$d=\sqrt(3.3125^(2) +0.3251^(2) +1.9479^( 2) ) \ cca 3.8565$ lin. jedinice

Neka su ravne date u prostoru l I m. Kroz neku tačku A prostora povlačimo prave linije l 1 || l I m 1 || m(Sl. 138).

Imajte na umu da se tačka A može izabrati proizvoljno; posebno, može ležati na jednoj od ovih pravih. Ako je ravno l I m seku, tada se A može uzeti kao tačka preseka ovih pravih ( l 1 = l I m 1 = m).

Ugao između neparalelnih linija l I m je vrijednost najmanjeg od susjednih uglova formiranih linijama koje se seku l 1 I m 1 (l 1 || l, m 1 || m). Ugao između paralelnih linija smatra se jednakim nuli.

Ugao između pravih linija l I m označeno sa $\widehat((l;m))$. Iz definicije sledi da ako se meri u stepenima, onda 0° < $\widehat((l;m)) $ < 90°, a ako je u radijanima, onda 0 < $\widehat((l;m)) $ < π / 2 .

Zadatak. Zadata je kocka ABCDA 1 B 1 C 1 D 1 (sl. 139).

Pronađite ugao između pravih AB i DC 1.

Ukrštanje pravih AB i DC 1. Kako je prava DC paralelna pravoj liniji AB, ugao između pravih AB i DC 1, prema definiciji, jednak je $\widehat(C_(1)DC)$.

Prema tome, $\widehat((AB;DC_1))$ = 45°.

Direktno l I m su pozvani okomito, ako je $\widehat((l;m)) $ = π / 2. Na primjer, u kocki

Proračun ugla između pravih linija.

Problem izračunavanja ugla između dve prave u prostoru rešava se na isti način kao i u ravni. Označimo sa φ veličinu ugla između pravih l 1 I l 2, a kroz ψ - veličina ugla između vektora pravca A I b ove prave linije.

Onda ako

ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (Sl. 206.6), tada φ = 180° - ψ. Očigledno, u oba slučaja je tačna jednakost cos φ = |cos ψ|. Prema formuli (kosinus ugla između vektora a i b koji nisu nula jednak je skalarni proizvod ovih vektora podijeljenih umnoškom njihovih dužina) imamo

$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$

dakle,

$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$

Neka su linije zadane njihovim kanonskim jednadžbama

$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; I \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$

Tada se ugao φ između linija određuje pomoću formule

$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2 )\sqrt((b_1)^2+(b_2)^2+(b_3)^2)) (1)$$

Ako je jedna od linija (ili obje) data nekanonskim jednadžbama, tada za izračunavanje kuta morate pronaći koordinate vektora smjera ovih linija, a zatim koristiti formulu (1).

Zadatak 1. Izračunajte ugao između linija

$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;and\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$

Vektori pravca pravih linija imaju koordinate:

a = (-√2 ; √2 ; -2), b = (√3 ; √3 ; √6 ).

Koristeći formulu (1) nalazimo

$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)( 2\sqrt2\cdot 2\sqrt3)=\frac(1)(2) $$

Dakle, ugao između ovih linija je 60°.

Zadatak 2. Izračunajte ugao između linija

$$ \begin(slučajevi)3x-12z+7=0\\x+y-3z-1=0\end(slučajevi) i \begin(slučajevi)4x-y+z=0\\y+z+1 =0\kraj (slučajevi) $$

Iza vodećeg vektora A uzmi prvu pravu liniju vektorski proizvod normalni vektori n 1 = (3; 0; -12) i n 2 = (1; 1; -3) ravni koje definišu ovu pravu. Koristeći formulu $=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) $ dobijamo

$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$

Slično, nalazimo vektor smjera druge prave linije:

$$ b=\begin(vmatrix) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatrix)=-2i-4i+4k $$

Ali pomoću formule (1) izračunavamo kosinus željenog ugla:

$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2) ^2+4^2+4^2))=0 $$

Dakle, ugao između ovih linija je 90°.

Zadatak 3. U trouglastoj piramidi MABC, ivice MA, MB i MC su međusobno okomite (Sl. 207);

njihove dužine su 4, 3, 6. Tačka D je sredina [MA]. Pronađite ugao φ između pravih CA i DB.

Neka su CA i DB vektori pravca CA i DB.

Uzmimo tačku M kao početak koordinata. Po uslovu jednačine imamo A (4; 0; 0), B(0; 0; 3), C(0; 6; 0), D (2; 0; 0). Stoga $\overrightarrow(CA)$ = (4; - 6;0), $\overrightarrow(DB)$= (-2; 0; 3). Koristimo formulu (1):

$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9) )) $$

Koristeći kosinusnu tablicu, nalazimo da je ugao između pravih CA i DB približno 72°.

UGAO IZMEĐU RAVNI

Razmotrimo dvije ravni α 1 i α 2, definirane jednadžbama:

Ispod ugao između dvije ravni razumjet ćemo jedan od diedarskih uglova koje formiraju ove ravni. Očigledno je da je ugao između vektora normale i ravni α 1 i α 2 jednak jednom od naznačenih susednih diedarskih uglova ili . Zbog toga . Jer I , To

Primjer. Odredite ugao između ravnina x+2y-3z+4=0 i 2 x+3y+z+8=0.

Uslov za paralelnost dve ravni.

Dvije ravni α 1 i α 2 su paralelne ako i samo ako su njihovi normalni vektori paralelni, te stoga .

Dakle, dvije ravni su paralelne jedna s drugom ako i samo ako su koeficijenti odgovarajućih koordinata proporcionalni:

ili

Uslov okomitosti ravnina.

Jasno je da su dvije ravni okomite ako i samo ako su njihovi normalni vektori okomiti, i stoga, ili .

Dakle, .

Primjeri.

PRAVO U PROSTOR.

VEKTORSKA JEDNAČINA ZA PRAVU.

PARAMETRIČKE DIREKTNE JEDNAČINE

Položaj prave u prostoru u potpunosti je određen specificiranjem bilo koje njene fiksne tačke M 1 i vektor paralelan ovoj pravoj.

Poziva se vektor paralelan pravoj vodiči vektor ove linije.

Dakle, neka prava linija l prolazi kroz tačku M 1 (x 1 , y 1 , z 1), koja leži na pravoj paralelnoj vektoru .

Razmotrite proizvoljnu tačku M(x,y,z) na pravoj liniji. Iz slike je jasno da .

Vektori i su kolinearni, tako da postoji takav broj t, šta , gdje je množitelj t mogu prihvatiti bilo koje numerička vrijednost zavisno od položaja tačke M na pravoj liniji. Faktor t naziva parametar. Nakon što smo odredili radijus vektore tačaka M 1 i M odnosno, kroz i , Dobijamo . Ova jednačina se zove vektor jednačina prave linije. To pokazuje da za svaku vrijednost parametra t odgovara radijus vektoru neke tačke M, leži na pravoj liniji.

Zapišimo ovu jednačinu u koordinatnom obliku. Obratite pažnju da, i odavde

Rezultirajuće jednačine se nazivaju parametarski jednačine prave linije.

Prilikom promjene parametra t promene koordinata x, y I z i tačka M kreće se pravolinijski.

KANONIČKE JEDNAČINE DIREKTNE

Neka M 1 (x 1 , y 1 , z 1) – tačka koja leži na pravoj liniji l, And je njegov vektor smjera. Uzmimo opet proizvoljnu tačku na pravoj M(x,y,z) i razmotrimo vektor .

Jasno je da su i vektori kolinearni, pa njihove odgovarajuće koordinate moraju biti proporcionalne, dakle,

– kanonski jednačine prave linije.

Napomena 1. Imajte na umu da se kanonske jednačine prave mogu dobiti iz parametarskih eliminacijom parametra t. Zaista, iz parametarskih jednačina dobijamo ili .

Primjer. Zapišite jednačinu prave u parametarskom obliku.

Označimo , odavde x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Napomena 2. Neka je prava okomita na jednu od koordinatnih osa, na primjer na os Ox. Tada je vektor smjera prave okomit Ox, dakle, m=0. Shodno tome, parametarske jednačine prave će poprimiti oblik

Isključivanje parametra iz jednačina t, dobijamo jednadžbe prave u obliku

Međutim, i u ovom slučaju pristajemo da formalno zapišemo kanonske jednačine prave u obliku . Dakle, ako je nazivnik jednog od razlomaka nula, to znači da je prava okomita na odgovarajuću koordinatnu osu.

Slično kanonskim jednačinama odgovara pravoj liniji okomitoj na osi Ox I Oy ili paralelno sa osom Oz.

Primjeri.

OPĆE JEDNAČINE PRAVE KAO PRAVE PRESEKA DVIJE RAVNE

Kroz svaku pravu liniju u svemiru postoji bezbroj ravni. Bilo koja dva od njih, ukrštajući se, definiraju ga u prostoru. Prema tome, jednačine bilo koje dvije takve ravni, razmatrane zajedno, predstavljaju jednačine ove prave.

Općenito, bilo koje dvije neparalelne ravni date općim jednačinama

odrediti pravu liniju njihovog preseka. Ove jednačine se nazivaju opšte jednačine ravno.

Primjeri.

Konstruirajte pravu zadanu jednadžbama

Za konstruiranje prave linije dovoljno je pronaći bilo koje dvije njene tačke. Najlakši način je da odaberete tačke preseka linije sa koordinatne ravni. Na primjer, tačka preseka sa ravninom xOy dobijamo iz jednačina prave linije, pod pretpostavkom z= 0:

Nakon što smo riješili ovaj sistem, nalazimo poentu M 1 (1;2;0).

Slično, pod pretpostavkom y= 0, dobijamo tačku preseka prave sa ravninom xOz:

Od opštih jednačina prave linije može se preći na njene kanonske ili parametarske jednačine. Da biste to učinili, morate pronaći neku tačku M 1 na pravoj liniji i vektor smjera prave linije.

Koordinate tačaka M 1 dobijamo iz ovog sistema jednačina, dajući jednoj od koordinata proizvoljnu vrijednost. Da biste pronašli vektor smjera, imajte na umu da ovaj vektor mora biti okomit na oba normalni vektori I . Dakle, izvan vektora smjera prave linije l možete uzeti vektorski proizvod normalnih vektora:

Primjer. Olovo opšte jednačine ravno kanonskom obliku.

Nađimo tačku koja leži na pravoj. Da bismo to učinili, proizvoljno biramo jednu od koordinata, na primjer, y= 0 i riješi sistem jednačina:

Vektori normale ravni koje definiraju pravu imaju koordinate Stoga će vektor smjera biti ravan

. dakle, l: .

UGAO IZMEĐU RAVNIH

Ugao između pravih u prostoru nazvat ćemo bilo koji od susjednih uglova formiranih od dvije prave povučene kroz proizvoljnu tačku paralelnu sa podacima.

Neka su u prostoru date dvije linije:

Očigledno, ugao φ između pravih linija može se uzeti kao ugao između njihovih vektora smjera i . Budući da , onda koristeći formulu za kosinus kuta između vektora dobivamo