Матричное умножение. Математика для чайников. Матрицы и основные действия над ними. Случай прямоугольных матриц

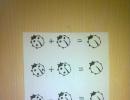
Сложение матриц $ A $ и $ B $ это арифметическая операция, в результате которой, должна получаться матрица $ C $, каждый элемент которой равен сумме соответствующих элементов складываемых матриц:

$$ c_{ij} = a_{ij} + b_{ij} $$

Более подробно формула сложения двух матриц выглядит так:

$$ A + B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} + b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \\ a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} \end{pmatrix} = C $$

Обратите внимание, что складывать и вычитать матрицы можно только одинаковой размерности. При сумме или разности будет получаться матрица $ C $ такой же размерности как и слагаемые (вычитаемые) матрицы $ A $ и $ B $. Если матрицы $ A $ и $ B $ отличаются друг от друга размерами, то сложение (вычитание) таких матриц будет ошибкой!

В формуле складываются матрицы 3 на 3, значит и получиться должна матрица 3 на 3.

Вычитание матриц полностью аналогично по алгоритму сложения, только знак минус. Каждый элемент искомой матрицы $ C $ получается благодаря вычитанию соответствующих элементов матриц $ A $ и $ B $:

$$ c_{ij} = a_{ij} - b_{ij} $$

Запишем подробную формулу вычитания двух матриц:

$$ A - B = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} - \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} = $$

$$ = \begin{pmatrix} a_{11} - b_{11} & a_{12}-b_{12} & a_{13}-b_{13} \\ a_{21}-b_{21} & a_{22}-b_{22} & a_{23}-b_{23} \\ a_{31}-b_{31} & a_{32}-b_{32} & a_{33}-b_{33} \end{pmatrix} = C $$

Стоит так же заметить, что нельзя складывать и вычитать матрицы с обычными числами, а так же с другими какими-то элементами

Будет полезно знать для дальнейших решений задач с матрицами знать свойства сложения (вычитания).

Свойства

Если матрицы $ A,B,C $ одинаковые по размеру, тогда для них действует свойство ассоциативности: $$ A + (B + C) = (A + B) + C $$
Для каждой матрицы существует нулевая матрица, обозначаемая $ O $, при сложении (вычитании) с которой исходная матрица не изменяется: $$ A \pm O = A $$
Для каждой ненулевой матрицы $ A $ есть противоположная матрица $ (-A) $ сумма с которой обращается в нуль: $$ A + (-A) = 0 $$
При сложении (вычитании) матриц допустимо свойство коммутативности, то есть матрицы $ A $ и $ B $ можно менять местами: $$ A + B = B + A $$ $$ A - B = B - A $$

Примеры решений

Пример 1
Даны матрицы $ A = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} $ и $ B = \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} $. Выполнить сложение матриц, а затем вычитание.
Решение
Первым делом проверяем матрицы на размерность. У матрицы $ A $ размерность $ 2 \times 2 $, у второй матрицы $ B $ размерность тоже $ 2 \times 2 $. Это значит, что с данными матрицами можно провести совместную операцию по сложению и вычитанию. Напомним, что для суммы нужно выполнить попарное сложение соответствующих элементов матриц $ A \text{ и } B $. $$ A + B = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} + \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} = $$ $$ = \begin{pmatrix} 2 + 1 & 3 + (-3) \\ -1 + 2 & 4 + 5 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 1 & 9 \end{pmatrix} $$ Аналогично сумме находим разность матриц с помощью замены знака "плюс" на "минус": $$ A - B = \begin{pmatrix} 2&3 \\ -1& 4 \end{pmatrix} + \begin{pmatrix} 1&-3 \\ 2&5 \end{pmatrix} = $$ $$ = \begin{pmatrix} 2 - 1 & 3 - (-3) \\ -1 - 2 & 4 - 5 \end{pmatrix} = \begin{pmatrix} 1 & 6 \\ -3 & -1 \end{pmatrix} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ A + B = \begin{pmatrix} 3 & 0 \\ 1 & 9 \end{pmatrix}; A - B = \begin{pmatrix} 1 & 6 \\ -3 & -1 \end{pmatrix} $$

В статье: "Сложение и вычитание матриц" были даны определения, правила, замечания, свойства операций и практические примеры решения.

Прежде всего, ЧТО должно получиться в результате умножения трёх матриц ? Кошка не родит мышку. Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)

Произведение трёх матриц можно вычислить двумя способами:

1) найти , а затем домножить на матрицу «цэ»: ;

2) либо сначала найти , потом выполнить умножение .

Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения :

Пример 6

Перемножить матрицы двумя способами

Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц.

1) Используем формулу

Действие первое:

Действие второе:

2) Используем формулу

Действие первое:

Действие второе:

Ответ :

Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных матриц – лишь бы они умножались:

Пример 7

Найти произведение трёх матриц

Это пример для самостоятельного решения. В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения имеет место быть и для бОльшего количества множителей.

Теперь самое время вернуться к степеням матриц. Квадрат матрицы рассмотрен в самом начале и на повестке дня вопрос.

Это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.

Произведением матрицы A m × n на матрицу B n × k будет матрица C m × k такая, что элемент матрицы C , находящийся в i -ой строке и j -ом столбце, то есть элемент c ij равен сумме произведений элементов i -ой строки матрицы A на соответствующие элементы j -ого столбца матрицы B .

Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример:
Можно ли умножить матрицу на матрицу ?

m = n , значит, умножать данные матрицы можно.

Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.

m ≠ n , таким образом, выполнять умножение нельзя:

Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы , умножение которых заведомо невозможно.

Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, и возможно как умножение MN , так и умножение NM.

Это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.

Начнем с самого простого примера:

Необходимо умножить на . Первым делом приведем формулу для данного случая:

- здесь хорошо прослеживается закономерность.

Умножить на .

Формула для этого случая: .

Умножение матриц и результат:

В результате получена т.н. нулевая матрица.

Очень важно помнить, что здесь не работает «правило перестановки мест слагаемых» так как почти всегда MN ≠ NM . Поэтому, производя операцию умножения матриц их ни в коем случае нельзя менять местами.

Теперь рассмотрим примеры умножения матриц третьего порядка:

Умножить на .

Формула очень похожа на прошлые:

Решение матрицы: .

Это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.

Пример умножения матрицы на число:

Тут все понятно - для того, чтобы умножить матрицу на число , необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае - на 3.

Еще один полезный пример:

- умножение матрицы на дробное число.

Первым делом покажем то, чего делать не надо:

При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

И, тем более, не нужно делить каждый элемент матрицы на -7:

Что стоит сделать в данном случае - это внести минус в матрицу:

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление - это частный случай умножения.

Главные применения матриц связаны м операцией умножения.

Даны две матрицы:

А – размера mn

B – размера nk

Т.к. длина строки в матрице А совпадает с высотой столбца в матрице В, можно определить матрицу С=АВ, которая будет иметь размеры mk. Элемент матрицы С, расположенный в произвольнойi-й строке (i=1,…,m) и произвольном j-м столбце (j=1,…,k), по определению равен скалярному проиведению двух векторов из
:i-й строк марицы А и j-го столбца матрицы В:

Свойства:

Как определяется операция умножения матрицы А на число λ?

Произведением А на число λ называется матрица, каждый элемент которой равен произведению соответствующего элемента А на λ. Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

13. Определение обратной матрицы и ее свойства.

Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А -1 .

Cвойства обратных матриц

Укажем следующие свойства обратных матриц:

1) (A -1) -1 = A;

2) (AB) -1 = B -1 A -1

3) (A T) -1 = (A -1) T .

1. Если обратная матрица существует, то она единственная.

2. Не у всякой ненулевой квадратной матрицы существует обратная.

14. Приведите основные свойства определителей. Проверьте справедливость свойства |АВ|=|А|*|В| для матриц

А= и В=

Свойства определителей:

1. Если какая-либо строка определителя состоит из нулей, то и сам определитель равен нулю.

2. При перестановке двух строк определитель умножается на -1.

3. Определитель с двумя одинаковыми строками равен нулю.

4. Общий множитель элементов любой строки можно вынести за знак определителя.

5. Если элементы некоторой строки определителя А представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей Б и Д. В определителе Б указанная строка состоит из первых слагаемых, в Д - из вторых слагаемых. Остальные строки определителей Б и Д - те же, что и в А.

6. Величина определителя не изменится, если к одной из строк прибавить другую строку, умноженную на какое угодно число.

7. Сумма произведений элементов любой строки на алгебраические дополнения к соответствующим элементам другой строки равны 0.

8. Определитель матрицы А равен определителю транспонированной матрицы А т, т.е. определитель не меняется при транспонировании.

15. Дайте определение модуля и аргумента комплексного числа. Запишите в тригонометрической форме числа √3+ i , -1+ i .

Каждому комплексному числу z=a+ib может быть поставлен в соответствие вектор (a,b)€R 2. Длина этого вектора, равная √a 2 + b 2 называется модулем комплексного числа z и обозначается через |z|. Угол φ между данным вектором и положительным направлением оси Ox называется аргументом комплексного числа z и обозначается arg z.

Любое комплексное число z≠0 может быть представлено в виде z=|z|(cosφ +isinφ).

Такая форма записи комплексного числа называется тригонометрической.

√3+i=2(√3/2+1/2i)=2(cosπ/6+isinπ/6);

1+i=2(-√2/2+i√2/2)=2(cosπ/4+isinπ/4).

Каждому комплексному числу Z = a + ib может быть поставлен вектор (а; b), принадлежащий R^2. Длина этого вектора, равная КВ из a^2 + b^2, называется модулем комплексного числа и обозначается через модуль Z. Угол между данным вектором и положительным направлением оси Оx называется аргументом комплексного числа (обозначается arg Z).

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m ×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В .

В общем виде матрицу размером m ×n записывают так

Числа, составляющие матрицу, называются элементами матрицы . Элементы матрицы удобно снабжать двумя индексами a ij : первый указывает номер строки, а второй – номер столбца. Например, a 23 – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной , причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной . В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом .

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц . Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a ij = b ij . Так если и , то A=B , если a 11 = b 11 , a 12 = b 12 , a 21 = b 21 и a 22 = b 22 .

Транспонирование . Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A , а переход от A к B транспонированием .

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A , обычно обозначают A T .

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры . Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B , стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C , которая определяется по правилу, например,

Примеры. Найти сумму матриц:

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B )+C =A +(B+C ).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

Примеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB , элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C ) элемент, стоящий в 1-ой строке и 3-м столбце c 13 , нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a ij) размера m ×n на матрицу B = (b ij) размера n ×p , то получим матрицу C размера m ×p , элементы которой вычисляются следующим образом: элемент c ij получается в результате произведения элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

Примеры.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A . Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC .

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A , причём AE=EA=A .

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например , если , то

ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка , соответствующим данной матрице, называется число, получаемое следующим образом: a 11 a 22 – a 12 a 21 .

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка , соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a 11 , a 12 , a 13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.